Signal Separation Operator Based on Wavelet Transform for Non-Stationary Signal Decomposition
Abstract
1. Introduction
2. Main Result
- (a)
- The set can be expressed as a disjoint union of exactly K non-empty sets, i.e.,
- (b)
- Letthenandas .
| Algorithm 1: CWTSSO for non-stationary signal decomposition |
|
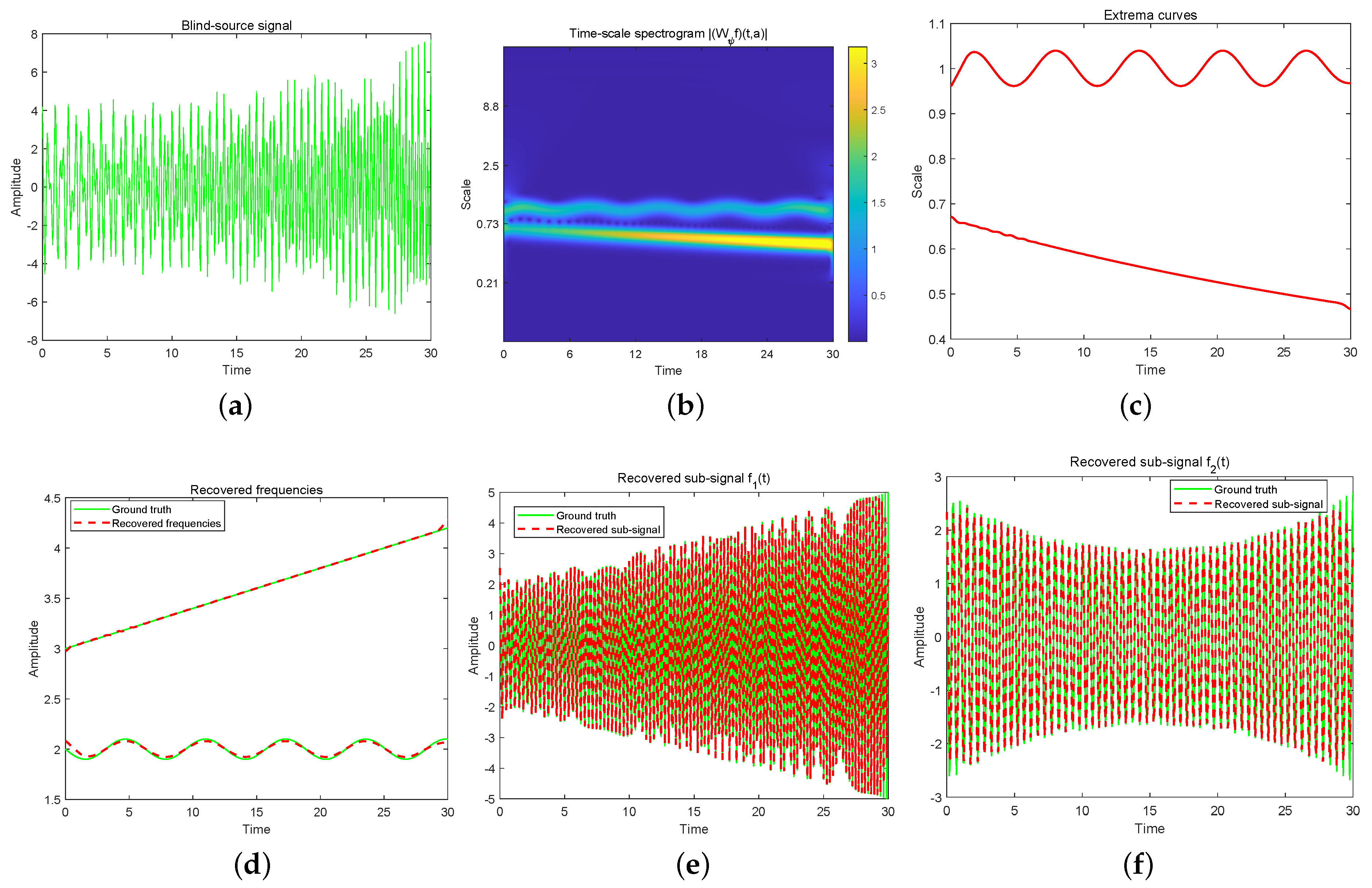
3. Experimentation and Examples
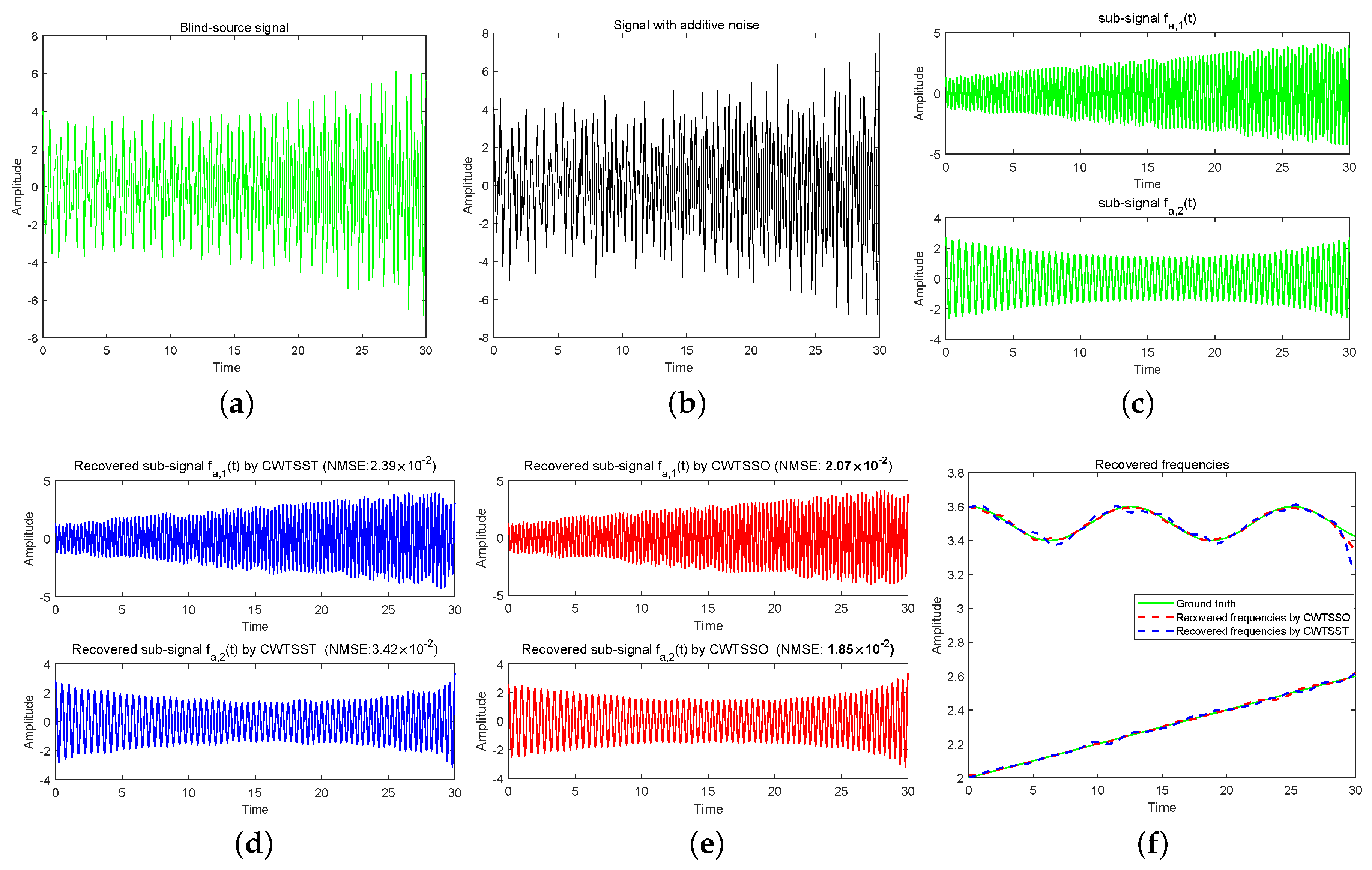

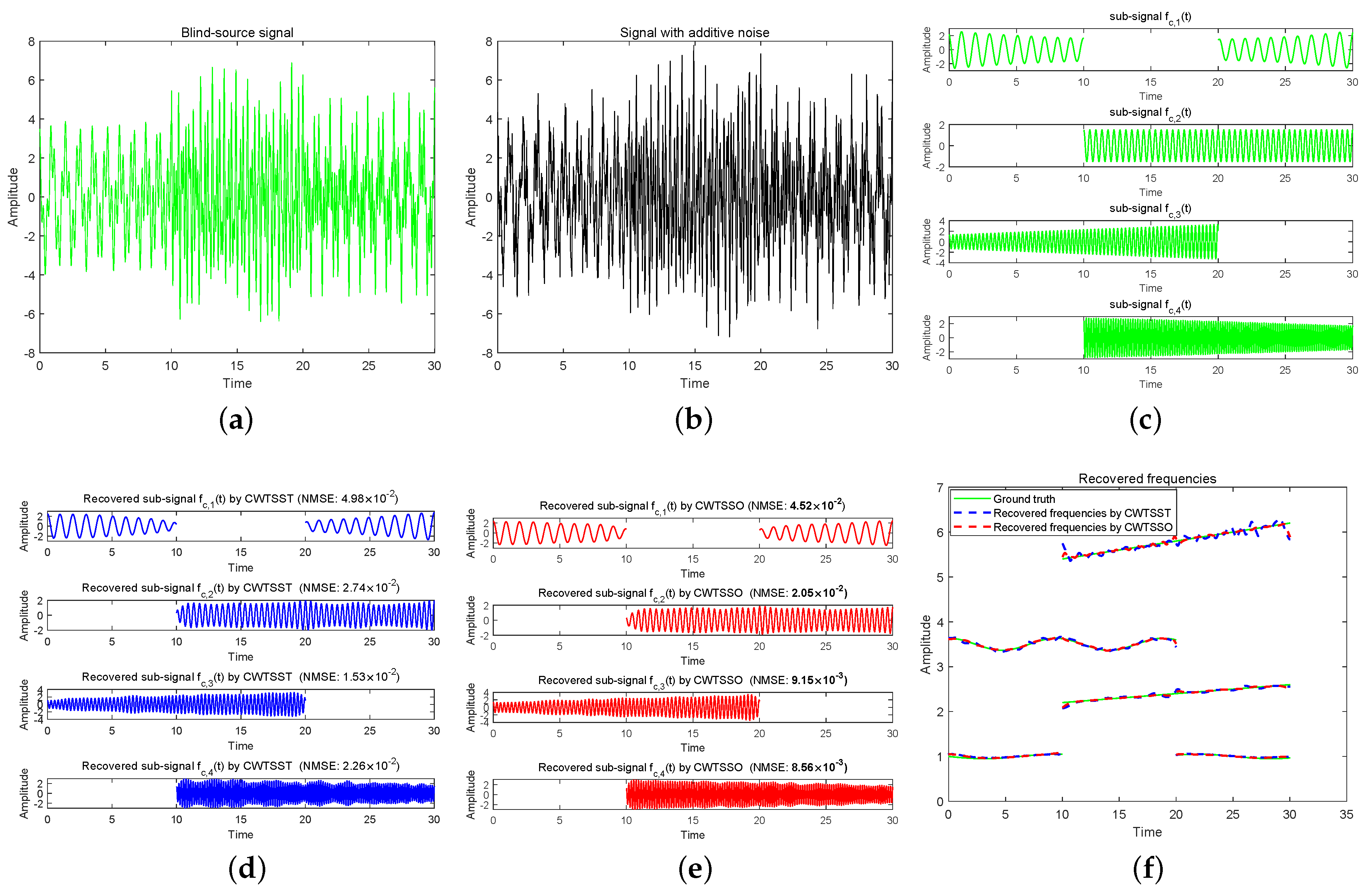
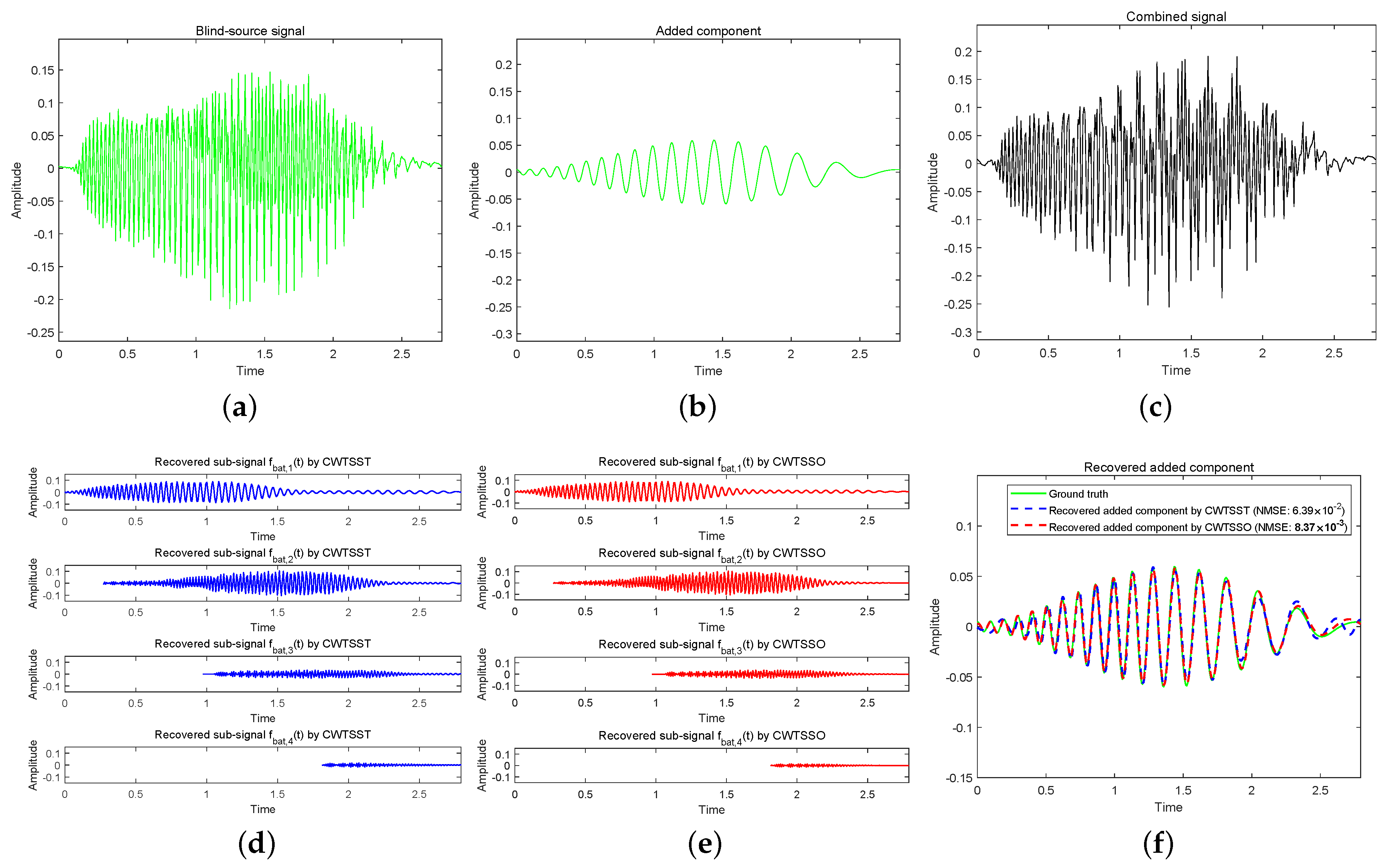
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Pustelnik, N.; Borgnat, P.; Flandrin, P. Empirical mode decomposition revisited by multicomponent non-smooth convex optimization. Signal Process. 2014, 102, 313–331. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P. One or two frequencies? The empirical mode decomposition answers. IEEE Trans. Signal Process. 2008, 56, 85–95. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Empirical mode decomposition for trivariate signals. IEEE Trans. Signal Process. 2010, 58, 1059–1068. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Filter bank property of multivariate empirical mode decomposition. IEEE Trans. Signal Process. 2011, 59, 2421–2426. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. An alternative formulation for the empirical mode decomposition. IEEE Trans. Signal Process. 2012, 60, 2236–2246. [Google Scholar] [CrossRef]
- Hou, T.Y.; Shi, Z. Data-driven time-frequency analysis. Appl. Comput. Harmon. Anal. 2013, 35, 284–308. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Chen, S.; Dong, X.; Peng, Z.; Zhang, W.; Meng, G. Nonlinear chirp mode decomposition: A variational method. IEEE Trans. Signal Process. 2017, 65, 6024–6037. [Google Scholar] [CrossRef]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmon. Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef]
- Cicone, A.; Dell’Acqua, P. Study of boundary conditions in the iterative filtering method for the decomposition of nonstationary signals. J. Comput. Appl. Math. 2020, 373, 112248. [Google Scholar] [CrossRef]
- Kowalski, M.; Meynard, A.; Wu, H.T. Convex Optimization approach to signals with fast varying instantaneous frequency. Appl. Comput. Harmon. Anal. 2018, 41, 89–112. [Google Scholar] [CrossRef]
- Kodera, K.; Gendrin, R.; Villedary, C. Analysis of time-varying signals with small BT values. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 64–76. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Auger, F.; Chassande-Mottin, E.; Flandrin, P. Making reassignment adjustable: The levenberg-marquardt approach. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3889–3892. [Google Scholar]
- Chassande-Mottin, E.; Auger, F.; Flandrin, P. Time-frequency/timescale reassignment. In Wavelets and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2003; pp. 233–267. [Google Scholar]
- Auger, F.; Flandrin, P.; Lin, Y.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.-T. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Daubechies, I.; Maes, S. A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models. In Wavelets in Medicine and Biology; Routledge: London, UK, 1996; pp. 527–546. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Yang, H. Synchrosqueezed wave packet transforms and diffeomorphism based spectral analysis for 1D general mode decompositions. Appl. Comput. Harmon. Anal. 2015, 39, 33–66. [Google Scholar] [CrossRef]
- Yang, H.; Ying, L. Synchrosqueezed curvelet transform for two-dimensional mode decomposition. Siam J. Math. Anal. 2014, 46, 2052–2083. [Google Scholar] [CrossRef]
- Huang, Z.L.; Zhang, J.; Zhao, T.H.; Sun, Y. Synchrosqueezing S-transform and its application in seismic spectral decomposition. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 817–825. [Google Scholar] [CrossRef]
- Thakur, G.; Wu, H.T. Synchrosqueezing-based recovery of instantaneous frequency from nonuniform samples. Siam J. Math. Anal. 2011, 43, 2078–2095. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. The Fourier-based synchrosqueezing transform. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar]
- Chen, Y.C.; Cheng, M.Y.; Wu, H.T. Non-parametric and adaptive modelling of dynamic periodicity and trend with heteroscedastic and dependent errors. J. R. Stat. Soc. Ser. Stat. Methodol. 2014, 76, 651–682. [Google Scholar] [CrossRef]
- Meignen, S.; Oberlin, T.; McLaughlin, S. A new algorithm for multicomponent signals analysis based on synchrosqueezing: With an application to signal sampling and denoising. IEEE Trans. Signal Process. 2012, 60, 5787–5798. [Google Scholar] [CrossRef]
- Thakur, G.; Brevdo, E.; Fckar, N.S.; Wu, H.T. The synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications. Signal Process. 2012, 93, 1079–1094. [Google Scholar] [CrossRef]
- Yang, H. Statistical analysis of synchrosqueezed transforms. Appl. Comput. Harmon. Anal. 2018, 45, 526–550. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]
- Pham, D.H.; Meignen, S. High-order synchrosqueezing transform for multicomponent signals analysis with an application to gravitational-wave signal. IEEE Trans. Signal Process. 2017, 65, 3168–3178. [Google Scholar] [CrossRef]
- Behera, R.; Meignen, S.; Oberlin, T. Theoretical analysis of the second-order synchrosqueezing transform. Appl. Comput. Harmon. Anal. 2018, 45, 379–404. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.H.; Mclaughlin, S. On demodulation, ridge detection and synchrosqueezing for multicomponent signals. IEEE Trans. Signal Process. 2017, 65, 2093–2103. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Cai, G.; Chen, B.; Li, X.; He, Z. Matching demodulation transform and synchrosqueezing in time–frequency analysis. IEEE Trans. Signal Process. 2014, 62, 69–84. [Google Scholar] [CrossRef]
- Li, L.; Cai, H.Y.; Han, H.X.; Jiang, Q.T.; Ji, H.B. Adaptive short-time Fourier transform and synchrosqueezing transform for non-stationary signal separation. Signal Process. 2020, 166, 107–231. [Google Scholar] [CrossRef]
- Li, L.; Cai, H.Y.; Jiang, Q.T. Adaptive synchrosqueezing transform with a time-varying parameter for non-stationary signal separation. Appl. Comput. Harmon. Anal. 2020, 49, 1075–1106. [Google Scholar] [CrossRef]
- Chui, C.K.; Mhaskar, H.N. Signal decomposition and analysis via extraction of frequencies. Appl. Comput. Harmon. Anal. 2016, 40, 97–136. [Google Scholar] [CrossRef]
- Chui, C.K.; Han, N.N. Wavelet thresholding for recovery of active sub-signals of a composite signal from its discrete samples. Appl. Comput. Harmon. Anal. 2021, 52, 1–24. [Google Scholar] [CrossRef]
| Example 1 | Example 2 | Example 3 | Example 4 | |
|---|---|---|---|---|
| CWTSST | 15.46 | 28.62 | 133.27 | 13.81 |
| CWTSSO | 2.78 | 3.87 | 17.77 | 1.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, N.; Pei, Y.; Song, Z. Signal Separation Operator Based on Wavelet Transform for Non-Stationary Signal Decomposition. Sensors 2024, 24, 6026. https://doi.org/10.3390/s24186026
Han N, Pei Y, Song Z. Signal Separation Operator Based on Wavelet Transform for Non-Stationary Signal Decomposition. Sensors. 2024; 24(18):6026. https://doi.org/10.3390/s24186026
Chicago/Turabian StyleHan, Ningning, Yongzhen Pei, and Zhanjie Song. 2024. "Signal Separation Operator Based on Wavelet Transform for Non-Stationary Signal Decomposition" Sensors 24, no. 18: 6026. https://doi.org/10.3390/s24186026
APA StyleHan, N., Pei, Y., & Song, Z. (2024). Signal Separation Operator Based on Wavelet Transform for Non-Stationary Signal Decomposition. Sensors, 24(18), 6026. https://doi.org/10.3390/s24186026







