Optimized Design of Direct Digital Frequency Synthesizer Based on Hermite Interpolation
Abstract
:1. Introduction
- Utilizing the smooth characteristics of cubic Hermite interpolation to effectively address waveform spurs caused by accumulator truncation. A dual-port ROM structure is employed to obtain the parameters required for interpolation calculations.
- By leveraging the derivative relationship between sine and cosine functions in the ROM table design, this approach avoids excessive ROM resource consumption. Additionally, a single-quadrant ROM compression method is introduced to further reduce ROM size.
2. DDFS Architectural Design
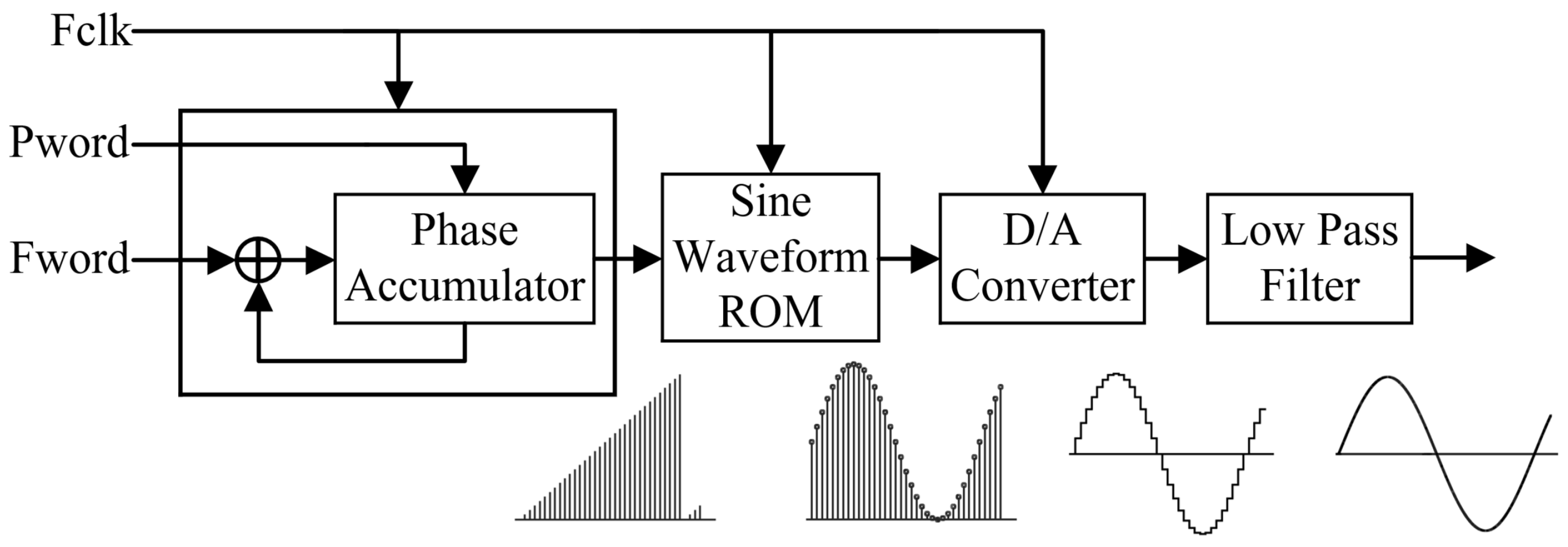
2.1. Traditional DDFS Architecture
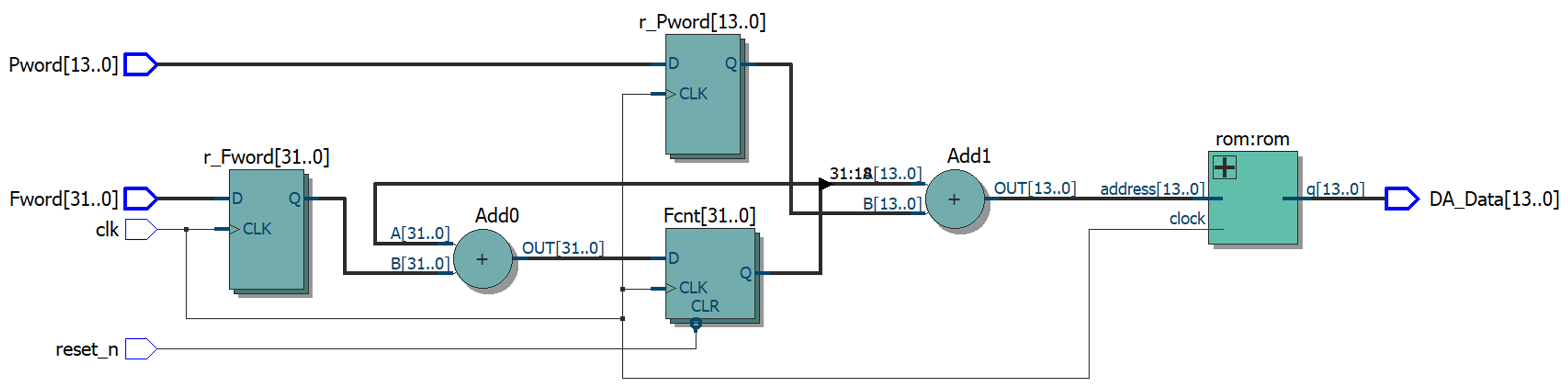
2.2. FPGA-Based DDFS Architectural Design
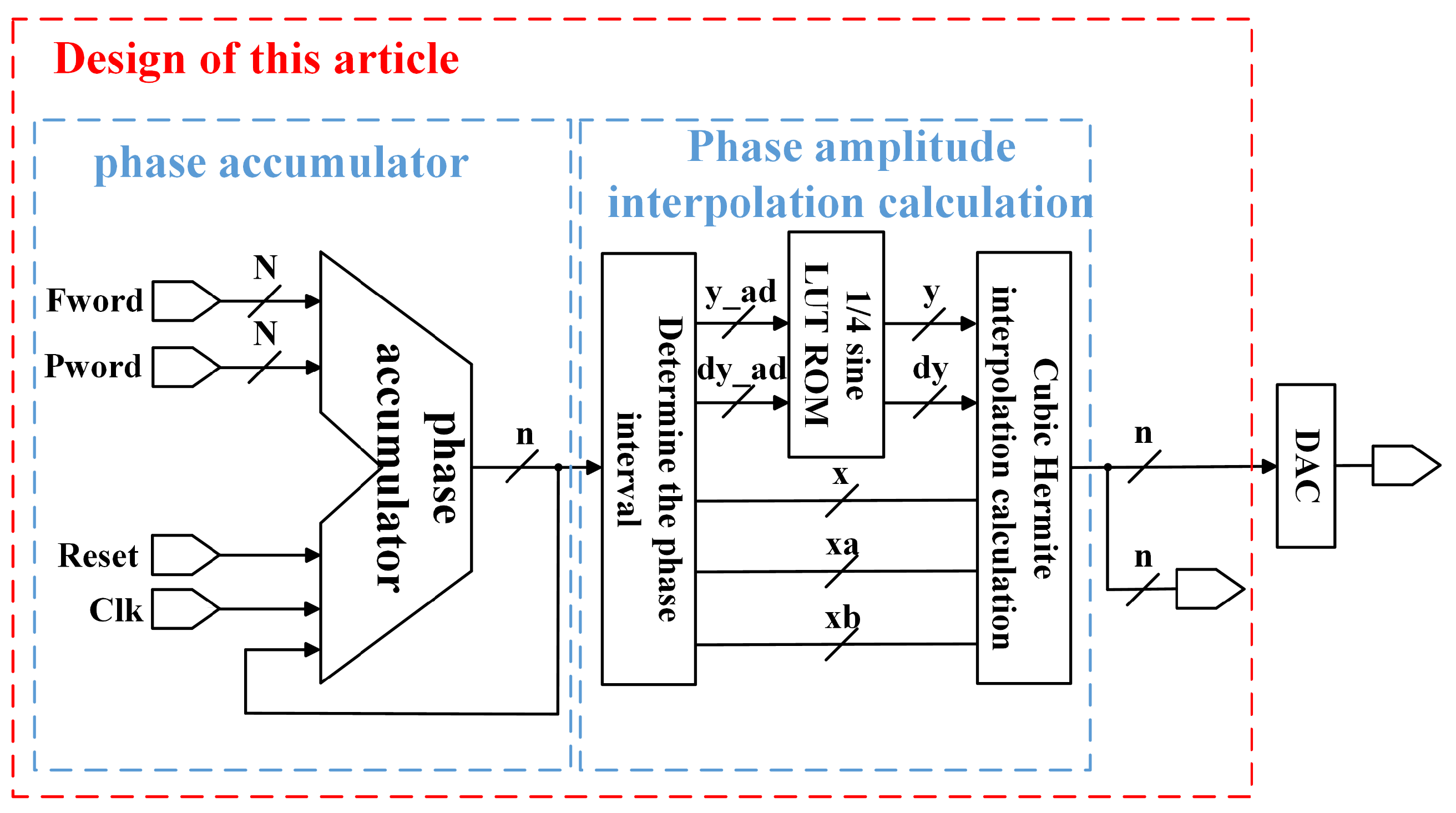
3. Optimized Design of DDFS Architecture
3.1. Optimization of Interpolation Algorithm
- Approximate the curve between two sampling points as a cubic polynomial;
- Specify both function values and first-order derivatives at the two sampling points;
- Solve for the coefficients of the polynomial;
- Use the polynomial for interpolation between the two sampling points.
- The error in the traditional method mainly stems from linear quantization noise. As the quantization step size increases, the error power also increases.
- The error in Hermite interpolation is due to the approximation error of higher-order derivative terms. The interpolation method reduces the quantization error, particularly in cases of higher resolution and more complex signals, making the effect of the interpolation method more pronounced.
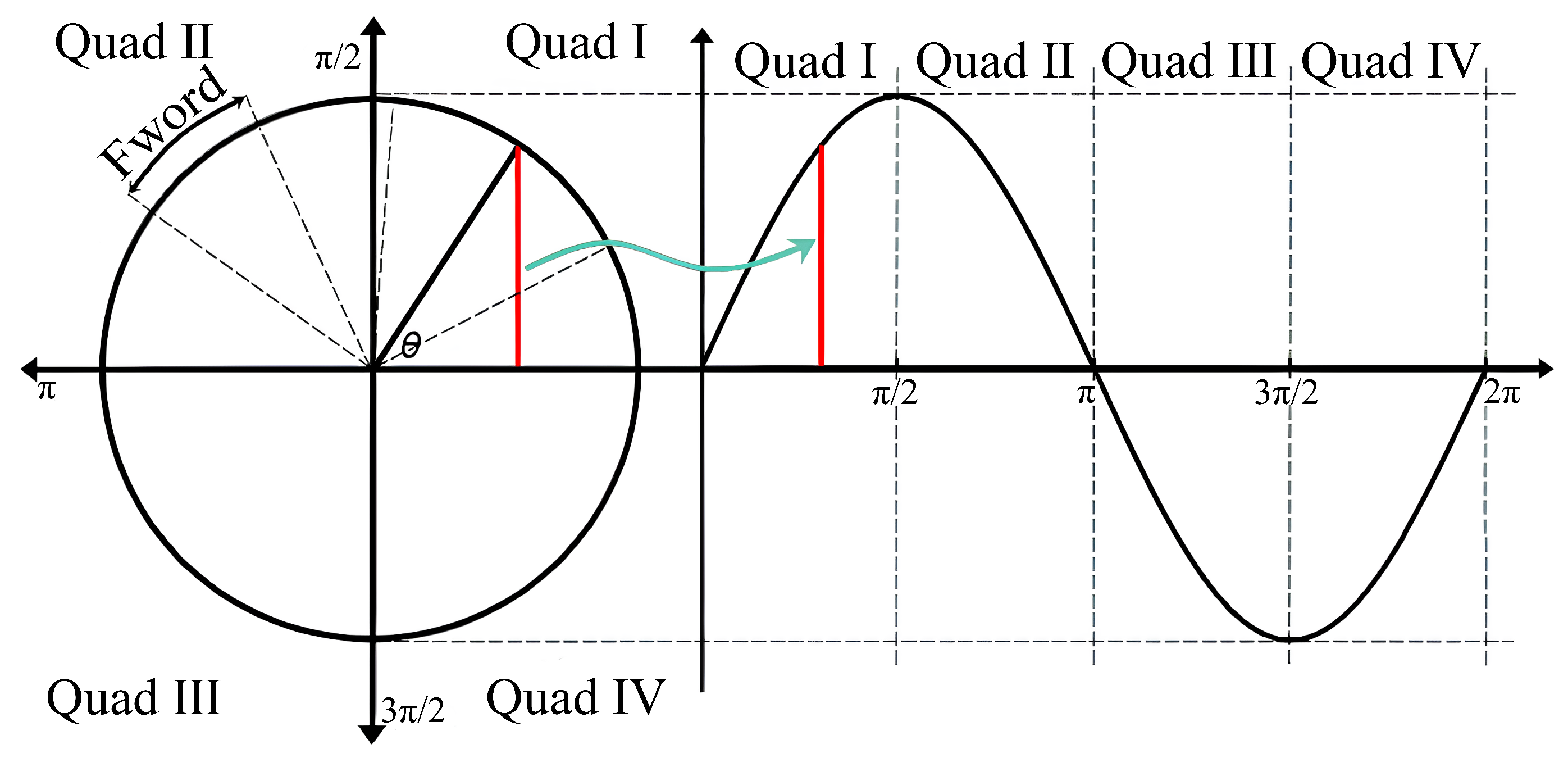
3.2. Single-Quadrant ROM Table Design
3.3. Delayed Structural Design
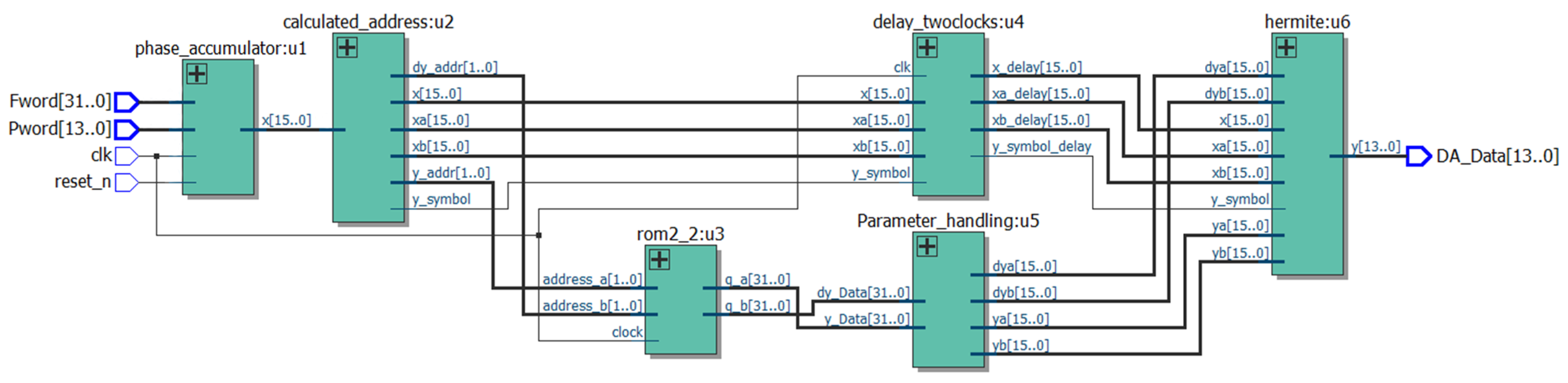
3.4. Optimized Architecture Logic Design
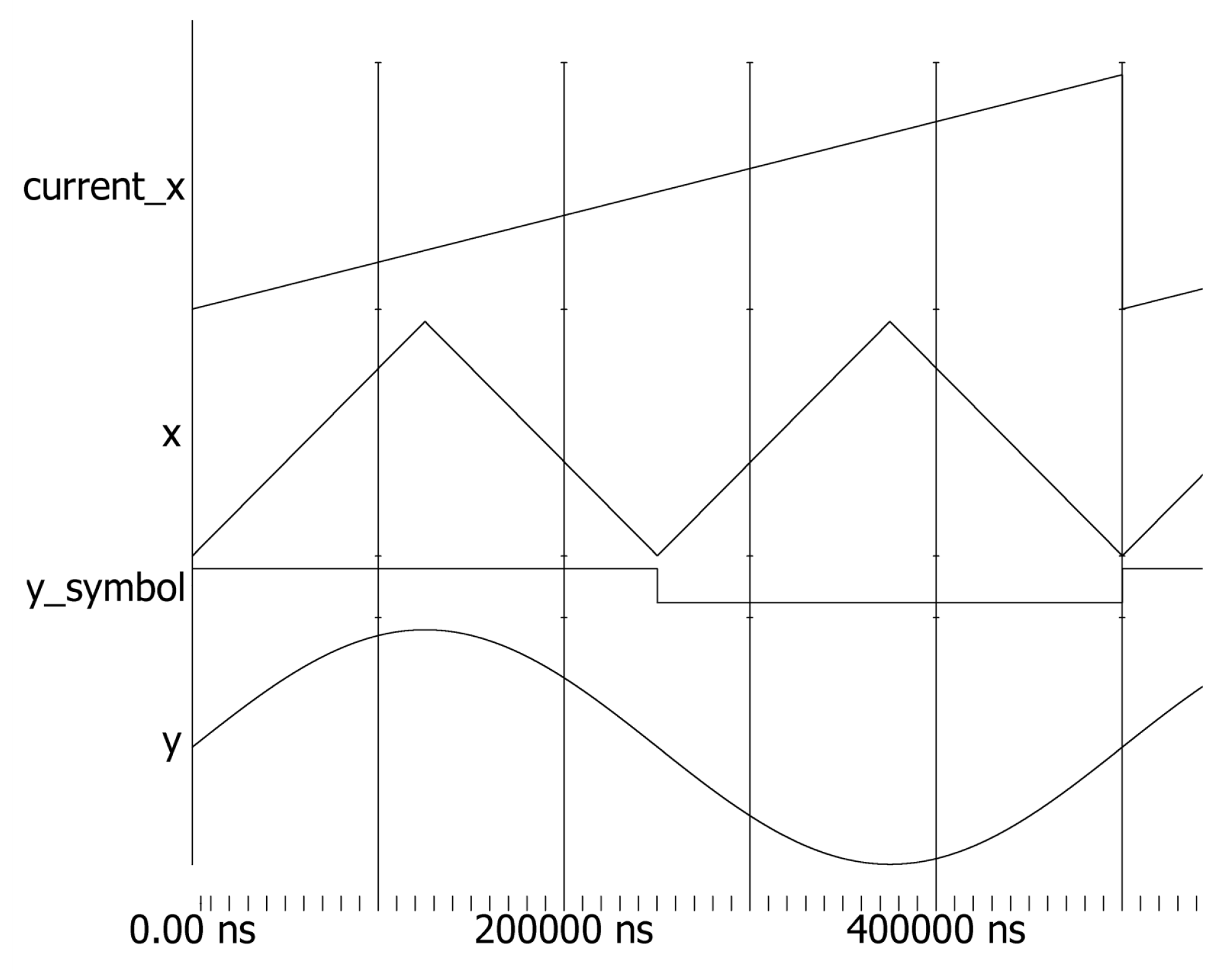
- Phase calculation and adjustment.The phase of the node is calculated using a phase accumulator. A single-quadrant storage method is employed to perform phase reversal operations and sign changes at specific phase points (1/4, 1/2, and 3/4 cycles) to generate the desired sinusoidal phase data for the cycle.
- Phase data handling.After acquiring the phase data, the key bits (determined by the number of bits in the ROM storage table) are retained, while the remaining bits are cleared to obtain the node data . The other node data are then computed using the sum of and the interval width, along with the delayed structure, to ensure synchronized input of parameters for the cubic Hermite interpolation.
- ROM table structure application.A single-quadrant storage method and a dual-port ROM table structure are utilized. Based on the interval node data, the address information for the magnitude and derivative data of the two nodes in the interval are obtained from the ROM.
- Data read and shift operations.Using the obtained address information, the magnitude and derivative data for the two nodes in the interval are read from the ROM. Since each data entry in the ROM table contains information about two nodes in an interval, a shift operation is performed after reading to separately access the data for the two nodes.
- Cubic Hermite interpolation calculations.Based on the parameters derived from the previous steps, the cubic Hermite interpolation algorithm is executed to generate the interpolated waveform data.
| Algorithm 1 Cubic Hermite interpolation for DDFS. |
| Input: Phase accumulator, ROM //Phase increment and ROM with nodes and derivatives Output: Output waveform value
|
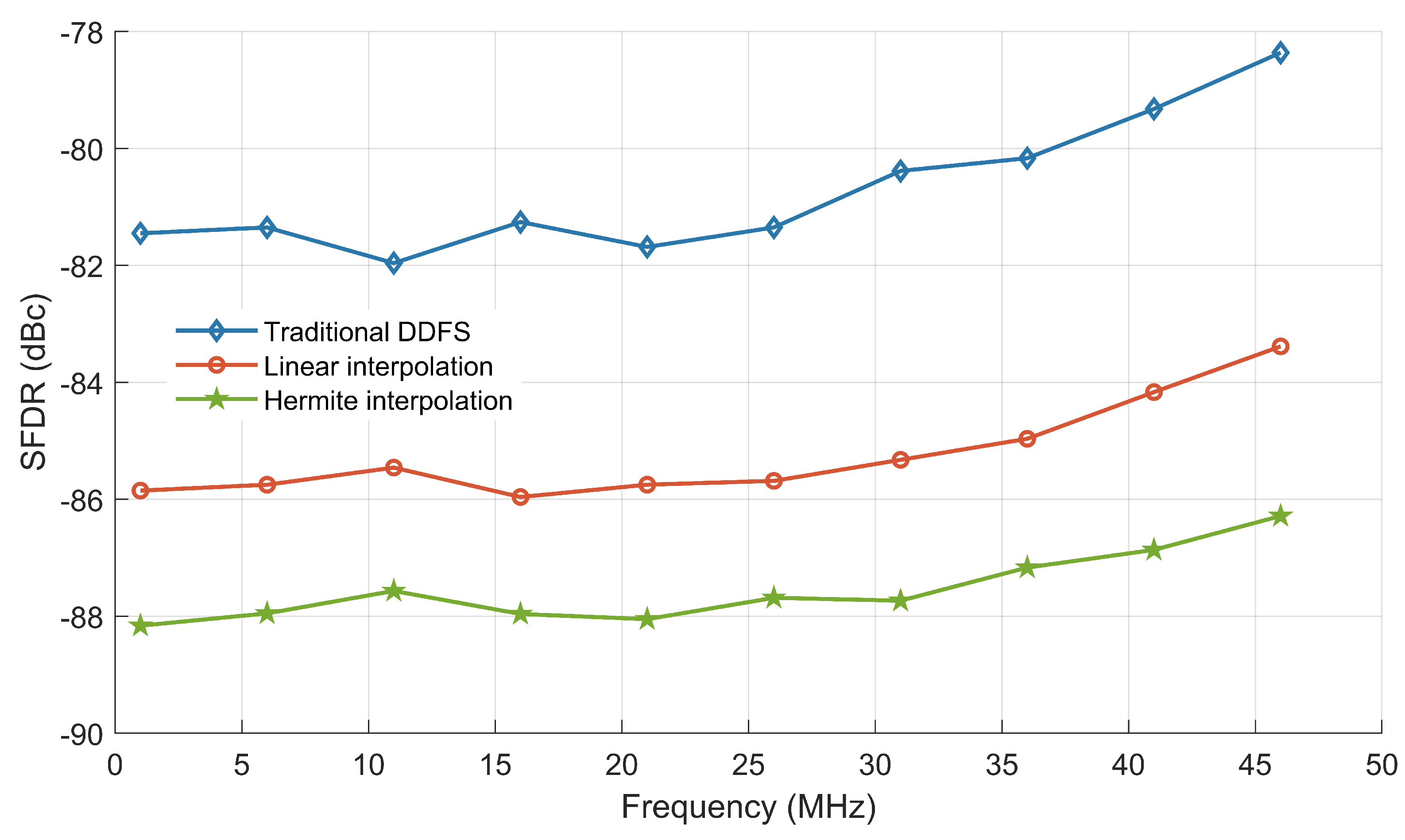
4. Experiment and Analysis
4.1. ModelSim Software Simulation
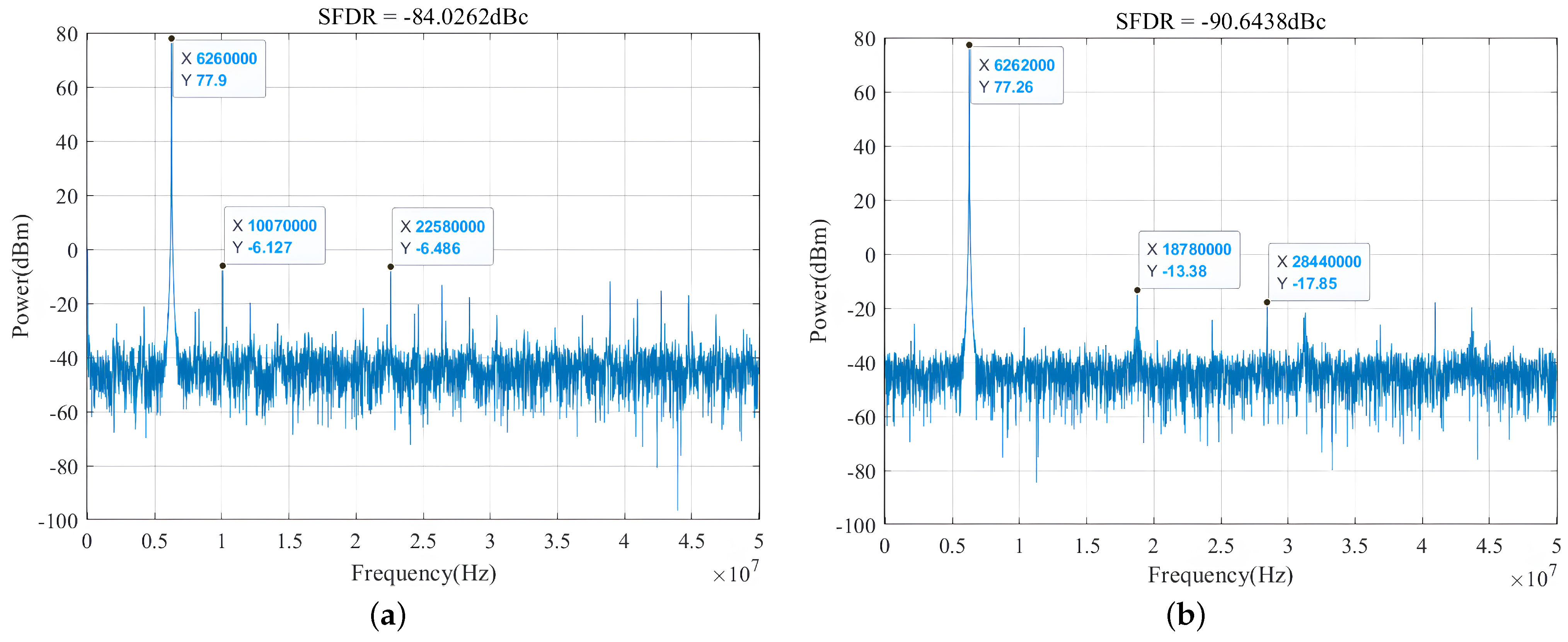
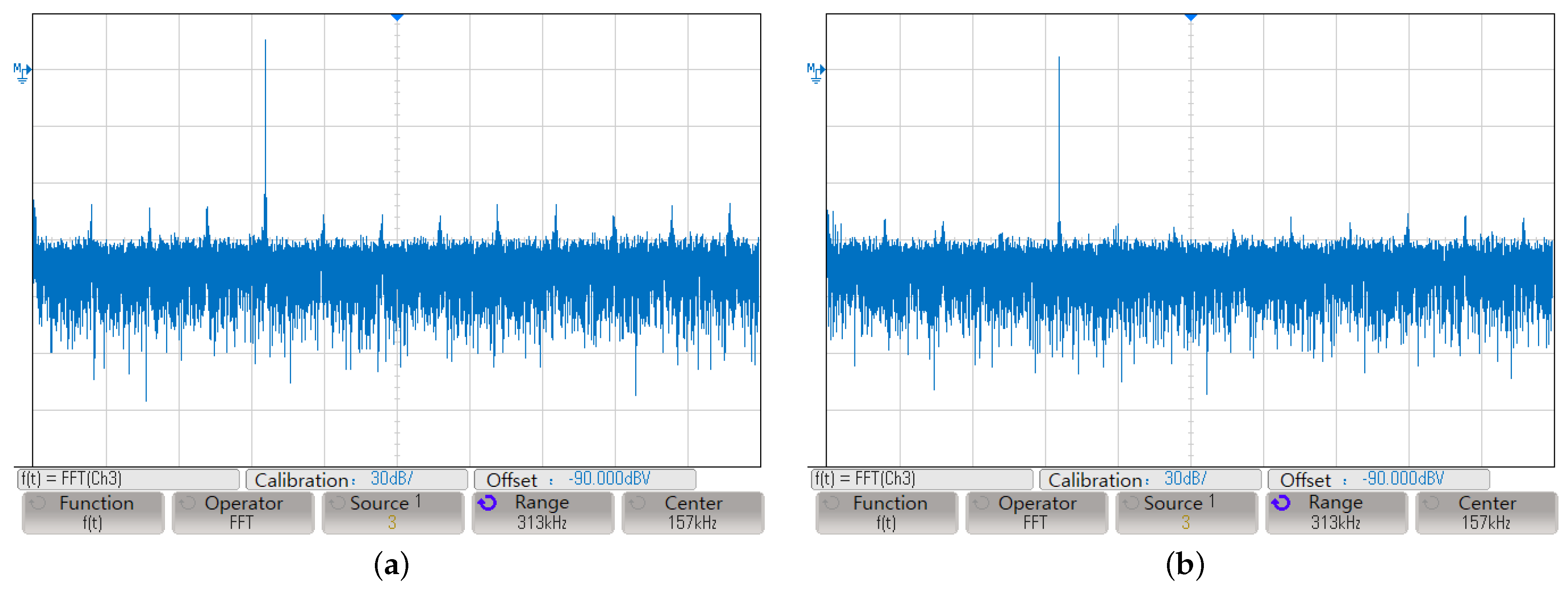
4.2. FPGA Platform Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horlbeck, M.; Scheiner, B.; Weigel, R.; Lurz, F. Fast rf-synthesizer based on direct digital synthesis for an instantaneous frequency measurement system. In Proceedings of the 2021 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNeT), San Diego, CA, USA, 17–22 January 2021; pp. 1–4. [Google Scholar]
- Tang, S.; Li, C.; Hou, Y. A suppressing method for spur caused by amplitude quantization in dds. IEEE Access 2019, 7, 62344–62351. [Google Scholar] [CrossRef]
- Choi, J.M.; Yoon, D.H.; Jung, D.K.; Seong, K.; Han, J.S.; Lee, W.; Baek, K.H. Design and analysis of low power and high sfdr direct digital frequency synthesizer. IEEE Access 2020, 8, 67581–67590. [Google Scholar] [CrossRef]
- Wang, C.; Sulistiyanto, N.; Shih, H.Y.; Lin, Y.C.; Wang, W. Power-effective rom-less ddfs design approach with high sfdr performance. J. Signal Process. Syst. 2019, 92, 213–224. [Google Scholar] [CrossRef]
- Wang, C.C.; Lou, P.Y.; Tsai, T.Y.; Shih, H.Y. 74-dBc sfdr 71-Mhz four-stage pipeline rom-less ddfs using factorized second-order parabolic equations. IEEE Trans. on Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2464–2468. [Google Scholar] [CrossRef]
- Beheshti, M.; Jannesari, A. A 2-ghz rom-less direct digital frequency synthesizer based on an analog sine-mapper circuit. In Proceedings of the 2016 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 10–12 May 2016; pp. 1603–1608. [Google Scholar]
- Wu, X.; Zhao, Z.; Pan, Y.P.; Jiang, M.M. Design of arbitrary waveform generator based on labview. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 6382–6386. [Google Scholar]
- Yang, D.; Xu, J.; Du, H. A high performance frequency synthesis method based on pll and dds. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shanghai, China, 17–20 May 2020; pp. 1–3. [Google Scholar]
- Bommi, R.M.; Raja, S.S. High performance reversible direct data synthesizer for radio frequency applications. Mob. Netw. Appl. 2019, 24, 224–233. [Google Scholar] [CrossRef]
- Huang, L.; Tian, S.; Liu, K.; Guo, G.; Xiao, Y.; Zhao, W.; Yang, X. The design of a wide bandwidth time marker generator. Rev. Sci. Instruments 2018, 89, 115103. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Sun, Y.; Simpson, O. Design and implementation of a re-configurable versatile direct digital synthesis-based pulse generator. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, Y.; Liu, K.; Huang, L.; Yang, X. A sampling rate selecting algorithm for the arbitrary waveform generator. IEEE Access 2019, 7, 83761–83770. [Google Scholar] [CrossRef]
- Yan, C.; Sun, J.; Liu, W. An efficient high sfdr pdds using high-pass-shaped phase dithering. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 2003–2007. [Google Scholar] [CrossRef]
- Hou, Y.; Li, C.; Tang, S. An accurate dds method using compound frequency tuning word and its fpga implementation. Electronics 2018, 7, 330. [Google Scholar] [CrossRef]
- Jeng, S.S.; Lin, H.C.; Lin, C.H. A novel rom compression architecture for ddfs utilizing the parabolic approximation of equi-section division. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2603–2612. [Google Scholar] [CrossRef] [PubMed]
- Calbaza, D.E.; Savaria, Y. Jitter model of direct digital synthesis clock generators. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems (ISCAS), Orlando, FL, USA, 30 May–2 June 1999; pp. 1–4. [Google Scholar]
- Das, K.; Pradhan, S.N. Field-programmable gate array-based design for real-time computation of ensemble empirical mode decomposition. Int. J. Circuit Theory Appl. 2021, 49, 2312–2328. [Google Scholar] [CrossRef]
- George, G.C.; Moitra, A.; Caculo, S.; AmalinPrince, A. Efficient architecture for implementation of hermite interpolation on fpga. In Proceedings of the 2018 Conference on Design and Architectures for Signal and Image Processing (DASIP), Porto, Portugal, 10–12 October 2018; pp. 7–12. [Google Scholar]
- Samila, A.; Hotra, O.; Majewski, J.A. Implementation of the configuration structure of an integrated computational core of a pulsed NQR sensor based on FPGA. Sensors 2021, 21, 6029. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yang, M.; Long, J.; Xu, D.; Blaabjerg, F. A dds-based wait-free phase-continuous carrier frequency modulation strategy for emi reduction in fpga-based motor drive. IEEE Trans. Power Electron. 2019, 34, 9619–9631. [Google Scholar] [CrossRef]
- D’souza, A.V.; Ravi, D.J. In-phase and quadrature-phase sinusoidal signal generation using dds technique. IETE J. Res. 2021, 69, 4273–4280. [Google Scholar] [CrossRef]
- Damnjanović, V.D.; Petrović, M.L.; Milovanović, V.M. A parameterizable chisel generator of numerically controlled oscillators for direct digital synthesis. In Proceedings of the 2021 24th International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Vienna, Austria, 7–9 April 2021; pp. 141–144. [Google Scholar]
- Bio, M.; Gietler, H.; Plazonic, J.; Ley, M.; Zangl, H.; Scherr, W. Prototyping for a dds-based i/q reference signal generation on a capacitive sensing chip in 65nm cmos using systemc ams, c hls and vhdl. In Proceedings of the 2021 Austrochip Workshop on Microelectronics (Austrochip), Linz, Austria, 14 October 2021; pp. 37–40. [Google Scholar]
- Petrinović, D.; Brezović, M. Spline-based high-accuracy piecewise-polynomial phase-to-sinusoid amplitude converters. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 711–729. [Google Scholar] [CrossRef] [PubMed]
- Boukhtache, S.; Blaysat, B.; Grédiac, M.; Berry, F. Alternatives to bicubic interpolation considering fpga hardware resource consumption. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 247–258. [Google Scholar] [CrossRef]
- George, G.C.; Moitra, A.; Caculo, S.; Prince, A.A.; Buch, J.J.U.; Pathak, S.K. A novel and efficient hardware accelerator architecture for signal normalization. Circuits Syst. Signal Process. 2019, 39, 2425–2441. [Google Scholar] [CrossRef]
- Wijaya, R.I.; Ros, S.; Bagus, E.S.; Dadan, M. FPGA-based I/Q chirp generator using first quadrant DDS compression for pulse compression radar. AIP Conf. Proc. 2016, 1755, 170005. [Google Scholar]
- Turner, S.E.; Cali, J.D. Phase coherent frequency hopping in direct digital synthesizers and phase locked loops. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1815–1823. [Google Scholar] [CrossRef]
- Annafianto, N.F.R.; Jabir, M.V.; Burenkov, I.A.; Ugurdag, H.F.; Battou, A.; Polyakov, S.V. FPGA Implementation of a Low Latencyand High SFDR Direct Digital Synthesizer for Resource-Efficient Quantum-Enhanced Communication. In Proceedings of the 2020 IEEE East-West Design & Test Symposium (EWDTS), Varna, Bulgaria, 4–7 September 2020; pp. 1–8. [Google Scholar]


| Logic Unit | Equation (7) | Optimized |
|---|---|---|
| Adder | 19 | 11 |
| Multiplier | 14 | 11 |
| Defaulter | 6 | 1 |
| Total Logic Elements | Total Memory Bits | |
|---|---|---|
| Using the single-quadrant method | 1394 | 128 |
| Single-quadrant method not used | 1326 | 507 |
| Parameter Name | Set Value |
|---|---|
| 100 MHz | |
| 32 bit | |
| 14 bit | |
| DAC | 14 bit |
| [5] TVLSI | [4] JSPS | [3] ACCESS | [29] EWDTS | [13] TVLSI | This Work | |
|---|---|---|---|---|---|---|
| Year | 2018 | 2019 | 2020 | 2020 | 2021 | 2023 |
| Process (nm CMOS) | 180 | FPGA | 65 | FPGA | 45 | FPGA |
| (bits) | 32 | 32 | 32 | 32 | 25 | 32 |
| Output resolution (bits) | 24 | 24 | 9 | 16 | 25 | 14 |
| Clock rate (MHz) | 71.9 | 100 | 2000 | 251 | 2000 | 100 |
| Verification | Mears. | Mears. | Sim. | Mears. | Sim. | Mears. |
| SFDR (dBc) | 74 | 68.4242 | 70.8 | 72.2 | 41 | 88.134 |
| Resource Utilization Rate | Traditional Method | Piecewise Linear Approximation Method [2] | Pulse Width Modulation Method [11] | Proposed Method |
|---|---|---|---|---|
| Device | EP4CE10F17C8 | EP1C12Q24017 | EP4CE55F23C6 | EP4CE10F17C8 |
| Total logic elements | 94/10,320 (<1%) | 1104/12,060 (9%) | 36,011/55,856 (64%) | 1394/10,320 (14%) |
| Total memory bits | 229,376/423,936 (54%) | 180,275/23,9616 (75%) | 1,286,144/2,396,160 (54%) | 128/423,936 (<1%) |
| Total pins | 19/180 (11%) | 19/173(11%) | 181/325 (56%) | 19/180 (11%) |
| Embedded multiplier 9-bit elements | 0/46 (0%) | N/A | 184/308 (60%) | 46/46 (100%) |
| Total PLLs | 1/2 (50%) | 1/2 (50%) | 2/4 (50%) | 1/2 (50%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Xu, Q.; Zhang, T. Optimized Design of Direct Digital Frequency Synthesizer Based on Hermite Interpolation. Sensors 2024, 24, 6285. https://doi.org/10.3390/s24196285
Zhou K, Xu Q, Zhang T. Optimized Design of Direct Digital Frequency Synthesizer Based on Hermite Interpolation. Sensors. 2024; 24(19):6285. https://doi.org/10.3390/s24196285
Chicago/Turabian StyleZhou, Kunpeng, Qiaoyu Xu, and Tianle Zhang. 2024. "Optimized Design of Direct Digital Frequency Synthesizer Based on Hermite Interpolation" Sensors 24, no. 19: 6285. https://doi.org/10.3390/s24196285
APA StyleZhou, K., Xu, Q., & Zhang, T. (2024). Optimized Design of Direct Digital Frequency Synthesizer Based on Hermite Interpolation. Sensors, 24(19), 6285. https://doi.org/10.3390/s24196285





