Sowing Depth Monitoring System for High-Speed Precision Planters Based on Multi-Sensor Data Fusion
Abstract
1. Introduction
2. Materials and Methods
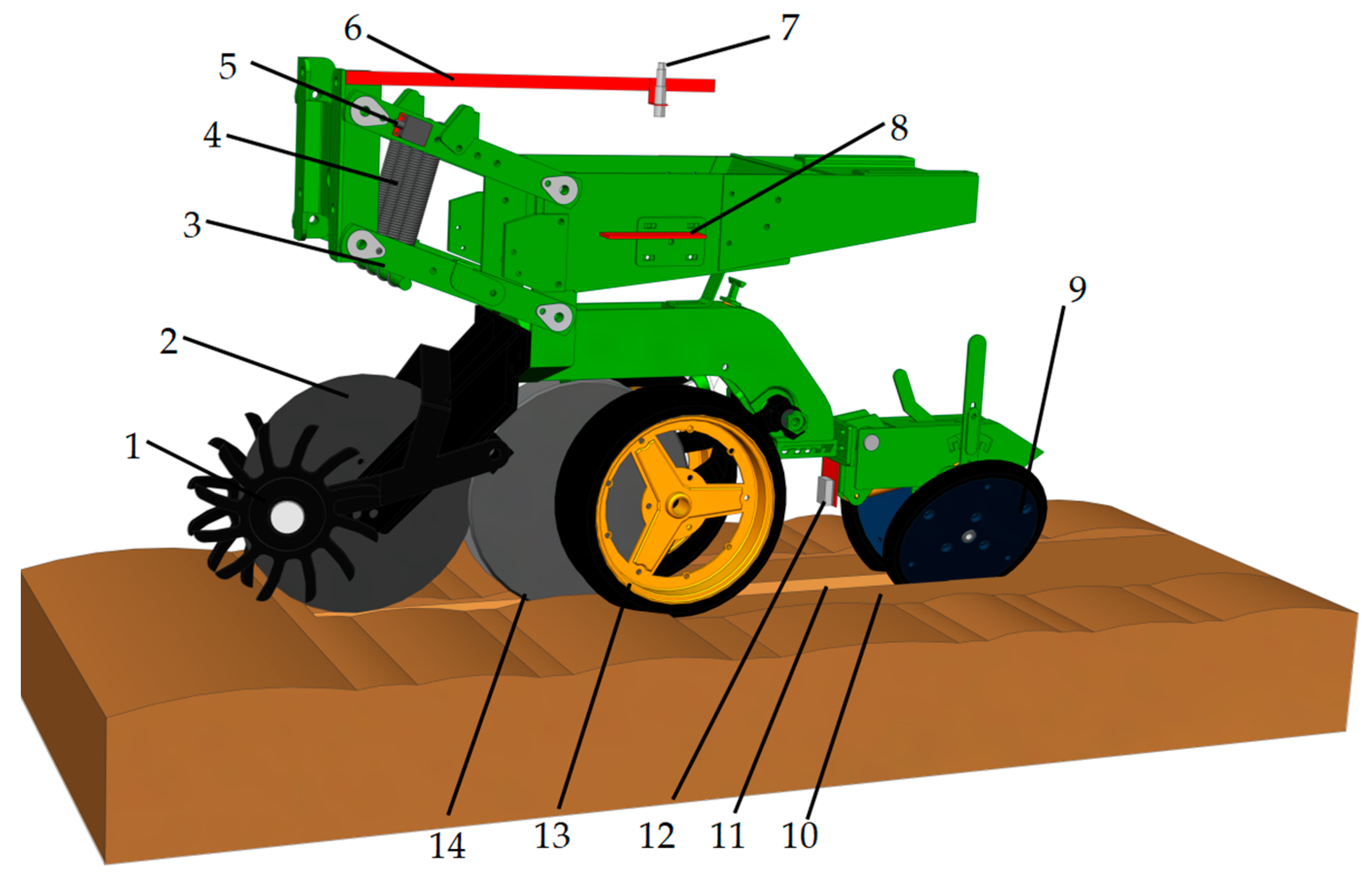
2.1. Sowing Depth Monitoring Methods
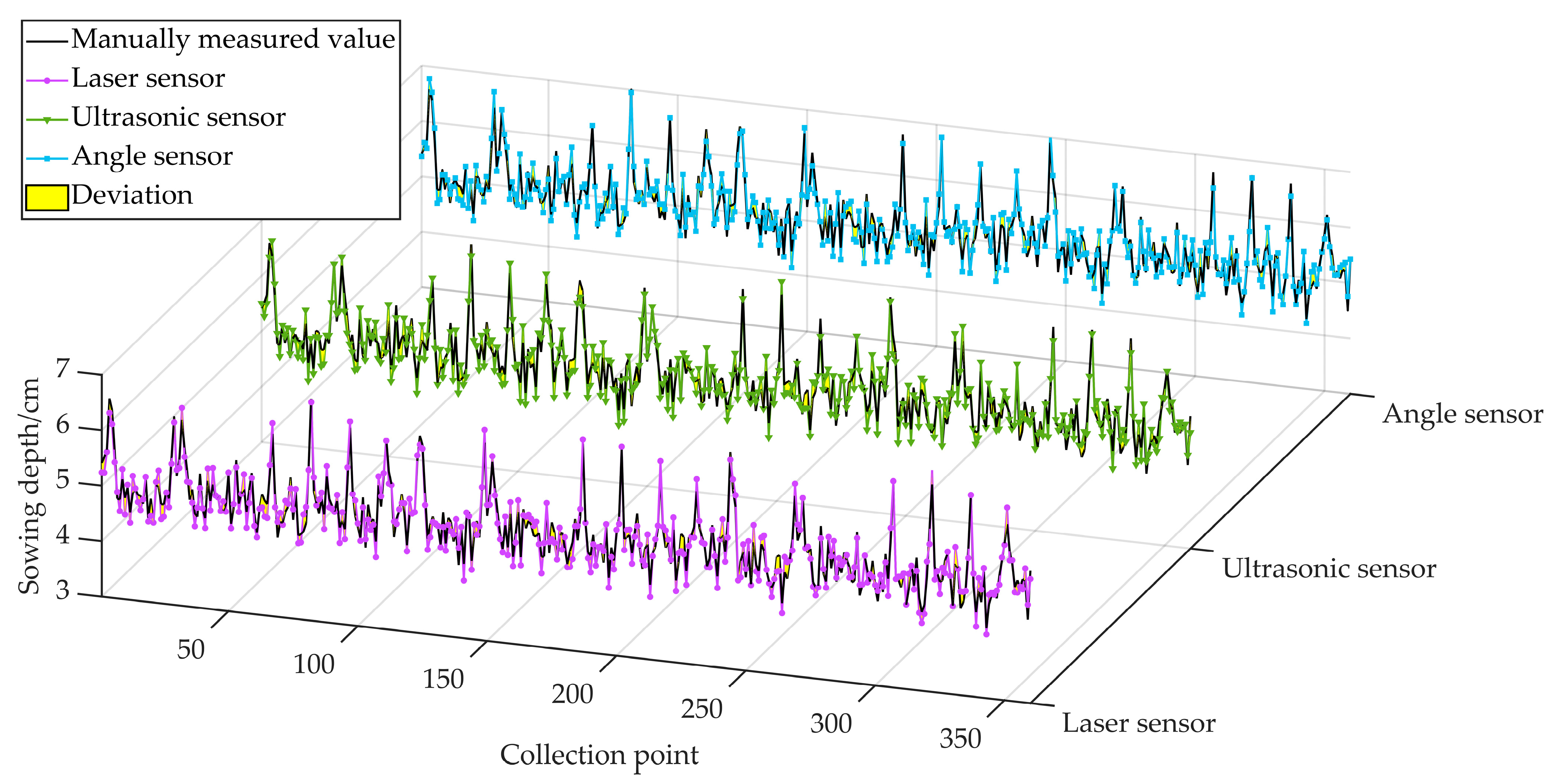
2.2. Sowing Depth Raw Data Collection
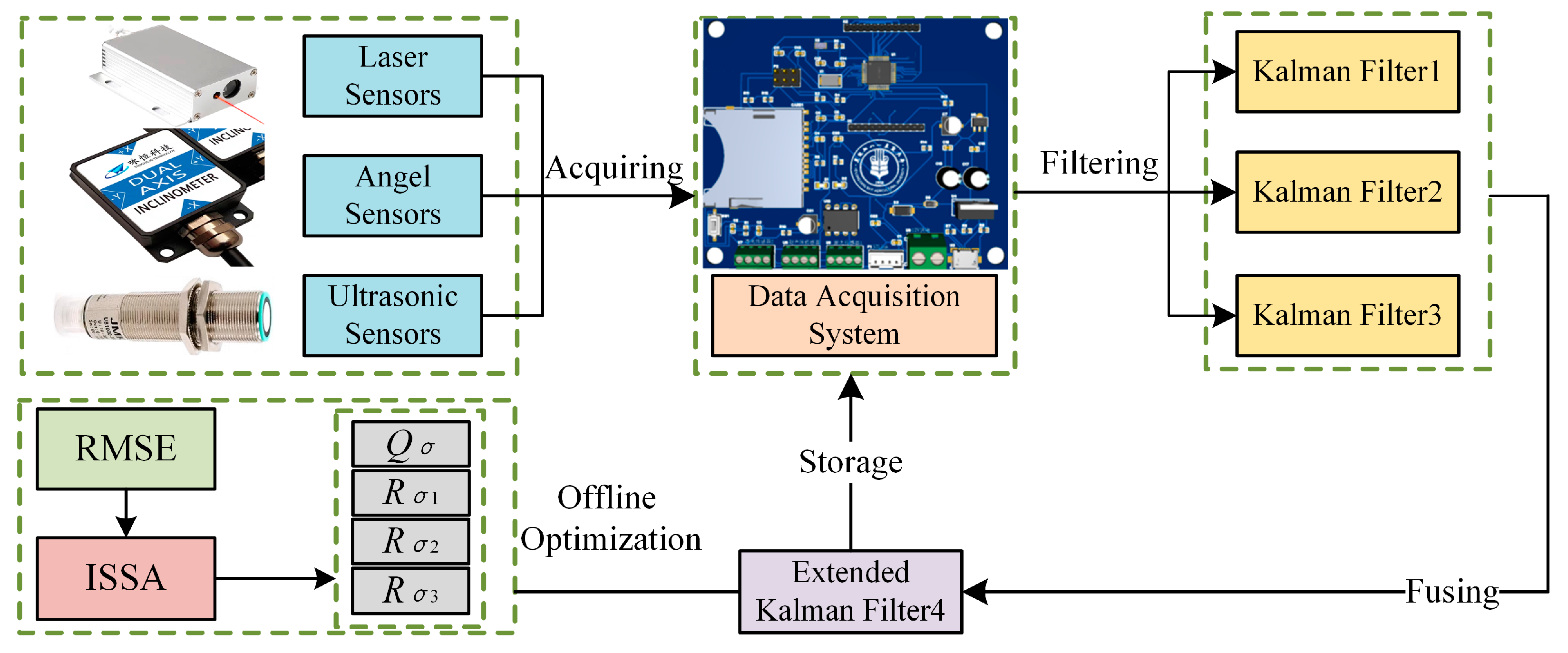
2.3. EKF Multi-Sensor Fusion Algorithm
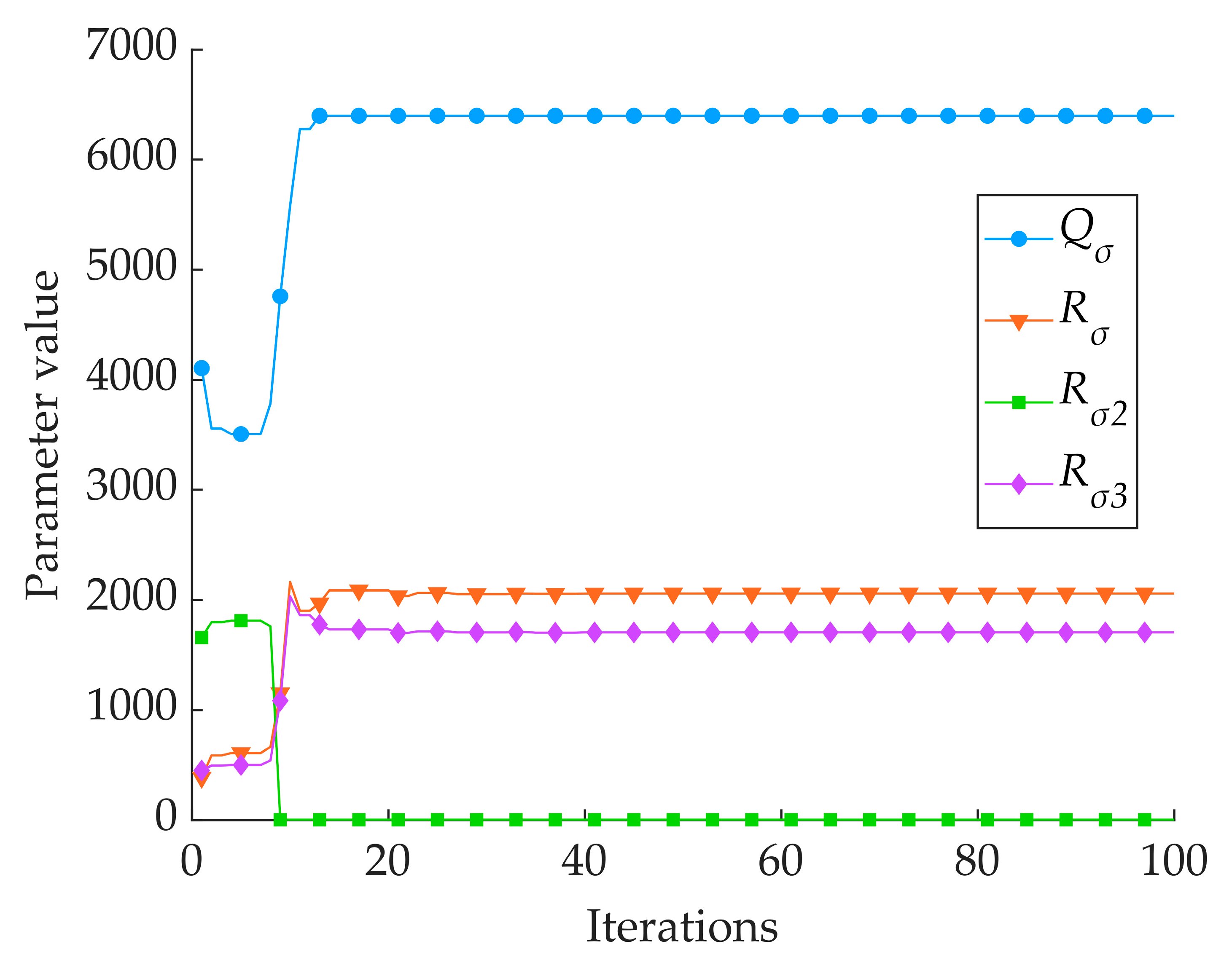
2.4. Improved Sparrow Search Algorithm
2.5. ISSA-EKF
3. Results
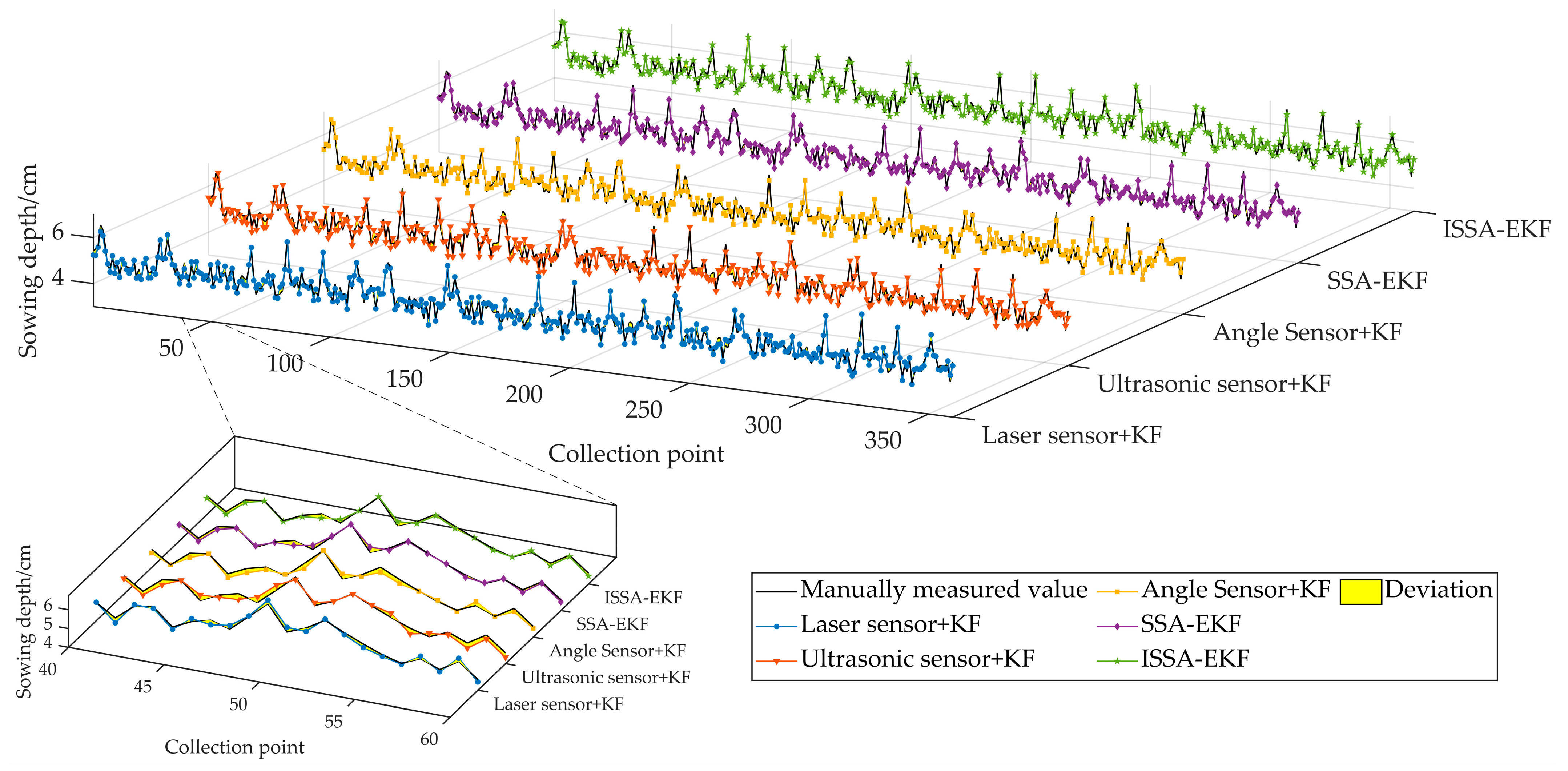
3.1. Simulation Test
3.2. Field Test
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yadav, N.; Khanduri, V.P.; Singh, B.; Dhanai, C.S.; Riyal, M.K.; Rawat, D.; Ahmad, T.; Kumar, M. Effect of temperature, seed size, sowing depth, and position on seed germination and seedling growth of bauhinia retusa roxb. and bauhinia variegata L. Forests 2023, 14, 1664. [Google Scholar] [CrossRef]
- Thani, P.R.; Johnson, J.B.; Bhattarai, S.; Trotter, T.; Walsh, K.; Broszczak, D.; Naiker, M. An in-depth examination into how genotype, planting density, and time of sowing affect key phytochemical constituents in nigella sativa seed. Seeds 2024, 3, 357–380. [Google Scholar] [CrossRef]
- Orzech, K.; Wanic, M.; Załuski, D. The effects of soil compaction and different tillage systems on the bulk density and moisture content of soil and the yields of winter oilseed rape and cereals. Agriculture 2021, 11, 666. [Google Scholar] [CrossRef]
- Nemergut, K.; Thomison, P.; Carter, P.; Lindsey, A. Planting depth affects corn emergence, growth and development, and yield. Agron. J. 2021, 113, 3351–3360. [Google Scholar] [CrossRef]
- Dwivedi, A.; Groll, H.; Beckerle, P. A systematic review of sensor fusion methods using peripheral bio-signals for human intention decoding. Sensors 2022, 22, 6319. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Ma, Y.; Zhou, H.; Niu, K.; Zhao, B.; Wei, L.; Bai, S.; Zheng, Y.; Zhang, W. Design and test of sowing depth measurement and control system for no-till corn seeder based on integrated electro-hydraulic drive. Appl. Sci. 2023, 13, 5823. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, R.; Liu, Q.; Yin, X.; He, X.; Cui, T.; Zhang, D. Row cleaner and depth control unit improving sowing performance of maize no-till precision planter. Trans. CSAE 2016, 32, 18–23. [Google Scholar]
- Li, M.; Xia, X.; Zhu, L.; Zhou, R.; Huang, D. Intelligent sowing depth regulation system based on Flex sensor and Mamdani fuzzy model for a no-till planter. Int. J. Agric. Biol. Eng. 2021, 14, 145–152. [Google Scholar] [CrossRef]
- Gao, Y.; Zhai, C.; Yang, S.; Zhao, X.; Wang, X.; Zhao, C. Measurement method and mathematical model for the seeding downforce of planter row unit. Trans. CSAE 2020, 36, 1–9. [Google Scholar]
- Gao, Y.; Wang, X.; Yang, S.; Zhai, C.; Zhao, X.; Zhao, C. Development of CAN-based sowing depth monitoring and evaluation system. Trans. CSAM 2019, 50, 23–32. [Google Scholar]
- Gao, Y.; Zhai, C.; Yang, S.; Zhao, X.; Wang, X.; Zhao, C. Development of CAN-based downforce and sowing depth monitoring and evaluation system for precision planter. Trans. CSAM 2020, 51, 15–28. [Google Scholar]
- Galibjon, M.; Dimitris, S.; Hans, W. Implementation of a magnetorheological damper on a no-till seeding assembly for optimising sowing depth. Comput. Electron. Agric. 2018, 150, 465–475. [Google Scholar]
- Wen, L.; Fan, X.; Liu, Z.; Yong, Z. The design and development of the precision planter sowing depth control system. Sens. Transducers 2014, 162, 53–58. [Google Scholar]
- Nielsen, S.; Norremark, M.; Green, O. Sensor and control for consistent seed drill coulter depth. Comput. Electron. Agric. 2016, 127, 690–698. [Google Scholar] [CrossRef]
- Pasi, S.; Timo, O. Automatic working depth control for seed drill using ISO 11783 remote control messages. Comput. Electron. Agric. 2015, 116, 30–35. [Google Scholar]
- ISO11783; Tractors and Machinery for Agriculture and Forestry-Serial Control and Communications Data Network. ISO: Geneva, Switzerland, 2002.
- Jamil, H.; Qayyum, F.; Iqbal, N.; Kim, D. Enhanced harmonics reactive power control strategy based on multilevel inverter using ML-FFNN for dynamic power load management in microgrid. Sensors 2022, 22, 6402. [Google Scholar] [CrossRef] [PubMed]
- Bruijn, F.; Gill, E. Influence of sensor and actuator errors on impulsive satellite formation control methods. Acta Astronautica 2014, 94, 608–618. [Google Scholar] [CrossRef]
- Song, Y.; Fang, X.; Wu, G.; Chen, N.; Liang, M.; Xu, Z.; Zhang, F. Research on straightness perception compensation model of FBG scraper conveyor based on rotation error angle. Sensors 2022, 22, 6399. [Google Scholar] [CrossRef]
- Zhai, C.; Yang, S.; Wang, X.; Zhang, C.; Song, J. Status and prospect of intelligent measurement and control technology for agricultural equipment. Trans. CSAM 2022, 53, 1–20. [Google Scholar]
- Ding, Y.; Liu, Z.; Chen, C.; Liu, H.; Luo, J.; Yu, H. Functional detection method of application rate based on principle of dynamic weighing. Trans. CSAM 2021, 52, 146–154. [Google Scholar]
- Wang, Q.; Cao, X.; Wang, C.; Li, H.; He, J.; Lu, C. Research progress of no/minimum tillage corn seeding technology and machine in northeast black land of China. Trans. CSAM 2021, 52, 1–15. [Google Scholar]
- Fu, G.; Yang, C.; Zhang, S.; Huang, W.; Chen, T.; Zhu, L. Research on laser and ultrasonic combined ranging method for robot navigation at banana plantation. Trans. CSAM 2021, 52, 159–168. [Google Scholar]
- Xia, J.; Li, D.; Liu, G.; Cheng, J.; Zheng, K.; Luo, C. Design and test of electro-hydraulic monitoring device for hitch tillage depth based on measurement of tractor pitch angle. Trans. CSAM 2021, 52, 386–395. [Google Scholar]
- Yang, Z.; Yan, Z.; Lu, Y.; Wang, W.; Yu, L.; Geng, Y. Double DOF strategy for continuous-wave pulse generator based on extended Kalman filter and adaptive linear active disturbance rejection control. IEEE Trans. Power Electron. 2022, 37, 1382–1393. [Google Scholar] [CrossRef]
- Oehler, F.; Nurnberger, K.; Sturm, J.; Jossen, A. Embedded real-time state observer implementation for lithium-ion cells using an electrochemical model and extended Kalman filter. J. Power Sources 2022, 525, 231018. [Google Scholar] [CrossRef]
- Hoshiya, M.; Saito, E. Structural identification by extended Kalman filter. J. Eng. Mech. 1984, 110, 1757–1770. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Li, M.; Xu, R.; Yang, Z.; Hong, W.; An, X.; Yi, H. Optimization approach of berth-quay crane-truck allocation by the tide, environment and uncertainty factors based on chaos quantum adaptive seagull optimization algorithm. J. Appl. Soft Comput. 2024, 152, 111197. [Google Scholar] [CrossRef]
- Ahmed, M.; Kamel, S.; Abbasy, N.; Abouelseoud, Y. A Gaussian random walk salp swarm algorithm for optimal dynamic charging of electric vehicles. Appl. Soft Comput. 2023, 147, 110838. [Google Scholar] [CrossRef]
- NY/T1143-2006; Technical Specification for Quality Evaluation of Sowing Machines. National Standard of the People’s Republic of China: Beijing, China, 2006.








| Sensor Type | Main Parameters | Parameter Value |
|---|---|---|
| Laser sensor | Measurement accuracy/mm | 0.5 |
| Measurement range/m | 0.05~80 | |
| Spot size/mm | 6 | |
| Ultrasonic sensor | Beam angle/(°) | 10 |
| Sensing range/cm | 7~100 | |
| Measurement blindness/cm | 0~7 | |
| Angle sensor | Measurement resolution/(°) | 0.01 |
| Measurement accuracy/(°) | 0.05 | |
| Measuring range/(°) | ±90 |
| Data Source | Key Performance Evaluation Parameters | ||
|---|---|---|---|
| MAE/cm | RMSE/cm | R | |
| Laser sensor | 0.154 | 0.179 | 0.943 |
| Ultrasonic sensor | 0.169 | 0.195 | 0.930 |
| Angle sensor | 0.147 | 0.169 | 0.945 |
| Data Source | Key Performance Evaluation Parameters | ||
|---|---|---|---|
| MAE/cm | RMSE/cm | R | |
| Laser sensor + KF | 0.148 | 0.172 | 0.944 |
| Ultrasonic sensor + KF | 0.162 | 0.188 | 0.932 |
| Angle sensor + KF | 0.143 | 0.166 | 0.946 |
| SSA-EKF | 0.096 | 0.120 | 0.971 |
| ISSA-EKF | 0.083 | 0.103 | 0.979 |
| Optimisation Algorithm | Key Parameters | Number of Iterations | Fitness | |||
|---|---|---|---|---|---|---|
| Qσ | Rσ1 | Rσ2 | Rσ3 | |||
| SSA | 395 | 68 | 60 | 0.03 | 20 | 0.120 |
| ISSA | 6400 | 2057 | 1705 | 4 | 92 | 0.103 |
| Theoretical Sowing Depth/cm | Data Source | Key Performance Evaluation Parameters | ||
|---|---|---|---|---|
| MAE/cm | RMSE/cm | R | ||
| 3 | Laser sensor | 0.152 | 0.175 | 0.943 |
| Ultrasonic sensor | 0.166 | 0.189 | 0.934 | |
| Angle sensor | 0.139 | 0.159 | 0.953 | |
| ISSA-EKF | 0.082 | 0.103 | 0.979 | |
| 5 | Laser sensor | 0.154 | 0.178 | 0.948 |
| Ultrasonic sensor | 0.164 | 0.188 | 0.936 | |
| Angle sensor | 0.137 | 0.158 | 0.955 | |
| ISSA-EKF | 0.080 | 0.097 | 0.982 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yi, S.; Zhao, B.; Li, Y.; Li, S.; Tao, G.; Mao, X.; Sun, W. Sowing Depth Monitoring System for High-Speed Precision Planters Based on Multi-Sensor Data Fusion. Sensors 2024, 24, 6331. https://doi.org/10.3390/s24196331
Wang S, Yi S, Zhao B, Li Y, Li S, Tao G, Mao X, Sun W. Sowing Depth Monitoring System for High-Speed Precision Planters Based on Multi-Sensor Data Fusion. Sensors. 2024; 24(19):6331. https://doi.org/10.3390/s24196331
Chicago/Turabian StyleWang, Song, Shujuan Yi, Bin Zhao, Yifei Li, Shuaifei Li, Guixiang Tao, Xin Mao, and Wensheng Sun. 2024. "Sowing Depth Monitoring System for High-Speed Precision Planters Based on Multi-Sensor Data Fusion" Sensors 24, no. 19: 6331. https://doi.org/10.3390/s24196331
APA StyleWang, S., Yi, S., Zhao, B., Li, Y., Li, S., Tao, G., Mao, X., & Sun, W. (2024). Sowing Depth Monitoring System for High-Speed Precision Planters Based on Multi-Sensor Data Fusion. Sensors, 24(19), 6331. https://doi.org/10.3390/s24196331







