Nonprehensile Manipulation for Rapid Object Spinning via Multisensory Learning from Demonstration
Abstract
:1. Introduction
- (1)
- In order to realize more agile and fast nonprehensile manipulation, in this paper, we propose a systematic way to generate reliable and efficient reference trajectories through LfD. This is in contrast to conventional approaches where desired motion profiles are obtained from mathematical models of the manipulator and the target object.
- (2)
- We make explicit use of multimodal sensory data (i.e., vision, force, and position data) for both LfD (i.e., reference trajectory generation) and motion control processes. Compared to approaches based only on positional signal, our strategy can be particularly useful for nonprehensile manipulation involving impulsive actions such as the one considered in this paper.
2. Related Works
3. Background
3.1. Gaussian Mixture Model
- E step:
3.2. Gaussian Mixture Regression
3.3. Dynamic Time Warping
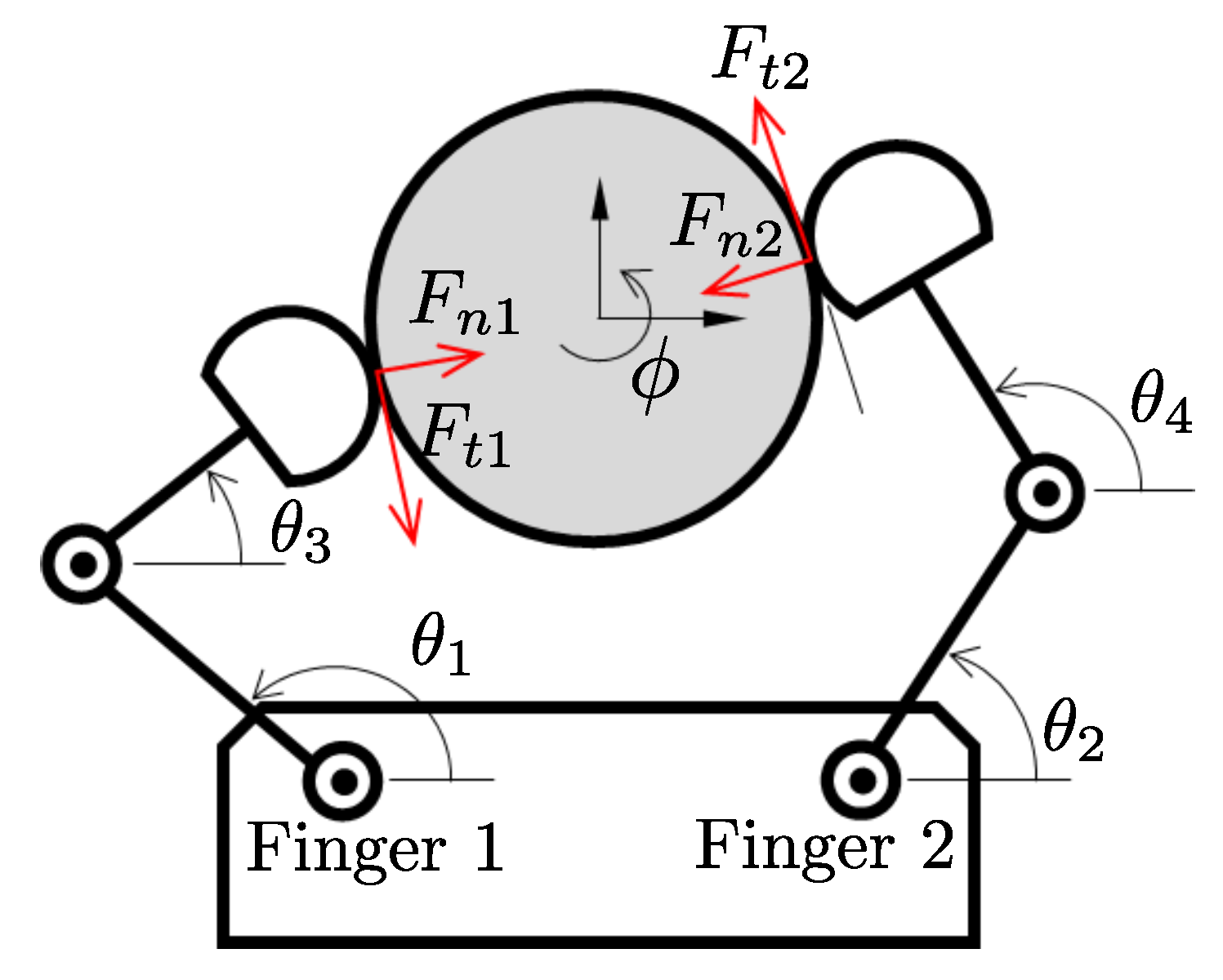
4. Methods and Approach
4.1. System Overview
4.2. Multisensory Learning from Demonstration
4.2.1. Data Collection
4.2.2. Data Preprocessing for Temporal Alignment
4.2.3. Trajectory Modeling and Reproduction
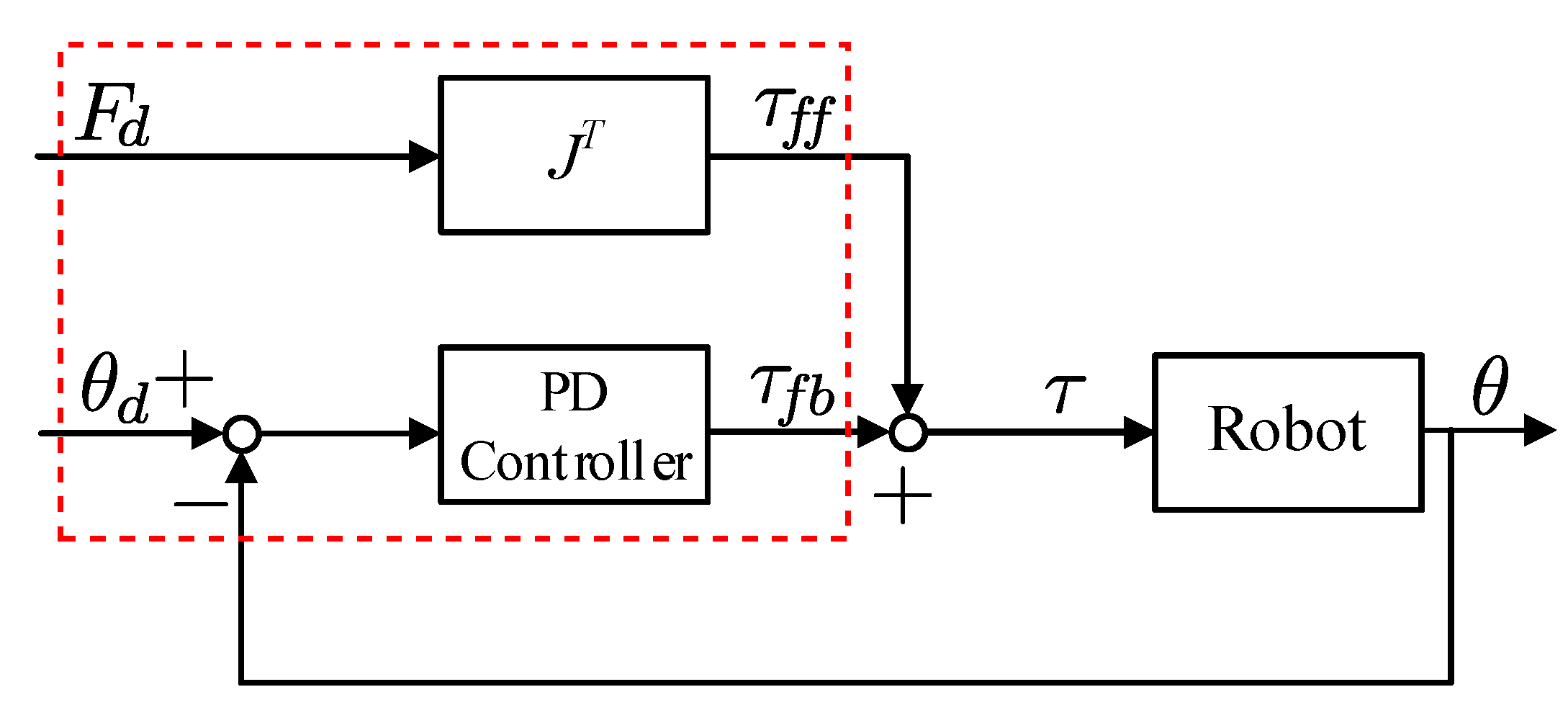
4.3. Motion Control with Multisensory GMR Trajectories
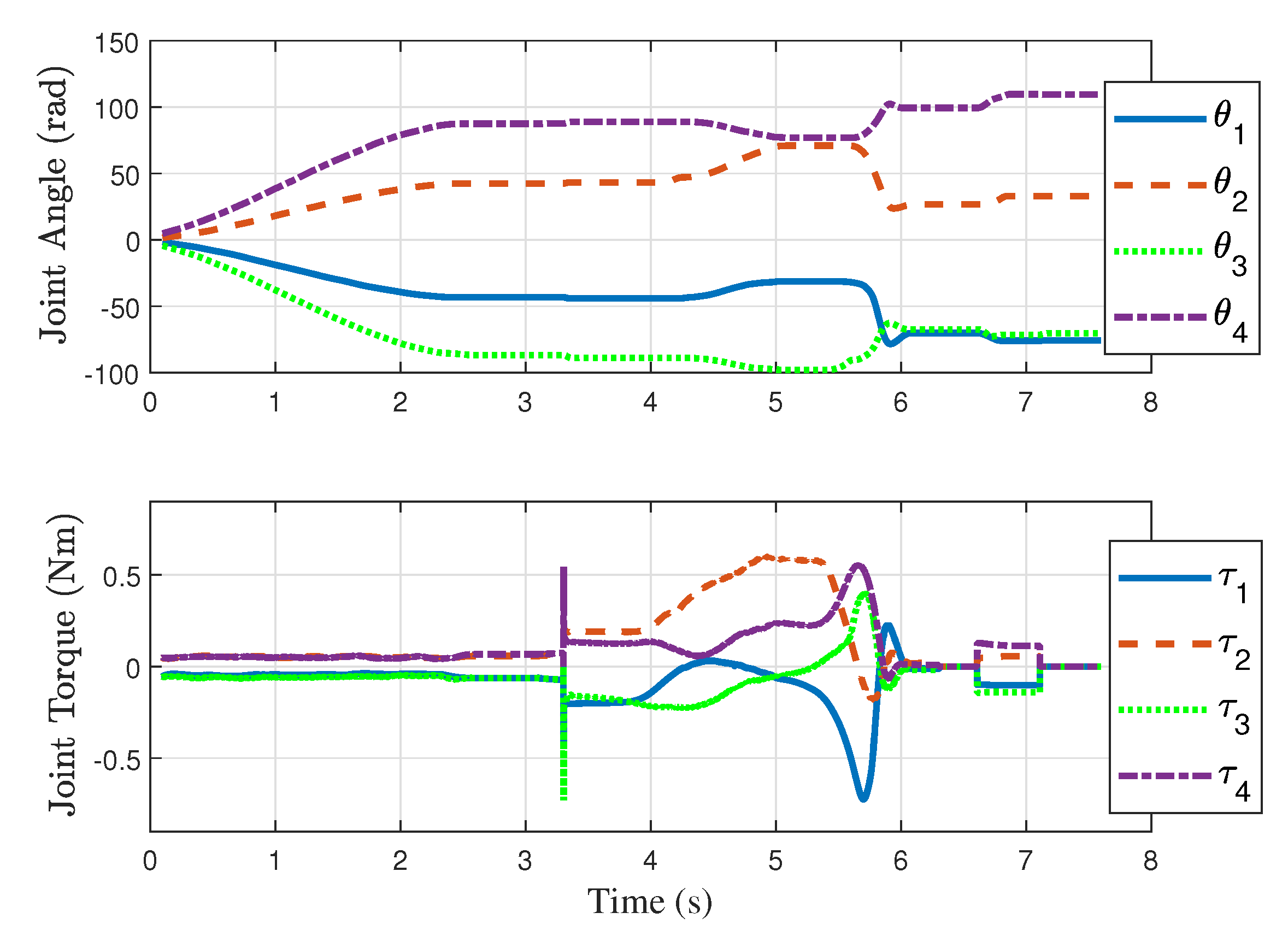
5. Experimental Results
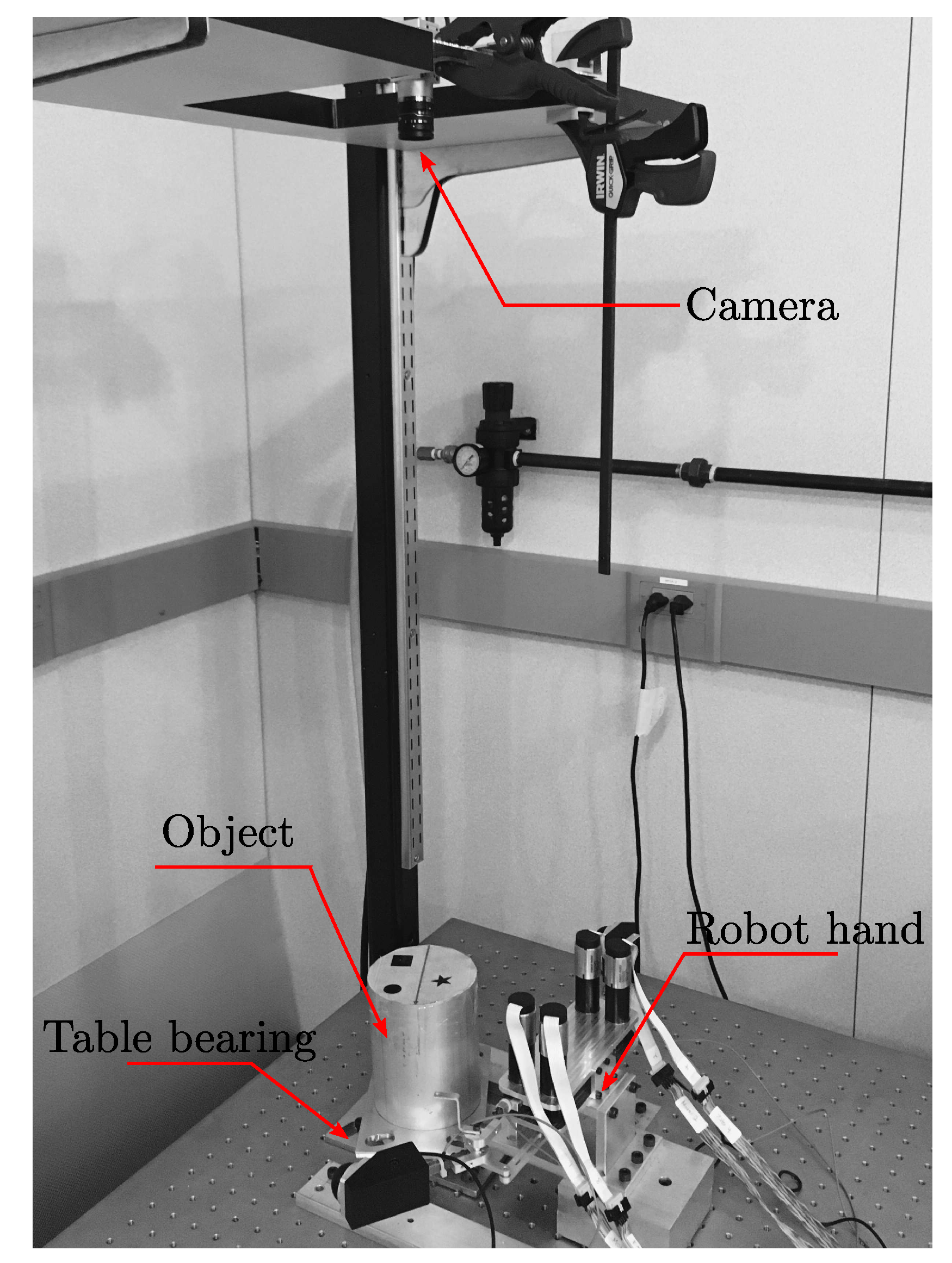
5.1. Experimental Setup
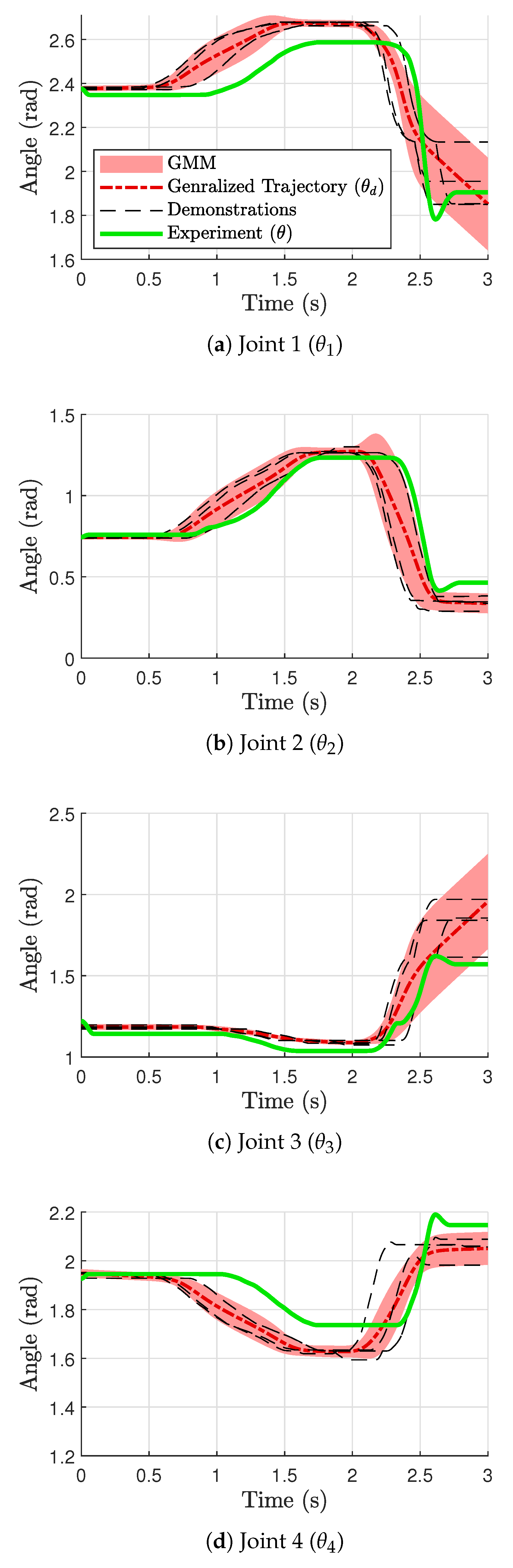
5.2. Experimental Results
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okamura, A.M.; Smaby, N.; Cutkosky, M.R. An overview of dexterous manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Francisco, CA, USA, 24–28 April 2000; pp. 255–262. [Google Scholar]
- Christensen, H.; Amato, N.; Yanco, H.; Mataric, M.; Choset, H.; Drobnis, A.; Goldberg, K.; Grizzle, J.; Hager, G.; Hollerbach, J.; et al. A roadmap for us robotics–from internet to robotics 2020 edition. Found. Trends® Robot. 2021, 8, 307–424. [Google Scholar] [CrossRef]
- Zhou, C.; Long, Y.; Shi, L.; Zhao, L.; Zheng, Y. Differential Dynamic Programming based Hybrid Manipulation Strategy for Dynamic Grasping. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar]
- Bai, Y.; Liu, C.K. Dexterous manipulation using both palm and fingers. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1560–1565. [Google Scholar]
- Xie, J.; Chakraborty, N. Rigid body dynamic simulation with line and surface contact. In Proceedings of the IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), San Francisco, CA, USA, 13–16 December 2016; pp. 9–15. [Google Scholar]
- Bicchi, A. On the Closure Properties of Robotic Grasping. Int. J. Robot. Res. 1995, 14, 319–334. [Google Scholar] [CrossRef]
- Imtiaz, M.B.; Qiao, Y.; Lee, B. Prehensile and non-prehensile robotic pick-and-place of objects in clutter using deep reinforcement learning. Sensors 2023, 23, 1513. [Google Scholar] [CrossRef]
- Lynch, K.M.; Mason, M.T. Dynamic Nonprehensile Manipulation: Controllability, Planning, and Experiments. Int. J. Robot. Res. 1999, 18, 64–92. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Siciliano, B. Nonprehensile Dynamic Manipulation: A Survey. IEEE Robot. Autom. Lett. 2018, 3, 1711–1718. [Google Scholar] [CrossRef]
- Bätz, G.; Yaqub, A.; Wu, H.; Kühnlenz, K.; Wollherr, D.; Buss, M. Dynamic manipulation: Nonprehensile ball catching. In Proceedings of the Mediterranean Conference on Control and Automation (MED), Marrakech, Morocco, 23–25 June 2010; pp. 365–370. [Google Scholar]
- Erdmann, M. An Exploration of Nonprehensile Two-Palm Manipulation: Planning and Execution. In Proceedings of the Robotics Research, Minneapolis, MN, USA, 22–28 April 1996; Giralt, G., Hirzinger, G., Eds.; Springer: London, UK, 1996; pp. 16–27. [Google Scholar]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.; Hudspeth, A. Principles of Neural Science; McGraw Hill: New York, NY, USA, 2000. [Google Scholar]
- Krakauer, J.W.; Mazzoni, P. Human sensorimotor learning: Adaptation, skill, and beyond. Curr. Opin. Neurobiol. 2011, 21, 636–644. [Google Scholar] [CrossRef] [PubMed]
- Correia, A.; Alexandre, L.A. A Survey of Demonstration Learning. arXiv 2023, arXiv:2303.11191. [Google Scholar]
- Kana, S.; Gurnani, J.; Ramanathan, V.; Ariffin, M.Z.; Turlapati, S.H.; Campolo, D. Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation. Sensors 2023, 23, 8721. [Google Scholar] [CrossRef] [PubMed]
- Calinon, S. Robot Programming by Demonstration—A Probabilistic Approach; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Jeon, S. State estimation based on kinematic models considering characteristics of sensors. In Proceedings of the American Control Conference (ACC), Baltimore, ML, USA, 30 June–2 July 2010; pp. 640–645. [Google Scholar]
- Tomizuka, H.M.; Cheng, C.C.W. Sensing rich drive trains for modern mechatronic systems: First year progress report. In Proceedings of the SPIE, San Diego, CA, USA, 10–13 March 2007; Volume 6529. [Google Scholar]
- Salisbury, J.K., Jr. Recent Advances in Robotics; Chapter Kinematic and Force Analysis of Articulated Hands; John Wiley & Sons, Inc.: New York, NY, USA, 1985; pp. 131–174. [Google Scholar]
- Bicchi, A.; Kumar, V. Robotic grasping and contact: A review. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 348–353. [Google Scholar]
- Bicchi, A. Hands for dexterous manipulation and robust grasping: A difficult road toward simplicity. IEEE Trans. Robot. Autom. 2000, 16, 652–662. [Google Scholar] [CrossRef]
- Murray, R.M.; Sastry, S.S.; Zexiang, L. A Mathematical Introduction to Robotic Manipulation, 1st ed.; CRC Press, Inc.: Boca Raton, FL, USA, 1994. [Google Scholar]
- Stoeter, S.A.; Voss, S.; Papanikolopoulos, N.P.; Mosemann, H. Planning of regrasp operations. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 245–250. [Google Scholar]
- Ma, R.R.; Dollar, A.M. On dexterity and dexterous manipulation. In Proceedings of the Int. Conf. on Advanced Robotics (ICAR), Dubai, United Arab Emirates, 12–13 December 2011; pp. 1–7. [Google Scholar]
- Cole, A.A.; Hsu, P.; Sastry, S.S. Dynamic control of sliding by robot hands for regrasping. IEEE Trans. Robot. Autom. 1992, 8, 42–52. [Google Scholar] [CrossRef]
- Rizzi, A.A.; Koditschek, D.E. An active visual estimator for dexterous manipulation. IEEE Trans. Robot. Autom. 1996, 12, 697–713. [Google Scholar] [CrossRef]
- Yousef, H.; Boukallel, M.; Althoefer, K. Tactile sensing for dexterous in-hand manipulation in robotics—A review. Sens. Actuators Phys. 2011, 167, 171–187. [Google Scholar] [CrossRef]
- Bae, H.; Jeon, S.; Huissoon, J.P. Vision and force/torque integration for realtime estimation of fast-moving object under intermittent contacts. ROBOMECH J. 2016, 3, 15. [Google Scholar] [CrossRef]
- van Hoof, H.; Hermans, T.; Neumann, G.; Peters, J. Learning robot in-hand manipulation with tactile features. In Proceedings of the IEEE-RAS Internatinoal Conference on Humanoid Robots (Humanoids), Seoul, Republic of Korea, 3–5 November 2015; pp. 121–127. [Google Scholar]
- Li, M.; Bekiroglu, Y.; Kragic, D.; Billard, A. Learning of grasp adaptation through experience and tactile sensing. In Proceedings of the IEEE/RSJ Internatinoal Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 3339–3346. [Google Scholar]
- Maekawa, H.; Tanie, K.; Komoriya, K. Tactile sensor based manipulation of an unknown object by a multifingered hand with rolling contact. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Nagoya, Japan, 21–27 May 1995; Volume 1, pp. 743–750. [Google Scholar]
- Allen, P.K.; Miller, A.T.; Oh, P.Y.; Leibowitz, B.S. Using tactile and visual sensing with a robotic hand. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Albuquerque, NM, USA, 20–25 April 1997; Volume 1, pp. 676–681. [Google Scholar]
- Cheah, C.C.; Han, H.Y.; Kawamura, S.; Arimoto, S. Grasping and position control for multi-fingered robot hands with uncertain Jacobian matrices. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Leuven, Belgium, 16–20 May 1998; Volume 3, pp. 2403–2408. [Google Scholar]
- Calli, B.; Dollar, A.M. Vision-based precision manipulation with underactuated hands: Simple and effective solutions for dexterity. In Proceedings of the IEEE/RSJ Internatinoal Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1012–1018. [Google Scholar]
- Calinon, S.; Guenter, F.; Billard, A. On Learning, Representing, and Generalizing a Task in a Humanoid Robot. IEEE Trans. Syst. Man Cybern. Part (Cybern.) 2007, 37, 286–298. [Google Scholar] [CrossRef]
- Calinon, S.; Bruno, D.; Caldwell, D.G. A task-parameterized probabilistic model with minimal intervention control. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3339–3344. [Google Scholar]
- Deng, Z.; Mi, J.; Chen, Z.; Einig, L.; Zou, C.; Zhang, J. Learning human compliant behavior from demonstration for force-based robot manipulation. In Proceedings of the IEEE Internatinoal Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 319–324. [Google Scholar]
- Lin, Y.; Ren, S.; Clevenger, M.; Sun, Y. Learning grasping force from demonstration. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), St Paul, MI, USA, 14–18 May 2012; pp. 1526–1531. [Google Scholar]
- Lee, A.X.; Lu, H.; Gupta, A.; Levine, S.; Abbeel, P. Learning force-based manipulation of deformable objects from multiple demonstrations. In Proceedings of the IEEE Internatinoal Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 177–184. [Google Scholar]
- Rozo, L.; Bruno, D.; Calinon, S.; Caldwell, D.G. Learning optimal controllers in human-robot cooperative transportation tasks with position and force constraints. In Proceedings of the IEEE/RSJ Internatinoal Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 1024–1030. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. (Methodol.) 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Chiu, C.Y.; Chao, S.P.; Wu, M.Y.; Yang, S.N.; Lin, H.C. Content-based retrieval for human motion data. J. Vis. Commun. Image Represent. 2004, 15, 446–466. [Google Scholar] [CrossRef]
- Akgun, B.; Cakmak, M.; Yoo, J.W.; Thomaz, A.L. Trajectories and keyframes for kinesthetic teaching: A human-robot interaction perspective. In Proceedings of the ACM/IEEE Internatinoal Conference on Human-Robot Interaction (HRI), Boston, MA, USA, 5–8 March 2012; pp. 391–398. [Google Scholar]
- Shin, K.J. Nonprehensile Manipulation via Multisensory Learning from Demonstration. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2018. [Google Scholar]
- Shin, K.; Jeon, S. Video of Nonprehensile Spinning. Available online: https://youtu.be/qp-Pve0raoY (accessed on 10 December 2023).
- Shin, K.; Jeon, S. Video of Finger Gating. Available online: https://youtu.be/K-3Djf7-7KE (accessed on 10 December 2023).







| Component | Manufacturer/Model | Specification |
|---|---|---|
| Geared Motor Set | Maxon Motor (Sachseln, Switzerland) (222053, 201937, 201937) | Max speed: 9270 rpm Rated torque: 11.6 mNm Gear ratio: 84:1 Encoder resolution: 512 ppr |
| Strain Gauge | Strain Measurement Device (Wallingford, CT, USA) (S220) | Max load: 6 lbs |
| Three-Axis Force Sensor | OnRobot (Budapest, Hungary) (OMD-30-SE-100N) | Nominal capacity: 100 N ( compression), N () |
| Vision Sensor | Basler (cA2000-340km) | Resolution: 2048 px × 1088 px |
| Desired Angle | Average Final Angle | Average Time of Completion | Std. Dev. of Angle Error |
|---|---|---|---|
| 90° | 91.63° | 3.46 s | 2.007° |
| 120° | 119.4° | 3.97 s | 2.1739° |
| 180° | 182.1° | 3.77 s | 2.4612° |
| Desired Angle | Average Final Angle | Average Time of Completion | Std. Dev. of Angle Error |
|---|---|---|---|
| 90° | 91.03° | 19.520 s | 0.464° |
| 120° | 120.8° | 22.109 s | 0.355° |
| 180° | 180.4° | 35.782 s | 0.450° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, K.J.; Jeon, S. Nonprehensile Manipulation for Rapid Object Spinning via Multisensory Learning from Demonstration. Sensors 2024, 24, 380. https://doi.org/10.3390/s24020380
Shin KJ, Jeon S. Nonprehensile Manipulation for Rapid Object Spinning via Multisensory Learning from Demonstration. Sensors. 2024; 24(2):380. https://doi.org/10.3390/s24020380
Chicago/Turabian StyleShin, Ku Jin, and Soo Jeon. 2024. "Nonprehensile Manipulation for Rapid Object Spinning via Multisensory Learning from Demonstration" Sensors 24, no. 2: 380. https://doi.org/10.3390/s24020380
APA StyleShin, K. J., & Jeon, S. (2024). Nonprehensile Manipulation for Rapid Object Spinning via Multisensory Learning from Demonstration. Sensors, 24(2), 380. https://doi.org/10.3390/s24020380






