Non-Contact Current Measurement for Three-Phase Rectangular Busbars Using TMR Sensors
Abstract
:1. Introduction
2. Method
2.1. The Relationship between the Three-Phase Currents and the Measured Magnetic Fields
2.2. Determination of the Coefficient Matrix [Kf]
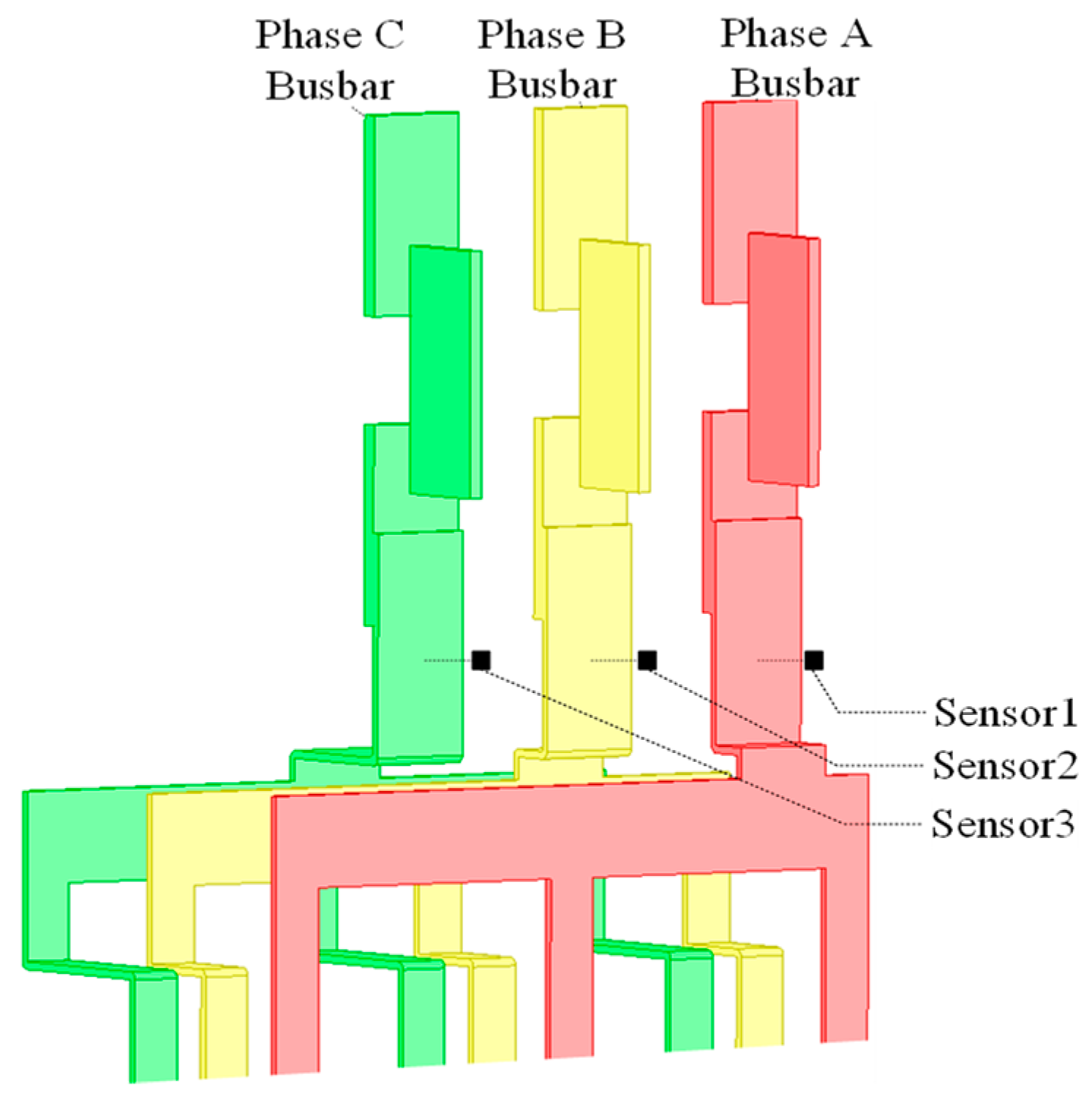
3. Sensor Position Optimization
4. Circuit Design
4.1. Current Measurement Circuit
4.2. Calibrator Circuit
5. Results and Discussions
5.1. Sensor Calibration
5.2. Current Measurement
5.3. Non-Linearity Evaluation of the Developed Current Sensor
5.4. Harmonic Interference and Noise Immunity Test
5.5. Error Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brandolini, A.; Faifer, M.; Ottoboni, R. A simple method for the calibration of traditional and electronic measurement current and voltage transformers. IEEE Trans. Instrum. Meas. 2009, 58, 1345–1353. [Google Scholar] [CrossRef]
- Emanuel, A.; Orr, J. Current harmonics measurement by means of current transformers. IEEE Trans. Power Deliv. 2007, 22, 1318–1325. [Google Scholar] [CrossRef]
- Li, X.; Qin, S.; Xiao, D. Technical analysis of the application of photoelectric transformer in extra-high voltage power grid. High Volt. Technol. 2007, 33, 13–15. [Google Scholar]
- Jogschies, L.; Klaas, D.; Kruppe, R.; Rittinger, J.; Taptimthong, P.; Wienecke, A.; Rissing, L.; Wurz, M.C. Recent Developments of Magnetoresistive Sensors for Industrial Applications. Sensors 2015, 15, 28665–28689. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Liu, X.; Philip, W.P. Performance study on commercial magnetic sensors for measuring current of unmanned aerial vehicles. IEEE Trans. Instrum. Meas. 2019, 69, 1397–1407. [Google Scholar] [CrossRef]
- Xu, X.; Liu, T.; Zhu, M.; Wang, J. New small-volume high-precision TMR busbar DC current sensor. IEEE Trans. Magn. 2020, 56, 4000105. [Google Scholar] [CrossRef]
- Qian, S.; Deng, H.; Chen, C.; Huang, H.; Liang, Y.; Guo, J.; Hu, Z. Design of a Nonintrusive Current Sensor with Large Dynamic Range Based on Tunneling Magnetoresistive Devices. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; IEEE: New York City, NY, USA, 2022; pp. 3405–3409. [Google Scholar]
- Shao, S.; Yu, N.; Xu, X.; Bai, J.; Wu, X.; Zhang, J. Tunnel magnetoresistance-based short-circuit and over-current protection for IGBT module. IEEE Trans. Power Electron. 2020, 35, 10930–10944. [Google Scholar] [CrossRef]
- Li, P.; Tian, B.; Li, L.; Wang, Z.; Lv, Q.; Zhou, K.; Xu, C.; Liu, Z.; Yin, X.; Zhang, J. A Contactless Current Sensor Based on TMR Chips. IEEE Trans. Instrum. Meas. 2022, 71, 9511711. [Google Scholar] [CrossRef]
- Qian, S.; Guo, J.; Huang, H.; Chen, C.; Wang, H.; Li, Y. Measurement of Small-Magnitude Direct Current Mixed With Alternating Current by Tunneling Magnetoresistive Sensor. IEEE Sens. Lett. 2022, 6, 5501004. [Google Scholar] [CrossRef]
- Xie, F.; Roland, W.; Robert, W. Improved mathematical operations based calibration method for giant magnetoresistive current sensor applying B-Spline modeling. Sens. Actuators A Phys. 2017, 254, 109–115. [Google Scholar] [CrossRef]
- Wang, H.; Guo, H.; Wang, Y. Development of current sensor based on TMR element. Electr. Meas. Instrum. 2018, 55, 103–107. [Google Scholar]
- Ma, X.; Guo, Y.; Chen, X.; Xiang, Y.; Chen, K. Impact of Coreless Current Transformer Position on Current Measurement. IEEE Trans. Instrum. Meas. 2019, 68, 3801–3809. [Google Scholar] [CrossRef]
- Xu, X.; Liu, T.; Zhu, M.; Wang, J. Nonintrusive Installation of the TMR Busbar DC Current Sensor. J. Sens. 2021, 2021, 8827131. [Google Scholar] [CrossRef]
- Xu, X.; Wang, S.; Liu, T.; Zhu, M.; Wang, J. TMR busbar current sensor with good frequency characteristics. IEEE Trans. Instrum. Meas. 2021, 70, 1504109. [Google Scholar] [CrossRef]
- Zhang, H.; Li, F.; Guo, H.; Yang, Z.; Yu, N. Current Measurement with 3-D coreless TMR Sensor Array for Inclined Conductor. IEEE Sens. J. 2019, 19, 6684–6690. [Google Scholar] [CrossRef]
- Liu, X.; He, W.; Guo, P.; Guo, T.; Xu, Z. Semi-Contactless Power Measurement Method for Single-Phase Enclosed Two-Wire Residential Entrance Lines. IEEE Trans. Instrum. Meas. 2022, 71, 9508216. [Google Scholar] [CrossRef]
- Gao, P.; Lin, S.; Xu, W. A Novel Current Sensor for Home Energy Use Monitoring. IEEE Trans. Smart Grid 2014, 5, 2021–2028. [Google Scholar] [CrossRef]
- IEC 61730-1; Photovoltaic (PV) Module Safety Qualification—Part 1: Requirements for Construction. IEC: Geneva, Switzerland, 2004.
- TMR2104—Magnetic Field Sensors—Sensors—Multi-Dimension Technology, The Leading Supplier of TMR Magnetic Sensors—MultiDimension Technology. Available online: http://www.dowaytech.com/en/1800.html (accessed on 1 November 2023).
- Bernieri, A.; Ferrigno, L.; Laracca, M.; Rasile, A. An AMR-Based Three-Phase Current Sensor for Smart Grid Applications. IEEE Sens. J. 2017, 17, 7704–7712. [Google Scholar] [CrossRef]














| Distance (cm) | 12 | 9 | 6 | 3 |
|---|---|---|---|---|
| Amplitude of harmonic component at150 Hz (A) | 0.256 | 0.201 | 0.145 | 0.478 |
| Relative Error (%) | −20.9 | −40.0 | −56.7 | 42.68 |
| Distance (cm) | 12 | 9 | 6 | 3 |
|---|---|---|---|---|
| Amplitude of fundamental component (A) | 14.83 | 14.91 | 15.16 | 15.57 |
| Relative error (%) | 0.54 | 1.08 | 2.78 | 5.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Li, H.; Liang, W.; Shen, C.; Xu, Z. Non-Contact Current Measurement for Three-Phase Rectangular Busbars Using TMR Sensors. Sensors 2024, 24, 388. https://doi.org/10.3390/s24020388
Su H, Li H, Liang W, Shen C, Xu Z. Non-Contact Current Measurement for Three-Phase Rectangular Busbars Using TMR Sensors. Sensors. 2024; 24(2):388. https://doi.org/10.3390/s24020388
Chicago/Turabian StyleSu, Huafeng, Haojun Li, Weihao Liang, Chaolan Shen, and Zheng Xu. 2024. "Non-Contact Current Measurement for Three-Phase Rectangular Busbars Using TMR Sensors" Sensors 24, no. 2: 388. https://doi.org/10.3390/s24020388
APA StyleSu, H., Li, H., Liang, W., Shen, C., & Xu, Z. (2024). Non-Contact Current Measurement for Three-Phase Rectangular Busbars Using TMR Sensors. Sensors, 24(2), 388. https://doi.org/10.3390/s24020388







