Comparison of Shoulder Range of Motion Quantified with Mobile Phone Video-Based Skeletal Tracking and 3D Motion Capture—Preliminary Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
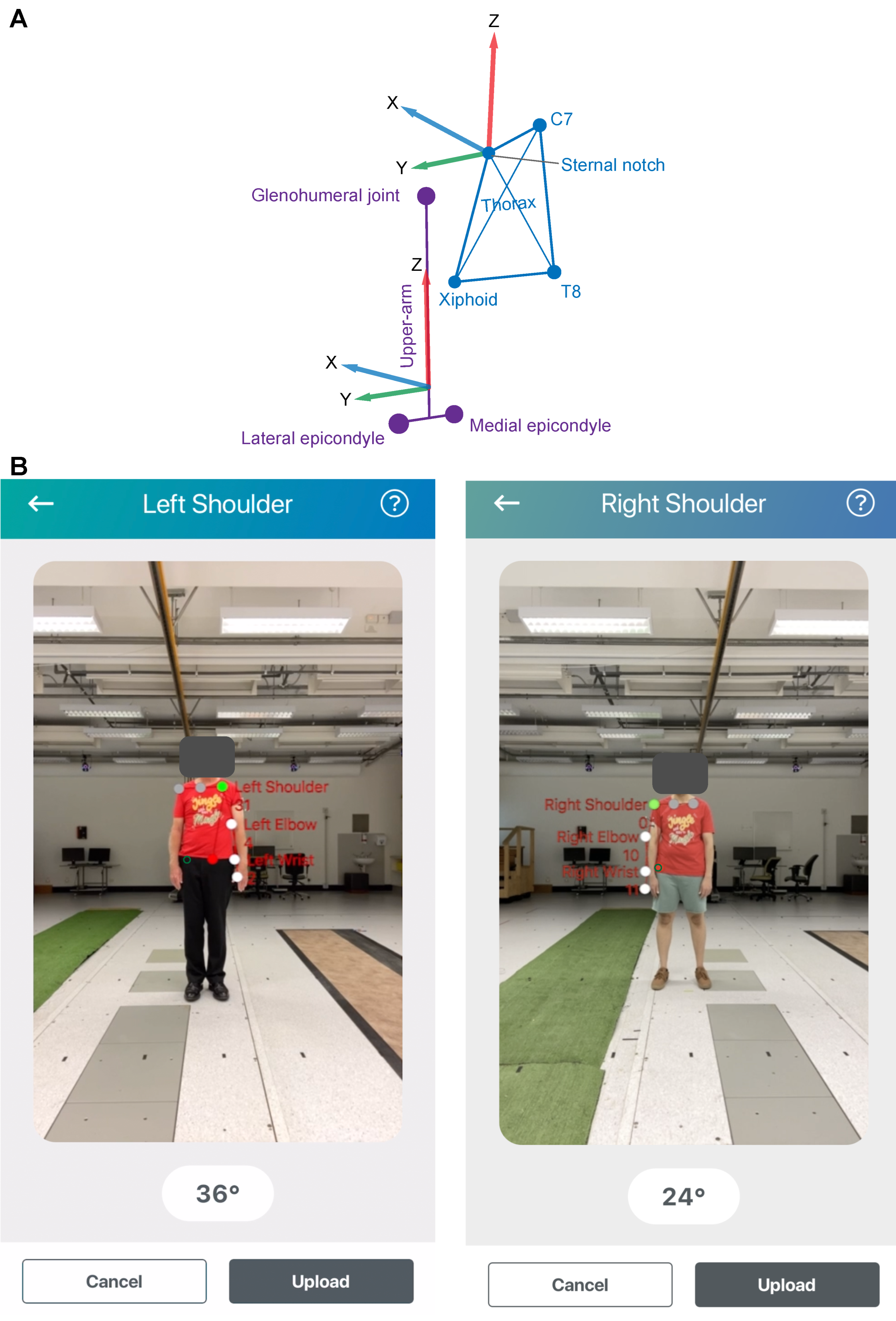
2.2. Experimental Setup
2.3. Data Collection
2.4. Data Analysis
2.5. Statistics
3. Results
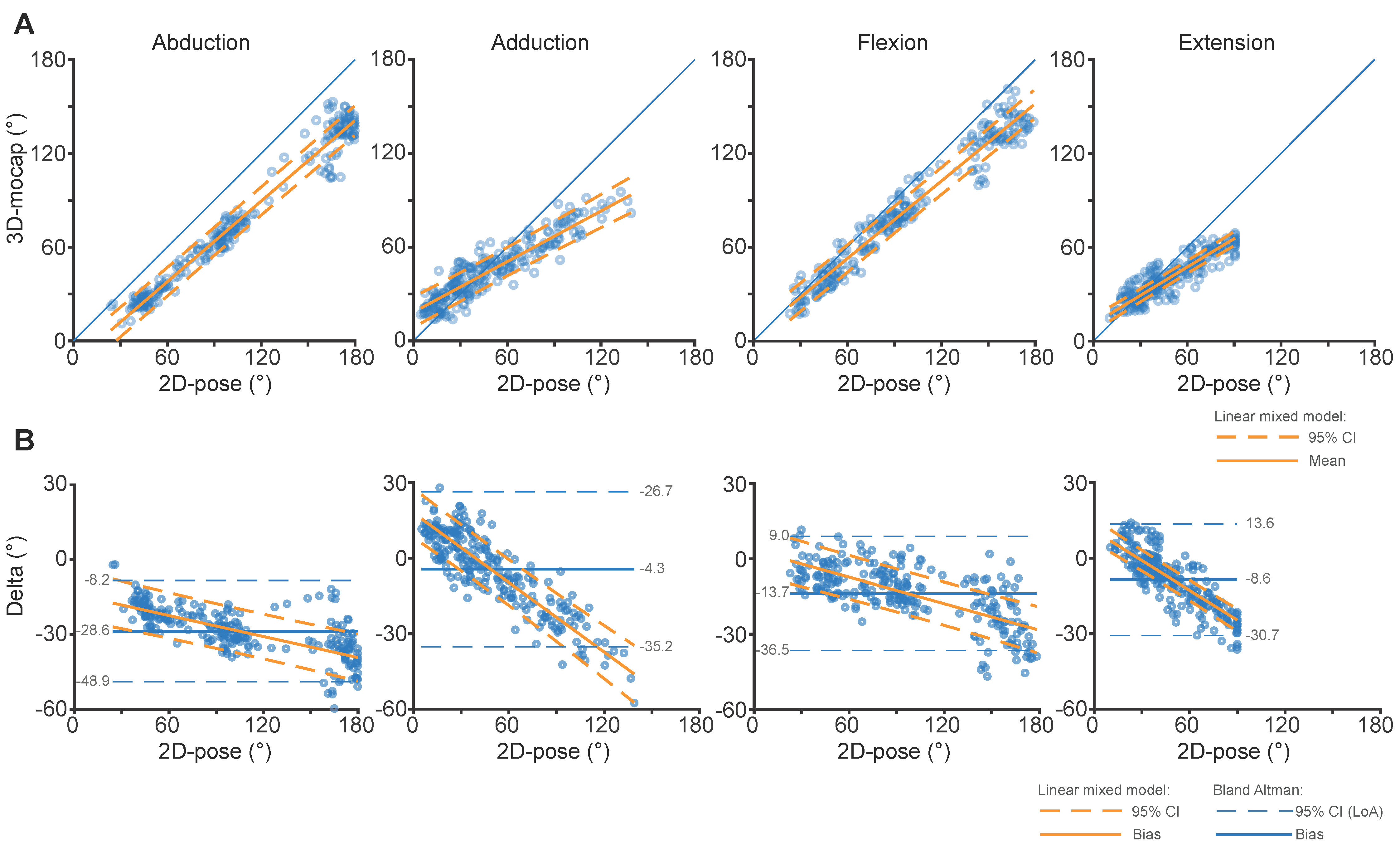
3.1. Comparison between 2D-Pose and 3D Motion Capture (ISB-Based Euler Decomposition): Consistency
3.2. Comparison between 2D-Pose and 3D Motion Capture (ISB-Based Euler Decomposition): Agreement
3.3. Comparison between 2D-Pose and 2D View of 3D Motion Capture
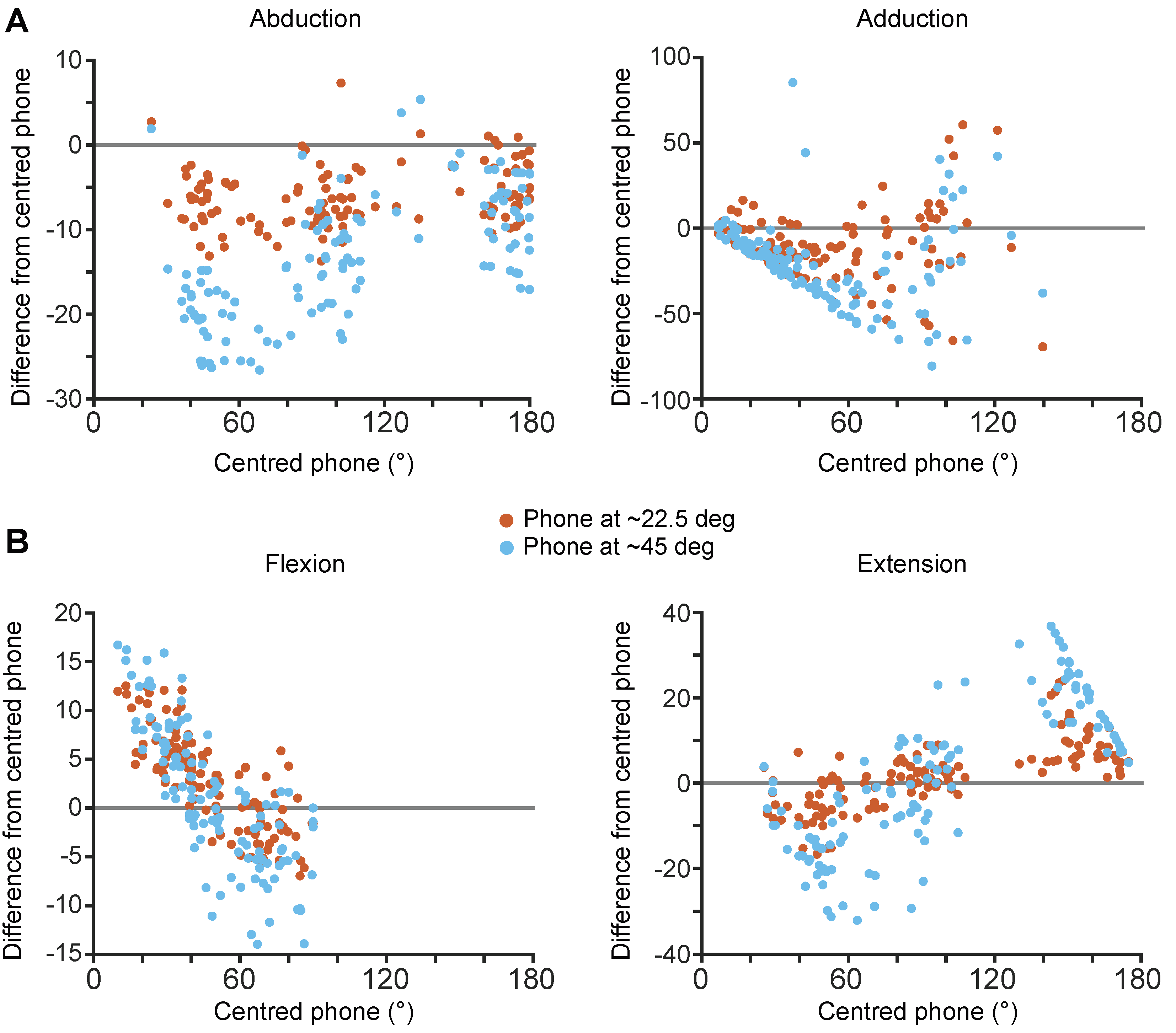
3.4. Impact of Out-of-Plane Movements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. iPhone’s Pitch Angle Correction
Appendix A.2. iPhone’s Heading Angle Correction
Appendix B
| 2D-Pose vs. 2D-View of 3D-Mocap | |||||
|---|---|---|---|---|---|
| Movement | Intercept (95% CI) | p-Value | Coeff (95% CI) | p-Value | Adjusted R2 |
| Abduction | −19.4 (−22.0, −16.7) | <0.001 | 0.983 (0.966, 1.01) | <0.001 | 0.98 |
| Adduction | 10.0 (6.3, 13.8) | <0.001 | 0.549 (0.512, 0.586) | <0.001 | 0.85 |
| Flexion | 3.36 (0.25, 6.46) | 0.034 | 0.837 (0.822, 0.851) | <0.001 | 0.98 |
| Extension | 6.30 (3.85, 8.74) | <0.001 | 0.673 (0.652, 0.693) | <0.001 | 0.96 |
| Agreement | |||||
| Abduction | −19.4 (−22.0, −16.7) | <0.001 | −0.017 (−0.034, −0.01) | 0.062 | 0.52 |
| Adduction | 10.0 (6.3, 13.8) | <0.001 | −0.451 (−0.488, −0.414) | <0.001 | 0.80 |
| Flexion | 3.36 (0.25, 6.46) | 0.034 | −0.163 (−0.178, −0.149) | <0.001 | 0.76 |
| Extension | 6.30 (3.85, 8.74) | <0.001 | −0.327 (−0.348, −0.307) | <0.001 | 0.92 |
Appendix C
Comparison between 2D-Pose and 3D-Mocap Using Alternative Cardan Decomposition Sequences

| 2D-Pose vs. 2D-View of 3D-Mocap | |||||
|---|---|---|---|---|---|
| Movement | Intercept (95% CI) | p-Value | Coeff (95% CI) | p-Value | Adjusted R2 |
| Abduction | −1.5 (−6.4, 3.3) | 0.534 | B1: 0.491 (0.398, 0.584) | <0.001 | 0.99 |
| B2: 0.0023 (0.0019, 0.0027) | <0.001 | ||||
| Adduction | 5.9 (0.8, 11.0) | 0.024 | 0.220 (0.180, 0.260) | <0.001 | 0.66 |
| Flexion | −1.6 (−4.7, 1.6) | 0.336 | 0.892 (0.878, 0.906) | <0.001 | 0.98 |
| Extension | 11.2 (8.8, 13.5) | <0.001 | 0.571 (0.553, 0.589) | <0.001 | 0.96 |
| Agreement | |||||
| Abduction | −1.5 (−6.4, 3.3) | 0.534 | B1: −0.509 (−0.602, −0.416) | <0.001 | 0.55 |
| B2: 0.0023 (0.0019, 0.0027) | <0.001 | ||||
| Adduction | 5.9 (0.8, 11.0 | 0.024 | −0.780 (−0.820, −0.738) | <0.001 | 0.92 |
| Flexion | −1.6 (−4.7, 1.6) | 0.336 | −0.108 (−0.122, −0.094) | <0.001 | 0.72 |
| Extension | 11.2 (8.8, 13.5) | <0.001 | −0.429 (−0.447, −0.411) | <0.001 | 0.96 |
References
- Pope, D.P.; Croft, P.R.; Pritchard, C.M.; Silman, A.J. Prevalence of shoulder pain in the community: The influence of case definition. Ann. Rheum. Dis. 1997, 56, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Constant, C.R.; Murley, A.H. A clinical method of functional assessment of the shoulder. Clin. Orthop. Relat. Res. 1987, 214, 160–164. [Google Scholar] [CrossRef]
- Riddle, D.L.; Rothstein, J.M.; Lamb, R.L. Goniometric reliability in a clinical setting. Shoulder measurements. Phys. Ther. 1987, 67, 668–673. [Google Scholar] [CrossRef] [PubMed]
- van de Pol, R.J.; van Trijffel, E.; Lucas, C. Inter-rater reliability for measurement of passive physiological range of motion of upper extremity joints is better if instruments are used: A systematic review. J. Physiother. 2010, 56, 7–17. [Google Scholar] [CrossRef]
- Terwee, C.B.; de Winter, A.F.; Scholten, R.J.; Jans, M.P.; Deville, W.; van Schaardenburg, D.; Bouter, L.M. Interobserver reproducibility of the visual estimation of range of motion of the shoulder. Arch. Phys. Med. Rehabil. 2005, 86, 1356–1361. [Google Scholar] [CrossRef] [PubMed]
- Gorce, P.; Jacquier-Bret, J. Three-month work-related musculoskeletal disorders assessment during manual lymphatic drainage in physiotherapists using Generic Postures notion. J. Occup. Health 2023, 65, e12420. [Google Scholar] [CrossRef] [PubMed]
- Ke-Li, C.; Ruo-Feng, T.; Min, T.; Jing-Ye, Q.; Sarkis, M. Parametric Human Body Reconstruction Based on Sparse Key Points. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2467–2479. [Google Scholar]
- Qiao, S.; Wang, Y.; Li, J. Real-time human gesture grading based on OpenPose. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–6. [Google Scholar]
- Apple Detecting Human Body Poses in Images. Available online: https://developer.apple.com/documentation/vision/detecting_human_body_poses_in_images (accessed on 3 February 2022).
- Kingma, I.; de Looze, M.P.; van Dieen, J.H.; Toussaint, H.M.; Adams, M.A.; Baten, C.T.M. 2D Analysis of 3D Lifting: How Far can we go. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2000, 44, 601–604. [Google Scholar] [CrossRef]
- Ota, M.; Tateuchi, H.; Hashiguchi, T.; Kato, T.; Ogino, Y.; Yamagata, M.; Ichihashi, N. Verification of reliability and validity of motion analysis systems during bilateral squat using human pose tracking algorithm. Gait Posture 2020, 80, 62–67. [Google Scholar] [CrossRef]
- Ota, M.; Tateuchi, H.; Hashiguchi, T.; Ichihashi, N. Verification of validity of gait analysis systems during treadmill walking and running using human pose tracking algorithm. Gait Posture 2021, 85, 290–297. [Google Scholar] [CrossRef]
- Zhu, Q.; Fan, J.; Gu, F.; Lv, L.; Zhang, Z.; Zhu, C.; Qi, J. Validation of a Human Pose Tracking Algorithm for Measuring Upper Limb Joints: Comparison With Photography-based Goniometry. Res. Sq. 2022, 23, 1–10. [Google Scholar] [CrossRef]
- Wu, G.; Helm, F.C.T.v.d.; Veeger, H.E.J.; Makhsous, M.; Roy, P.V.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Warner, M.B.; Chappell, P.H.; Stokes, M.J. Measurement of dynamic scapular kinematics using an acromion marker cluster to minimize skin movement artifact. J. Vis. Exp. 2015, 96, e51717. [Google Scholar] [CrossRef]
- Metzger, M.F.; Senan, N.A.F.; O’Reilly, O.M.; Lotz, J.C. Minimizing errors associated with calculating the location of the helical axis for spinal motions. J. Biomech. 2010, 43, 2822–2829. [Google Scholar] [CrossRef] [PubMed]
- Spoor, C.W.; Veldpaus, F.E. Rigid body motion calculated from spatial co-ordinates of markers. J. Biomech. 1980, 13, 391–393. [Google Scholar] [CrossRef]
- Bet-Or, Y.; van den Hoorn, W.; Johnston, V.; O’Leary, S. Reliability and Validity of an Acromion Marker Cluster for Recording Scapula Posture at End Range Clavicle Protraction, Retraction, Elevation, and Depression. J. Appl. Biomech. 2017, 33, 379–383. [Google Scholar] [CrossRef]
- Lempereur, M.; Brochard, S.; Leboeuf, F.; Remy-Neris, O. Validity and reliability of 3D marker based scapular motion analysis: A systematic review. J. Biomech. 2014, 47, 2219–2230. [Google Scholar] [CrossRef]
- Alexander, N.; Wegener, R.; Zdravkovic, V.; North, D.; Gawliczek, T.; Jost, B. Reliability of scapular kinematics estimated with three-dimensional motion analysis during shoulder elevation and flexion. Gait Posture 2018, 66, 267–272. [Google Scholar] [CrossRef]
- Renomart Standard Kitchen Benchtop Height. Available online: https://renomart.com.au/standard-dimensions-for-australian-kitchens (accessed on 7 February 2022).
- RJLiving Coffee Table Height & Size Guide. Available online: https://www.rjliving.com.au/blogs/design-tips/coffee-table-height-and-size-guide (accessed on 7 February 2022).
- Brezlin Brezlin Shelving Guidelines. Available online: http://www.brezlin.com/design/shelvingguidelines.html (accessed on 7 February 2022).
- Schreven, S.; Beek, P.J.; Smeets, J.B. Optimising filtering parameters for a 3D motion analysis system. J. Electromyogr. Kinesiol. 2015, 25, 808–814. [Google Scholar] [CrossRef]
- Marques, O. Image Processing and Computer Vision in IOS; Springer International Publishing AG: Cham, Switzerland, 2020. [Google Scholar]
- Campeau-Lecours, A.; Vu, D.S.; Schweitzer, F.; Roy, J.S. Alternative Representation of the Shoulder Orientation Based on the Tilt-and-Torsion Angles. J. Biomech. Eng. 2020, 142, 074504. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. J. R. Stat. Society. Ser. D Stat. 1983, 32, 307–317. [Google Scholar] [CrossRef]
- De Vet, H.C.W.; Terwee, C.B.; Mokkink, L.B.; Knol, D.L. Measurement in Medicine; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wilkinson, G.N.; Rogers, C.E. Symbolic Description of Factorial Models for Analysis of Variance. J. R. Stat. Society. Ser. C Appl. Stat. 1973, 22, 392–399. [Google Scholar] [CrossRef]
- Hayes, K.; Walton, J.R.; Szomor, Z.R.; Murrell, G.A. Reliability of five methods for assessing shoulder range of motion. Aust. J. Physiother. 2001, 47, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.E.; Seitz, A.L.; Leeser, M.; Sternad, D. Validity and reliability of Kinect skeleton for measuring shoulder joint angles: A feasibility study. Physiotherapy 2015, 101, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Vitali, A.; Regazzoni, D.; Rizzi, C.; Maffioletti, F. A New Approach for Medical Assessment of Patient’s Injured Shoulder. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019; Volume 1. [Google Scholar]
- Matsui, K.; Shimada, K.; Andrew, P.D. Deviation of skin marker from bone target during movement of the scapula. J. Orthop. Sci. 2006, 11, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Lavaill, M.; Martelli, S.; Kerr, G.K.; Pivonka, P. Statistical Quantification of the Effects of Marker Misplacement and Soft-Tissue Artifact on Shoulder Kinematics and Kinetics. Life 2022, 12, 819. [Google Scholar] [CrossRef] [PubMed]



| RoM | Abduction | Adduction | Flexion | Extension |
|---|---|---|---|---|
| Small | 28 (9) | 25 (10) | 40 (15) | 28 (7) |
| Medium | 67 (10) | 39 (14) | 77 (14) | 37 (8) |
| Large | 146 (16) | 57 (17) | 138 (15) | 52 (8) |
| 2D-Pose vs. 3D-Mocap | |||||
|---|---|---|---|---|---|
| Movement | Intercept (95% CI) | p-Value | Coeff (95% CI) | p-Value | Adjuster R2 |
| Abduction | −13.8 (−16.5, −11.1) | <0.001 | 0.859 (0.845, 0.873) | <0.001 | 0.98 |
| Adduction | 18.2 (15.6, 20.7) | <0.001 | 0.539 (0.514, 0.565) | <0.001 | 0.92 |
| Flexion | 3.56 (0.07, 6.65) | 0.046 | 0.824 (0.810, 0.839) | <0.001 | 0.98 |
| Extension | 10.87 (8.34, 13.39) | <0.001 | 0.606 (0.590, 0.623) | <0.001 | 0.97 |
| Agreement | |||||
| Abduction | −13.8 (−16.5, −11.1) | <0.001 | −0.141 (−0.155, −0.127) | <0.001 | 0.73 |
| Adduction | 18.2 (15.6, 20.7) | <0.001 | −0.461 (−0.486, −0.435) | <0.001 | 0.90 |
| Flexion | 3.56 (0.07, 6.65) | 0.046 | −0.176 (−0.190, −0.162) | <0.001 | 0.82 |
| Extension | 10.87 (8.34, 13.39) | <0.001 | −0.394 (−0.410, −0.378) | <0.001 | 0.96 |
| 2D-Pose vs. 3D-Mocap | |||||||
|---|---|---|---|---|---|---|---|
| Range (°) | 0 | 30 | 60 | 90 | 120 | 150 | 180 |
| Abduction | −13.8 (−23.8, −3.8) | −18.0 (−27.6, −8.5) | −22.2 (−31.4, −13.1) | −26.5 (−35.5, −17.4) | −30.7 (−39.7, −21.7) | −34.9 (−44.1, −25.7) | −39.1 (−48.7, −29.6) |
| Adduction | 18.2 (8.3, 28.0) | 4.3 (−4.9, 13.6) | −9.5 (−18.6, −0.3) | −23.3 (−32.9, −13.7) | |||
| Flexion | 3.6 (−6.2, 12.9) | −1.9 (−10.9, 7.1) | −7.2 (−15.9, 1.5) | −12.5 (−21.0, −3.9) | −17.7 −26.3, −9.1) | −23.0 (−31.9, −14.1) | −28.3 (−37.5, −19.0) |
| Extension | 10.9 (6.2, 15.6) | −0.9 (−5.1, 3.2) | −12.8 (−16.8, −8.7) | −24.6 (−29.1, −20.1) | |||
| 2D-pose vs. 2D view of 3D-Mocap | |||||||
| Range (°) | 0 | 30 | 60 | 90 | 120 | 150 | 180 |
| Abduction | −19.4 (−31.2, −7.5) | −19.9 (−31.1, −8.6) | −20.4 (−31.2, −9.5) | −20.9 (−31.5, −10.2) | −21.4 (−32.0, −10.7) | −21.9 (−32.8, −10.9) | −22.3 (−33.7, −11.0) |
| Adduction | 10.0 (−5.7, 25.8) | −3.5 (−18.6, 11.6) | −17.0 (−32.1, −1.9) | −30.6 (−46.4, −14.7) | |||
| Flexion | 3.4 (−6.9, 13.6) | −1.5 (−11.3, 8.2) | −6.4 (−15.9, 3.0) | −11.3 (−20.6, −2.0) | −16.2 (−25.6, −6.9) | −21.1 (−30.7, −11.6) | −26.0 (−36.0, −16.1) |
| Extension | 6.3 (0.6, 12.0) | −3.5 (−8.4, 1.4) | −13.3 (−18.1, −8.6) | −23.2 (−28.5, −17.8) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van den Hoorn, W.; Lavaill, M.; Cutbush, K.; Gupta, A.; Kerr, G. Comparison of Shoulder Range of Motion Quantified with Mobile Phone Video-Based Skeletal Tracking and 3D Motion Capture—Preliminary Study. Sensors 2024, 24, 534. https://doi.org/10.3390/s24020534
van den Hoorn W, Lavaill M, Cutbush K, Gupta A, Kerr G. Comparison of Shoulder Range of Motion Quantified with Mobile Phone Video-Based Skeletal Tracking and 3D Motion Capture—Preliminary Study. Sensors. 2024; 24(2):534. https://doi.org/10.3390/s24020534
Chicago/Turabian Stylevan den Hoorn, Wolbert, Maxence Lavaill, Kenneth Cutbush, Ashish Gupta, and Graham Kerr. 2024. "Comparison of Shoulder Range of Motion Quantified with Mobile Phone Video-Based Skeletal Tracking and 3D Motion Capture—Preliminary Study" Sensors 24, no. 2: 534. https://doi.org/10.3390/s24020534
APA Stylevan den Hoorn, W., Lavaill, M., Cutbush, K., Gupta, A., & Kerr, G. (2024). Comparison of Shoulder Range of Motion Quantified with Mobile Phone Video-Based Skeletal Tracking and 3D Motion Capture—Preliminary Study. Sensors, 24(2), 534. https://doi.org/10.3390/s24020534







