Detection of Degraded Star Observation Using Singular Values for Improved Attitude Determination
Abstract
:1. Introduction
2. Background
2.1. Invariance of Singular Values
2.2. Attitude Determination
3. Quality Level Calculation
3.1. Variation of Singular Values
3.2. Quality Value Calculation
4. Simulation Results
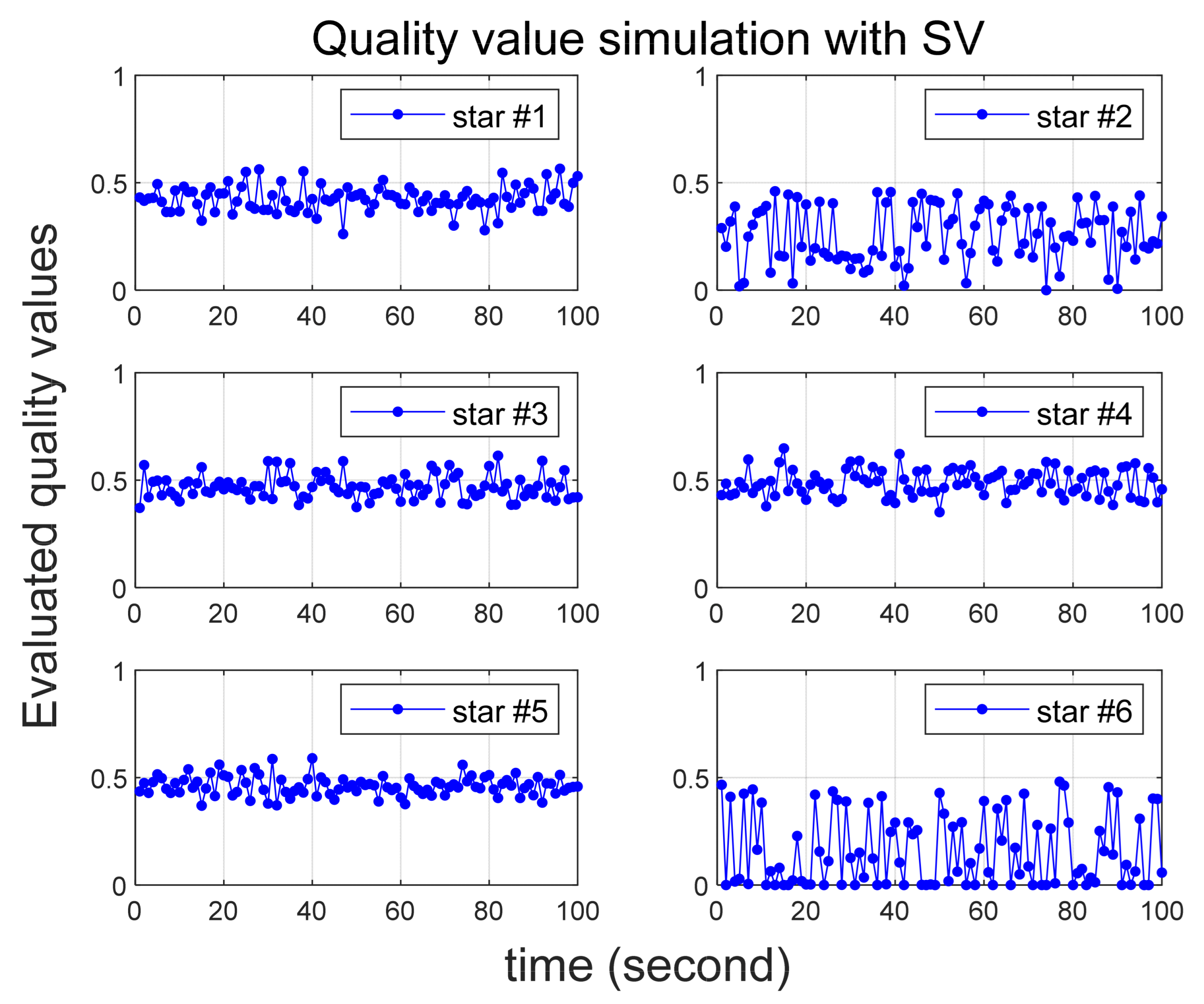
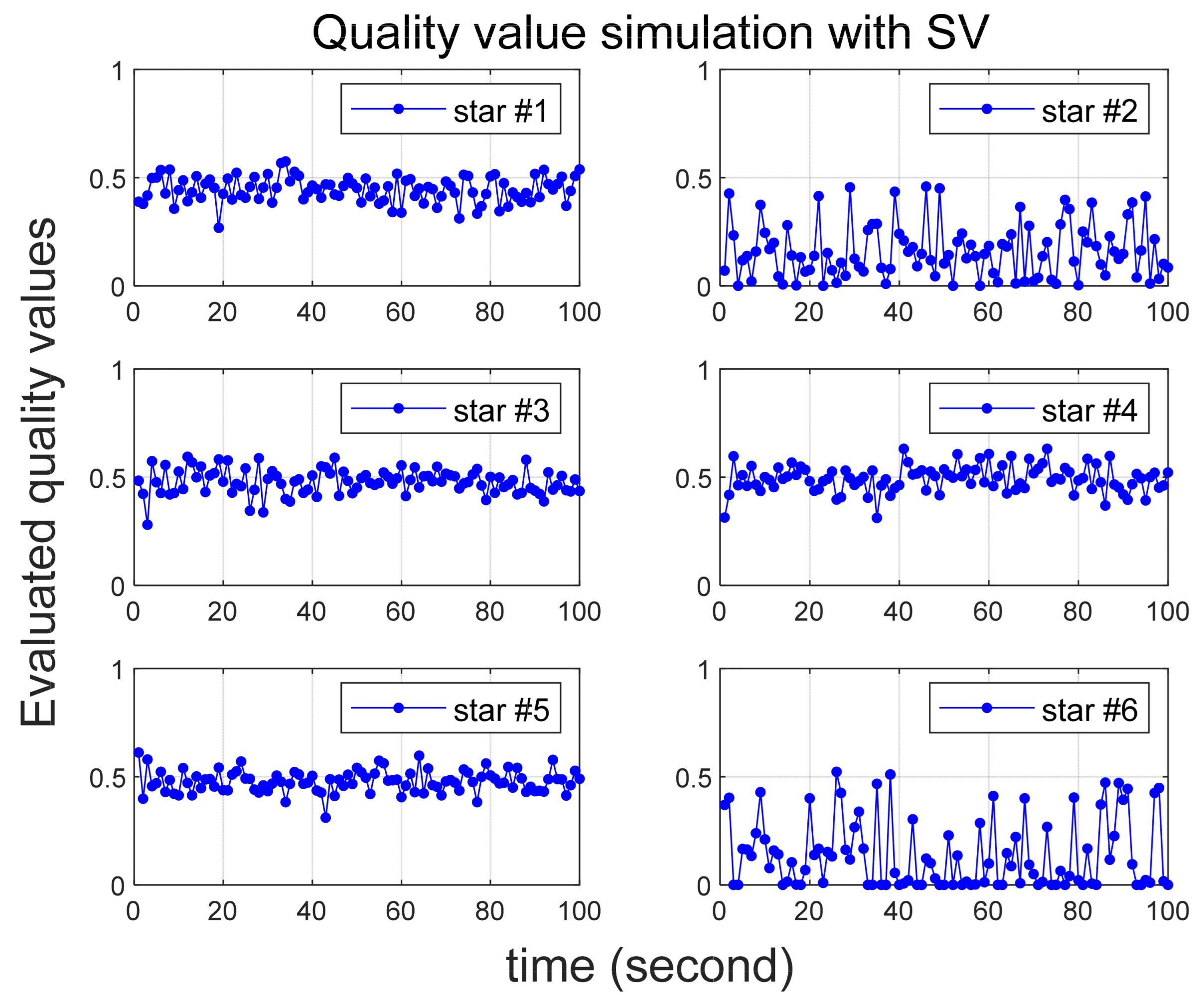
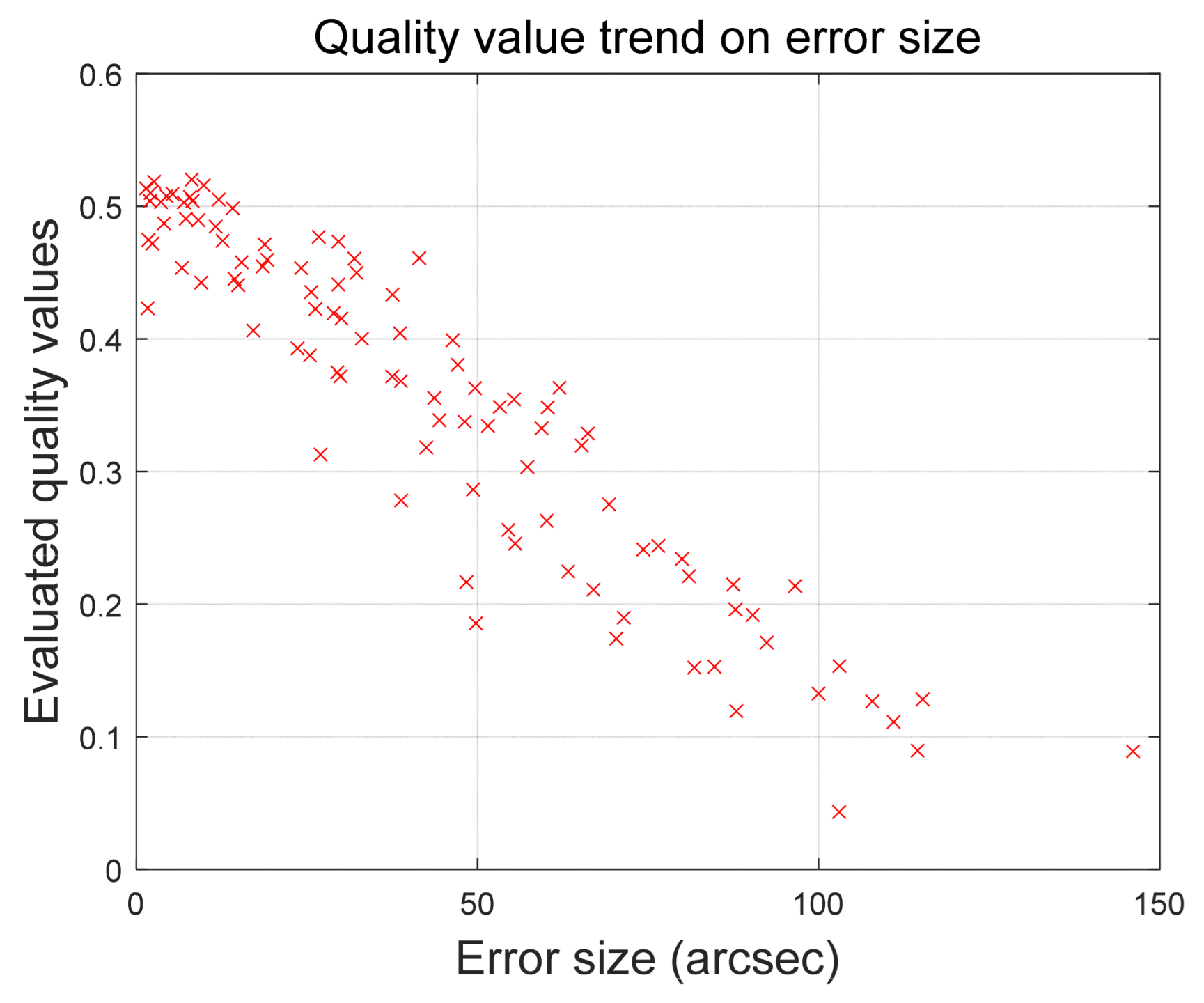
4.1. Quality Value Verification
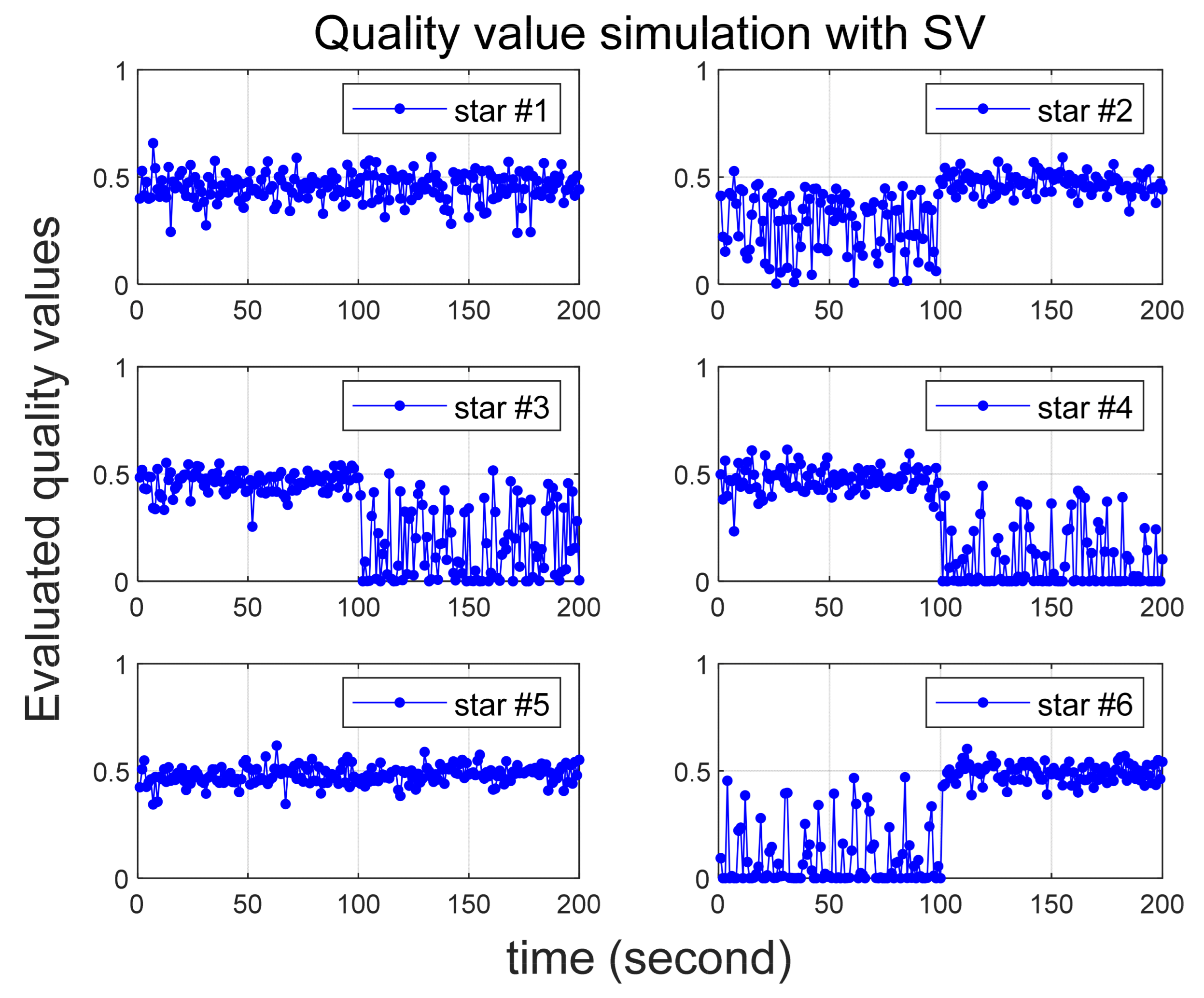
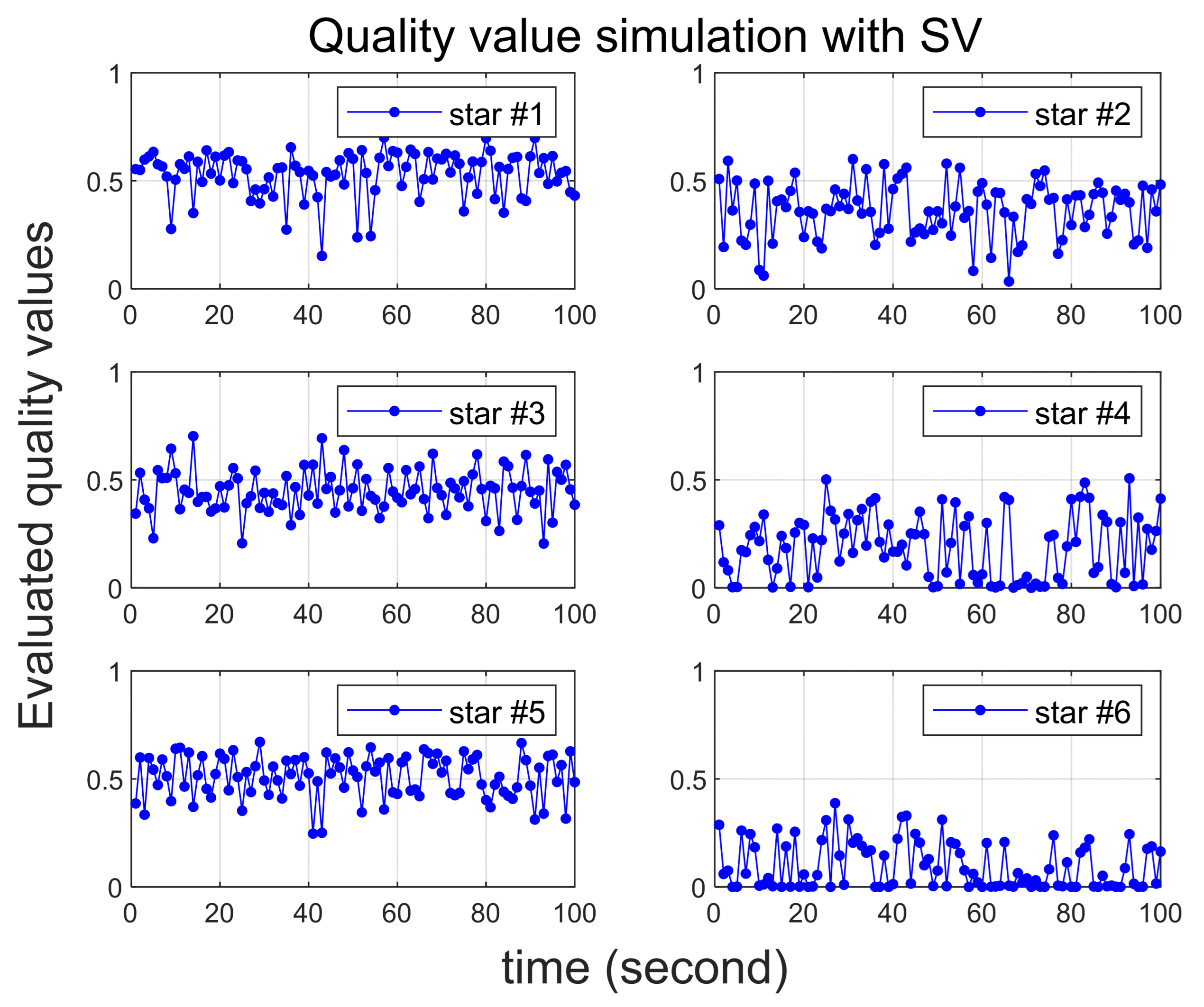
4.2. Effects Depending on the Number of Abnormal Stars
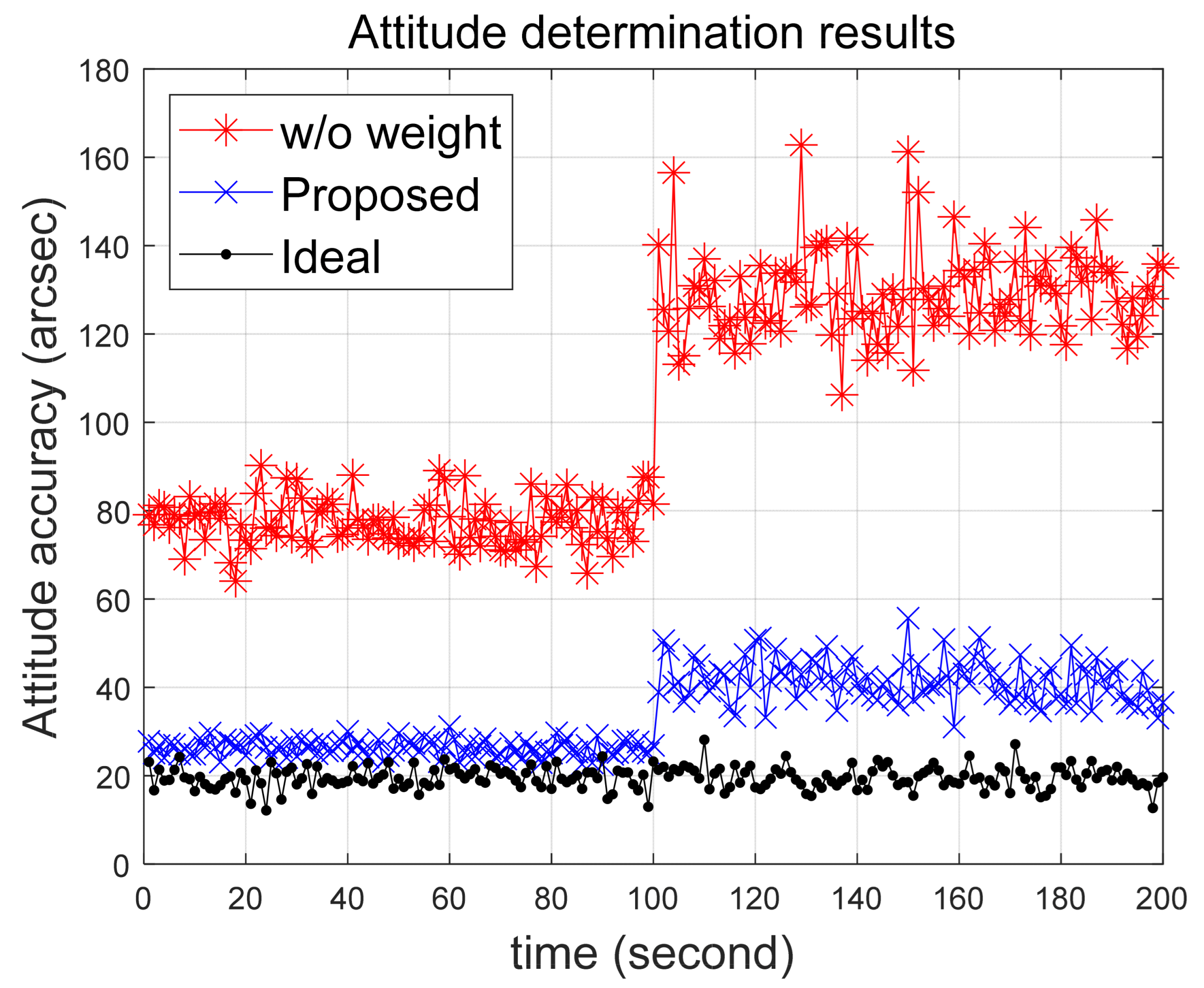
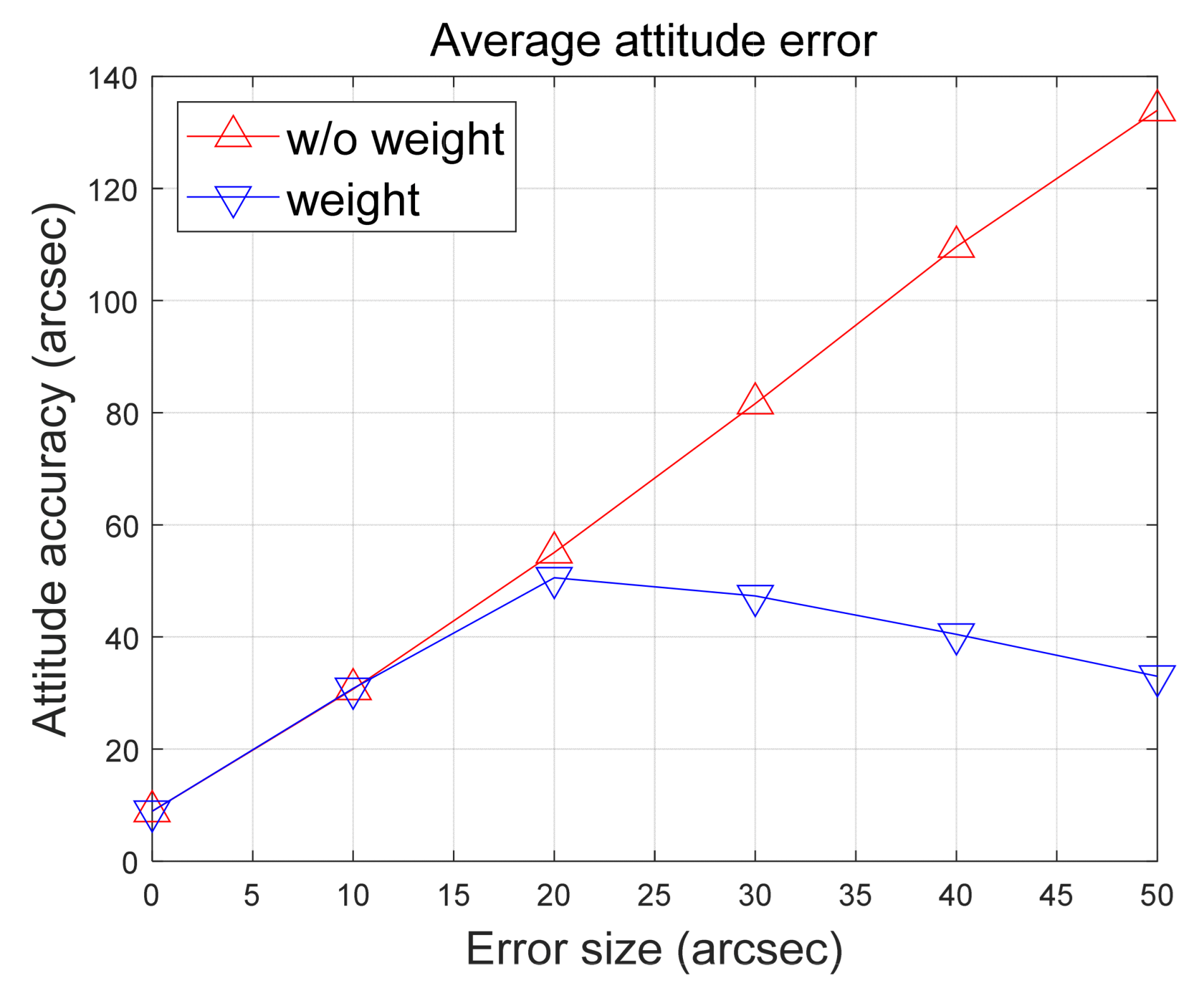
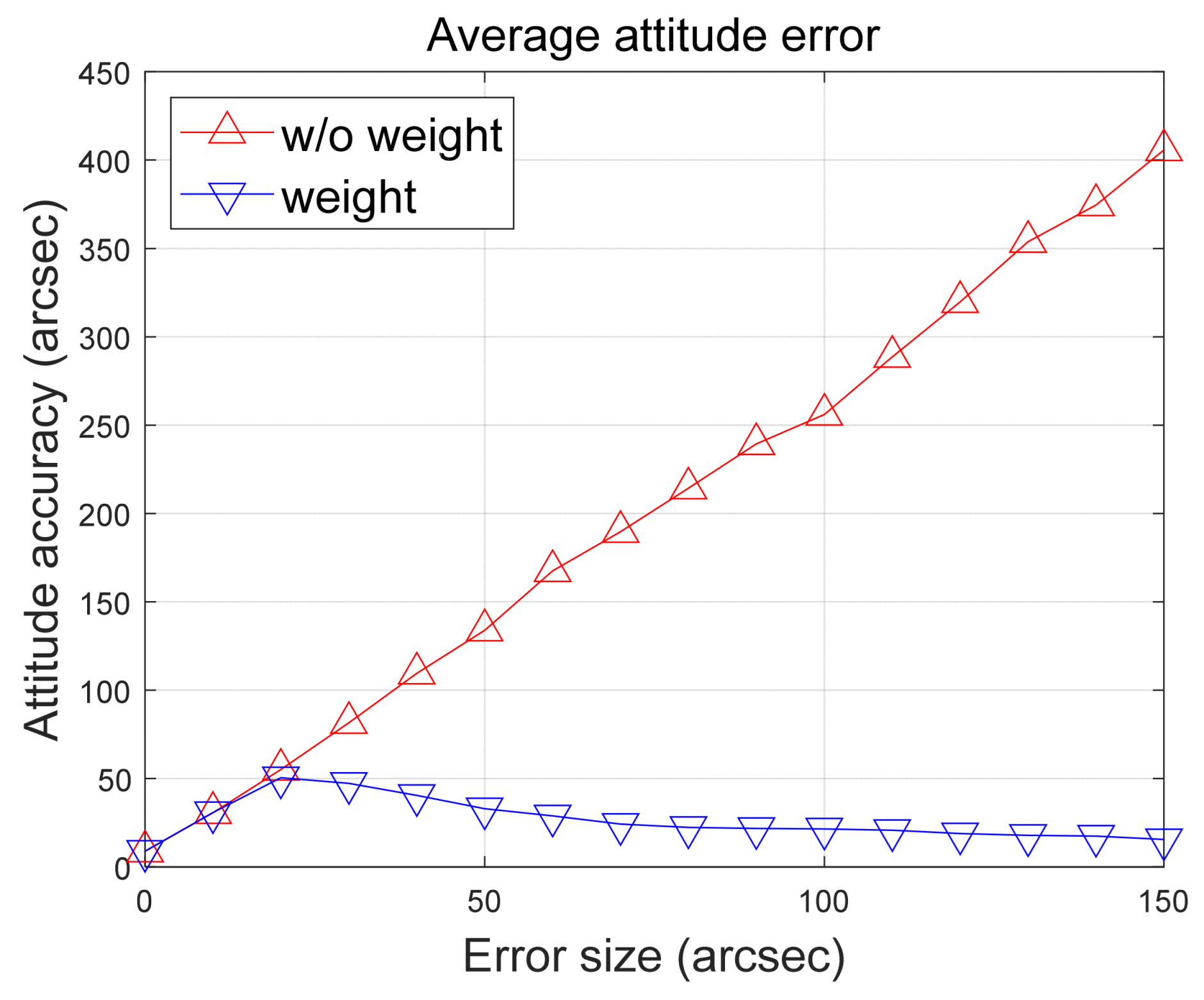
4.3. Attitude Determination
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kirkpatrick, D. Space Mission Analysis and Design; Wertz, J.R., Larson, W.J., Klungle, D., Eds.; Microcosm: Torrance, CA, USA, 1999; Volume 8. [Google Scholar]
- Fallon, L., III. Star Sensors Spacecraft Attitude Determination and Control; Wertz, J.R., Ed.; Springer Science & Business Media: Berlin, Germany, 1978. [Google Scholar]
- Wang, X. Research on Technology of High-Precision Star Sensor with Large Field of View; Graduate University of Chinese Academy of Sciences, Changchun Institute of Optics, Fine Mechanics and Physics: Changchun, China, 2003. [Google Scholar]
- Schulz, V.H.; Marcelino, G.M.; Seman, L.O.; Santos Barros, J.; Kim, S.; Cho, M.; Villarrubia González, G.; Leithardt, V.R.Q.; Bezerra, E.A. Universal verification platform and star simulator for fast star tracker design. Sensors 2021, 21, 907. [Google Scholar] [CrossRef] [PubMed]
- Liebe, C.C. Accuracy performance of star trackers-a tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar]
- Lappas, V.J.; Steyn, W.H.; Underwood, C.I. Attitude control for small satellites using control moment gyros. Acta Astronaut. 2002, 51, 101–111. [Google Scholar] [CrossRef]
- Samaan, M.A.; Pollock, T.C.; Junkins, J.L. Predictive centroiding for star trackers with the effect of image smear. J. Astronaut. Sci. 2002, 50, 113–123. [Google Scholar]
- Schiattarella, V.; Spiller, D.; Curti, F. Star identification robust to angular rates and false objects with rolling shutter compensation. Acta Astronaut. 2020, 166, 243–259. [Google Scholar]
- Liao, Y.; Liu, E.; Zhong, J.; Zhang, H. Processing centroids of smearing star image of star sensor. Math. Probl. Eng. 2014, 2014, 534698. [Google Scholar] [CrossRef]
- Curti, F.; Spiller, D.; Ansalone, L.; Becucci, S.; Procopio, D.; Boldrini, F.; Fidanzati, P. Determining high rate angular velocity from star tracker measurements. In International Astronautical Congress: Iac Proceedings; International Astronautical Federation, IAF: New Delhi, India, 2015; Volume 7, pp. 5666–5678. [Google Scholar]
- Kazemi, L.; Enright, J. Enabling technologies for high slew rate star trackers. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Liebe, C.C.; Gromov, K.; Meller, D.M. Toward a stellar gyroscope for spacecraft attitude determination. J. Guid. Control. Dyn. 2004, 27, 91–99. [Google Scholar] [CrossRef]
- Zhang, W.; Quan, W.; Guo, L. Blurred star image processing for star sensors under dynamic conditions. Sensors 2012, 12, 6712–6726. [Google Scholar]
- Wan, X.; Wang, G.; Wei, X.; Li, J.; Zhang, G. Star centroiding based on fast Gaussian fitting for star sensors. Sensors 2018, 18, 2836. [Google Scholar]
- Wan, X.; Wang, G.; Wei, X.; Li, J.; Zhang, G. ODCC: A dynamic star spots extraction method for star sensors. IEEE Trans. Instrum. Meas. 2021, 70, 5009114. [Google Scholar] [CrossRef]
- Accardo, D.; Rufino, G. Brightness-independent start-up routine for star trackers. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 813–823. [Google Scholar] [CrossRef]
- Padgett, C.; Kreutz-Delgado, K.; Udomkesmalee, S. Evaluation of star identification techniques. J. Guid. Control Dyn. 1997, 20, 259–267. [Google Scholar]
- Mu, Z.; Wang, J.; He, X.; Wei, Z.; He, J.; Zhang, L.; Lv, Y.; He, D. Restoration method of a blurred star image for a star sensor under dynamic conditions. Sensors 2019, 19, 4127. [Google Scholar] [CrossRef]
- Han, J.; Yang, X.; Xu, T.; Fu, Z.; Chang, L.; Yang, C.; Jin, G. An end-to-end identification algorithm for smearing star image. Remote Sens. 2021, 13, 4541. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. A survey of lost-in-space star identification algorithms since 2009. Sensors 2020, 20, 2579. [Google Scholar] [CrossRef]
- Mehta, D.S.; Chen, S.; Low, K.S. A robust star identification algorithm with star shortlisting. Adv. Space Res. 2018, 61, 2647–2660. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A star identification algorithm based on radial and dynamic cyclic features of star pattern. Adv. Space Res. 2019, 63, 2245–2259. [Google Scholar] [CrossRef]
- Juang, J.N.; Wang, Y.C. Further studies on singular value method for star pattern recognition and attitude determination. J. Astronaut. Sci. 2012, 59, 370–380. [Google Scholar]
- Yin, H.; Song, X.; Yan, Y. Robustness analysis and improvement of singular value decomposition algorithm for autonomous star identification. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1757–1770. [Google Scholar]
- Wu, L.; Xu, Q.; Heikkilä, J.; Zhao, Z.; Liu, L.; Niu, Y. A star sensor on-orbit calibration method based on singular value decomposition. Sensors 2019, 19, 3301. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Andrews, H.; Patterson, C. Singular value decompositions and digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 26–53. [Google Scholar]
- Markley, F.L. Attitude determination using vector observations and the singular value decomposition. J. Astronaut. Sci. 1988, 36, 245–258. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hashim, H.A.; Brown, L.J.; Mcisaac, K. Guaranteed performance of nonlinear attitude filters on the special orthogonal group SO(3). IEEE Access 2018, 7, 3731–3745. [Google Scholar] [CrossRef]
- Wahba, G. A least square estimate of satellite attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude determination using vector observations: A fast optimal matrix algorithm. In Flight Mechanics (Estimation Theory Symposium; NASA: Greenbelt, MD, USA, 1992. [Google Scholar]
- Davenport, P.B. A Vector Approach to the Algebra of Rotations with Applications; National Aeronautics and Space Administration: Washington, DC, USA, 1968; Volume 4696.
- Perryman, M.A.; Lindegren, L.; Kovalevsky, J.; Hoeg, E.; Bastian, U.; Bernacca, P.L.; Crézé, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The HIPPARCOS catalogue. Astron. Astrophys. 1997, 323, L49–L52. [Google Scholar]

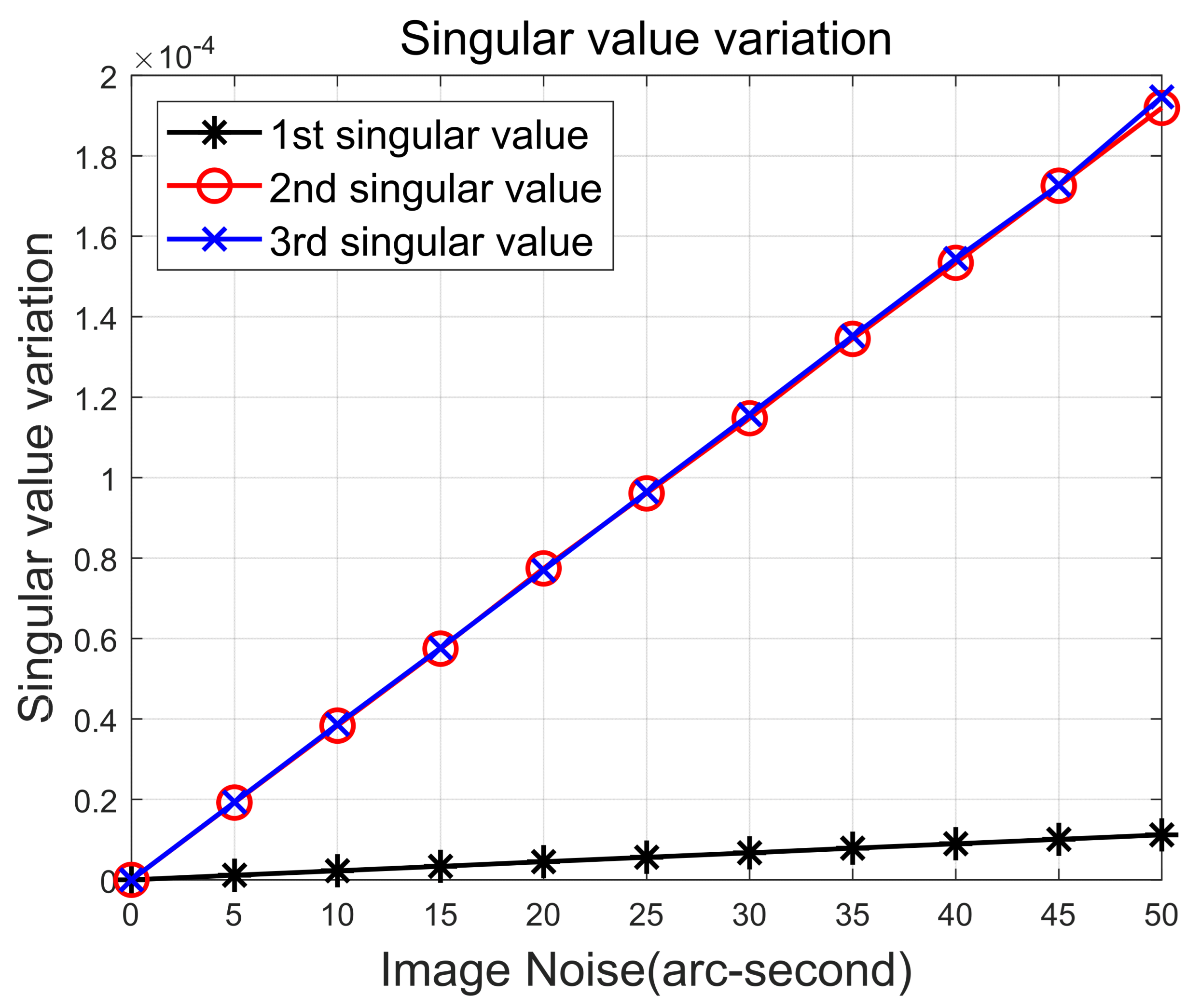


| 1st Singular Value | 2nd Singular Value | 3rd Singular Value | |
|---|---|---|---|
| Magnitude | 1.7288 | 0.0947 | 0.0291 |
| Variation w/o noise | 3.5374 | 7.3239 | 5.1625 |
| Variation w/10 arcsec | 2.7827 | 3.8214 | 3.8230 |
| Standard deviation w/10 arcsec | 2.9367 | 4.8097 | 4.8389 |
| Perturbed Star | Error Magnitude (Arc-Seconds) | Simulation Time (s) | |
|---|---|---|---|
| Scenario 1 | Star #2 | 25 | 0 to 100 |
| Star #6 | 60 | 0 to 100 | |
| Scenario 2 | Star #2 | 35 | 0 to 100 |
| Star #6 | 70 | 0 to 100 | |
| Scenario 3 | Star #2 | 25 | 0 to 100 |
| Star #3 | 35 | 100 to 200 | |
| Star #4 | 70 | 100 to 200 | |
| Star #6 | 60 | 0 to 100 |
| Star #1 | Star #2 | Star #3 | Star #4 | Star #5 | Star #6 |
|---|---|---|---|---|---|
| 89,962 | 91,117 | 92,175 | 90,135 | 91,845 | 91,726 |
| Perturbed Star | Error Magnitude (Arc-Seconds) | Simulation Time (s) | |
|---|---|---|---|
| Scenario 4 | Star #2 | 25 | 0 to 100 |
| Star #4 | 35 | 0 to 100 | |
| Star #6 | 60 | 0 to 100 | |
| Scenario 5 | Star #2 | 25 | 0 to 100 |
| Star #4 | 35 | 0 to 100 | |
| Star #5 | 25 | 0 to 100 | |
| Star #6 | 60 | 0 to 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K. Detection of Degraded Star Observation Using Singular Values for Improved Attitude Determination. Sensors 2024, 24, 593. https://doi.org/10.3390/s24020593
Kim K. Detection of Degraded Star Observation Using Singular Values for Improved Attitude Determination. Sensors. 2024; 24(2):593. https://doi.org/10.3390/s24020593
Chicago/Turabian StyleKim, Kiduck. 2024. "Detection of Degraded Star Observation Using Singular Values for Improved Attitude Determination" Sensors 24, no. 2: 593. https://doi.org/10.3390/s24020593
APA StyleKim, K. (2024). Detection of Degraded Star Observation Using Singular Values for Improved Attitude Determination. Sensors, 24(2), 593. https://doi.org/10.3390/s24020593





