A Fast Self-Calibration Method for Dual-Axis Rotational Inertial Navigation Systems Based on Invariant Errors
Abstract
1. Introduction
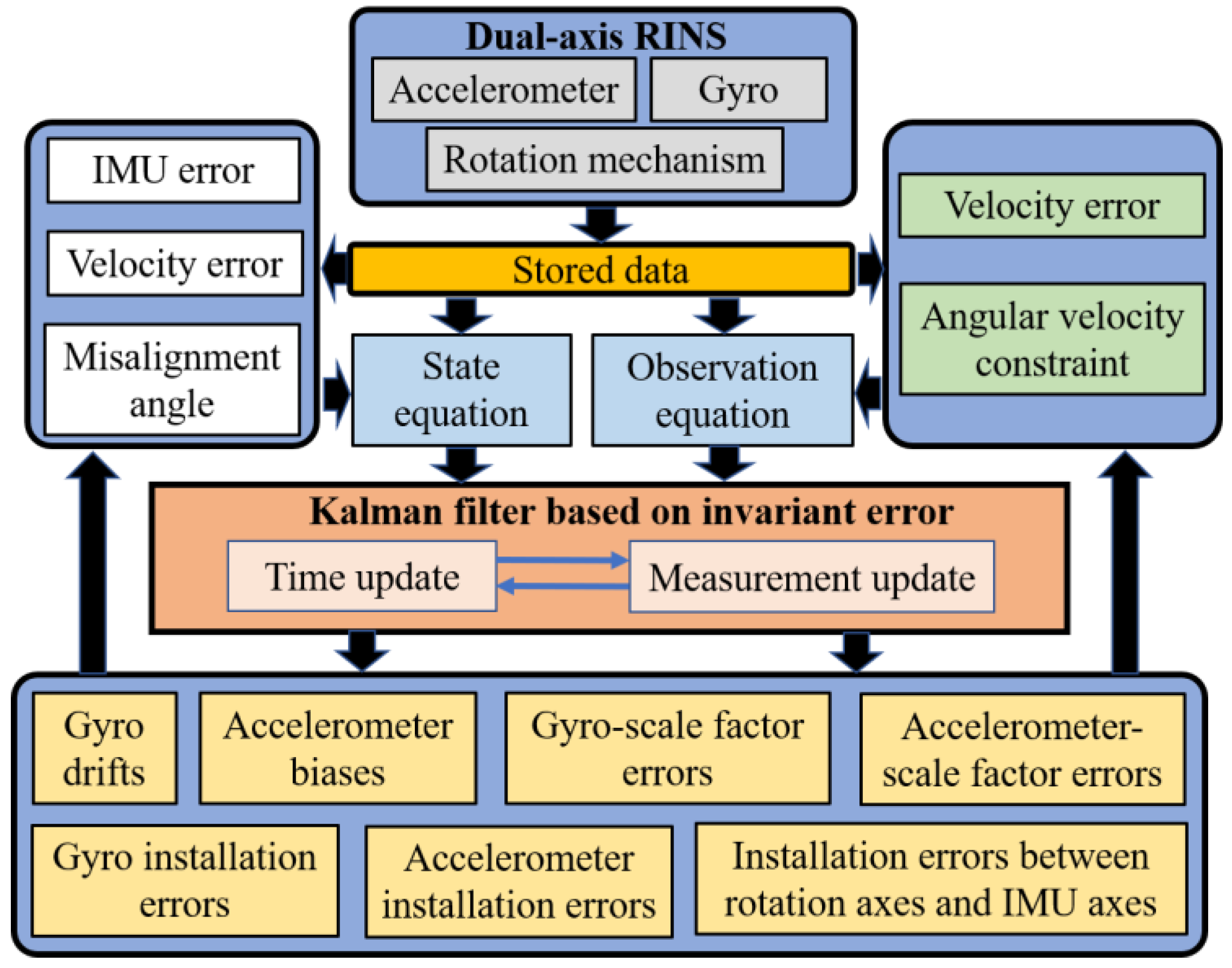
2. Mathematical Preliminaries and the Framework of the Proposed Method
3. Gimbal Mechanism Installation Error Model, IMU Error Model, and Navigation Error Model
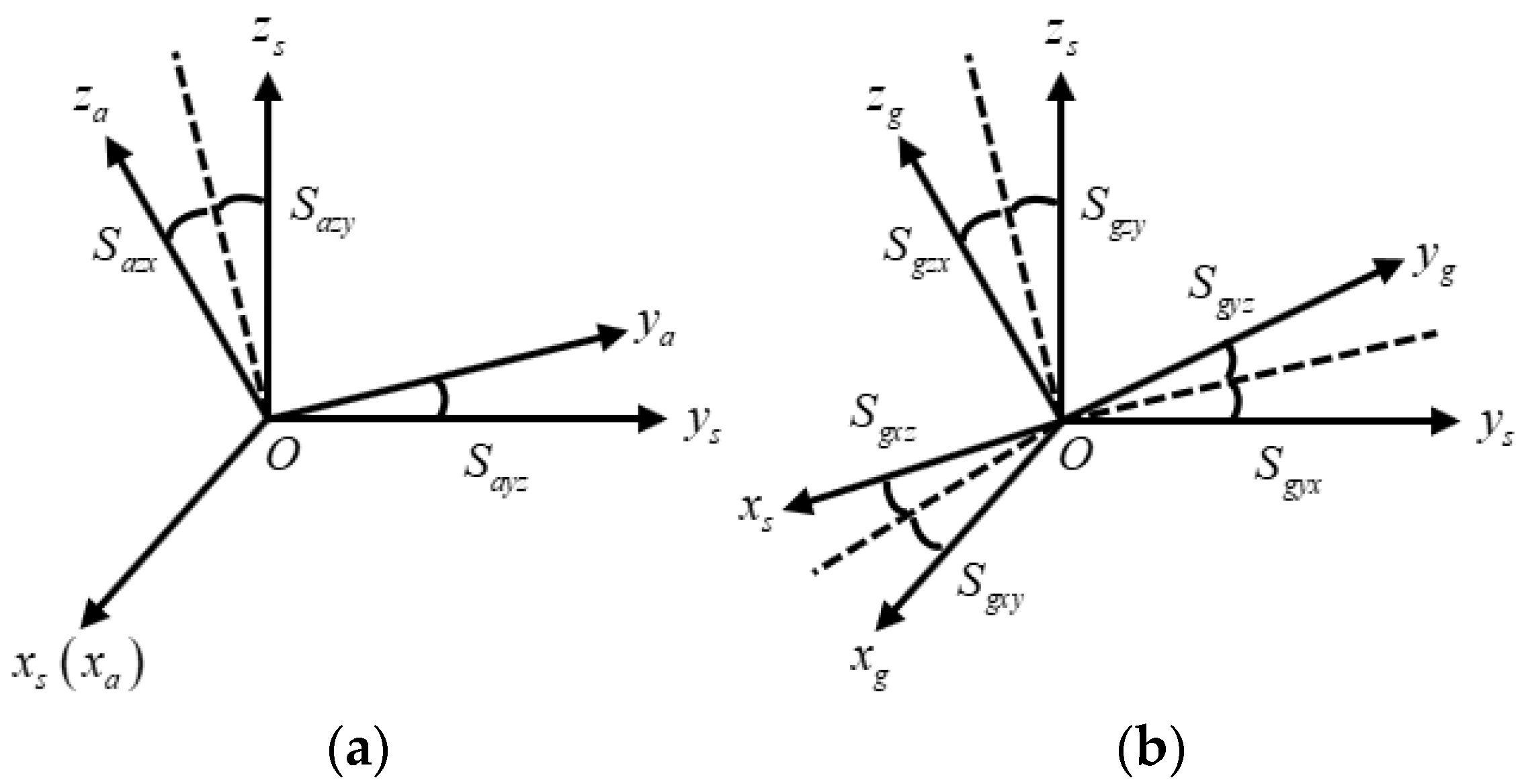
3.1. Gimbal Mechanism Installation Error Model
3.2. IMU Error Model
3.3. Navigation Error State Model in the Inertial Frame
3.3.1. Error State Model Based on
3.3.2. Right-Invariant Error State Model Based on
3.3.3. Left-Invariant Error State Model Based on
| Algorithm 1 Discrete Kalman filter algorithm flow |
| (1) State and variance matrix initialization |
| (2) State propagation process |
| (3) Update filter state |
| (4) Update navigation state |
| where is the discrete time. and are device random noise. |
4. The Fast Self-Calibration Method and Observability Analysis of the Dual-Axis RINS
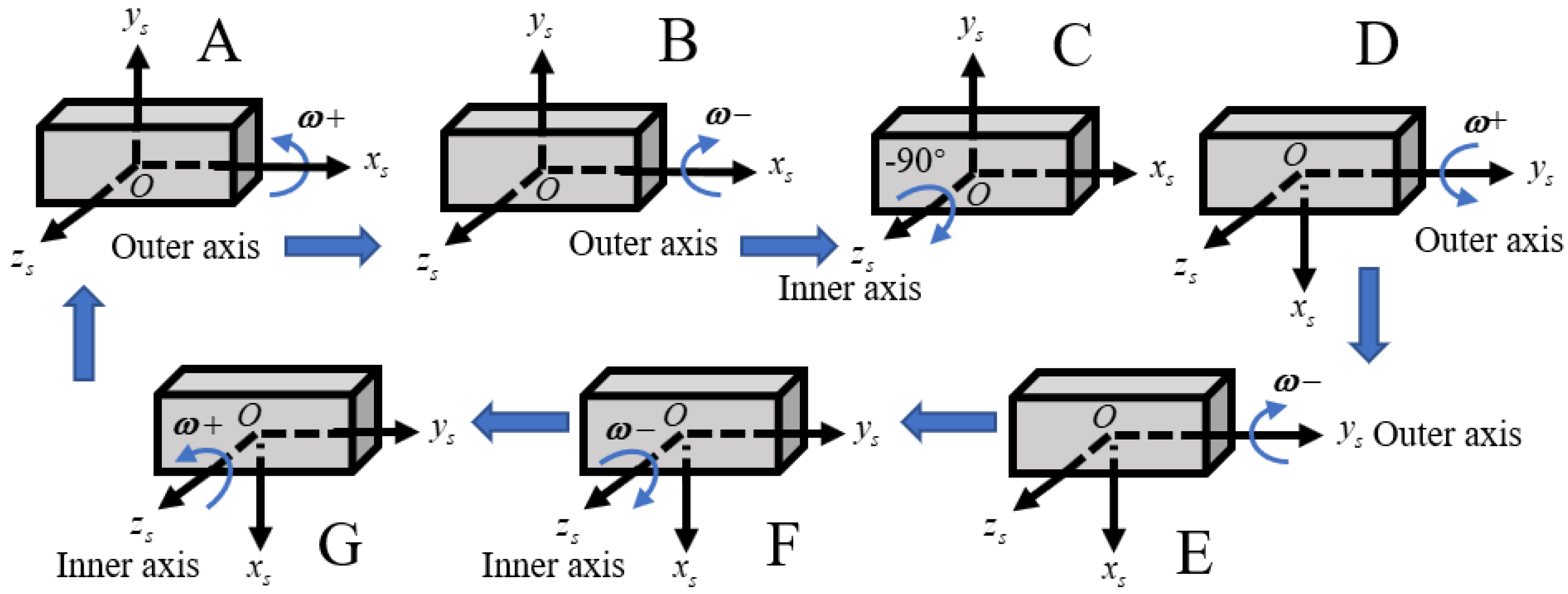
4.1. Rotation Scheme Design and Observability Analysis
4.2. Angular Velocity Constraint Equation
4.3. Backtracking Scheme Design in the Inertial Frame
5. Simulation Test and Experimental Analysis
5.1. Simulation Test
5.1.1. Verification of the Observability Analysis
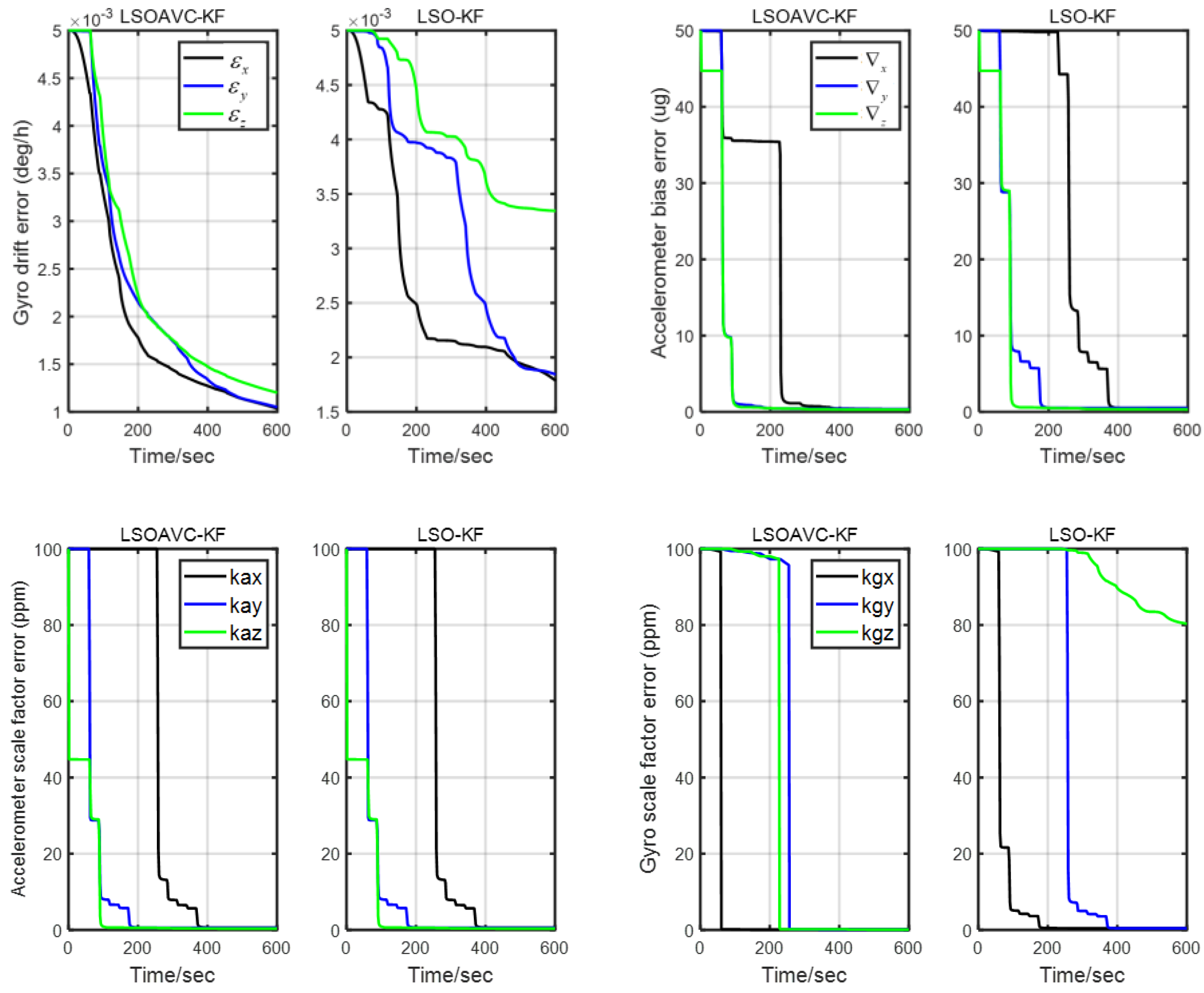
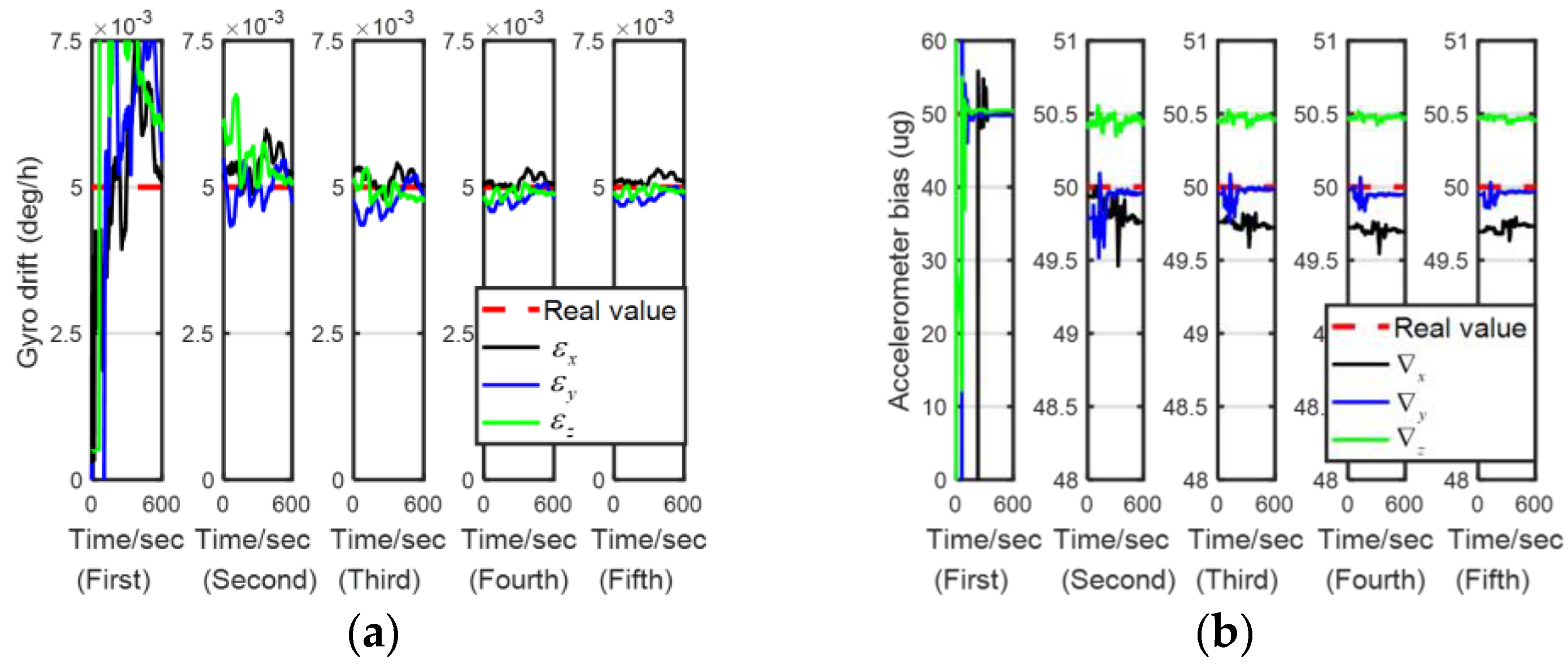
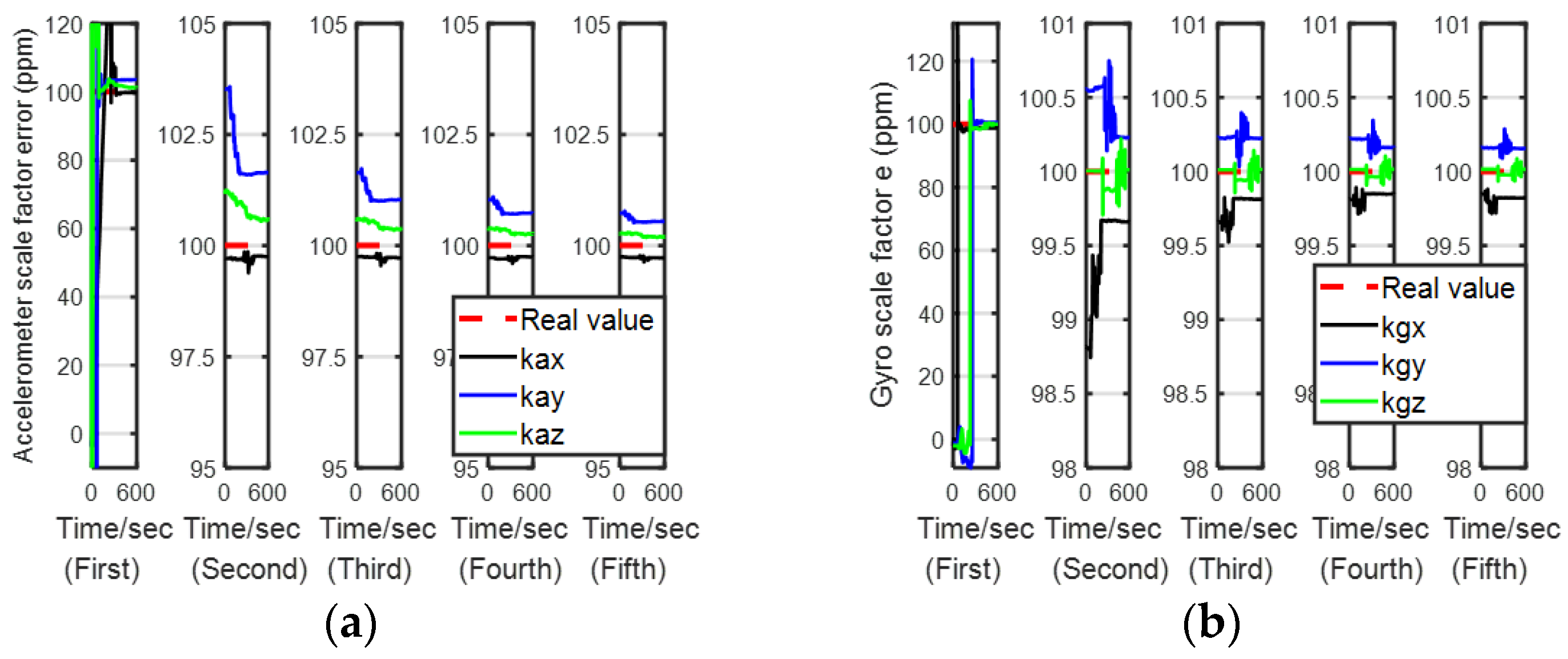
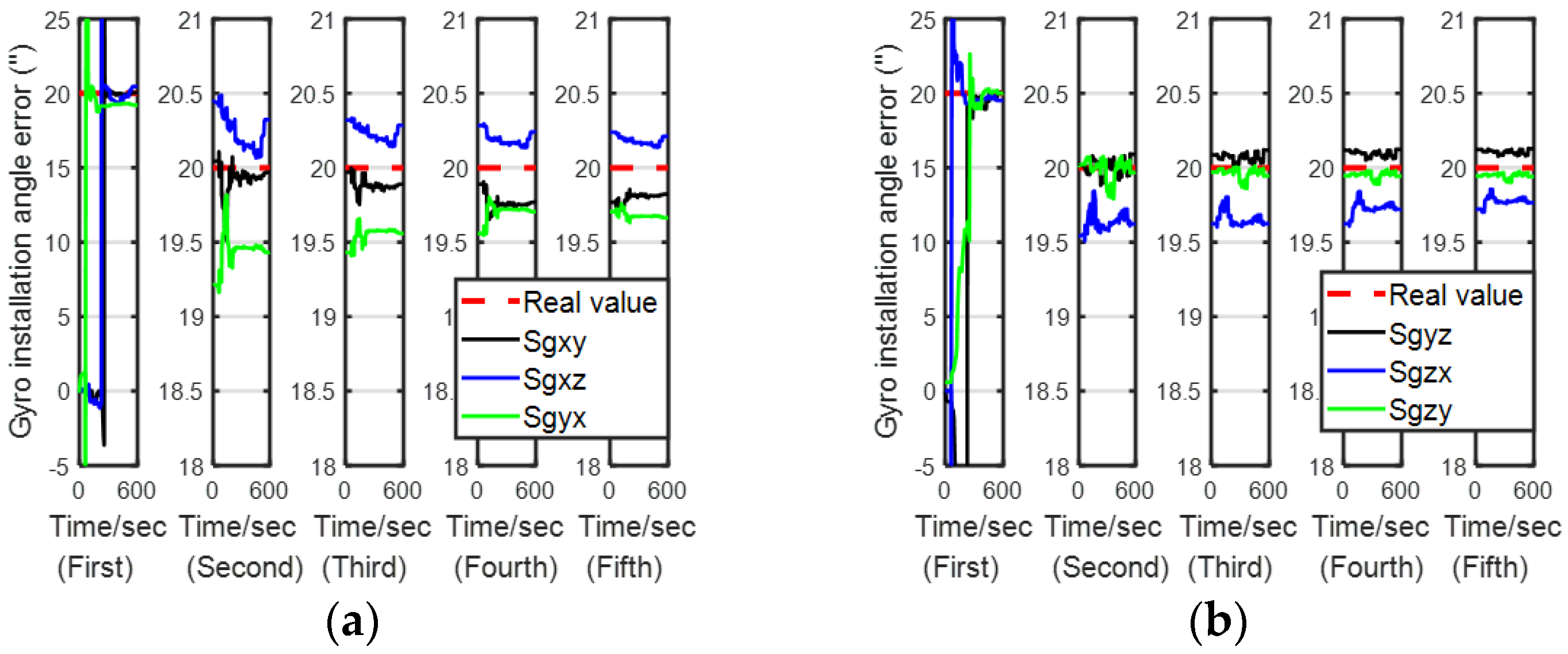
5.1.2. Comparison of the Calibration Accuracy
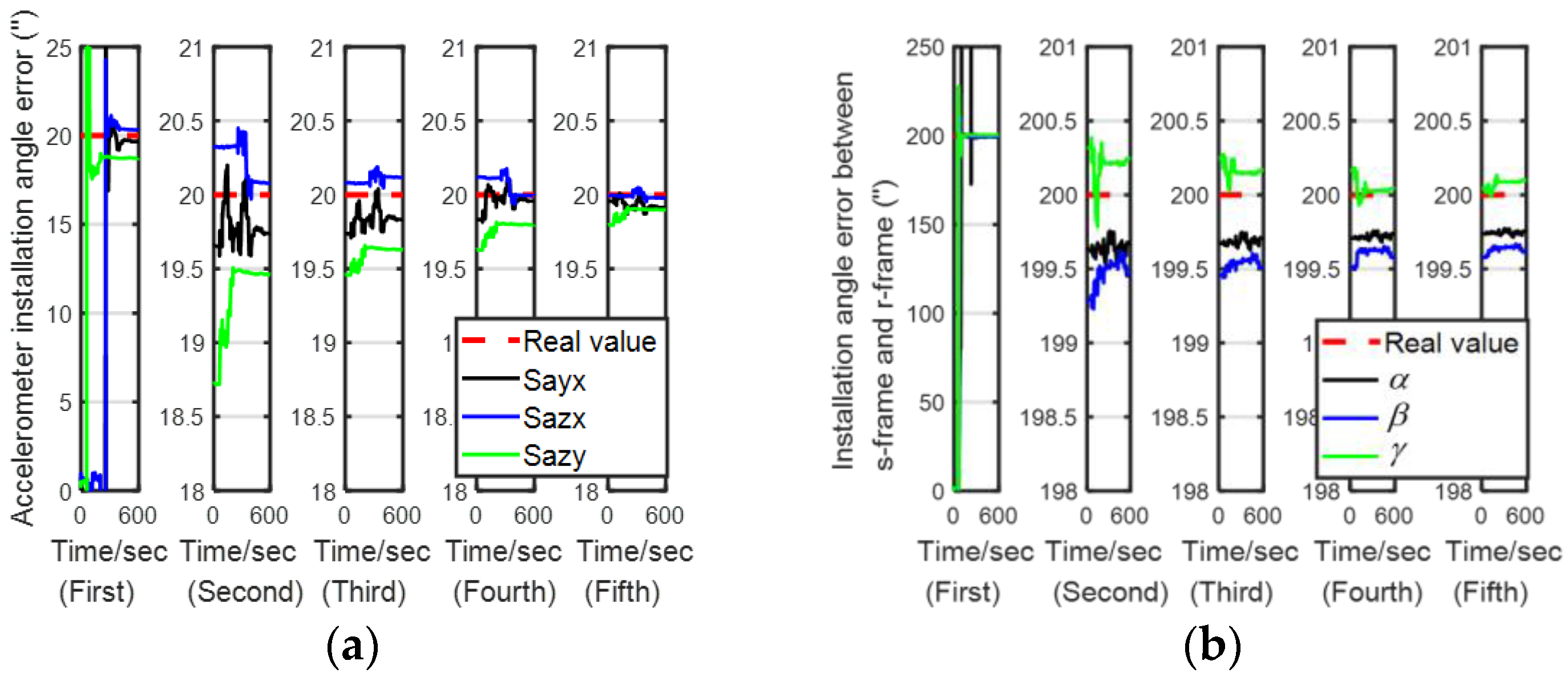
5.2. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Groves, P.D. Principles of GNSS, inertial, and multisensor integrated navigation systems, [Book review]. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Wang, B.; Ren, Q.; Deng, Z.; Fu, M. A self-calibration method for nonorthogonal angles between gimbals of rotational inertial navigation system. IEEE Trans. Ind. Electron. 2014, 62, 2353–2362. [Google Scholar] [CrossRef]
- Ren, Q.; Wang, B.; Deng, Z.; Fu, M. A multi-position self-calibration method for dual-axis rotational inertial navigation system. Sens. Actuators A Phys. 2014, 219, 24–31. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Liu, Z.; Zhang, Y. Innovative self-calibration method for accelerometer scale factor of the missile-borne RINS with fiber optic gyro. Opt. Express 2016, 24, 21228–21243. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zha, F.; Chang, L. Novel rotation scheme for dual-axis rotational inertial navigation system based on body diagonal rotation of inertial measurement unit. Meas. Sci. Technol. 2022, 33, 095105. [Google Scholar] [CrossRef]
- Li, Q.; Li, K.; Liang, W. A Dual-Axis Rotation Scheme for Long-Endurance Inertial Navigation Systems. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tsukioka, S.; Yoshida, H.; Hyakudome, T.; Sawa, T.; Tahara, J.; Aoki, T.; Ishikawa, A. Accuracy Improvement of an Inertial Navigation System brought about by the Rotational Motion. In Proceedings of the OCEANS 2007—Europe, Aberdeen, Scotland, 18–21 June 2007; pp. 1–5. [Google Scholar]
- Gao, J.; Li, K.; Chen, Y. Study on Integration of FOG Single-Axis Rotational INS and Odometer for Land Vehicle. IEEE Sens. J. 2018, 18, 752–763. [Google Scholar] [CrossRef]
- Zhang, Q.; Niu, X.; Shi, C. Impact Assessment of Various IMU Error Sources on the Relative Accuracy of the GNSS/INS Systems. IEEE Sens. J. 2020, 20, 5026–5038. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, W.; Tang, G. Stellar/inertial integrated guidance for responsive launch vehicles. Aerosp. Sci. Technol. 2012, 18, 35–41. [Google Scholar] [CrossRef]
- Bo, X.; Feng, S. A FOG Online Calibration Research Based on High-precision three-axis Turntable. In Proceedings of the 2009 International Asia Conference on Informatics in Control, Automation and Robotics, Bangkok, Thailand, 1–2 February 2009; pp. 454–458. [Google Scholar]
- Zheng, Z.; Han, S.; Zheng, K. An eight-position self-calibration method for a dual-axis rotational Inertial Navigation System. Sens. Actuators A-Phys. 2015, 232, 39–48. [Google Scholar] [CrossRef]
- Sun, F.; Xia, J.; Ben, Y.; Zhang, X.; IEEE. Four-position Drift Measurement of SINS Based on Single-axis Rotation. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 818–823. [Google Scholar]
- Wei, Q.; Zha, F.; He, H.; Li, B. An Improved System-Level Calibration Scheme for Rotational Inertial Navigation Systems. Sensors 2022, 22, 7610. [Google Scholar] [CrossRef]
- Hu, P.; Xu, P.; Chen, B.; Wu, Q. A Self-Calibration Method for the Installation Errors of Rotation Axes Based on the Asynchronous Rotation of Rotational Inertial Navigation Systems. IEEE Trans. Ind. Electron. 2018, 65, 3550–3558. [Google Scholar] [CrossRef]
- Bai, S.; Lai, J.; Lyu, P.; Xu, X.; Liu, M.; Huang, K. A System-Level Self-Calibration Method for Installation Errors in A Dual-Axis Rotational Inertial Navigation System. Sensors 2019, 19, 4005. [Google Scholar] [CrossRef]
- Huang, Z.; Du, P.; Kosterev, D.; Yang, B. Application of extended Kalman filter techniques for dynamic model parameter calibration. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, D.; Yuan, P.; Wang, T.; Cai, Y.; Tang, H. A normal sensor calibration method based on an extended Kalman filter for robotic drilling. Sensors 2018, 18, 3485. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Chen, Y. Common Frame Based Unscented Quaternion Estimator for Inertial-Integrated Navigation. IEEE ASME Trans. Mechatron. 2018, 23, 2413–2423. [Google Scholar] [CrossRef]
- Scherzinger, B.M.; Reid, D.B. Modified strapdown inertial navigator error models. In Proceedings of the 1994 IEEE Position, Location and Navigation Symposium (PLANS’94), Las Vegas, NV, USA, 11–15 April 1994; pp. 426–430. [Google Scholar] [CrossRef]
- Wang, M.; Wu, W.; Zhou, P.; He, X. State transformation extended Kalman filter for GPS/SINS tightly coupled integration. GPS Solut. 2018, 22, 112. [Google Scholar] [CrossRef]
- He, H.; Tang, H.; Xu, J.; Liang, Y.; Li, F. A SINS/USBL System-Level Installation Parameter Calibration With Improved RDPSO. IEEE Sens. J. 2023, 23, 17214–17223. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, P.; Wei, Z.; Luo, G. A novel MEMS-RIMU self-calibration method based on gravity vector observation. Meas. Sci. Technol. 2021, 32, 055108. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, K.; Song, J.; Huang, S.; Dissanayake, G. Convergence and Consistency Analysis for a 3-D Invariant-EKF SLAM. IEEE Robot. Autom. Lett. 2017, 2, 733–740. [Google Scholar] [CrossRef]
- Potokar, E.; Norman, K.; Mangelson, J. Invariant Extended Kalman Filtering for Underwater Navigation. IEEE Robot. Autom. Lett. 2021, 6, 5792–5799. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. The Invariant Extended Kalman Filter as a Stable Observer. IEEE Trans. Autom. Control. 2017, 62, 1797–1812. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Xu, J. Strapdown Inertial Navigation System Initial Alignment Based on Group of Double Direct Spatial Isometries. IEEE Sens. J. 2022, 22, 803–818. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Invariant kalman filtering. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 237–257. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, C.; You, S.; Hu, J.; Liu, J. SE2 (3) based Extended Kalman Filter and Smoothing for Inertial-Integrated Navigation. arXiv 2021, arXiv:2102.12897. [Google Scholar]
- Chang, L.B. SE(3) based extended Kalman filter for attitude estimation. J. Chin. Inert. Technol. 2020, 28, 499–504, 550. [Google Scholar]
- Wang, J.; Chen, X.; Shao, X. An Adaptive Multiple Backtracking UKF Method Based on Krein Space Theory for Marine Vehicles Alignment Process. IEEE Trans. Veh. Technol. 2023, 72, 3214–3226. [Google Scholar] [CrossRef]
- Lin, Y.; Miao, L.; Zhou, Z. A high-accuracy initial alignment method based on backtracking process for strapdown inertial navigation system. Measurement 2022, 201, 111712. [Google Scholar] [CrossRef]
- Sola, J.; Deray, J.; Atchuthan, D. A micro Lie theory for state estimation in robotics. arXiv 2018, arXiv:1812.01537. [Google Scholar]
- Tang, H.; Xu, J.; Chang, L.; Shi, W.; He, H. Invariant Error-Based Integrated Solution for SINS/DVL in Earth Frame: Extension and Comparison. IEEE Trans. Instrum. Meas. 2023, 72, 1–17. [Google Scholar] [CrossRef]
- Gao, P.; Li, K.; Wang, L.; Liu, Z. A Self-Calibration Method for Accelerometer Nonlinearity Errors in Triaxis Rotational Inertial Navigation System. IEEE Trans. Instrum. Meas. 2017, 66, 243–253. [Google Scholar] [CrossRef]





| Reference Frame | Definition |
|---|---|
| a-frame | Accelerometer installation frame |
| g-frame | Gyro installation frame |
| s-frame | Sensor frame |
| s0-frame | Sensor frame in the initial state |
| b-frame | Body frame, which is the orthogonal reference frame of a dual-axis RINS. In this paper, the b-frame coincides with the s0-frame |
| n-frame | The navigation frame, which is the orthogonal reference frame aligned with the east-north-up geodetic axes |
| in0-frame | The navigation inertial frame, which is the fixed axes of the n-frame in the inertial space at the beginning of the calibration process |
| e-frame | Earth-centered earth-fixed (ECEF) frame |
| e0-frame | ECEF inertial frame in the initial state |
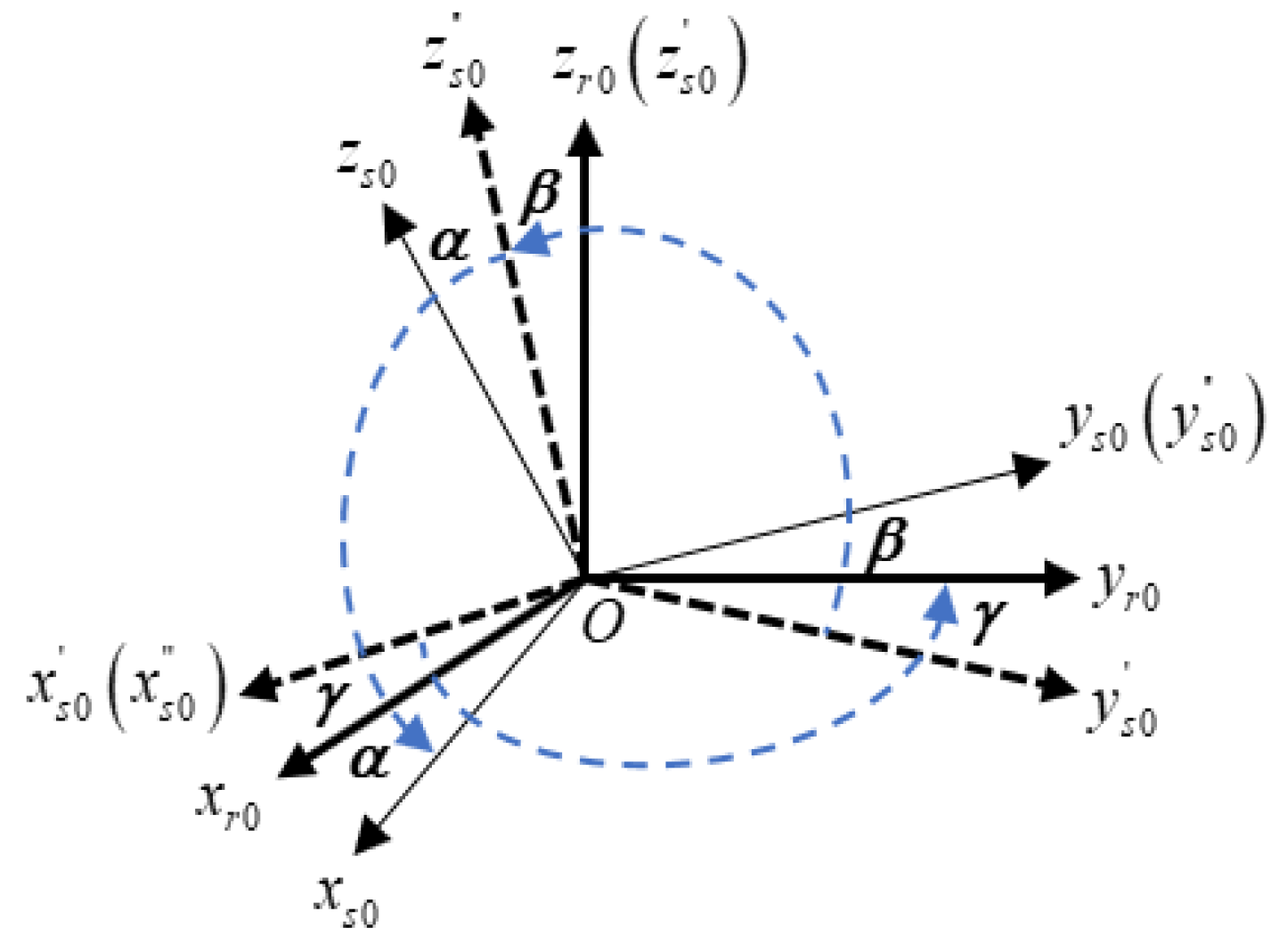
| r-frame | r-frame, which is the orthogonal reference frame of the gimbal mechanism. Its three axes are defined by . coincides with the outer axis, coincides with the inner axis, while forms a right-handed orthogonal frame with and |
| r0-frame | r-frame in the initial state |
| Invariant Error Model Based on | Name | Corresponds to Error Model Based on |
| (26) | Right Invariant | (27) |
| (28) | Left Invariant | (29) |
| Parameter | RSEAVC-KF | RSOAVC-KF | LSEAVC-KF | LSOAVC-KF | ||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | ME | RMSE | ME | RMSE | ME | RMSE | |
| (°/h) | 0.0003 | 0.0042 | 0.0005 | 0.0058 | 0.0002 | 0.0035 | 0.0004 | 0.0052 |
| (°/h) | 0.0006 | 0.0041 | 0.0003 | 0.0042 | 0.0005 | 0.0039 | 0.0002 | 0.0042 |
| (°/h) | −0.0003 | 0.0034 | −0.0004 | 0.0039 | −0.0001 | 0.0020 | −0.0005 | 0.0039 |
| (μg) | −0.2131 | 0.8136 | −0.2794 | 0.8935 | −0.1434 | 0.7252 | −0.2327 | 0.868 |
| (μg) | 0.1595 | 0.74 | 0.3689 | 0.8136 | 0.0796 | 0.7375 | 0.2049 | 0.744 |
| (μg) | 0.053 | 0.3953 | 0.1245 | 0.4452 | 0.0436 | 0.3771 | 0.0983 | 0.44 |
| (ppm) | 0.1447 | 0.1668 | 0.1808 | 0.1938 | 0.1429 | 0.1644 | 0.1644 | 0.169 |
| (ppm) | −0.1493 | 0.1658 | −0.152 | 0.169 | −0.1464 | 0.1646 | −0.1517 | 0.1674 |
| (ppm) | −0.1449 | 0.1584 | −0.1561 | 0.1739 | −0.1396 | 0.1535 | −0.1553 | 0.1585 |
| (ppm) | 0.0321 | 0.7175 | −0.2059 | 0.7305 | −0.0222 | 0.6592 | −0.1809 | 0.7255 |
| (ppm) | 0.4286 | 0.704 | 0.5241 | 1.911 | 0.3087 | 0.6776 | 0.5095 | 0.9855 |
| (ppm) | 0.0267 | 0.3216 | 0.0654 | 0.4094 | 0.0055 | 0.298 | 0.061 | 0.389 |
| (″) | 0.0376 | 0.3052 | 0.1986 | 0.3549 | 0.015 | 0.2579 | 0.1828 | 0.3166 |
| (″) | 0.0594 | 0.2630 | 0.0811 | 0.2888 | 0.0523 | 0.2264 | 0.0697 | 0.2843 |
| (″) | 0.2352 | 0.3658 | 0.4452 | 0.5174 | 0.2215 | 0.3441 | 0.3935 | 0.51 |
| (″) | 0.0532 | 0.1663 | 0.0762 | 0.1759 | 0.0526 | 0.1375 | 0.07 | 0.1702 |
| (″) | 0.3509 | 0.4442 | 0.4905 | 0.5414 | 0.3338 | 0.4142 | 0.4750 | 0.4712 |
| (″) | 0.4519 | 0.4801 | 0.4741 | 0.4991 | 0.3329 | 0.3547 | 0.4523 | 0.4833 |
| (″) | 0.1472 | 0.3518 | 0.4257 | 0.5364 | 0.1296 | 0.3454 | 0.3866 | 0.4828 |
| (″) | 0.3752 | 0.5953 | 0.542 | 0.6552 | 0.365 | 0.4648 | 0.5214 | 0.6058 |
| (″) | 0.3949 | 0.4742 | 0.5194 | 0.5836 | 0.3363 | 0.4468 | 0.5133 | 0.5067 |
| (″) | 0.1522 | 0.2978 | 0.2748 | 0.3139 | 0.1301 | 0.1754 | 0.2526 | 0.3022 |
| (″) | −0.115 | 0.3132 | −0.2536 | 0.3381 | −0.112 | 0.2757 | −0.2136 | 0.3158 |
| (″) | 0.0036 | 0.295 | 0.1852 | 0.3563 | 0.0025 | 0.2461 | 0.1637 | 0.3353 |
| Parameter | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
|---|---|---|---|---|---|---|---|
| (°/h) | 0.0001 | 0.0002 | 0.0003 | 0.0004 | 0.0002 | 0.0003 | 0.0004 |
| (°/h) | 0.0002 | 0.0002 | 0.0003 | 0.0004 | 0.00005 | 0.0004 | 0.0005 |
| (°/h) | −0.0002 | 0.0003 | −0.0003 | 0.0003 | −0.0003 | 0.0002 | −0.0003 |
| (μg) | −0.8282 | 0.8047 | −0.7621 | 0.678 | −0.6723 | 0.9058 | −1.1413 |
| (μg) | −0.4469 | 0.4493 | −0.4953 | 0.4189 | −0.4932 | 0.5359 | −0.7016 |
| (μg) | 0.2836 | 0.003 | 0.4408 | 0.5425 | 0.0634 | 0.3509 | 0.8046 |
| (ppm) | 0.2310 | 0.2100 | 0.1528 | 0.3561 | 0.1059 | 0.4795 | 0.2095 |
| (ppm) | −0.1640 | −0.1014 | −0.1108 | −0.1751 | −0.2135 | 0.1915 | −0.1813 |
| (ppm) | −0.1199 | −0.1785 | −0.1568 | −0.1210 | −0.1812 | −0.1964 | −0.2170 |
| (ppm) | 0.0834 | 0.5543 | −0.7975 | 1.1018 | 0.9184 | −0.1006 | −0.9222 |
| (ppm) | 0.5652 | 0.4680 | 0.2568 | 0.4750 | 0.5810 | −0.7252 | 1.1168 |
| (ppm) | 0.0618 | 0.3218 | 0.0911 | 0.6660 | 0.2012 | 0.3106 | −0.6793 |
| (″) | −0.1669 | 0.1989 | −0.1252 | 0.2270 | −0.1389 | 0.1585 | 0.5027 |
| (″) | 0.2890 | 0.3614 | 0.1423 | 0.5180 | 0.0331 | 0.3029 | 0.5712 |
| (″) | −0.3021 | −0.3992 | −0.2673 | −0.5448 | −0.3001 | −0.5239 | −0.7781 |
| (″) | 0.1665 | 0.1887 | 0.3553 | 0.7222 | 0.3628 | 0.6499 | 0.9026 |
| (″) | 0.1506 | 0.2519 | 0.2645 | 0.4042 | 0.1984 | 0.2353 | 0.5648 |
| (″) | −0.2413 | −0.1235 | −0.3786 | −0.4283 | −0.4807 | −0.4395 | −0.5220 |
| (″) | 0.3448 | 0.8615 | 0.4011 | 0.7038 | 0.3126 | 0.5732 | 0.9560 |
| (″) | 0.1160 | 0.3993 | 0.3379 | 0.3820 | 0.5392 | 0.3255 | 0.9529 |
| (″) | 0.4830 | 0.3893 | 0.4517 | 0.4436 | 0.3257 | 0.3720 | 0.7392 |
| (″) | 0.0563 | 0.0611 | 0.2052 | 0.2174 | 0.2938 | 0.2404 | 0.3120 |
| (″) | −0.1074 | 0.5557 | −0.1808 | 0.3342 | −0.3589 | 0.5153 | −0.7725 |
| (″) | 0.0307 | 0.0573 | 0.0952 | 0.0495 | 0.3831 | 0.6351 | 0.6807 |
| Characteristics | Description |
|---|---|
| Sampling frequency | 200 Hz |
| Gyro-constant drift | 0.005 deg/h |
| Gyro-stochastic drift | 0.001 deg/sqrt(h) |
| Gyro-scale factor repeatability | 50 ppm |
| Gyro-constant drift repeatability | 0.001 deg/h |
| Gyro installation error | 0.001 rad |
| Accelerometer constant bias | 10 μg |
| Accelerometer-scale factor repeatability | 50 ppm |
| Accelerometer constant bias repeatability | 10 μg |
| Accelerometer installation error | 0.001 rad |
| Rotation angle accuracy | 0.5″ |
| Rotation velocity accuracy | 0.7″/s |
| Parameter | LSEAVC-KF | LSOAVC-KF | |
|---|---|---|---|
| Ve error (m/s) | RMSE Maximum | 0.0595 0.0870 | 0.1002 0.1515 |
| Vn error (m/s) | RMSE Maximum | 0.0403 0.0661 | 0.0706 0.1092 |
| Pe error (m) | RMSE Maximum | 110.0472 175.9277 | 130.3365 216.0348 |
| Pn error (m) | RMSE Maximum | 40.4820 100.6326 | 82.8674 185.4080 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Lai, J.; Lyu, P.; Liu, R.; Gao, W. A Fast Self-Calibration Method for Dual-Axis Rotational Inertial Navigation Systems Based on Invariant Errors. Sensors 2024, 24, 597. https://doi.org/10.3390/s24020597
Sun X, Lai J, Lyu P, Liu R, Gao W. A Fast Self-Calibration Method for Dual-Axis Rotational Inertial Navigation Systems Based on Invariant Errors. Sensors. 2024; 24(2):597. https://doi.org/10.3390/s24020597
Chicago/Turabian StyleSun, Xin, Jizhou Lai, Pin Lyu, Rui Liu, and Wentao Gao. 2024. "A Fast Self-Calibration Method for Dual-Axis Rotational Inertial Navigation Systems Based on Invariant Errors" Sensors 24, no. 2: 597. https://doi.org/10.3390/s24020597
APA StyleSun, X., Lai, J., Lyu, P., Liu, R., & Gao, W. (2024). A Fast Self-Calibration Method for Dual-Axis Rotational Inertial Navigation Systems Based on Invariant Errors. Sensors, 24(2), 597. https://doi.org/10.3390/s24020597







