Performance Analysis and Prediction of 5G Round-Trip Time Based on the VMD-LSTM Method
Abstract
:1. Introduction
2. Related Works
2.1. Measurement and Analysis of 5G RTT
2.2. Prediction of 5G RTT
2.2.1. Models Based on 5G RTT Theory
2.2.2. Methods Based on 5G RTT Timing
2.2.3. Examples of 5G RTT Prediction
2.3. The Contributions of This Paper
- For real factory scenarios, we propose a 5G RTT prediction method with low prediction error and good transferability, demonstrating the feasibility of applying 5G in factory scenarios with low latency requirements;
- The sensitivity analysis of the model’s prediction performance to parameters provides readers with a basis for selecting model parameters;
- The proposed model prediction accuracy metric TC, combined with the control domain, offers a new perspective on how to select control periods and when to retrain the model.
3. Test Environment Setting
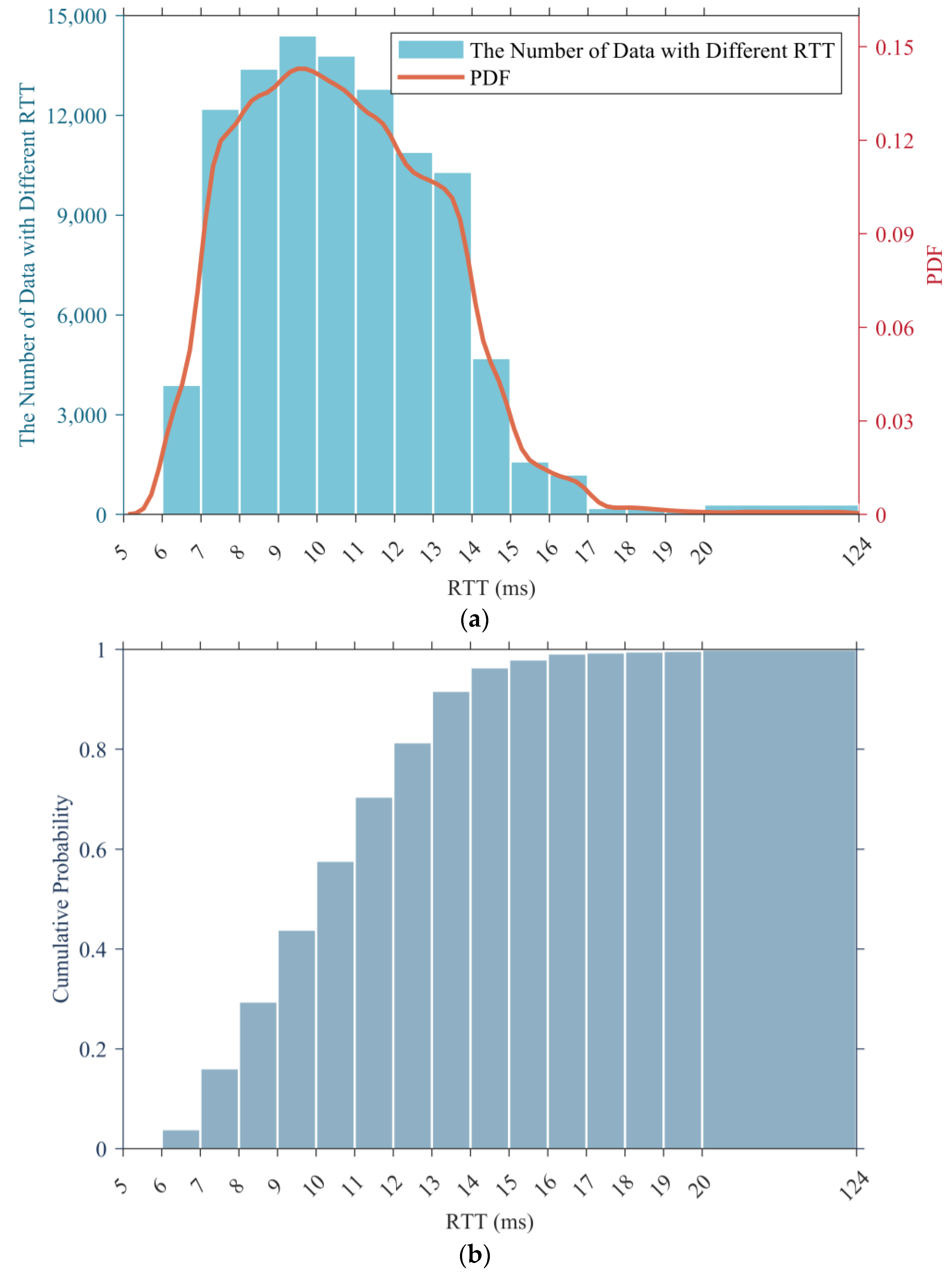
4. Statistical Analysis of 5G RTT Data
5. Time Series Analysis of 5G RTT Data
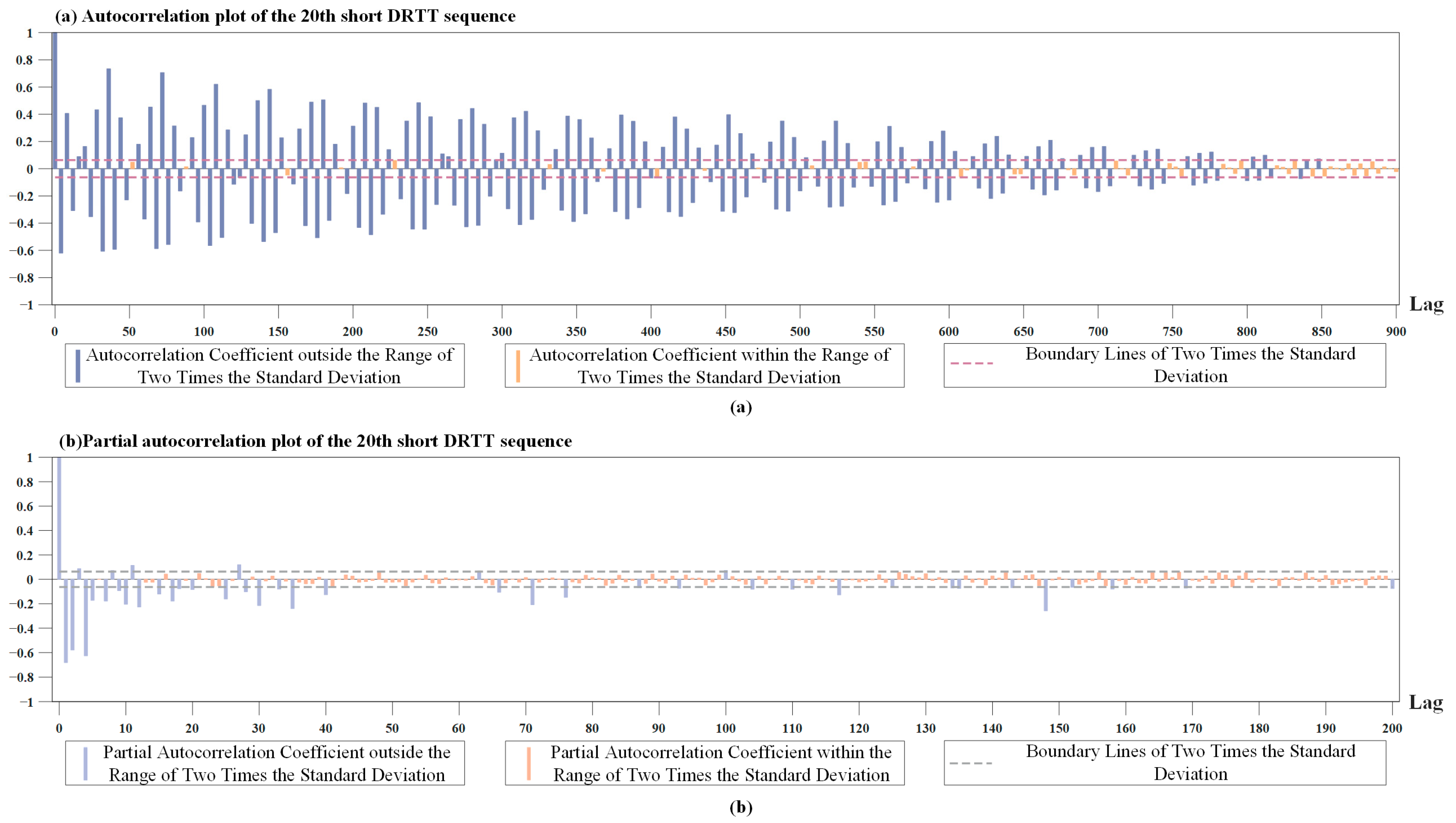
5.1. Stationary Analysis of RTT Series
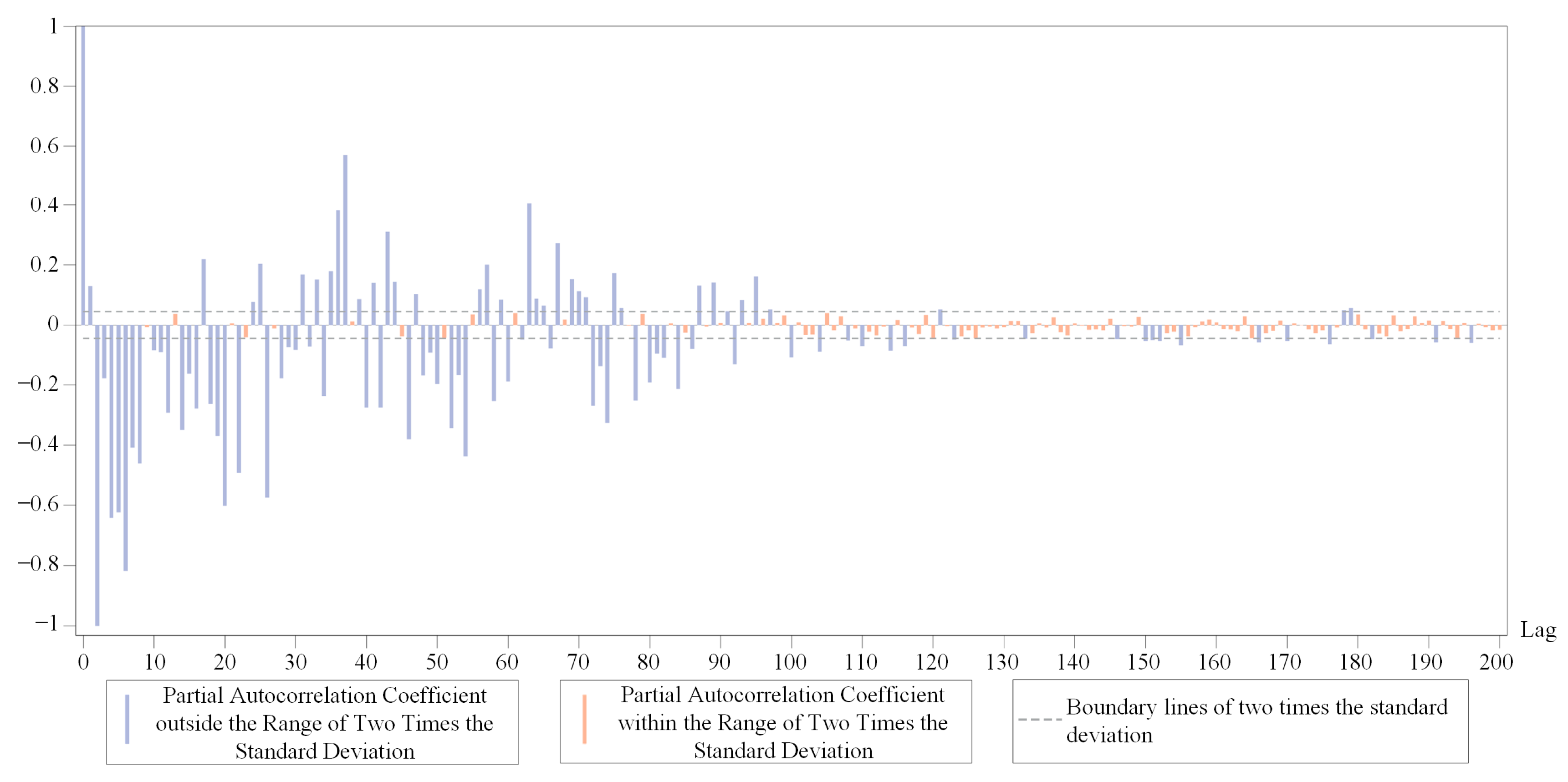
5.2. Correlation Coefficient Analysis of Differential RTT Series
6. 5G RTT Prediction with the Time Series Analysis-Based VMD-LSTM Method
6.1. Decomposing the 5G DRTT Series with the VMD Method
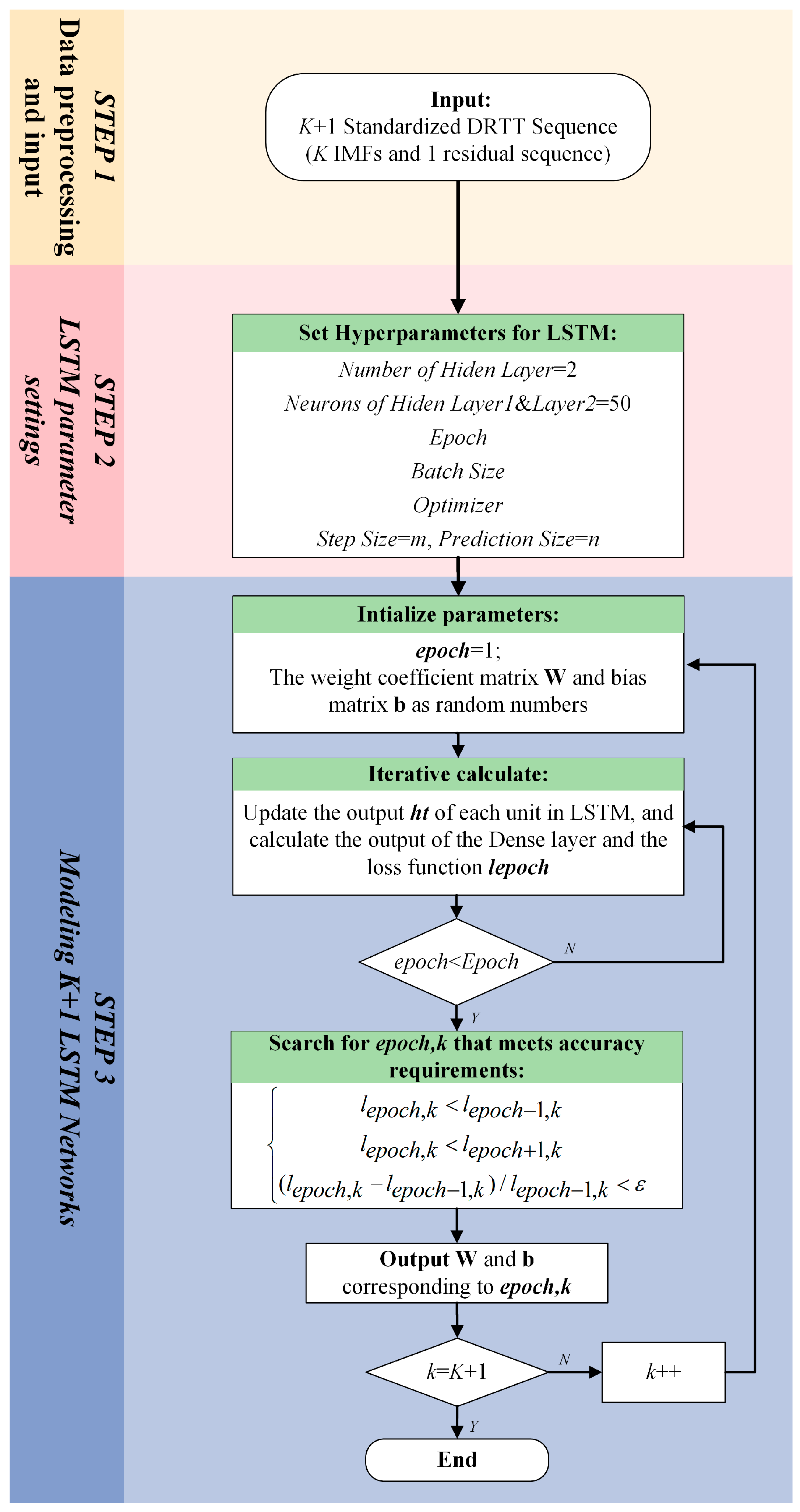
6.2. 5G RTT Prediction Method Based on VMD-LSTM
7. Results and Discussion
7.1. Prediction Performance Evaluation Metrics
- (1)
- Before sending motion commands, the central controller must take into account the offsets caused by the latency time on the AGV’s position and speed in order to calculate the appropriate command values. Therefore, the accuracy of RTT prediction determines the accuracy of the synchronous motion commands;
- (2)
- When the 5G RTT exceeds the AGV’s synchronous control cycle value, it indicates that the commands issued by the central controller were not received by the AGV within the current cycle. If the AGV misses multiple synchronous commands, the system may lose stability. To avoid this situation, a compensation control strategy should be preset and then activated when it is predicted that the AGV will soon be unable to receive synchronous commands. Therefore, accurately predicting whether control commands can be received within each control cycle is crucial for the stability of the system.
7.1.1. Prediction Accuracy Metrics
7.1.2. Early Warning Accuracy Metrics for Control Issues
- (1)
- Indicating when to retrain the model.
- (2)
- Indicating the setting of the control cycle.
7.2. Impact of Hyperparameters on Predictive Performance
7.2.1. Epoch
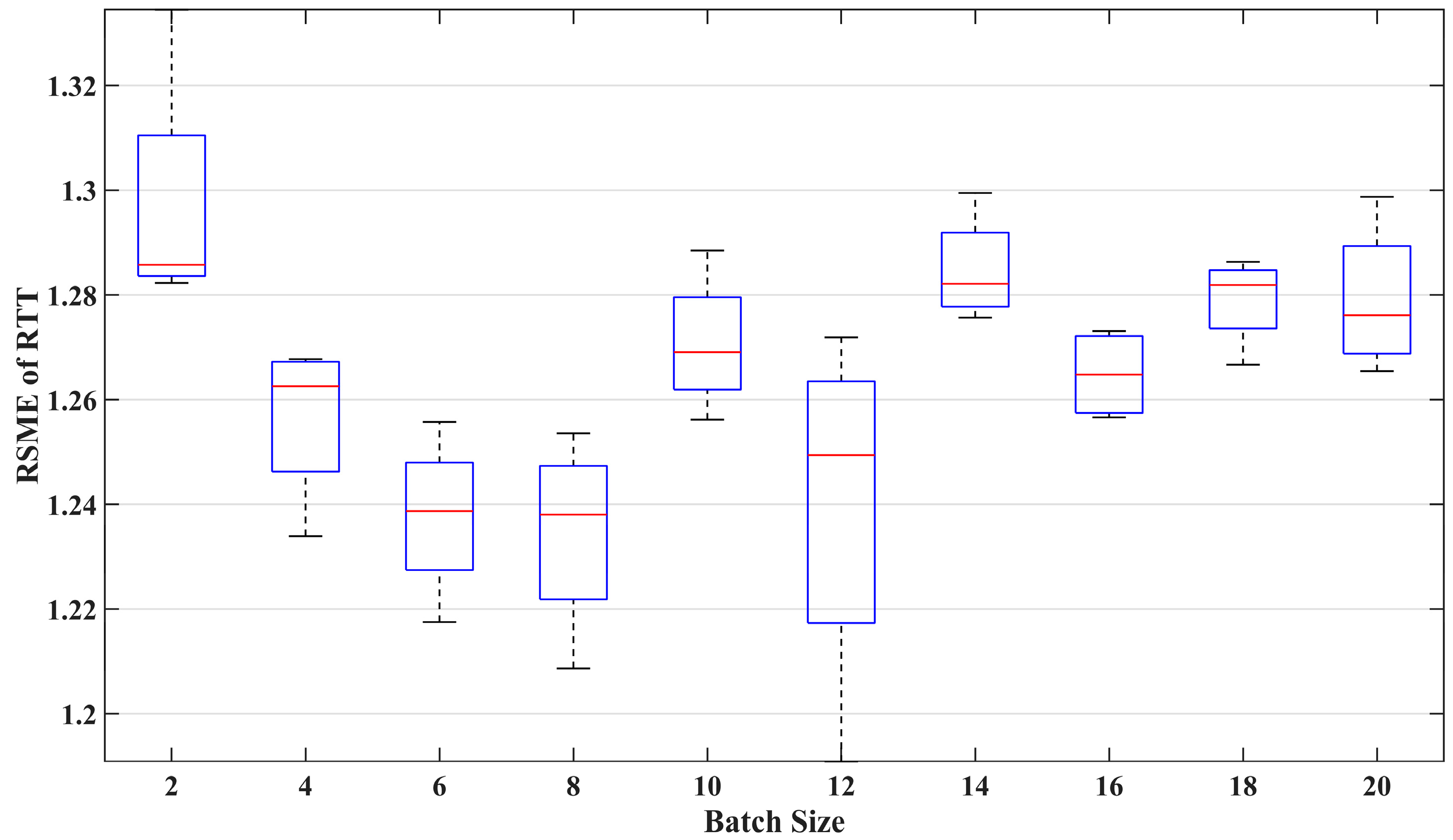
7.2.2. Batch Size
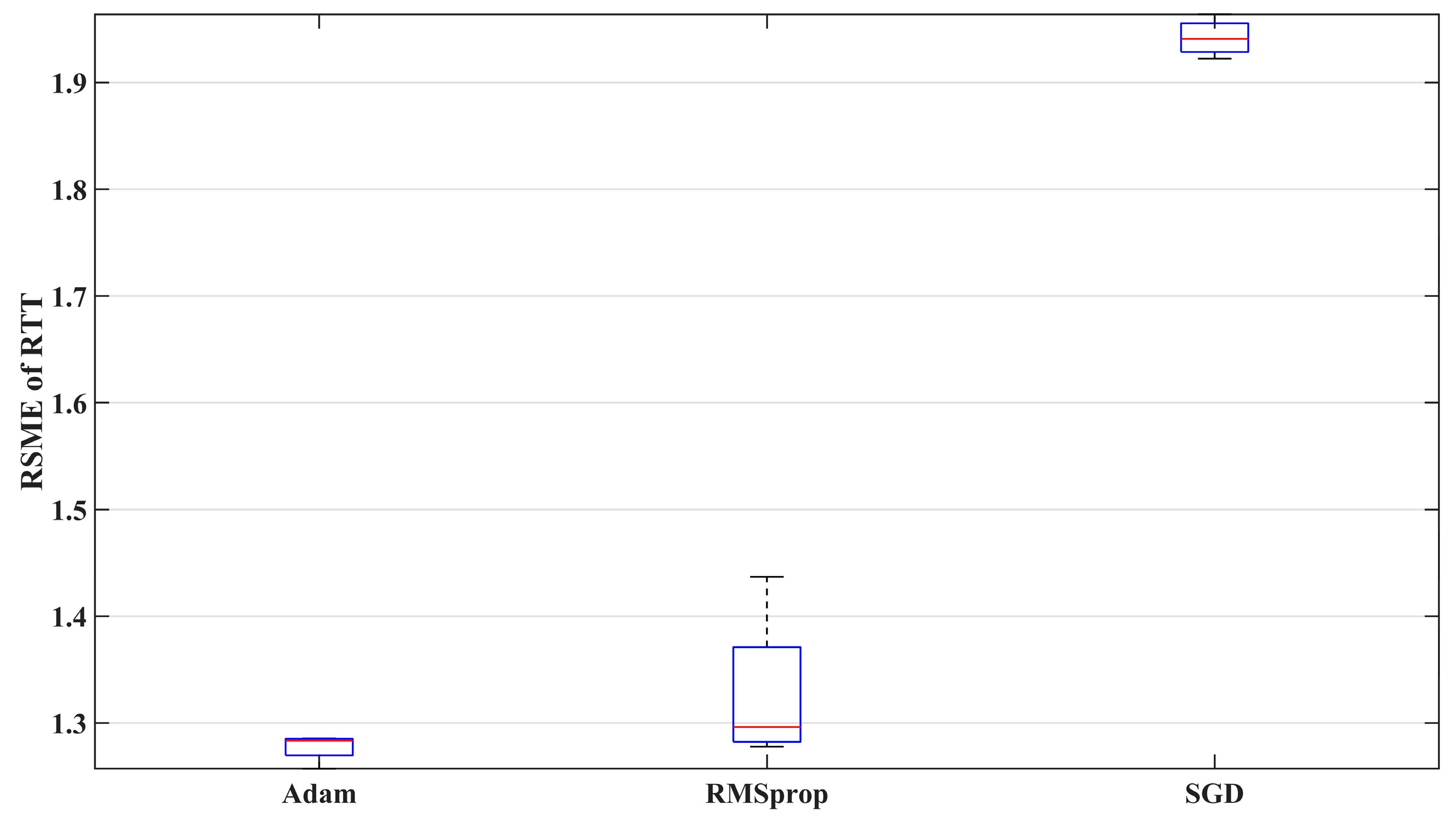
7.2.3. Optimizer
7.2.4. Time Step
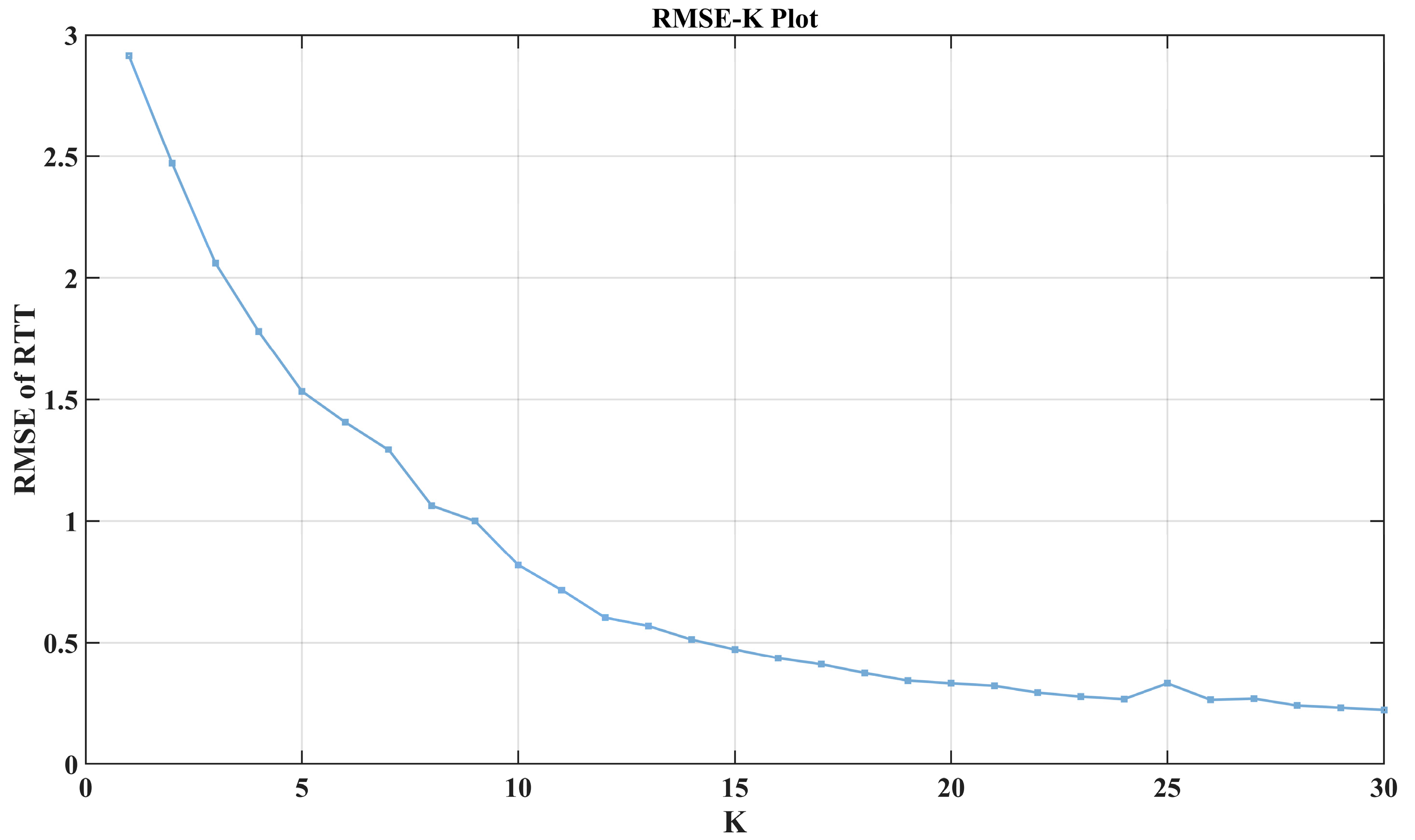
7.2.5. K
- (1)
- Randomly extract a continuous 2000 data points from Dataset 8 to test the prediction errors of the existing models.
- (2)
- For each fixed K value, the trained K-th model set is used to predict the data selected in step (1), and the corresponding RTT prediction error RMSE is calculated. This results in 30 RMSE values for different K values (from 1 to 30), referred to as a set of RMSE values for Dataset 8.
- (3)
- Steps (1) and (2) are repeated a total of 10 times, resulting in 10 sets of RMSE values.
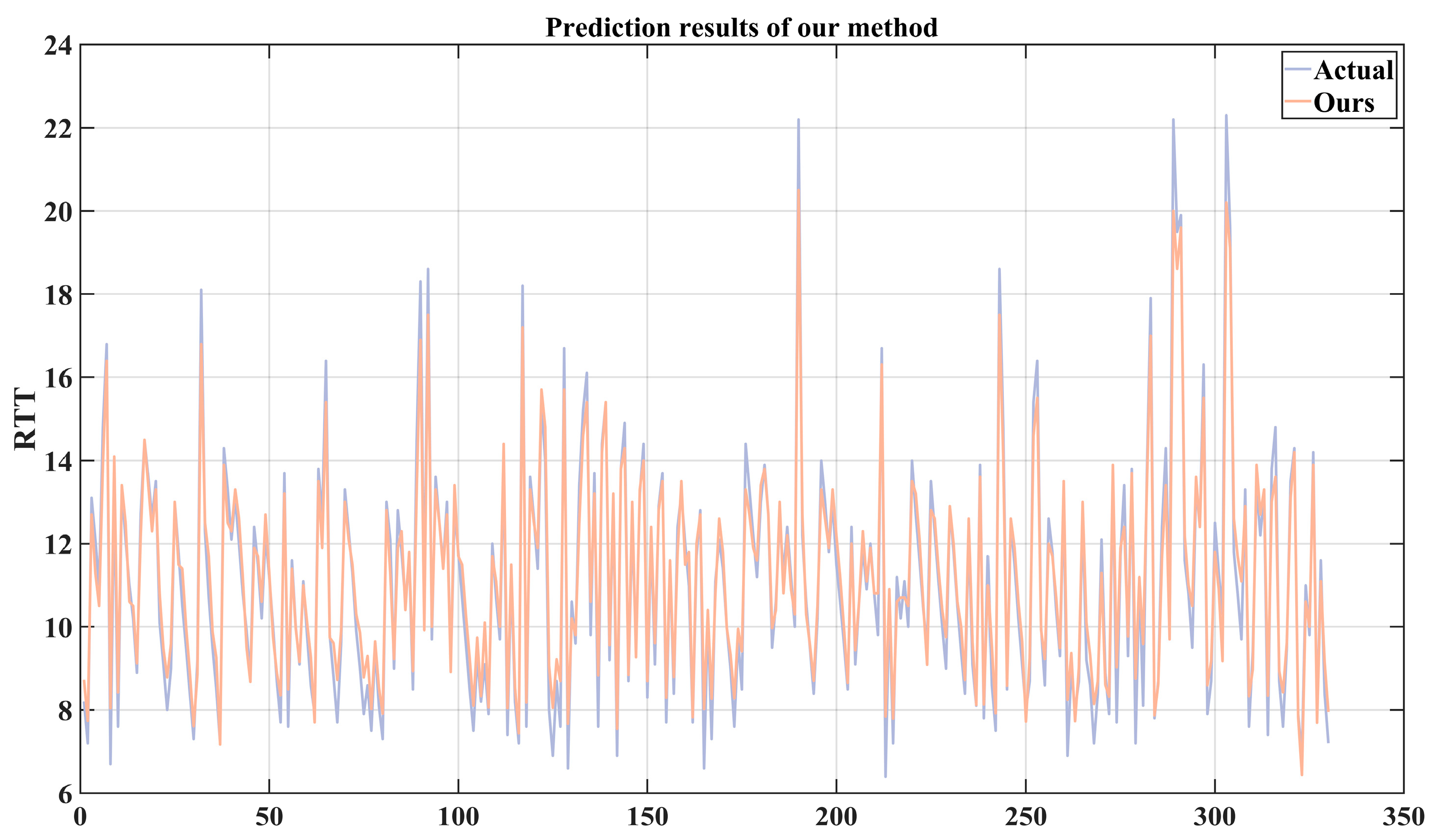
7.3. Comparison of Prediction Performance of Different Methods
- a.
- LSTM
- b.
- EEMD-LSTM
- c.
- VMD-LSTM
- d.
- The time series analysis-based VMD-LSTM prediction method proposed in this paper.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, J.-R. An Improved Cyber-Physical Systems Architecture for Industry 4.0 Smart Factories. Adv. Mech. Eng. 2018, 10, 1687814018784192. [Google Scholar] [CrossRef]
- Ding, K.; Chan, F.; Zhang, X.; Zhou, G.; Zhang, F. Defining a Digital Twin-Based Cyber-Physical Production System for Autonomous Manufacturing in Smart Shop Floors. Int. J. Prod. Res. 2019, 57, 6315–6334. [Google Scholar] [CrossRef]
- Xu, H.; Yu, W.; Griffith, D.; Golmie, N. A Survey on Industrial Internet of Things: A Cyber-Physical Systems Perspective. IEEE Access 2018, 6, 78238–78259. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, W.; Tao, F.; Lin, C.-L. Industrial IoT in 5G Environment towards Smart Manufacturing. J. Ind. Inf. Integr. 2018, 10, 10–19. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, J. Comparative Examination on Architecture and Protocol of Industrial Wireless Sensor Network Standards. IEEE Commun. Surv. Tutor. 2016, 18, 2197–2219. [Google Scholar] [CrossRef]
- Liang, W.; Zheng, M.; Zhang, J.; Shi, H.; Yu, H.; Yang, Y.; Liu, S.; Yang, W.; Zhao, X. WIA-FA and Its Applications to Digital Factory: A Wireless Network Solution for Factory Automation. Proc. IEEE 2019, 107, 1053–1073. [Google Scholar] [CrossRef]
- Willig, A.; Matheus, K.; Wolisz, A. Wireless Technology in Industrial Networks. Proc. IEEE 2005, 93, 1130–1151. [Google Scholar] [CrossRef]
- Gungor, V.C.; Hancke, G.P. Industrial Wireless Sensor Networks: Challenges, Design Principles, and Technical Approaches. IEEE Trans. Ind. Electron. 2009, 56, 4258–4265. [Google Scholar] [CrossRef]
- Zand, P.; Chatterjea, S.; Das, K.; Havinga, P. Wireless Industrial Monitoring and Control Networks: The Journey So Far and the Road Ahead. J. Sens. Actuator Netw. 2012, 1, 123–152. [Google Scholar] [CrossRef]
- Case Studies—5G in Verticals in China 2022. Connected Manufacturing. Available online: https://www.gsma.com/solutions-and-impact/industries/connected-manufacturing/gsma_resources/greater-china-5g-vertical-2022/ (accessed on 3 June 2023).
- Bazzi, A.; Chafii, M. On Outage-Based Beamforming Design for Dual-Functional Radar-Communication 6G Systems. IEEE Trans. Wirel. Commun. 2023, 22, 5598–5612. [Google Scholar] [CrossRef]
- Chafii, M.; Bariah, L.; Muhaidat, S.; Debbah, M. Twelve Scientific Challenges for 6G: Rethinking the Foundations of Communications Theory. IEEE Commun. Surv. Tutor. 2023, 25, 868–904. [Google Scholar] [CrossRef]
- Lackner, T.; Hermann, J.; Dietrich, F.; Kuhn, C.; Angos, M.; Jooste, J.L.; Palm, D. Measurement and Comparison of Data Rate and Time Delay of End-Devices in Licensed Sub-6 GHz 5G Standalone Non-Public Networks. Procedia CIRP 2022, 107, 1132–1137. [Google Scholar] [CrossRef]
- Rischke, J.; Sossalla, P.; Itting, S.; Fitzek, F.H.P.; Reisslein, M. 5G Campus Networks: A First Measurement Study. IEEE Access 2021, 9, 121786–121803. [Google Scholar] [CrossRef]
- Ficzere, D.; Soos, G.; Varga, P.; Szalay, Z. Real-Life V2X Measurement Results for 5G NSA Performance on a High-Speed Motorway. In Proceedings of the 2021 IFIP/IEEE International Symposium on Integrated Network Management (IM), Bordeaux, France, 17–21 May 2021; pp. 836–841. [Google Scholar]
- del Peral-Rosado, J.A.; Gunnarsson, F.; Dwivedi, S.; Razavi, S.M.; Renaudin, O.; López-Salcedo, J.A.; Seco-Granados, G. Exploitation of 3D City Maps for Hybrid 5G RTT and GNSS Positioning Simulations. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 9205–9209. [Google Scholar]
- Wang, L.; Liu, Q.; Zang, C.; Zhu, S.; Gan, C.; Liu, Y. Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks. Machines 2021, 9, 318. [Google Scholar] [CrossRef]
- Zinno, S.; Affinito, A.; Pasquino, N.; Ventre, G.; Botta, A. Prediction of RTT Through Radio-Layer Parameters in 4G/5G Dual-Connectivity Mobile Networks. In Proceedings of the 2023 IEEE Symposium on Computers and Communications (ISCC), Gammarth, Tunisia, 9–12 July 2023; pp. 213–218. [Google Scholar]
- Liu, Z.; Sheng, Z. URLLC Occasional Large Time Delay Prediction Based on Unbalanced Regression and LSTM. Phys. Commun. 2022, 54, 101785. [Google Scholar] [CrossRef]
- On the Performance of an Indoor Open-Source 5G Standalone Deployment. Available online: https://ieeexplore.ieee.org/abstract/document/10118776 (accessed on 30 September 2024).
- Kourtis, M.-A.; Oikonomakis, A.; Santorinaios, D.; Anagnostopoulos, T.; Xilouris, G.; Kourtis, A.; Chochliouros, I.; Zarakovitis, C. 5G NPN Performance Evaluation for I4.0 Environments. Appl. Sci. 2022, 12, 7891. [Google Scholar] [CrossRef]
- Thuy, H.; Anh, D.T.; Chau, V. Efficient segmentation-based methods for anomaly detection in static and streaming time series under dynamic time warping. J. Intell. Inf. Syst. 2021, 56, 121–146. [Google Scholar] [CrossRef]
- Anvari, H.; Lu, P. Learning Mixed Traffic Signatures in Shared Networks. In Proceedings of the 20th Annual International Conference on Computational Science (ICCS), Amsterdam, Netherlands, 3–5 June 2020; pp. 524–537. [Google Scholar]
- Yu, Y.; Zhu, Y.; Wan, D.; Liu, H.; Zhao, Q. A Novel Symbolic Aggregate Approximation for Time Series. In Proceedings of the 13th International Conference on Ubiquitous Information Management and Communication (IMCOM), Phuket, Thailand, 4–6 January 2019; pp. 805–822. [Google Scholar]
- Pan, H.; Lin, Z.; Gui, G. Enabling Damage Identification of Structures Using Time Series-Based Feature Extraction Algorithms. J. Aerosp. Eng. 2019, 32, 04019014. [Google Scholar] [CrossRef]
- Severin, I.C.; Dobrea, D.M. 6DOF Inertial IMU Head Gesture Detection: Performance Analysis Using Fourier Transform and Jerk-Based Feature Extraction. In Proceedings of the 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2020; pp. 118–123. [Google Scholar]
- Kiskin, I.; Zilli, D.; Li, Y.; Sinka, M.; Willis, K.; Roberts, S. Bioacoustic Detection with Wavelet-Conditioned Convolutional Neural Networks. Neural Comput. Appl. 2020, 32, 915–927. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Li, J.; Shi, G.; Zhang, C.; Ma, H. Time Series Prediction of 5G Network Data Based on Improved EEMD-BiLSTM Prediction Model. In Advanced Intelligent Computing Technology and Applications; Lecture Notes in Computer Science; Huang, D.-S., Premaratne, P., Jin, B., Qu, B., Jo, K.-H., Hussain, A., Eds.; Springer Nature: Singapore, 2023; Volume 14090, pp. 409–420. ISBN 978-981-9947-60-7. [Google Scholar]
- Li, Y.; Liu, R.; Liu, Z.; Liu, J. Similarity Grouping-Guided Neural Network Modeling for Maritime Time Series Prediction. IEEE Access 2019, 7, 72647–72659. [Google Scholar] [CrossRef]
- Chengsong, H. Time Delay Analysis of Deterministic Network 5G-A Terminals. Adv. Comput. Signals Syst. 2023, 7, 57–61. [Google Scholar] [CrossRef]
- Bi, J.; Ma, H.; Yuan, H.; Zhang, J. Accurate Prediction of Workloads and Resources with Multi-Head Attention and Hybrid LSTM for Cloud Data Centers. IEEE Trans. Sustain. Comput. 2023, 8, 375–384. [Google Scholar] [CrossRef]
- Wu, K.; Lu, J.; Lin, F.; Huang, Y.; Zhan, C.; Sun, L. A Realistic Network Traffic Forecasting Method Based on VMD and LSTM Network. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhou, T.; Wu, W.; Peng, L.; Zhang, M.; Li, Z.; Xiong, Y.; Bai, Y. Evaluation of Urban Bus Service Reliability on Variable Time Horizons Using a Hybrid Deep Learning Method. Reliab. Eng. Syst. Saf. 2022, 217, 108090. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, W. A Method of Combining Hidden Markov Model and Convolutional Neural Network for the 5G RCS Message Filtering. Appl. Sci. 2021, 11, 6350. [Google Scholar] [CrossRef]
- Hou, Y.; Kawasaki, S.; Denno, S. Busy/Idle Duration Prediction for Video and Audio WLAN Traffics Using Autoregressive Predictor with Data Categorization. In Proceedings of the 2022 24th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 13–16 February 2022; pp. 259–264. [Google Scholar]
- Lin, Y.; Gao, Y.; Dong, W. Bandwidth Prediction for 5G Cellular Networks. In Proceedings of the 2022 IEEE/ACM 30th International Symposium on Quality of Service (IWQoS), Oslo, Norway, 10–12 June 2022; pp. 1–10. [Google Scholar]
- Benslimen, Y.; Sedjelmaci, H.; Manenti, A. Attacks and Failures Prediction Framework for a Collaborative 5G Mobile Network. Computing 2021, 103, 1165–1181. [Google Scholar] [CrossRef]
- Ji, S.-Y.; Jeong, B.K.; Kamhoua, C.; Leslie, N.; Jeong, D.H. Forecasting Network Events to Estimate Attack Risk: Integration of Wavelet Transform and Vector Auto Regression with Exogenous Variables. J. Netw. Comput. Appl. 2022, 203, 103392. [Google Scholar] [CrossRef]
- Bai, P.; Safikhani, A.; Michailidis, G. Multiple Change Points Detection in Low Rank and Sparse High Dimensional Vector Autoregressive Models. IEEE Trans. Signal Process. 2020, 68, 3074–3089. [Google Scholar] [CrossRef]
- Dong, A.; Du, Z.; Yan, Z. Round Trip Time Prediction Using Recurrent Neural Networks with Minimal Gated Unit. IEEE Commun. Lett. 2019, 23, 584–587. [Google Scholar] [CrossRef]
- He, T.; Mao, H.; Yi, Z. Subtraction Gates: Another Way to Learn Long-Term Dependencies in Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1740–1751. [Google Scholar] [CrossRef]
- Apolinario, G.F.D.G.; Hong, Y.; Lee, Y.; Jiang, J.; Wang, S. Comparative Studies on Use of Discrete Wavelet Transform-based Feature Extraction for Peak Load Forecasting Using LSTM. In Proceedings of the 2021 IEEE 4th International Conference on Power and Energy Applications (ICPEA), Busan, Republic of Korea, 9–11 October 2021; pp. 88–92. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Zeng, C.; Ma, C.; Wang, K.; Cui, Z. Parking Occupancy Prediction Method Based on Multi Factors and Stacked GRU-LSTM. IEEE Access 2022, 10, 47361–47370. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef] [PubMed]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- 3GPP. 5G from 3GPP: Release 15; 3GPP: Geneva, Switzerland, 2020. [Google Scholar]
- Aumiwalker. Product Center. Available online: http://www.aumiwalker.com/product/85.html (accessed on 28 August 2022).
- Dai, L.; Fang, Y.; Guan, Y.; Mohsen, G. Design of Protograph LDPC-coded MIMO-VLC Systems with Generalized Spatial Modulation. China Commun. 2024, 21, 118–136. [Google Scholar]
- Shao, S.; Hailes, P.; Wang, T.Y.; Wu, J.Y.; Maunder, R.G.; Al-Hashimi, B.M.; Hanzo, L. Survey of Turbo, LDPC, and Polar Decoder ASIC Implementations. IEEE Commun. Surv. Tutor. 2019, 21, 2309–2333. [Google Scholar] [CrossRef]
- Paparoditis, E.; Politis, D.N. The Asymptotic Size and Power of the Augmented Dickey–Fuller Test for a Unit Root. Economet. Rev. 2018, 37, 955–973. [Google Scholar] [CrossRef]
- Ng, S.; Perron, P. Unit Root Tests in ARMA Models with Data-Dependent Methods for the Selection of the Truncation Lag. J. Am. Stat. Assoc. 1994, 90, 268–281. [Google Scholar] [CrossRef]
- Wang, Y. Applied Time Series Analysis, 6th ed.; China Renmin University Press: Beijing, China, 2022; p. 44. ISBN 978-73-0030-743-5. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- How to Tune LSTM Hyperparameters with Keras for Time Series Forecasting. Available online: https://machinelearningmastery.com/tune-lstm-hyperparameters-keras-time-series-forecasting/ (accessed on 28 August 2023).
- IEC. Industrial Networks—Wireless Communication Network and Communication Profiles—WIA-FA; IEC: Geneva, Switzerland, 2017. [Google Scholar]





| MCS Index | Modulation Index | Target Code Rate R × [1024] | Spectral Efficiency |
|---|---|---|---|
| 0 | 2 | 120 | 0.2344 |
| 1 | 2 | 157 | 0.3066 |
| 2 | 2 | 193 | 0.3770 |
| 3 | 2 | 251 | 0.4902 |
| 4 | 2 | 308 | 0.6016 |
| 5 | 2 | 379 | 0.7402 |
| 6 | 2 | 449 | 0.8770 |
| 7 | 2 | 526 | 1.0273 |
| 8 | 2 | 602 | 1.1758 |
| 9 | 2 | 679 | 1.3262 |
| 10 | 4 | 340 | 1.3281 |
| 11 | 4 | 378 | 1.4766 |
| 12 | 4 | 434 | 1.6953 |
| 13 | 4 | 490 | 1.9141 |
| 14 | 4 | 553 | 2.1602 |
| 15 | 4 | 616 | 2.4063 |
| 16 | 4 | 658 | 2.5703 |
| 17 | 6 | 438 | 2.5664 |
| 18 | 6 | 466 | 2.7305 |
| 19 | 6 | 517 | 3.0293 |
| 20 | 6 | 567 | 3.3223 |
| 21 | 6 | 616 | 3.6094 |
| 22 | 6 | 666 | 3.9023 |
| 23 | 6 | 719 | 4.2129 |
| 24 | 6 | 772 | 4.5234 |
| 25 | 6 | 822 | 4.8164 |
| 26 | 6 | 873 | 5.1152 |
| 27 | 6 | 910 | 5.3320 |
| 28 | 6 | 948 | 5.5547 |
| 29 | 2 | Reserved | |
| 30 | 4 | Reserved | |
| 31 | 6 | Reserved | |
| Parameters | Value |
|---|---|
| Sub-frame Ratio | 7:3 |
| Carrier Frequency | 3.5 GHz |
| Bandwidth | 100 MHz |
| Cyclic Prefix (CP) Length | Normal |
| Intercarrier Spacing | 30 kHz |
| Channel Coding | Service Channel: LDPC |
| Control Channel: Polar | |
| Modulation Scheme | AMC |
| Frame Duration | 10 ms |
| Number of Slots | 1 Frame: 20 Slots |
| Number of Symbols | 1 Slot: 14 Symbols |
| Duplex Mode | Time Division Duplex (TDD) |
| NR Band | 3.5 GHz–3.6 GHz |
| Dataset Number | Packet Sending Interval (ms) | Packet Length (byte) | Min RTT (ms) | Max RTT (ms) | Mean (ms) | Standard Deviation (ms) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| 1 | 16 | 32 | 6.4 | 123.7 | 10.57 | 2.61 | 8.60 | 352.65 |
| 2 | 16 | 128 | 6.3 | 39.5 | 10.75 | 2.66 | 1.30 | 5.32 |
| 3 | 16 | 640 | 6.4 | 29.3 | 11.16 | 3.03 | 0.96 | 1.97 |
| 4 | 16 | 1024 | 6.5 | 34.4 | 11.13 | 2.74 | 0.57 | 0.56 |
| 5 | 32 | 32 | 6.5 | 186.9 | 11.16 | 3.45 | 19.55 | 902.73 |
| 6 | 32 | 128 | 6.4 | 186.0 | 11.31 | 3.86 | 18.11 | 694.31 |
| 7 | 32 | 640 | 6.4 | 99.2 | 11.10 | 2.67 | 4.24 | 120.96 |
| 8 | 32 | 1024 | 6.5 | 161.5 | 11.23 | 3.32 | 15.00 | 584.45 |
| Short Sequence Number | Lag | p-Value | τ-Statistic | Critical Value (0.05) |
|---|---|---|---|---|
| 1 | 27 | 0.6718 | 0.0548 | −1.9413 |
| 11 | 66 | 0.9374 | 1.1642 | −1.9413 |
| 21 | 36 | 0.8666 | 0.7028 | −1.9413 |
| 31 | 29 | 0.7129 | 0.1671 | −1.9413 |
| 41 | 14 | 0.8302 | 0.5309 | −1.9413 |
| Subsquence Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Epoch | |||||||||
| 25 | *0.0030* | 0.0050 | 0.0040 | 0.0070 | 0.0040 | 0.0060 | 0.0025 | *0.1930* | |
| 50 | 0.0030 | *0.0045* | 0.0040 | *0.0065* | 0.0075 | *0.0055* | 0.0020 | 0.3535 | |
| 100 | 0.0030 | 0.0065 | 0.0040 | 0.0075 | *0.0040* | 0.0065 | 0.0020 | 1.1585 | |
| 200 | 0.0035 | 0.0125 | *0.0020* | 0.0085 | 0.0045 | 0.0075 | *0.0010* | 1.4915 | |
| 300 | 0.0040 | 0.0205 | 0.0110 | 0.0100 | 0.0085 | 0.0080 | 0.0030 | 1.1625 | |
| 400 | 0.0050 | 0.0380 | 0.0135 | 0.0175 | 0.0090 | 0.0080 | 0.0030 | 1.4560 | |
| Time Step | RMSE (ms) | MAPE (%) |
|---|---|---|
| 80 | 1.06 | 7.682 |
| 81 | 1.04 | 7.652 |
| 82 * | 1.05 | 7.655 |
| 83 | 1.05 | 7.701 |
| 84 | 1.06 | 7.654 |
| 70 | 1.069 | 7.925 |
| 50 | 1.08 | 8.288 |
| 30 | 1.112 | 8.657 |
| 10 | 1.134 | 8.926 |
| Methods | RMSE (ms) | MAPE (%) |
|---|---|---|
| LSTM | 2.891 | 20.900 |
| EEMD-LSTM | 2.451 | 16.177 |
| VMD-LSTM | 2.786 | 19.132 |
| Ours | 0.608 | 4.481 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Zhou, S.; Wang, L.; Zang, C.; Liu, Y.; Liu, Q. Performance Analysis and Prediction of 5G Round-Trip Time Based on the VMD-LSTM Method. Sensors 2024, 24, 6542. https://doi.org/10.3390/s24206542
Zhu S, Zhou S, Wang L, Zang C, Liu Y, Liu Q. Performance Analysis and Prediction of 5G Round-Trip Time Based on the VMD-LSTM Method. Sensors. 2024; 24(20):6542. https://doi.org/10.3390/s24206542
Chicago/Turabian StyleZhu, Sanying, Shutong Zhou, Liuquan Wang, Chenxin Zang, Yanqiang Liu, and Qiang Liu. 2024. "Performance Analysis and Prediction of 5G Round-Trip Time Based on the VMD-LSTM Method" Sensors 24, no. 20: 6542. https://doi.org/10.3390/s24206542
APA StyleZhu, S., Zhou, S., Wang, L., Zang, C., Liu, Y., & Liu, Q. (2024). Performance Analysis and Prediction of 5G Round-Trip Time Based on the VMD-LSTM Method. Sensors, 24(20), 6542. https://doi.org/10.3390/s24206542







