A Comparative Study of Geometric Phase Change- and Sideband Peak Count-Based Techniques for Monitoring Damage Growth and Material Nonlinearity
Abstract
:1. Introduction
- (1)
- The GPC-I is proposed for the first time as a damage indicator with high sensitivity;
- (2)
- The effects of linear and nonlinear responses on the behavior of GPC-I are investigated in depth;
- (3)
- A comparison between the available SPC-I technique and the proposed GPC-I technique can reveal the mechanism GPC-I uses to capture linear and nonlinear responses, and thus can provide guidance for SHM applications;
- (4)
- The effects of material nonlinearity on SPC-I and GPC-I are compared;
- (5)
- A fundamental understanding of geometric phase change in practical applications is clarified.
2. Methodology and Theory
3. Model Description and Numerical Modeling
3.1. Peri-Ultrasound and FEM Modeling for Cracked Geometry
3.2. FEM Modeling for Material Nonlinearity Problems
4. Numerical Modeling Results
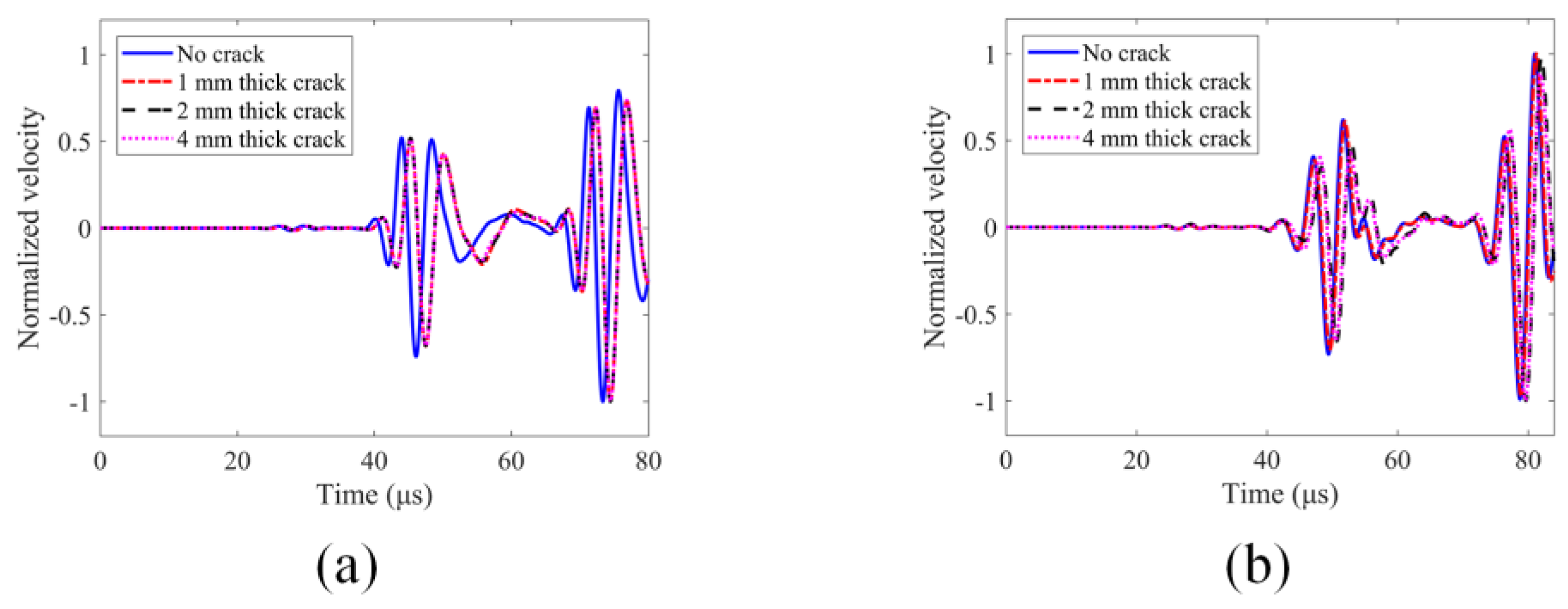
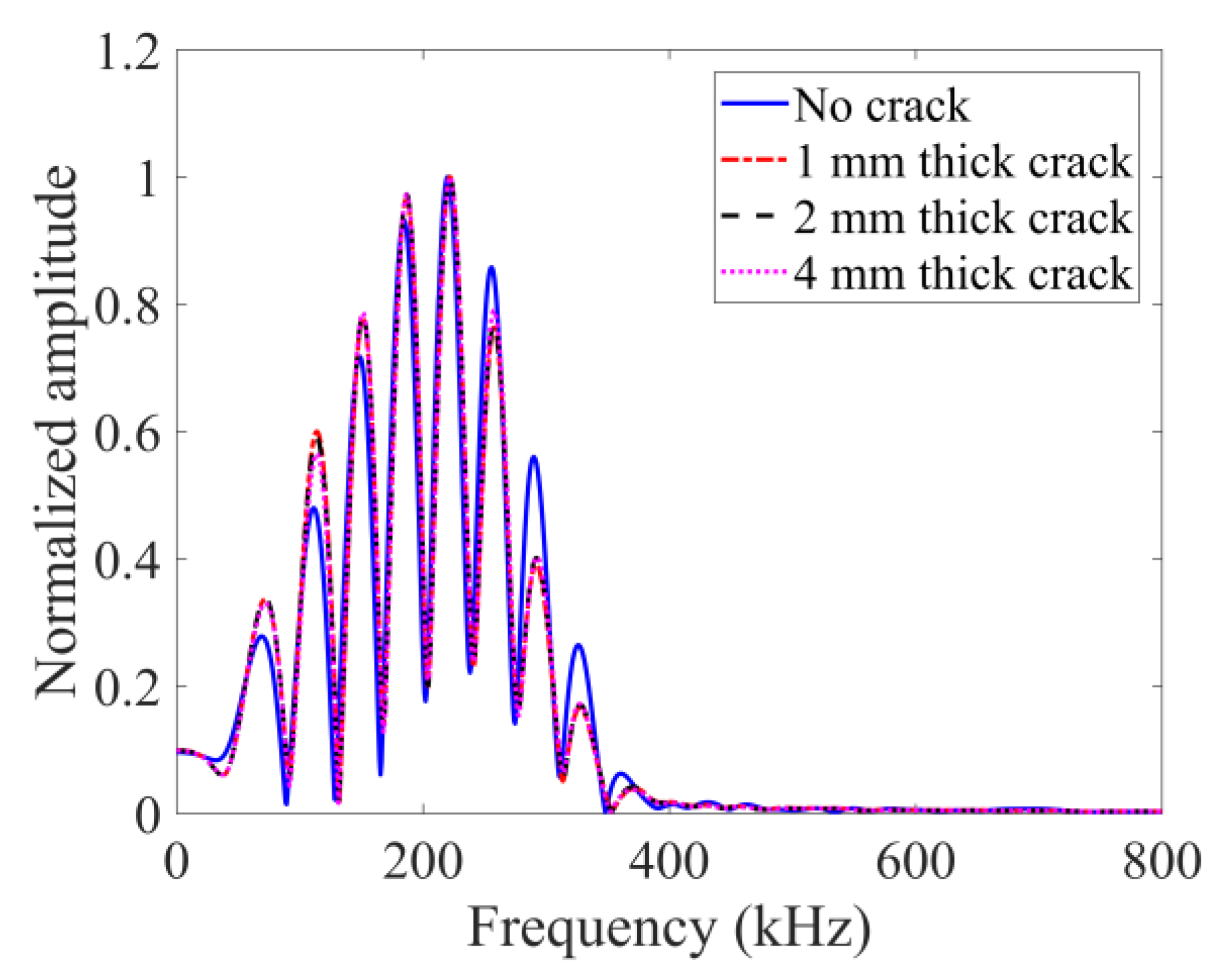
4.1. Effects of FEM and Peri-Ultrasound Modeling on Wave Propagation
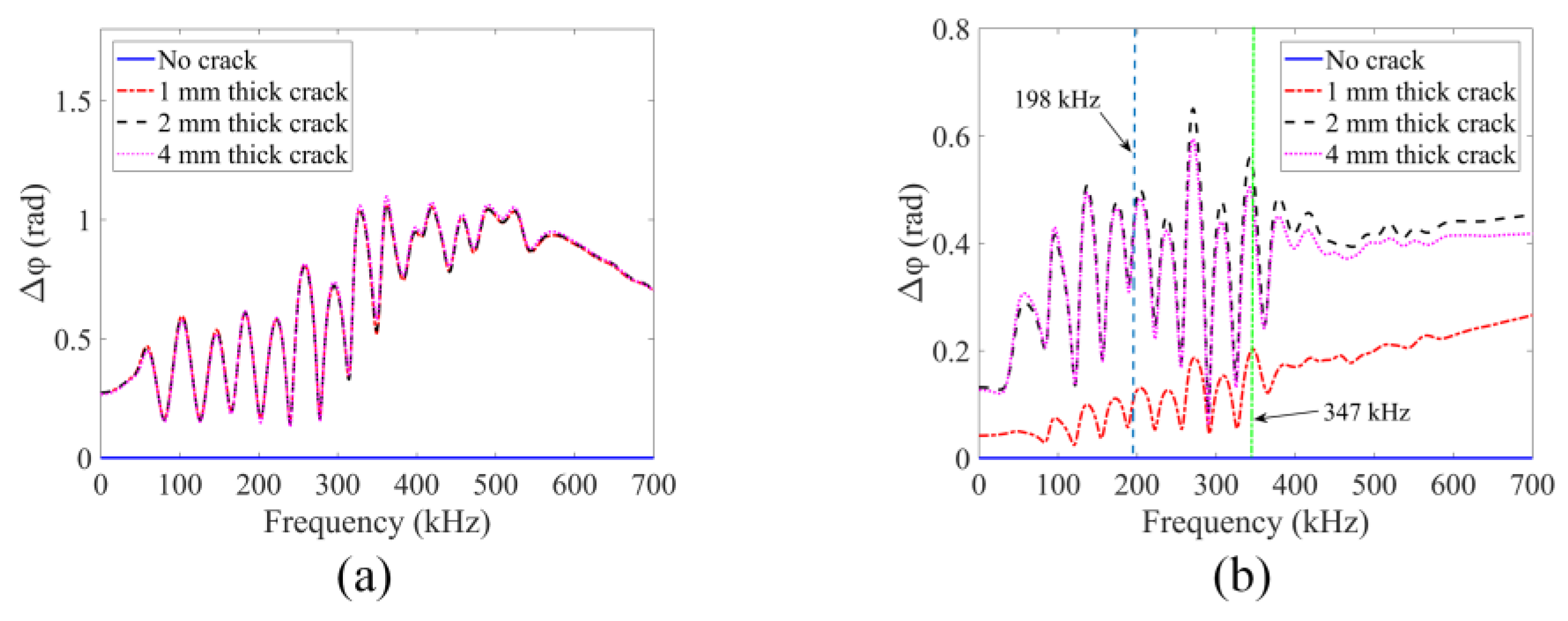
4.2. GPC Computation for Damage Growth
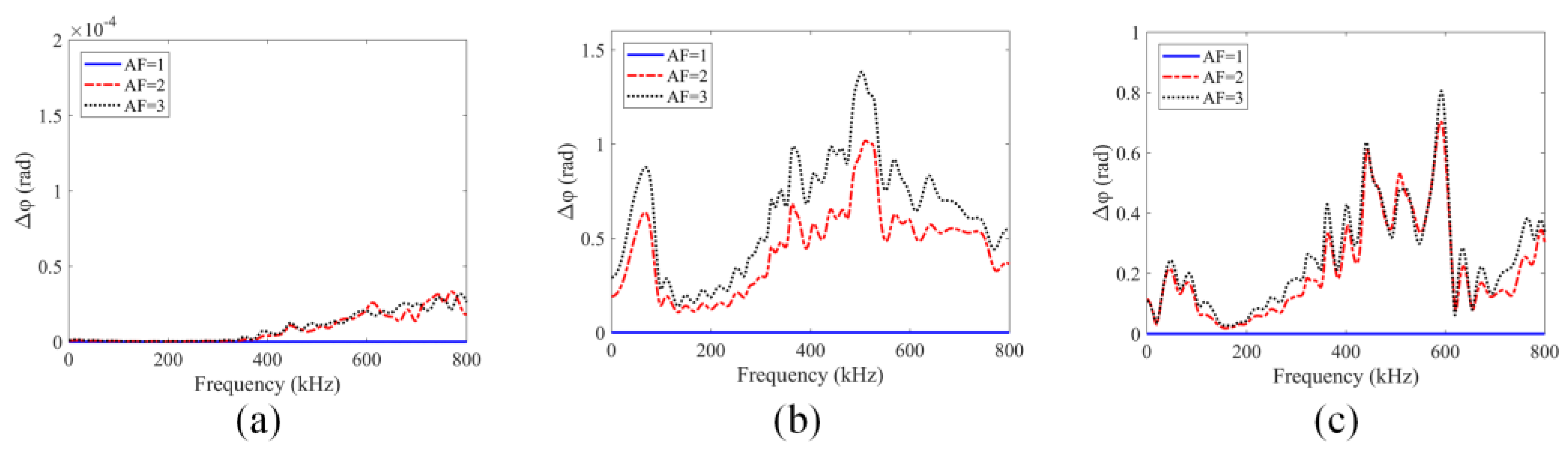
4.3. GPC Computation for Material Nonlinearity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Hashim, K.; Yeboah, D. Recent advancements in non-destructive testing techniques for structural health mon-itoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Li, T.; Kundu, T. Monitoring elastoplastic deformation in ductile metallic materials using sideband peak count-index (SPC-I) technique. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2023, 6, 1–15. [Google Scholar]
- Park, S.; Alnuaimi, H.N.; Hayes, A.; Sitkiewicz, M.; Amjad, U.; Muralidharan, K.; Kundu, T. Nonlinear Acoustic Technique for Monitoring Porosity in Additively Manufactured Parts. J. Nondestruct. Evaluation, Diagn. Progn. Eng. Syst. 2022, 5, 021008. [Google Scholar] [CrossRef]
- Park, S.H.; Kundu, T. A modified sideband peak count based nonlinear ultrasonic technique for material characterization. Ultrasonics 2023, 128, 106858. [Google Scholar] [CrossRef]
- Lata, T.D.; Deymier, P.A.; Runge, K.; Clark, W. Topological Acoustic Sensing Using Nonseparable Superpositions of Acoustic Waves. Vibration 2022, 5, 513–529. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Li, X.; Chen, C.; Zhou, K. Evaluating the reinforcement content and elastic properties of Mg-based composites using dual-mode ultrasonic velocities. Ultrasonics 2017, 81, 167–173. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, X.; Li, X.; Song, Y.; Zhang, S. Measurement of shear wave attenuation coefficient using a contact pulse-echo method with con-sideration of partial reflection effects. Meas. Sci. Technol. 2019, 30, 115601. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Zhang, S.; Kundu, T. Investigation of frequency-dependent attenuation coefficients for multiple solids using a reliable pulse-echo ultrasonic measurement technique. Measurement 2021, 177, 109270. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Zhang, G. A Crack Size Quantification Method Using High-Resolution Lamb Waves. Sensors 2021, 21, 6941. [Google Scholar] [CrossRef]
- Marino, D.; Kim, J.-Y.; Ruiz, A.; Joo, Y.-S.; Qu, J.; Jacobs, L.J. Using nonlinear ultrasound to track microstructural changes due to thermal aging in modified 9%Cr ferritic martensitic steel. NDT E Int. 2016, 79, 46–52. [Google Scholar] [CrossRef]
- Doerr, C.; Kim, J.-Y.; Singh, P.; Wall, J.J.; Jacobs, L.J. Evaluation of sensitization in stainless steel 304 and 304L using nonlinear Rayleigh waves. NDT E Int. 2017, 88, 17–23. [Google Scholar] [CrossRef]
- Thiele, S.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Air-coupled detection of nonlinear Rayleigh surface waves to assess material nonlinearity. Ultrasonics 2014, 54, 1470–1475. [Google Scholar] [CrossRef]
- Donskoy, D.M.; Sutin, A.M. Vibro-Acoustic Modulation Nondestructive Evaluation Technique. J. Intell. Mater. Syst. Struct. 1998, 9, 765–771. [Google Scholar] [CrossRef]
- Duffour, P.; Morbidini, M.; Cawley, P. A study of the vibro-acoustic modulation technique for the detection of cracks in metals. J. Acoust. Soc. Am. 2006, 119, 1463–1475. [Google Scholar] [CrossRef]
- Van Den Abeele, K.E.A.; Johnson, P.A.; Sutin, A. Nonlinear elastic wave spectroscopy (NEWS) techniques to discern material damage, part I: Nonlinear wave modulation spectroscopy (NWMS). J. Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar] [CrossRef]
- Van Den Abeele, K.E.A.; Carmeliet, J.; Ten Cate, J.A.; Johnson, P.A. Nonlinear elastic wave spectroscopy (NEWS) techniques to discern material damage, Part II: Single-mode nonlinear resonance acoustic spectroscopy. J. Res. Nondestruct. Eval. 2000, 12, 31–42. [Google Scholar] [CrossRef]
- Alnuaimi, H.; Amjad, U.; Russo, P.; Lopresto, V.; Kundu, T. Monitoring damage in composite plates from crack initiation to macro-crack propagation combining linear and nonlinear ultrasonic techniques. Struct. Heal. Monit. 2021, 20, 139–150. [Google Scholar] [CrossRef]
- Alnuaimi, H.; Amjad, U.; Park, S.; Russo, P.; Lopresto, V.; Kundu, T. An improved nonlinear ultrasonic technique for detecting and monitoring impact induced damage in composite plates. Ultrasonics 2022, 119, 106620. [Google Scholar] [CrossRef]
- Alnuaimi, H.N.; Sasmal, S.; Amjad, U.; Nikvar-Hassani, A.; Zhang, L.; Kundu, T. Monitoring Concrete Curing by Linear and Nonlinear Ultrasonic Methods. ACI Mater. J. 2022, 118, 61–69. [Google Scholar] [CrossRef]
- Basu, S.; Thirumalaiselvi, A.; Sasmal, S.; Kundu, T. Nonlinear ultrasonics-based technique for monitoring damage progression in reinforced concrete structures. Ultrasonics 2021, 115, 106472. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Bokhari, I.; Alnuaimi, H.; Amjad, U.; Fleischman, R.; Kundu, T. Early detection of steel tube welded joint failure using SPC-I nonlinear ultrasonic technique. Struct. Heal. Monit. 2024, 14759217241235057. [Google Scholar] [CrossRef]
- Arumaikani, T.; Sasmal, S.; Kundu, T. Detection of initiation of corrosion induced damage in concrete structures using nonlinear ultrasonic techniques. J. Acoust. Soc. Am. 2022, 151, 1341–1352. [Google Scholar] [CrossRef] [PubMed]
- Castellano, A.; Fraddosio, A.; Paparella, F.; Piccioni, M.D.; Kundu, T. The evaluation of the adhesion defects in FRCM reinforcements for masonry constructions by Sideband Peak Count based nonlinear acoustic technique. J. Vib. Control. 2023. [Google Scholar] [CrossRef]
- Wang, M.; Pau, A.; Zhang, G.; Kundu, T. Monitoring prestress in plates by sideband peak count-index (SPC-I) and nonlinear higher harmonics techniques. Nonlinear Dyn. 2023, 111, 15749–15766. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, B.; Alnuaimi, H.; Amjad, U.; Kundu, T. Numerical modeling with experimental verification investigating the effect of various nonlinearities on the sideband peak count-index technique. Ultrasonics 2024, 138, 107259. [Google Scholar] [CrossRef]
- Lata, T.D.; Deymier, P.A.; Runge, K.; Le Tourneau, F.-M.; Ferrière, R.; Huettmann, F. Topological acoustic sensing of spatial patterns of trees in a model forest landscape. Ecol. Model. 2020, 419, 108964. [Google Scholar] [CrossRef]
- Lata, T.D.; Deymier, P.A.; Runge, K.; Ferrière, R.; Huettmann, F. Topological acoustic sensing of ground stiffness: Presenting a potential means of sensing warming permafrost in a forest. Cold Reg. Sci. Technol. 2022, 199, 103569. [Google Scholar] [CrossRef]
- Hasan, M.A.; Deymier, P.A. Modeling and simulations of a nonlinear granular metamaterial: Application to geometric phase-based mass sensing. Model. Simul. Mater. Sci. Eng. 2022, 30, 074002. [Google Scholar] [CrossRef]
- Lata, T.D.; Deymier, P.A.; Runge, K.; Uehara, G.S.; Hodges, T.M.W. Underwater acoustic sensing using the geometric phase. J. Acoust. Soc. Am. 2023, 154, 2869–2877. [Google Scholar] [CrossRef]
- Zhang, G.; Deymier, P.A.; Runge, K.; Kundu, T. Monitoring damage growth and topographical changes in plate structures using sideband peak count-index and topological acoustic sensing techniques. Ultrasonics 2024, 141, 107354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Li, X.; Kundu, T. Ordinary state-based peri-ultrasound modeling to study the effects of multiple cracks on the nonlinear response of plate structures. Ultrasonics 2023, 133, 107028. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Li, X.; Zhang, S.; Kundu, T. Sideband peak count-index technique for monitoring multiple cracks in plate structures using ordinary state-based peri-ultrasound theory. J. Acoust. Soc. Am. 2022, 152, 3035–3048. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Li, X.; Li, T.; Kundu, T. Ordinary state-based peri-ultrasound modeling for monitoring crack propagation in plate structures using sideband peak count-index technique. J. Sound Vib. 2024, 568, 117962. [Google Scholar] [CrossRef]
- Jhang, K.-Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135, Erratum in Int. J. Precis. Eng. Manuf. 2017, 18, 139. [Google Scholar] [CrossRef]
- Kawashima, K.; Omote, R.; Ito, T.; Fujita, H.; Shima, T. Nonlinear acoustic response through minute surface cracks: FEM simulation and ex-perimentation. Ultrasonics 2002, 40, 611–615. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, S.; Jhang, K.-Y.; Kim, T. Experimental Verification of Contact Acoustic Nonlinearity at Rough Contact Interfaces. Materials 2021, 14, 2988. [Google Scholar] [CrossRef]
- He, Y.; Xiao, Y.; Su, Z.; Pan, Y.; Zhang, Z. Contact acoustic nonlinearity effect on the vibro-acoustic modulation of delaminated composite structures. Mech. Syst. Signal Process. 2022, 163, 108161. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Kundu, T. Peri-Ultrasound Modeling to Investigate the Performance of Different Nonlinear Ultrasonic Techniques for Damage Monitoring in Plate Structures. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2024, 7, 031003. [Google Scholar] [CrossRef]
- Guan, L.; Zou, M.; Wan, X.; Li, Y. Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Appl. Sci. 2020, 10, 2135. [Google Scholar] [CrossRef]
- Castellano, A.; Fraddosio, A.; Piccioni, M.D.; Kundu, T. Linear and Nonlinear Ultrasonic Techniques for Monitoring Stress-Induced Damages in Concrete. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2021, 4, 041001. [Google Scholar] [CrossRef]
- Alnuaimi, H.N.; Amjad, U.; Russo, P.; Lopresto, V.; Kundu, T. Advanced non-linear ultrasonic sideband peak count-index technique for efficient detection and monitoring of defects in composite plates. J. Vib. Control. 2023, 10775463231168228. [Google Scholar] [CrossRef]
- Ho, I.-T.; Muralidharan, K.; Runge, K.; Granados, A.H.; Kundu, T.; Deymier, P.A. Monitoring defects in plates using topological acoustic sensing and sideband peak counting. Ultrasonics, 2024; Under review. [Google Scholar]
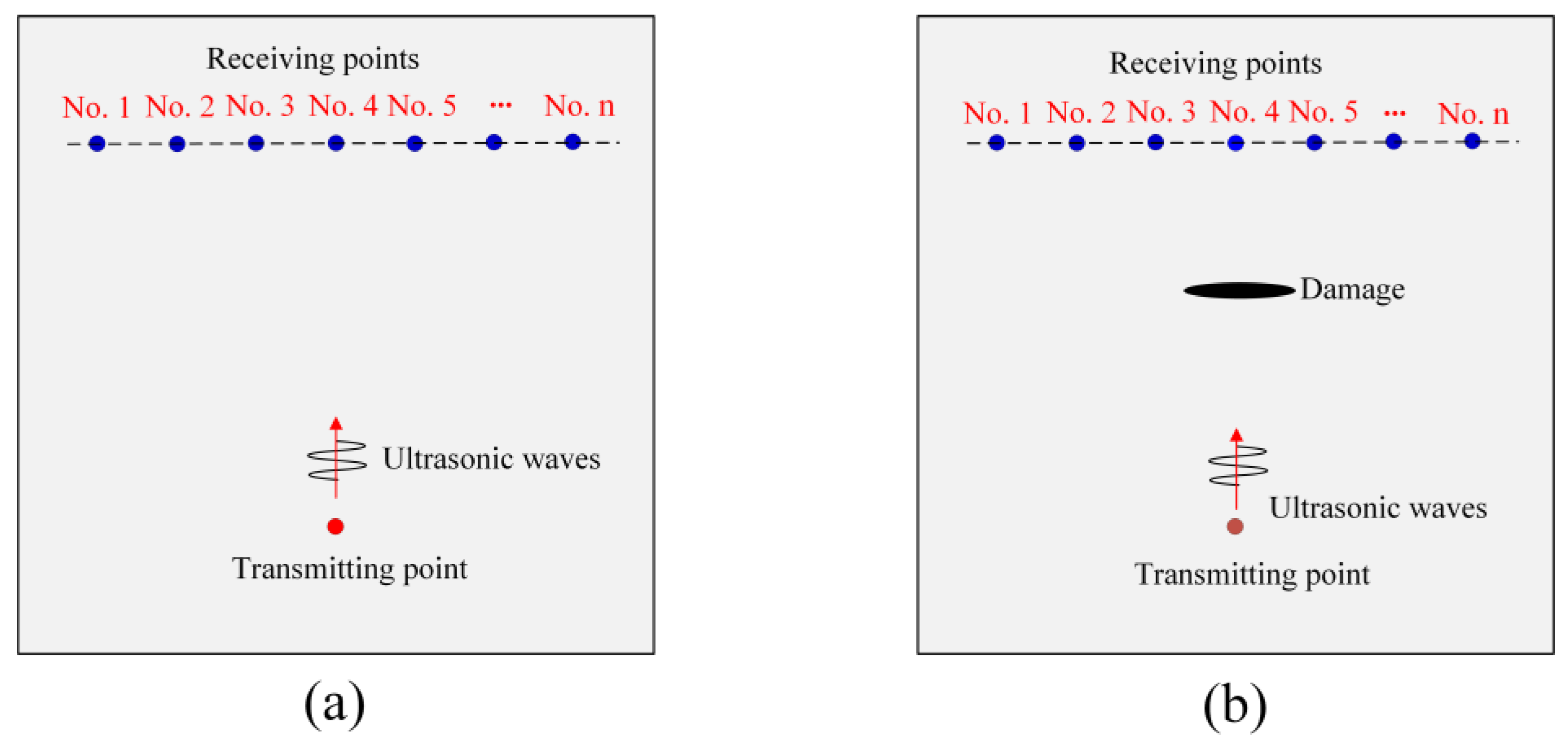
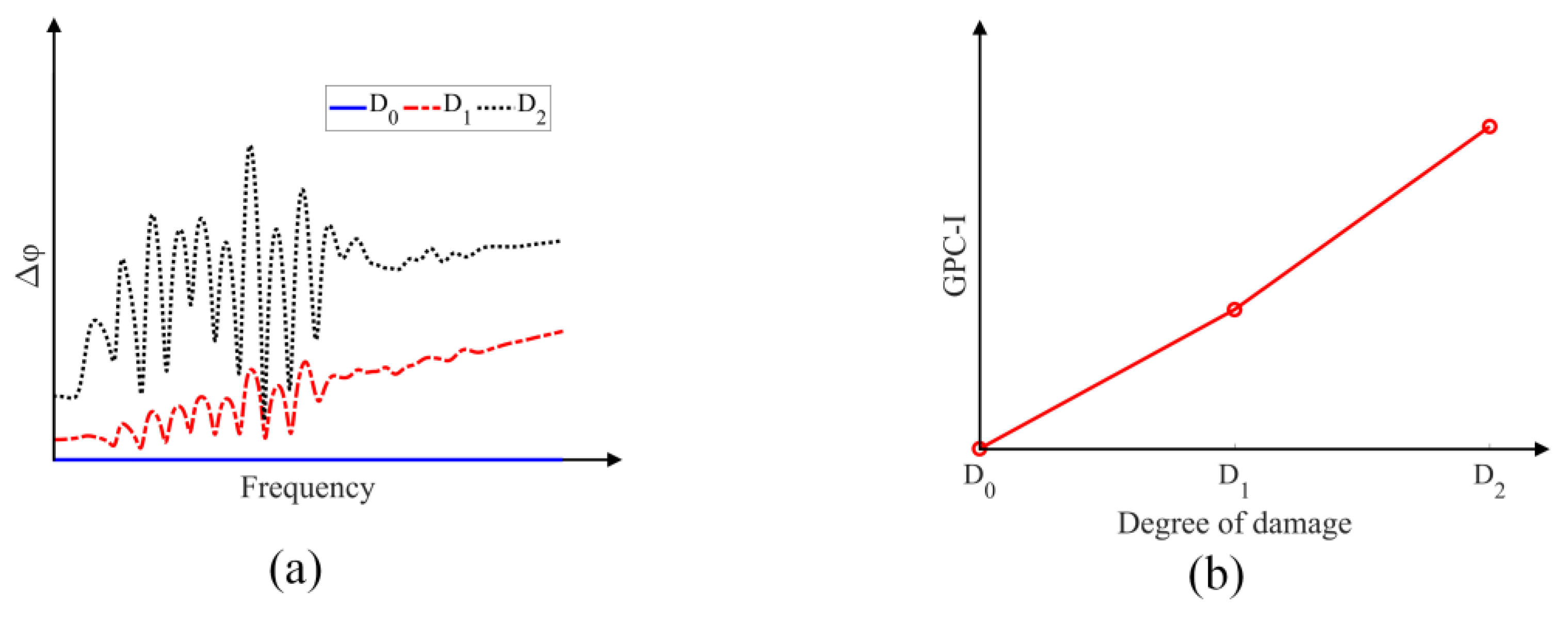
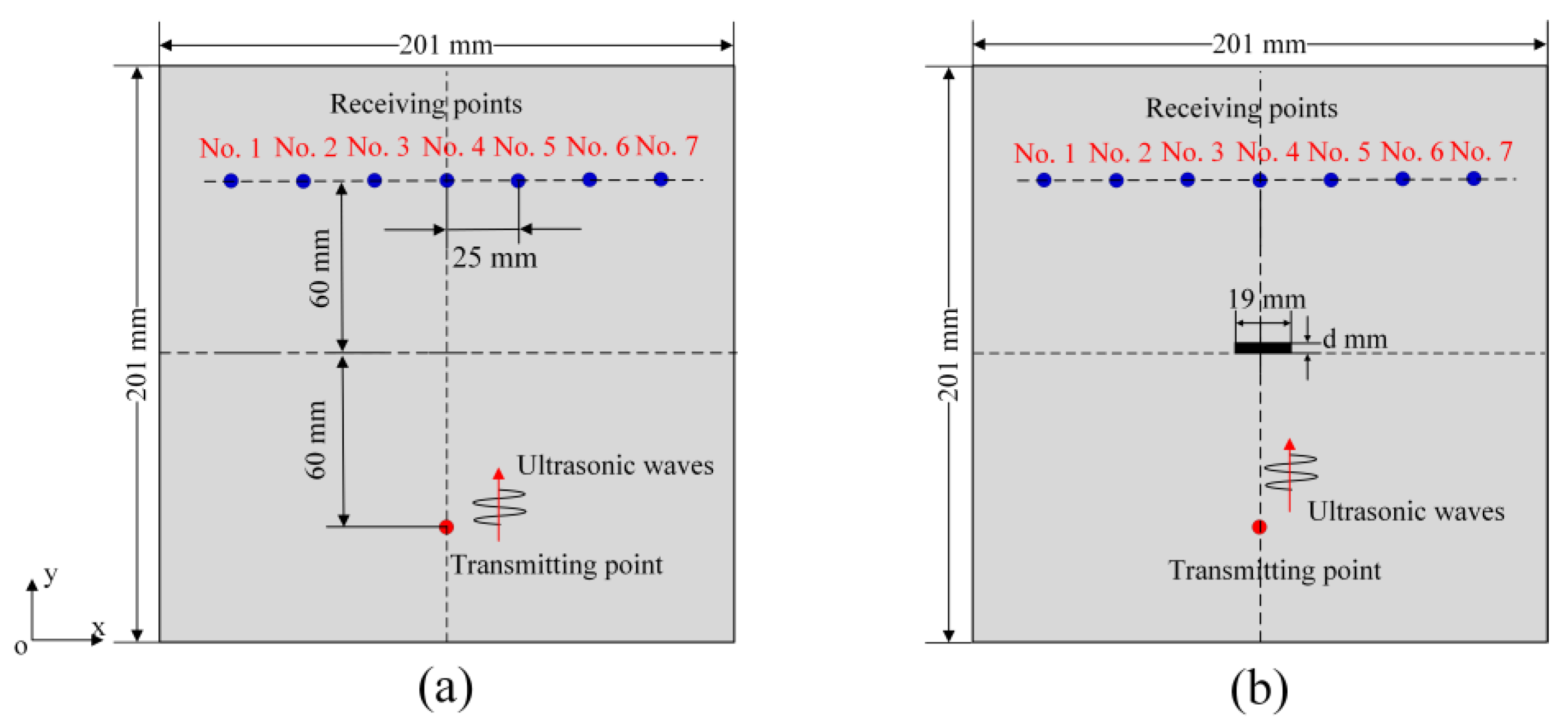
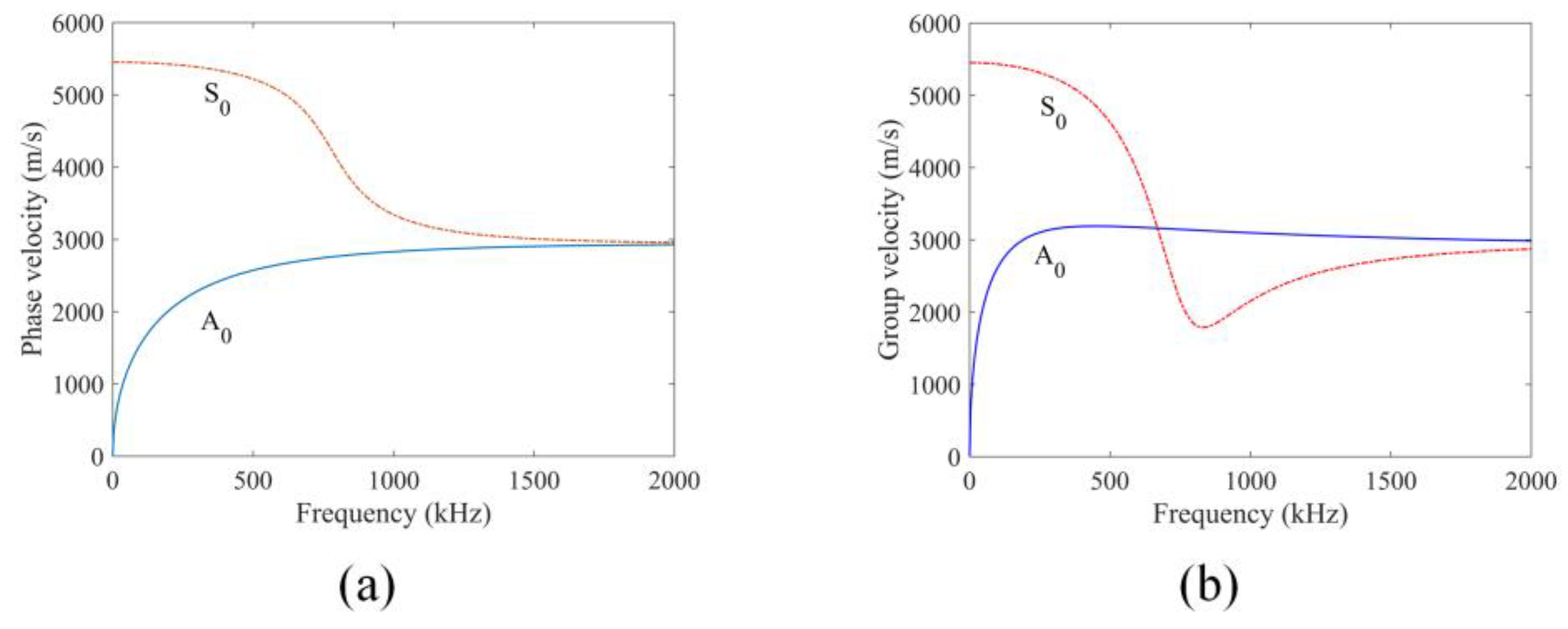






| Parameter | Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m³) |
|---|---|---|---|
| Values | 71.50 | 0.33 | 2700.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Kundu, T.; Deymier, P.A.; Runge, K. A Comparative Study of Geometric Phase Change- and Sideband Peak Count-Based Techniques for Monitoring Damage Growth and Material Nonlinearity. Sensors 2024, 24, 6552. https://doi.org/10.3390/s24206552
Zhang G, Kundu T, Deymier PA, Runge K. A Comparative Study of Geometric Phase Change- and Sideband Peak Count-Based Techniques for Monitoring Damage Growth and Material Nonlinearity. Sensors. 2024; 24(20):6552. https://doi.org/10.3390/s24206552
Chicago/Turabian StyleZhang, Guangdong, Tribikram Kundu, Pierre A. Deymier, and Keith Runge. 2024. "A Comparative Study of Geometric Phase Change- and Sideband Peak Count-Based Techniques for Monitoring Damage Growth and Material Nonlinearity" Sensors 24, no. 20: 6552. https://doi.org/10.3390/s24206552
APA StyleZhang, G., Kundu, T., Deymier, P. A., & Runge, K. (2024). A Comparative Study of Geometric Phase Change- and Sideband Peak Count-Based Techniques for Monitoring Damage Growth and Material Nonlinearity. Sensors, 24(20), 6552. https://doi.org/10.3390/s24206552






