Interior Profile Accuracy Assessment Method of Deep-Hole Parts Based on Servo Drive System
Abstract
:1. Introduction
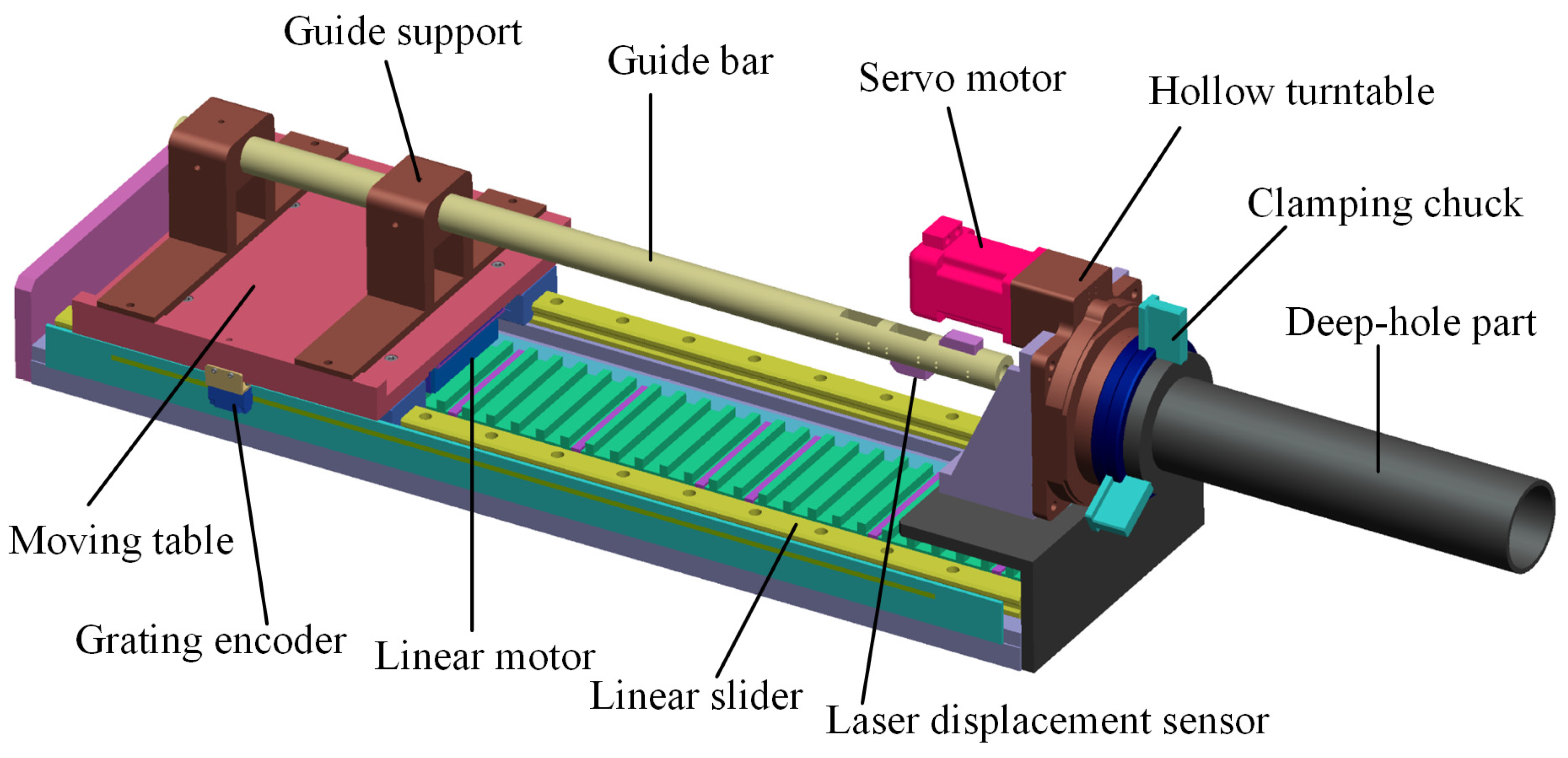
2. Measuring Device Based on a Servo Drive System
2.1. Device Design
2.2. System Construction
2.3. Measurement Principle
3. Accuracy Assessment Method
3.1. Assessment of Roundness Accuracy
3.2. Assessment of Straightness Accuracy
3.3. Assessment of Cylindricity Accuracy
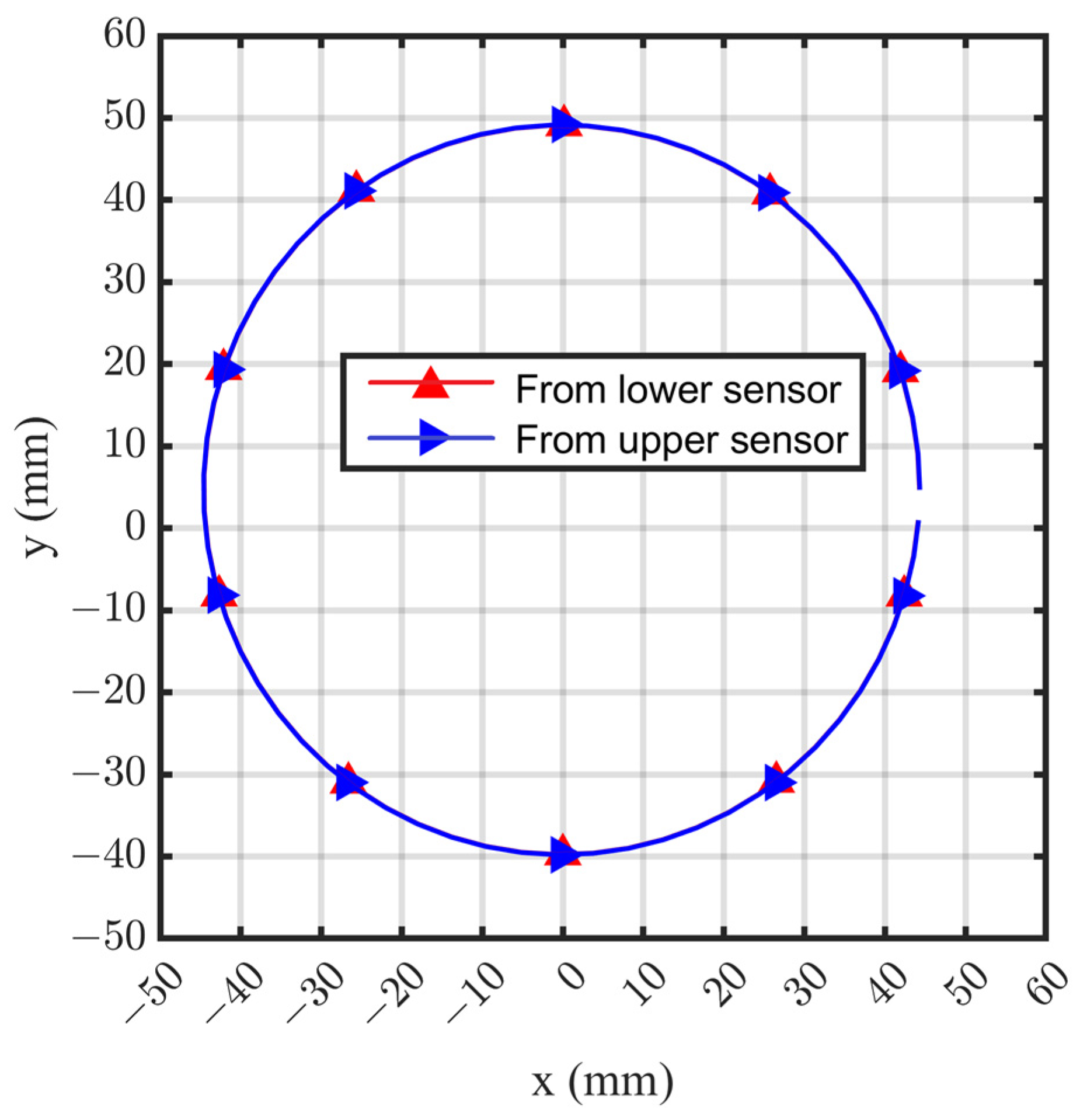
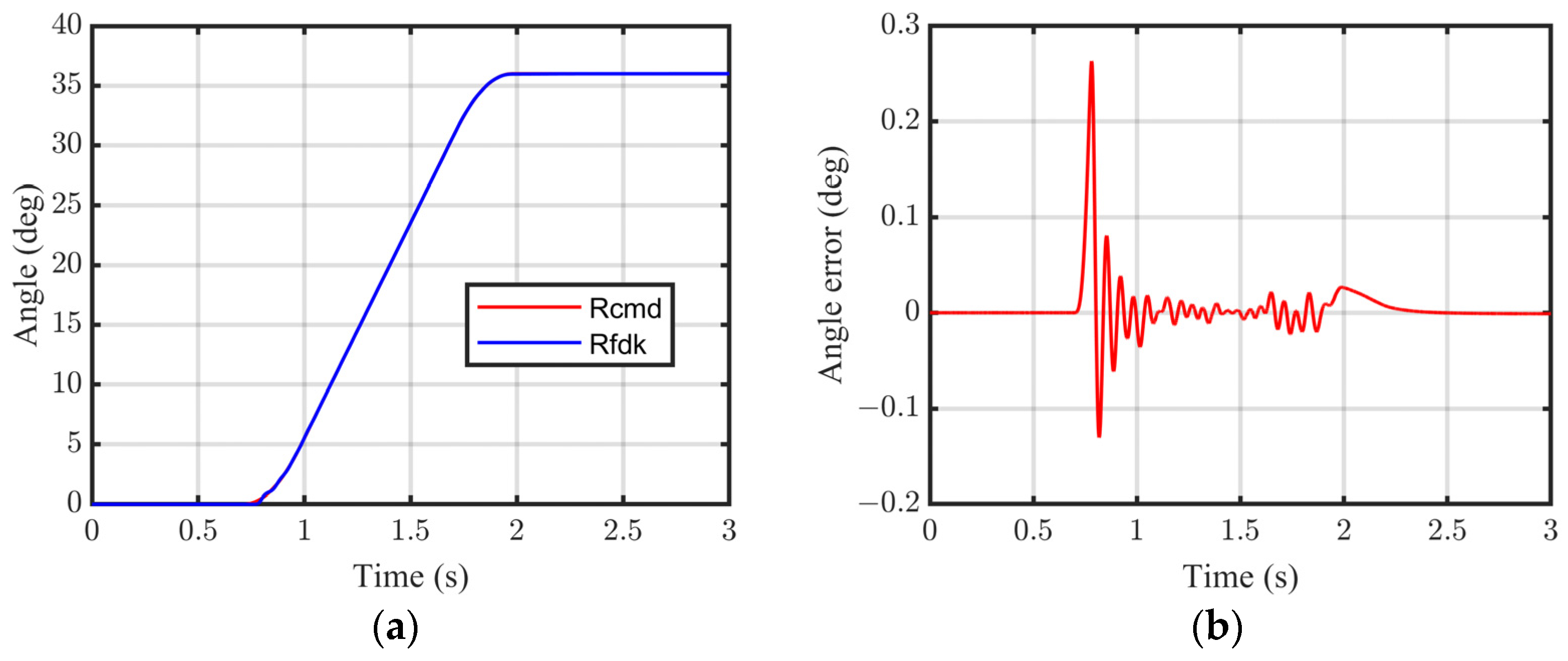
4. Experiment
5. Assessment Error Analysis
5.1. Sensor Error
5.2. Surface Finish Error
5.3. Positioning Error of Measured Points
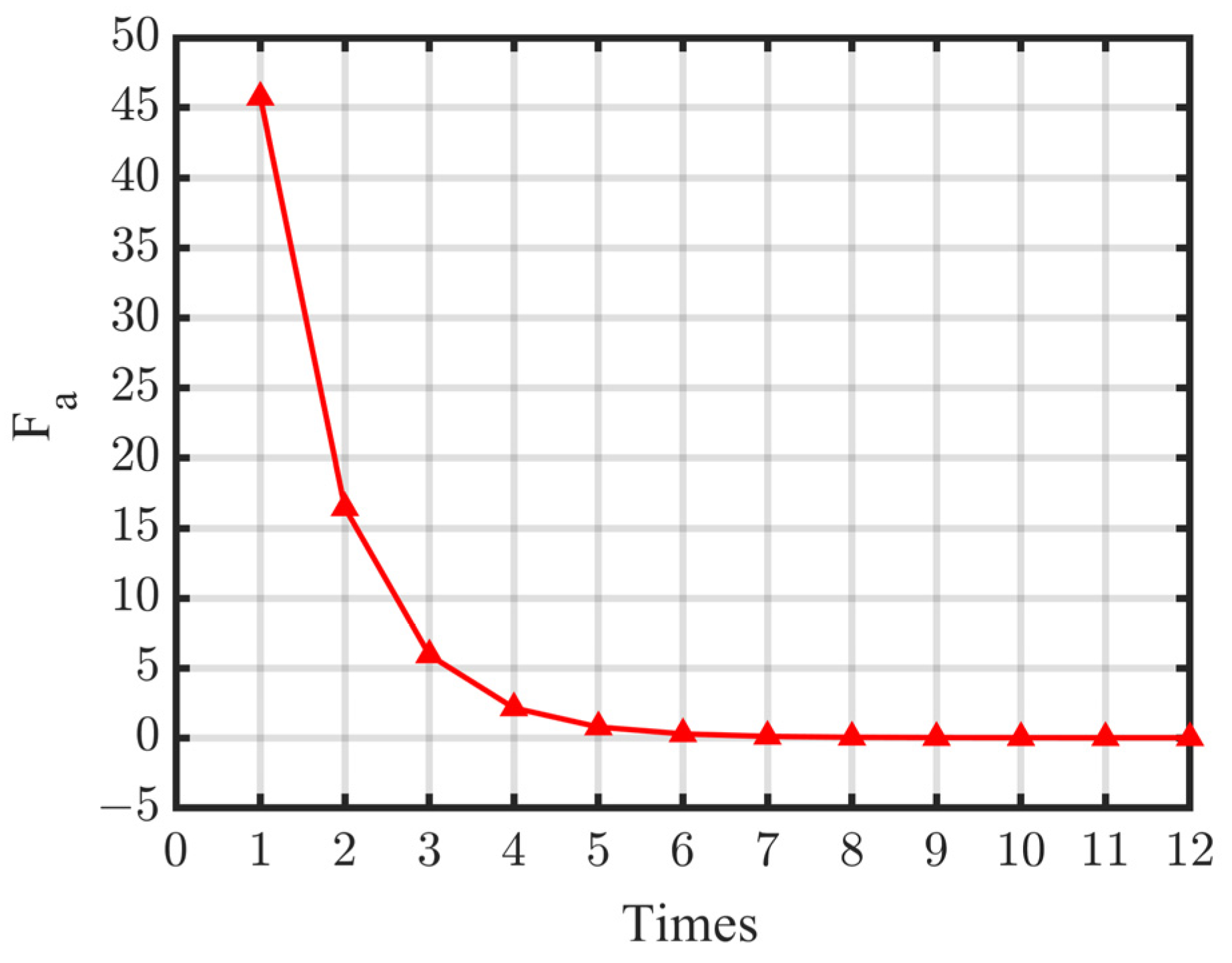
5.4. Assessment Method Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1. Circular-section parameter calculation based on LSM with GDM |
| %%Matlab program for rotating axial error compensation based on the gradient descent method, as follows: %% |
| function [p] = Circ_grad(ya,yb) |
| N = size(ya,2); |
| xr = sym(‘xr’); |
| yr = sym(‘yr’); |
| for i = 1:1:N |
| xna(i) = (0-xr)*cos((N-i)*2*pi/N)-(ya(i)-yr)*sin((N-i)*2*pi/N) + xr; |
| yna(i) = (0-xr)*sin((N-i)*2*pi/N)+(ya(i)-yr)*cos((N-i)*2*pi/N) + yr; |
| xnb(i) = (0-xr)*cos((N-i)*2*pi/N)-(yb(i)-yr)*sin((N-i)*2*pi/N) + xr; |
| ynb(i) = (0-xr)*sin((N-i)*2*pi/N)+(yb(i)-yr)*cos((N-i)*2*pi/N) + yr; |
| end |
| sum_xa = 0; |
| sum_ya = 0; |
| sum_xxa = 0; |
| sum_yya = 0; |
| sum_xxxa = 0; |
| sum_yyya = 0; |
| sum_xya = 0; |
| sum_xyya = 0; |
| sum_xxya = 0; |
| sum_xb = 0; |
| sum_yb = 0; |
| sum_xxb = 0; |
| sum_yyb = 0; |
| sum_xxxb = 0; |
| sum_yyyb = 0; |
| sum_xyb = 0; |
| sum_xyyb = 0; |
| sum_xxyb = 0; |
| for i = 1:1:N |
| sum_xa = sum_xa + xna(i); |
| sum_ya = sum_ya + yna(i); |
| sum_xxa = sum_xxa + xna(i) * xna(i); |
| sum_yya = sum_yya + yna(i) * yna(i); |
| sum_xxxa = sum_xxxa + xna(i) * xna(i) * xna(i); |
| sum_yyya = sum_yyya + yna(i) * yna(i) * yna(i); |
| sum_xya = sum_xya + xna(i) * yna(i); |
| sum_xxya = sum_xxya + xna(i) * xna(i) * yna(i); |
| sum_xyya = sum_xyya + xna(i) * yna(i) * yna(i); |
| sum_xb = sum_xb + xnb(i); |
| sum_yb = sum_yb + ynb(i); |
| sum_xxb = sum_xxb + xnb(i) * xnb(i); |
| sum_yyb = sum_yyb + ynb(i) * ynb(i); |
| sum_xxxb = sum_xxxb + xnb(i) * xnb(i) * xnb(i); |
| sum_yyyb = sum_yyyb + ynb(i) * ynb(i) * ynb(i); |
| sum_xyb = sum_xyb + xnb(i) * ynb(i); |
| sum_xxyb = sum_xxyb + xnb(i) * xnb(i) * ynb(i); |
| sum_xyyb = sum_xyyb + xnb(i) * ynb(i) * ynb(i); |
| end |
| Da = N * sum_xya - sum_xa * sum_ya; |
| Ca = N * sum_xxa - sum_xa * sum_xa; |
| Ea = N * sum_xxxa + N*sum_xyya -(sum_xxa + sum_yya) * sum_xa; |
| Ga = N * sum_yya - sum_ya * sum_ya; |
| Ha = N * sum_yyya + N * sum_xxya - (sum_xxa + sum_yya) * sum_ya; |
| Db = N * sum_xyb - sum_xb * sum_yb; |
| Cb = N * sum_xxb - sum_xb * sum_xb; |
| Eb = N * sum_xxxb + N*sum_xyyb -(sum_xxb + sum_yyb) * sum_xb; |
| Gb = N * sum_yyb - sum_yb * sum_yb; |
| Hb = N * sum_yyyb + N * sum_xxyb - (sum_xxb + sum_yyb) * sum_yb; |
| aa = (Ha*Da-Ea*Ga)/(Ca*Ga-Da*Da); |
| ba = (Ha*Ca-Ea*Da)/(Da*Da-Ga*Ca); |
| ca = -((sum_xxa + sum_yya) + aa * sum_xa + ba * sum_ya)/N; |
| xca = -0.5*aa; |
| yca = -0.5*ba; |
| Ra = 0.5 * sqrt(aa*aa+ba*ba-4*ca); |
| ab = (Hb*Db-Eb*Gb)/(Cb*Gb-Db*Db); |
| bb = (Hb*Cb-Eb*Db)/(Db*Db-Gb*Cb); |
| cb = -((sum_xxb + sum_yyb) + ab * sum_xb + bb * sum_yb)/N; |
| xcb = -0.5*ab; |
| ycb = -0.5*bb; |
| Rb = 0.5 * sqrt(ab*ab+bb*bb-4*cb); |
| Fa = (xca-xcb)^2+(yca-ycb)^2; |
| df = gradient(Fa,[xr,yr]); |
| xr = 0; |
| yr = 0; |
| FAA = eval(Fa); |
| dff = eval(df); |
| d = 100; |
| M = 100; |
| while (FAA > 0.0001)&&(M > 0) |
| xr = xr-dff(1)*d; |
| yr = yr-dff(2)*d; |
| FAA = eval(Fa); |
| dff = eval(df); |
| M = M-1; |
| end |
| p(1) = xr; |
| p(2) = yr; |
| p(3) = FAA; |
| p(4) = eval(xca); |
| p(5) = eval(yca); |
| p(6) = eval(xcb); |
| p(7) = eval(ycb); |
| p(8) = eval(Ra); |
| p(9) = eval(Rb); |
| p(10) = M; |
| %%END%%. |
References
- Biermann, D.; Bleicher, F.; Heisel, U.; Klocke, F.; Möhring, H.C.; Shih, A. Deep hole drilling. CIRP Ann.—Manuf. Technol. 2018, 67, 673–694. [Google Scholar] [CrossRef]
- Chandar, J.B.; Nagarajan, L.; Kumar, M.S. Recent research progress in deep hole drilling process: A review. Surf. Rev. Lett. 2021, 28, 2130003. [Google Scholar] [CrossRef]
- Woon, K.; Chaudhari, A.; Rahman, M.; Wan, S.; Kumar, A.S. The effects of tool edge radius on drill deflection and hole misalignment in deep hole gundrilling of Inconel-718. CIRP Ann.—Manuf. Technol. 2014, 63, 125–128. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Tnay, G.L.; Liu, K.; Kumar, A.S. Effect of apex offset inconsistency on hole straightness deviation in deep hole gun drilling of Inconel 718. Int. J. Mach. Tools Manuf. 2018, 125, 123–132. [Google Scholar] [CrossRef]
- Thil, J.; Haddag, B.; Nouari, M.; Barlier, C.; Papillon, L. Experimental and analytical analyses of the cutting process in the deep hole drilling with BTA (Boring Trepanning Association) system. Mech. Ind. 2013, 14, 413–429. [Google Scholar] [CrossRef]
- Li, X.B.; Zhai, C.M.; He, W.Q.; Lu, Y.; Zhang, B.D. Experimental investigation of tool wear and machining quality of BTA deep-hole drilling in low-carbon alloy steel SA-5083. Materials 2023, 16, 6686. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Yu, Y.X.; Wang, X.H. Diameter measuring technique based on capacitive probe for deep hole or oblique hole monitoring. Measurement 2014, 47, 42–44. [Google Scholar] [CrossRef]
- Elfurjani, S.; Ko, J.; Jun, M.B. Micro-scale hole profile measurement using rotating wire probe and acoustic emission contact detection. Measurement 2016, 89, 215–222. [Google Scholar] [CrossRef]
- Arunkumar, N.; Thanikasalam, A.; Sankaranarayanan, V.; Senthilkumar, E. Parametric optimization of deep-hole drilling on AISI 1045 steel and online tool condition monitoring using an accelerometer. Mater. Manuf. Process. 2018, 33, 1751–1764. [Google Scholar] [CrossRef]
- Shi, Y.; Hao, L.; Cai, M.; Wang, Y.; Yao, J.; Li, R.; Feng, Q.; Li, Y. High-precision diameter detector and three-dimensional reconstruction method for oil and gas pipelines. J. Pet. Sci. Eng. 2018, 165, 842–849. [Google Scholar] [CrossRef]
- Bian, X.Y.; Cui, J.N.; Lu, Y.S.; Tan, J.B. Ultraprecision diameter measurement of small holes with large depth-to-diameter ratios based on spherical scattering electrical-field probing. Appl. Sci. 2019, 9, 242. [Google Scholar] [CrossRef]
- Katsuki, A.; Sajima, T.; Murakami, H.; Hazrat, A.M.; Ohnishi, O.; Akashi, K. Development of a laser-guiding-type deep small-sized hole-measurement. Precis. Eng. 2020, 63, 18–32. [Google Scholar] [CrossRef]
- Song, C.; Jiao, L.; Wang, X.B.; Liu, Z.B.; Shen, W.H.; Chen, H.; Qian, Y.H. Development and testing of a muti-sensor measurement system for roundness and axis straightness errors of deep-hole parts. Measurement 2022, 198, 111069. [Google Scholar] [CrossRef]
- Zhao, X.; Du, H.; Yu, D. Improving measurement accuracy of deep hole measurement instruments through perspective transformation. Sensors 2024, 24, 3158. [Google Scholar] [CrossRef]
- Liang, J.T.; Ming, Z.F.; Li, P.D. System construction of a four-side primary permanent-magnet linear motor drive mechanical press. Front. Mech. Eng. 2020, 15, 600–609. [Google Scholar] [CrossRef]
- Liang, J.T.; Ming, Z.F.; Ji, X.P. Feeding apparatus directly driven by optimal topology flux switching permanent magnet linear motor. Electr. Power Compon. Syst. 2019, 47, 903–913. [Google Scholar] [CrossRef]
- Jan, H.U.; Khan, F.; Ullah, B.; Qasim, M.; Milyani, A.H.; Azhari, A.A. Design and thermal analysis of linear hybrid excited flux switching machine using ferrite magnets. Energies 2022, 15, 5275. [Google Scholar] [CrossRef]
- Gu, T.Q.; Lin, S.W.; Fang, B.; Luo, T.Z. An improved total least square calibration method for straightness error of coordinate measuring machine. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 1665–1672. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Lin, M.X.; Yeh, K.T. Measuring parametric and volumetric errors in a four-axis CMM using a hole plate. Int. J. Precis. Eng. Manuf. 2024, 25, 959–979. [Google Scholar] [CrossRef]
- Sever, K.; Golušin, L.M.; Lončar, J. Optimization of gradient descent parameters in attitude estimation algorithms. Sensors 2023, 23, 2298. [Google Scholar] [CrossRef]
- Balamurali, A.; Feng, G.D.; Lai, C.Y.; Tjong, J.; Kar, N.C. Maximum efficiency control of PMSM drives considering system losses using gradient descent algorithm based on DC power measurement. IEEE Trans. Energy Convers. 2023, 23, 2298. [Google Scholar] [CrossRef]










| Laser Sensor | Point 1 (mm) | Point 2 (mm) | Point 3 (mm) | Point 4 (mm) | Point 5 (mm) | Point 6 (mm) | Point 7 (mm) | Point 8 (mm) | Point 9 (mm) | Point 10 (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| Sensor 1 | 39.71 | 39.33 | 38.79 | 38.23 | 37.89 | 37.93 | 38.37 | 38.91 | 39.47 | 39.75 |
| Sensor 2 | 49.26 | 49.71 | 50.31 | 50.86 | 51.08 | 50.95 | 50.49 | 49.77 | 49.44 | 49.21 |
| Measurement No. | Roundness Error (mm) | Straightness Error (mm) | Cylindricity Error (mm) |
|---|---|---|---|
| 1st measurement with the proposed system | 0.0609 | 0.2869 | 1.0097 |
| 2nd measurement with the proposed system | 0.055 | 0.2868 | 0.924 |
| 3rd measurement with the proposed system | 0.0615 | 0.2873 | 0.916 |
| 1st measurement with the CMM | 0.0519 | 0.206 | NCD |
| Part Number | Roundness Error (mm) | Straightness Error (mm) | Cylindricity Error (mm) |
|---|---|---|---|
| No. 1 | 0.0615 | 0.2873 | 0.916 |
| No. 2 | 0.0578 | 0.3999 | 0.956 |
| No. 3 | 0.0708 | 0.2001 | 0.7548 |
| No. 4 | 0.1026 | 0.2616 | 0.6095 |
| No. 5 | 0.0713 | 0.1772 | 0.6543 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Wang, K.; Song, X.; Han, X. Interior Profile Accuracy Assessment Method of Deep-Hole Parts Based on Servo Drive System. Sensors 2024, 24, 6554. https://doi.org/10.3390/s24206554
Liang J, Wang K, Song X, Han X. Interior Profile Accuracy Assessment Method of Deep-Hole Parts Based on Servo Drive System. Sensors. 2024; 24(20):6554. https://doi.org/10.3390/s24206554
Chicago/Turabian StyleLiang, Jintao, Kaixin Wang, Xiaotian Song, and Xiaolan Han. 2024. "Interior Profile Accuracy Assessment Method of Deep-Hole Parts Based on Servo Drive System" Sensors 24, no. 20: 6554. https://doi.org/10.3390/s24206554
APA StyleLiang, J., Wang, K., Song, X., & Han, X. (2024). Interior Profile Accuracy Assessment Method of Deep-Hole Parts Based on Servo Drive System. Sensors, 24(20), 6554. https://doi.org/10.3390/s24206554








