A Small-Sample Classification Strategy for Extracting Fractional Cover of Native Grass Species and Noxious Weeds in the Alpine Grasslands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Hyperspectral Image
2.1.1. Study Area
2.1.2. Hyperspectral Image
2.2. Field Investigation
2.2.1. Sample Data Collection
2.2.2. Vegetation Spectral Survey
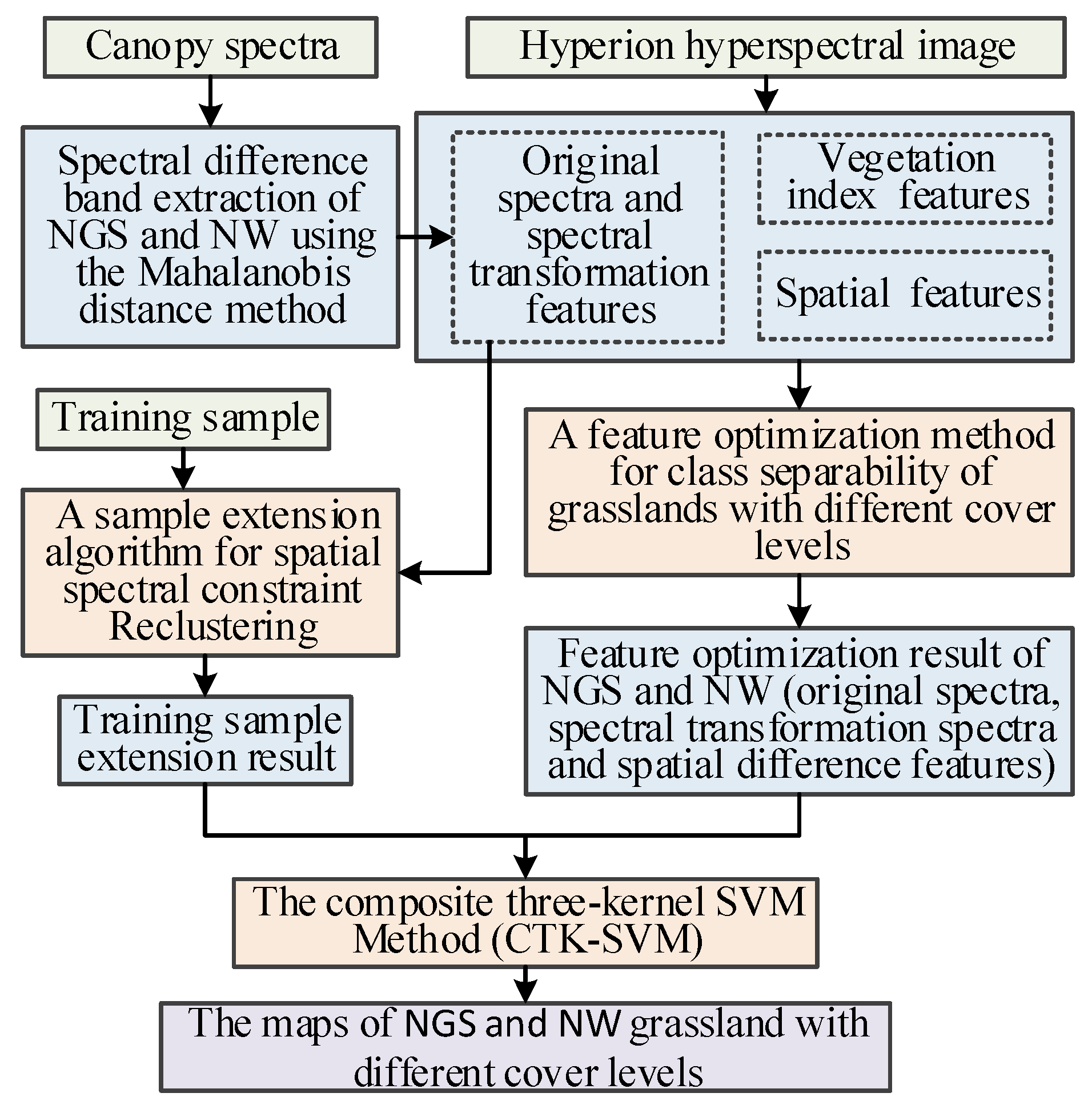
2.3. Feature Extraction and Optimization Method
2.3.1. Difference Feature Extraction Method
- (1).
- Spectral difference features
- (2).
- Vegetation index features
- (3).
- Spatial texture difference features
2.3.2. Feature Optimization Method
- (1).
- The spectral values corresponding to the field sampling points are extracted from the difference features; these values form a data matrix.
- (2).
- The data matrix is classified according to different cover levels, the average spectral values of each cover level are obtained, and the average spectral curves of different cover levels are obtained.
- (3).
- The spectral curves of different cover levels are plotted and the differentiation of the spectral curves of different cover levels is checked.
- (4).
- The bands with the smallest intervals in the spectral curves should be deleted in order to obtain the final features.
2.4. Training Sample Extension Method
2.5. Composite Three-Kernel SVM Method
- (1).
- SVM mothed
- (2).
- Three-kernel construction method
- (3).
- Three-kernel construction method of training samples
2.6. The Technical Flow Chart of the Small-Sample Classification Strategy
3. Results and Discussion
3.1. The Results of Feature Extraction and Optimization
3.1.1. The Difference Features of NGS and NW
- (1).
- Spectral difference feature
- (2).
- Vegetation indices feature
- (3).
- Spatial difference feature
3.1.2. The Optimization Results of Difference Features
- (1).
- Spectral feature optimization results
- (2).
- Continuum Removal feature optimization results
- (3).
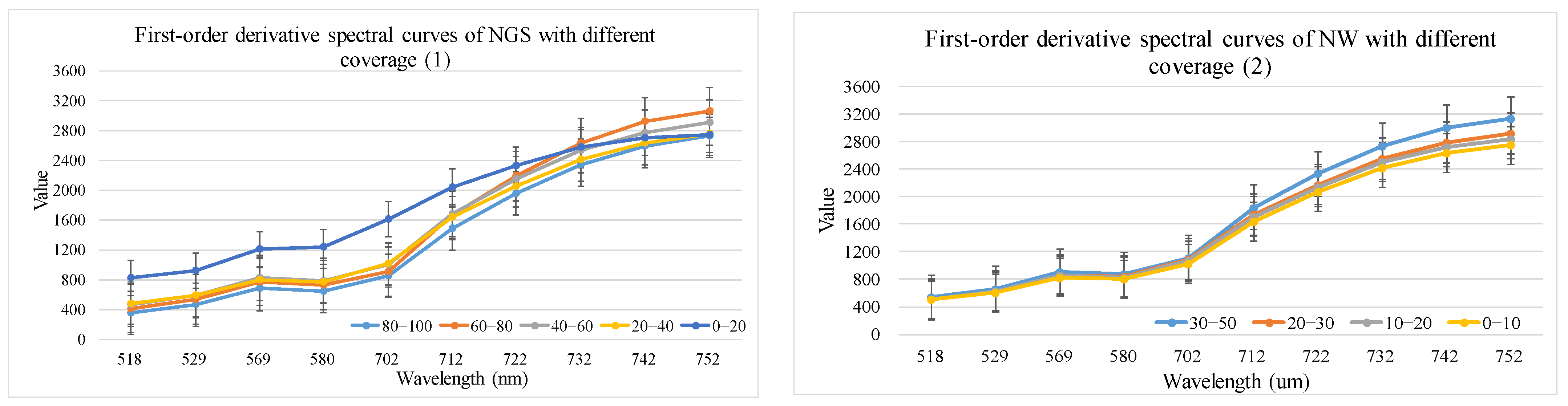
- First-order derivative feature optimization results
- (4).
- Vegetation index feature optimization results
- (5).
- Texture features optimization results
3.2. The Results of Training Sample Extension
3.3. The Fractional Cover Maps of GNS and NW
3.3.1. Accuracy Verification
3.3.2. Map of NGS with Different Coverage Levels
3.3.3. Map of NW with Different Coverage Levels
3.4. Discussion
3.4.1. The Impact of Feature Reduction on Recognition Accuracy
3.4.2. The Main Factors Affecting the Recognition Accuracy
- (1).
- Field samples
- (2).
- Different features
- (3).
- Identification methods
4. Conclusions
- (1).
- A new feature optimization method for class separability of grasslands with different cover levels was proposed. Based on this method, the difference features of NGS and NW were optimized, and the difference feature ranges of original spectra, spectral transformations, and spatial features of NGS and NW were further reduced. The method is also applicable to the optimization of difference features for other grass species.
- (2).
- A new spectral–spatial constrained re-clustering training sample extension method was proposed. This method is able to effectively increase the number of training samples by adjusting the spatial distance and spectral angle. Furthermore, it is able to exclude the samples with large errors by re-clustering. This method is also applicable to the extension of training samples when classifying similar vegetation types.
- (3).
- A composite three-kernel SVM method was constructed, which includes an original spectral kernel, a spectral transformation kernel, and a spatial feature kernel. Based on the mothed, the fractional cover maps of NGS and NW were produced, and the overall accuracies are approximately 65%. The RMSE of NGS and NW is approximately 16% and 11%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bardgett, R.D.; Bullock, J.M.; Lavorel, S.; Manning, P.; Schaffner, U.; Ostle, N.; Chomel, M.; Durigan, G.; LFry, E.; Johnson, D.; et al. Combatting global grassland degradation. Nat. Rev. Earth Environ. 2021, 2, 720–735. [Google Scholar] [CrossRef]
- Jiyuan, L.; Xinliang, X.; Quanqin, S. Grassland degradation in the “three-river headwaters” region, qinghai province. J. Geogr. Sci. 2008, 18, 259–273. [Google Scholar]
- Qu, R.; Li, S.; Xu, X. Progress on methods of grassland degradation and weed invasion monitoring based on remote sensing. J. Geo-Inf. Sci. 2013, 5, 761–767. [Google Scholar] [CrossRef]
- Xing, F.; An, R.; Guo, X.; Shen, X.; Soubry, I.; Wang, B.; Mu, Y.; Huang, X. Mapping alpine grassland fraction coverage using zhuhai-1 ohs imagery in the three river headwaters region, china. Remote Sens. 2023, 15, 2289. [Google Scholar] [CrossRef]
- Ziyu, S.; Junbang, W. The 30m-ndvi-based alpine grassland changes and climate impacts in the three-river headwaters region on the qinghai-tibet plateau from 1990 to 2018. J. Resour. Ecol. 2022, 13, 186–195. [Google Scholar] [CrossRef]
- Liu, N.; Yang, Y.; Ling, Y.; Yue, X. A regionalized study on the spatial-temporal changes of grassland cover in the three-river headwaters region from 2000 to 2016. Sustainability 2018, 10, 3539. [Google Scholar] [CrossRef]
- Ru, A.; Danping, J.; Xiaoxue, L.; Zhe, W.; Quaye-Ballard, J.A. Using hyperspectral data to determine spectral characteristics of grassland vegetation in central and eastern parts of three river source. Remote Sens. Technol. Appl. 2014, 29, 202–211. [Google Scholar]
- Zhou, W.; Li, H.; Shi, P.; Xie, L.; Yang, H. Spectral characteristics of vegetation of poisonous weed degraded grassland in the “three-river headwaters” region. J. Geo-Inf. Sci. 2020, 22, 1735–1742. [Google Scholar]
- Yina, H.; Ru, A.; Zetia, A.; Weibing, D. Researches on grass species fine identification based on uav hyperspectral images in three-river source region. Remote Sens. Technol. Appl. 2021, 36, 926–935. [Google Scholar]
- Ru, A.; Caihong, L.; Huilin, W.; Mengqiu, J.D.; Ballard, J.A.Q. Remote sensing identification of rangeland degradation using hyperion hyperspectral image in a typical area for three -river headwater region, qinghai, china. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 399–405. [Google Scholar]
- Ai, Z.; An, R.; Lu, C.; Chen, Y. Mapping of native plant species and noxious weeds to investigate grassland degradation in the three-river headwaters region using hj-1a/hsi imagery. Int. J. Remote Sens. 2020, 41, 1813–1838. [Google Scholar] [CrossRef]
- Binge, C.; Xiudan, M.; Xiaoyun, X. Hyperspectral image de-noising and classification with small training samples. J. Remote Sens. 2017, 21, 728–738. [Google Scholar]
- Zheng, C.; Wang, N.; Cui, J. Hyperspectral image classification with small training sample size using superpixel-guided training sample enlargement. IEEE Trans. Geoence Remote Sens. 2019, 57, 7307–7316. [Google Scholar] [CrossRef]
- Kun, S.; Xia, Z.; Yan-li, S.; Lifu, Z.; Shudong, W.; Zhi, Z. Sophisticated v egetation classification based on feature band set using hyperspectral image. Spectrosc. Spectr. Anal. 2015, 35, 1669–1676. [Google Scholar]
- Galvão, L.S.; Formaggio, A.R.; Tisot, D.A. Discrimination of sugarcane varieties in southeastern brazil with eo-1 hyperion data. Remote Sens. Environ. 2005, 94, 523–534. [Google Scholar] [CrossRef]
- Pengra, B.W.; Johnston, C.A.; Loveland, T.R. Mapping an invasive plant, phragmites australis, in coastal wetlands using the eo-1 hyperion hyperspectral sensor. Remote Sens. Environ. 2007, 108, 74–81. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, B.; Palm, H.L. Detecting invasive sericea lespedeza (lespedeza cuneata) in mid-missouri pastureland using hyperspectral imagery. Environ. Manag. 2008, 41, 853–862. [Google Scholar] [CrossRef]
- Phinn, S.; Roelfsema, C.; Dekker, A.; Brando, V.; Anstee, J. Mapping seagrass species, cover and biomass in shallow waters: An assessment of satellite multi-spectral and airborne hyper-spectral imaging systems in moreton bay (australia). Remote Sens. Environ. 2008, 112, 3413–3425. [Google Scholar] [CrossRef]
- Guo, F.; Fan, J.; Tang, X. Comparison of methods for grassland classification based on hj-1a hyperspectral image data in north tibet. Remote Sens. Inf. 2013, 28, 77–82, 88. [Google Scholar]
- Xue, Z.; Du, P.; Li, J.; Su, H. Sparse graph regularization for robust crop mapping using hyperspectral remotely sensed imagery with very few in situ data. ISPRS J. Photogramm. Remote Sens. 2017, 124, 1–15. [Google Scholar] [CrossRef]
- Ren, R.; Bao, W.X. Hyperspectral image classification based on belief propagation with multi-features and small sample learning. J. Indian Soc. Remote Sens. 2019, 47, 307–316. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. A Nonlinear Regression Classification Algorithm with Small Sample Set for Hyperspectral Image. In Proceedings of the Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013; pp. 441–444. [Google Scholar]
- Binol, H.; Bilgin, G.; Dinc, S.; Bal, A. Kernel fukunaga-koontz transform subspaces for classification of hyperspectral images with small sample sizes. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1287–1291. [Google Scholar] [CrossRef]
- Chen, J.; Xia, J.; Du, P.; Chanussot, J.; Xie, X. Kernel supervised ensemble classifier for the classification of hyperspectral data using few labeled samples. Remote Sens. 2016, 8, 601. [Google Scholar] [CrossRef]
- Weixiao, L.; Jun, X.; Yaqing, Y.; Zhicai, Z. Temporal and spatial change characteristics of vegetaion cover(ndvl) in the three-river headwater region on tibetan plateau under global warming. Mt. Res. 2021, 39, 473–482. [Google Scholar]
- Fassnacht, F.E.; Li, L.; Fritz, A. Mapping degraded grassland on the eastern tibetan plateau with multi-temporal landsat 8 data—Where do the severely degraded areas occur? Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 115–127. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, J. Research on the spectral characteristic of grassland in arid regions based on hyperspectral image. Spectrosc. Spectr. Ananlysis 2012, 32, 445–448. [Google Scholar]
- Feng, H.; Chen, Y.; Song, J.; Lu, B.; Shu, C.; Qiao, J.; Liao, Y.; Yang, W. Maturity classification of rapeseed using hyperspectral image combined with machine learning. Plant Phenomics 2024, 6, 0139. [Google Scholar] [CrossRef]
- Lingli, W.; Wenquan, Z.; Nan, J. Evaluation of distance measure methods for vegetation index time-series data. J. Remote Sens. 2012, 16, 644–662. [Google Scholar]
- Lin, H.; Zhang, H.; Gao, Y.; Li, X. Mahalanobis distance based hyperspectral characteristic discrimination of leaves of different tree species. Spectrosc. Spectr. Anal. 2014, 34, 3358–3362. [Google Scholar]
- Song, W.; Mu, X.; Ruan, G.; Gao, Z.; Li, L.; Yan, G. Estimating fractional vegetation cover and the vegetation index of bare soil and highly dense vegetation with a physically based method. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 168–176. [Google Scholar] [CrossRef]
- Hollberg, J.; Schellberg, J. Distinguishing intensity levels of grassland fertilization using vegetation indices. Remote Sens. 2017, 9, 81. [Google Scholar] [CrossRef]
- Kong, B.; He, B.; Huan, Y.; Liu, Y. An integrated field and hyperspectral remote sensing method for the estimation of pigments content of stipa purpurea in shenzha, tibet. Math. Probl. Eng. 2017, 2017, 4787054. [Google Scholar] [CrossRef]
- Jia, S.; Hu, J.; Xie, Y.; Shen, L.; Jia, X.; Li, Q. Gabor cube selection based multitask joint sparse representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3174–3187. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Gabor-filtering-based nearest regularized subspace for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1012–1022. [Google Scholar] [CrossRef]
- Rajadell, O.; Garcia-Sevilla, P.; Pla, F. Spectral—Spatial pixel characterization using gabor filters for hyperspectral image classification. Geosci. Remote Sens. Lett. IEEE 2013, 10, 860–864. [Google Scholar] [CrossRef]
- Patra, S.; Bhardwaj, K.; Bruzzone, L. A spectral-spatial multicriteria active learning technique for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5213–5227. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological attribute filters for the analysis of very high resolution remote sensing images. In Proceedings of the Geoscience & Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Dalla Mura, M.; Atli Benediktsson, J.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-spatial classification of hyperspectral data using loopy belief propagation and active learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Imani, M. Difference-based target detection using mahalanobis distance and spectral angle. Int. J. Remote Sens. 2019, 40, 811–831. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized composite kernel framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral–spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Ranjan, S.; Sarvaiya, J.N.; Patel, J.N. Integrating spectral and spatial features for hyperspectral image classification with a modified composite kernel framework. PFG—J. Photogramm. Remote Sens. Geoinf. Ence 2019, 87, 275–296. [Google Scholar] [CrossRef]
- Yuhong, M.; Min, Y.; Guojun, W. Sophisticated vegetation classification based on multi-dimensional features of hyperspectral lmage. J. Atmos. Environ. Opt. 2020, 15, 117–124. [Google Scholar]
- Guoli, J.; Hongqi, W.; Yanmin, F. Degradation class identification based on high spectral in seriphidium transiliense desert grassland. Acta Grestia Sin. 2017, 25, 893–895+900. [Google Scholar]
- Li, S.; Xu, X.; Fu, Y. A study on classification of different degradation level alpine meadows based on hyperspectral image data in three-river headwater region. Remote Sens. Technol. Appl. 2015, 30, 50–57. [Google Scholar]
- Liu, J.; Wu, Z.; Wei, Z.; Xiao, L.; Sun, L. Spatial-spectral kernel sparse representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2462–2471. [Google Scholar] [CrossRef]












| Grassland Coverage Level | Number of the Training Samples | Grassland Coverage Level | Number of the Training Samples | ||
|---|---|---|---|---|---|
| NGS | NW | NGS | NW | ||
| 0 ≤ C < 10 | 15 | 39 | 50 ≤ C < 60 | 15 | 0 |
| 10 ≤ C < 20 | 33 | 41 | 60 ≤ C < 70 | 33 | 0 |
| 20 ≤ C < 30 | 46 | 24 | 70 ≤ C < 80 | 46 | 0 |
| 30 ≤ C < 40 | 19 | 11 | 80 ≤ C < 90 | 19 | 0 |
| 40 ≤ C < 50 | 5 | 3 | 90 ≤ C < 100 | 5 | 0 |
| Inputs: the locations and classes of the field samples, hyperspectral images |
| The method consists of three steps: A: Spatial distance constraints to select extended samples. Based on the location of the field samples, the locations of the 5 × 5 pixels around the field sample are extracted to form the extended pixel set, which is used as the extended samples. B: Spectral similarity constraints to select alternative samples. Based on the hyperspectral image, the spectral information of the extended samples is extracted. Then, the spectral angular distances between the field samples and each extended sample are calculated and a threshold (usually less than 0.05) is set to further select the alternative samples. C: Intra-class re-clustering to select extended samples. For the same class of alternative samples selected in the second step, the Fuzzy C-mean algorithm is used for re-clustering by setting two cluster centers, the samples of the cluster center containing the field samples are retained, and these samples are used as the final extended samples. |
| Output: The locations, classes, and numbers of the extended samples. |
| Spectral Type | Range of Canopy Spectral Difference | Corresponding Hyperion Imaging Bands | Number of Bands |
|---|---|---|---|
| Canopy spectra | 345–523 nm, 853–946 nm, 985–1069 nm. | 1–10 (345–523 nm), 44–50 (853–946 nm), 51–64 (985–1069 nm). Blue Valley (671 nm, 681 nm), Green Peak (691 nm) | 35 |
| First-order derivative | 693–752 nm. | 5–10 (460–523 nm), 16–28 (572–705 nm). | 19 |
| Continuum Removal | 460–523 nm, 572–705 nm. | 28–33 (693–752 nm). trilateral parametric band: 518 and 528 nm, 569 and 579. | 10 |
| Name | Formula | Name | Formula |
|---|---|---|---|
| NDVI | (R852 − R651)/(R852 + R651) | nLCI | (R850 − R710)/(R850 + R680) |
| nGNDVI | (R780 − R550)/(R780 + R550) | VOG2 | (R734 − R747)/(R715 + R726) |
| nNDVI | (R800 − R670)/(R800 + R670) | ARI2 | R800 × [(R550)-1-(R700)-1] |
| PRI | (R531 − R570)/(R531 + R570) | VARI | (R555 − R680)/(R555 + R680 − R480) |
| nPRI | (R550 − R530)/(R550 + R530) |
| Feature | Difference Features of NGS | Difference Features of NW |
|---|---|---|
| 35 Hyperion hyperspectral bands | 477–523 nm (5 bands), 852–885 nm (8 bands), 985–1069 nm (14 bands), Blue Valley (671 nm, 681.2 nm), Green Peak (691 nm). A total of 30 bands. | 852–885 nm (8 bands), 985–1069 nm (14 bands). A total of 22 bands. |
| 19 Continuum Removal features | 467–508 nm (5 bands), 671–702 nm (4 bands). A total of 9 bands | all unavailable |
| 10 first-order derivative features | 518 nm, 529 nm, 569 nm, 580 nm, 702 nm. A total of 5 bands. | 712 nm, 722 nm, 732 nm, 742 nm, 752 nm. A total of 5 bands |
| 9 vegetation index features | NDVI, NGDVI, NNDVI, VAVI. A total of 4 bands. | all unavailable |
| 12 Gabor features | all unavailable | all unavailable |
| 18 EMP features | The B1–B5 of EMP features are based on PCA1. A total of 5 bands. | The B1–B9 of EMP features are based on PCA1. A total of 9 bands. |
| Grassland Coverage Level | Number of Training Samples | Grassland Coverage Level | Number of Training Samples | ||
|---|---|---|---|---|---|
| Field | Extended | Field | Extended | ||
| 0 ≤ C < 10 | 3 | 16 | 50 ≤ C < 60 | 8 | 80 |
| 10 ≤ C < 20 | 4 | 22 | 60 ≤ C < 70 | 7 | 62 |
| 20 ≤ C < 30 | 6 | 50 | 70 ≤ C < 80 | 2 | 24 |
| 30 ≤ C < 40 | 10 | 76 | 80 ≤ C < 100 | 2 | 31 |
| 40 ≤ C < 50 | 18 | 118 | |||
| Grassland Coverage Level | Number of Training Samples | Grassland Coverage Level | Number of Training Samples | ||
|---|---|---|---|---|---|
| Field | Extended | Field | Extended | ||
| 0 ≤ C < 10 | 20 | 147 | 20 ≤ C < 30 | 13 | 131 |
| 10 ≤ C < 20 | 22 | 161 | 30 ≤ C < 50 | 5 | 43 |
| Accuracy Index (Estimated and Measured) | Weight Ratios of the Composite Three-Kernel | ||||
|---|---|---|---|---|---|
| 0.4:0.4:0.2 | 0.5:0.4:0.1 | 0.6:0.3:0.1 | 0.7:0.2:0.1 | 0.8:0.1:0.1 | |
| Less than 10 | 27 | 27 | 26 | 25 | 24 |
| Less than 15 | 34 | 34 | 33 | 32 | 31 |
| Less than 20 | 38 | 38 | 37 | 37 | 37 |
| Less than 25 | 46 | 46 | 45 | 45 | 45 |
| RMSE | 16.94% | 17.17% | 17.78% | 17.89% | 17.72% |
| Accuracy Index (Estimated and Measured) | Weight Ratios of the Composite Three-Kernel | |||
|---|---|---|---|---|
| 0.5:0.2:0.3 | 0.6:0.2:0.2 | 0.7:0.1:0.2 | 0.8:0.1:0.1 | |
| Less than 10 | 25 | 24 | 24 | 24 |
| Less than 15 | 34 | 33 | 33 | 33 |
| Less than 20 | 46 | 46 | 46 | 46 |
| RMSE | 10.87% | 11.00% | 11.00% | 11.00% |
| Accuracy Index (Estimated and Measured) | Half Features | Third Features | Full Features |
|---|---|---|---|
| Less than 10 | 26 | 26 | 27 |
| Less than 15 | 37 | 36 | 34 |
| Less than 20 | 38 | 38 | 38 |
| RMSE | 16.70% | 16.59% | 17.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, Z.; An, R. A Small-Sample Classification Strategy for Extracting Fractional Cover of Native Grass Species and Noxious Weeds in the Alpine Grasslands. Sensors 2024, 24, 6571. https://doi.org/10.3390/s24206571
Ai Z, An R. A Small-Sample Classification Strategy for Extracting Fractional Cover of Native Grass Species and Noxious Weeds in the Alpine Grasslands. Sensors. 2024; 24(20):6571. https://doi.org/10.3390/s24206571
Chicago/Turabian StyleAi, Zetian, and Ru An. 2024. "A Small-Sample Classification Strategy for Extracting Fractional Cover of Native Grass Species and Noxious Weeds in the Alpine Grasslands" Sensors 24, no. 20: 6571. https://doi.org/10.3390/s24206571
APA StyleAi, Z., & An, R. (2024). A Small-Sample Classification Strategy for Extracting Fractional Cover of Native Grass Species and Noxious Weeds in the Alpine Grasslands. Sensors, 24(20), 6571. https://doi.org/10.3390/s24206571





