Circumferential Crack Detection in Ultra-High-Pressure Tubular Reactors with Pulsed Eddy Current Testing
Abstract
1. Introduction
2. PECT Method and Experimental Platform
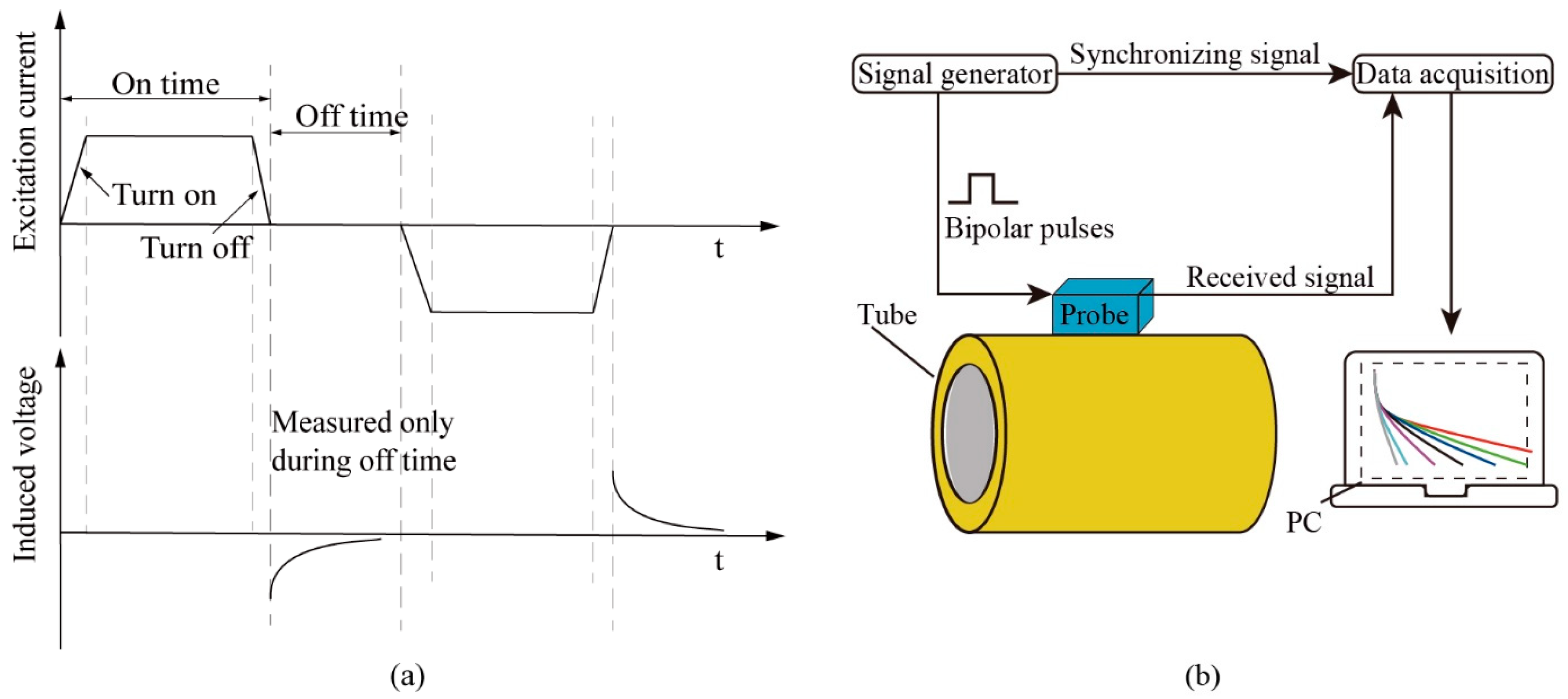
2.1. PECT Method
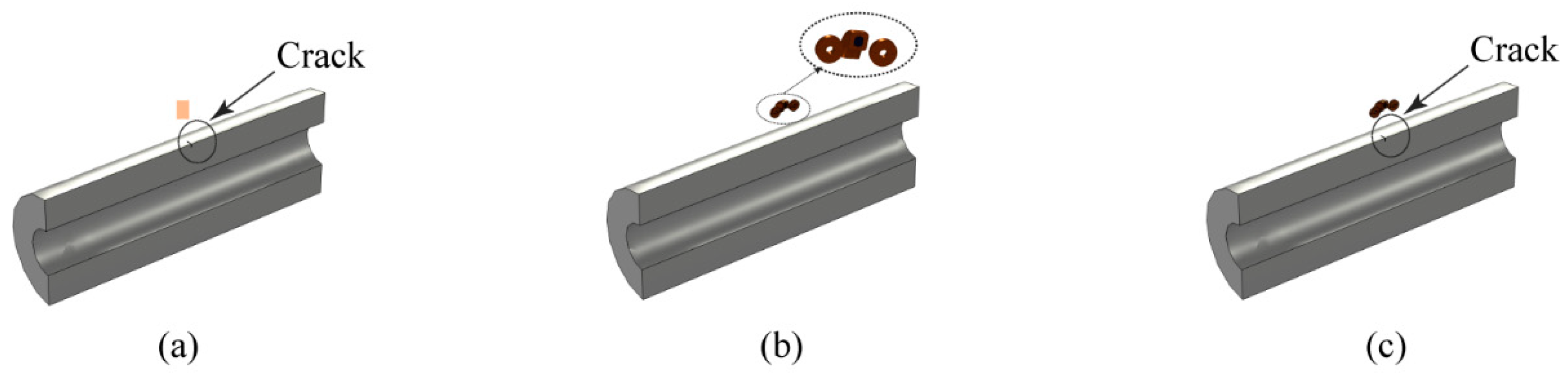
2.2. Experimental Platform and Specimens
3. Simulation Modeling and Validation
3.1. Setup of Simulation Models
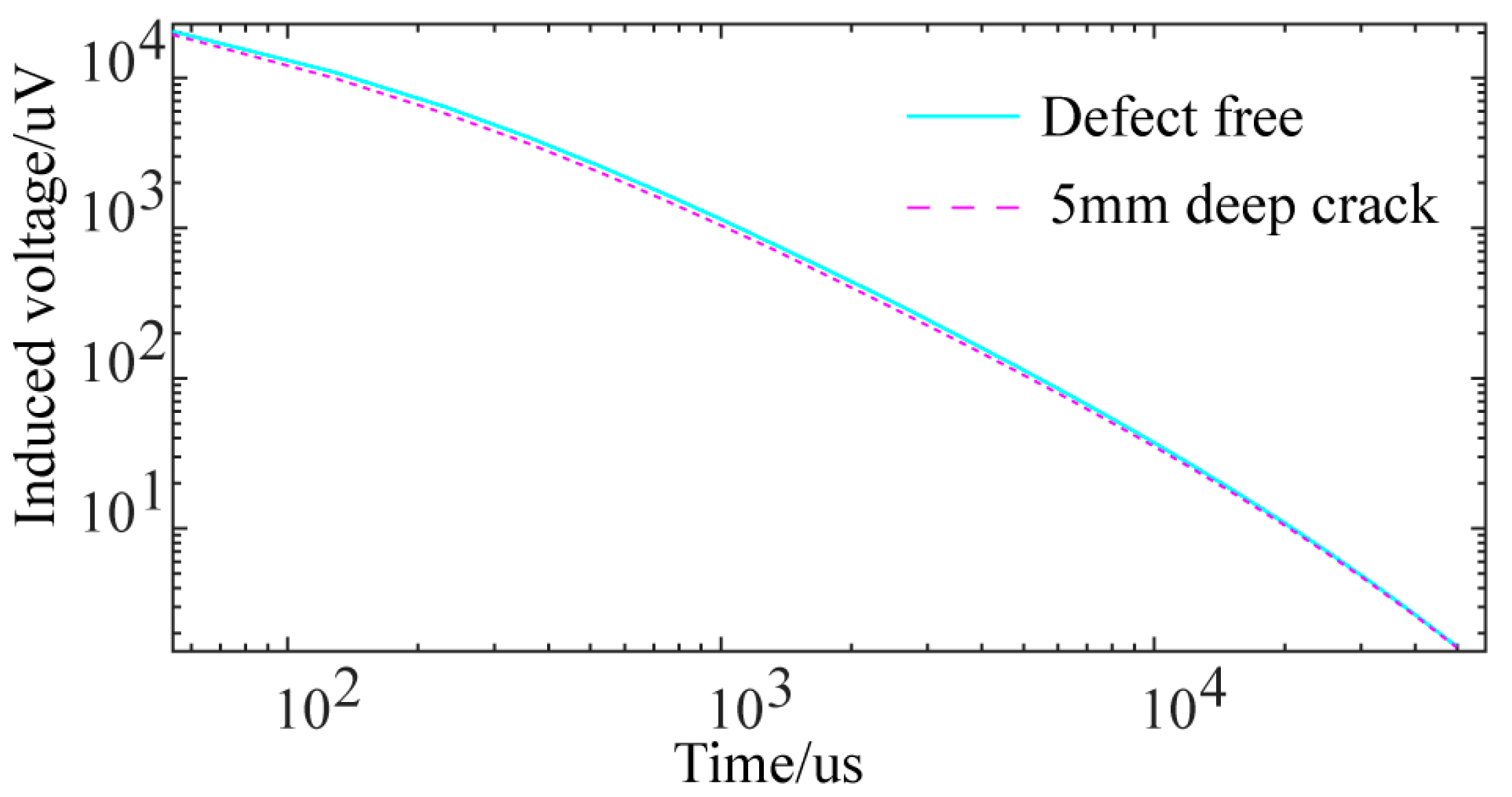
3.2. Modeling Validation
4. Simulation Results
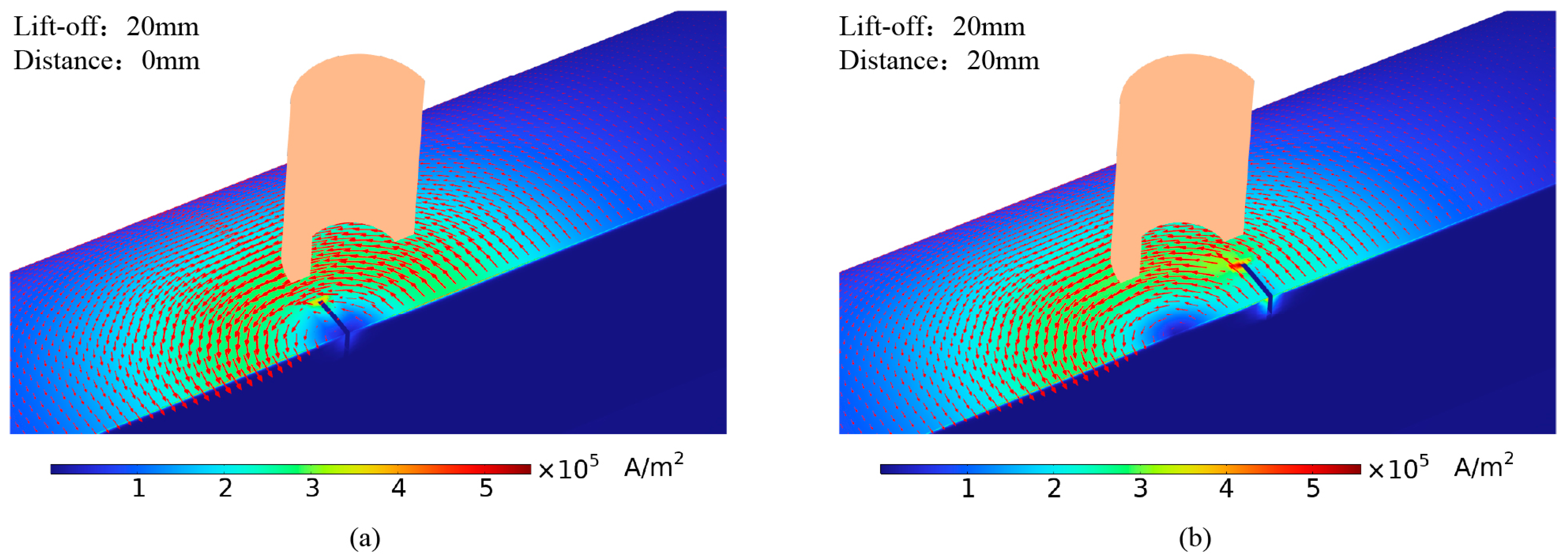
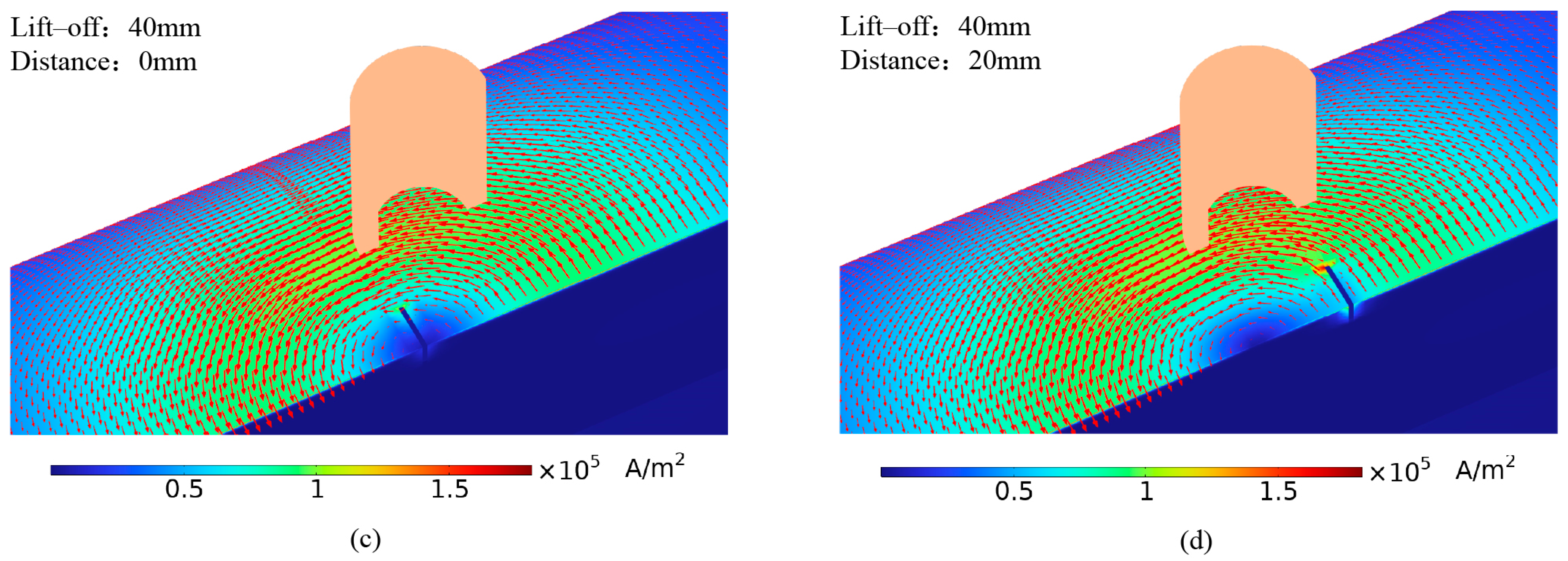
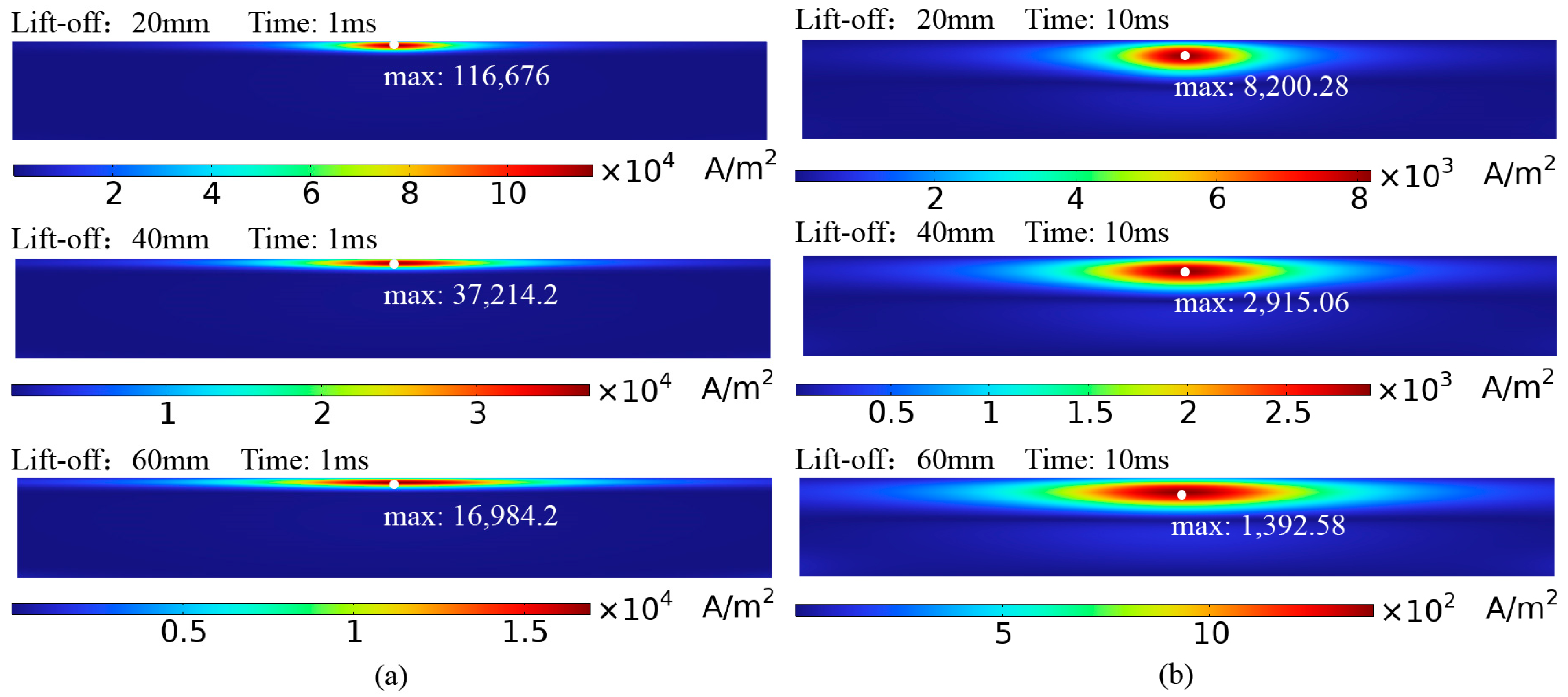
4.1. Perturbation Analysis of Eddy Currents by Cracks under Conventional Cylindrical Probe Excitation
4.2. Perturbation of Eddy Current Field and Received Signal by Cracks under Semi-Circular Excitation Probe
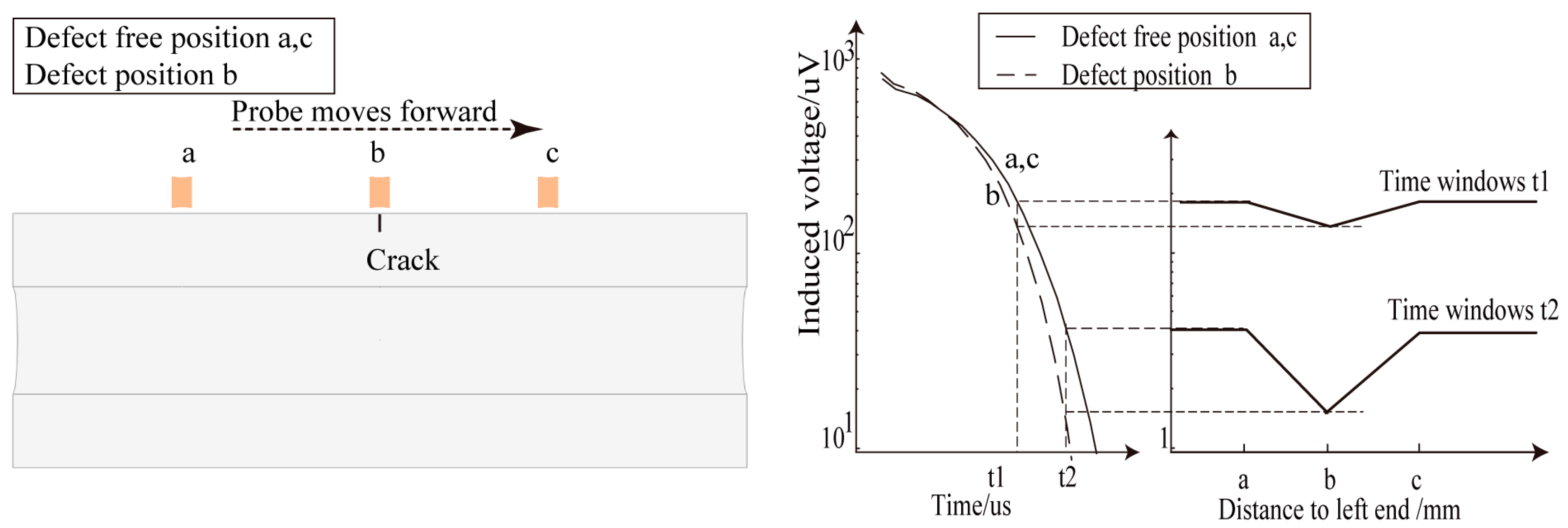
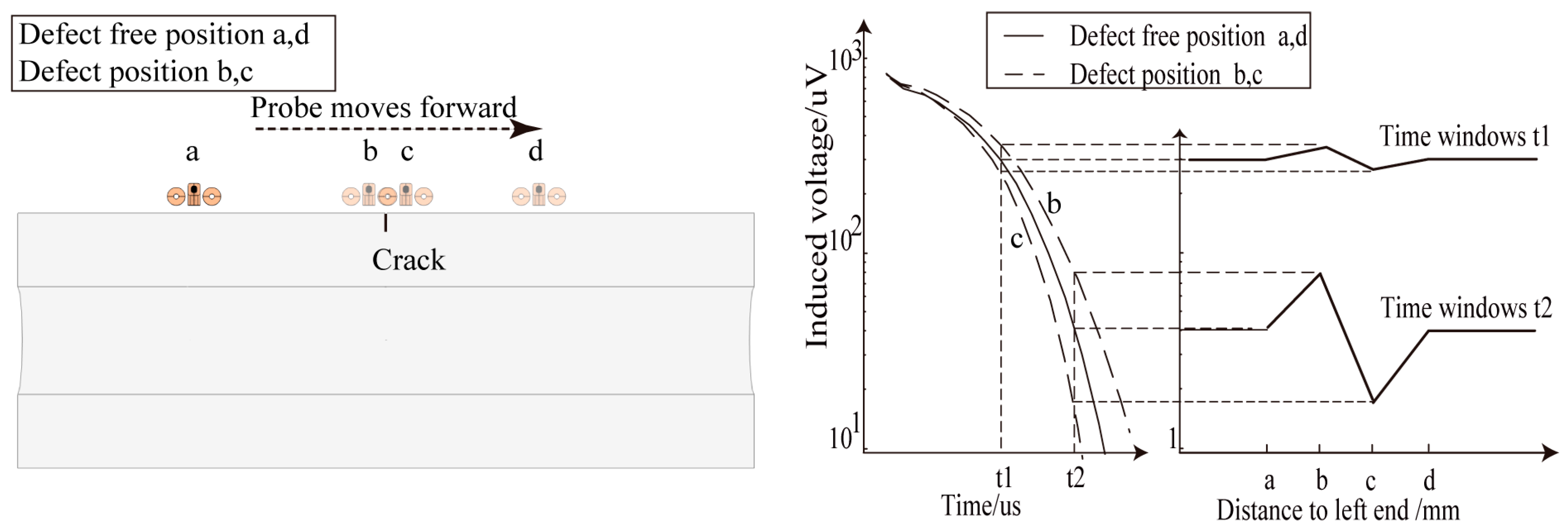
4.3. Simulation Analysis of Crack Detection Signals at Different Positions in the Detection Area of the Semi-Circular Probes
5. Experimental Results
5.1. Signal Processing Method
5.2. Experimental Design
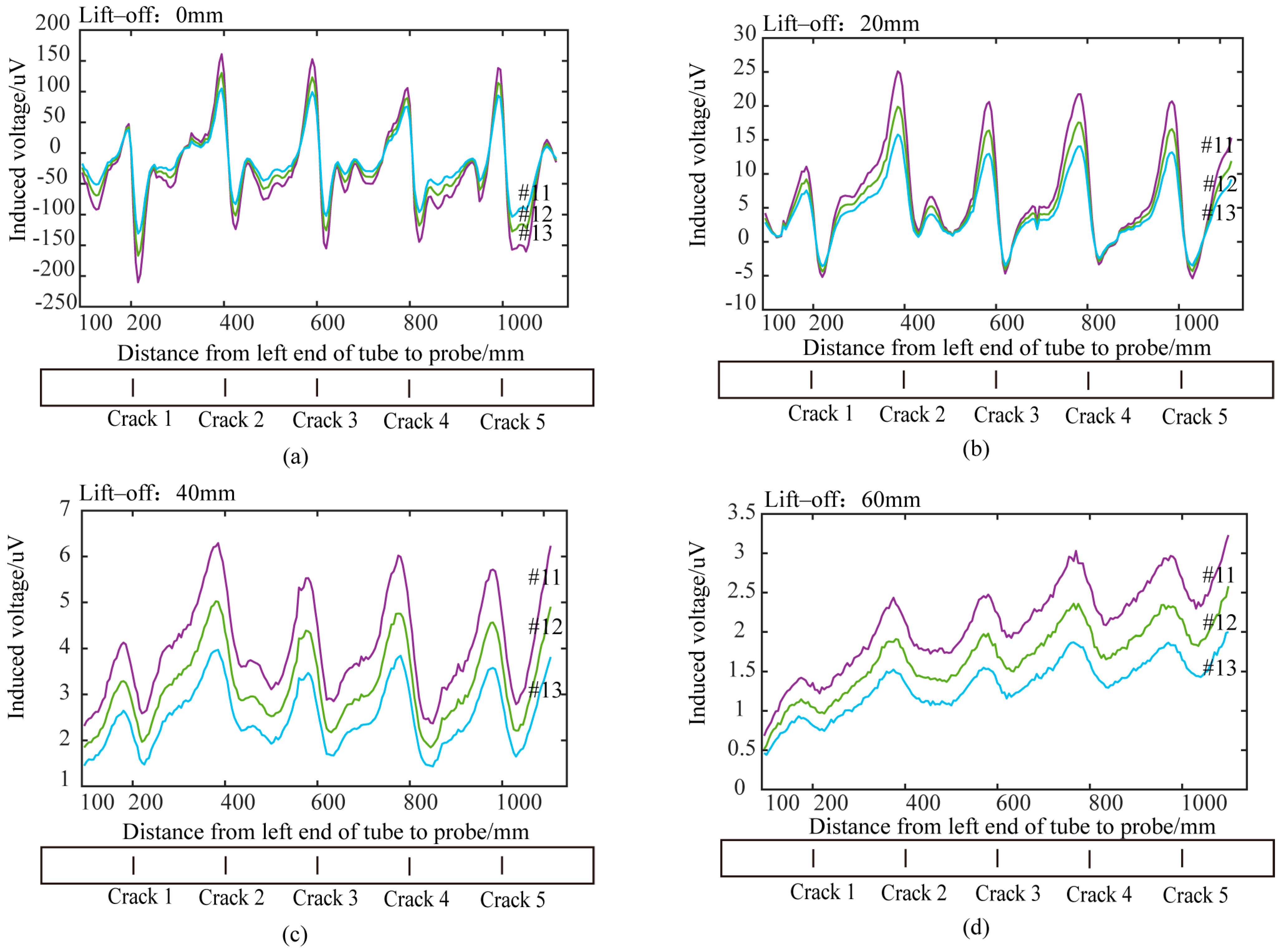
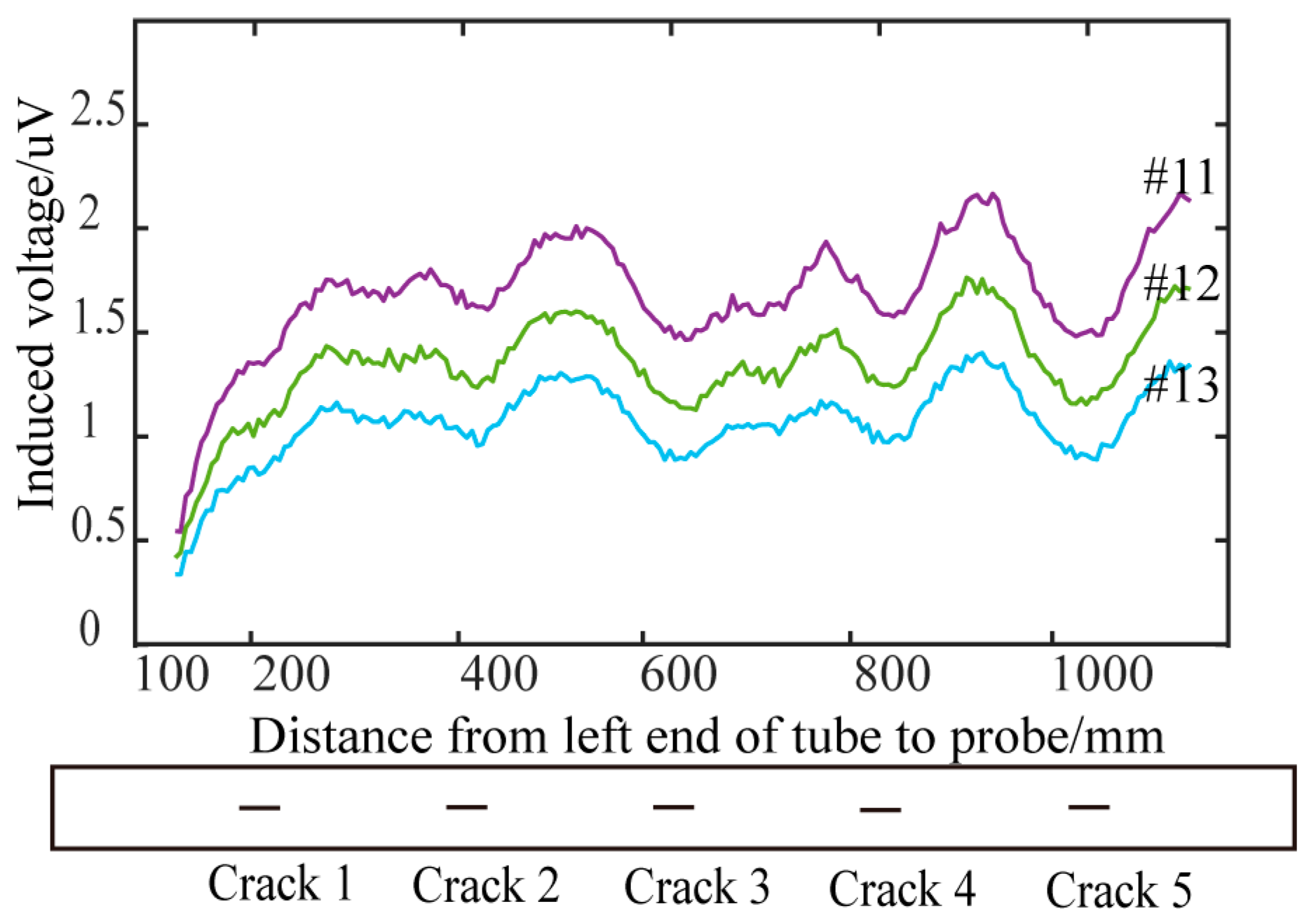
5.3. Analysis of Experimental Results of Conventional Cylindrical Absolute Probe
5.4. Analysis of Experimental Results of Differential Probes with Semi-Circular Excitation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, Z.; Seong, H.J.; Jang, Y.-S. Environmental toxicity and decomposition of polyethylene. Ecotoxicol. Environ. Saf. 2022, 242, 113933. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Zhu, W. Theoretical and Experimental Research on the Ultimate Pressure of In-Service Polyethylene Ultra-High Pressure Reactor Tubes. In Advanced Pressure Vessel Technology, Proceedings of the Ninth National Pressure Vessel Conference, Hefei, China, 5 September 2017; Elsevier: Amsterdam, The Netherlands, 2017; pp. 633–636. [Google Scholar]
- Kamal, S.M.; Borsaikia, A.C.; Dixit, U.S. Experimental assessment of residual stresses induced by the thermal autofrettage of thick-walled cylinders. J. Strain Anal. Eng. Des. 2015, 51, 144–160. [Google Scholar] [CrossRef]
- Li, G.; Deng, X.; Song, H.; Zhang, B. Research on Autofrettage Mechanism in Ultra-High Pressure Thick-walled Vessel. J. Phys. Conf. Ser. 2021, 1802, 022001. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Q.; Shen, G. A Review of Pulsed Eddy Current Nondestructive Testing Technology. J. Instrum. Meas. 2016, 37, 1698–1712. [Google Scholar]
- Sophian, A.; Tian, G.; Fan, M. Pulsed Eddy Current Non-destructive Testing and Evaluation: A Review. Chin. J. Mech. Eng. 2017, 30, 500–514, Erratum in Chin. J. Mech. Eng. 2017, 30, 1474. [Google Scholar] [CrossRef]
- Fu, Y.; Underhill, P.R.; Krause, T.W. Factors Affecting Spatial Resolution in Pulsed Eddy Current Inspection of Pipe. J. Nondestruct. Eval. 2020, 39, 34. [Google Scholar] [CrossRef]
- Shen, G.; Li, J.; Wu, X. Research and Application of Pulsed Eddy Current Testing Technology for Pressure Equipment. J. Mech. Eng. 2017, 53, 49–58. [Google Scholar] [CrossRef]
- Slobodnk, K. Detection and evaluation of subsurface defects using pulse eddy current differential probe. In Proceedings of the 2017 18th International Conference “Computational Problems of Electrical Engineering” (CPEE), Kutna Hora, Czech Republic, 11–13 September 2017; pp. 1–4. [Google Scholar]
- Faurschou, K.F.; Underhill, P.R.; Morelli, J.; Krause, T.W. Pulsed eddy current probe optimization for steel pipe wall thickness measurement. In Proceedings of the 45th Annual Review of Progress in Quantitative Nondestructive Evaluation, Burlington, VT, USA, 15–19 July 2018; p. 080002. [Google Scholar]
- Vasic, D.; Bilas, V.; Ambrus, D. Pulsed Eddy-Current Nondestructive Testing of Ferromagnetic Tubes. IEEE Trans. Instrum. Meas. 2004, 53, 1289–1294. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, M.; Li, Z.; Gu, Z.; Yang, H.; Cao, A.; Sun, J. Lift-off effect reduction based on the dynamic trajectories of the received-signal fast Fourier transform in pulsed eddy current testing. NDT E Int. 2017, 87, 85–92. [Google Scholar] [CrossRef]
- Li, P.; Xie, S.; Wang, K.; Zhao, Y.; Zhang, L.; Chen, Z.; Uchimoto, T.; Takagi, T. A novel frequency-band-selecting pulsed eddy current testing method for the detection of a certain depth range of defects. NDT E Int. 2019, 107, 102154. [Google Scholar] [CrossRef]
- Yu, Z.; Fu, Y.; Jiang, L.; Yang, F. Detection of circumferential cracks in heat exchanger tubes using pulsed eddy current testing. NDT E Int. 2021, 121, 102444. [Google Scholar] [CrossRef]
- Nafiah, F.; Sophian, A.; Khan, R.; Abidin, I.M.Z. Quantitative evaluation of crack depths and angles for pulsed eddy current non-destructive testing. NDT E Int. 2018, 102, 180–188. [Google Scholar] [CrossRef]
- Yuan, F.; Yu, Y.; Liu, B.; Tian, G. Investigation on Velocity Effect in Pulsed Eddy Current Technique for Detection Cracks in Ferromagnetic Material. IEEE Trans. Magn. 2020, 56, 1–8. [Google Scholar] [CrossRef]
- Wang, C.; Wu, S.; Xin, J.; He, R.; Chen, J.; Wang, D. Numerical Simulation of Oil and Gas Pipeline Crack Detection Based on Pulsed Eddy Current Testing Technology. In Proceedings of the 2021 4th International Conference on Electron Device and Mechanical Engineering (ICEDME), Guangzhou, China, 19–21 March 2021; pp. 46–50. [Google Scholar]
- Chen, Z.; Fan, M.; Cao, B.; Hu, B.; Sha, J. Characterization of image sequences of a defect using pulsed eddy current signals. J. Magn. Magn. Mater. 2021, 534, 168007. [Google Scholar] [CrossRef]
- Yu, Y.; Guan, J. Investigation of signal features of pulsed eddy current testing technique by experiments. Insight Non-Destr. Test. Cond. Monit. 2013, 55, 487–491. [Google Scholar] [CrossRef]
- Lin, J.; Li, T.; Yu, S. Nonuniform sampling and robust stacking of transient electromagnetic signal. In Proceedings of the ICSP’98 Fourth International Conference on Signal Processing, Beijing, China, 12–16 October 1998; Volume 2, pp. 1696–1699. [Google Scholar]







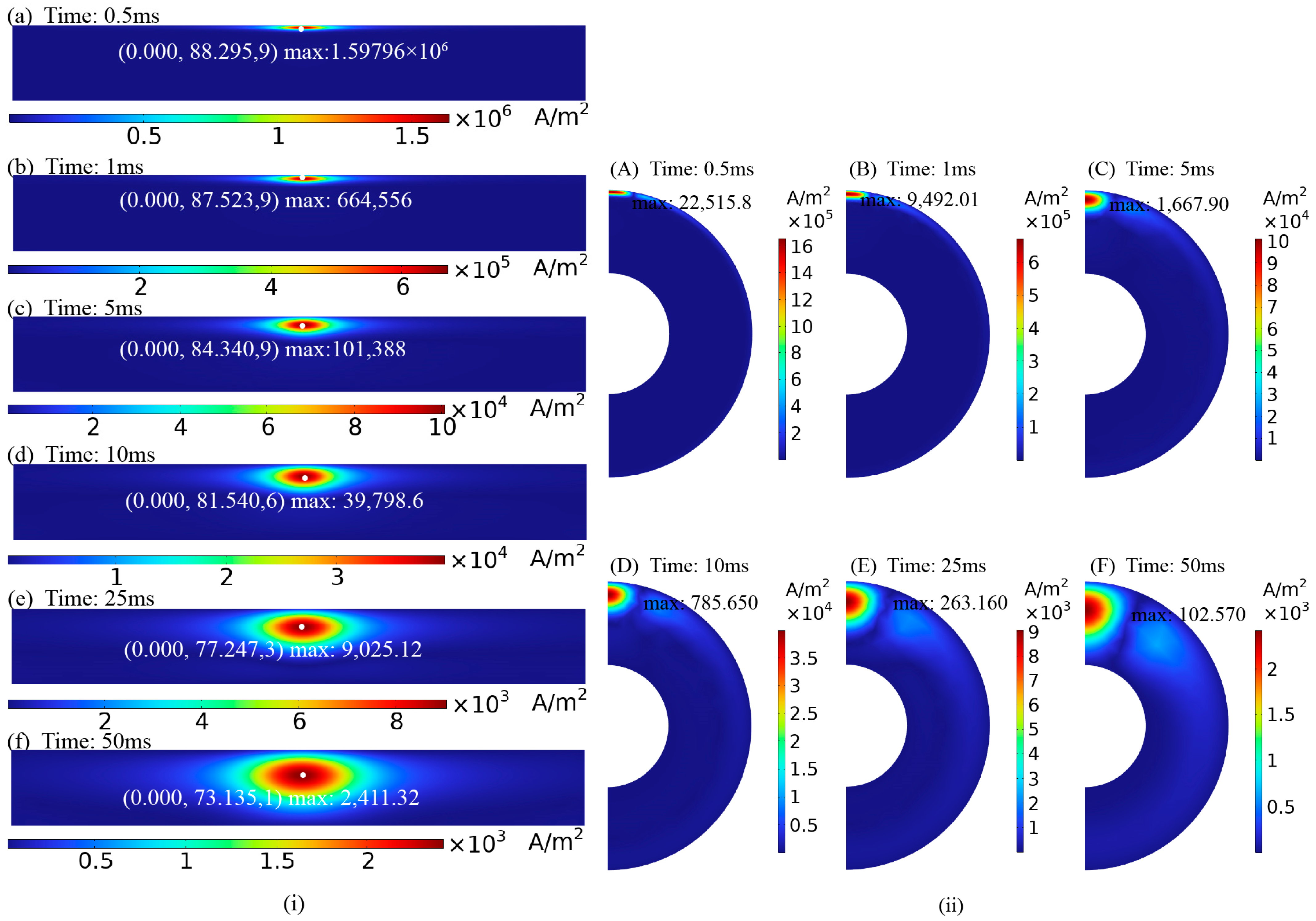
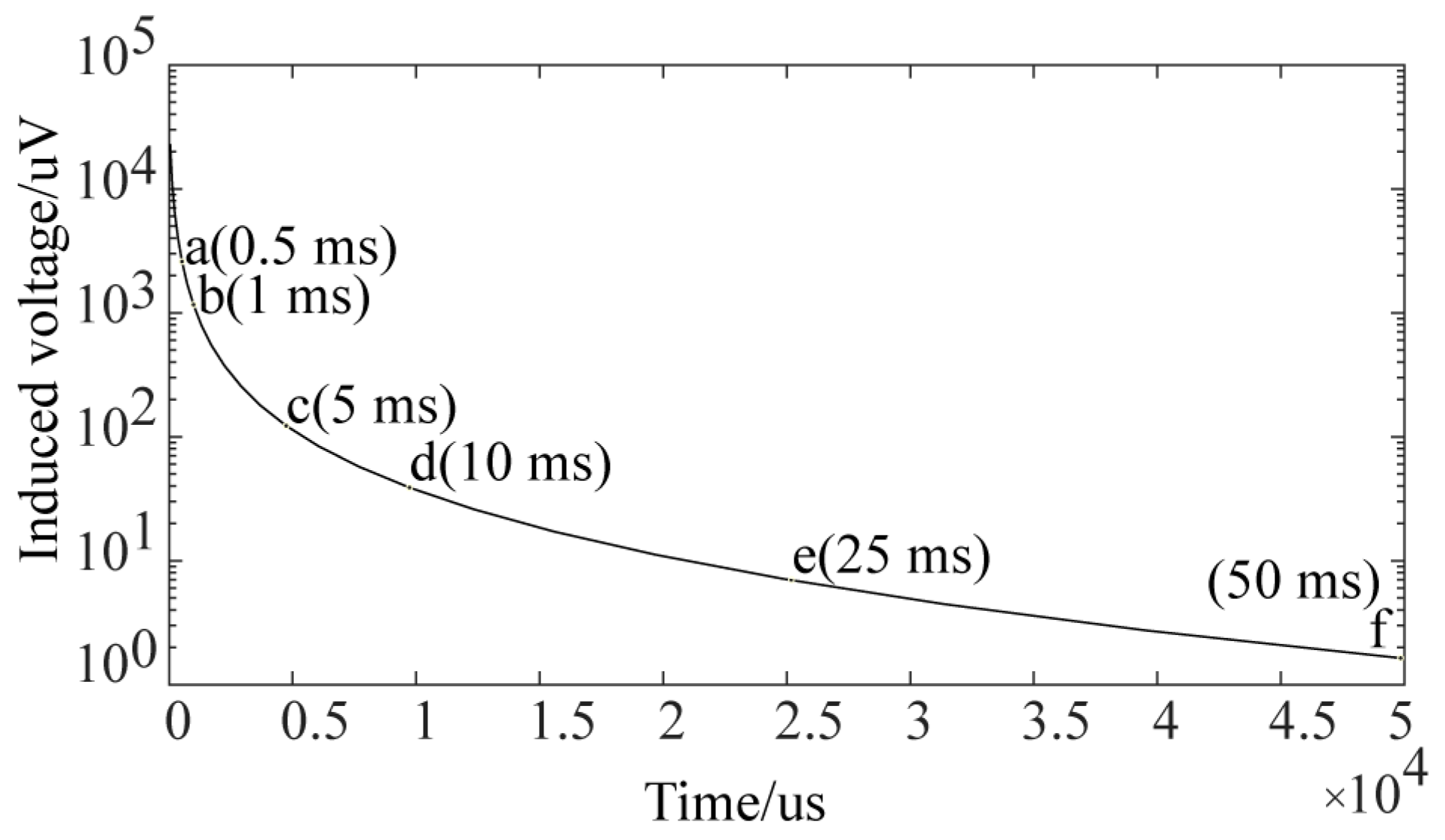
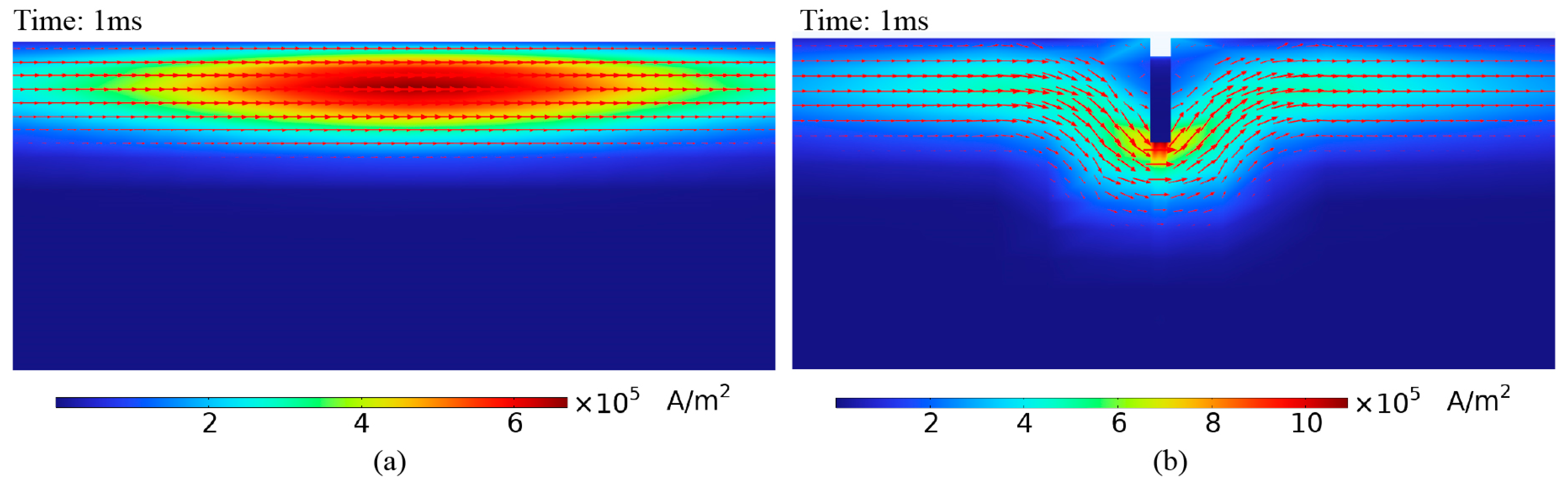
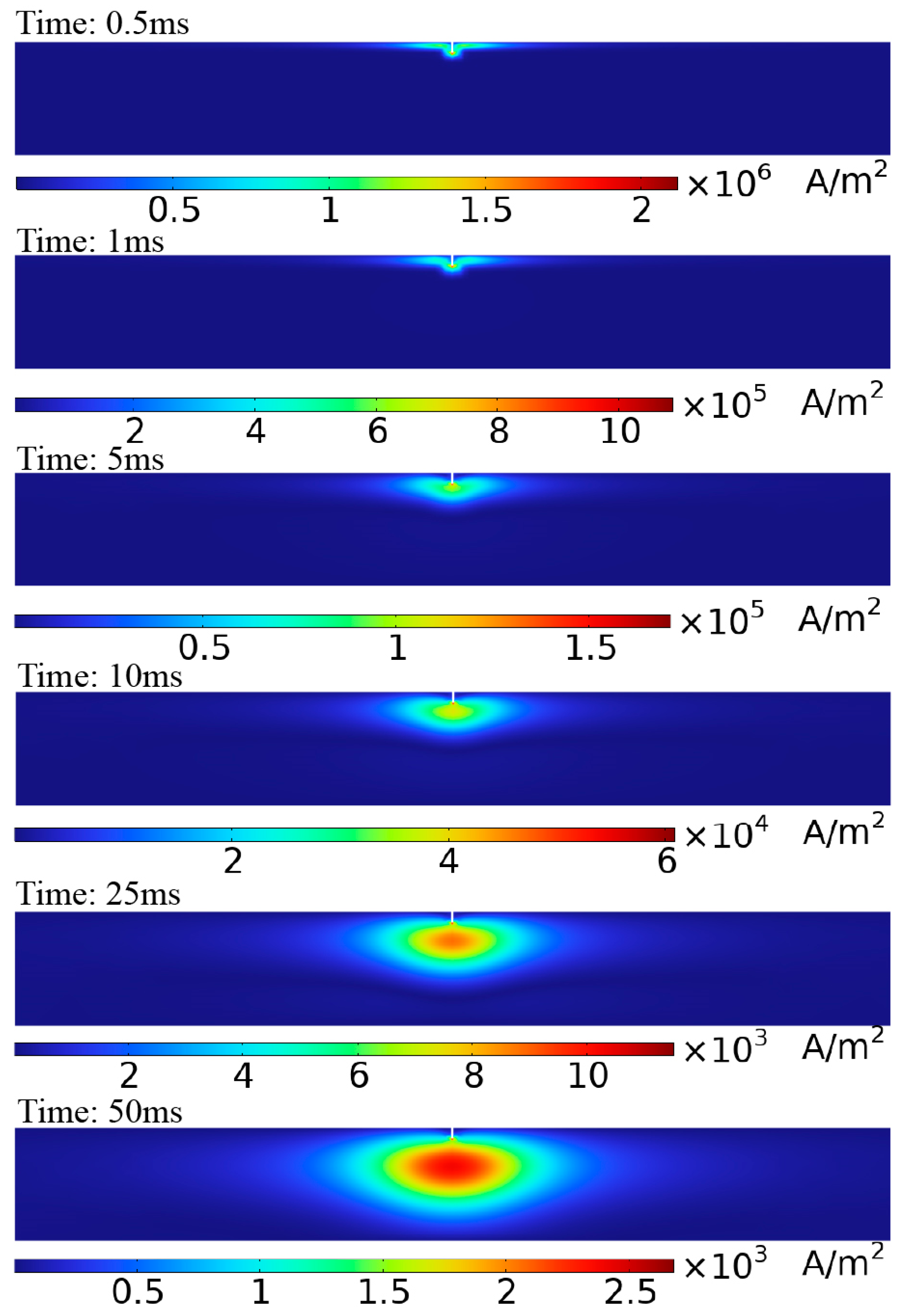



| Window Number | Center Time (μs) | Window Number | Center Time (μs) | Window Number | Center Time (μs) | Window Number | Center Time (μs) |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 9 | 335 | 17 | 2011 | 25 | 12,598 |
| 2 | 46 | 10 | 414 | 18 | 2528 | 26 | 15,856 |
| 3 | 79 | 11 | 518 | 19 | 3172 | 27 | 19,965 |
| 4 | 104 | 12 | 645 | 20 | 3990 | 28 | 25,131 |
| 5 | 135 | 13 | 804 | 21 | 5024 | 29 | 31,632 |
| 6 | 176 | 14 | 1010 | 22 | 6319 | 30 | 39,817 |
| 7 | 215 | 15 | 1273 | 23 | 7956 | 31 | 50,117 |
| 8 | 271 | 16 | 1598 | 24 | 10,015 |
| Lift-Off Height | 0 mm | 20 mm | 40 mm | 60 mm |
| Detection Area | 45 mm | 60 mm | 75 mm | >100 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, J.; Hu, H.; Hu, B.; Bin, W.; Shi, W.; Fu, Y. Circumferential Crack Detection in Ultra-High-Pressure Tubular Reactors with Pulsed Eddy Current Testing. Sensors 2024, 24, 6599. https://doi.org/10.3390/s24206599
Wang Y, Sun J, Hu H, Hu B, Bin W, Shi W, Fu Y. Circumferential Crack Detection in Ultra-High-Pressure Tubular Reactors with Pulsed Eddy Current Testing. Sensors. 2024; 24(20):6599. https://doi.org/10.3390/s24206599
Chicago/Turabian StyleWang, Yaxing, Jie Sun, Huasheng Hu, Bo Hu, Weiqi Bin, Wen Shi, and Yuewen Fu. 2024. "Circumferential Crack Detection in Ultra-High-Pressure Tubular Reactors with Pulsed Eddy Current Testing" Sensors 24, no. 20: 6599. https://doi.org/10.3390/s24206599
APA StyleWang, Y., Sun, J., Hu, H., Hu, B., Bin, W., Shi, W., & Fu, Y. (2024). Circumferential Crack Detection in Ultra-High-Pressure Tubular Reactors with Pulsed Eddy Current Testing. Sensors, 24(20), 6599. https://doi.org/10.3390/s24206599





