A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers
Abstract
1. Introduction
2. Key Developments in Grating Fabrication
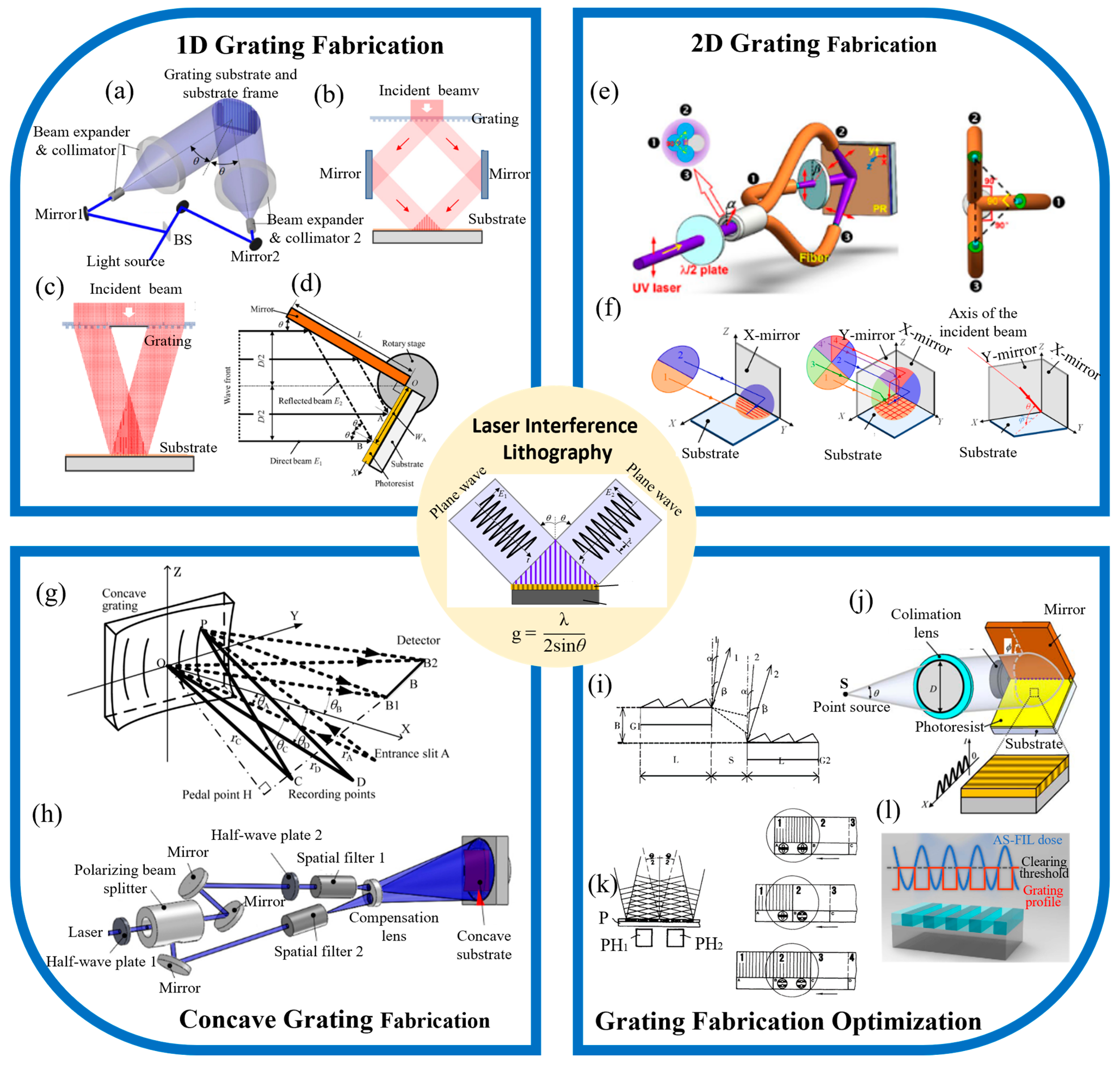
2.1. Principle of LIL
2.2. 1-D Grating Fabrication
2.3. 2-D Grating Fabrication
2.4. Concave Grating Fabrication
2.5. Exposure Field Drift Control

3. Key Developments in Grating Interferometry
3.1. High-Precision Measurement
3.1.1. Multiple Optical Subdivision
3.1.2. Multiple Electronic Subdivision

3.1.3. Using Gratings with Smaller Periods
3.1.4. Laser Frequency Stabilization
3.2. Absolute Measurement
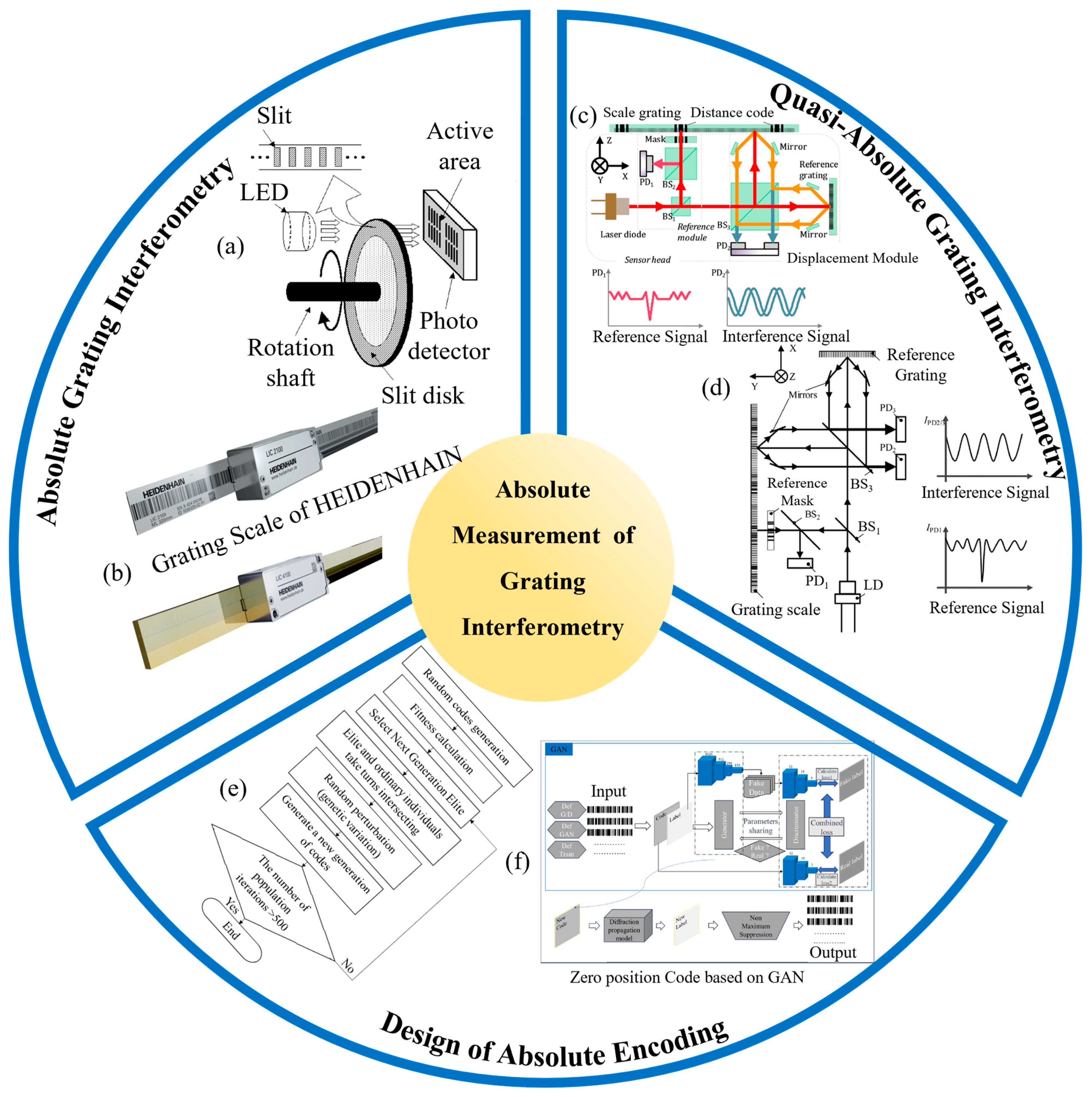
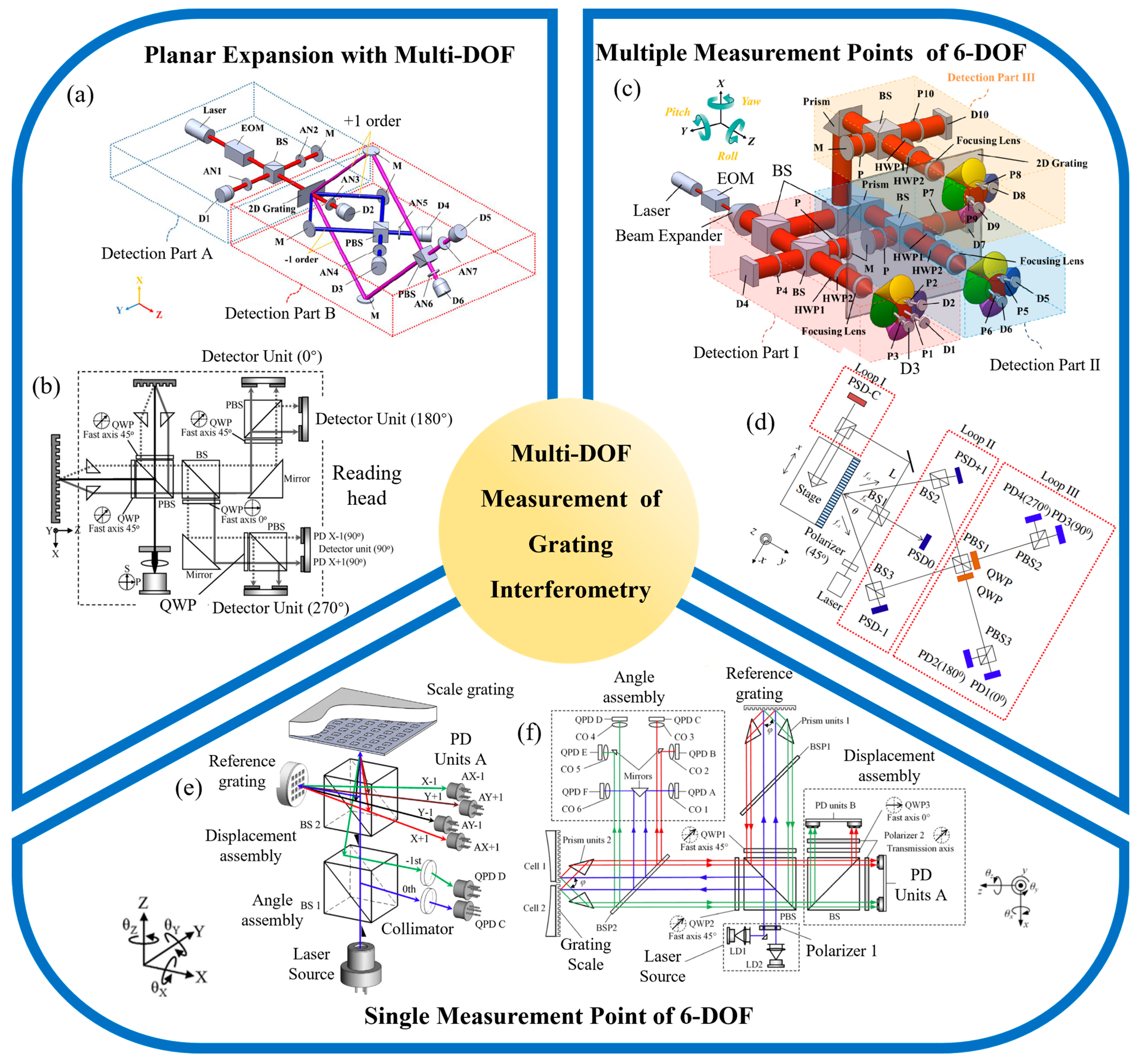
3.3. Multi-Degree-of-Freedom Measurement
3.4. Industrialization Modules of Grating Interferometry
3.4.1. Mature Industrial Products
3.4.2. Diffraction Light Modulation Module
3.4.3. Interferometric Optical Path Integration Module
3.4.4. Signal Processing Systems
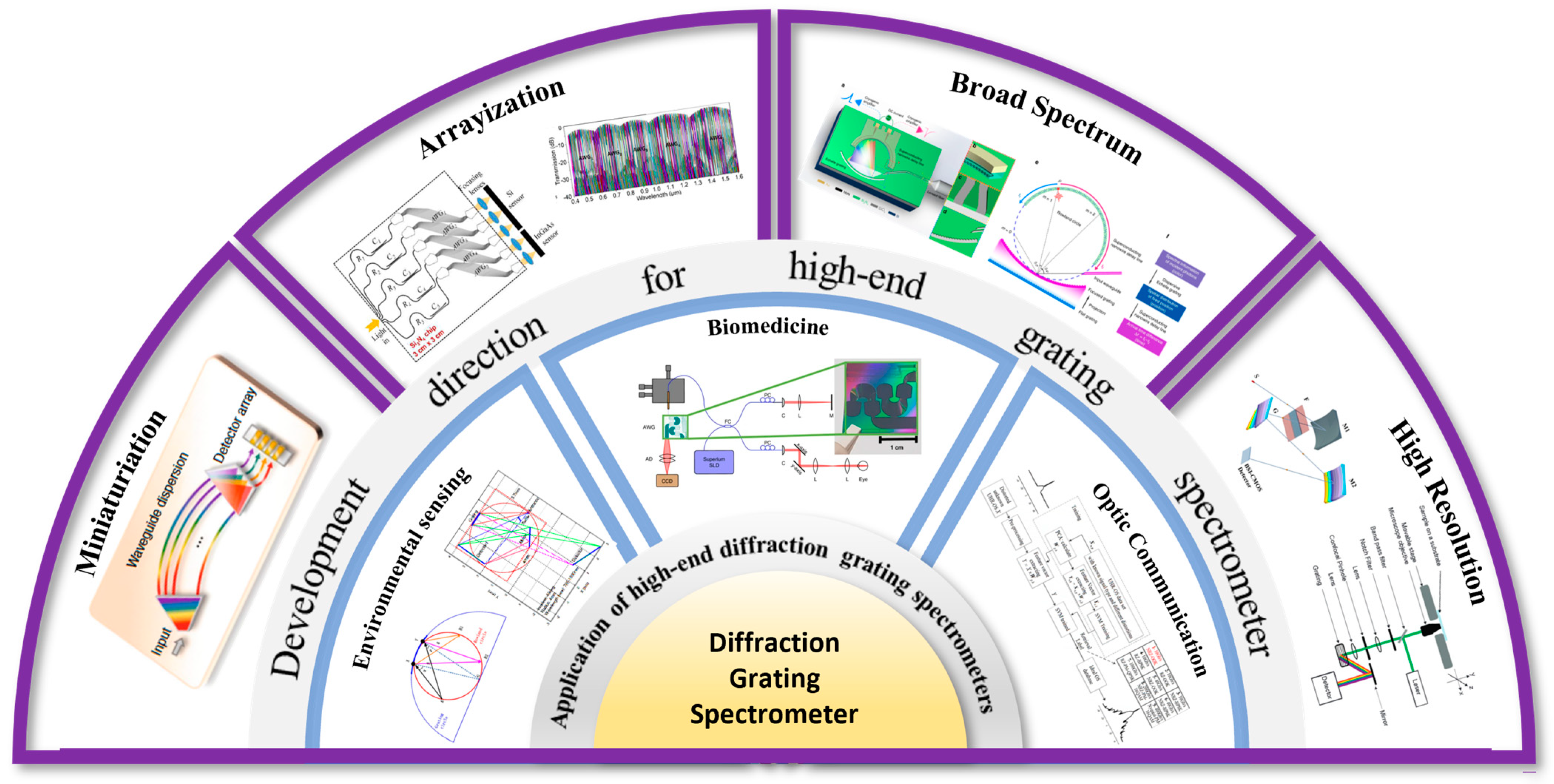
4. Gratings in Miniature Spectrometers
4.1. Concave Grating Spectrometer
4.2. Fresnel Grating Spectrometer
4.3. Novel Microlens Grating Spectrometer
5. Conclusions and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Noda, H.; Namioka, T.; Seya, M. Geometric theory of the grating. J. Opt. Soc. Am. 1974, 64, 1031–1036. [Google Scholar] [CrossRef]
- Silberstein, E.; Lalanne, P.; Hugonin, J.-P.; Cao, Q. Use of grating theories in integrated optics. J. Opt. Soc. Am. A 2001, 18, 2865–2875. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Y.-L.; Chu, F.; Li, N.-N.; Li, Z.-S.; Lee, S.-D.; Nie, Z.-Q.; Liu, C.; Wang, Q.-H. Color liquid crystal grating based color holographic 3D display system with large viewing angle. Light Sci. Appl. 2024, 13, 16. [Google Scholar] [CrossRef] [PubMed]
- Vitali, V.; Domínguez Bucio, T.; Lacava, C.; Marchetti, R.; Mastronardi, L.; Rutirawut, T.; Churchill, G.; Faneca, J.; Gates, J.C.; Gardes, F. High-efficiency reflector-less dual-level silicon photonic grating coupler. Photonics Res. 2023, 11, 1275–1283. [Google Scholar] [CrossRef]
- Chen, R.; Li, Y.; Xue, G.; Tao, Y.; Li, X. Laser triangulation measurement system with Scheimpflug calibration based on the Monte Carlo optimization strategy. Opt. Express 2022, 30, 25290–25307. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Zhao, S.; Deng, X. Biological sensors based on long period fiber grating. Opt. Laser Technol. 2023, 158, 108936. [Google Scholar] [CrossRef]
- Branduardi-Raymont, G.; denBoggende, A.; Audard, M.; Thomsen, K.; Brinkman, A.; denHerder, J.; Bixler, J.; Aarts, H.; Kahn, S. The Reflection Grating Spectrometer on Board XMM-Newton. Astron. Astrophys. 2001, 365, L7–L17. [Google Scholar]
- Fortin, G.; McCarthy, N. Chirped holographic grating used as the dispersive element in an optical spectrometer. Appl. Opt. 2005, 44, 4874–4883. [Google Scholar] [CrossRef]
- Sokolova, E. Holographic diffraction gratings for flat-field spectrometers. J. Mod. Opt. 2000, 47, 2377–2389. [Google Scholar] [CrossRef]
- Glaser, T. High-end spectroscopic diffraction gratings: Design and manufacturing. Adv. Opt. Technol. 2015, 4, 25–46. [Google Scholar] [CrossRef]
- Li, X.; Zhu, X.; Zhou, Q.; Wang, H.; Ni, K. Low-cost lithography for fabrication of one-dimensional diffraction gratings by using laser diodes. In Proceedings of the 2015 International Conference on Optical Instruments and Technology: Micro/Nano Photonics and Fabrication, Beijing, China, 17–19 May 2015; Zhou, Z., Zhou, C., Cheben, P., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9624. [Google Scholar]
- Carr, J.; Desmulliez, M.; Weston, N.; McKendrick, D.; Cunningham, G.; McFarland, G.; Meredith, W.; McKee, A.; Langton, C. Miniaturised optical encoder for ultra precision metrology systems. Precis. Eng. 2009, 33, 263–267. [Google Scholar] [CrossRef]
- Han, M.; Lei, F.; Shi, W.; Lu, S.; Li, X. Uniaxial MEMS-based 3D reconstruction using pixel refinement. Opt. Express 2022, 31, 536–554. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Qiao, X.; Ni, K.; Li, X.; Wang, X. Depth detection in interactive projection system based on one-shot black-and-white stripe pattern. Opt. Express 2017, 25, 5341–5351. [Google Scholar] [CrossRef] [PubMed]
- Lei, F.; Han, M.; Jiang, H.; Wang, X.; Li, X. A phase-angle inspired calibration strategy based on MEMS projector for 3D reconstruction with markedly reduced calibration images and parameters. Opt. Lasers Eng. 2024, 176, 108078. [Google Scholar] [CrossRef]
- Chen, H.; Guan, H.; Zeng, L.; Jin, Y. Fabrication of broadband, high-efficiency, metal-multilayer-dielectric gratings. Opt. Commun. 2014, 329, 103–108. [Google Scholar] [CrossRef]
- Clausnitzer, T.; Limpert, J.; Zöllner, K.; Zellmer, H.; Fuchs, H.-J.; Kley, E.-B.; Tünnermann, A.; Jupe, M.; Ristau, D. Highly efficient transmission gratings in fused silica for chirped-pulse amplification systems. Appl. Opt. 2003, 42, 6934–6938. [Google Scholar] [CrossRef]
- Canova, F.; Uteza, O.; Chambaret, J.-P.; Flury, M.; Tonchev, S.; Fechner, R.; Parriaux, O. High-efficiency, broad band, high-damage threshold high-index gratings for femtosecond pulse compression. Opt. Express 2007, 15, 15324–15334. [Google Scholar] [CrossRef]
- Kessler, T.J.; Bunkenburg, J.; Huang, H.; Kozlov, A.; Meyerhofer, D.D. Demonstration of coherent addition of multiple gratings for high-energy chirped-pulse-amplified lasers. Opt. Lett. 2004, 29, 635–637. [Google Scholar] [CrossRef] [PubMed]
- Habara, H.; Xu, G.; Jitsuno, T.; Kodama, R.; Suzuki, K.; Sawai, K.; Kondo, K.; Miyanaga, N.; Tanaka, K.A.; Mima, K. Pulse compression and beam focusing with segmented diffraction gratings in a high-power chirped-pulse amplification glass laser system. Opt. Lett. 2010, 35, 1783–1785. [Google Scholar] [CrossRef] [PubMed]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef]
- Agrawal, G.P. Optical communication: Its history and recent progress. In Optics in Our Time; Springer: Cham, Switzerland, 2016; pp. 177–199. [Google Scholar]
- Essiambre, R.-J.; Tkach, R.W. Capacity trends and limits of optical communication networks. Proc. IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
- Ho, K.-P. Phase-Modulated Optical Communication Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Goedgebuer, J.-P.; Levy, P.; Larger, L.; Chen, C.-C.; Rhodes, W.T. Optical communication with synchronized hyperchaos generated electrooptically. IEEE J. Quantum Electron. 2002, 38, 1178–1183. [Google Scholar] [CrossRef]
- Han, Y.; Zang, Z.; Wu, L.; Hao, Y.; Zhu, Q.; Liu, X.; Chang-Hasnain, C.; Fu, H. Wide-field multipass spectral-scanning 3D imaging LiDAR using an echelle grating. In Proceedings of the 2023 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 7–12 May 2023; pp. 1–2. [Google Scholar]
- Lei, F.; Ma, R.; Li, X. Use of Phase-Angle Model for Full-Field 3D Reconstruction under Efficient Local Calibration. Sensors 2024, 24, 2581. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Wang, X.; Li, X. Projection superimposition for the generation of high-resolution digital grating. Opt. Lett. 2024, 49, 4473–4476. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, Z.; Zhang, C.; Han, M.; Lei, F.; Liang, X.; Wang, X.; Gui, W.; Li, X. Deep learning-driven one-shot dual-view 3D reconstruction for dual-projector system. IEEE Trans. Instrum. Meas. 2023, 73, 1–14. [Google Scholar]
- Han, M.; Shi, W.; Lu, S.; Lei, F.; Li, Y.; Wang, X.; Li, X. Internal-External Layered Phase-shifting for Phase Retrieval. IEEE Trans. Instrum. Meas. 2023, 73, 1–13. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Liang, X.; Huang, H.; Qian, X.; Feng, F.; Zhang, C.; Wang, X.; Gui, W.; Li, X. Global phase accuracy enhancement of structured light system calibration and 3D reconstruction by overcoming inevitable unsatisfactory intensity modulation. Measurement 2024, 236, 114952. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, Z.; Sun, Y.; Teng, H.; Wang, W.; Li, W. Bidirectional Littrow double grating interferometry for quadruple optical interpolation. Opt. Laser Technol. 2024, 175, 110751. [Google Scholar] [CrossRef]
- Ban, Y.; Zhao, G.; Liu, H.; Zhang, Z.; Chen, B.; Lu, B.; Liu, H. Two-dimensional grating interferometer with nanometer accuracy. AIP Adv. 2023, 13, 125125. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Tsai, C.-M.; Ye, C.-Y.; Chen, P.-L.; Lee, T.-T.; Dai, Z.-X. Period measurement of a periodic structure by using a heterodyne grating interferometer. Appl. Opt. 2024, 63, 4211–4218. [Google Scholar] [CrossRef]
- Rohan, R.; Venkadeshwaran, K.; Ranjan, P. Recent advancements of fiber Bragg grating sensors in biomedical application: A review. J. Opt. 2024, 53, 282–293. [Google Scholar] [CrossRef]
- Singh, M.J.; Choudhary, S.; Chen, W.-B.; Wu, P.-C.; Goyal, M.K.; Rajput, A.; Borana, L. Applications of fibre Bragg grating sensors for monitoring geotechnical structures: A comprehensive review. Measurement 2023, 218, 113171. [Google Scholar] [CrossRef]
- Wu, Y.; Long, X.; Lu, J.; Zhou, R.; Liu, L.; Wu, Y. Long-life in-situ temperature field monitoring using Fiber Bragg grating sensors in electromagnetic launch high-rate hardcase lithium-ion battery. J. Storage Mater. 2023, 57, 106207. [Google Scholar] [CrossRef]
- Presti, D.L.; Dimo, A.; Zoboli, L.; Bianchi, D.; Massaroni, C.; Altomare, V.; Grasso, A.; Oddo, C.; Gizzi, A.; Schena, E. A 3D-printed tactile probe based on fiber Bragg grating sensors for non-invasive breast cancer identification. IEEE Sens. J. 2023, 23, 24489–24499. [Google Scholar] [CrossRef]
- Xue, G.; Zhai, Q.; Lu, H.; Zhou, Q.; Ni, K.; Lin, L.; Wang, X.; Li, X. Polarized holographic lithography system for high-uniformity microscale patterning with periodic tunability. Microsyst. Nanoeng. 2021, 7, 31. [Google Scholar] [CrossRef]
- Xue, G.; Lin, L.; Zhai, Q.; Zeng, C.; Wang, X.; Li, X. Development of dielectric-film-based polarization modulation scheme for patterning highly uniform 2d array structures with periodic tunability. Opt. Lasers Eng. 2023, 167, 107627. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhu, X.; Lu, H.; Yang, L.; Ma, D.; Sun, J.; Ni, K.; Wang, X. Holographic fabrication of an arrayed one-axis scale grating for a two-probe optical linear encoder. Opt. Express 2017, 25, 16028–16039. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lu, H.; Zhou, Q.; Wu, G.; Ni, K.; Wang, X. An orthogonal type two-axis Lloyd’s mirror for holographic fabrication of two-dimensional planar scale gratings with large area. Appl. Sci. 2018, 8, 2283. [Google Scholar] [CrossRef]
- Brueck, S.R. Optical and interferometric lithography-nanotechnology enablers. Proc. IEEE 2005, 93, 1704–1721. [Google Scholar] [CrossRef]
- Gui, X.; Li, Z.; Fu, X.; Guo, H.; Wang, Y.; Wang, C.; Wang, J.; Jiang, D. Distributed optical fiber sensing and applications based on large-scale fiber Bragg grating array. J. Light. Technol. 2023, 41, 4187–4200. [Google Scholar] [CrossRef]
- Ropp, C.; Maurya, D.; Yulaev, A.; Westly, D.; Simelgor, G.; Aksyuk, V. Scalable and robust beam shaping using apodized fish-bone grating couplers. Opt. Express 2023, 31, 40792–40802. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, K.; Zhang, X.; Popmintchev, D.; Xu, H.; Wang, Y.; Li, R.; Zhang, G.; Tang, J.; Niu, J. Highly efficient and aberration-free off-plane grating spectrometer and monochromator for EUV—Soft X-ray applications. Light Sci. Appl. 2024, 13, 12. [Google Scholar] [CrossRef] [PubMed]
- Shcheglov, A.; Nie, Y.; Thienpont, H.; Ottevaere, H. Miniaturized two-channel broadband spectrometer based on variable-spacing concave blazed gratings. J. Opt. Microsyst. 2023, 3, 024501. [Google Scholar] [CrossRef]
- Kliss, N.; Wengrowicz, J.; Papeer, J.; Mazuz-Herpaz, Y.; Porat, E.; Zigler, A.; Frank, Y. Sinusoidal transmission grating spectrometer for extreme ultraviolet measurement. Rev. Sci. Instrum. 2024, 95, 049902. [Google Scholar] [CrossRef] [PubMed]
- Chu, Q.; Li, X.; Sun, Y.; Jirigalantu; Sun, C.; Chen, J.; Li, F.; Bayanheshig. Theoretical analysis of a multi-grating-based cross-dispersed spatial heterodyne spectrometer. Opt. Express 2023, 31, 18190–18209. [Google Scholar] [CrossRef] [PubMed]
- Heilmann, R.K.; Bruccoleri, A.R.; Gregory, J.A.; Gullikson, E.M.; Günther, H.M.; Hertz, E.; Lambert, R.D.; Young, D.J.; Schattenburg, M.L. Transmission grating arrays for the X-ray spectrometer on Arcus Probe. arXiv 2024, arXiv:2405.15977. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, W.; Zhang, A.; Yan, Y.; Huang, H.; Geng, Y.; Li, C. Fabrication of micro-nano hierarchical grating using revolving trajectory of nanoindenter. J. Manuf. Process. 2024, 127, 77–97. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, Q.; Shimada, K.; Liu, P.; He, Y.; Hu, Y.; Wang, X.; Zhou, T.; Mizutani, M. High-precision and high-efficiency fabrication of blazed grating by ultrasonic-assisted ultraprecision planing. J. Mater. Process. Technol. 2023, 311, 117802. [Google Scholar] [CrossRef]
- Mumtaz, F.; Tekle, H.; Zhang, B.; Smith, J.D.; O’Malley, R.J.; Huang, J. Highly cascaded first-order sapphire optical fiber Bragg gratings fabricated by a femtosecond laser. Opt. Lett. 2023, 48, 4380–4383. [Google Scholar] [CrossRef]
- Gao, J.; Chen, P.; Wu, L.; Yu, B.; Qian, L. A review on fabrication of blazed gratings. J. Phys. D Appl. Phys. 2021, 54, 313001. [Google Scholar] [CrossRef]
- Xue, B.; Yang, C.; Geng, Y.; Yan, Y. A novel fabrication of micro/nano hierarchical grating structures for structural coloration by using revolving tip-based machining method. J. Manuf. Process. 2021, 62, 202–212. [Google Scholar] [CrossRef]
- Sideris, C.; Khachaturian, A.; White, A.D.; Bruno, O.P.; Hajimiri, A. Foundry-fabricated grating coupler demultiplexer inverse-designed via fast integral methods. Commun. Phys. 2022, 5, 68. [Google Scholar] [CrossRef]
- Chen, M.-Q.; He, T.-Y.; Zhao, Y.; Yang, G. Ultra-short phase-shifted fiber Bragg grating in a microprobe for refractive index sensor with temperature compensation. Opt. Laser Technol. 2023, 157, 108672. [Google Scholar] [CrossRef]
- He, W.; Lin, Y.; Cui, L.; Chen, T.; Qian, L.; Yu, B. Roles of overlapped scratching in grating fabrications assisted by selective wet etching. J. Mater. Sci. 2023, 58, 15647–15659. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, X.; Chen, Y.; Qin, L.; Ning, Y.; Wang, L. The development progress of surface structure diffraction gratings: From manufacturing technology to spectroscopic applications. Appl. Sci. 2022, 12, 6503. [Google Scholar] [CrossRef]
- Rothschild, M.; Bloomstein, T.M.; Fedynyshyn, T.H.; Kunz, R.R.; Liberman, V.; Switkes, M.; Efremow, N.N.; Palmacci, S.T.; Sedlacek, J.H.; Hardy, D.E. Recent trends in optical lithography. Linc. Lab. J. 2003, 14, 221–236. [Google Scholar]
- Bossung, J.W.; Muraski, E.S. Optical advances in projection photolithography. In Proceedings of the Developments in Semiconductor Microlithography III, San Jose, CA, USA, 10–11 April 1978; pp. 16–23. [Google Scholar]
- Stokes, K.; Clark, K.; Odetade, D.; Hardy, M.; Goldberg Oppenheimer, P. Advances in lithographic techniques for precision nanostructure fabrication in biomedical applications. Discov. Nano 2023, 18, 153. [Google Scholar] [CrossRef]
- Barcelo, S.; Li, Z. Nanoimprint lithography for nanodevice fabrication. Nano Converg. 2016, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; S Rajput, N.; Luo, X. Nanoimprint lithography-the past, the present and the future. Curr. Nanosci. 2016, 12, 712–724. [Google Scholar] [CrossRef]
- Unno, N.; Mäkelä, T. Thermal nanoimprint lithography—A review of the process, mold fabrication, and material. Nanomaterials 2023, 13, 2031. [Google Scholar] [CrossRef]
- Chen, Y. Nanofabrication by electron beam lithography and its applications: A review. Microelectron. Eng. 2015, 135, 57–72. [Google Scholar] [CrossRef]
- Seo, J.-H.; Park, J.H.; Kim, S.-I.; Park, B.J.; Ma, Z.; Choi, J.; Ju, B.-K. Nanopatterning by laser interference lithography: Applications to optical devices. J. Nanosci. Nanotechnol. 2014, 14, 1521–1532. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Z.-H.; Yu, Y.-H.; Sun, H.-B. Laser interference fabrication of large-area functional periodic structure surface. Front. Mech. Eng. 2018, 13, 493–503. [Google Scholar] [CrossRef]
- Lasagni, A.F.; Mulko, L.; Soldera, M. Ultrarapid Industrial Large-Area Processing Using Laser Interference Patterning Methods. In Ultrafast Laser Nanostructuring: The Pursuit of Extreme Scales; Springer: Berlin/Heidelberg, Germany, 2023; pp. 951–977. [Google Scholar]
- Gao, W.; Kim, S.-W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Castillo, J.E.; Castro, J.M.; Kostuk, R.K.; Geraghty, D.F. Study of multichannel parallel anti-symmetric waveguide Bragg gratings for telecom applications. IEEE Photonics Technol. Lett. 2007, 19, 85–87. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X.; Zhou, Q.; Wang, X.; Ni, K. A blu-ray laser diode based dual-beam interference lithography for fabrication of diffraction gratings for surface encoders. In Proceedings of the Advanced Laser Processing and Manufacturing, Beijing, China, 13 October 2016; pp. 27–32. [Google Scholar]
- Wang, G.; Xue, G.; Zhai, Q.; Zhu, J.; Yu, K.; Huang, G.; Wang, M.; Zhong, A.; Zhu, L.; Yan, S. Planar diffractive grating for magneto-optical trap application: Fabrication and testing. Appl. Opt. 2021, 60, 9358–9364. [Google Scholar] [CrossRef]
- van Wijk, A.C.; Doerr, C.R.; Akca, I.B. Custom Arrayed Waveguide Gratings with Improved Performance. Adv. Photonics Res. 2023, 4, 2300198. [Google Scholar] [CrossRef]
- Perry, M.; Shore, B.; Boyd, R.; Britten, J. Multilayer dielectric gratings: Increasing the power of light. Sci. Technol. Rev. 1995, 9, 25–33. [Google Scholar]
- Zhou, Q.; Li, X.; Ni, K.; Tian, R.; Pang, J. Holographic fabrication of large-constant concave gratings for wide-range flat-field spectrometers with the addition of a concave lens. Opt. Express 2016, 24, 732–738. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y. Laser interference lithography for fabrication of planar scale gratings for optical metrology. Nanomanufacturing Metrol. 2021, 4, 3–27. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Y.; Kong, W.; Liu, K.; Du, W.; Zhao, C.; Gao, P.; Zhao, Z.; Wang, C.; Pu, M. Large area deep subwavelength interference lithography with a 35 nm half-period based on bulk plasmon polaritons. Opt. Mater. Express 2018, 8, 199–209. [Google Scholar] [CrossRef]
- Pang, L.; Nakagawa, W.; Fainman, Y. Fabrication of two-dimensional photonic crystals with controlled defects by use of multiple exposures and direct write. Appl. Opt. 2003, 42, 5450–5456. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Feng, B.; Lu, B.; Chen, Y.; Li, W.; Zhang, W.; Li, T. A study of nano-structural effect on the polarization characteristics of metallic sub-wavelength grating polarizers in visible wavelengths. Microelectron. Eng. 2020, 227, 111327. [Google Scholar] [CrossRef]
- Luo, X. Extraordinary Young’s interferences and super-diffraction laser lithography. In Handbook of Laser Micro- and Nano-Engineering; Springer: Cham, Switzerland, 2020; pp. 1–40. [Google Scholar]
- Wang, X.; Jiang, Y.; Zheng, Z.; Wang, W.; Chi, Z.; Li, W. Reconstruction design method of an aspherical recording optical system for the varied line-space grating. Opt. Lett. 2022, 47, 4487–4490. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, W.; Zhang, T.; Zheng, Z.; Chi, Z.; Jiang, Y.; Wu, N. A large-size and polarization-independent two dimensional grating fabricated by scanned reactive-ion-beam etching. Nanophotonics 2022, 11, 4649–4657. [Google Scholar] [CrossRef]
- Liu, R.; Cao, L.; Liu, D.; Wang, L.; Saeed, S.; Wang, Z. Laser Interference Lithography—A Method for the Fabrication of Controlled Periodic Structures. Nanomaterials 2023, 13, 1818. [Google Scholar] [CrossRef]
- Capraro, G.; Lipkin, M.; Möller, M.; Bolten, J.; Lemme, M.C. Phase mask pinholes as spatial filters for laser interference lithography. Adv. Photonics Res. 2023, 4, 2300225. [Google Scholar] [CrossRef]
- Liu, R.; Cao, L.; Liu, D.; Lian, Z.; Wang, Z. One-step laser interference lithography for large-scale preparation of a superhydrophobic Ti6Al4V surface with improved hardness, friction reduction and corrosion resistance. Colloids Surf. A 2024, 702, 134898. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, X.; Di, X.; Jia, T.; Chen, T.; Zhang, L.; Yang, H.; Qi, Y.; Tang, C. Theoretical study on fabrication of sub-wavelength structures via combining low-order guided mode interference lithography with sample rotation. J. Opt. 2022, 25, 015001. [Google Scholar] [CrossRef]
- Park, J.H.; Yun, D.H.; Ma, Y.W.; Gwak, C.Y.; Shin, B.S. Prism-based laser interference lithography system for simple multibeam interference lithography. Sci. Adv. Mater. 2020, 12, 398–402. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Kim, W.; Hosono, K.; Shimizu, Y.; Shi, L.; Zeng, L. A sub-nanometric three-axis surface encoder with short-period planar gratings for stage motion measurement. Precis. Eng. 2012, 36, 576–585. [Google Scholar] [CrossRef]
- Chen, C.G.; Konkola, P.T.; Heilmann, R.K.; Joo, C.; Schattenburg, M.L. Nanometer-accurate grating fabrication with scanning beam interference lithography. In Proceedings of the Nano-and Microtechnology: Materials, Processes, Packaging, and Systems, Melbourne, Australia, 16–18 December 2002; pp. 126–134. [Google Scholar]
- Buitrago, E.; Fallica, R.; Fan, D.; Kulmala, T.S.; Vockenhuber, M.; Ekinci, Y. SnOx high-efficiency EUV interference lithography gratings towards the ultimate resolution in photolithography. Microelectron. Eng. 2016, 155, 44–49. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, S.; Gao, W. Fabrication of scale gratings for surface encoders by using laser interference lithography with 405 nm laser diodes. Int. J. Precis. Eng. Manuf. 2013, 14, 1979–1988. [Google Scholar] [CrossRef]
- He, J.; Fang, X.; Lin, Y.; Zhang, X. Polarization control in flexible interference lithography for nano-patterning of different photonic structures with optimized contrast. Opt. Express 2015, 23, 11518–11525. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Aihara, R.; Ren, Z.; Chen, Y.-L.; Ito, S.; Gao, W. Influences of misalignment errors of optical components in an orthogonal two-axis Lloyd’s mirror interferometer. Opt. Express 2016, 24, 27521–27535. [Google Scholar] [CrossRef]
- Chen, C.G. Beam Alignment and Image Metrology for Scanning Beam Interference Lithography: Fabricating Gratings with Nanometer Phase Accuracy. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Li, X.; Ni, K.; Zhou, Q.; Wang, X.; Tian, R.; Pang, J. Fabrication of a concave grating with a large line spacing via a novel dual-beam interference lithography method. Opt. Express 2016, 24, 10759–10766. [Google Scholar] [CrossRef]
- Turukhano, B.; Gorelik, V.; Kovalenko, S.; Turukhano, N. Phase synthesis of a holographic metrological diffraction grating of unlimited length. Opt. Laser Technol. 1996, 28, 263–268. [Google Scholar] [CrossRef]
- Xue, D.; Deng, X.; Dun, X.; Wang, J.; Wang, Z.; Cheng, X. Improving grating duty cycle uniformity: Amplitude-splitting flat-top beam laser interference lithography. Appl. Opt. 2024, 63, 2065–2069. [Google Scholar] [CrossRef]
- Lindau, S. The groove profile formation of holographic gratings. Opt. Acta Int. J. Opt. 1982, 29, 1371–1381. [Google Scholar] [CrossRef]
- Kodate, K.; Kamiya, T.; Takenaka, H.; Yanai, H. Analysis of two-dimensional etching effect on the profiles of fine holographic grating made of positive photoresist AZ2400. Jpn. J. Appl. Phys. 1978, 17, 121. [Google Scholar] [CrossRef]
- Britten, J.A.; Boyd, R.D.; Shore, B.W. In situ end-point detection during development of submicrometer grating structures in photoresist. Opt. Eng. 1995, 34, 474–479. [Google Scholar] [CrossRef]
- Leclere, P.; Renotte, Y.; Lion, Y. Measure of the diffraction efficiency of a holographic grating created by two Gaussian beams. Appl. Opt. 1992, 31, 4725–4733. [Google Scholar] [CrossRef] [PubMed]
- Shore, B.; Perry, M.; Britten, J.; Boyd, R.; Feit, M.; Nguyen, H.; Chow, R.; Loomis, G.; Li, L. Design of high-efficiency dielectric reflection gratings. J. Opt. Soc. Am. A 1997, 14, 1124–1136. [Google Scholar] [CrossRef]
- Ma, D.; Zhao, Y.; Zeng, L. Achieving unlimited recording length in interference lithography via broad-beam scanning exposure with self-referencing alignment. Sci. Rep. 2017, 7, 926. [Google Scholar] [CrossRef]
- Lloyd, H. On a new case of interference of the rays of light. Trans. R. Ir. Acad. 1831, 17, 171–177. [Google Scholar]
- Titchmarsh, P. Lloyd’s single-mirror interference fringes. Proc. Phys. Soc. 1941, 53, 391. [Google Scholar] [CrossRef]
- Xie, Q.; Hong, M.; Tan, H.; Chen, G.; Shi, L.; Chong, T. Fabrication of nanostructures with laser interference lithography. J. Alloys Compd. 2008, 449, 261–264. [Google Scholar] [CrossRef]
- Ku, H.M.; Huang, C.Y.; Chao, S. Fabrication of three-dimensional autocloned photonic crystal on sapphire substrate. Appl. Opt. 2011, 50, C1–C4. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, S.; Gao, W.; Zeng, L. Fabrication of diffraction gratings for surface encoders by using a Lloyd’s mirror interferometer with a 405 nm laser diode. In Proceedings of the Eighth International Symposium on Precision Engineering Measurement and Instrumentation, Chengdu, China, 8–11 August 2012; pp. 1182–1188. [Google Scholar]
- He, J.; Lin, Y.; Zhang, X. Fiber-based flexible interference lithography for photonic nanopatterning. Opt. Express 2014, 22, 26386–26391. [Google Scholar] [CrossRef]
- Yang, M.; Kong, X.; Li, X. Impact of Grating Duty-Cycle Randomness on DFB Laser Performance. Photonics 2024, 11, 574. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.; Lin, J.; Zhao, H.; Ma, H.; Yao, H.; Kang, M.; Fu, B.; Liu, S. The fabrication of high-performance diffraction gratings via vibration-assisted UV nanoimprinting lithography. Colloids Surf. A 2023, 679, 132569. [Google Scholar] [CrossRef]
- Korre, H.; Fucetola, C.P.; Johnson, J.A.; Berggren, K.K. Development of a simple, compact, low-cost interference lithography system. J. Vac. Sci. Technol. B 2010, 28, C6Q20–C26Q24. [Google Scholar] [CrossRef]
- Kondo, T.; Matsuo, S.; Juodkazis, S.; Mizeikis, V.; Misawa, H. Multiphoton fabrication of periodic structures by multibeam interference of femtosecond pulses. Appl. Phys. Lett. 2003, 82, 2758–2760. [Google Scholar] [CrossRef]
- Chua, J.; Murukeshan, V. Patterning of two-dimensional nanoscale features using grating-based multiple beams interference lithography. Phys. Scr. 2009, 80, 015401. [Google Scholar] [CrossRef]
- Stankevičius, E.; Daugnoraitė, E.; Račiukaitis, G. Mechanism of pillars formation using four-beam interference lithography. Opt. Lasers Eng. 2019, 116, 41–46. [Google Scholar] [CrossRef]
- Solak, H.; David, C.; Gobrecht, J.; Wang, L.; Cerrina, F. Four-wave EUV interference lithography. Microelectron. Eng. 2002, 61, 77–82. [Google Scholar] [CrossRef]
- Berger, V.; Gauthier-Lafaye, O.; Costard, E. Photonic band gaps and holography. J. Appl. Phys. 1997, 82, 60–64. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Shimizu, Y.; Ito, S. A two-axis Lloyd’s mirror interferometer for fabrication of two-dimensional diffraction gratings. CIRP Ann. 2014, 63, 461–464. [Google Scholar] [CrossRef]
- Vala, M.; Homola, J. Flexible method based on four-beam interference lithography for fabrication of large areas of perfectly periodic plasmonic arrays. Opt. Express 2014, 22, 18778–18789. [Google Scholar] [CrossRef]
- de Boor, J.; Geyer, N.; Gösele, U.; Schmidt, V. Three-beam interference lithography: Upgrading a Lloyd’s interferometer for single-exposure hexagonal patterning. Opt. Lett. 2009, 34, 1783–1785. [Google Scholar] [CrossRef]
- Zhou, H.; Zeng, L. Method to fabricate orthogonal crossed gratings based on a dual Lloyd’s mirror interferometer. Opt. Commun. 2016, 360, 68–72. [Google Scholar] [CrossRef]
- Solak, H.H.; David, C.; Gobrecht, J.; Golovkina, V.; Cerrina, F.; Kim, S.O.; Nealey, P. Sub-50 nm period patterns with EUV interference lithography. Microelectron. Eng. 2003, 67, 56–62. [Google Scholar] [CrossRef]
- Xue, G.; Lu, H.; Li, X.; Zhou, Q.; Wu, G.; Wang, X.; Zhai, Q.; Ni, K. Patterning nanoscale crossed grating with high uniformity by using two-axis Lloyd’s mirrors based interference lithography. Opt. Express 2020, 28, 2179–2191. [Google Scholar] [CrossRef]
- Chen, X.; Ren, Z.; Shimizu, Y.; Chen, Y.-L.; Gao, W. Optimal polarization modulation for orthogonal two-axis Lloyd’s mirror interference lithography. Opt. Express 2017, 25, 22237–22252. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Mano, K.; Zhang, K.; Matsukuma, H.; Gao, W. Accurate polarization control in nonorthogonal two-axis Lloyd’s mirror interferometer for fabrication of two-dimensional scale gratings. Opt. Eng. 2019, 58, 092611. [Google Scholar] [CrossRef]
- Shimizu, Y.; Mano, K.; Murakami, H.; Hirota, S.; Matsukuma, H.; Gao, W. Design optimization of a non-orthogonal two-axis Lloyd’s mirror interferometer for fabrication of large-area two-dimensional scale gratings. Precis. Eng. 2019, 60, 280–290. [Google Scholar] [CrossRef]
- Chen, X.; Shimizu, Y.; Chen, C.; Chen, Y.-L.; Gao, W. Generalized method for probing ideal initial polarization states in multibeam Lloyd’s mirror interference lithography of 2D scale gratings. J. Vac. Sci. Technol. B 2018, 36, 021601. [Google Scholar] [CrossRef]
- Hung, Y., Jr.; Chang, H.-J.; Chang, P.-C.; Lin, J.-J.; Kao, T.-C. Employing refractive beam shaping in a Lloyd’s interference lithography system for uniform periodic nanostructure formation. J. Vac. Sci. Technol. B 2017, 35, 030601. [Google Scholar] [CrossRef]
- Sokolova, E.; Kruizinga, B.; Valkenburg, T.V.; Schaarsberg, J.G. Recording of concave diffraction gratings in counterpropagating beams using meniscus blanks. J. Mod. Opt. 2002, 49, 1907–1917. [Google Scholar] [CrossRef]
- Sokolova, E. Simulation of mechanically ruled concave diffraction gratings by use of an original geometric theory. Appl. Opt. 2004, 43, 20–28. [Google Scholar] [CrossRef]
- Grabarnik, S.; Emadi, A.; Wu, H.; De Graaf, G.; Wolffenbuttel, R. Concave diffraction gratings fabricated with planar lithography. In Proceedings of the Micro-Optics 2008, Strasbourg, France, 7–9 April 2008; pp. 344–351. [Google Scholar]
- Xie, Y.; Lu, Z.; Li, F.; Zhao, J.; Weng, Z. Lithographic fabrication of large diffractive optical elements on a concave lens surface. Opt. Express 2002, 10, 1043–1047. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Li, L.; Zeng, L. A method to fabricate convex holographic gratings as master gratings for making flat-field concave gratings. In Proceedings of the Holography and Diffractive Optics III, Beijing, China, 12–15 November 2007; SPIE: Bellingham, WA, USA, 2008; pp. 218–226. [Google Scholar]
- Chen, Y.-P.; Lee, Y.-P.; Chang, J.-H.; Wang, L.A. Fabrication of concave gratings by curved surface UV-nanoimprint lithography. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2008, 26, 1690–1695. [Google Scholar] [CrossRef]
- Shi, Z.; He, J.-J.; He, S. Analysis and design of a concave diffraction grating with total-internal-reflection facets by a hybrid diffraction method. J. Opt. Soc. Am. A 2004, 21, 1198–1206. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Kalb, A.; Guardalben, M.; King, G.; Canning, D.; Kelly, J. Large-aperture grating tiling by interferometry for petawatt chirped-pulse-amplification systems. Opt. Express 2007, 15, 9562–9574. [Google Scholar] [CrossRef]
- Konkola, P.T.; Chen, C.G.; Heilmann, R.K.; Joo, C.; Montoya, J.C.; Chang, C.-H.; Schattenburg, M.L. Nanometer-level repeatable metrology using the Nanoruler. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2003, 21, 3097–3101. [Google Scholar] [CrossRef]
- Wang, R.; Han, J.; Xiao, D.; Ye, H.Q.; Tang, L.; Hao, J.; Zhai, Y.; Hao, Z.B. Accurate Adjustment Technology for Longitudinal Piston Error in Echelle Grating Tiling. Acta Opt. Sin. 2022, 42, 1812006. [Google Scholar] [CrossRef]
- Shi, L.; Zeng, L. Fabrication of optical mosaic gratings: A self-referencing alignment method. Opt. Express 2011, 19, 8985–8993. [Google Scholar] [CrossRef]
- Zhou, H.; Zeng, L. Method to fabricate orthogonal crossed gratings by an interference fringe based alignment technique. In Proceedings of the Optical Measurement Technology and Instrumentation, Taipei, Taiwan, 23–26 May 2016; pp. 960–967. [Google Scholar]
- Schattenburg, M.L.; Chen, C.G.; Heilmann, R.K.; Konkola, P.T.; Pati, G. Progress toward a general grating patterning technology using phase-locked scanning beams. In Proceedings of the Optical Spectroscopic Techniques, Remote Sensing, and Instrumentation for Atmospheric and Space Research IV, San Diego, CA, USA, 30 July–2 August 2001; SPIE: Bellingham, WA, USA, 2002; pp. 378–384. [Google Scholar]
- Song, Y.; Zhao, X.; Jiang, Y.; Bayanheshig; Qi, X. Interference Fringe Locking by Grating-Shifting Holographic Grating Exposure. Chin. J. Lasers 2017, 44, 0509001. [Google Scholar] [CrossRef]
- Gao, L.; Lin, H.; Zeng, L. A close-loop feedback system used for improving the stability of interference fringes. Opt. Optoelectron. Technol. 2004, 2, 23–25. [Google Scholar]
- Zhao, J.; Cheng, H.; Feng, Y.; Yan, S.; Cheng, W. Multi-wavelength confocal displacement sensing using a highly dispersive flat-field concave grating. Appl. Opt. 2024, 63, 1347–1354. [Google Scholar] [CrossRef]
- Chen, C.G.; Konkola, P.T.; Heilmann, R.K.; Pati, G.; Schattenburg, M.L. Image metrology and system controls for scanning beam interference lithography. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2001, 19, 2335–2341. [Google Scholar] [CrossRef]
- Heilmann, R.K.; Konkola, P.T.; Chen, C.G.; Pati, G.; Schattenburg, M.L. Digital heterodyne interference fringe control system. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2001, 19, 2342–2346. [Google Scholar] [CrossRef]
- Pati, G.; Heilmann, R.; Konkola, P.; Joo, C.; Chen, C.; Murphy, E.; Schattenburg, M. Generalized scanning beam interference lithography system for patterning gratings with variable period progressions. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2002, 20, 2617–2621. [Google Scholar] [CrossRef]
- Chen, C.G.; Heilmann, R.K.; Joo, C.; Konkola, P.T.; Pati, G.; Schattenburg, M.L. Beam alignment for scanning beam interference lithography. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2002, 20, 3071–3074. [Google Scholar] [CrossRef]
- Heilmann, R.K.; Chen, C.G.; Konkola, P.T.; Schattenburg, M.L. Dimensional metrology for nanometre-scale science and engineering: Towards sub-nanometre accurate encoders. Nanotechnology 2004, 15, S504. [Google Scholar] [CrossRef]
- Traut, S.; Herzig, H.P. Holographically recorded gratings on microlenses for a miniaturized spectrometer array. Opt. Eng. 2000, 39, 290–298. [Google Scholar] [CrossRef]
- Jitsuno, T.; Motokoshi, S.; Okamoto, T.; Mikami, T.; Smith, D.; Schattenburg, M.; Kitamura, H.; Matsuo, H.; Kawasaki, T.; Kondo, K. Development of 91 cm size gratings and mirrors for LEFX laser system. J. Phys. Conf. Ser. 2008, 112, 032002. [Google Scholar] [CrossRef]
- Shi, J.; Huang, Y.-S.; Peng, L.-N.; Ni, Z.-J.; Zhang, D.-W. Grating/microlens arrays fabricated by hot-melting, self-assembly and replication. Opt. Mater. 2020, 104, 109733. [Google Scholar] [CrossRef]
- Song, Y.; Bayanheshig; Qi, X.-d.; Zhang, N.; Tang, Y.-g. Design of frequency-shift interference fringe locking system in holographic grating exposure. Opt. Precis. Eng. 2014, 22, 318–324. [Google Scholar] [CrossRef]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng.-J. Am. Soc. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Fan, K.-C.; Lai, Z.-F.; Wu, P.; Chen, Y.-C.; Chen, Y.; Jäger, G. A displacement spindle in a micro/nano level. Meas. Sci. Technol. 2007, 18, 1710. [Google Scholar] [CrossRef]
- Zhao, X.; Bayanheshig; Li, W.; Yanxiu, J.; Song, Y.; Li, X.; Jiang, S.; Wu, N. Moiré alignment algorithm for an aberration-corrected holographic grating exposure system and error analysis. Appl. Opt. 2016, 55, 8683–8689. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Bayanheshig; Li, W.; Zhang, J. Merit function to design holographic gratings for moderate-resolution monochromators. Appl. Opt. 2011, 50, 6179–6183. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, W.; Bayanheshig; Li, X.; Jiang, S.; Song, Y.; Lv, Q. Two-color heterodyne laser interferometry for long-distance stage measurement with correction of uncertainties in measured optical distances. Sci. Rep. 2017, 7, 8173. [Google Scholar] [CrossRef]
- Perry, M.; Orr, P.; Niewczas, P.; Johnston, M. High-speed interferometric FBG interrogator with dynamic and absolute wavelength measurement capability. J. Light. Technol. 2013, 31, 2897–2903. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, X.; Zhang, Q. Phase subdivision of absolute coding grating and application in displacement measurement. Acta Opt. Sin 2011, 31, 0812005. [Google Scholar] [CrossRef]
- Ni, K.; Wang, H.; Li, X.; Wang, X.; Xiao, X.; Zhou, Q. Measurement uncertainty evaluation of the three degree of freedom surface encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IV, Beijing, China, 12–14 October 2016; pp. 187–192. [Google Scholar]
- Ren, W.; Cui, J.; Tan, J. A three-dimensional small angle measurement system based on autocollimation method. Rev. Sci. Instrum. 2022, 93, 055102. [Google Scholar] [CrossRef]
- Han, Y.; Ni, K.; Li, X.; Wu, G.; Yu, K.; Zhou, Q.; Wang, X. An FPGA Platform for Next-Generation Grating Encoders. Sensors 2020, 20, 2266. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Guan, J.; Wen, F.; Tan, J. High-resolution and wide range displacement measurement based on planar grating. Opt. Commun. 2017, 404, 132–138. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Lee, J.Y.; Wu, W.T.; Chen, J.C.; Deturche, R.; Lerondel, G. Quasi-common-optical-path heterodyne grating interferometer for displacement measurement. Meas. Sci. Technol. 2010, 21, 9. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Ni, K.; Zhou, Q.; Mao, X.; Zeng, L.; Wang, X.; Xiao, X. Two-probe optical encoder for absolute positioning of precision stages by using an improved scale grating. Opt. Express 2016, 24, 21378–21391. [Google Scholar] [CrossRef]
- Lee, C.B.; Kim, G.-H.; Lee, S.-K. Uncertainty investigation of grating interferometry in six degree-of-freedom motion error measurements. Int. J. Precis. Eng. Manuf. 2012, 13, 1509–1515. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.; Zhu, J.; Wang, S.; Wu, Y.; Li, X. Method and system for phase measurement of the heterodyne interference system. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; pp. 431–442. [Google Scholar]
- Harrison, G.R.; Archer, J.E. Interferometric calibration of precision screws and control of ruling engines. J. Opt. Soc. Am. 1951, 41, 495–503. [Google Scholar] [CrossRef]
- Cai, Y.; Lou, Z.; Ling, S.; Liao, B.-s.; Fan, K.-c. Development of a compact three-degree-of-freedom laser measurement system with self-wavelength correction for displacement feedback of a nanopositioning stage. Appl. Sci. 2018, 8, 2209. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, G.; Wang, S.; Li, X. A reflective-type heterodyne grating interferometer for three-degree-of-freedom subnanometer measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Cheng, F.; Fan, K.-C. Linear diffraction grating interferometer with high alignment tolerance and high accuracy. Appl. Opt. 2011, 50, 4550–4556. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhou, Q.; Li, X.; Ni, K.; Wang, X. Design and testing of a linear encoder capable of measuring absolute distance. Sens. Actuators A 2020, 308, 111935. [Google Scholar] [CrossRef]
- Incremental Grating Scale of Magnescale. Available online: https://www.magnescale.com/zh/company_design/ (accessed on 24 September 2024).
- Zhu, Y.; Wang, L.; Hu, J.; Li, X. Grating Interferometer with Redundant Design for Performing Wide-Range Displacement Measurements. Sensors 2022, 22, 3738. [Google Scholar] [CrossRef]
- Pan, S.-W.; Hsieh, H.-L.; Wang, W.-C. 6-DOF displacement and angle measurements using heterodyne laser encoder. In Proceedings of the Instrumentation, Metrology, and Standards for Nanomanufacturing, Optics, and Semiconductors VII, San Diego, CA, USA, 28 August 2013; pp. 38–45. [Google Scholar]
- Hu, P.C.; Chang, D.; Tan, J.B.; Yang, R.T.; Yang, H.X.; Fu, H.J. Displacement measuring grating interferometer: A review. Front. Inf. Technol. Electron. Eng. 2019, 20, 631–654. [Google Scholar] [CrossRef]
- Wang, S.T.; Luo, L.B.; Zhu, J.H.; Shi, N.N.; Li, X.H. An Ultra-Precision Absolute-Type Multi-Degree-of-Freedom Grating Encoder. Sensors 2022, 22, 9047. [Google Scholar] [CrossRef]
- Wang, S.; Ma, R.; Cao, F.; Luo, L.; Li, X. A Review: High-Precision Angle Measurement Technologies. Sensors 2024, 24, 1755. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.C.; Lü, H.; Zhao, S. Research on long-range grating interferometry with nanometer resolution. Meas. Sci. Technol. 2008, 19, 017001. [Google Scholar] [CrossRef]
- Xing, X.; Chang, D.; Hu, P.C.; Tan, J.B. Spatially separated heterodyne grating interferometer for eliminating periodic nonlinear errors. Opt. Express 2017, 25, 31384–31393. [Google Scholar] [CrossRef] [PubMed]
- Ye, G.Y.; Liu, H.Z.; Wang, Y.; Lei, B.A.; Shi, Y.S.; Yin, L.; Lu, B.H. Ratiometric-Linearization-Based High-Precision Electronic Interpolator for Sinusoidal Optical Encoders. IEEE Trans. Ind. Electron. 2018, 65, 8224–8231. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, J.; Hou, C.; Bai, J.; Yang, G. Optical accelerometer based on grating interferometer with phase modulation technique. Appl. Opt. 2012, 51, 7005–7010. [Google Scholar] [CrossRef]
- Shimizu, Y.; Chen, L.C.; Kim, D.W.; Chen, X.G.; Li, X.H.; Matsukuma, H. An insight into optical metrology in manufacturing. Meas. Sci. Technol. 2021, 32, 042003. [Google Scholar] [CrossRef]
- Wei, L.; Wang, H.; Zhao, Z.; Feng, X. Envelope-Modulated X-ray Grating Interferometry. AIP Adv. 2023, 14, 193701. [Google Scholar]
- Hsieh, H.L.; Chen, J.C.; Lerondel, G.; Lee, J.Y. Two-dimensional displacement measurement by quasi-common-optical-path heterodyne grating interferometer. Opt. Express 2011, 19, 9770–9782. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lu, M.P. Optical heterodyne grating shearing interferometry for long-range positioning applications. Opt. Commun. 2011, 284, 857–862. [Google Scholar] [CrossRef]
- Fan, K.C.; Liu, Y.S.; Chen, Y.J.; Cheng, F. A linear diffraction grating interferometer with high accuracy. In Proceedings of the 3rd International Symposium on Precision Mechanical Measurements, Ürümqi, China, 2–6 August 2006. [Google Scholar]
- Chen, Y.D.; Zhou, C.H.; Wang, Y.H.; Li, X.X.; Jia, W.; Wang, J. A new high-precision device for one-dimensional grating period measurement. In Proceedings of the Conference on Holography, Diffractive Optics, and Applications XII Part of SPIE/COS Photonics Asia Conference, Electr Network, Online, 5–11 December 2022. [Google Scholar]
- Ping, S.; Haojie, X.I.A.; Yetai, F.E.I. Research status and developing trends of diffraction grating interferometer measurement system. Opt. Technol. 2011, 37, 313–316. [Google Scholar]
- Chang, L.W.; Lee, C.T.; Chien, P.Y. Displacement measurement by synthesized light source based on fiber Bragg gratings. Opt. Commun. 1998, 154, 261–267. [Google Scholar] [CrossRef]
- Wang, G.-c.; Yan, S.-h.; Gao, L.; Xie, X.-d.; Tian, Z. Development of displacement measurement technologies based on grating interferometry. Laser Technol. 2010, 34, 661–664. [Google Scholar] [CrossRef]
- Lin, Y.; Ji, C.; Zhang, H.; Yang, J. Design of grating encoder displacement measurement system. J. Phys. Conf. Ser. 2024, 2825, 012011. [Google Scholar]
- Guo, D.; Shi, L.; Yu, Y.; Xia, W.; Wang, M. Micro-displacement reconstruction using a laser self-mixing grating interferometer with multiple-diffraction. Opt. Express 2017, 25, 31394–31406. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Yan, X.; Wei, C.; Liu, S.; Yang, W. Eightfold Optical Encoder with High-Density Grating. Appl. Opt. 2018, 57, 2366–2375. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Niu, D.; Zhao, G.; Ban, Y.; Wang, X.; Wei, P.; Jiang, W.; Chen, J.; Liu, H. Improving the optical subdivision ability of a grating interferometer via double-row reverse blazed gratings. Opt. Lasers Eng. 2023, 168, 107676. [Google Scholar] [CrossRef]
- Hu, H.; Qiu, X.; Wang, J.; Ju, A.; Zhang, Y. Subdivision and direction recognition of λ/16 of orthogonal fringes for nanometric measurement. Appl. Opt. 2009, 48, 6479–6484. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.K.; Tang, K.-Z. Adaptive online correction and interpolation of quadrature encoder signals using radial basis functions. IEEE Trans. Control. Syst. Technol. 2005, 13, 370–377. [Google Scholar]
- Van Hoang, H.; Jeon, J.W. An efficient approach to correct the signals and generate high-resolution quadrature pulses for magnetic encoders. IEEE Trans. Ind. Electron. 2010, 58, 3634–3646. [Google Scholar] [CrossRef]
- Benammar, M.; Ben-Brahim, L.; Alhamadi, M.A. A high precision resolver-to-DC converter. IEEE Trans. Instrum. Meas. 2005, 54, 2289–2296. [Google Scholar] [CrossRef]
- Ye, G.; Fan, S.; Liu, H.; Li, X.; Yu, H.; Shi, Y.; Yin, L.; Lu, B. Design of a precise and robust linearized converter for optical encoders using a ratiometric technique. Meas. Sci. Technol. 2014, 25, 125003. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Z.; Zuo, Z. A novel design method for resolver-to-digital conversion. IEEE Trans. Ind. Electron. 2014, 62, 3724–3731. [Google Scholar] [CrossRef]
- Peng, K.; Liu, X.; Chen, Z.; Yu, Z.; Pu, H. Sensing mechanism and error analysis of a capacitive long-range displacement nanometer sensor based on time grating. IEEE Sens. J. 2017, 17, 1596–1607. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, G.; Liu, H.; Lei, B.; Li, X.; Han, W.; Liu, H. Electronic interpolation interface based on linear subdivision method for sinusoidal optical encoders. IEEE Sens. J. 2019, 20, 3646–3654. [Google Scholar] [CrossRef]
- Li, X.; Yuan, W.; Ni, K.; Zhou, Q.; Wang, X. A two-probe linear encoder by using an arrayed scale grating stitched by multiple separate short gratings. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Bellingham, WA, USA, 2019; pp. 207–212. [Google Scholar]
- Hsu, C.-C.; Wu, C.-C.; Lee, J.-Y.; Chen, H.-Y.; Weng, H.-F. Reflection type heterodyne grating interferometry for in-plane displacement measurement. Opt. Commun. 2008, 281, 2582–2589. [Google Scholar] [CrossRef]
- Wang, G.; Gao, L.; Huang, G.; Lei, X.; Cui, C.; Wang, S.; Yang, M.; Zhu, J.; Yan, S.; Li, X. A wavelength-stabilized and quasi-common-path heterodyne grating interferometer with sub-nanometer precision. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Shimizu, Y.; Matsukuma, H.; Gao, W. Optical sensors for multi-axis angle and displacement measurement using grating reflectors. Sensors 2019, 19, 5289. [Google Scholar] [CrossRef]
- Zhu, C.; Zhuang, Y.; Liu, B.; Huang, J. Review of fiber optic displacement sensors. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Lou, J.; Wang, Y.; Tong, L. Microfiber optical sensors: A review. Sensors 2014, 14, 5823–5844. [Google Scholar] [CrossRef]
- Yacoot, A.; Cross, N. Measurement of picometre non-linearity in an optical grating encoder using X-ray interferometry. Meas. Sci. Technol. 2002, 14, 148. [Google Scholar] [CrossRef]
- Zhai, Q.; Xue, G.; Lin, L.; Zhou, Q.; Ni, K.; Wang, X.; Li, X. A mechanical mosaic method for reflective grating based on diffracted beams orientation. In Proceedings of the Holography, Diffractive Optics, and Applications XI, Nantong, China, 10–19 October 2021; pp. 125–131. [Google Scholar]
- Lu, Y.; Wei, C.; Jia, W.; Li, S.; Yu, J.; Li, M.; Xiang, C.; Xiang, X.; Wang, J.; Ma, J. Two-degree-freedom displacement measurement based on a short period grating in symmetric Littrow configuration. Opt. Commun. 2016, 380, 382–386. [Google Scholar] [CrossRef]
- Li, X.H.; Shimizu, Y.; Muto, H.; Ito, S.; Gao, W. Design of a three-axis surface encoder with a blue-ray laser diode. Key Eng. Mater. 2012, 523, 913–918. [Google Scholar] [CrossRef]
- Apostol, D.; Udrea, C.; Garoi, F.; Vasile, T.; Logofătu, P.C. High diffraction order grating interferometer for pitch measurement. Opt. Eng. 2011, 50, 105601–105604. [Google Scholar] [CrossRef]
- Wu, C.-C.; Cheng, C.-Y.; Yang, Z.-Y. Optical homodyne common-path grating interferometer with sub-nanometer displacement resolution. In Proceedings of the Interferometry XV: Applications, San Diego, CA, USA, 2–5 August 2010; pp. 48–55. [Google Scholar]
- Xia, H.; Fei, Y. Precise stage design with planar diffraction grating interferometer. In Proceedings of the Sixth International Symposium on Precision Engineering Measurements and Instrumentation, Hangzhou, China, 8–10 August 2010; pp. 258–262. [Google Scholar]
- Xu, Y.; Sasaki, O.; Suzuki, T. Double-grating interferometer for measurement of cylinder diameters. Appl. Opt. 2004, 43, 537–541. [Google Scholar] [CrossRef]
- Jie, W.; Guangyao, H.; Guochao, W.; Yaning, W.; Mei, H.; Qixue, L.; Lingxiao, Z.; Xinghui, L.; Shuhua, Y.; Jun, Y. One-thousandth-level laser power stabilization based on optical feedback from a well-designed high-split-ratio and nonpolarized beam splitter. Appl. Opt. 2021, 60, 7798–7803. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zhu, J.; Huang, G.; Wang, G.; Wang, S.; Ni, K.; Wang, X.; Li, X. A polarization adjustment module for frequency aliasing of heterodyne grating interferometer. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–11 December 2022; pp. 362–369. [Google Scholar]
- Yu, H.; Liu, H.; Li, X.; Ye, G.; Shi, Y.; Yin, L.; Jiang, W.; Chen, B.; Liu, X. Calibration of non-contact incremental linear encoders using a macro–micro dual-drive high-precision comparator. Meas. Sci. Technol. 2015, 26, 095103. [Google Scholar] [CrossRef]
- Ma, S.; Xie, F.; Li, Z. Research on a multiplexed interferometry technique for absolute displacement measurement. In Proceedings of the 2011 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Beijing, China, 6–9 November 2011; pp. 160–166. [Google Scholar]
- Chen, M.; Xie, S.; Zhou, G.; Wei, D.; Wu, H.; Takahashi, S.; Matsumoto, H.; Takamasu, K. Absolute distance measurement based on spectral interferometer using the effect of the FSR of a Fabry–Perot etalon. Opt. Lasers Eng. 2019, 123, 20–27. [Google Scholar] [CrossRef]
- Tao, Z.; Cui, J.; Tan, J. Simultaneous multi-channel absolute position alignment by multi-order grating interferometry. Opt. Express 2016, 24, 802–816. [Google Scholar] [CrossRef]
- Matsuzoe, Y.; Tsuji, N.; Nakayama, T.; Fujita, K.; Yoshizawa, T. High-performance absolute rotary encoder using multitrack and M-code. Opt. Eng. 2003, 42, 124–131. [Google Scholar] [CrossRef]
- Wang, H.; Shi, Y.; Li, X.; Ni, K.; Zhou, Q.; Wang, X. Improvement of absolute positioning of precision stage based on cooperation the zero position pulse signal and incremental displacement signal. J. Phys. Conf. Ser. 2018, 986, 012002. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, K.; Li, X.; Zhou, Q.; Wang, X. Highly accurate, absolute optical encoder using a hybrid-positioning method. Opt. Lett. 2019, 44, 5258–5261. [Google Scholar] [CrossRef]
- Absolute Linear Encoders of Heidenhain. Available online: https://www.heidenhain.com/products/linear-encoders/exposed/ (accessed on 5 September 2024).
- Wang, S.; Luo, L.; Gao, L.; Ma, R.; Wang, X.; Li, X. Long binary coding design for absolute positioning using genetic algorithm. In Proceedings of the Optical Metrology and Inspection for Industrial Applications X, Beijing, China, 15–16 October 2023; pp. 8–15. [Google Scholar]
- Wang, S.; Luo, L.; Li, X. Design and Parameter Optimization of Zero Position Code Considering Diffraction Based on Deep Learning Generative Adversarial Networks. Nanomanufacturing Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Cao, F.; Li, X. Nanoscale Absolute Grating Encoder with Wide Range Directional Discrimination Based on Asymmetric Code and Hybrid Positioning. In Proceedings of the CLEO: Fundamental Science, Charlotte, NC, USA, 5–10 May 2024; p. JTh2A. 159. [Google Scholar]
- Wang, S.; Gao, L.; Luo, L.; Deng, F.; Wang, X.; Li, X.; Ma, R. Codes coupling optimization for absolute measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications X, Beijing, China, 15–16 October 2023; pp. 178–185. [Google Scholar]
- Liu, L.; Lou, Z.-F.; Huang, Y.-B.; Fan, K.-C.; Zhang, J.-Y. A five degrees-of-freedom errors measurement system for rotary axis with reference laser for reference axis alignment. Rev. Sci. Instrum. 2020, 91, 075101. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.-C.; Wang, H.-Y.; Yang, H.-W.; Chen, L.-M. Techniques of multi-degree-of-freedom measurement on the linear motion errors of precision machines. Adv. Opt. Technol. 2014, 3, 375–386. [Google Scholar] [CrossRef]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A three-axis autocollimator for detection of angular error motions of a precision stage. CIRP Ann. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Arai, Y.; Zeng, L. Design and construction of a two-degree-of-freedom linear encoder for nanometric measurement of stage position and straightness. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2010, 34, 145–155. [Google Scholar] [CrossRef]
- Kimura, A.; Hosono, K.; Kim, W.; Shimizu, Y.; Gao, W.; Zeng, L. A two-degree-of-freedom linear encoder with a mosaic scale grating. Int. J. Nanomanuf. 2011, 7, 73–91. [Google Scholar] [CrossRef]
- Hsieh, H.-L.; Pan, S.-W. Three-degree-of-freedom displacement measurement using grating-based heterodyne interferometry. Appl. Opt. 2013, 52, 6840–6848. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, K.; Xue, G.; Shi, N.; Zhou, Q.; Wang, X.; Li, X. A simplified two-phase differential decoding algorithm for high precision grating encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications VIII, Nantong, China, 10–19 October 2021; pp. 49–58. [Google Scholar]
- Hsieh, H.-L.; Pan, S.-W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef]
- Lee, C.; Kim, G.H.; Lee, S.-K. Design and construction of a single unit multi-function optical encoder for a six-degree-of-freedom motion error measurement in an ultraprecision linear stage. Meas. Sci. Technol. 2011, 22, 105901. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Muto, H.; Shimizu, Y.; Ito, S.; Dian, S. A six-degree-of-freedom surface encoder for precision positioning of a planar motion stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Yu, K.; Zhu, J.; Yuan, W.; Zhou, Q.; Xue, G.; Wu, G.; Wang, X.; Li, X. Two-channel six degrees of freedom grating-encoder for precision-positioning of sub-components in synthetic-aperture optics. Opt. Express 2021, 29, 21113–21128. [Google Scholar] [CrossRef]
- Fan, K.-C.; Chen, M.-J. A 6-degree-of-freedom measurement system for the accuracy of XY stages. Precis. Eng. 2000, 24, 15–23. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in cross-talk errors in a six-degree-of-freedom surface encoder. Nanomanufacturing Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Chang, D.; Hu, P.; Tan, J. Fused-like angles: Replacement for roll-pitch-yaw angles for a six-degree-of-freedom grating interferometer. Front. Inf. Technol. Electron. Eng. 2021, 22, 1677–1684. [Google Scholar] [CrossRef]
- Zhu, J.H.; Wang, S.T.; Li, X.H. Ultraprecision Grating Positioning Technology for Wafer Stage of Lithography Machine. Laser Optoelectron. Prog. 2022, 59, 0922019. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Li, W. Grating-based 2D displacement measurement with quadruple optical subdivision of a single incident beam. Opt. Express 2021, 29, 24169–24181. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Jiri, G.; Hao, Q.; Li, W. High-precision 2D grating displacement measurement system based on double-spatial heterodyne optical path interleaving. Opt. Lasers Eng. 2022, 158, 107167. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, N.; Li, L.; Ni, K.; Li, X. Instantaneous grating signal subdivision system with non-linear Kalman filters. In Proceedings of the Optical Design and Testing XII, Online, 5–11 December 2022; pp. 90–96. [Google Scholar]
- Heidenhain. Available online: https://www.heidenhain.com/ (accessed on 5 September 2024).
- LF 185 Incremental Sealed Linear Encoder with Large Cross Section for Highest Repeatability. Available online: https://www.heidenhain.com/products/linear-encoders/sealed/lf-185 (accessed on 5 September 2024).
- LIP382 Incremental Exposed Encoder for High Accuracy. Available online: https://www.heidenhain.com/service-support/infobase/349981-01 (accessed on 5 September 2024).
- Incremental Exposed Two-Coordinate Encoder. Available online: https://www.heidenhain.com/products/linear-encoders/exposed/pp-281 (accessed on 5 September 2024).
- TTR ECA 4402 Scaledrum for Absolute Angle Encoder without Integral Bearing. Available online: https://www.heidenhain.com/service-support/infobase/1042970-10 (accessed on 5 September 2024).
- BS78 Grating Scale with the High-Resolution. Available online: https://www.magnescale.com/zh/products/bs78/ (accessed on 5 September 2024).
- Gao, W.; Kimura, A. A three-axis displacement sensor with nanometric resolution. CIRP Ann. 2007, 56, 529–532. [Google Scholar] [CrossRef]
- Wang, S.; Liao, B.; Shi, N.; Li, X. A compact and high-precision three-degree-of-freedom grating encoder based on a quadrangular frustum pyramid prism. Sensors 2023, 23, 4022. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Ultraprecision real-time displacements calculation algorithm for the grating interferometer system. Sensors 2019, 19, 2409. [Google Scholar] [CrossRef] [PubMed]
- Köchert, P.; Flügge, J.; Weichert, C.; Köning, R.; Manske, E. Phase measurement of various commercial heterodyne He–Ne-laser interferometers with stability in the picometer regime. Meas. Sci. Technol. 2012, 23, 074005. [Google Scholar] [CrossRef]
- Magnescale. Available online: https://www.magnescale.com/ (accessed on 5 September 2024).
- Kimura, A.; Gao, W.; Lijiang, Z. Position and out-of-straightness measurement of a precision linear air-bearing stage by using a two-degree-of-freedom linear encoder. Meas. Sci. Technol. 2010, 21, 054005. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhang, M.; Zhu, Y.; Wu, Y.F.; Hu, C.X.; Liu, Z. A novel heterodyne grating interferometer system for in-plane and out-of-plane displacement measurement with nanometer resolution. In Proceedings of the 29th Annual Meeting of the American Society for Precision Engineering, Boston, MA, USA, 9–15 November 2014; pp. 173–177. [Google Scholar]
- Yin, Y.; Liu, L.; Bai, Y.; Jirigalantu; Yu, H.; Bayanheshig; Liu, Z.; Li, W. Littrow 3D measurement based on 2D grating dual-channel equal-optical path interference. Opt. Express 2022, 30, 41671–41684. [Google Scholar] [CrossRef] [PubMed]
- Liao, B.; Wang, S.; Lin, J.; Dou, Y.; Wang, X.; Li, X. A research on compact short-distance grating interferometer based on ridge prism. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; pp. 411–418. [Google Scholar]
- Masui, S.; Goda, S.; Kadoya, S.; Michihata, M.; Takahashi, S. Grating periods measurement of multi-pitched grating using Littrow configuration external cavity diode laser. Appl. Phys Express 2021, 14, 076501. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, Z.; Wang, W.; Jiang, S.; Bayanheshig; Li, W. Fast method to detect and calculate displacement errors in a Littrow grating-based interferometer. Appl. Opt. 2019, 58, 3193–3199. [Google Scholar] [CrossRef]
- Guo, C.; Zeng, L. Measurement of period difference in grating pair based on analysis of far-field intensity patterns. Opt. Commun. 2008, 281, 3611–3616. [Google Scholar] [CrossRef]
- Chang, D.; Yin, Z.; Sun, Y.; Hu, P.; Tan, J.; Fan, Z. Spatially separated heterodyne grating interferometer for in-plane and out-of-plane displacement measurements. Photonics 2022, 9, 830. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.; Gao, W. Design and testing of a four-probe optical sensor head for three-axis surface encoder with a mosaic scale grating. Meas. Sci. Technol. 2014, 25, 094002. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and Testing of a Compact Optical Prism Module for Multi-Degree-of-Freedom Grating Interferometry Application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Wang, G.-C.; Li, X.-H.; Yan, S.-H.; Tan, L.-L.; Guan, W.-L. Real-time absolute distance measurement by multi-wavelength interferometry synchronously multi-channel phase-locked to frequency comb and analysis for the potential non-ambiguity range. Acta Phys. Sin. 2021, 70, 040601. [Google Scholar]
- Cheng, F.; Fei, Y.-T.; Fan, K.-C. New method on real-time signal correction and subdivision for grating-based nanometrology. In Proceedings of the 4th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Design, Manufacturing, and Testing of Micro-and Nano-Optical Devices and Systems, Chengdu, China, 19–21 November 2008; SPIE: Bellingham, WA, USA, 2009; pp. 17–22. [Google Scholar]
- Hu, W.; Zhang, Y.; Fu, J. An introduction to CPU and DSP design in China. Sci. China. Inf. Sci. 2016, 59, 1–8. [Google Scholar] [CrossRef]
- Wirtz, S.F.; Cunha, A.P.; Labusch, M.; Marzun, G.; Barcikowski, S.; Söffker, D. Development of a low-cost FPGA-based measurement system for real-time processing of acoustic emission data: Proof of concept using control of pulsed laser ablation in liquids. Sensors 2018, 18, 1775. [Google Scholar] [CrossRef]
- Vera-Salas, L.A.; Moreno-Tapia, S.V.; Garcia-Perez, A.; de Jesus Romero-Troncoso, R.; Osornio-Rios, R.A.; Serroukh, I.; Cabal-Yepez, E. FPGA-based smart sensor for online displacement measurements using a heterodyne interferometer. Sensors 2011, 11, 7710–7723. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, P.; Anstotz, F.; Johnson, G.; Kiefer, R. Real time surface morphology analysis of semiconductor materials and devices using 4D interference microscopy. J. Mater. Sci. Mater. Electron. 2008, 19, 194–198. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Liu, C.; Cai, G.; Wang, W. A survey on the grating based optical position encoder. Opt. Laser Technol. 2021, 143, 107352. [Google Scholar] [CrossRef]
- Spence, T.; Calzada, M.; Gardner, H.; Leefe, E.; Fontenot, H.; Gilevicius, L.; Hartsock, R.; Boyson, T.; Harb, C. Real-time FPGA data collection of pulsed-laser cavity ringdown signals. Opt. Express 2012, 20, 8804–8814. [Google Scholar] [CrossRef]
- Jamro, E.; Wielgosz, M.; Bieniasz, S.; Cioch, W. FPGA–ARM heterogeneous system for high speed signal analysis. Solid State Phenom. 2012, 180, 207–213. [Google Scholar] [CrossRef]
- Li, X.; Xiao, S.; Zhou, Q.; Ni, K.; Wang, X. A real-time distance measurement data processing platform for multi-axis grating interferometry type optical encoders. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Bellingham, WA, USA, 2019; pp. 1028–1035. [Google Scholar]
- Shi, N.; Wang, S.; Xue, G.; Liu, M.; Han, Y.; Zhu, J.; Ni, K.; Wang, X.; Li, X. A real-time processing system for dual-channel six-degree-of-freedom grating ruler based on FPGA. In Proceedings of the Optical Design and Testing XI, Nantong, China, 10–19 October 2021; pp. 250–260. [Google Scholar]
- Shi, N.; Zhu, J.; Wang, S.; Han, Y.; Yu, K.; Li, X.; Wang, X. FPGA displacement calculation platform and test of two-phase grating interference encoder. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; pp. 372–383. [Google Scholar]
- Liu, Q.; Ohba, R. A simple real-time method for checking parallelism between the two gratings in Talbot interferometry. Opt. Commun. 2000, 175, 19–26. [Google Scholar] [CrossRef]
- Shan, X.; Kuo, S.-K.; Zhang, J.; Menq, C.-H. Ultra precision motion control of a multiple degrees of freedom magnetic suspension stage. IEEE/ASME Trans. Mechatron. 2002, 7, 67–78. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Translational displacement computational algorithm of the grating interferometer without geometric error for the wafer stage in a photolithography scanner. Opt. Express 2018, 26, 34734–34752. [Google Scholar] [CrossRef] [PubMed]
- Rank, E.A.; Sentosa, R.; Harper, D.J.; Salas, M.; Gaugutz, A.; Seyringer, D.; Nevlacsil, S.; Maese-Novo, A.; Eggeling, M.; Muellner, P. Toward optical coherence tomography on a chip: In vivo three-dimensional human retinal imaging using photonic integrated circuit-based arrayed waveguide gratings. Light Sci. Appl. 2021, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Li, X.; Wang, X.; Zhou, Q.; Ni, K. Chromatic confocal displacement sensor with optimized dispersion probe and modified centroid peak extraction algorithm. Sensors 2019, 19, 3592. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Li, Z.; Deen, M.J.; Fang, Q.; Selvaganapathy, P. Design of a flat field concave-grating-based micro-Raman spectrometer for environmental applications. Appl. Opt. 2012, 51, 6855–6863. [Google Scholar] [CrossRef]
- Lu, H.; Cui, S.; Ke, C.; Liu, D. Automatic reference optical spectrum retrieval method for ultra-high resolution optical spectrum distortion analysis utilizing integrated machine learning techniques. Opt. Express 2017, 25, 32491–32503. [Google Scholar] [CrossRef]
- Cheng, R.; Zou, C.-L.; Guo, X.; Wang, S.; Han, X.; Tang, H.X. Broadband on-chip single-photon spectrometer. Nat. Commun. 2019, 10, 4104. [Google Scholar] [CrossRef]
- Jiang, A.-Q.; Zang, K.-Y.; Tu, H.-T.; Chen, J.-K.; Lu, W.-J.; Yoshie, O.; Wang, X.-P.; Xiang, X.-D.; Lee, Y.-P.; Chen, B. Ultrahigh-resolution spectrometer based on 19 integrated gratings. Sci. Rep. 2019, 9, 10211. [Google Scholar] [CrossRef]
- Xu, B.; Jia, Z.; Li, X.; Chen, Y.-L.; Shimizu, Y.; Ito, S.; Gao, W. Surface form metrology of micro-optics. In Proceedings of the International Conference on Optics in Precision Engineering and Nanotechnology (icOPEN2013), Singapore, 9–11 April 2013; p. 876902. [Google Scholar]
- Bai, J.; Wang, Y.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. Three-probe error separation with chromatic confocal sensors for roundness measurement. Nanomanufacturing Metrol. 2021, 4, 247–255. [Google Scholar] [CrossRef]
- Bonod, N.; Neauport, J. Diffraction gratings: From principles to applications in high-intensity lasers. Adv. Opt. Photonics 2016, 8, 156–199. [Google Scholar] [CrossRef]
- Burkhardt, M.; Rathje, T.; Lehr, D.; Erdmann, L.; Helgert, M.; Triebel, P.; Diehl, T.; Gatto, A.; vd Valk, N.; Vink, R. Manufacturing method for monolithic freeform Offner-gratings for hyper-spectral imaging. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Strasbourg, France, 9–12 September 2019; pp. 146–157. [Google Scholar]
- Li, A.; Yao, C.; Xia, J.; Wang, H.; Cheng, Q.; Penty, R.; Fainman, Y.; Pan, S. Advances in cost-effective integrated spectrometers. Light Sci. Appl. 2022, 11, 174. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Wen, Z.-Y.; Liang, Y.-Q.; Du, X.-Q.; Zhang, B. Microbiochemical analyzer based on continuous spectrum and its test for clinic use. Guang Pu Xue Yu Guang Pu Fen Xi = Guang Pu 2006, 26, 1769–1773. [Google Scholar] [PubMed]
- Zhou, Q.; Pang, J.; Li, X.; Ni, K.; Tian, R. Concave grating miniature spectrometer with an expanded spectral band by using two entrance slits. Chin. Opt. Lett. 2015, 13, 110501. [Google Scholar] [CrossRef]
- Ren, T.; Qiu, K.; Li, A.; Huan, S.; Lou, Z.; Ji, L.; Li, S.; Hong, Y. High diffraction efficiency varied-line-space concave gratings for the Lyman ultraviolet explorer. Appl. Opt. 2023, 62, 9414–9421. [Google Scholar] [CrossRef]
- Geng, M.; Zhou, Q.; Li, X.; Lu, H.; Wang, W.; Liu, Y.; Ni, K.; Hui, L. Design and fabrication of a variable-line-space grating surface for a Fresnel-grating lens based miniature spectrometer. In Proceedings of the Holography, Diffractive Optics, and Applications VIII, Beijing, China, 11–13 October 2018; pp. 367–373. [Google Scholar]
- Zhou, Q.; Li, X.; Geng, M.; Hu, H.; Ni, K.; Zhong, L.; Yan, P.; Wang, X. Economic fabrication of a novel hybrid planar Grating/Fresnel lens for miniature spectrometers. Opt. Express 2018, 26, 6079–6089. [Google Scholar] [CrossRef]
- Shan, S.; Li, J.; Liu, P.; Li, Q.; Wang, X.; Li, X. A Microlens Array Grating for Miniature Multi-Channel Spectrometers. Sensors 2023, 23, 8381. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Edwards, P.; Shi, K.; Liu, Z. Proposal and demonstration of a spectrometer using a diffractive optical element with dual dispersion and focusing functionality. Opt. Lett. 2011, 36, 2023–2025. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, G.; Edwards, P.; Zhou, M.-D.; Zheng, S.; Liu, Z. G-Fresnel smartphone spectrometer. Lab Chip 2016, 16, 246–250. [Google Scholar] [CrossRef]



| Grating Fabrication Tech | Advantages | Disadvantages |
|---|---|---|
| Mechanical Ruling | With the development of Fast Tool Servo (FTS) technology, complex pattern structures can be machined. | Tool wear and high running accuracy, minimum encoder pitch is limited by the tool (typically up to a few micrometers). |
| Nanoimprint Lithography | High resolution for small cycle grating fabrication; high productivity. | The cost of the equipment is high, and the precision of the mask is required. |
| Projection Exposure | Higher productivity and resolution. | High equipment and mask cost. |
| Electron Beam Lithography (EBL) | High resolution for grating fabrication of small apertures (less than 100 nm). | High costs, only small areas can be processed (no more than 100 × 100 µm2). |
| Laser Interference Lithography (LIL) | Sub-micron periodic grating fabrication at high efficiency and low cost. | Has difficulty processing complex structural patterns. |
| Main Development Directions for Advanced Grating Interferometry Technology | Development Status | Developmental Limitations |
|---|---|---|
| Ultra-high-precision measurement | Sub-nanometer-level resolution Sub-nanometer-level accuracy | Complex structure Lack of stability |
| Absolute measurement | Nanometer-level resolution Nanometer-level accuracy | Absolute encoding design Lack of ultra-high accuracy |
| Multi-DOF measurement | Expandable to 6-DOF measurement | Complex structure |
| Industrialization development | Partially industrializable modules | Lack of mature modules |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Shan, S.; Li, X. A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers. Sensors 2024, 24, 6617. https://doi.org/10.3390/s24206617
Luo L, Shan S, Li X. A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers. Sensors. 2024; 24(20):6617. https://doi.org/10.3390/s24206617
Chicago/Turabian StyleLuo, Linbin, Shuonan Shan, and Xinghui Li. 2024. "A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers" Sensors 24, no. 20: 6617. https://doi.org/10.3390/s24206617
APA StyleLuo, L., Shan, S., & Li, X. (2024). A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers. Sensors, 24(20), 6617. https://doi.org/10.3390/s24206617