Performance of a Radio-Frequency Two-Photon Atomic Magnetometer in Different Magnetic Induction Measurement Geometries
Abstract
:1. Introduction
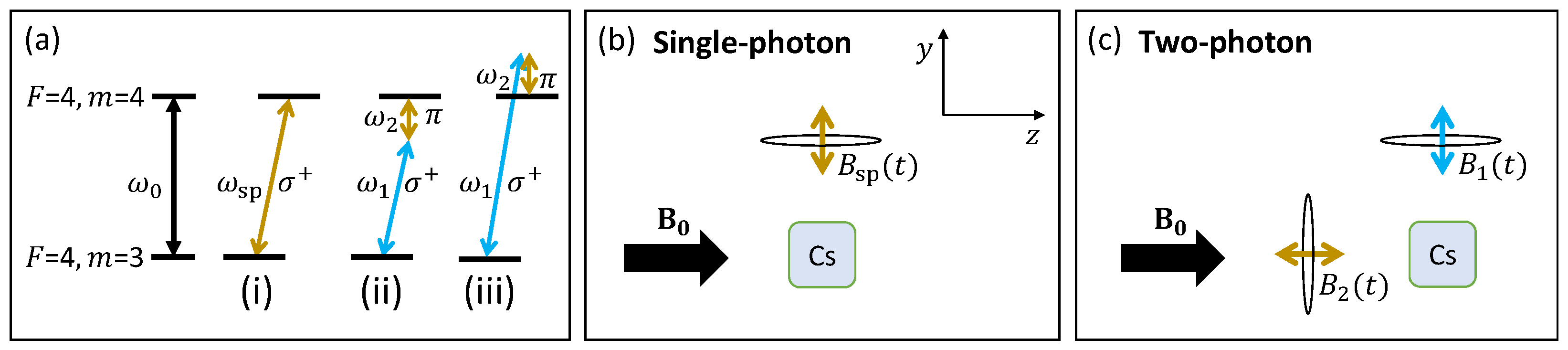
2. Experimental Setup
3. Results
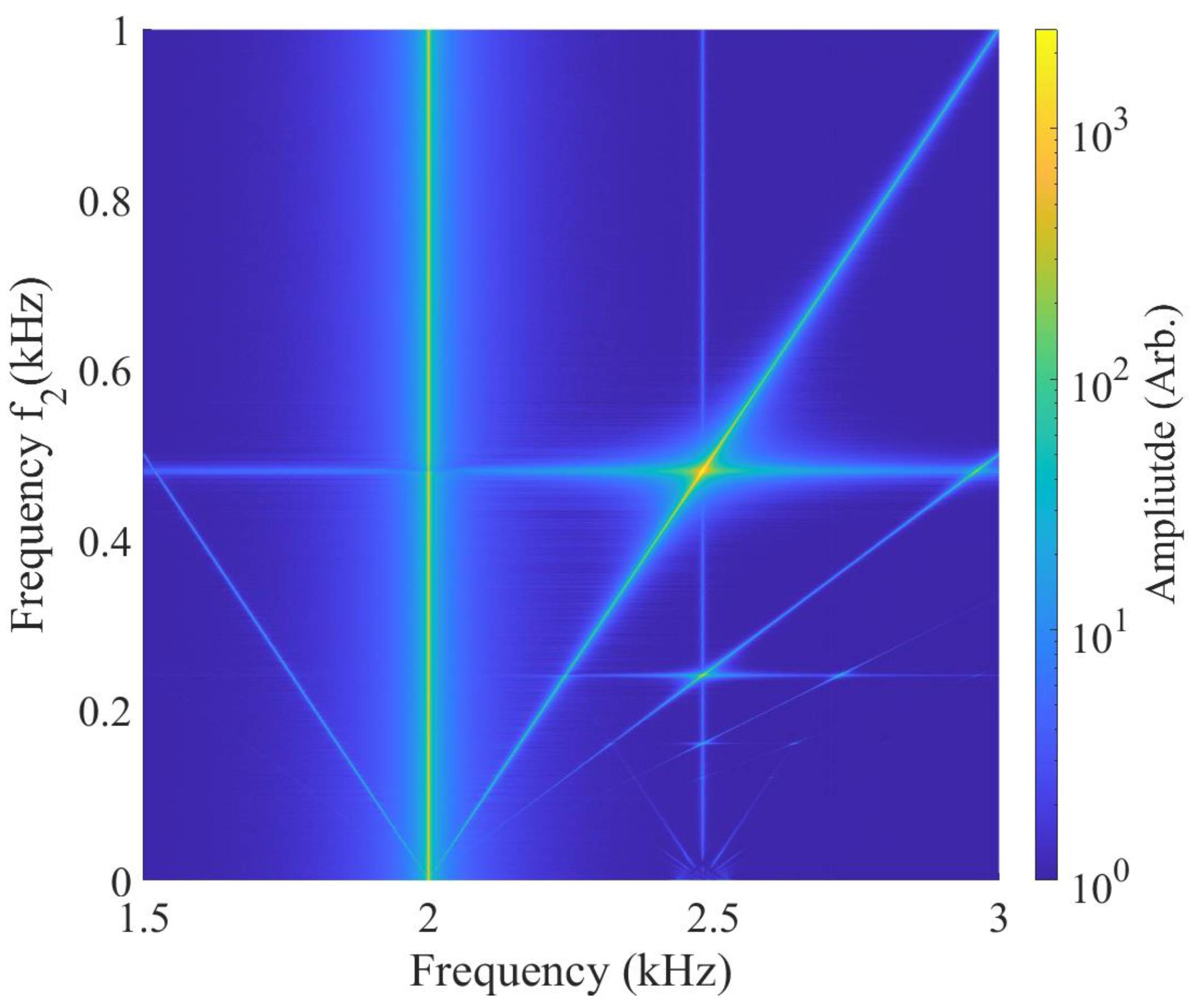
3.1. Spectral Components by Non-Linear Interactions
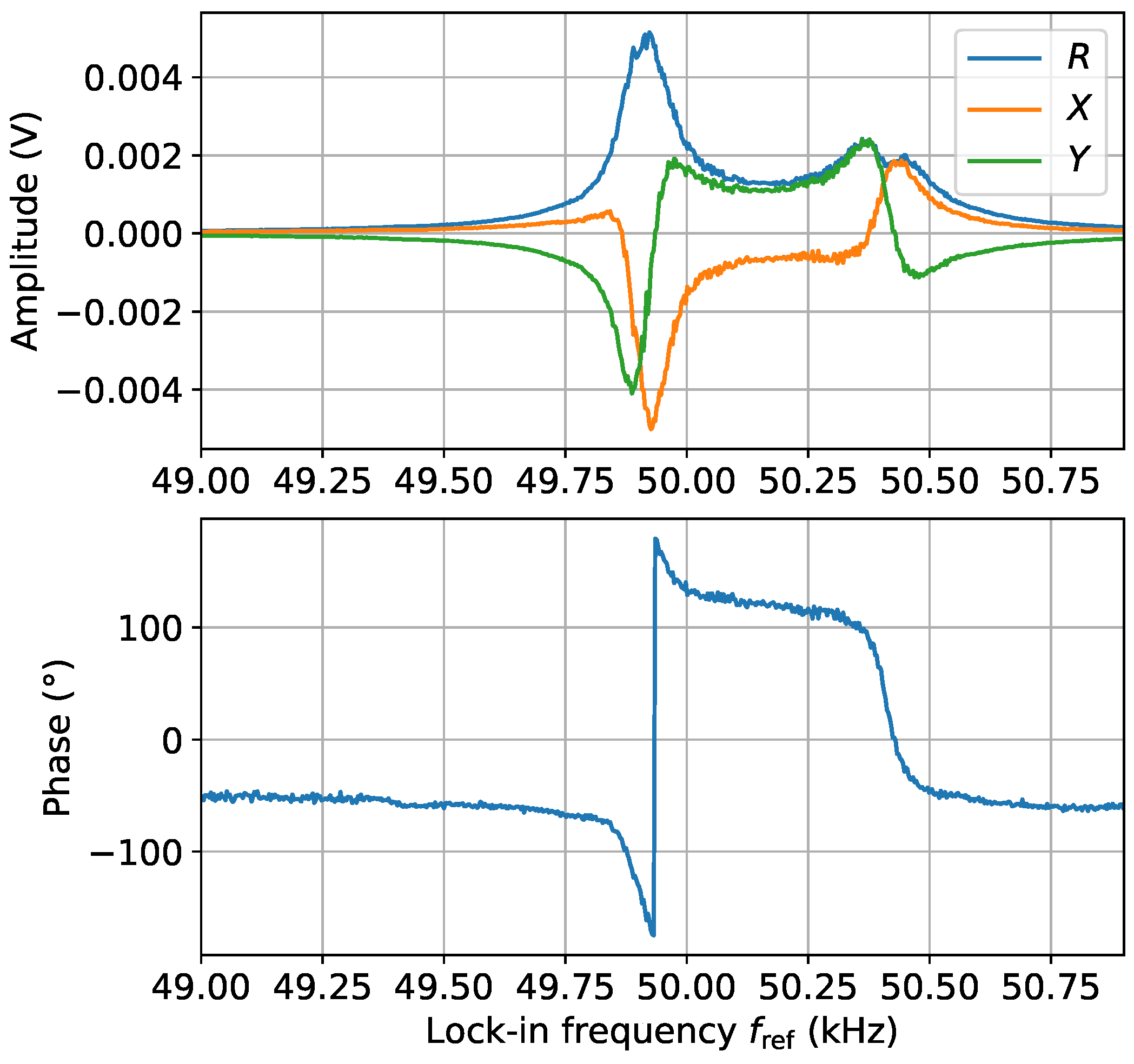
3.2. Phase Information
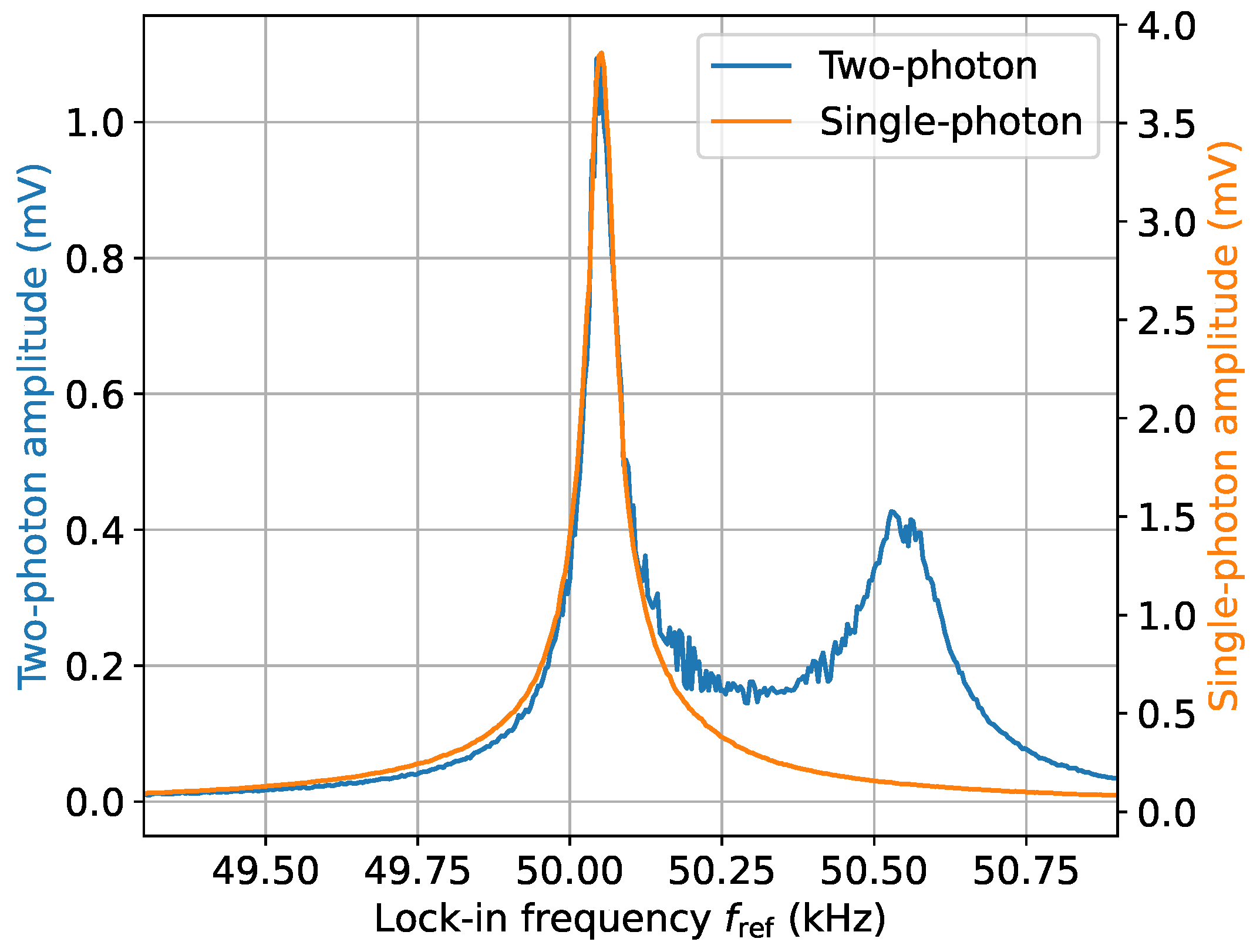
3.3. Comparison of Single- and Two-Photon Process Efficiencies
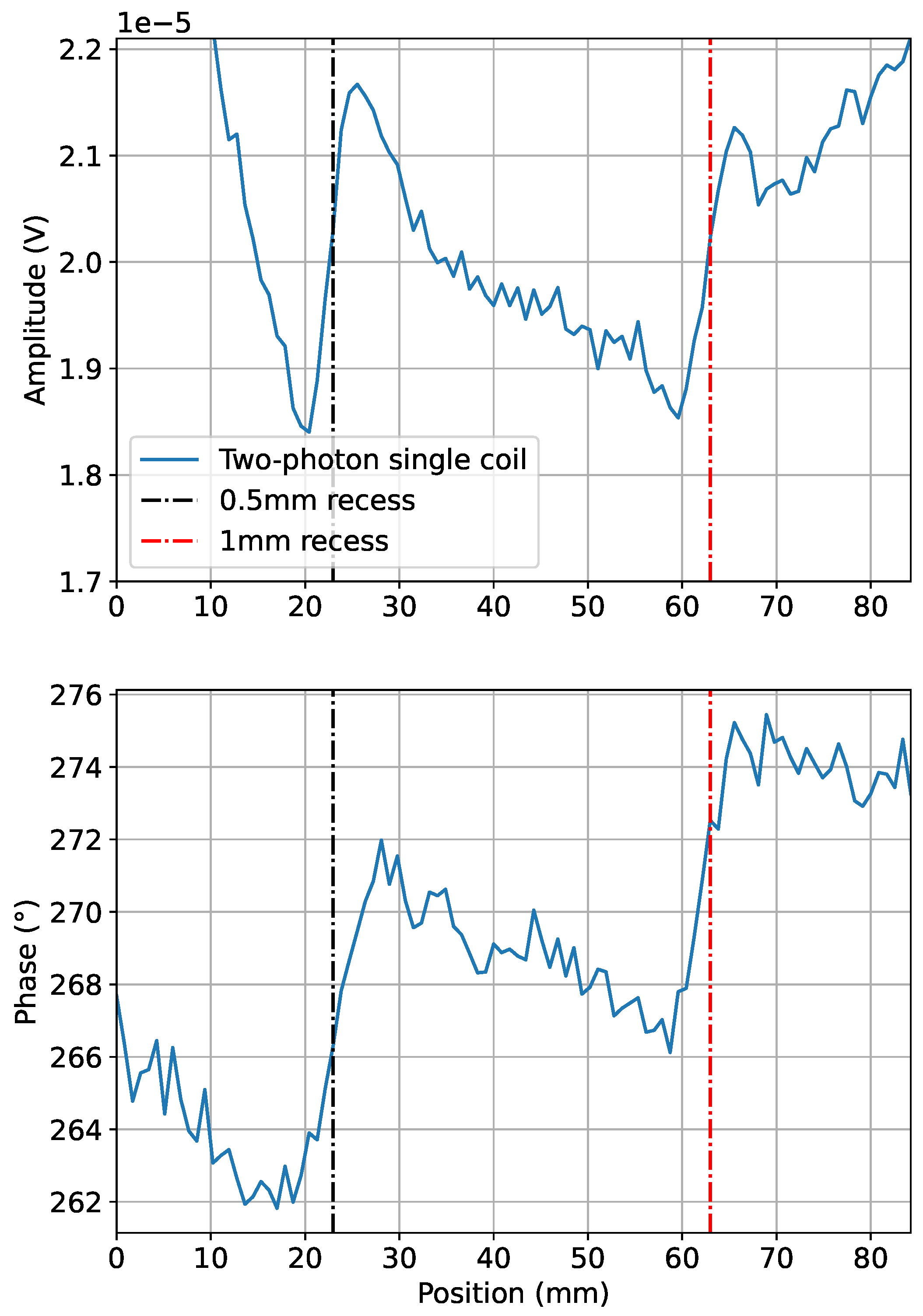
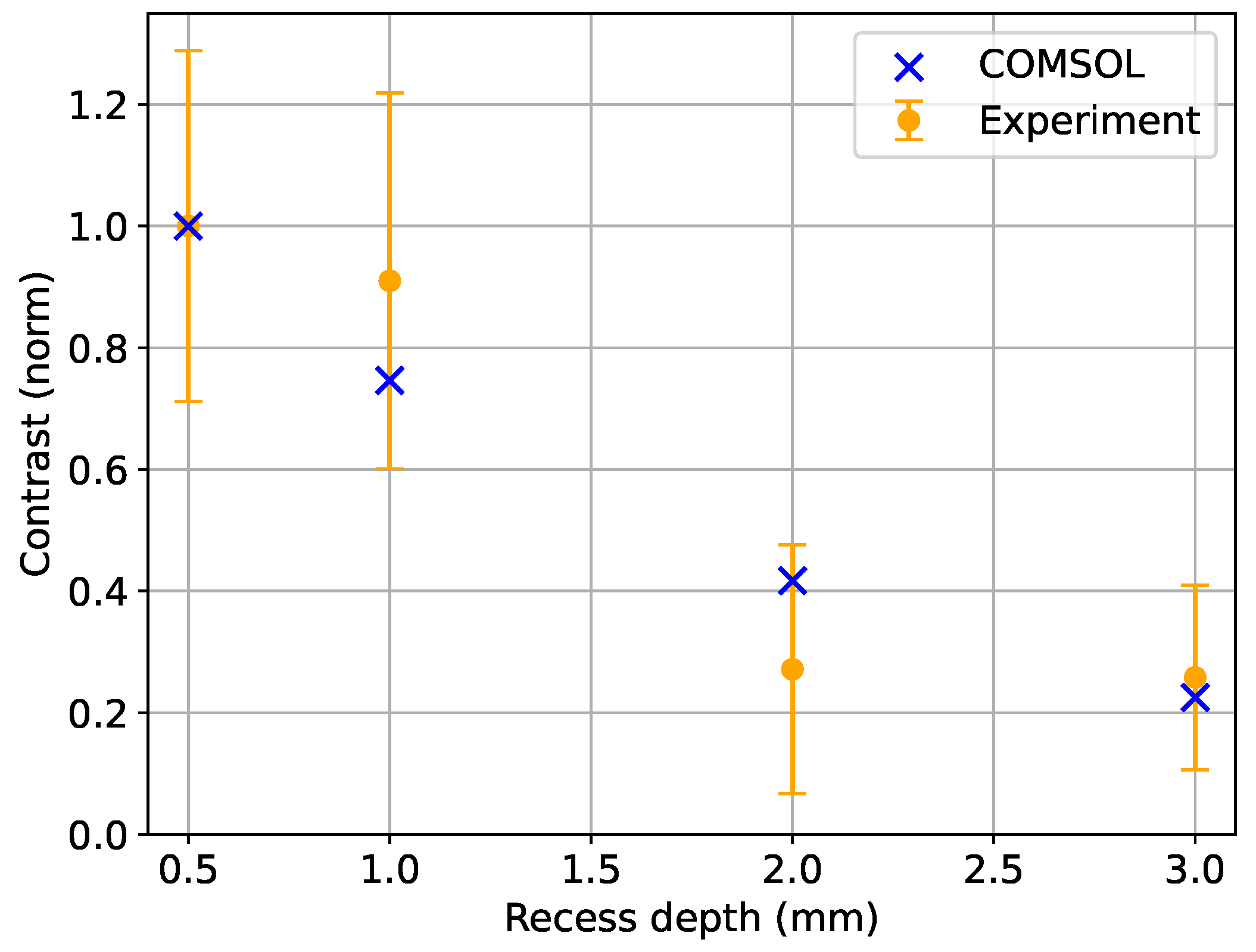
3.4. Inductive Measurements with Two-Photon-Based Detection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Helifa, B.; Oulhadj, A.; Benbelghit, A.; Lefkaier, I.K.; Boubenider, F.; Boutassouna, D. Detection and measurement of surface cracks in ferromagnetic materials using eddy current testing. NDT E Int. 2006, 39, 384–390. [Google Scholar] [CrossRef]
- Libin, M.N.; Balasubramaniam, K.; Maxfield, B.W.; Krishnamurthy, C.V. Simulations and measurements of artificial cracks and pits in flat stainless steel plates using tone burst eddy-currents thermography. Rev. Prog. Quant. Nondestruct. Eval. 2013, 32, 539–546. [Google Scholar]
- Liu, X.; Lin, H. Research on Coating Thickness Measurement with Eddy Current. In Proceedings of the 2018 Eighth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 19–21 July 2018; pp. 101–105. [Google Scholar]
- Wickenbrock, A.; Leefer, N.; Blanchard, J.W.; Budker, D. Eddy current imaging with an atomic radio-frequency magnetometer. Appl. Phys. Lett. 2016, 108, 183507. [Google Scholar] [CrossRef]
- Marmugi, L.; Deans, C.; Renzoni, F. Electromagnetic induction imaging with atomic magnetometers: Unlocking the low conductivity regime. Appl. Phys. Lett. 2019, 115, 083503. [Google Scholar] [CrossRef]
- Wickenbrock, A.; Jurgilas, S.; Dow, A.; Marmugi, L.; Renzoni, F. Magnetic induction tomography using an all-optical 87Rb atomic magnetometer. Opt. Lett. 2014, 39, 6367. [Google Scholar] [CrossRef]
- Elson, L.; Meraki, A.; Rushton, L.M.; Pyragius, T.; Jensen, K. Detection and characterisation of conductive objects using electromagnetic induction and a fluxgate magnetometer. Sensors 2022, 22, 5934. [Google Scholar] [CrossRef]
- Dogaru, T.; Smith, S.T. Giant magnetoresistance-based eddy-current sensor. IEEE Trans. Magn. 2001, 37, 3831–3838. [Google Scholar] [CrossRef]
- Heilman, D.J.; Sauer, K.L.; Prescott, D.W.; Motamedi, C.Z.; Dural, N.; Romalis, M.V.; Kornack, T.W. Large-scale, multi-pass, two-chamber rf atomic magnetometer. arXiv 2023, arXiv:2312.10228. [Google Scholar]
- Savukov, I.M.; Seltzer, S.J.; Romalis, M.V.; Sauer, K.L. Tunable atomic magnetometer for detection of radio-frequency magnetic fields. Phys. Rev. Lett. 2005, 95, 63004. [Google Scholar] [CrossRef] [PubMed]
- Keder, D.A.; Prescott, D.W.; Conovaloff, A.W.; Sauer, K.L. An unshielded radio-frequency atomic magnetometer with sub-femtotesla sensitivity. AIP Adv. 2014, 4, 127159. [Google Scholar] [CrossRef]
- Ledbetter, M.P.; Acosta, V.M.; Rochester, S.M.; Budker, D. Detection of radio-frequency magnetic fields using nonlinear magneto-optical rotation. Phys. Rev. A 2007, 75, 023405. [Google Scholar] [CrossRef]
- Zigdon, D.T.; Wilson-Gordon, A.D.; Guttikonda, S.; Bahr, E.J.; Neitzke, O.; Rochester, S.M.; Budker, D. Non-linear magneto-optical rotation in the presence of a radio-frequency field. Opt. Express 2010, 18, 25494. [Google Scholar] [CrossRef] [PubMed]
- Ingleby, S.J.; O’Dwyer, C.; Griffin, P.F.; Arnold, A.S.; Riis, E. Vector Magnetometry Exploiting Phase-Geometry Effects in a Double-Resonance Alignment Magnetometer. Phys. Rev. Appl. 2018, 10, 034035. [Google Scholar] [CrossRef]
- Dhombridge, J.E.; Claussen, N.R.; Iivanainen, J.; Schwindt, P.D.D. High-Sensitivity rf Detection Using an Optically Pumped Comagnetometer Based on Natural- Abundance Rubidium with Active Ambient-Field Cancellation. Phys. Rev. Appl. 2022, 18, 044052. [Google Scholar] [CrossRef]
- Rushton, L.M.; Pyragius, T.; Meraki, A.; Elson, L.; Jensen, K. Unshielded portable optically pumped magnetometer for the remote detection of conductive objects using eddy current measurements. Rev. Sci. Instrum. 2022, 93, 125103. [Google Scholar] [CrossRef]
- Yao, H.; Maddox, B.; Renzoni, F. High-sensitivity operation of an unshielded single cell radio-frequency atomic magnetometer. Opt. Express 2022, 30, 42015. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, X.; Wu, T.; Peng, X.; Guo, H. Radio-Frequency Magnetometry Based on Parametric Resonances. Phys. Rev. Lett. 2024, 133, 093201. [Google Scholar] [CrossRef]
- Liu, X.; Han, J.; Xiao, W.; Wu, T.; Peng, X.; Guo, H. Magnetic field imaging with radio-frequency optically pumped magnetometers. Chin. Opt. Lett. 2024, 22, 06006. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, H.; Schmieg, R.; Oesterle, A.; Polzik, E.S. Entanglement-Enhanced Magnetic Induction Tomograph. Phys. Rev. Lett. 2023, 130, 203602. [Google Scholar] [CrossRef] [PubMed]
- Lipka, M.; Sierant, A.; Troullinou, C.; Mitchell, M.W. Multiparameter quantum sensing and magnetic communication with a hybrid dc and rf optically pumped magnetometer. Phys. Rev. Appl. 2024, 21, 034054. [Google Scholar] [CrossRef]
- Wang, H.; Zugenmaier, M.; Jensen, K.; Zheng, W.; Polzik, E.S. Magnetic induction sensor based on a dual-frequency atomic magnetometer. Phys. Rev. Appl. 2024, 22, 034030. [Google Scholar] [CrossRef]
- Bevington, P.; Gartman, R.; Chalupczak, W. Imaging of material defects with a radio-frequency atomic magnetometer. Rev. Sci. Instrum. 2019, 90, 013103. [Google Scholar] [CrossRef] [PubMed]
- Bevington, P.; Gartman, R.; Chalupczak, W. Enhanced material defect imaging with a radio-frequency atomic magnetometer. J. Appl. Phys. 2019, 125, 094503. [Google Scholar] [CrossRef]
- Gerginov, V. Field-polarisation Sensitivity in rf Atomic Magnetometers. Phys. Rev. Appl. 2019, 11, 024008. [Google Scholar] [CrossRef]
- Rushton, L.M.; Ellis, L.M.; Zipfel, J.D.; Bevington, P.; Chalupczak, W. Polarization of radio-frequency magnetic fields in magnetic induction measurements with an atomic magnetometer. Phys. Rev. Appl. 2024, 22, 014002. [Google Scholar] [CrossRef]
- Motamedi, C.Z.; Sauer, K.L. Magnetic Jones Vector Detection with rf Atomic Magnetometer. Phys. Rev. Appl. 2024, 20, 014006. [Google Scholar] [CrossRef]
- Bevington, P.; Gartman, R.; Chalupczak, W. Alkali-metal spin maser for non-destructive tests. App. Phys. Lett. 2019, 115, 173502. [Google Scholar] [CrossRef]
- Bevington, P.; Gartman, R.; Chalupczak, W. Dual frequency caesium spin maser. Phys. Rev. A 2020, 102, 032804. [Google Scholar] [CrossRef]
- Xiao, W.; Sun, C.; Shen, L.; Feng, Y.; Liu, M.; Wu, Y.; Liu, X.; Wu, T.; Peng, X.; Guo, H. A movable unshielded magnetocardiography system. Sci. Adv. 2023, 9, eadg1746. [Google Scholar] [CrossRef]
- Savukov, I.M.; Seltzer, S.J.; Romalis, M.V. Detection of NMR signals with a radio-frequency atomic magnetometer. J. Magn. Res. 2007, 185, 214. [Google Scholar] [CrossRef] [PubMed]
- Maddox, B.; Renzoni, F. Two-photon electromagnetic induction imaging with an atomic magnetometer. Appl. Phys. Lett. 2023, 122, 144001. [Google Scholar] [CrossRef]
- Geng, X.; Yang, G.; Qi, P.; Tang, W.; Liang, S.; Li, G.; Huang, G. Laser-detected magnetic resonance induced by radio-frequency two-photon processes. Phys. Rev. A 2021, 103, 053112. [Google Scholar] [CrossRef]
- Chalupczak, W.; Godun, R.M.; Pustelny, S.; Gawlik, W. Room temperature femtotesla radio-frequency atomic magnetometer. Appl. Phys. Lett. 2012, 100, 242401. [Google Scholar]
- Budker, D.; Kimball, D.F.; DeMille, D.P. Atomic Physics: An Exploration through Problems and Solutions, 2nd ed.; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Jensen, K.; Zugenmaier, M.; Arnbak, J.; Stærkind, H.; Balabas, M.V.; Polzik, E.S. Detection of low-conductivity objects using eddy current measurements with an optical magnetometer. Phys. Rev. Res. 2019, 1, 033087. [Google Scholar] [CrossRef]
- Bevington, P.; Gartman, R.; Chalupczak, W. Inductive Imaging of the Concealed Defects with Radio-Frequency Atomic Magnetometers. Appl. Sci. 2020, 10, 6871. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rushton, L.M.; Ellis, L.M.; Zipfel, J.D.; Bevington, P.; Chalupczak, W. Performance of a Radio-Frequency Two-Photon Atomic Magnetometer in Different Magnetic Induction Measurement Geometries. Sensors 2024, 24, 6657. https://doi.org/10.3390/s24206657
Rushton LM, Ellis LM, Zipfel JD, Bevington P, Chalupczak W. Performance of a Radio-Frequency Two-Photon Atomic Magnetometer in Different Magnetic Induction Measurement Geometries. Sensors. 2024; 24(20):6657. https://doi.org/10.3390/s24206657
Chicago/Turabian StyleRushton, Lucas Martin, Laura Mae Ellis, Jake David Zipfel, Patrick Bevington, and Witold Chalupczak. 2024. "Performance of a Radio-Frequency Two-Photon Atomic Magnetometer in Different Magnetic Induction Measurement Geometries" Sensors 24, no. 20: 6657. https://doi.org/10.3390/s24206657
APA StyleRushton, L. M., Ellis, L. M., Zipfel, J. D., Bevington, P., & Chalupczak, W. (2024). Performance of a Radio-Frequency Two-Photon Atomic Magnetometer in Different Magnetic Induction Measurement Geometries. Sensors, 24(20), 6657. https://doi.org/10.3390/s24206657






