Adaptive Optimization and Dynamic Representation Method for Asynchronous Data Based on Regional Correlation Degree
Abstract
:1. Introduction
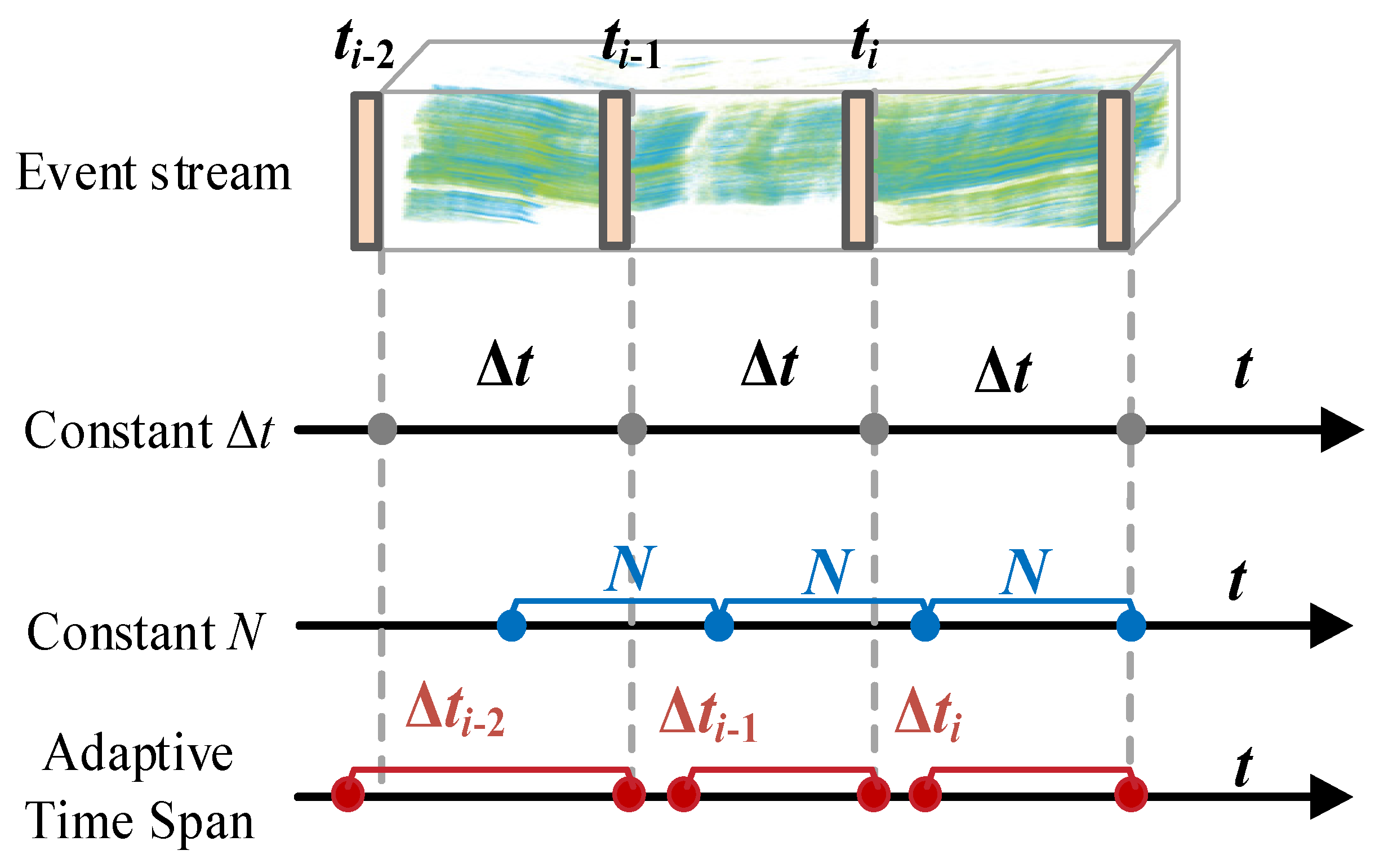
- We propose a Dynamic Asynchronous Data Metric and Slicing algorithm (ASDMS) that dynamically adjusts the slicing span of events based on the spatiotemporal structure and polarity information of the event stream;
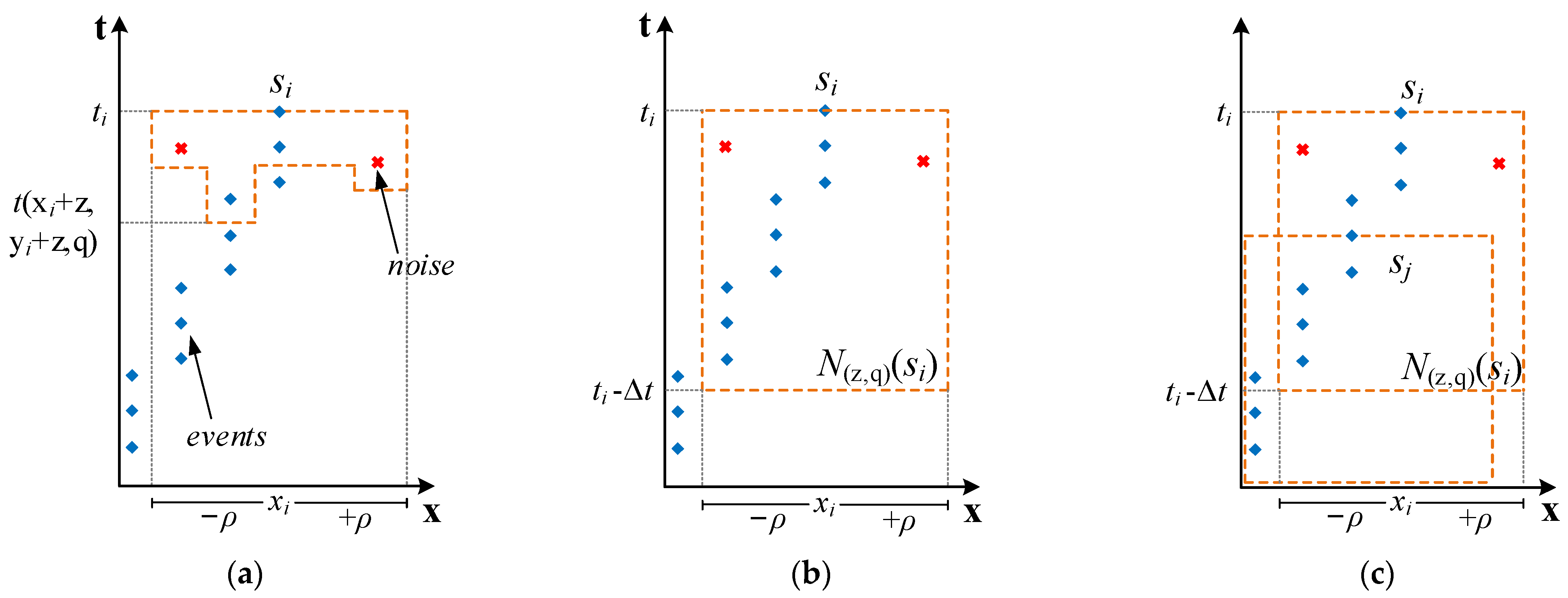
- We introduce an Adaptive Spatiotemporal Subject Surface Compensation algorithm (ASSSC) that repairs the main information-carrying parts of the new event stream after slicing based on the correlation between main and overall events, removing redundant events in the spatiotemporal correlation area;
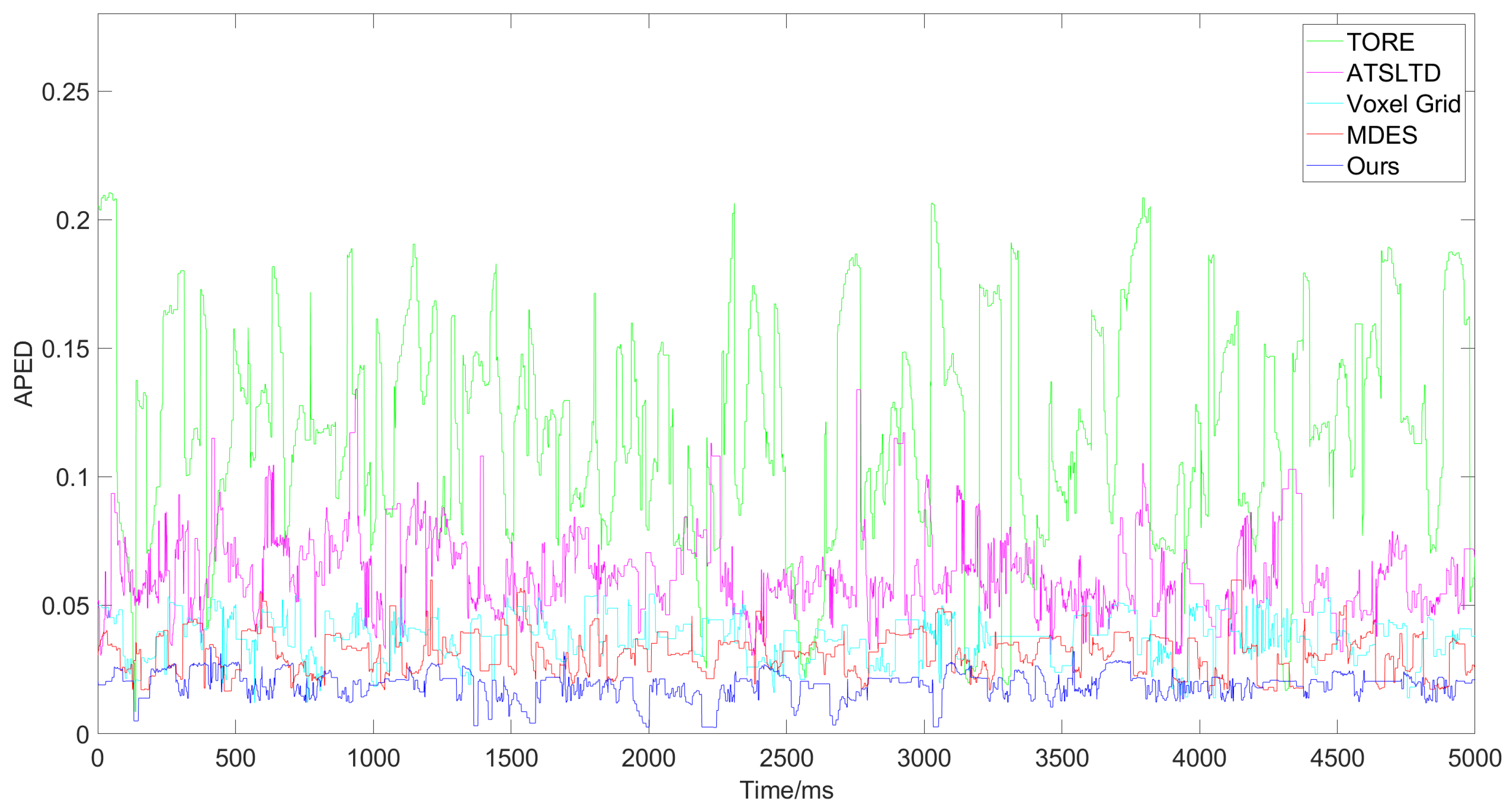
- We propose a new evaluation metric, Actual Performance Efficiency Discrepancy (APED), which quantifies the effectiveness of each representation method in handling the primary information-carrying events in the event stream.
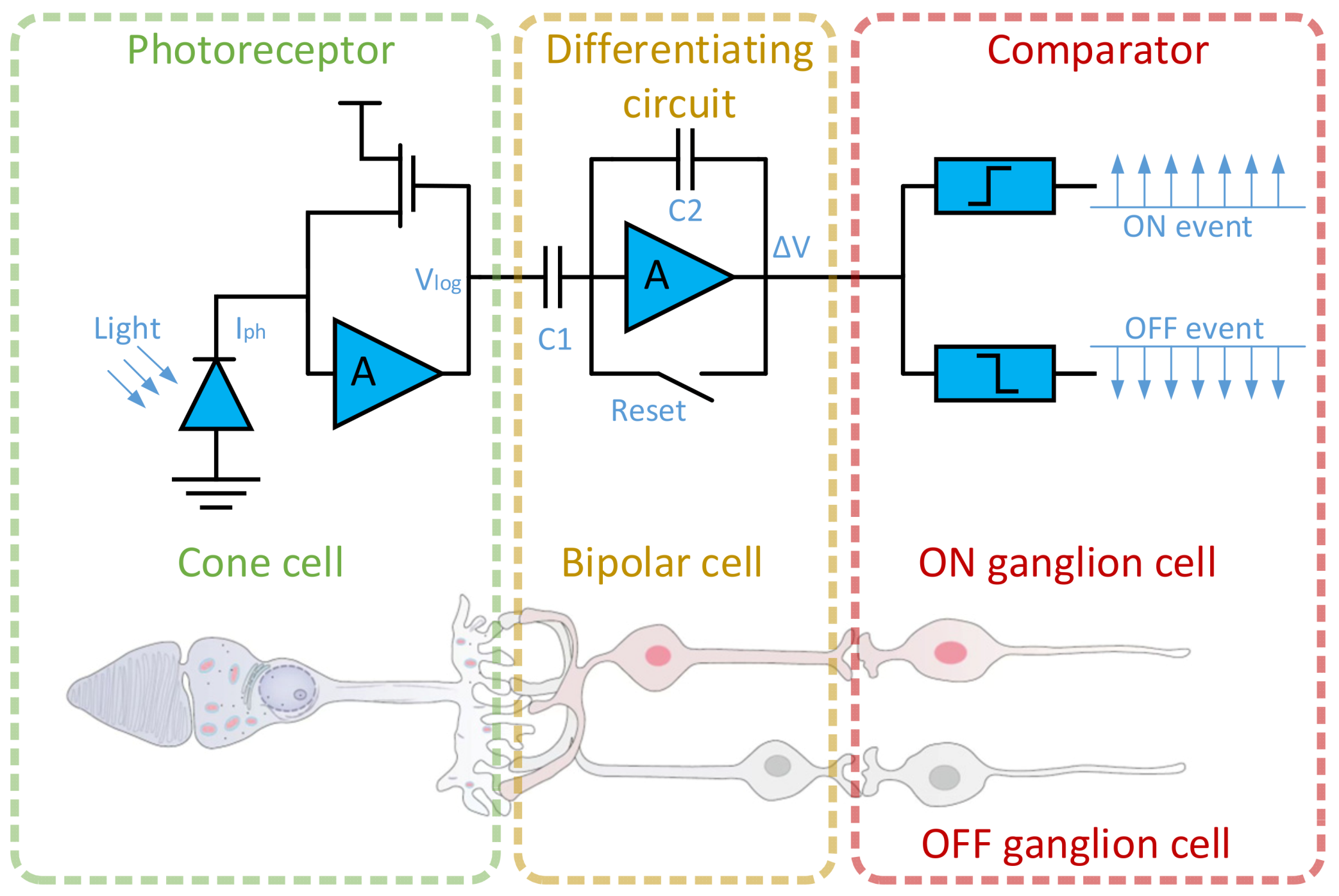
2. Materials and Methods
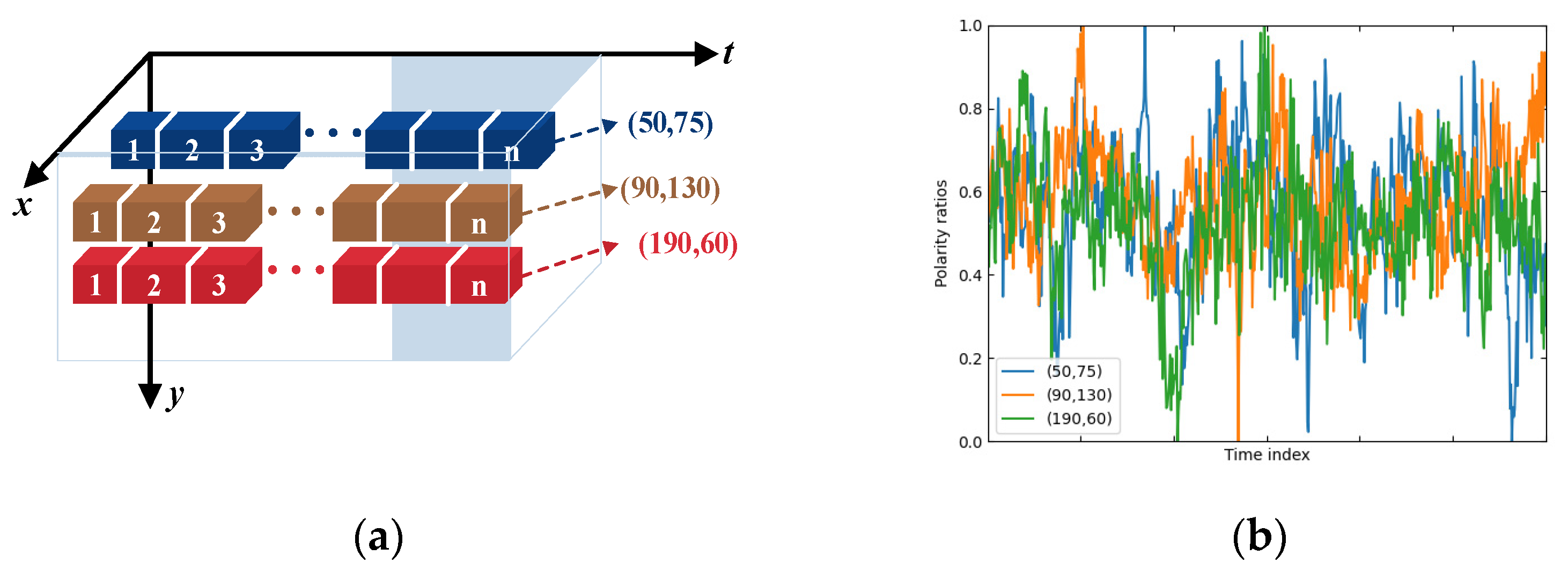
2.1. Asynchronous Spike Dynamic Metric and Slicing Algorithm
| Algorithm 1. Asynchronous Spike Dynamic Metric and Slicing. |
2 For k =1, 2 …, K do 8 End for |
2.2. Adaptive Spatiotemporal Subject Surface Compensation Algorithm
| Algorithm 2. Adaptive Spatiotemporal Subject Surface Compensation. |
| and initial cell of the main events, , Output: Cell and density of main compensation events 1 Obtain main compensation events and 2 Obtain time representation image and and 5 Update main compensation events and 6 Update time representation image and and 8 End 9 Obtain event count image and 10 Obtain event density and 12 Assign the value of to 13 Obtain event density 14 do 15 and 16 Update event count image and 17 End 18 End 19 Return , |
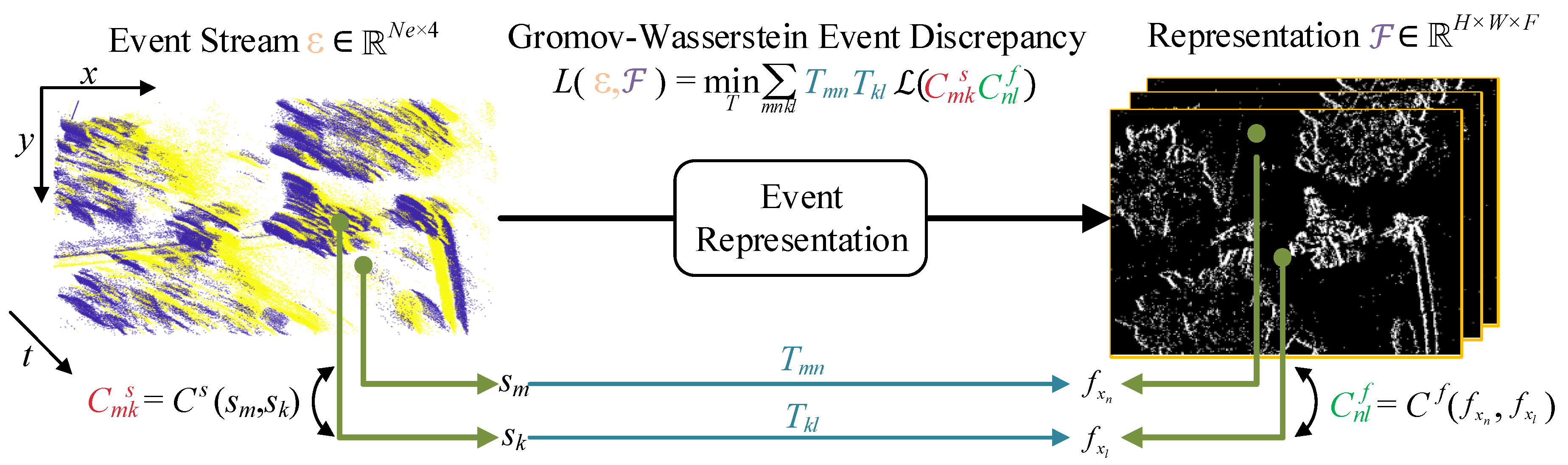
2.3. Actual Performance Efficiency Discrepancy
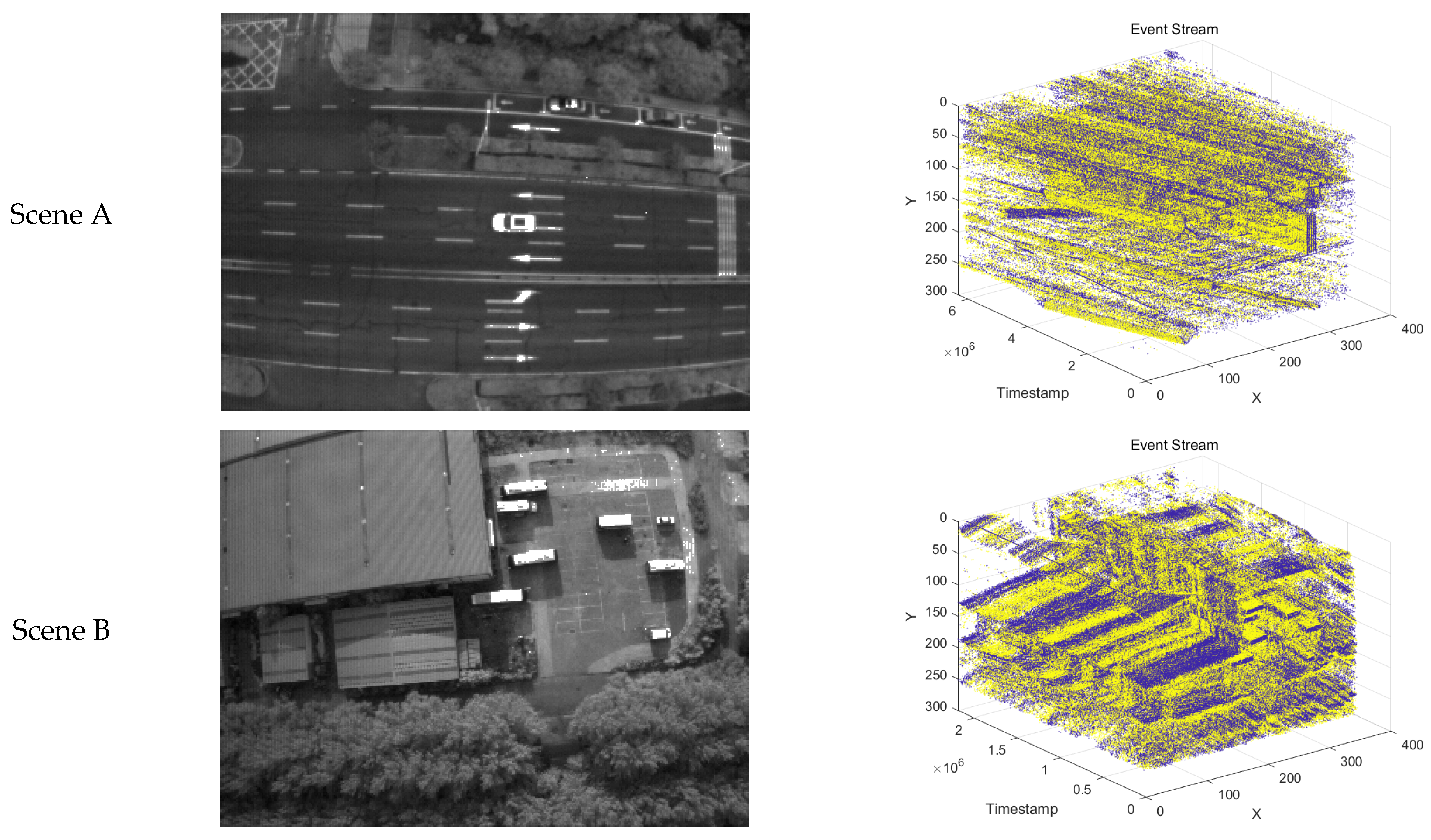
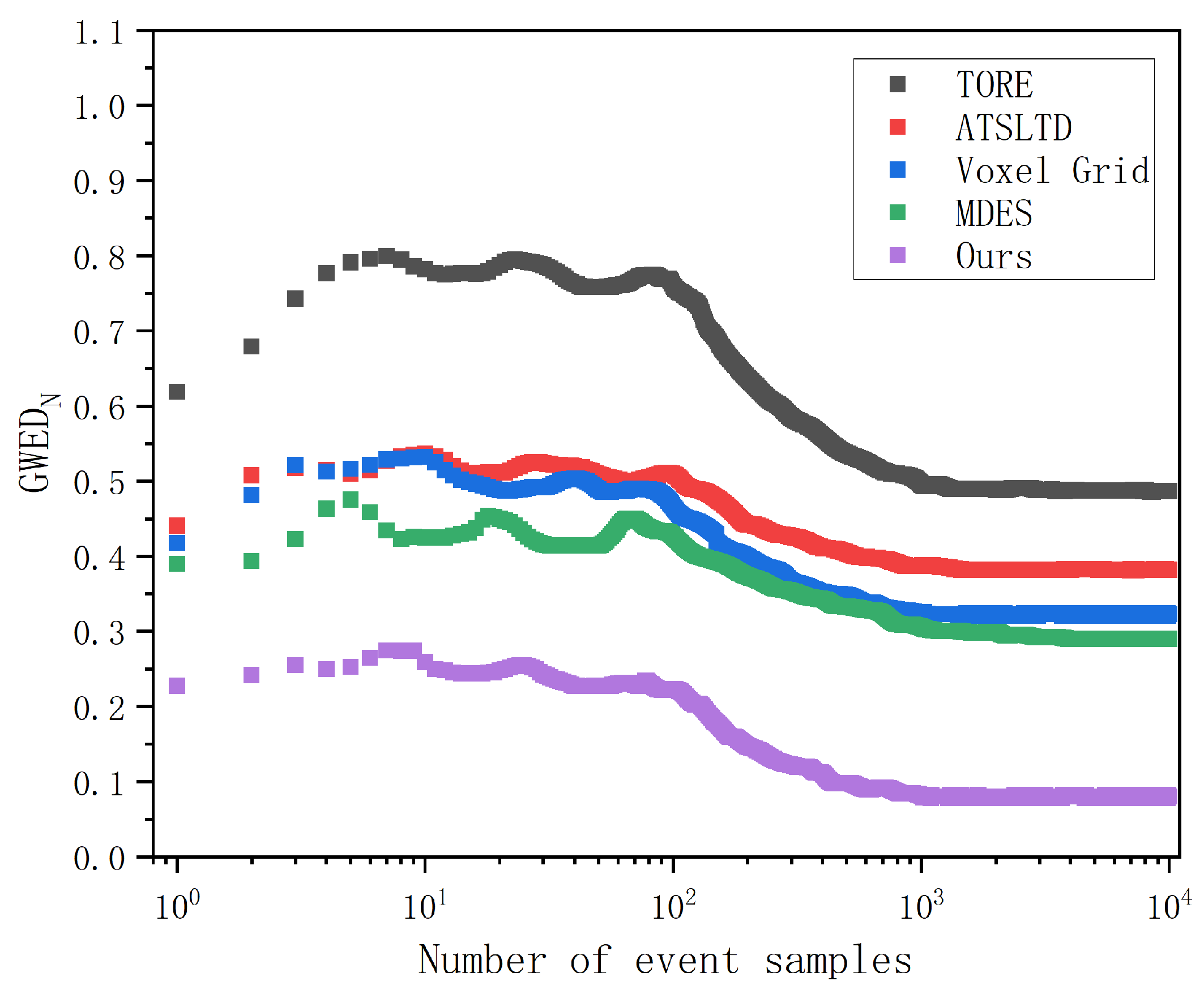
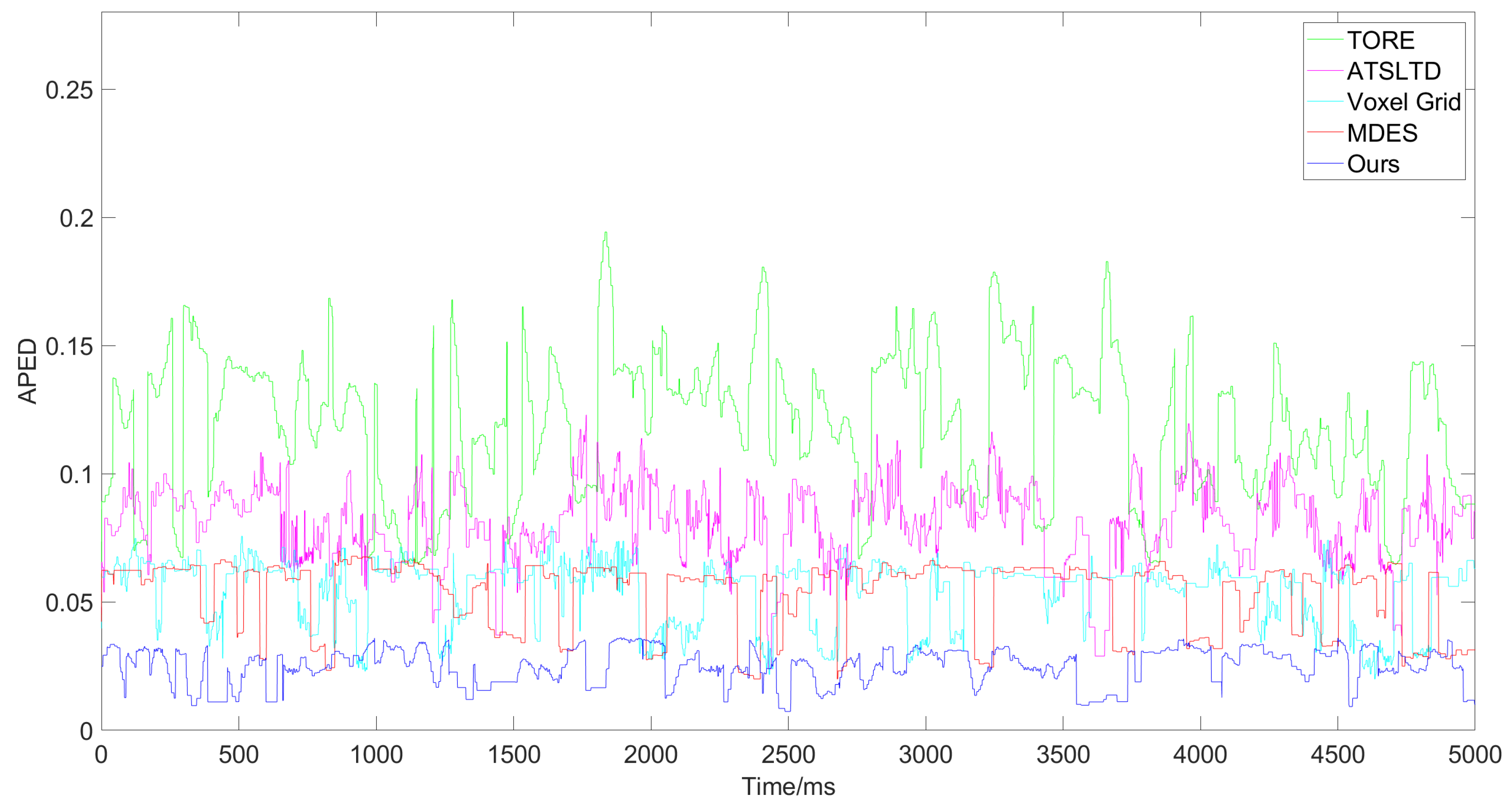
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Brandli, C.; Berner, R.; Yang, M.; Liu, S.-C.; Delbruck, T. A 240 × 180 130 db 3 µs latency global shutter spatiotemporal vision sensor. IEEE J. Solid-State Circuits 2014, 49, 2333–2341. [Google Scholar] [CrossRef]
- Posch, C.; Matolin, D.; Wohlgenannt, R. A QVGA 143 dB dynamic range frame-free PWM image sensor with lossless pixel-level video compression and time-domain CDS. IEEE J. Solid-State Circuits 2010, 46, 259–275. [Google Scholar] [CrossRef]
- Oyster, C. The analysis of image motion by the rabbit retina. J. Physiol. 1968, 199, 613–635. [Google Scholar] [CrossRef]
- Murphy-Baum, B.L.; Awatramani, G.B. An old neuron learns new tricks: Redefining motion processing in the primate retina. Neuron 2018, 97, 1205–1207. [Google Scholar] [CrossRef]
- Ölveczky, B.P.; Baccus, S.A.; Meister, M. Segregation of object and background motion in the retina. Nature 2003, 423, 401–408. [Google Scholar] [CrossRef]
- Wild, B. How does the brain tell self-motion from object motion? J. Neurosci. 2018, 38, 3875–3877. [Google Scholar] [CrossRef]
- Ghosh, R.; Gupta, A.; Nakagawa, A.; Soares, A.; Thakor, N. Spatiotemporal filtering for event-based action recognition. arXiv 2019, arXiv:1903.07067. [Google Scholar]
- Ghosh, R.; Gupta, A.; Tang, S.; Soares, A.; Thakor, N. Spatiotemporal feature learning for event-based vision. arXiv 2019, arXiv:1903.06923. [Google Scholar]
- Orchard, G.; Meyer, C.; Etienne-Cummings, R.; Posch, C.; Thakor, N.; Benosman, R. HFirst: A temporal approach to object recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2028–2040. [Google Scholar] [CrossRef]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training deep spiking neural networks using backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef]
- Zhao, B.; Ding, R.; Chen, S.; Linares-Barranco, B.; Tang, H. Feedforward categorization on AER motion events using cortex-like features in a spiking neural network. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1963–1978. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Carrasco, J.A.; Zhao, B.; Serrano, C.; Acha, B.; Serrano-Gotarredona, T.; Chen, S.; Linares-Barranco, B. Mapping from frame-driven to frame-free event-driven vision systems by low-rate rate coding and coincidence processing—Application to feedforward ConvNets. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2706–2719. [Google Scholar] [CrossRef] [PubMed]
- Sekikawa, Y.; Hara, K.; Saito, H. Eventnet: Asynchronous recursive event processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3887–3896. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Fan, H.; Yu, X.; Ding, Y.; Yang, Y.; Kankanhalli, M. Pstnet: Point spatio-temporal convolution on point cloud sequences. arXiv 2022, arXiv:2205.13713. [Google Scholar]
- Gehrig, M.; Scaramuzza, D. Recurrent vision transformers for object detection with event cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 13884–13893. [Google Scholar]
- Schaefer, S.; Gehrig, D.; Scaramuzza, D. Aegnn: Asynchronous event-based graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12371–12381. [Google Scholar]
- Bi, Y.; Chadha, A.; Abbas, A.; Bourtsoulatze, E.; Andreopoulos, Y. Graph-based spatio-temporal feature learning for neuromorphic vision sensing. IEEE Trans. Image Process. 2020, 29, 9084–9098. [Google Scholar] [CrossRef]
- Bi, Y.; Chadha, A.; Abbas, A.; Bourtsoulatze, E.; Andreopoulos, Y. Graph-based object classification for neuromorphic vision sensing. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019; pp. 491–501. [Google Scholar]
- Mondal, A.; Giraldo, J.H.; Bouwmans, T.; Chowdhury, A.S. Moving object detection for event-based vision using graph spectral clustering. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 876–884. [Google Scholar]
- Deng, Y.; Chen, H.; Liu, H.; Li, Y. A voxel graph cnn for object classification with event cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1172–1181. [Google Scholar]
- Maqueda, A.I.; Loquercio, A.; Gallego, G.; García, N.; Scaramuzza, D. Event-based vision meets deep learning on steering prediction for self-driving cars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5419–5427. [Google Scholar]
- Sironi, A.; Brambilla, M.; Bourdis, N.; Lagorce, X.; Benosman, R. HATS: Histograms of averaged time surfaces for robust event-based object classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1731–1740. [Google Scholar]
- Zhu, A.Z.; Yuan, L.; Chaney, K.; Daniilidis, K. Unsupervised event-based learning of optical flow, depth, and egomotion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 989–997. [Google Scholar]
- Wang, L.; Ho, Y.-S.; Yoon, K.-J. Event-based high dynamic range image and very high frame rate video generation using conditional generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10081–10090. [Google Scholar]
- Alonso, I.; Murillo, A.C. EV-SegNet: Semantic segmentation for event-based cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 1624–1633. [Google Scholar]
- Baldwin, R.W.; Liu, R.; Almatrafi, M.; Asari, V.; Hirakawa, K. Time-ordered recent event (tore) volumes for event cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2519–2532. [Google Scholar] [CrossRef]
- Nam, Y.; Mostafavi, M.; Yoon, K.-J.; Choi, J. Stereo depth from events cameras: Concentrate and focus on the future. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6114–6123. [Google Scholar]
- Zhang, Y.; Zhao, Y.; Lv, H.; Feng, Y.; Liu, H.; Han, C. Adaptive slicing method of the spatiotemporal event stream obtained from a dynamic vision sensor. Sensors 2022, 22, 2614. [Google Scholar] [CrossRef]
- Perot, E.; De Tournemire, P.; Nitti, D.; Masci, J.; Sironi, A. Learning to detect objects with a 1 megapixel event camera. Adv. Neural Inf. Process. Syst. 2020, 33, 16639–16652. [Google Scholar]
- Kim, J.; Bae, J.; Park, G.; Zhang, D.; Kim, Y.M. N-imagenet: Towards robust, fine-grained object recognition with event cameras. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 2146–2156. [Google Scholar]
- Gehrig, D.; Loquercio, A.; Derpanis, K.G.; Scaramuzza, D. End-to-end learning of representations for asynchronous event-based data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5633–5643. [Google Scholar]
- Zubic, N.; Gehrig, D.; Gehrig, M.; Scaramuzza, D. From Chaos Comes Order: Ordering Event Representations for Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023. [Google Scholar]
- Chen, H.; Wu, Q.; Liang, Y.; Gao, X.; Wang, H. Asynchronous tracking-by-detection on adaptive time surfaces for event-based object tracking. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 473–481. [Google Scholar]
- Tang, S.; Lv, H.; Zhao, Y.; Feng, Y.; Liu, H.; Bi, G. Denoising method based on salient region recognition for the spatiotemporal event stream. Sensors 2023, 23, 6655. [Google Scholar] [CrossRef]
- Park, I.M.; Seth, S.; Paiva, A.R.; Li, L.; Principe, J.C. Kernel methods on spike train space for neuroscience: A tutorial. IEEE Signal Process. Mag. 2013, 30, 149–160. [Google Scholar] [CrossRef]
- González, J.A.; Rodríguez-Cortés, F.J.; Cronie, O.; Mateu, J. Spatio-temporal point process statistics: A review. Spat. Stat. 2016, 18, 505–544. [Google Scholar] [CrossRef]
- Teixeira, R.F.; Leite, N.J. A new framework for quality assessment of high-resolution fingerprint images. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1905–1917. [Google Scholar] [CrossRef]
- Dong, S.; Bi, Z.; Tian, Y.; Huang, T. Spike coding for dynamic vision sensor in intelligent driving. IEEE Internet Things J. 2018, 6, 60–71. [Google Scholar] [CrossRef]
- Paiva, A.R.; Park, I.; Principe, J.C. A reproducing kernel Hilbert space framework for spike train signal processing. Neural Comput. 2009, 21, 424–449. [Google Scholar] [CrossRef] [PubMed]
- Tezuka, T. Multineuron spike train analysis with R-convolution linear combination kernel. Neural Netw. 2018, 102, 67–77. [Google Scholar] [CrossRef]
- Houghton, C.; Sen, K. A new multineuron spike train metric. Neural Comput. 2008, 20, 1495–1511. [Google Scholar] [CrossRef]
- Brockmeier, A.J.; Choi, J.S.; Kriminger, E.G.; Francis, J.T.; Principe, J.C. Neural decoding with kernel-based metric learning. Neural Comput. 2014, 26, 1080–1107. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhu, L.; Xiang, X.; Huang, T.; Tian, Y. Asynchronous spatio-temporal memory network for continuous event-based object detection. IEEE Trans. Image Process. 2022, 31, 2975–2987. [Google Scholar] [CrossRef]
- Gönen, M.; Alpaydın, E. Multiple kernel learning algorithms. J. Mach. Learn. Res. 2011, 12, 2211–2268. [Google Scholar]
- Fu, Y.; Li, J.; Dong, S.; Tian, Y.; Huang, T. Spike coding: Towards lossy compression for dynamic vision sensor. In Proceedings of the 2019 Data Compression Conference (DCC), Snowbird, UT, USA, 26–29 March 2019; p. 572. [Google Scholar]
- Scheerlinck, C.; Barnes, N.; Mahony, R. Continuous-time intensity estimation using event cameras. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 308–324. [Google Scholar]
- Rebecq, H.; Ranftl, R.; Koltun, V.; Scaramuzza, D. Events-to-video: Bringing modern computer vision to event cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3857–3866. [Google Scholar]
- Lagorce, X.; Orchard, G.; Galluppi, F.; Shi, B.E.; Benosman, R.B. Hots: A hierarchy of event-based time-surfaces for pattern recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1346–1359. [Google Scholar] [CrossRef] [PubMed]
- Marchisio, A.; Shafique, M. Embedded Neuromorphic Using Intel’s Loihi Processor. In Embedded Machine Learning for Cyber-Physical, IoT, and Edge Computing: Software Optimizations and Hardware/Software Codesign; Springer: Berlin/Heidelberg, Germany, 2023; pp. 137–172. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Zhu, A.Z.; Yuan, L.; Chaney, K.; Daniilidis, K. EV-FlowNet: Self-supervised optical flow estimation for event-based cameras. arXiv 2018, arXiv:1802.06898. [Google Scholar]
- Said, S.; Bombrun, L.; Berthoumieu, Y.; Manton, J.H. Riemannian Gaussian distributions on the space of symmetric positive definite matrices. IEEE Trans. Inf. Theory 2017, 63, 2153–2170. [Google Scholar] [CrossRef]
- Peyré, G.; Cuturi, M.; Solomon, J. Gromov-wasserstein averaging of kernel and distance matrices. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2664–2672. [Google Scholar]






| Method | Actual Performance Efficiency Discrepancy | ||
|---|---|---|---|
| Scene A | Scene B | Scene C | |
| TORE | 0.11575 | 0.11906 | 0.04819 |
| ATSLTD | 0.07921 | 0.06497 | 0.03415 |
| Voxel Grid | 0.05566 | 0.03737 | 0.02832 |
| MDES | 0.05356 | 0.03086 | 0.01336 |
| Ours | 0.02403 | 0.01896 | 0.00596 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Zhao, Y.; Lv, H.; Sun, M.; Feng, Y.; Zhang, Z. Adaptive Optimization and Dynamic Representation Method for Asynchronous Data Based on Regional Correlation Degree. Sensors 2024, 24, 7430. https://doi.org/10.3390/s24237430
Tang S, Zhao Y, Lv H, Sun M, Feng Y, Zhang Z. Adaptive Optimization and Dynamic Representation Method for Asynchronous Data Based on Regional Correlation Degree. Sensors. 2024; 24(23):7430. https://doi.org/10.3390/s24237430
Chicago/Turabian StyleTang, Sichao, Yuchen Zhao, Hengyi Lv, Ming Sun, Yang Feng, and Zeshu Zhang. 2024. "Adaptive Optimization and Dynamic Representation Method for Asynchronous Data Based on Regional Correlation Degree" Sensors 24, no. 23: 7430. https://doi.org/10.3390/s24237430
APA StyleTang, S., Zhao, Y., Lv, H., Sun, M., Feng, Y., & Zhang, Z. (2024). Adaptive Optimization and Dynamic Representation Method for Asynchronous Data Based on Regional Correlation Degree. Sensors, 24(23), 7430. https://doi.org/10.3390/s24237430





