Noise Variation Characteristics of the Superconducting Gravimeter at Jiufeng Station in Wuhan (China)
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
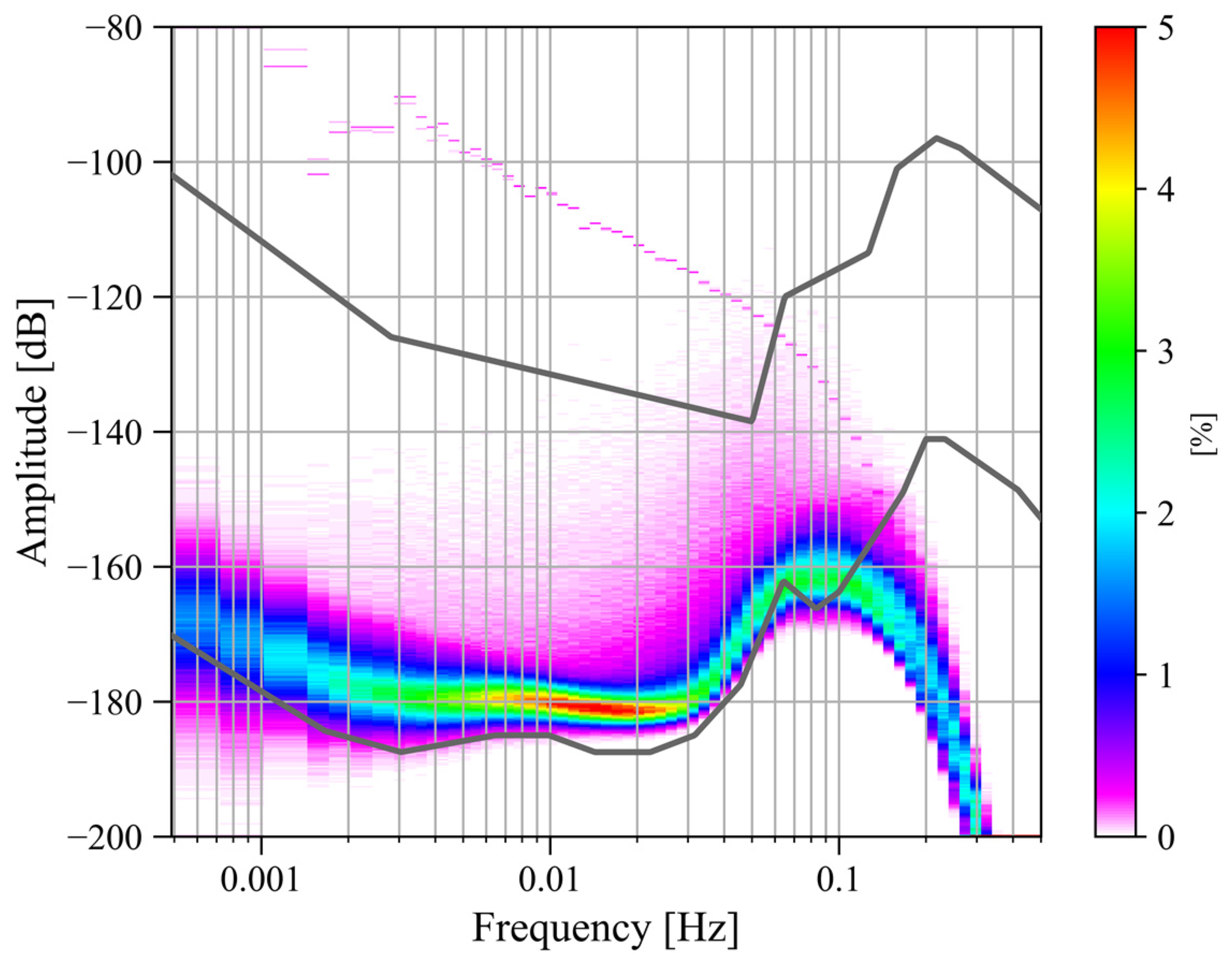
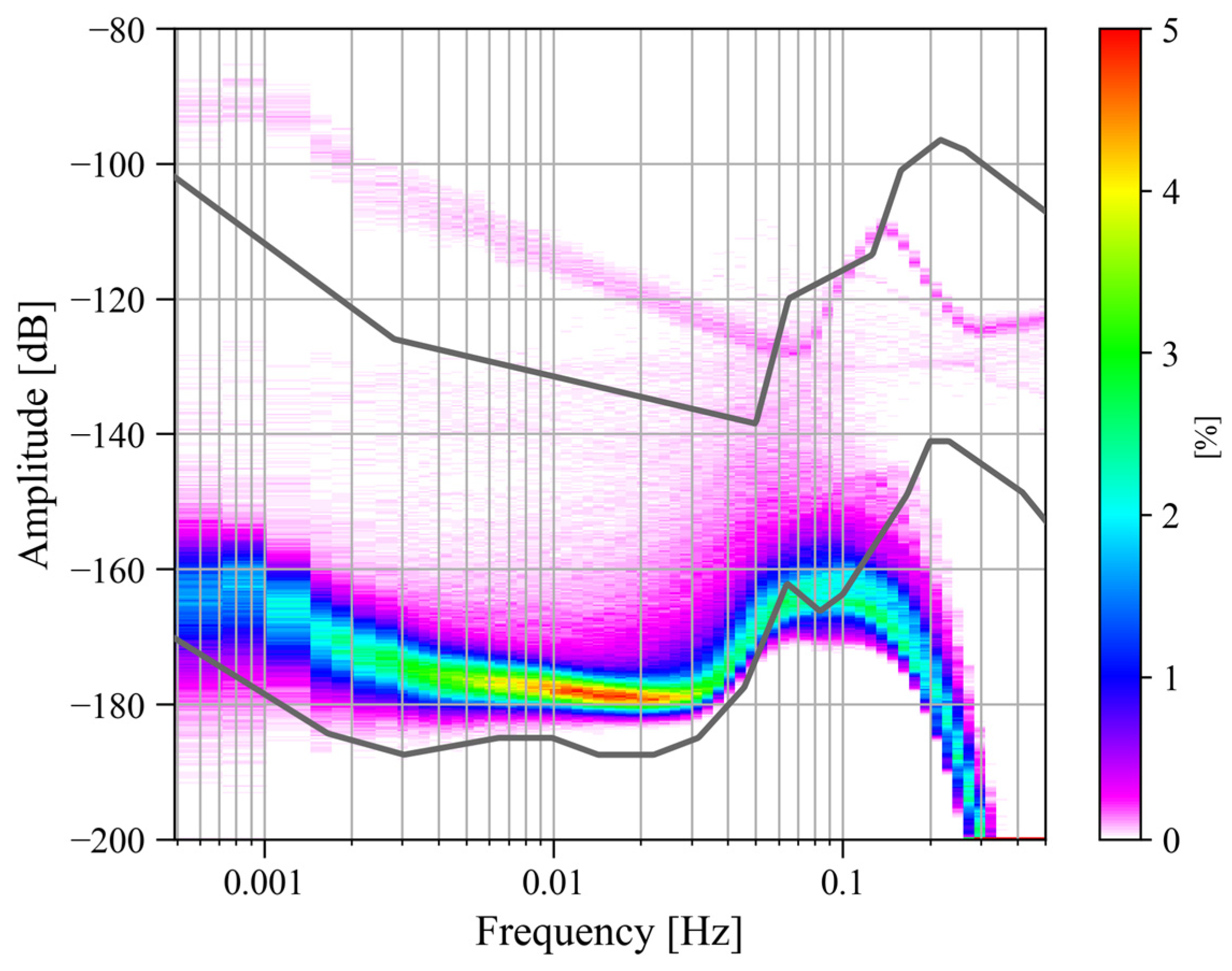
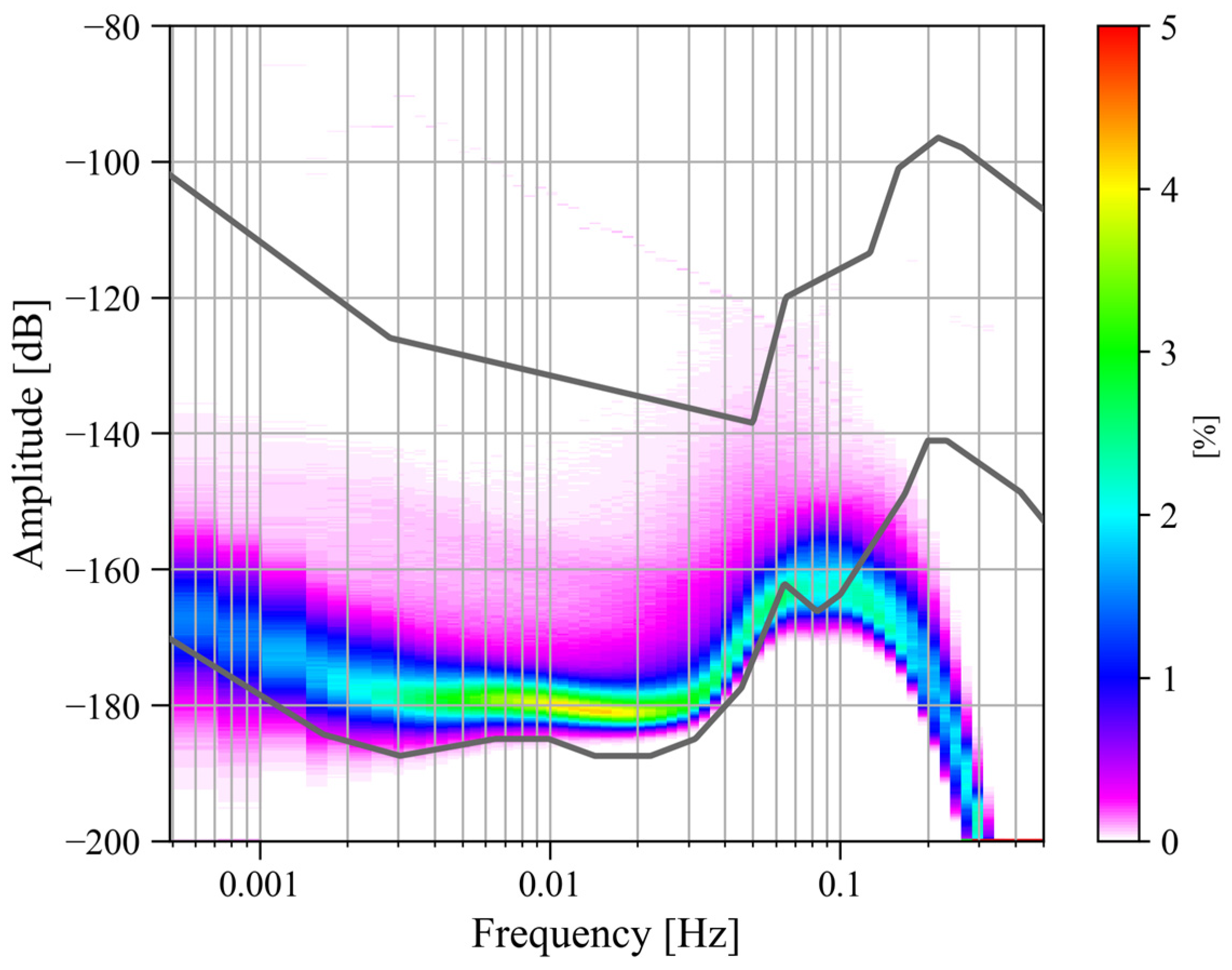
2.2.1. Power Spectrum Analysis
2.2.2. Probability Density Function
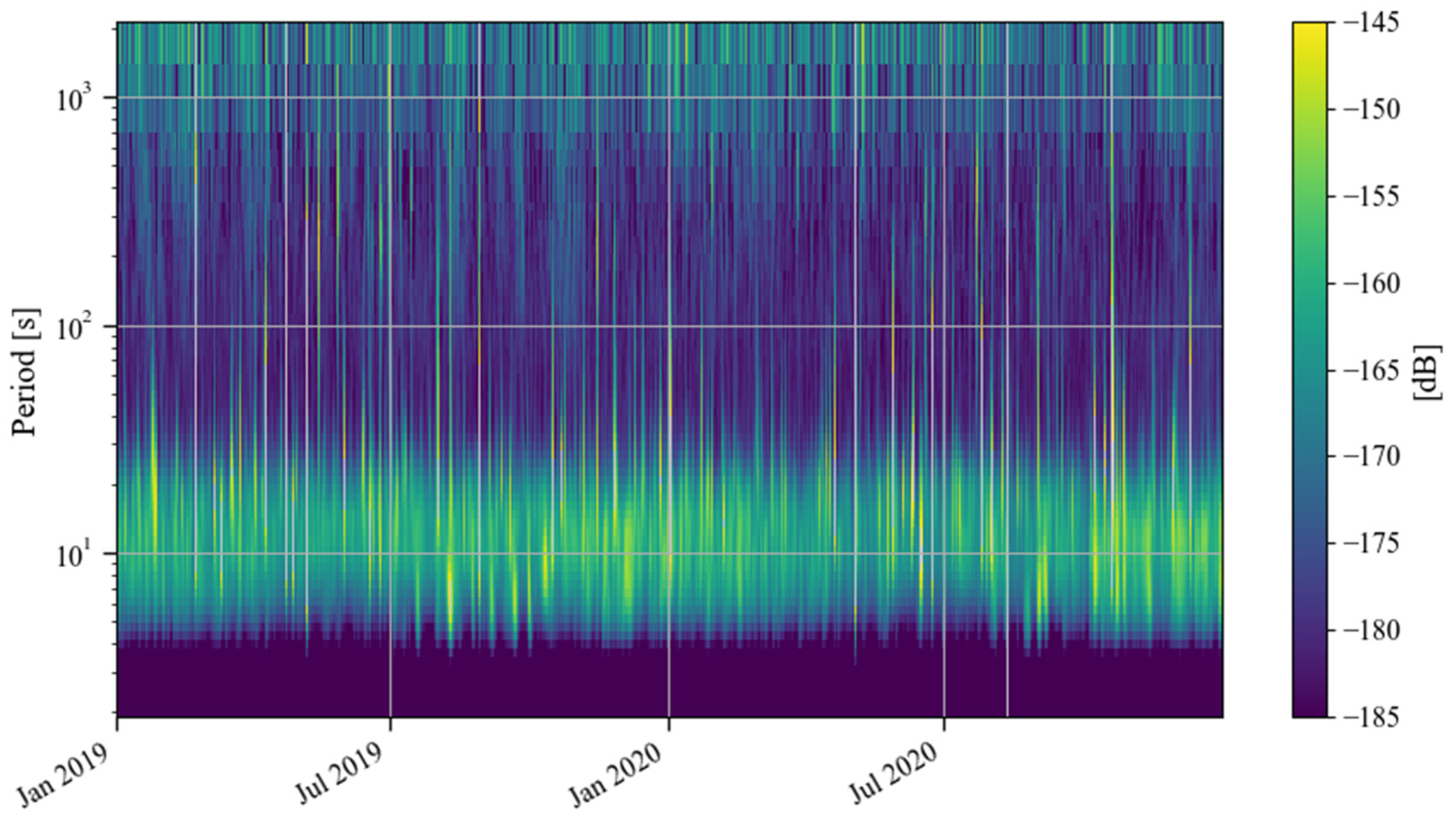
2.2.3. Continuous Wavelet Transform
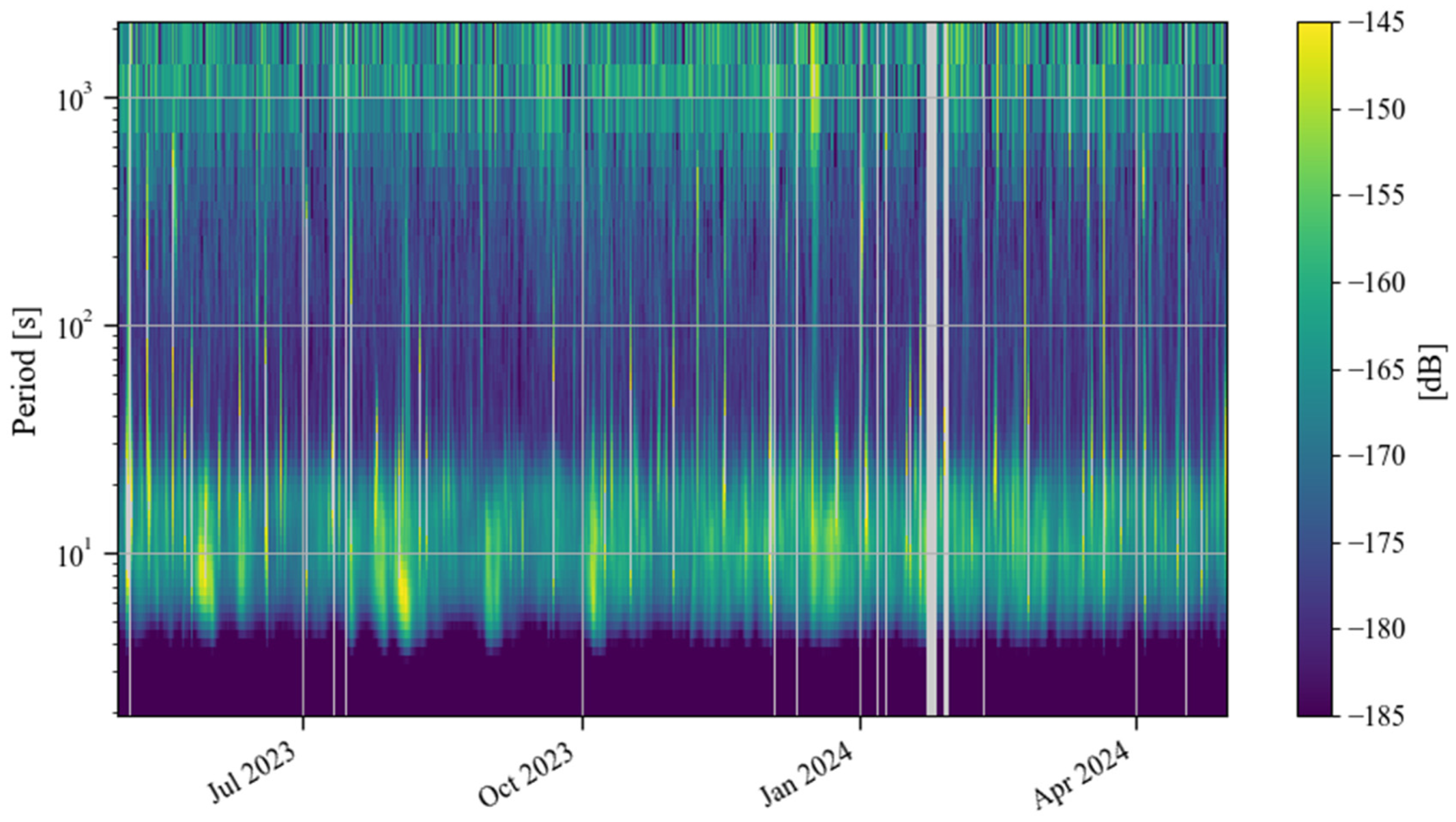
3. Results
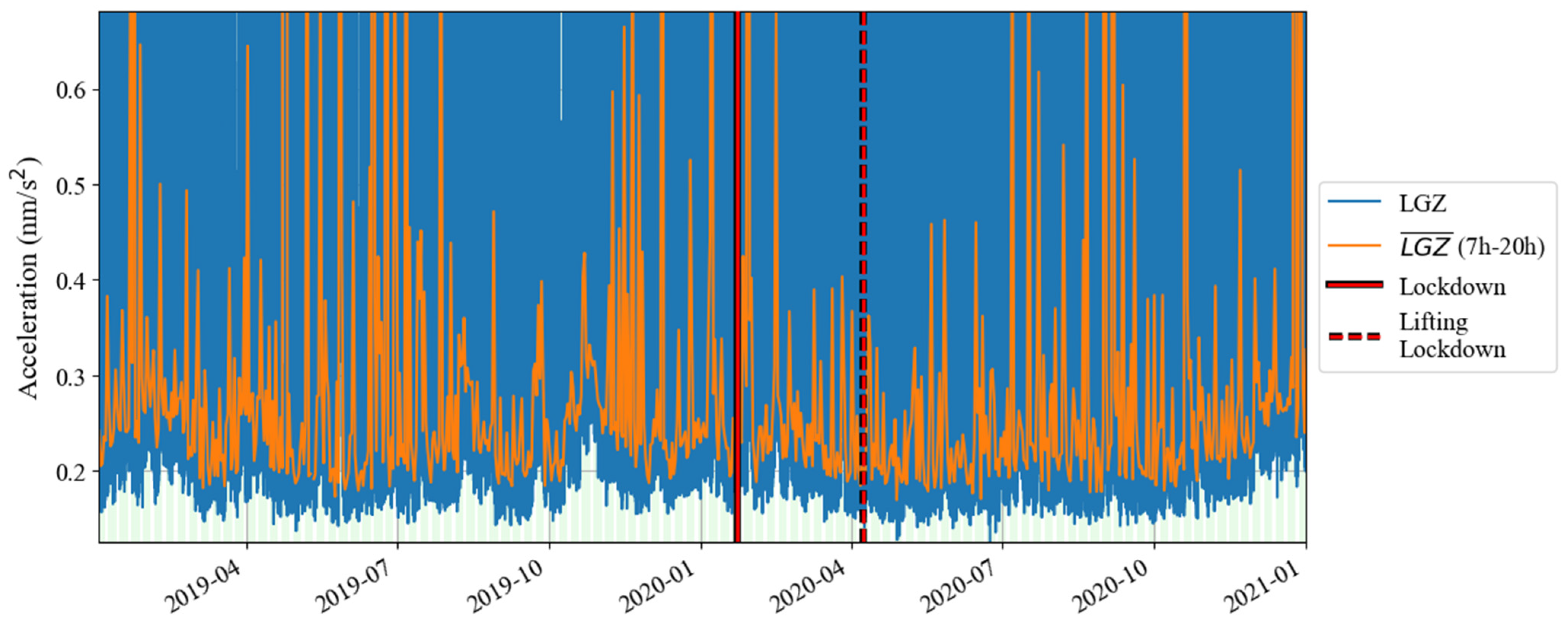
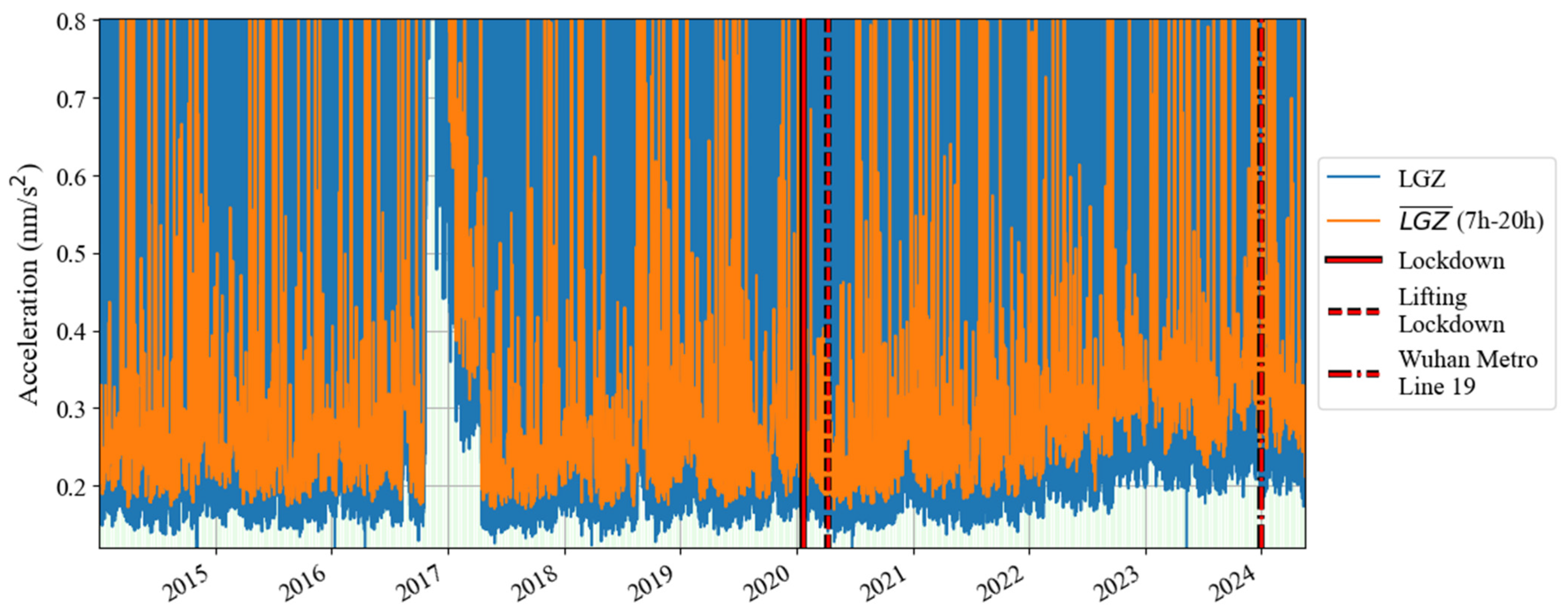
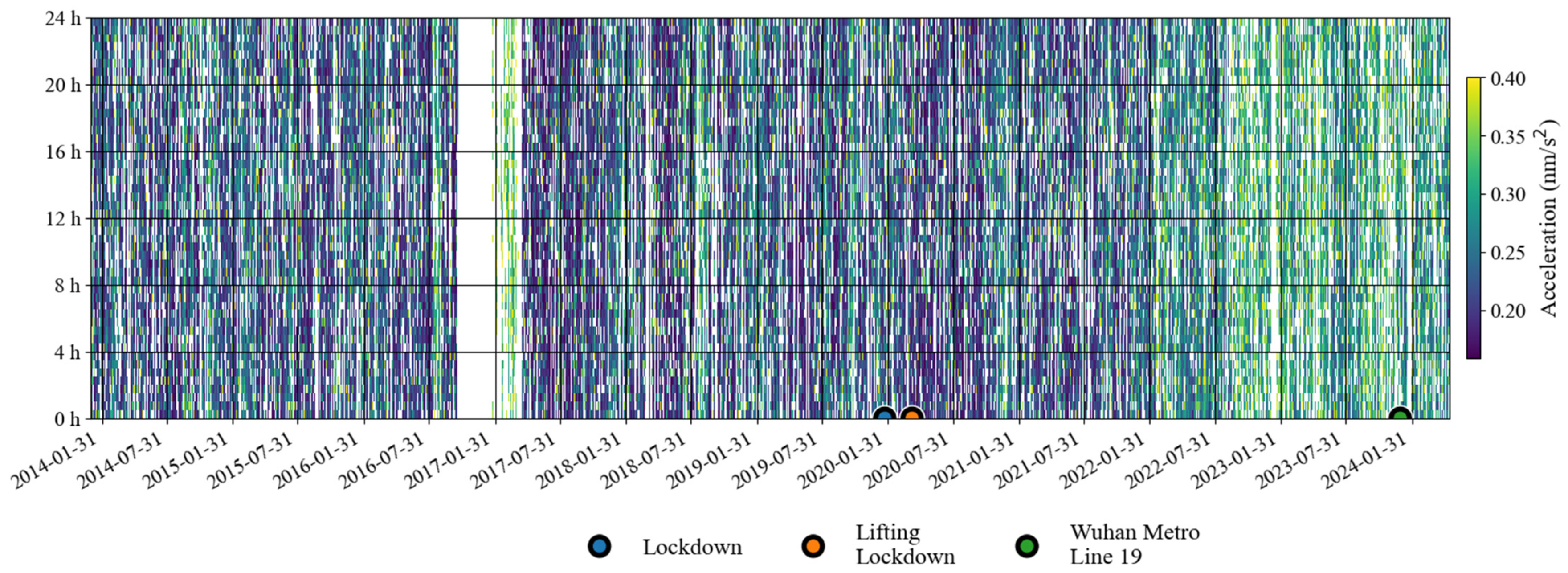
3.1. The Noise Levels Before and After the Lockdown of Wuhan in 2020
3.2. The Noise Level Before and After the Operation of Wuhan Metro Line 19
4. Discussion
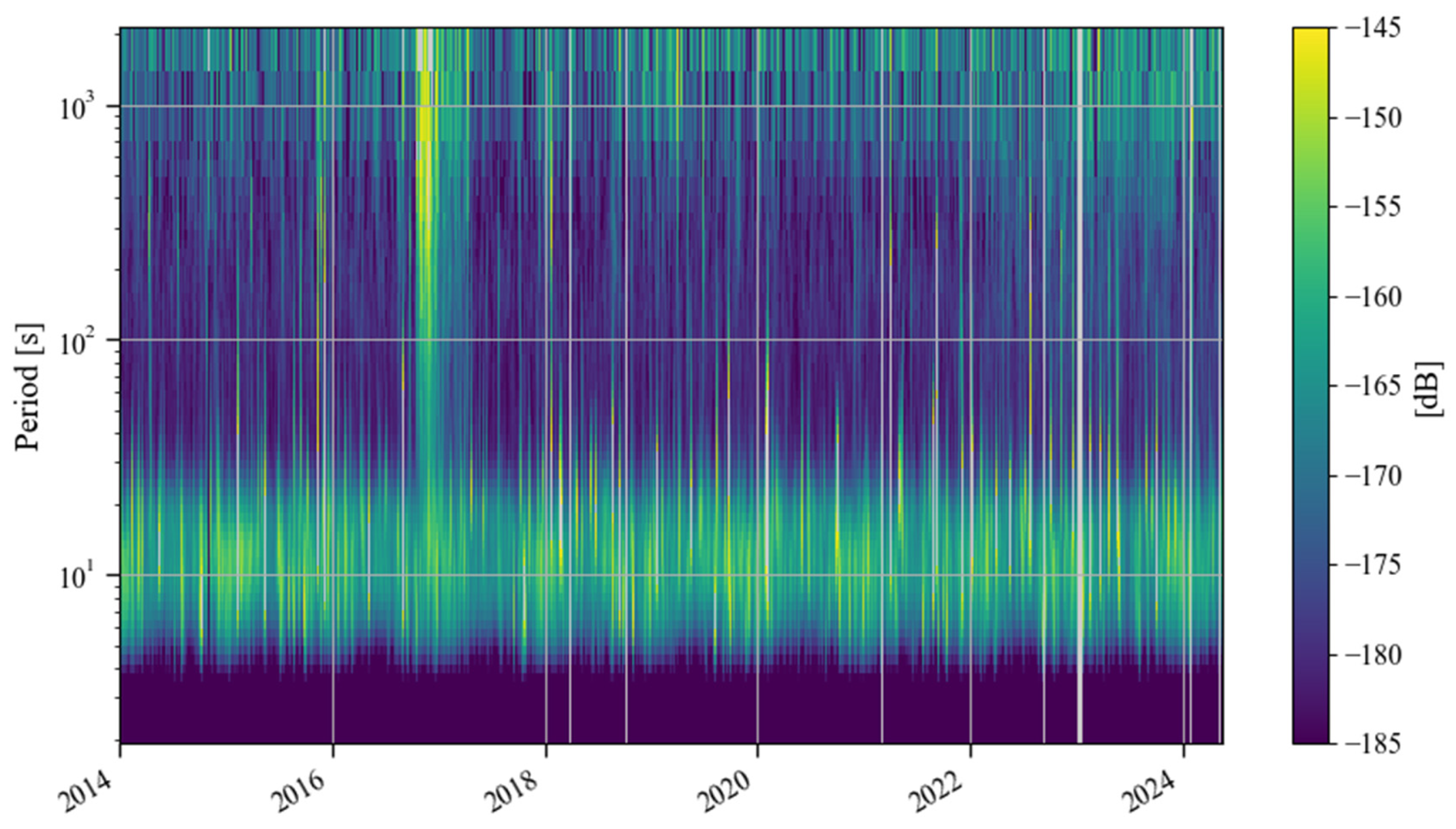
4.1. Variations in the Noise Level in the Last Decade
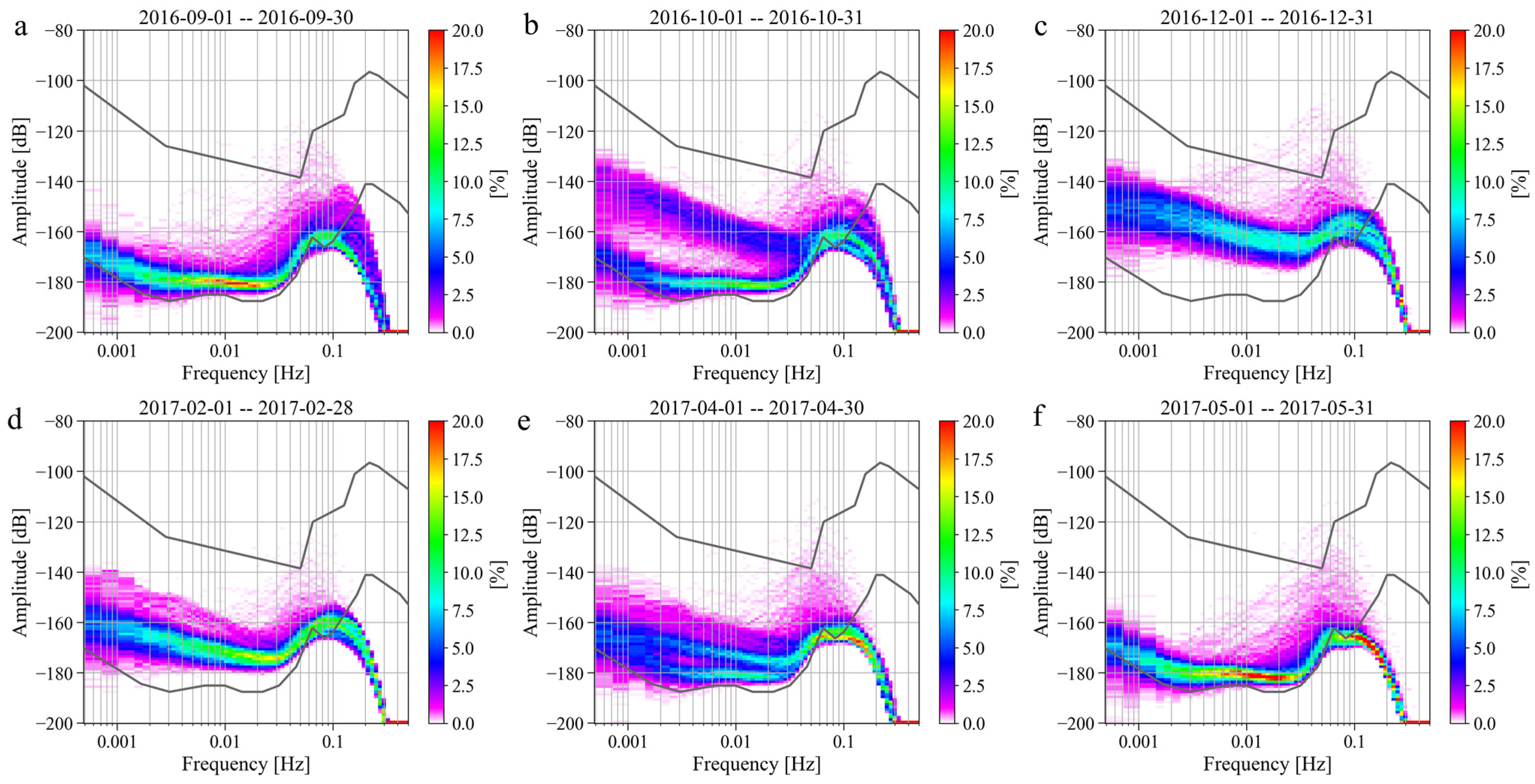
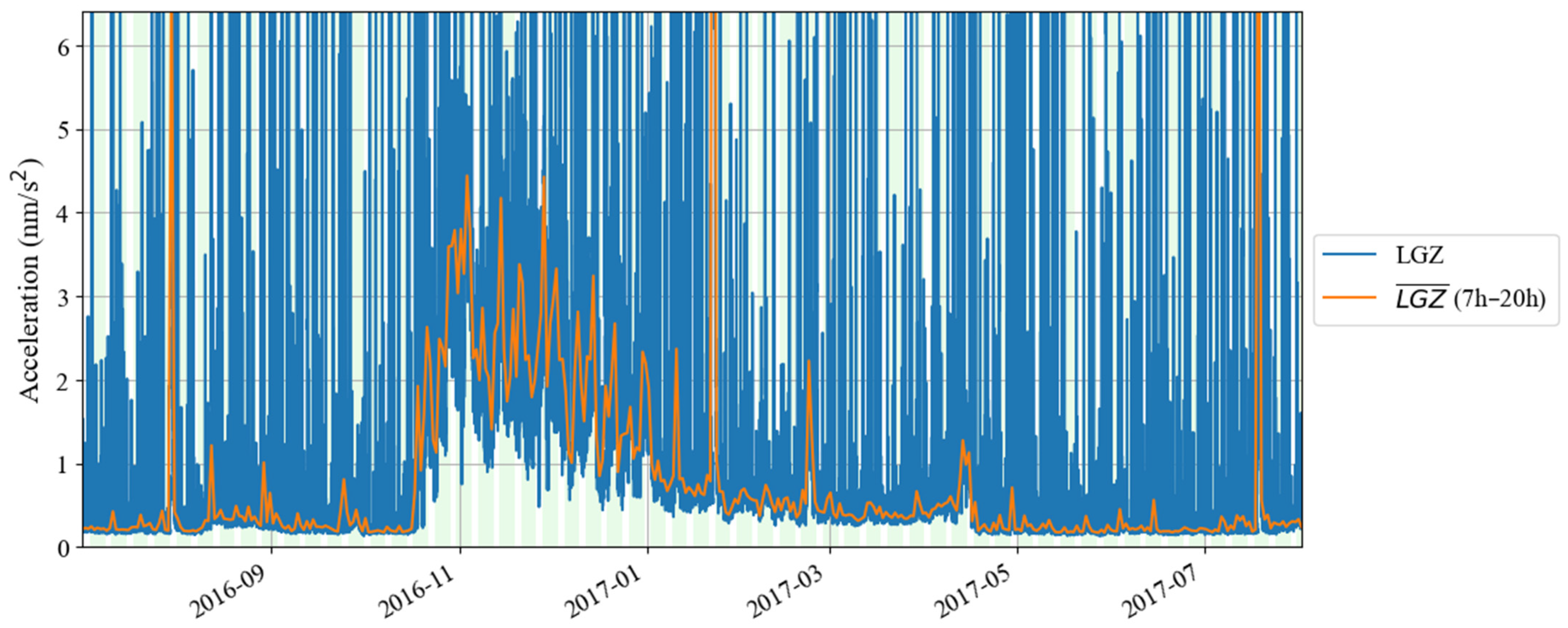
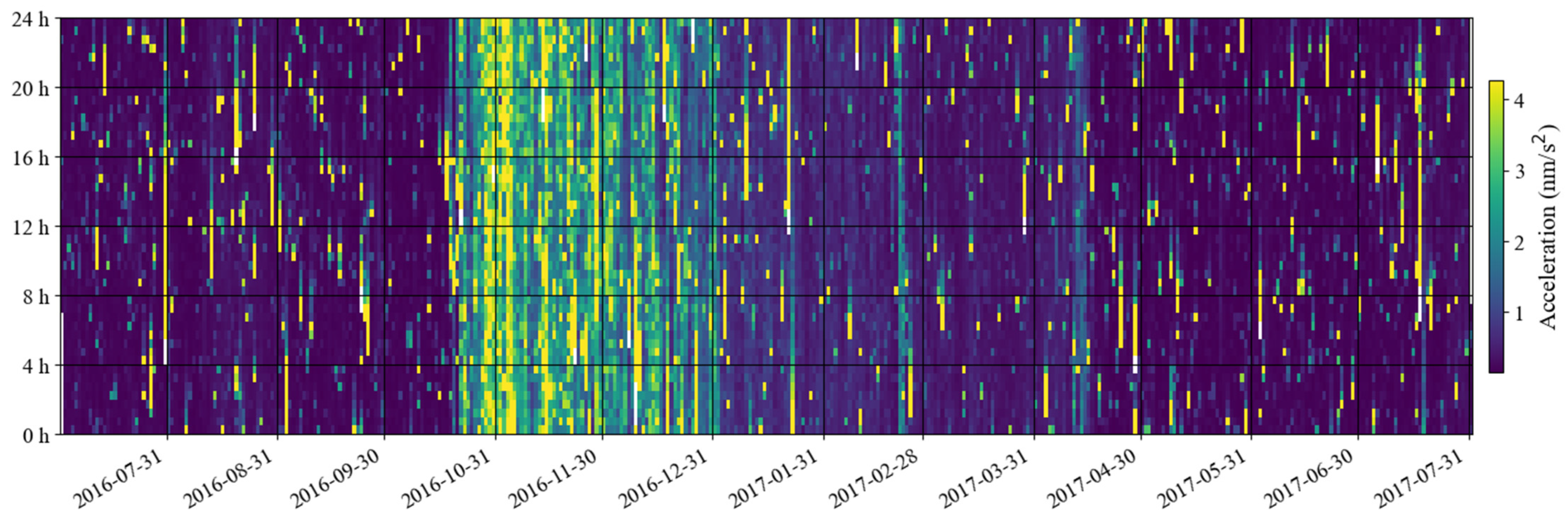
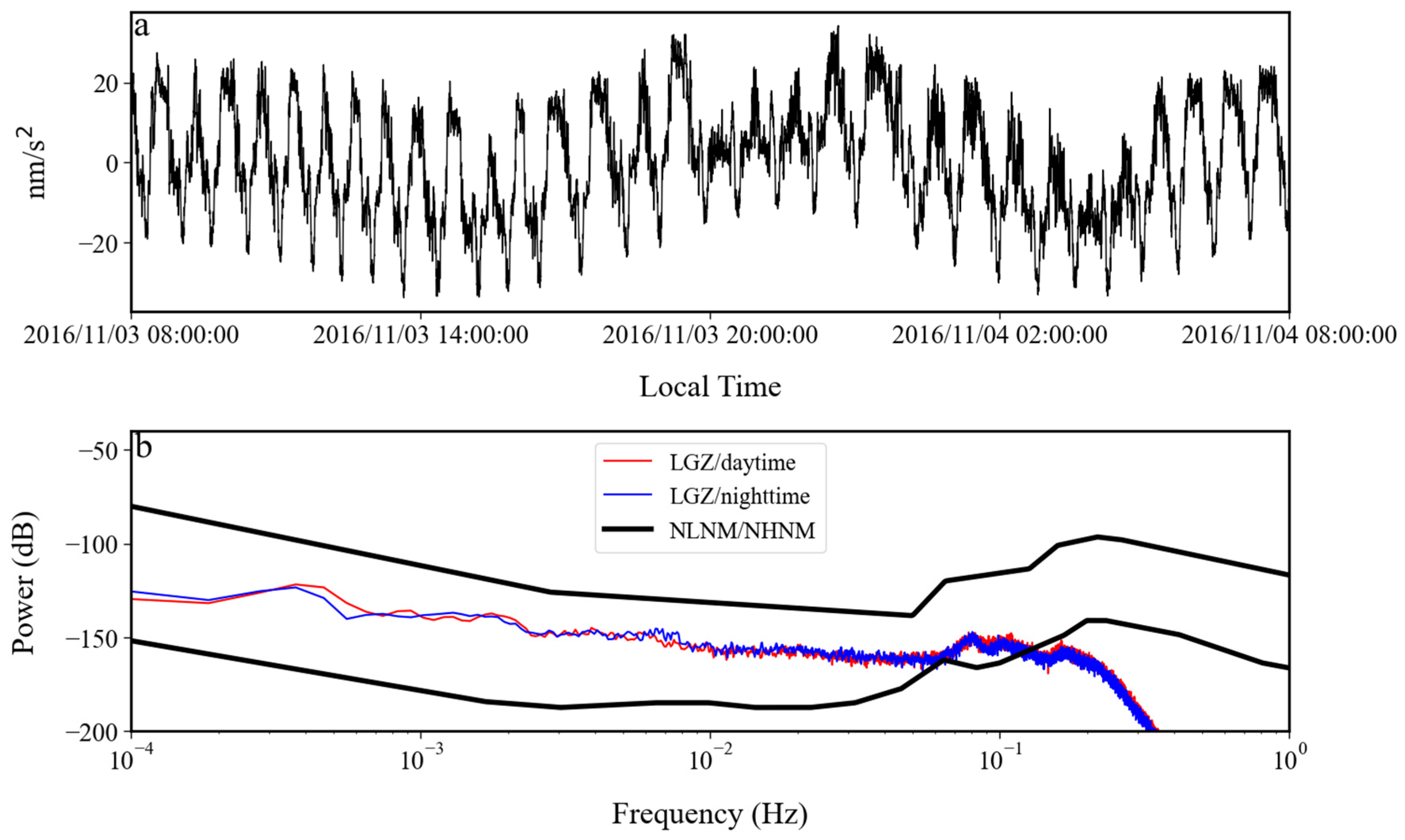
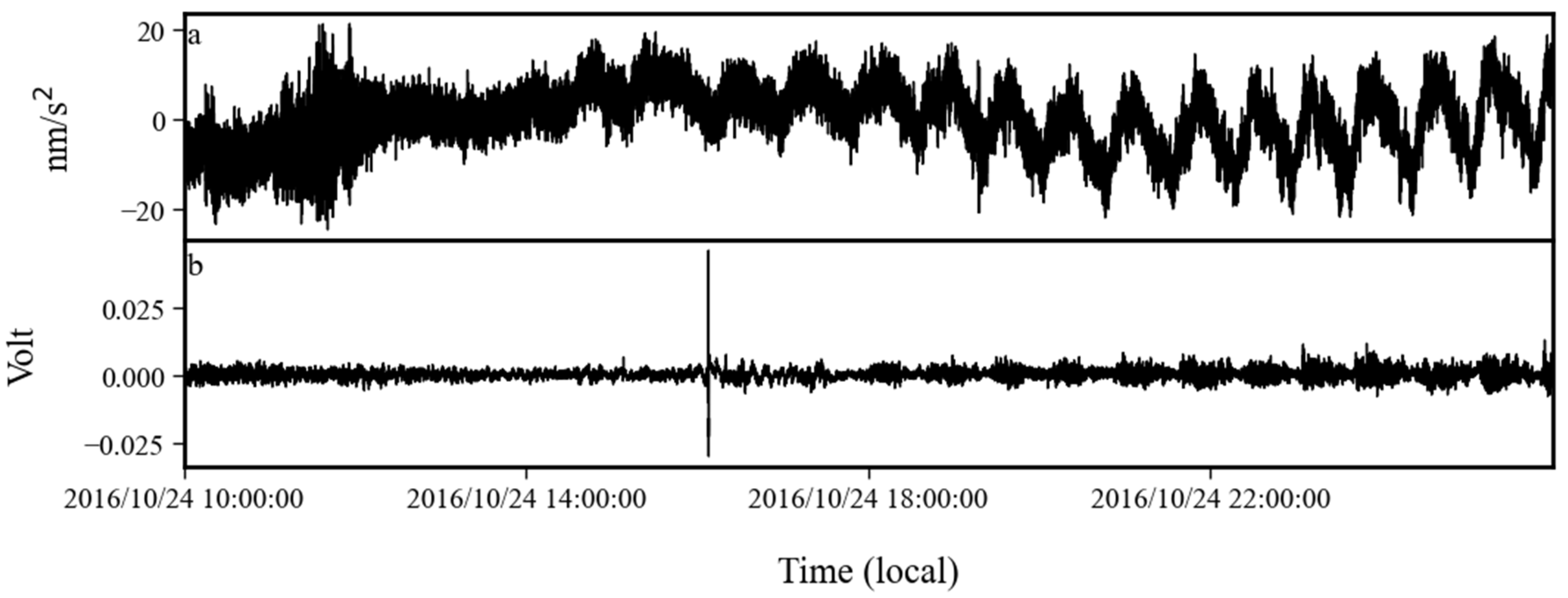
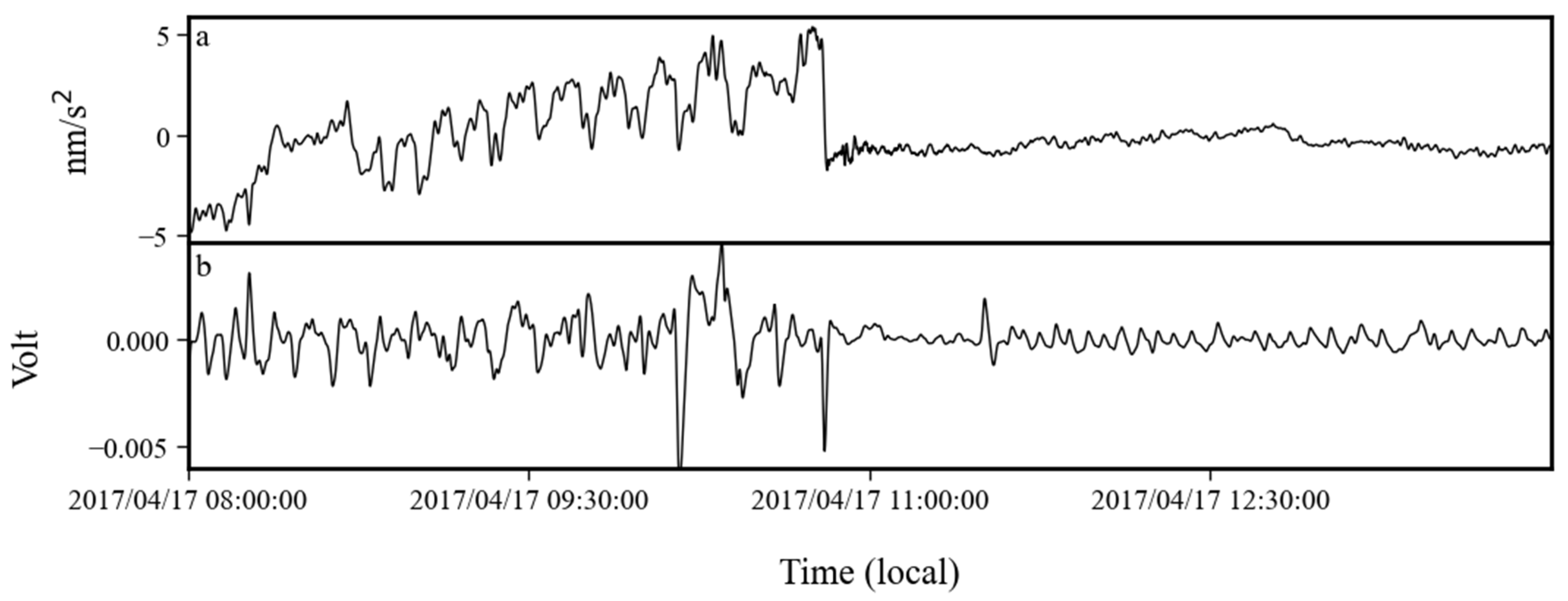
4.2. Analysis of Noise Anomalies Between 2016 and 2017
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banka, D.; Crossley, D. Noise Levels of Superconducting Gravimeters at Seismic Frequencies. Geophys. J. Int. 1999, 139, 87–97. [Google Scholar] [CrossRef]
- Rosat, S.; Hinderer, J.; Crossley, D.; Rivera, L. The Search for the Slichter Mode: Comparison of Noise Levels of Superconducting Gravimeters and Investigation of a Stacking Method. Phys. Earth Planet. Inter. Geochem. Evol. Deep Earth 2003, 140, 183–202. [Google Scholar] [CrossRef]
- Rosat, S.; Hinderer, J.; Crossley, D.; Boy, J.P. Performance of Superconducting Gravimeters from Long-Period Seismology to Tides. J. Geodyn. Varying Gravimenty GGP Vert. Crustal Motions 2004, 38, 461–476. [Google Scholar] [CrossRef]
- Rosat, S.; Hinderer, J. Noise Levels of Superconducting Gravimeters: Updated Comparison and Time Stability. Bull. Seismol. Soc. Am. 2011, 101, 1233–1241. [Google Scholar] [CrossRef]
- Rosat, S.; Hinderer, J. Limits of Detection of Gravimetric Signals on Earth. Sci. Rep. 2018, 8, 15324. [Google Scholar] [CrossRef]
- Lecocq, T.; Hicks, S.; Van Noten, K.; van Wijk, K.; Koelemeijer, P.; De Plaen, R.S.M.; Massin, F.; Hillers, G.; Anthony, R.E.; Apoloner, M.-T.; et al. Global Quieting of High-Frequency Seismic Noise Due to COVID-19 Pandemic Lockdown Measures. Science 2020, 369, 1338–1343. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Eilon, Z.; Ji, C.; Tanimoto, T. COVID-19 Societal Response Captured by Seismic Noise in China and Italy. Seismol. Res. Lett. 2020, 91, 2757–2768. [Google Scholar] [CrossRef]
- Poli, P.; Boaga, J.; Molinari, I.; Cascone, V.; Boschi, L. The 2020 Coronavirus Lockdown and Seismic Monitoring of Anthropic Activities in Northern Italy. Sci. Rep. 2020, 10, 9404. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, N.J.; Yuan, S.; Lellouch, A.; Gualtieri, L.; Lecocq, T.; Biondi, B. City-Scale Dark Fiber DAS Measurements of Infrastructure Use During the COVID-19 Pandemic. Geophys. Res. Lett. Res. Lett. 2020, 47, e2020GL089931. [Google Scholar] [CrossRef]
- Dias, F.L.; Assumpção, M.; Peixoto, P.S.; Bianchi, M.B.; Collaço, B.; Calhau, J. Using Seismic Noise Levels to Monitor Social Isolation: An Example From Rio de Janeiro, Brazil. Geophys. Res. Lett. Res. Lett. 2020, 47, e2020GL088748. [Google Scholar] [CrossRef]
- Hong, T.K.; Lee, J.; Lee, G.; Lee, J.; Park, S. Correlation between Ambient Seismic Noises and Economic Growth. Seismol. Res. Lett. 2020, 91, 2343–2354. [Google Scholar] [CrossRef]
- Diaz, J.; Schimmel, M.; Ruiz, M.; Carbonell, R. Seismometers Within Cities: A Tool to Connect Earth Sciences and Society. Front. Earth Sci. 2020, 8, 9. [Google Scholar] [CrossRef]
- Díaz, J.; Ruiz, M.; Sánchez-Pastor, P.S.; Romero, P. Urban Seismology: On the Origin of Earth Vibrations within a City. Sci. Rep. 2017, 7, 15296. [Google Scholar] [CrossRef] [PubMed]
- Sheen, D.-H.; Shin, J.S.; Kang, T.-S.; Baag, C.-E. Low Frequency Cultural Noise. Geophys. Res. Lett. Res. Lett. 2009, 36, L17314. [Google Scholar] [CrossRef]
- Kamal; Mansinha, L. A Test of the Superconducting Gravimeter as a Long-Period Seismometer. Phys. Earth Planet. Inter. 1992, 71, 52–60. [Google Scholar] [CrossRef]
- Freybourger, M.; Hinderer, J.; Trampert, J. Comparative Study of Superconducting Gravimeters and Broadband Seismometers STS-1/Z in Seismic and Subseismic Frequency Bands. Phys. Earth Planet. Inter. 1997, 101, 203–217. [Google Scholar] [CrossRef]
- Van Camp, M. Measuring Seismic Normal Modes with the GWR C021 Superconducting Gravimeter. Phys. Earth Planet. Inter. 1999, 116, 81–92. [Google Scholar] [CrossRef]
- Li, H.; Xu, J.; Chen, X.; Sun, H.; Zhang, M.; Zhang, L. Extracting Long-Period Surface Waves and Free Oscillations Using Ambient Noise Recorded by Global Distributed Superconducting Gravimeters. Seismol. Res. Lett. 2020, 91, 2234–2246. [Google Scholar] [CrossRef]
- Li, K.; Wang, L.; Ma, X.; Xie, Y.; Zhu, M. Dynamic Changes of Background Noise Level before and after COVID-19 Lockdown in Wuhan. J. Geod. Geodyn. 2023, 43, 1256–1260. [Google Scholar] [CrossRef]
- Rosat, S.; Hinderer, J.; Boy, J.P.; Littel, F.; Bernard, J.-D.; Boyer, D.; Mémin, A.; Rogister, Y.; Gaffet, S. A Two-Year Analysis of the iOSG-24 Superconducting Gravimeter at the Low Noise Underground Laboratory (LSBB URL) of Rustrel, France: Environmental Noise Estimate. J. Geodyn. 2018, 119, 1–8. [Google Scholar] [CrossRef]
- Sun, H.; Chen, X.; Wei, Z.; Zhang, M.; Zhang, G.; Ni, S.; Chu, R.; Xu, J.; Cui, X.; Xing, L. A Preliminary Study on the Ultra-Wide Band Ambient Noise of the Deep Underground Based on Observations of the Seismometer and Gravimeter. Chin. J. Geophys. 2022, 65, 4543–4554. [Google Scholar] [CrossRef]
- Rogister, Y.; Hinderer, J.; Riccardi, U.; Rosat, S. Subsurface Tidal Gravity Variation and Gravimetric Factor. Geophys. J. Int. 2024, 238, 848–859. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, J.; Xiaodong, C.; Heping, S. Long-Term Observations of Gravity Tides from a Superconducting Gravimeter at Wuhan. Chin. J. Geophys. 2014, 57, 3091–3102. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y. Absolute Gravity Measurement at Jiufeng Dynamic Geodesy Central Experiment Station. J. Geod. Geodyn. 2007, 27, 44–46. [Google Scholar] [CrossRef]
- McNamara, D.E.; Buland, R.P. Ambient Noise Levels in the Continental United States. Bull. Seismol. Soc. Am. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Peterson, J.R. Observations and Modeling of Seismic Background Noise; Open-File Report 93-322; U.S. Geological Survey: Reston, VA, USA, 1993. [CrossRef]
- Ardhuin, F.; Gualtieri, L.; Stutzmann, E. How Ocean Waves Rock the Earth: Two Mechanisms Explain Microseisms with Periods 3 to 300 s. Geophys. Res. Lett. 2015, 42, 765–772. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Jeffreys, H. A Theory of the Origin of Microseisms. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1950, 243, 1–35. [Google Scholar] [CrossRef]
- Hasselmann, K. A Statistical Analysis of the Generation of Microseisms. Rev. Geophys. 1963, 1, 177–210. [Google Scholar] [CrossRef]
- Ardhuin, F. Large-Scale Forces Under Surface Gravity Waves at a Wavy Bottom: A Mechanism for the Generation of Primary Microseisms. Geophys. Res. Lett. 2018, 45, 8173–8181. [Google Scholar] [CrossRef]
- Ardhuin, F.; Herbers, T.H.C. Noise Generation in the Solid Earth, Oceans and Atmosphere, from Nonlinear Interacting Surface Gravity Waves in Finite Depth. J. Fluid Mech. 2013, 716, 316–348. [Google Scholar] [CrossRef]
- Ardhuin, F.; Stutzmann, E.; Schimmel, M.; Mangeney, A. Ocean Wave Sources of Seismic Noise. J. Geophys. Res. 2011, 116, C09004. [Google Scholar] [CrossRef]
- Fukao, Y.; Nishida, K.; Kobayashi, N. Seafloor Topography, Ocean Infragravity Waves, and Background Love and Rayleigh Waves. J. Geophys. Res. 2010, 115, 2009JB006678. [Google Scholar] [CrossRef]
- Saito, T. Love-Wave Excitation Due to the Interaction between a Propagating Ocean Wave and the Sea-Bottom Topography: Ocean Wave Exciting Love Wave. Geophys. J. Int. 2010, 182, 1515–1523. [Google Scholar] [CrossRef]
- Kanamori, H.; Mori, J. Harmonic Excitation of Mantle Rayleigh Waves by the 1991 Eruption of Mount Pinatubo, Philippines. Geophys. Res. Lett. 1992, 19, 721–724. [Google Scholar] [CrossRef]
- Widmer, R.; Zürn, W. Bichromatic Excitation of Long-period Rayleigh and Air Waves by the Mount Pinatubo and El Chichon Volcanic Eruptions. Geophys. Res. Lett. 1992, 19, 765–768. [Google Scholar] [CrossRef]
- Ringler, A.T.; Anthony, R.E.; Aster, R.C.; Taira, T.; Shiro, B.R.; Wilson, D.C.; De Angelis, S.; Ebeling, C.; Haney, M.; Matoza, R.S.; et al. The Global Seismographic Network Reveals Atmospherically Coupled Normal Modes Excited by the 2022 Hunga Tonga Eruption. Geophys. J. Int. 2022, 232, 2160–2174. [Google Scholar] [CrossRef]
- Tanimoto, T. Continuous Free Oscillations: Atmosphere-Solid Earth Coupling. Annu. Rev. Earth Planet. Sci. 2001, 29, 563–584. [Google Scholar] [CrossRef]
- Nishida, K. Ambient Seismic Wave Field. Proc. Jpn. Academy. Ser. B Phys. Biol. Sci. 2017, 93, 423–448. [Google Scholar] [CrossRef]





| Data Gaps |
|---|
| 2018-03-29T10:22:32 to 2018-04-04T04:41:58 |
| 2018-10-07T04:49:59 to 2018-10-11T12:17:00 |
| 2023-01-06T13:32:40 to 2023-01-16T08:46:00 |
| 2023-07-11T12:25:59 to 2023-07-12T00:00:00 |
| 2023-07-15T09:19:59 to 2023-07-16T00:00:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, X.; Zhang, M.; Niu, X.; Xu, J.; Sun, H. Noise Variation Characteristics of the Superconducting Gravimeter at Jiufeng Station in Wuhan (China). Sensors 2024, 24, 7446. https://doi.org/10.3390/s24237446
Li H, Chen X, Zhang M, Niu X, Xu J, Sun H. Noise Variation Characteristics of the Superconducting Gravimeter at Jiufeng Station in Wuhan (China). Sensors. 2024; 24(23):7446. https://doi.org/10.3390/s24237446
Chicago/Turabian StyleLi, Hang, Xiaodong Chen, Miaomiao Zhang, Xiaowei Niu, Jianqiao Xu, and Heping Sun. 2024. "Noise Variation Characteristics of the Superconducting Gravimeter at Jiufeng Station in Wuhan (China)" Sensors 24, no. 23: 7446. https://doi.org/10.3390/s24237446
APA StyleLi, H., Chen, X., Zhang, M., Niu, X., Xu, J., & Sun, H. (2024). Noise Variation Characteristics of the Superconducting Gravimeter at Jiufeng Station in Wuhan (China). Sensors, 24(23), 7446. https://doi.org/10.3390/s24237446






