Fano Resonance-Associated Plasmonic Circular Dichroism in a Multiple-Dipole Interaction Born–Kuhn Model
Abstract
:1. Introduction
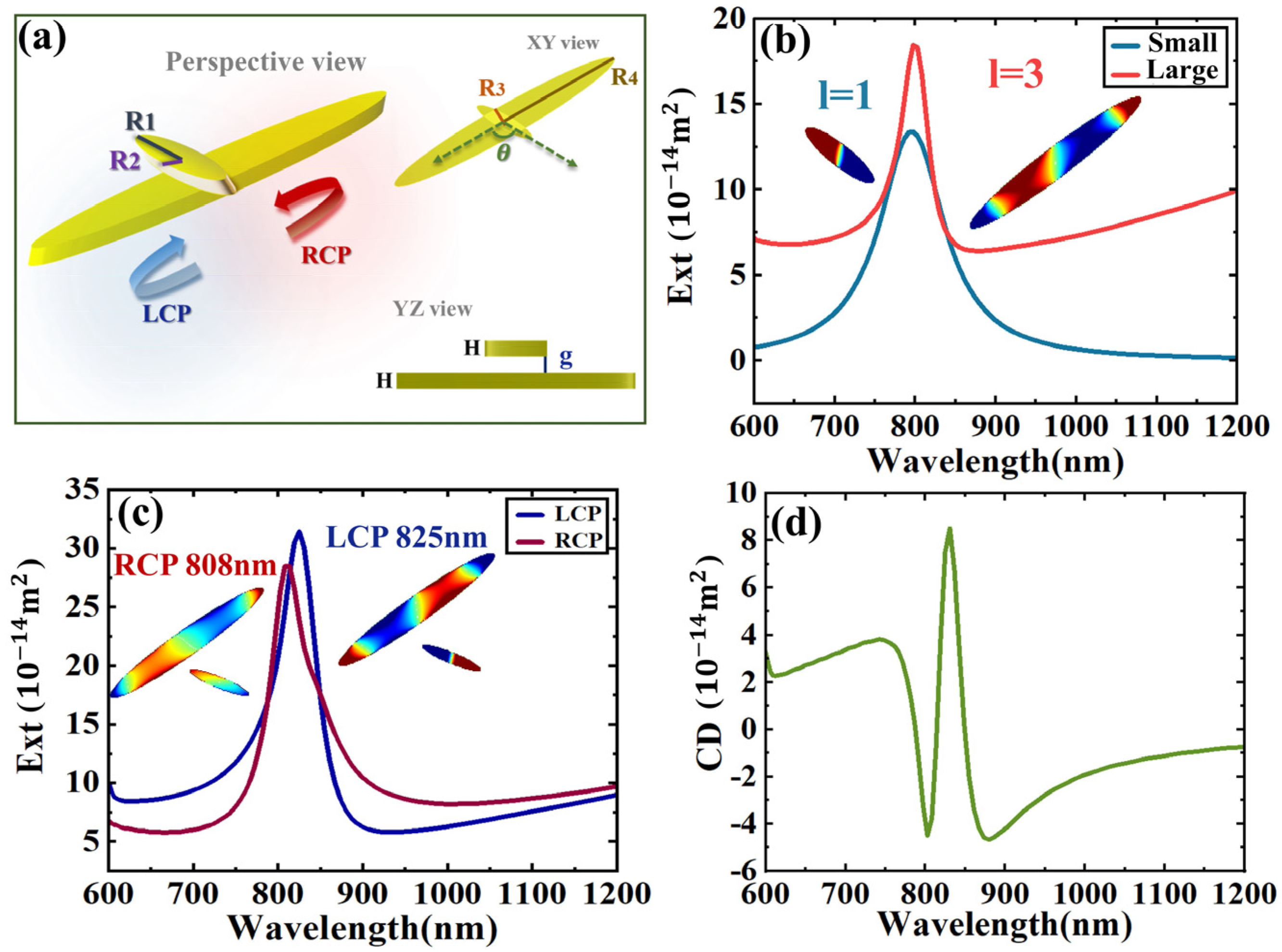
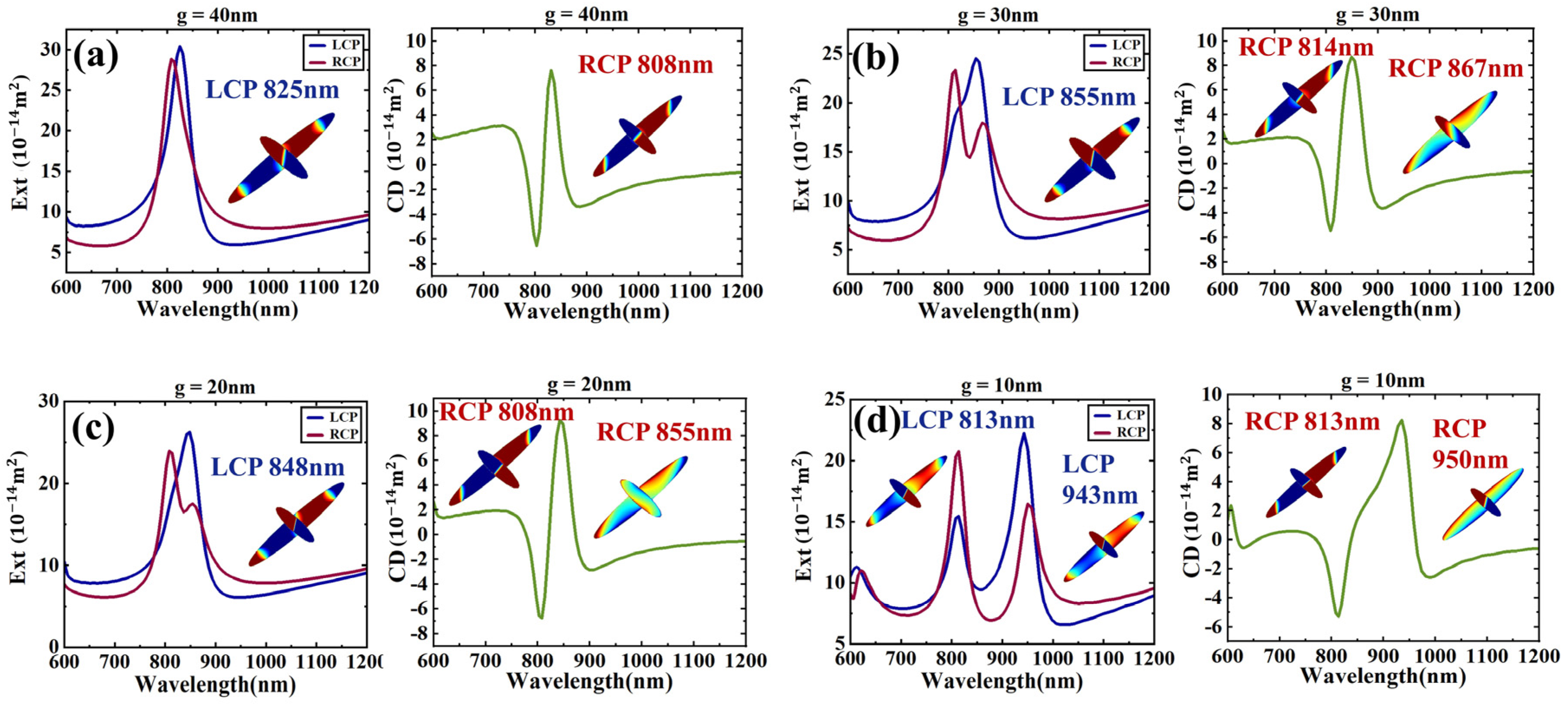
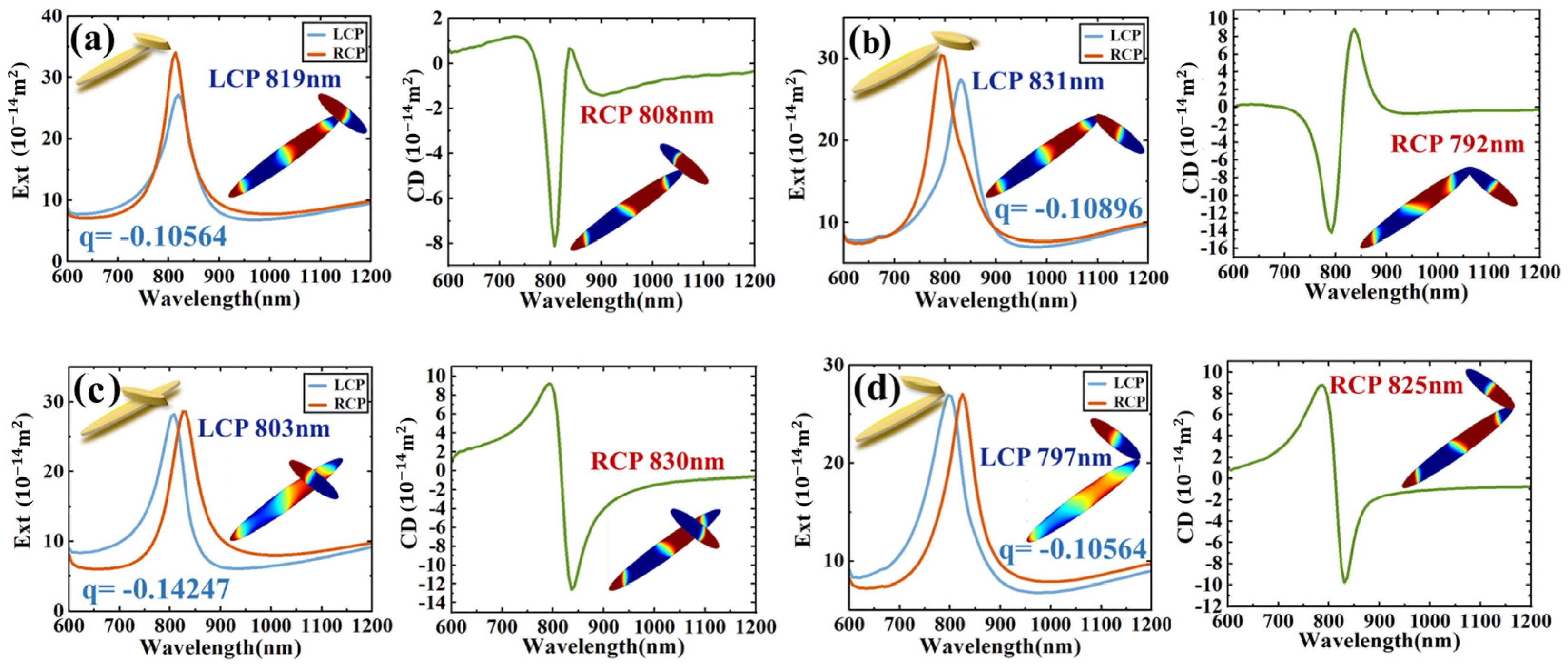
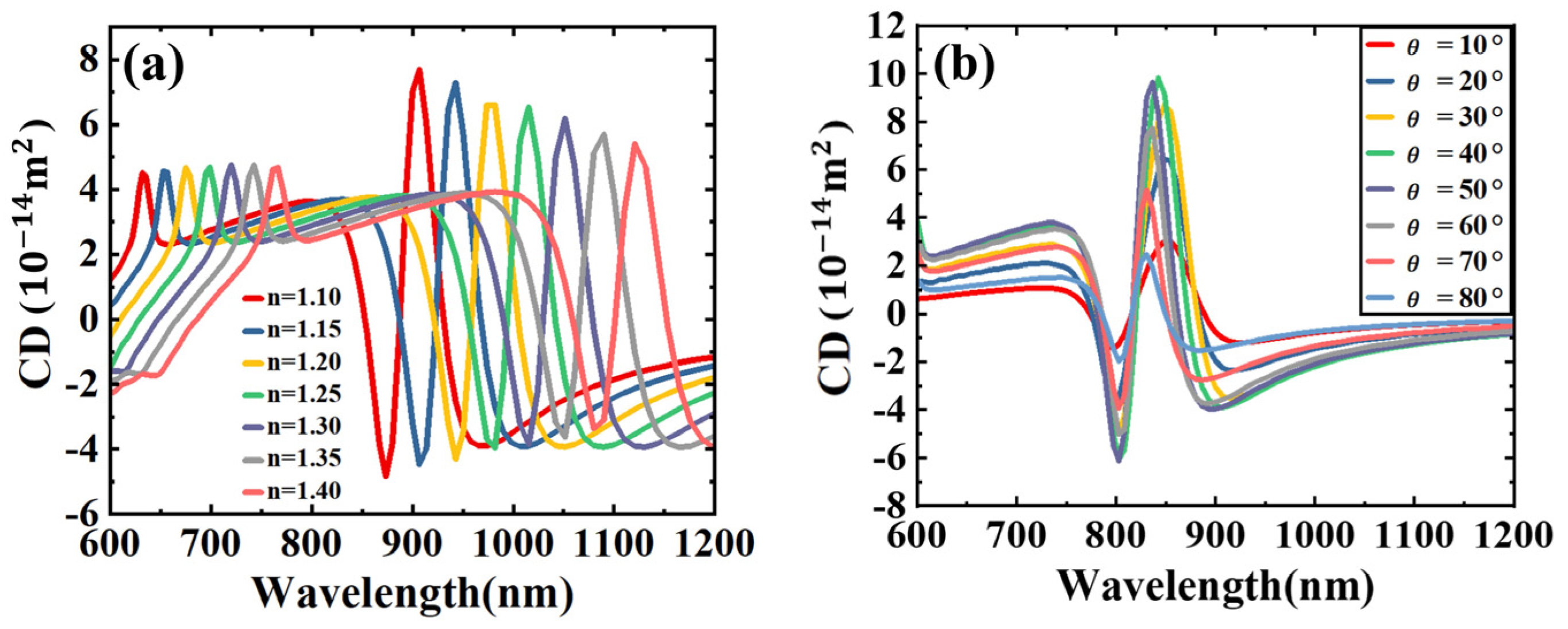
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barron, L.D. Molecular Light Scattering and Optical Activity, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Pu, J.; Wang, H.; Huang, C.; Bo, C.; Gong, B.; Ou, J. Progress of molecular imprinting technique for enantioseparation of chiral drugs in recent ten years. J. Chromatogr. A 2022, 1668, 462914. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Wang, J.H.; Wu, J.; Liu, J.; Chen, X.L.; Liu, L.M. Asymmetric assembly of high-value alpha-functionalized organic acids using a biocatalytic chiral-group-resetting process. Nat. Commun. 2018, 9, 3818. [Google Scholar] [CrossRef] [PubMed]
- Rey-Tarrio, F.; Quinoa, E.; Fernandez, G.; Freire, F. Multi-chiral materials comprising metallosupramolecular and covalent helical polymers containing five axial motifs within a helix. Nat. Commun. 2023, 14, 3348. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.T.; Besteiro, L.V.; Wang, Z.; Govorov, A.O. Plasmonic Chirality and Circular Dichroism in Bioassembled and Nonbiological Systems: Theoretical Background and Recent Progress. Adv. Mater. 2020, 32, e1801790. [Google Scholar] [CrossRef]
- Garcia-Guirado, J.; Svedendahl, M.; Puigdollers, J.; Quidant, R. Enhanced Chiral Sensing with Dielectric Nanoresonators. Nano Lett. 2020, 20, 585–591. [Google Scholar] [CrossRef]
- Merg, A.D.; Boatz, J.C.; Mandal, A.; Zhao, G.; Mokashi-Punekar, S.; Liu, C.; Wang, X.; Zhang, P.; van der Wel, P.C.A.; Rosi, N.L. Peptide-Directed Assembly of Single-Helical Gold Nanoparticle Superstructures Exhibiting Intense Chiroptical Activity. J. Am. Chem. Soc. 2016, 138, 13655–13663. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold Helix Photonic Metamaterial as Broadband Circular Polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Wozniak, P.; De Leon, I.; Hoflich, K.; Haverkamp, C.; Christiansen, S.; Leuchs, G.; Banzer, P. Chiroptical response of a single plasmonic nanohelix. Opt. Express 2018, 26, 19275–19293. [Google Scholar] [CrossRef]
- Wang, M.; Huang, Z.; Salut, R.; Suarez, M.A.; Lu, H.; Martin, N.; Grosjean, T. Plasmonic Helical Nanoantenna As a Converter between Longitudinal Fields and Circularly Polarized Waves. Nano Lett. 2021, 21, 3410–3417. [Google Scholar] [CrossRef]
- Bochenkov, V.E.; Sutherland, D.S. Chiral plasmonic nanocrescents: Large-area fabrication and optical properties. Opt. Express 2018, 26, 27101–27108. [Google Scholar] [CrossRef]
- Goerlitzer, E.S.A.; Mohammadi, R.; Nechayev, S.; Banzer, P.; Vogel, N. Large-Area 3D Plasmonic Crescents with Tunable Chirality. Adv. Opt. Mater. 2019, 7, 1801770. [Google Scholar] [CrossRef]
- Stevenson, P.R.; Du, M.; Cherqui, C.; Bourgeois, M.R.; Rodriguez, K.; Neff, J.R.; Abreu, E.; Meiler, I.M.; Tamma, V.A.; Apkarian, V.A.; et al. Active Plasmonics and Active Chiral Plasmonics through Orientation-Dependent Multipolar Interactions. ACS Nano 2020, 14, 11518–11532. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, Y.; Chui, K.K.; Zheng, J.; Ma, Y.; Liu, D.; Huang, Z.; Lei, D.; Wang, J. Synthesis of Bitten Gold Nanoparticles with Single-Particle Chiroptical Responses. Small 2023, 19, e2301476. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Nie, Y.; Cheng, Z.Z.; Gong, R.Z. Dual-band Circular Polarizer and Linear Polarization Transformer Based on Twisted Split-Ring Structure Asymmetric Chiral Metamaterial. Prog. Electromagn. Res. 2014, 145, 263–272. [Google Scholar] [CrossRef]
- Zhao, Y.; Engheta, N.; Alù, A. Homogenization of plasmonic metasurfaces modeled as transmission-line loads. Metamaterials 2011, 5, 90–96. [Google Scholar] [CrossRef]
- Karimullah, A.S.; Jack, C.; Tullius, R.; Rotello, V.M.; Cooke, G.; Gadegaard, N.; Barron, L.D.; Kadodwala, M. Disposable Plasmonics: Plastic Templated Plasmonic Metamaterials with Tunable Chirality. Adv. Mater. 2015, 27, 5610–5616. [Google Scholar] [CrossRef]
- Yin, X.; Schaferling, M.; Michel, A.K.; Tittl, A.; Wuttig, M.; Taubner, T.; Giessen, H. Active Chiral Plasmonics. Nano Lett. 2015, 15, 4255–4260. [Google Scholar] [CrossRef]
- Zhao, S.X.; Zhang, W. Plasmonic chirality of one-dimensional arrays of twisted nanorod dimers: The cooperation of local structure and collective effect. Opt. Express 2019, 27, 38614–38623. [Google Scholar] [CrossRef]
- Zhao, S.; Shao, L.; Wang, J.; Lin, H.-Q.; Zhang, W. Chirality-selective transparency induced by lattice resonance in bilayer metasurfaces. Photonics Res. 2021, 9, 484–493. [Google Scholar] [CrossRef]
- Ohnoutek, L.; Cho, N.H.; Allen Murphy, A.W.; Kim, H.; Răsădean, D.M.; Pantoş, G.D.; Nam, K.T.; Valev, V.K. Single Nanoparticle Chiroptics in a Liquid: Optical Activity in Hyper-Rayleigh Scattering from Au Helicoids. Nano Lett. 2020, 20, 5792–5798. [Google Scholar] [CrossRef]
- Bainova, P.; Joly, J.-P.; Urbanova, M.; Votkina, D.; Erzina, M.; Vokata, B.; Trelin, A.; Fitl, P.; Audran, G.; Vanthuyne, N.; et al. Plasmon-Assisted Chemistry Using Chiral Gold Helicoids: Toward Asymmetric Organic Catalysis. ACS Catal. 2023, 13, 12859–12867. [Google Scholar] [CrossRef]
- Xu, L.; Wang, X.; Wang, W.; Sun, M.; Choi, W.J.; Kim, J.-Y.; Hao, C.; Li, S.; Qu, A.; Lu, M.; et al. Enantiomer-dependent immunological response to chiral nanoparticles. Nature 2022, 601, 366–373. [Google Scholar] [CrossRef] [PubMed]
- Ayuso, D.; Ordonez, A.F.; Decleva, P.; Ivanov, M.; Smirnova, O. Enantio-sensitive unidirectional light bending. Nat. Commun. 2021, 12, 3951. [Google Scholar] [CrossRef] [PubMed]
- Roller, E.M.; Khorashad, L.K.; Fedoruk, M.; Schreiber, R.; Govorov, A.O.; Liedl, T. DNA-assembled nanoparticle rings exhibit electric and magnetic resonances at visible frequencies. Nano Lett. 2015, 15, 1368–1373. [Google Scholar] [CrossRef]
- Lan, X.; Wang, Q. Self-Assembly of Chiral Plasmonic Nanostructures. Adv. Mater. 2016, 28, 10499–10507. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, L.; Jiang, S.; Han, C.; Tang, P.; Yang, H.; Duan, X.; Liu, N.; Yan, H.; Lan, X. DNA Programmable Self-Assembly of Planar, Thin-Layered Chiral Nanoparticle Superstructures with Complex Two-Dimensional Patterns. ACS Nano 2021, 15, 16664–16672. [Google Scholar] [CrossRef]
- Li, C.; He, T.; Yang, X.; Feng, C.; Zhang, Z.; Zhu, J.; Dong, S.; Shi, Y.; Wei, Z.; Jiao, H.; et al. Enhanced Circular Dichroism for Achiral Sensing Based on a DNA-Origami-Empowered Anapole Metasurface. Nano Lett. 2024, 24, 9451–9458. [Google Scholar] [CrossRef]
- Zhu, G.; Wei, H.; Sun, Z.; Liu, J.; Wei, X.; Liang, Y.; Peng, W.; Fang, Y. Quantitative analysis of circular dichroism at higher-order resonance of extrinsic plasmonic chiral nanostructures using multipole decomposition combined with the optical theorem. New J. Phys. 2023, 25, 103044. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, Z.; Liu, J.; Fang, Y. Multipole Analysis of the Extinction Cross Section and Circular Dichroism of Chiral Metamolecules with Optical Theorem. Adv. Opt. Mater. 2023, 11, 2202677. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, H.; Tang, J.; Meng, S.; Xu, H.; Ding, T. Plasmon-Directed On-Wire Growth of Branched Silver Nanowires with Chiroptic Activity. ACS Nano 2021, 15, 16404–16410. [Google Scholar] [CrossRef]
- Wang, S.; Ding, T. Laser-Directed Asymmetric Growth of Plasmonic Chiral Ensembles. Laser Photonics Rev. 2022, 16, 2100526. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Wang, S.; Ding, T. Polarization-directed growth of spiral nanostructures by laser direct writing with vector beams. Nat. Commun. 2023, 14, 1422. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Schaferling, M.; Metzger, B.; Giessen, H. Interpreting chiral nanophotonic spectra: The plasmonic Born-Kuhn model. Nano Lett. 2013, 13, 6238–6243. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-H.; Kim, S.-H.; Bae, M.-C. Fano resonance by dipole–hexapole coupling in a χ-shaped plasmonic nanostructure. Appl. Opt. 2015, 54, 2710–2714. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Kim, R.M.; Im, S.W.; Balamurugan, M.; Nam, K.T. Plasmonic metamaterials for chiral sensing applications. Nanoscale 2020, 12, 58–66. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Hu, L.; Huang, Y.; Fang, L.; Chen, G.; Wei, H.; Fang, Y. Fano resonance assisting plasmonic circular dichroism from nanorice heterodimers for extrinsic chirality. Sci. Rep. 2015, 5, 16069. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, W.; Zhu, G.; Ma, F.; Zhu, T.; Fang, Y. Fano Resonance-Associated Plasmonic Circular Dichroism in a Multiple-Dipole Interaction Born–Kuhn Model. Sensors 2024, 24, 7517. https://doi.org/10.3390/s24237517
Bian W, Zhu G, Ma F, Zhu T, Fang Y. Fano Resonance-Associated Plasmonic Circular Dichroism in a Multiple-Dipole Interaction Born–Kuhn Model. Sensors. 2024; 24(23):7517. https://doi.org/10.3390/s24237517
Chicago/Turabian StyleBian, Wanlu, Guodong Zhu, Fengcai Ma, Tongtong Zhu, and Yurui Fang. 2024. "Fano Resonance-Associated Plasmonic Circular Dichroism in a Multiple-Dipole Interaction Born–Kuhn Model" Sensors 24, no. 23: 7517. https://doi.org/10.3390/s24237517
APA StyleBian, W., Zhu, G., Ma, F., Zhu, T., & Fang, Y. (2024). Fano Resonance-Associated Plasmonic Circular Dichroism in a Multiple-Dipole Interaction Born–Kuhn Model. Sensors, 24(23), 7517. https://doi.org/10.3390/s24237517






