Rolling Resistance Evaluation of Pavements Using Embedded Transducers on a Semi-Trailer Suspension
Abstract
:1. Introduction
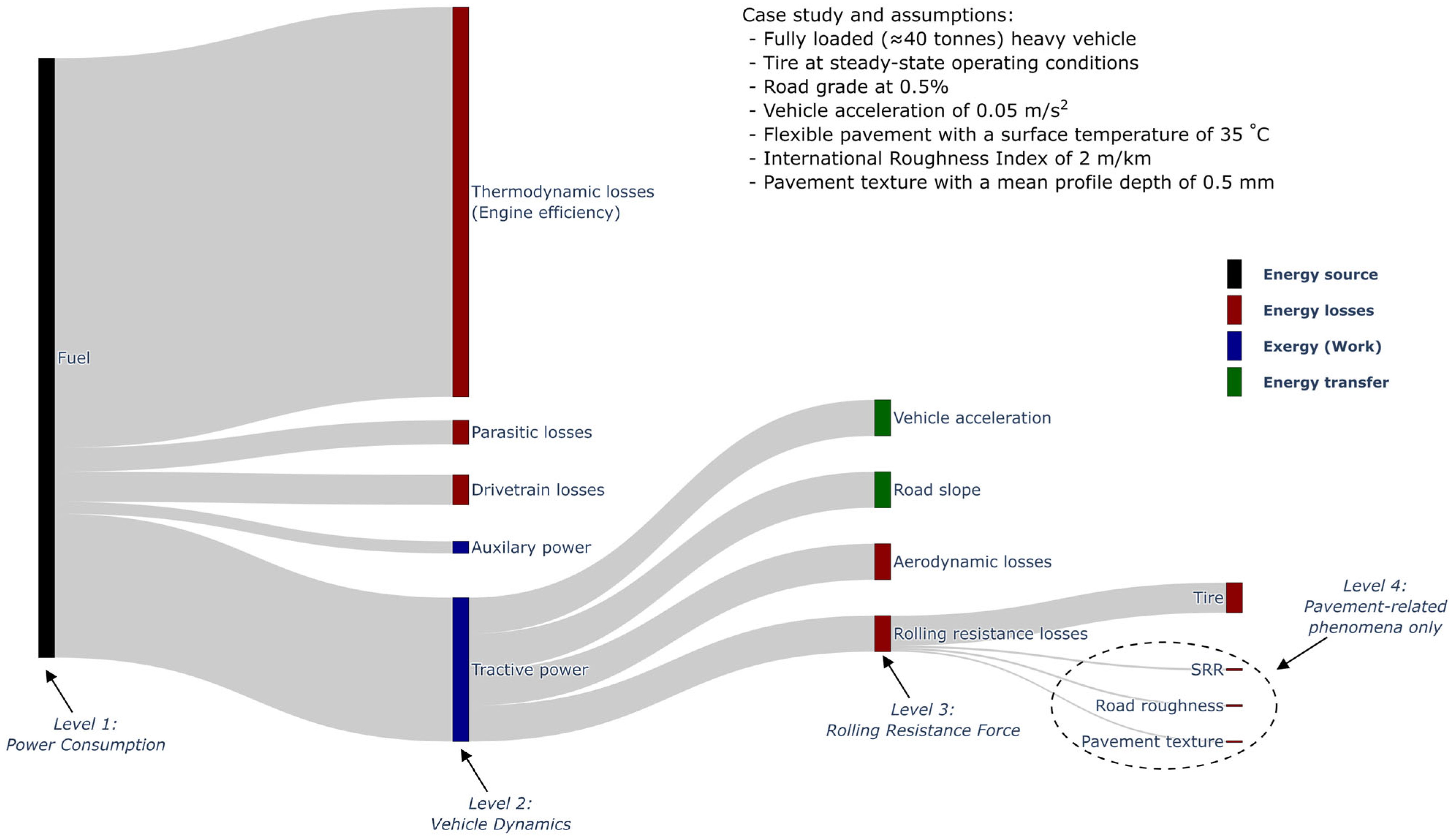
- Normalization of power consumption data to isolate the contribution of the pavement using mechanistic models (e.g., aerodynamic resistance, tire rolling resistance, road slope, etc.) and consideration for many parameters such as vehicle speed, wind conditions, and vehicle inefficiencies [17,18]. This focuses on the absolute value of the pavement’s contribution to energy consumption by emphasizing the physical interpretation
- Data mining on power consumption data using more advanced statistical and machine learning methods such as artificial neural networks, support vector regression, and random forest analysis [13,15,16]. This focuses on the statistical significance of the pavement’s contribution to energy consumption rather than emphasizing the physical interpretation.
- The pavement surface can have a significant effect on the rolling resistance coefficient, with differences of about 30% [22].
- Rolling resistance measurements performed in laboratory conditions, in accordance with ISO and SAE standards, correlate poorly with measurements performed on actual roads [35].
2. Materials and Methods
- All the tires of the heavy vehicle follow the same track (i.e., right and left). This means that they are all exposed to the same macrotexture of the pavement.
- Road roughness is typically quantified using the IRI, which is based on the simulation of a quarter-car model [38]. This means it is not common practice to consider the whole vehicle when assessing the effect of road roughness.
- Different wheels of the same heavy vehicle do not interact with each other in terms of SRR [37].
- Flexible: pavement with top layers made of bituminous materials on a granular base.
- Rigid: pavement made of jointed cement concrete slabs on which vehicles roll directly. In the dataset, all rigid pavement surfaces feature longitudinal grooving.
- Composite: pavement with top layers made of bituminous materials that were installed on an older cement-base foundation.
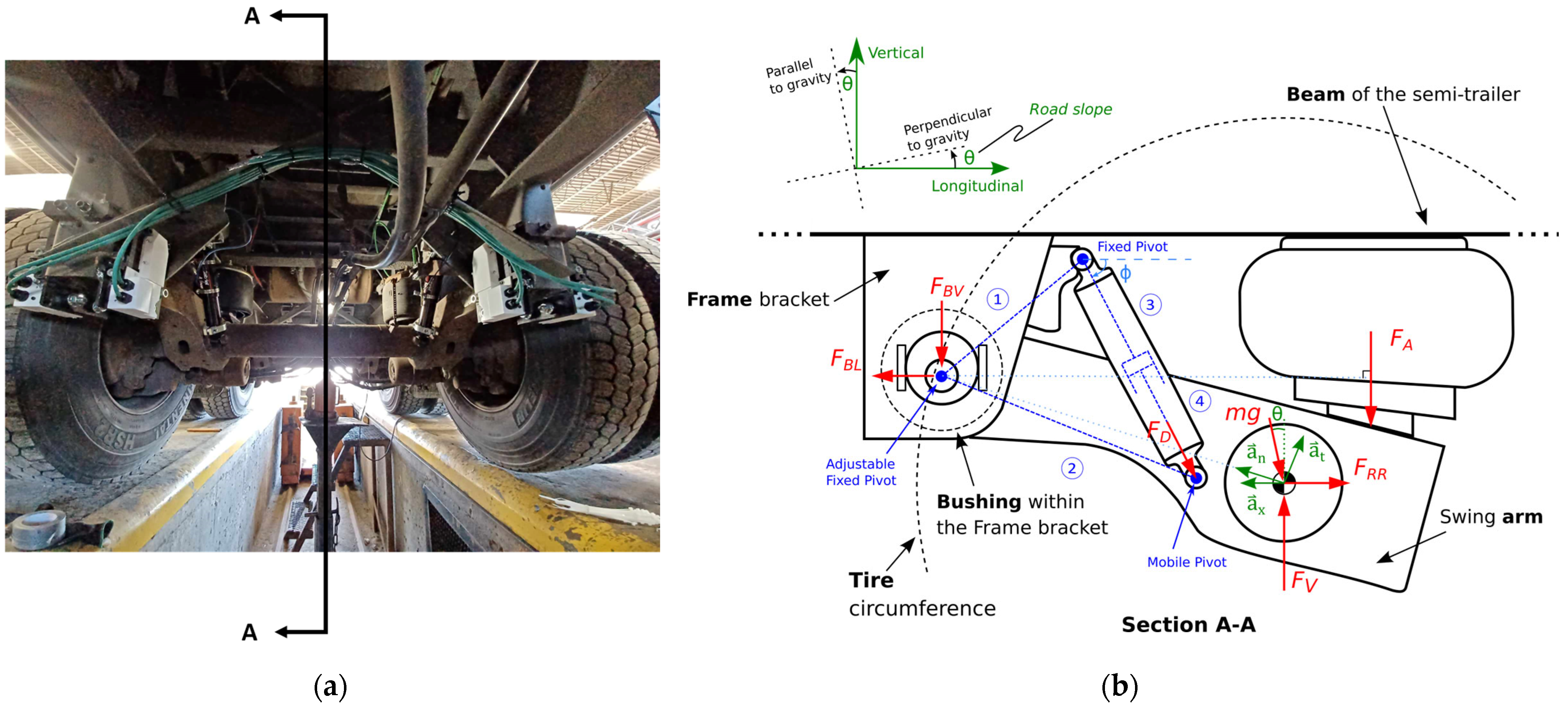
2.1. Conceptual Approach of the Measurement System
- The bushing within the frame bracket was considered rigid and represents the fixed pivot point of the suspension motion.
- The effect of the roll motion of the suspension was considered negligible, which justifies a two-dimensional model.
- The damper orientation was considered to be aligned with the vertical plane and its angle ϕ was assumed constant at 70 deg.
- The air bellow between the beam of the semi-trailer and the swing arm of the suspension was considered to only transmit a force (FA) in the vertical direction of the vehicle reference frame.
- This assumption was based on the uniform inflation pressure within the air bellow and its attachment to the beam of the semi-trailer.
- Additionally, the flexible material of the air bellow was assumed to transmit no shear forces due to its lower longitudinal stiffness compared to the bushing.
- Insensitive to power unit and power train efficiencies. As discussed in the introduction section, measuring the rolling resistance where it occurs (i.e., using a level 3 method) greatly limits the uncertainty addition as it does not depend on the power unit or the power train (e.g., level 1 method).
- Virtually insensitive to aerodynamic resistance. Since the measured forces are internal, they are not affected by the aerodynamics of the whole semi-trailer as in level 1 or 2 methods, but are influenced only by the aerodynamics of the suspension itself. The measured forces are influenced by the “fan effect” of the wheels rotating in the air [40], which can arguably be considered as part of the rolling resistance. The aerodynamic drag of the axle was assumed to be negligible, especially because the central axle was chosen.
- Low influence of road slope. The force transducers do not perceive the longitudinal gravitational force applied on the whole vehicle due to a non-zero road slope; they only measure the proportion related to the suspension mass. It was assumed that in the case of a non-zero road slope, the longitudinal gravitational force applied on the semi-trailer frame was compensated by the increase in tractive force from the tractor at the kingpin (for a constant vehicle speed). Moreover, the effect of the road slope on the weight supported by the suspension was assumed to be negligible in the context of this study. To illustrate, if a heavy vehicle travels on a positive 0.5% road slope, the longitudinal gravitational force applied on the whole heavy vehicle would be more or less the same as the total rolling resistance force, since a rolling resistance coefficient of 5 kg/tonne is a typical value [28]. This would be the effect on the measured value in a level 1 or level 2 method. However, for a 550 kg suspension [11] using the proposed level 3 method, the longitudinal force perceived by the transducers for a half-axle would be as follows:The relative significance of this bias error varies with cargo loading but would be a few percent for a loaded axle. More importantly, the bias error on the measured longitudinal force due to road slope should tend to zero if it is averaged over a longer distance with no altitude gain, since the average road slope will tend to zero as well.
- Low influence of vehicle acceleration. The vehicle acceleration perceived by the force transducers is attributable only to the suspension’s inertial resistance. For example, if a heavy vehicle increases from 0 to 100 km/h in 60 s, the vehicle acceleration would be around 0.5 m/s2, and the inertial force of the whole heavy vehicle would then be around one order of magnitude higher than the rolling resistance force during this 60s (assuming a 5 kg/tonne rolling resistance coefficient). Again, this would be the effect on the measured value in a level 1 or 2 method. However, for a 550 kg suspension [11] using the proposed level 3 method, the longitudinal force perceived by the transducers for a half-axle would be as follows:This value at high vehicle acceleration is less than the expected rolling resistance force for a loaded half-axle. This worst-case example illustrates the capacity of the measurement system to be relatively insensitive to vehicle acceleration, especially when the speed regulator is used under highway conditions.
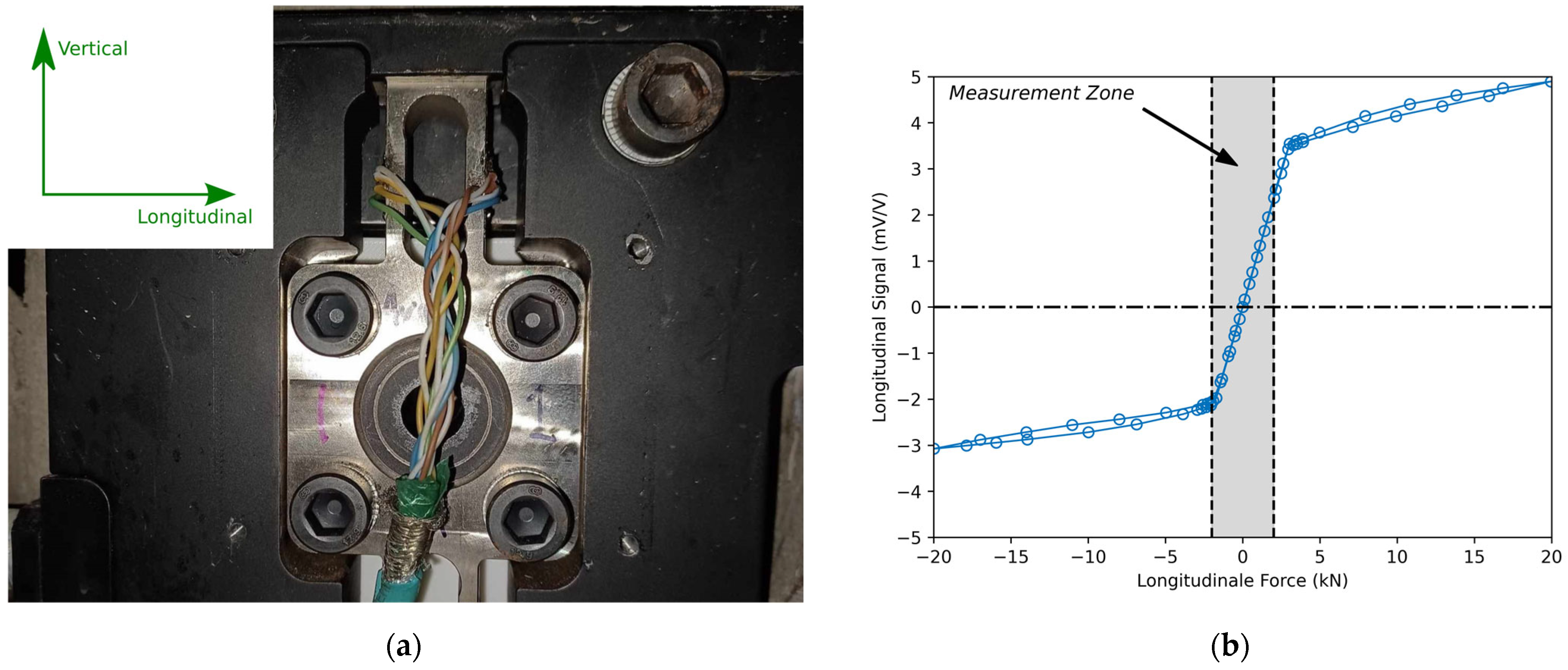
- Minimization of mechanical crosstalk. A primary technical challenge in measuring the rolling resistance under real driving conditions is the significant disparity between the vertical and longitudinal forces acting on a wheel, with the vertical force being approximately 200 times greater than the longitudinal force (assuming 5 kg/tonne of rolling resistance). This ratio, referred to as the force ratio, presents a challenge for measurements. If strain gauges are installed on a wheel and an encoder is used to estimate the longitudinal force, the resulting transducer must accurately measure and isolate a force that constitutes only 0.5% of its total load capacity, assuming the cargo load is significant enough to match the capacity of the wheel rim material. This is problematic because some commercial load cells typically exhibit a combined error (due to nonlinearity, hysteresis, repeatability, and creep) of about ±0.05% of their capacity, which represents approximately 10% of the force that needs to be measured in this case. The measurement system developed in this study effectively minimized mechanical crosstalk by leveraging two key factors: the air bellow’s inability to transmit shear forces and the placement of force transducers farther from the axle at the frame bracket rather than on the wheels or axle. This increased distance reduced the force ratio from approximately 200 to 10. Additionally, the force transducers installed at the frame bracket did not need to be axisymmetric (as is required for a wheel), allowing for higher sensitivity (and lower strength) in the longitudinal direction compared to the vertical direction, as presented in a previous study [39].
2.2. Force Measurements at the Frame Bracket
2.3. Asymmetric Damping Effect
2.4. Tire Operating Conditions
2.5. Data Acquisition and Processing
- Identification of the road segments with constant vehicle speed (i.e., 95 km/h);
- Subdivision of the road segments based on pavement types;
- Verification of the evolution of average tire temperature and road slope.
3. Results and Discussion
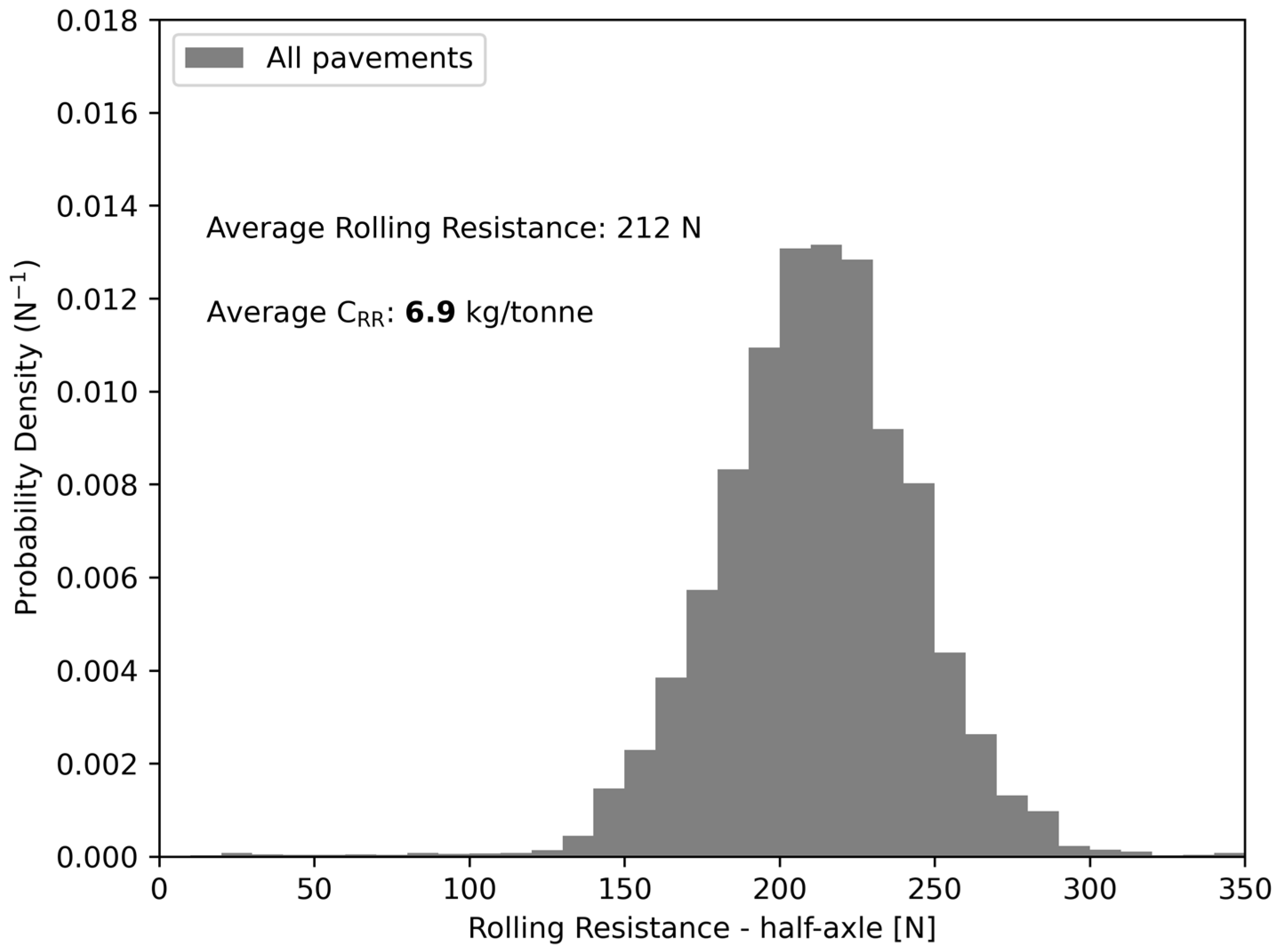
3.1. Measured Rolling Resistance
3.2. Uncertainty in the Measured Rolling Resistance Coefficient
- Nonlinearity (ε6) is the maximum deviation of the calibration curve from a straight line drawn between the minimum load and 75% of the rated capacity. This is caused by the change in geometry of the spring element under a load.
- Hysteresis (ε7) is defined as the maximum amplitude difference in a signal between the ascending and descending curve when measuring a load.
- Nonrepeatability (ε8) indicates the maximum difference between load cell signals at repeated loads under identical loading and environmental conditions. This is a random and uncorrelated error.
- Creep (ε9) refers to the change in load cell signal occurring with time under constant load and otherwise constant variables.
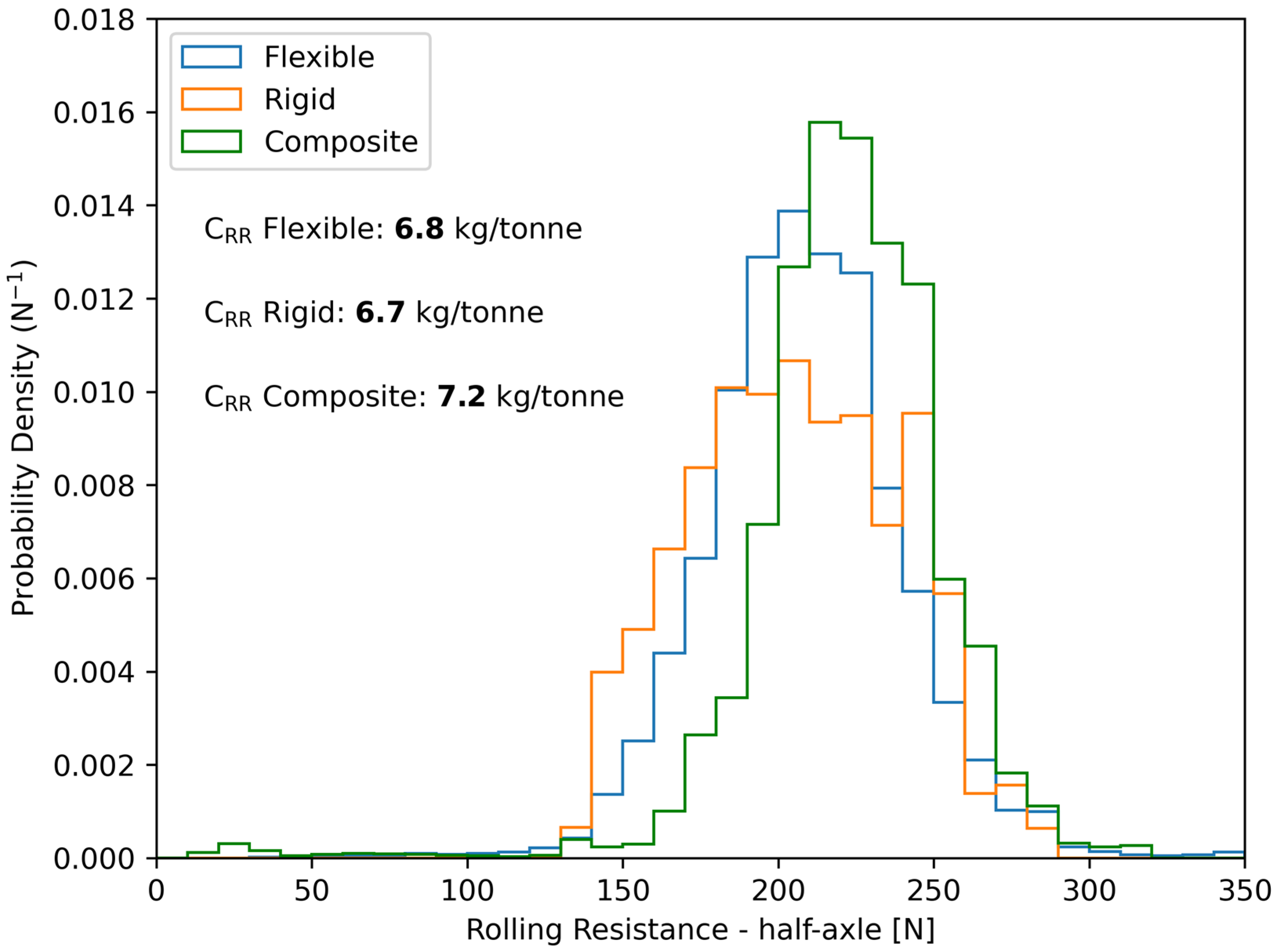
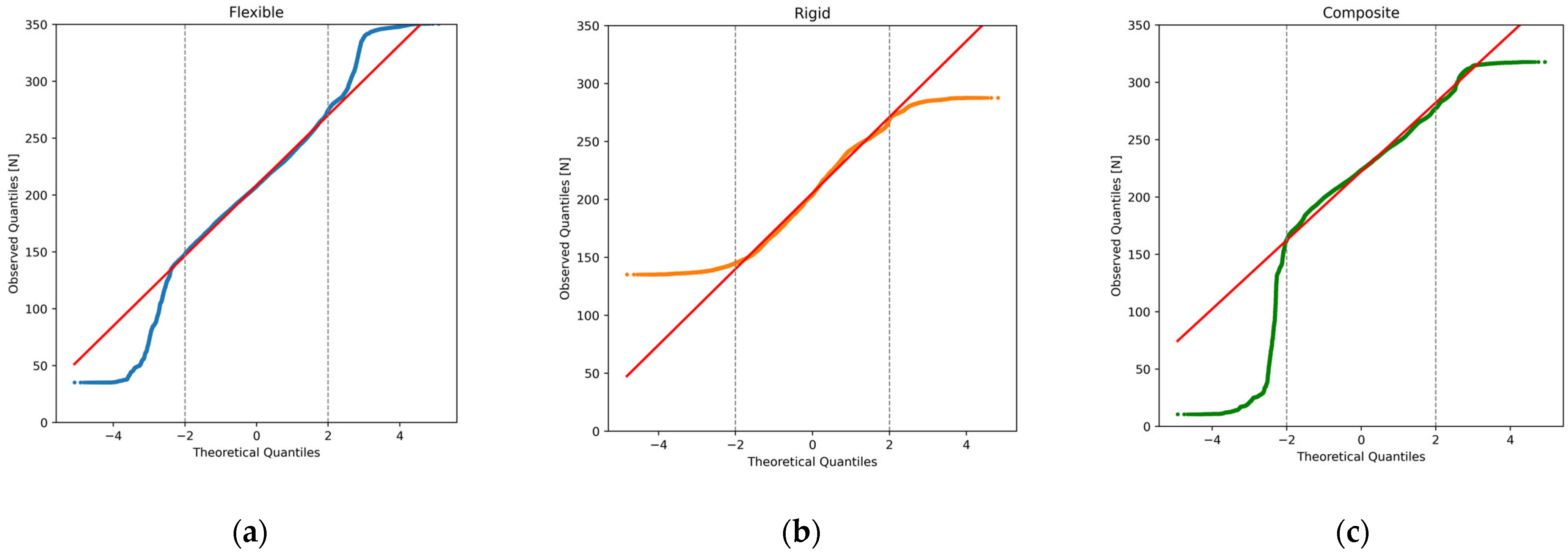
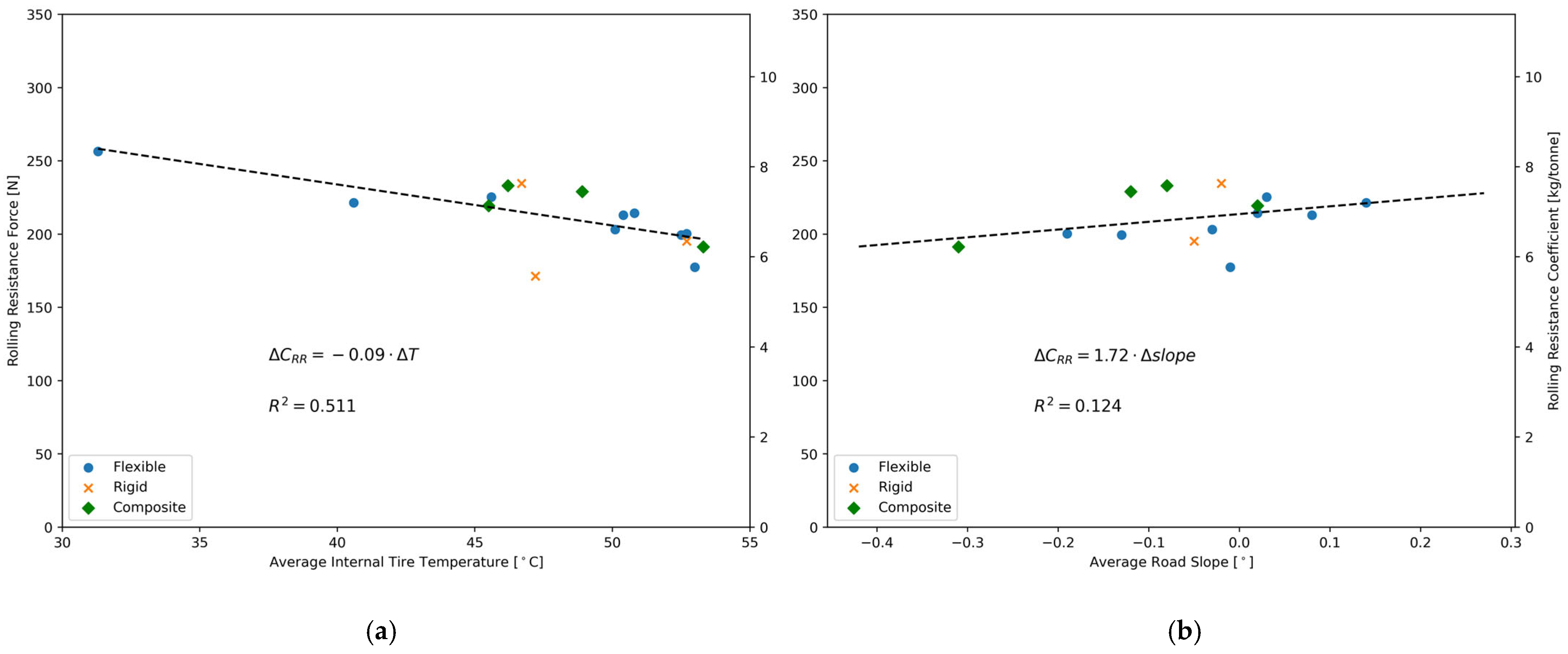
3.3. Pavement Type and Statistical Analysis
- Coasting events (extremely low values)
- Braking events (extremely high values)
- Vehicle turning (both extreme ends)
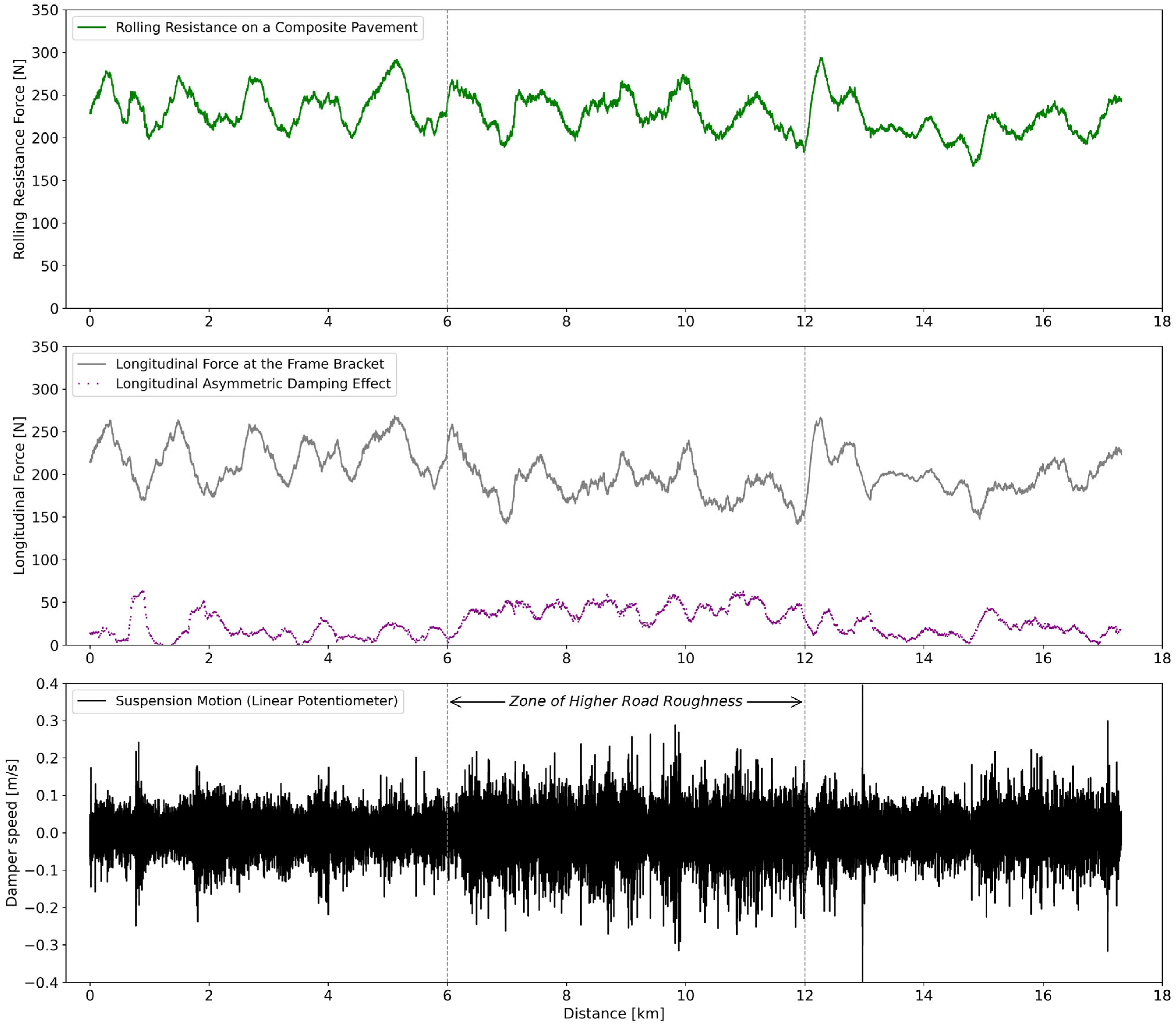
3.4. Rolling Resistance Measurements and Disturbing Factors
3.5. Rolling Resistance and Road Roughness
3.6. Road Segment Comparison
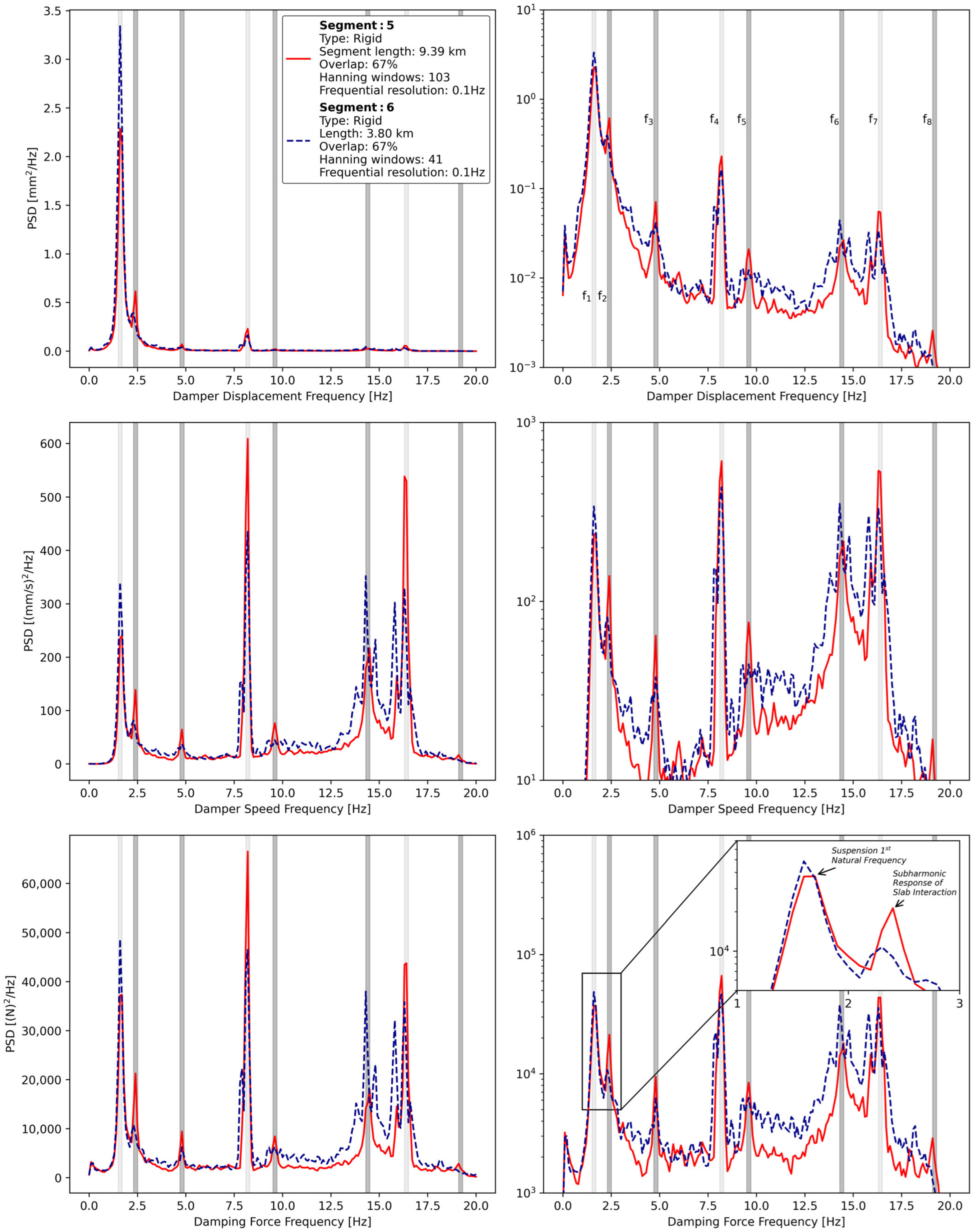
3.7. Rigid Pavement—Slab Interaction
- The deterioration of the slabs on the tested rigid pavements could lead to subharmonic responses in the vehicle suspension. This could be related to faults at the joints, where uneven slab alignment increases the probability of the suspension being excited at a frequency corresponding to two slabs. Inconsistent stiffness in the subbase could amplify this effect [66,67].
4. Conclusions
- Pavement type alone cannot fully explain rolling resistance variations. Future analyses should include factors like pavement age, macrotexture, and layer thickness.
- Tire internal temperature significantly impacts rolling resistance, with a reduction of 0.09 kg/tonne observed for every 1 °C increase in tire temperature. These findings highlight the limitations of laboratory-based methods, which fail to account for real-world factors such as vehicle speed, axle load, and ambient temperature [32,49].
- The study relied on measurements taken on a single day. To ensure the validity and generalizability of the results, future research should encompass a broader range of meteorological conditions.
- Improving rolling resistance computations by integrating accelerometer/gyroscope data could mitigate variability caused by road slope and provide more precise measurements.
- Vehicle speed was maintained at a constant 95 km/h in this study to focus on steady-state highway conditions. However, this may not accurately reflect conditions typically encountered in urban environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Environment Information and Observation Network (Eionet). Greenhouse Gas Emissions from Transport in Europe. Available online: https://www.eea.europa.eu/ims/greenhouse-gas-emissions-from-transport (accessed on 14 September 2022).
- US EPA. OAR Sources of Greenhouse Gas Emissions|US EPA. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions (accessed on 14 September 2022).
- Taylor, G.; Patten, J. Effects of Pavement Structure on Vehicle Fuel Consumption; Centre for Surface Transportation Technology (CSTT): Ottawa, ON, Canada; National Research Council of Canada (NRC): Ottawa, ON, Canada, 2006. [Google Scholar]
- Butt, A.A.; Harvey, J.T.; Fitch, D.; Kedarisetty, S.; Lea, J.D.; Lea, J.; Reger, D. Investigation of the Effect of Pavement Deflection on Vehicle Fuel Consumption: Field Testing and Empirical Analysis; University of California Pavement Research Center: Davis, CA, USA, 2022. [Google Scholar]
- Karlsson, R.; Hammarström, U.; Sörensen, H.; Eriksson, O. Road Surface Influence on Rolling Resistance: Coastdown Measurements for a Car and an HGV; Statens väg-och transportforskningsinstitut: Linköping, Sweden, 2011. [Google Scholar]
- Araújo, J.P.C.; Oliveira, J.R.M.; Silva, H.M.R.D. The Importance of the Use Phase on the LCA of Environmentally Friendly Solutions for Asphalt Road Pavements. Transp. Res. Part D Transp. Environ. 2014, 32, 97–110. [Google Scholar] [CrossRef]
- AzariJafari, H.; Gregory, J.; Kirchain, R. Potential Contribution of Deflection-Induced Fuel Consumption to U.S. Greenhouse Gas Emissions. Transp. Res. Rec. 2020, 2674, 931–937. [Google Scholar] [CrossRef]
- Levesque, W.; Bégin-Drolet, A.; Lépine, J. Effects of Pavement Characteristics on Rolling Resistance of Heavy Vehicles: A Literature Review. Transp. Res. Rec. 2023, 2677, 296–309. [Google Scholar] [CrossRef]
- Louhghalam, A.; Akbarian, M.; Ulm, F.J. Carbon Management of Infrastructure Performance: Integrated Big Data Analytics and Pavement-Vehicle-Interactions. J. Clean. Prod. 2017, 142, 956–964. [Google Scholar] [CrossRef]
- Ydrefors, L.; Hjort, M.; Kharrazi, S.; Jerrelind, J.; Stensson Trigell, A. Rolling Resistance and Its Relation to Operating Conditions—A Literature Review. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2931–2948. [Google Scholar] [CrossRef]
- Chatti, K.; Zaabar, I. Estimating the Effects of Pavement Condition on Vehicle Operating Costs; Transportation Research Board: Washington, DC, USA, 2012; Volume 720, ISBN 9780309258210. [Google Scholar]
- Amos, D. Pavement Smoothness and Fuel Efficiency: An Analysis of the Economic Dimensions of the Missouri Smooth Road Initiative; Missouri Department of Transportation: Jefferson City, MO, USA, 2006. [Google Scholar]
- Na, X.; Cebon, D. Quantifying Fuel-Saving Benefit of Low-Rolling-Resistance Tyres from Heavy Goods Vehicle In-Service Operations. SSRN Electron. J. 2022, 113, 103501. [Google Scholar] [CrossRef]
- Perrotta, F.; Parry, T.; Neves, L.C.; Buckland, T.; Benbow, E.; Mesgarpour, M. Verification of the HDM-4 Fuel Consumption Model Using a Big Data Approach: A UK Case Study. Transp. Res. Part D Transp. Environ. 2019, 67, 109–118. [Google Scholar] [CrossRef]
- Perrotta, F.; Parry, T.; Neves, L.C.; Mesgarpour, M.; Benbow, E.; Viner, H. On the Secondary Use of Truck Sensors and Asset Management Data to Monitor the Performance of Road Infrastructures. In TRUSS Training in Reducing Uncertainty in Structural Safety: D5. 2 Final Report: WP5-Rail; European Commission: Brussels, Belgium, 2019; pp. 43–48. [Google Scholar]
- Perrotta, F.; Parry, T.; Neves, L.C. A Machine Learning Approach for the Estimation of Fuel Consumption Related to Road Pavement Rolling Resistance for Large Fleets of Trucks. In Proceedings of the The Sixth International Symposium on Life-Cycle Civil Engineering (IALCCE 2018), Ghent, Belgium, 28–31 October 2018; pp. 1–5. [Google Scholar]
- Skar, A.; Vestergaard, A.M.; Pour, S.; Pettinari, M. Internet-of-Things (IoT) Platform for Road Energy Efficiency Monitoring. Sensors 2023, 23, 2756. [Google Scholar] [CrossRef]
- Skar, A.; Nielsen, N.R.; Pettinari, M.; Levenberg, E. Towards Infrastructure Energy Labelling Utilizing Data from a Connected Fleet of Electric Vehicles. Transp. Res. Procedia 2023, 72, 2676–2683. [Google Scholar] [CrossRef]
- Sandberg, T. Heavy Truck Modeling for Fuel Consumption Simulations and Measurements. Doctoral Dissertation, Linköping University, Linköping, Sweden, 2001. [Google Scholar]
- Hyttinen, J.; Wentzel, H.; Österlöf, R.; Jerrelind, J.; Drugge, L. Development and Analysis of an On-Road Torque Measurement Device for Trucks. Exp. Mech. 2024, 64, 455–466. [Google Scholar] [CrossRef]
- Nielsen, N.R. Investigating Pavement Response to a Moving Vehicle. Ph.D. Thesis, Roskilde University, Roskilde, Denmark, 2020. [Google Scholar]
- Ejsmont, J.A.; Ronowski, G.; Wilde, J. Rolling Resistance Measurements at the MnROAD Facility; Minnesota State University: Mankato, MN, USA, 2012. [Google Scholar]
- Ejsmont, J.; Sjögren, L.; Świeczko-Żurek, B.; Ronowski, G. Influence of Road Wetness on Tire-Pavement Rolling Resistance. J. Civ. Eng. Archit. 2015, 9, 1302–1310. [Google Scholar] [CrossRef]
- Ejsmont, J.A.; Świeczko-Żurek, B.; Ronowski, G.; Wilde, J. Rolling Resistance Measurements at the MnROAD Facility, Round 2; Transportation Research Board: Washington, DC, USA, 2014. [Google Scholar]
- Ejsmont, J.A.; Ronowski, G.; Świeczko-Żurek, B.; Sommer, S. Road Texture Influence on Tyre Rolling Resistance. Road Mater. Pavement Des. 2017, 18, 181–198. [Google Scholar] [CrossRef]
- Nielsen, N.R.; Chatti, K.; Nielsen, C.P.; Zaabar, I.; Hjorth, P.G.; Hecksher, T. Method for Direct Measurement of Structural Rolling Resistance for Heavy Vehicles. Transp. Res. Rec. 2020, 2674, 371–380. [Google Scholar] [CrossRef]
- Nielsen, N.R.; Hecksher, T.; Nielsen, C.P.; Hjorth, P.G. Measurement of Structural Rolling Resistance at Two Temperatures. In Proceedings of the Advances in Materials and Pavement Performance Prediction II, San Antonio, TX, USA, 27–29 May 2020; pp. 220–224. [Google Scholar]
- Madhusudhanan, A.K.; Ainalis, D.; Na, X.; Garcia, I.V.; Sutcliffe, M.; Cebon, D. Effects of Semi-Trailer Modifications on HGV Fuel Consumption. Transp. Res. Part D Transp. Environ. 2021, 92, 102717. [Google Scholar] [CrossRef]
- Vishay Precision Group. TN-511, Errors Due to Misalignment of Strain Gages; Vishay Precision Group: Malvern, PA, USA, 2010. [Google Scholar]
- Vishay Precision Group. TN-509, Errors Due To Transverse Sensitivity in Strain Gages; Vishay Precision Group: Malvern, PA, USA, 2011. [Google Scholar]
- Ronowski, G. Design and Calibration of Rolling Resistance Test Trailer R2Mk.2. IOP Conf. Ser. Mater. Sci. Eng. 2016, 148, 012026. [Google Scholar] [CrossRef]
- Ejsmont, J.; Ronowski, G.; Owczarzak, W.; Sommer, S. Temperature Influence on Tire Rolling Resistance Measurements Quality. Int. J. Automot. Technol. 2022, 23, 109–123. [Google Scholar] [CrossRef]
- Ejsmont, J.; Ronowski, G.; Taryma, S.; Świeczko-Żurek, B. The Influence of Road Surface Unevenness on Tyre Rolling Resistance. Arch. Automot. Eng. 2015, 70, 35–46. [Google Scholar] [CrossRef]
- Sandberg, U.; Hammarström, U.; Haider, M.; Conter, M.; Goubet, L.; Bergiers, A.; Glaeser, K.-P.; Boujard, O.; Karlsson, R.; Ejsmont, J.A.; et al. Rolling Resistance—Basic Information and State-of-the-Art on Measurement Methods. 2011. Available online: https://www.diva-portal.org/smash/get/diva2:674026/FULLTEXT02 (accessed on 20 October 2024).
- Ejsmont, J.; Ronowski, G.; Ydrefors, L.; Owczarzak, W.; Sommer, S.; Świeczko-Żurek, B. Comparison of Tire Rolling Resistance Measuring Methods for Different Surfaces. Int. J. Automot. Technol. 2024, 25, 965–976. [Google Scholar] [CrossRef]
- Ejsmont, J.; Ronowski, G.; Berge, T.; Sommer, S.; Owczarzak, W.; Szerszyńska, A. At What Temperature Should the Tire Rolling Resistance Be Measured? Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Chupin, O.; Piau, J.-M.; Chabot, A. Evaluation of the Structure-Induced Rolling Resistance (SRR) for Pavements Including Viscoelastic Material Layers. Mater. Struct. 2013, 46, 683–696. [Google Scholar] [CrossRef]
- Sayers, M.W.; Karamihas, S.M. The Little Book of Profiling: Basic Information about Measuring and Interpreting Road Profiles; University of Michigan, Ann Arbor, Transportation Research Institute: Ann Arbor, MI, USA, 1998; p. 100. [Google Scholar]
- Levesque, W.; Bégin-Drolet, A.; Lépine, J. Introducing a Novel Method for Measuring Rolling Resistance and Dynamic Vertical Load on a Semi-Trailer Suspension. In Proceedings of the Technology Convergence 2023: Setting the Wheels In Motion: Reimagining the Future of Heavy Vehicles, Roads and Freight, Brisbane, Australia, 6–10 November 2023. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Smith, M.C.; Swift, S.J. Power Dissipation in Automotive Suspensions. Veh. Syst. Dyn. 2011, 49, 59–74. [Google Scholar] [CrossRef]
- Clark, J.M.C.; Smith, M.C. Power Absorption Invariance for Brownian Spring Forcing. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 4396–4399. [Google Scholar]
- Opkon SLPC Potentiometer Body Series. Available online: https://www.opkon.com.tr/Content/product/pdf/pdf-fd2e6560.pdf (accessed on 20 October 2024).
- Fares, A.; Zayed, T. Industry- and Academic-Based Trends in Pavement Roughness Inspection Technologies over the Past Five Decades: A Critical Review. Remote Sens. 2023, 15, 2941. [Google Scholar] [CrossRef]
- Sensy Custom-Made Load Pins 5000. Available online: https://www.sensy.com/en/load-pins-configurator/load-pin-design (accessed on 4 November 2024).
- Zhang, B.; Li, Z.; Tan, C.A.; Liu, Z. LQR-Based Suspension for Heavy Vehicles Considering the Time-Varying Characteristics of Vehicle-Road Interaction. Int. J. Struct. Stab. Dyn. 2024, 2450256. [Google Scholar] [CrossRef]
- Liu, X.; Al-Qadi, I.L. Mechanistic Excess Fuel Consumption of a 3D Passenger Vehicle on Rough Pavements. J. Transp. Eng. Part B Pavements 2023, 149, 04022065. [Google Scholar] [CrossRef]
- Liu, X.; Al-Qadi, I.L. Development of a Simulated Three-Dimensional Truck Model to Predict Excess Fuel Consumption Resulting from Pavement Roughness. Transp. Res. Rec. 2021, 2675, 1444–1456. [Google Scholar] [CrossRef]
- Hyttinen, J.; Ussner, M.; Österlöf, R.; Jerrelind, J.; Drugge, L. Truck Tyre Transient Rolling Resistance and Temperature at Varying Vehicle Velocities—Measurements and Simulations. Polym. Test. 2023, 122, 108004. [Google Scholar] [CrossRef]
- Izze-Racing Tire Temperature and Pressure Monitoring System-Datasheet (Rev. D, 14 BAR). Available online: https://www.izzeracing.com/products/tire-temperature-pressure-monitoring-system.html (accessed on 1 October 2024).
- Ejsmont, J.; Stanislaw, T.; Ronowski, G.; Swieczko-Zurek, B. Influence of Temperature on the Tyre Rolling Resistance. Int. J. Automot. Technol. 2018, 19, 45–54. [Google Scholar] [CrossRef]
- Hyttinen, J.; Ussner, M.; Österlöf, R.; Jerrelind, J.; Drugge, L. Effect of Ambient and Tyre Temperature on Truck Tyre Rolling Resistance. Int. J. Automot. Technol. 2022, 23, 1651–1661. [Google Scholar] [CrossRef]
- GlobalTop Technology Inc. FGPMMOPA6H Standalone Module Sheet: V0A; GlobalTop Technology Inc.: Tainan, Taiwan, 2011. [Google Scholar]
- Paterlini, G.; Yucel, S.; Lucking, M.M.; Magnuson, J. Rolling Resistance Validation; Minnesota Department of Transportation: St. Paul, MN, USA, 2015. [Google Scholar]
- Micro-Measurements. Strain Gage Based Transducers: Application Note VMM-26; Vishay Precision Group: Malvern, PA, USA, 2010. [Google Scholar]
- Swarnakar, A.K.; Van Der Biest, O.; Baufeld, B. Young’s Modulus and Damping in Dependence on Temperature of Ti-6Al-4V Components Fabricated by Shaped Metal Deposition. J. Mater. Sci. 2011, 46, 3802–3811. [Google Scholar] [CrossRef]
- Scale Manufacturers Association Load Cell Application and Test Guideline; 2010. Available online: https://scalemanufacturers.org/PDF/LoadCellApplicationTestGuidelineApril2010.pdf (accessed on 20 October 2024).
- Zaabar, I.; Chatti, K. Estimating Vehicle Operating Costs Caused by Pavement Surface Conditions. Transp. Res. Rec. 2014, 2455, 63–76. [Google Scholar] [CrossRef]
- Sandberg, T.; Ramdén, C.; Gamberg, M. Tire Temperature Measurements for Validation of a New Rolling Resistance Model. IFAC Proc. Vol. 2004, 37, 589–594. [Google Scholar] [CrossRef]
- Sayers, M.W. On the Calculation of International Roughness Index from Longitudinal Road Profile. Transp. Res. Rec. 1995, 1501, 1–12. [Google Scholar]
- Liu, X.; Al-Qadi, I. Integrated Vehicle–Tire–Pavement Approach for Determining Pavement Structure–Induced Rolling Resistance under Dynamic Loading. Transp. Res. Rec. 2022, 2676, 398–409. [Google Scholar] [CrossRef]
- Hendrickson. UNDERSTANDING SUSPENSIONS. Available online: https://www.hendrickson-intl.com/getattachment/58b7a953-f534-4927-91ac-3a0f69baf0cf/L761.pdf (accessed on 9 October 2024).
- Pacejka, H.B. Short Wavelength Intermediate Frequency Tire Model; O’Reilly: Sebastopol, CA, USA, 2012; ISBN 9780080970165. [Google Scholar]
- Savoskin, A.; Vlasevskii, S. Aspects of Railway Vehicles Vibrations with Nonlinear Spring Suspension Characteristics. In VIII International Scientific Siberian Transport Forum. TransSiberia 2019. Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 109–116. [Google Scholar]
- Oberreiter, L.; Seifert, U.; Barato, A.C. Subharmonic Oscillations in Stochastic Systems under Periodic Driving. Phys. Rev. E 2019, 100, 012135. [Google Scholar] [CrossRef]
- American Concrete Pavement Association. Design and Construction of Joints for Concrete Streets. In Concrete Information; American Concrete Pavement Association: Rosemont, IL, USA, 1992; Available online: https://www.acpa.org/wpfd_file/design-and-construction-of-joints-for-concrete-streets/ (accessed on 20 October 2024).
- Xiao, W.; Wang, C.; Liu, J.; Gao, M.; Wu, J. Optimizing Faulting Prediction for Rigid Pavements Using a Hybrid SHAP-TPE-CatBoost Model. Appl. Sci. 2023, 13, 12862. [Google Scholar] [CrossRef]
- Deep, P.; Andersen, M.B.; Thom, N.; Lo Presti, D. Toward the Development of Load Transfer Efficiency Evaluation of Rigid Pavements by a Rolling Wheel Deflectometer. Infrastructures 2020, 5, 7. [Google Scholar] [CrossRef]
- Bazi, G.; Hajj, E.Y.; Ulloa-Calderon, A.; Ullidtz, P. Finite Element Modelling of the Rolling Resistance Due to Pavement Deformation. Int. J. Pavement Eng. 2020, 21, 365–375. [Google Scholar] [CrossRef]
- Balzarini, D.; Zaabar, I.; Chatti, K. Impact of PCC Pavement Structural Response on Rolling Resistance and Vehicle Fuel Economy. In Pavement Life-Cycle Assessment; CRC Press: Boca Raton, FL, USA, 2017; pp. 69–78. ISBN 9780367209896. [Google Scholar]
- Balzarini, D.; Zaabar, I.; Chatti, K. Impact of Concrete Pavement Structural Response on Rolling Resistance and Vehicle Fuel Economy. Transp. Res. Rec. 2017, 2640, 84–94. [Google Scholar] [CrossRef]






| Experimental Method | Level | Comments | References |
|---|---|---|---|
| Coast-down tests | N/A | Not in normal driving conditions | [5] |
| Vehicle operational data | 1 |
| [3,4,11,12,13,14,15,16,17,18] |
| Driving torque measurements | 2 |
| [19,20] |
| Instrumented axle | 3 | Found not suitable for rolling resistance measurements | [21] |
| Instrumented trailer | 3 | Currently exists only for passenger car tires, which cannot capture the structure-induced rolling resistance (SRR) of heavy vehicles | [22,23,24,25] |
| Traffic Speed Deflectometer (TSD) | 4 | Only useful for SRR measurements, hence not capturing the pavement macrotexture and roughness | [26,27] |
| Pavement Type | Number of Segments | Total Length [km] |
|---|---|---|
| Flexible | 9 | 102.3 |
| Composite | 4 | 45.7 |
| Rigid | 3 | 26.3 |
| Total | 16 | 174.4 |
| Symbol | Potential Source of Error | Origin | Effect on CRR Uncertainty [kg/Tonne] |
|---|---|---|---|
| ε1 | Analog-to-digital conversion | Data acquisition system | ±0.033 |
| ε2 | Random noise | Data acquisition system | ≅0 |
| ε3 | Difference in coefficient of thermal expansion | Strain gauges and spring element | ≅0 |
| ε4 | Temperature change on gauge factor | Strain gauges | ±0.0052 |
| ε5 | Temperature change on modulus of elasticity of Ti-6AL-4V | Spring element | ±0.017 |
| ε6 | Load cells—Linearity | Spring element | ≅0 |
| ε7 | Load cells—Hysteresis | Spring element | ≅0 |
| ε8 | Load cells—Repeatability | Strain gauges and spring element | ≅0 |
| ε9 | Load cells—Creep | Strain gauges and their bonding material | ≅0 |
| Pavement Type | Tire Temperature | Road Slope | Sum of Disturbing Factors | ||
|---|---|---|---|---|---|
| Average [°C] | Effect on CRR 1 [kg/Tonne] | Average [°] | Effect on CRR 2 [kg/Tonne] | Effect on CRR 3 [kg/Tonne] | |
| Flexible | 48.2 | 0.0022 | 0.015 | 0.026 | 0.028 |
| Composite | 47.5 | 0.070 | −0.070 | −0.12 | −0.050 |
| Rigid | 49.7 | −0.13 | 0.010 | 0.017 | −0.11 |
| All pavements | 48.3 | N/A (same tire temperature) | −0.0079 | −0.014 | N/A |
| Segment Number | Pavement Type | Length | Tire Temperature | Average Road Slope | Frame Bracket 1 | Longitudinal Asymmetric Damping Effect 2 | Rolling Resistance 3 | |
|---|---|---|---|---|---|---|---|---|
| [km] | [°C] | [°] | [N] | [N] | [N] | [kg/Tonne] | ||
| 1 | Flexible | 3.0 | 31.3 | −0.42 | 199 | 57 | 257 | 8.3 |
| 2 | Flexible | 22.7 | 40.6 | 0.14 | 170 | 52 | 221 | 7.2 |
| 3 | Flexible | 3.9 | 45.6 | 0.03 | 189 | 36 | 225 | 7.3 |
| 4 | Composite | 4.6 | 46.2 | −0.08 | 219 | 14 | 233 | 7.6 |
| 5 | Rigid | 9.4 | 46.7 | −0.02 | 224 | 10 | 235 | 7.6 |
| 6 | Rigid | 4.1 | 47.2 | 0.27 | 161 | 11 | 171 | 5.6 |
| 7 | Composite | 17.6 | 48.9 | −0.12 | 203 | 26 | 229 | 7.5 |
| 8 | Flexible | 7.0 | 50.1 | −0.03 | 193 | 10 | 203 | 6.6 |
| 9 | Flexible | 15.3 | 50.8 | 0.02 | 194 | 20 | 214 | 7.0 |
| 10 | Composite | 20.0 | 45.5 | 0.02 | 215 | 4 | 219 | 7.1 |
| 11 | Flexible | 20.5 | 50.4 | 0.08 | 209 | 4 | 213 | 6.9 |
| 12 | Flexible | 5.2 | 52.5 | −0.13 | 185 | 14 | 299 | 6.5 |
| 13 | Flexible | 17.4 | 53.0 | −0.01 | 172 | 6 | 178 | 5.8 |
| 14 | Composite | 3.5 | 53.3 | −0.31 | 185 | 6 | 191 | 6.2 |
| 15 | Rigid | 12.9 | 52.7 | −0.05 | 171 | 25 | 195 | 6.4 |
| 16 | Flexible | 7.3 | 52.7 | −0.19 | 176 | 24 | 200 | 6.5 |
| Label of the Frequency | Value [Hz] | Physical Interpretation | Mathematical Interpretation |
|---|---|---|---|
| f1 | 1.6 | Suspension characteristics | Suspension natural frequency |
| f2 | 2.4 | Two-slab distance | Subharmonic of slab interaction |
| f3 | 4.8 | One-Slab distance | Fundamental frequency of slab interaction |
| f4 | 8.2 | Rotation of wheels | Fundamental frequency of wheel rotation |
| f5 | 9.6 | Half-slab Distance | Second harmonic of slab interaction |
| f6 | 14.4 | Third-Slab Distance | Third harmonic of slab interaction (Confounded with the second natural frequency of the vehicle that is around 14 Hz) |
| f7 | 16.4 | Twice the Rotation of wheels | Second harmonic of wheel rotation |
| f8 | 19.2 | Quarter-Slab Distance | Fourth harmonic of slab interaction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levesque, W.; Bégin-Drolet, A.; Lépine, J. Rolling Resistance Evaluation of Pavements Using Embedded Transducers on a Semi-Trailer Suspension. Sensors 2024, 24, 7556. https://doi.org/10.3390/s24237556
Levesque W, Bégin-Drolet A, Lépine J. Rolling Resistance Evaluation of Pavements Using Embedded Transducers on a Semi-Trailer Suspension. Sensors. 2024; 24(23):7556. https://doi.org/10.3390/s24237556
Chicago/Turabian StyleLevesque, William, André Bégin-Drolet, and Julien Lépine. 2024. "Rolling Resistance Evaluation of Pavements Using Embedded Transducers on a Semi-Trailer Suspension" Sensors 24, no. 23: 7556. https://doi.org/10.3390/s24237556
APA StyleLevesque, W., Bégin-Drolet, A., & Lépine, J. (2024). Rolling Resistance Evaluation of Pavements Using Embedded Transducers on a Semi-Trailer Suspension. Sensors, 24(23), 7556. https://doi.org/10.3390/s24237556






