Effect of Dielectric Layer on Miniaturized Patch Antenna Sensor
Abstract
:1. Introduction
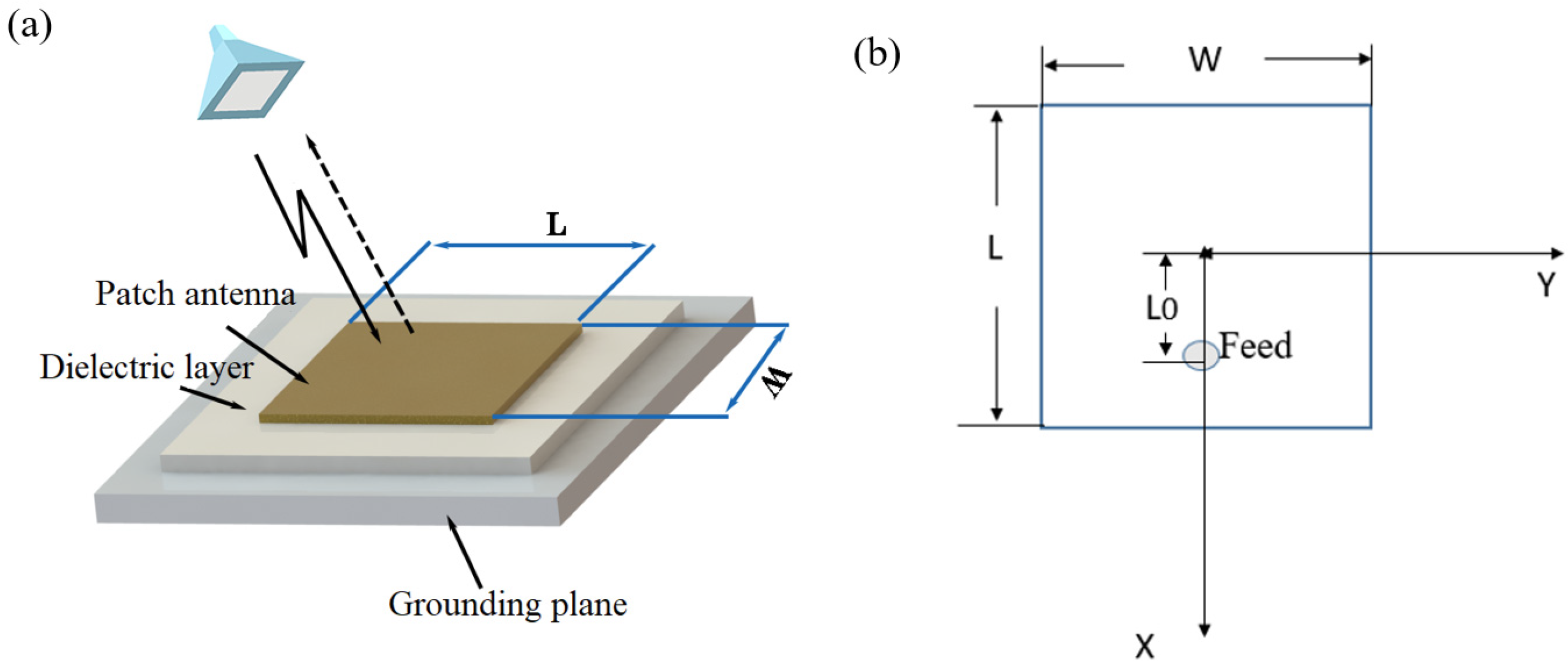
2. Size Calculation of Antenna Sensor
3. Results and Discussion
3.1. Effect of Relative Dielectric Constant of Dielectric Layer on Miniaturization of Antenna Sensor
3.2. Effect of Dielectric Loss of Dielectric Layer on Miniaturized Antenna Sensor
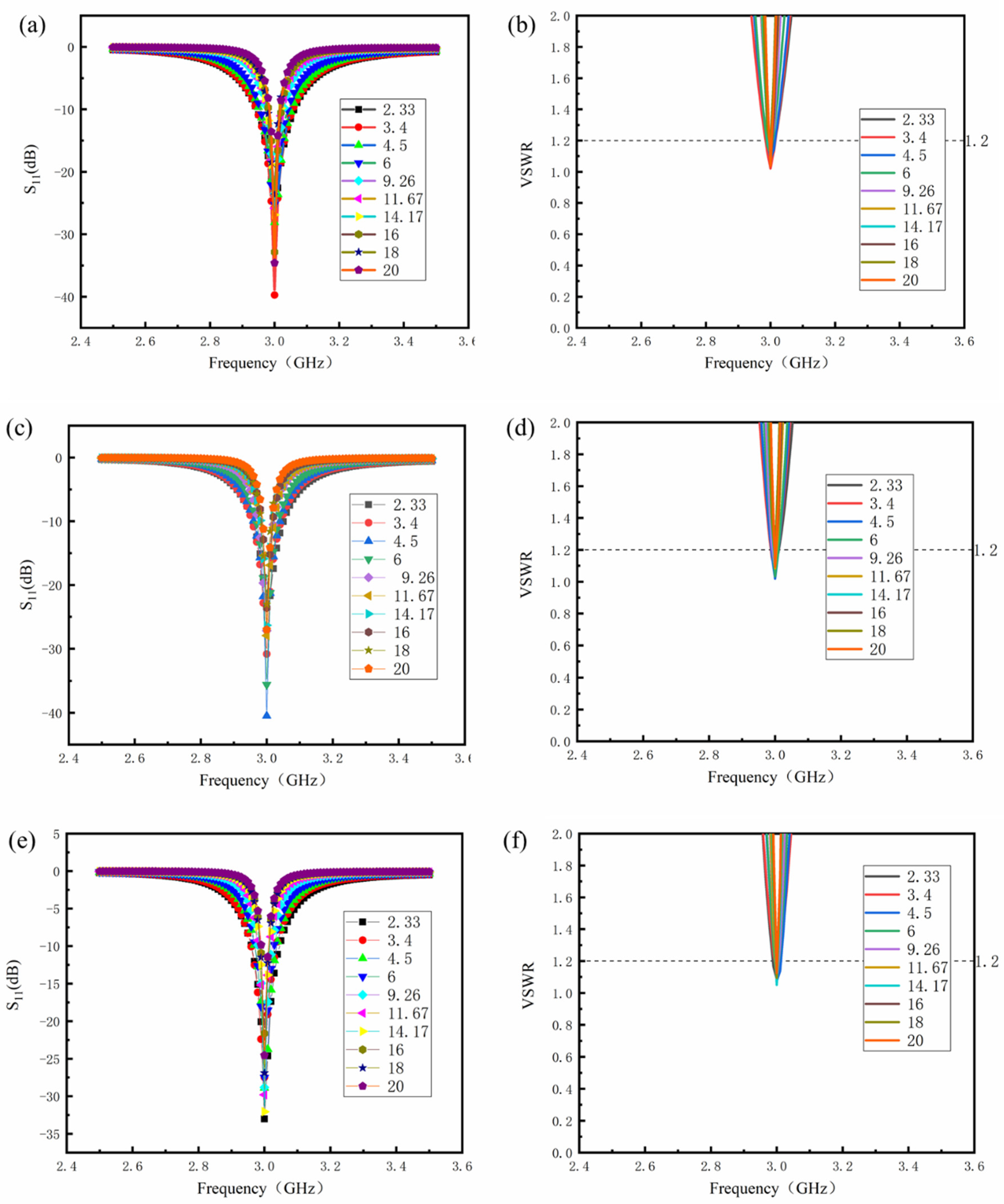
3.3. Relationship Between Relative Dielectric Constant and Dielectric Losses of Dielectric Layer at Specific Radiation Efficiency
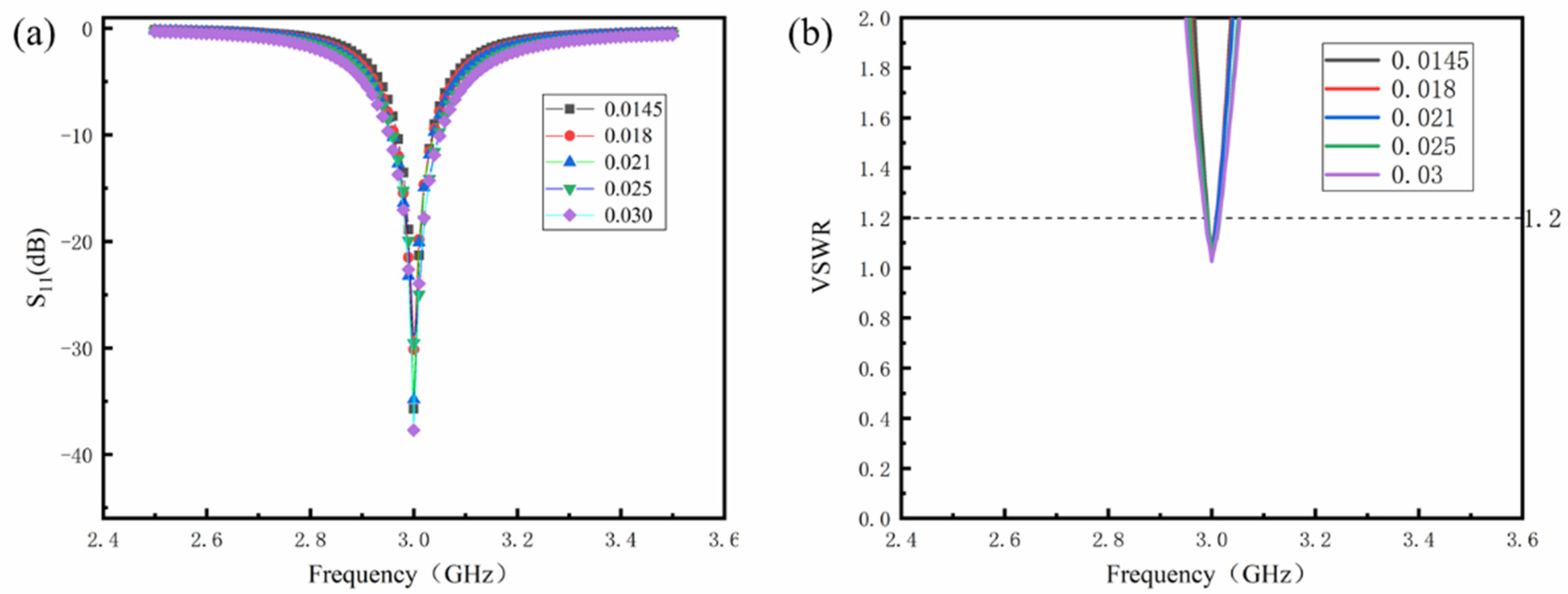
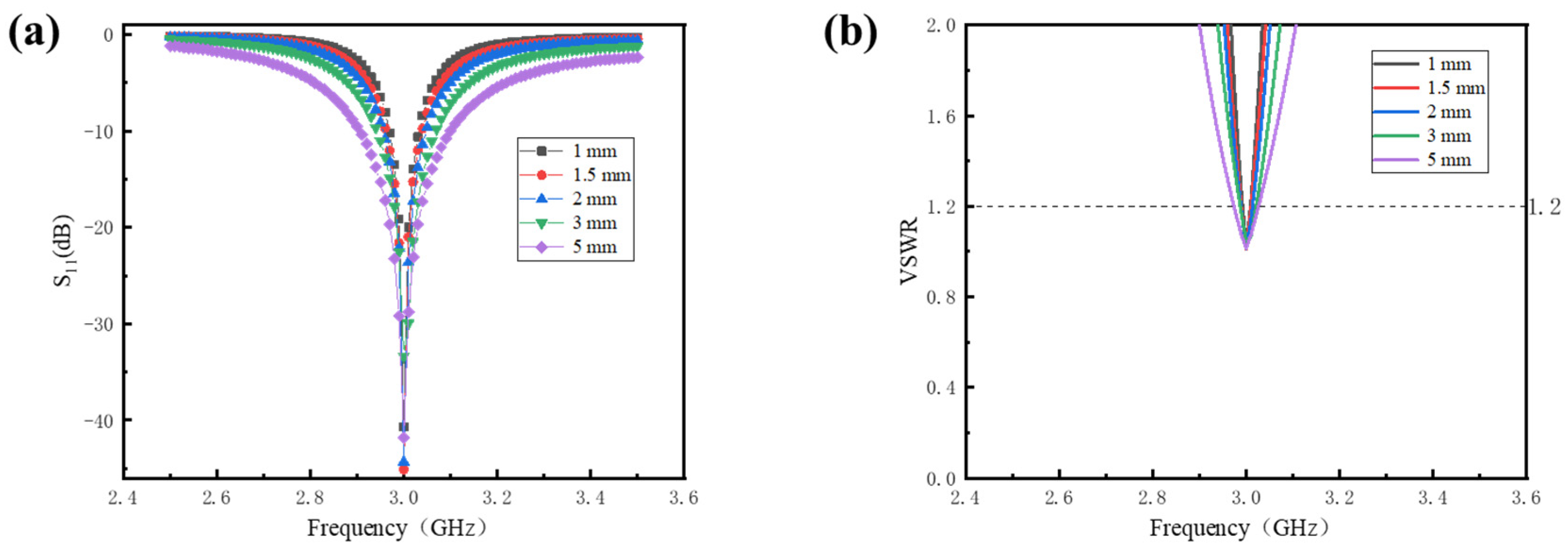
3.4. Effect of Dielectric Layer Thickness on Miniaturized Antenna Sensor
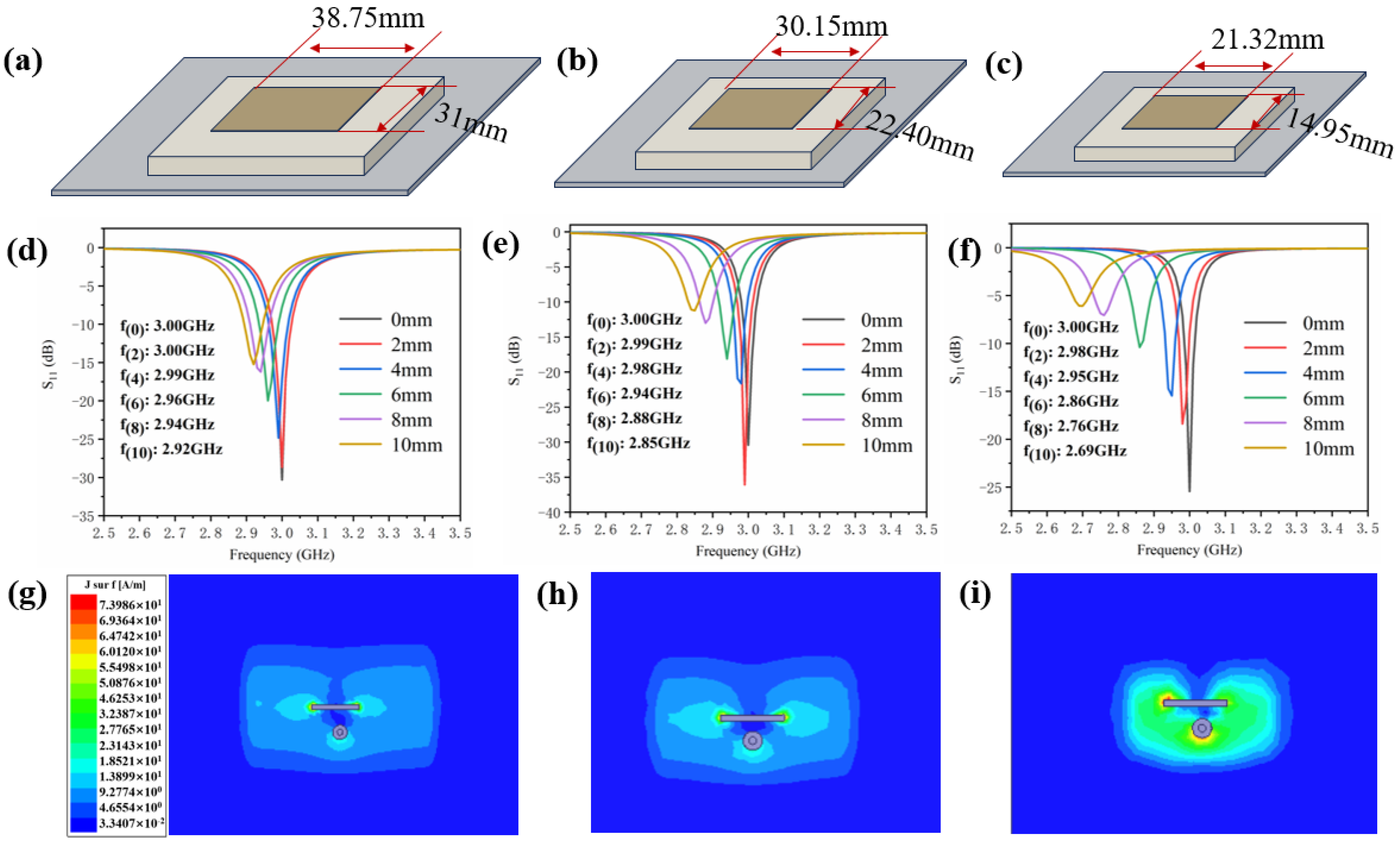
3.5. Effect of Crack Propagation on Miniaturized Antenna Sensor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, F.-G. Structural Health Monitoring/Management (SHM), In Aerospace Structures, 1st ed.; Woodhead Publishing: North Carolina State, NC, USA, 2024; pp. 3–14. ISBN 978-01-9850-970-7. [Google Scholar]
- Mieloszyk, M.; Majewska, K.; Ostachowicz, W. Application of embedded fibre Bragg grating sensors for structural health monitoring of complex composite structures for marine applications. Mar. Struct. 2021, 76, 102903. [Google Scholar] [CrossRef]
- Li, X.; Xue, S.; Xie, L.; Wan, G. A miniaturized passive wireless patch antenna sensor for structural crack sensing. Struct. Health Monit. 2024, 23, 3276–3295. [Google Scholar] [CrossRef]
- Yi, Z.; Xie, L.; Xue, S.; Wan, G. A Passive Wireless Acceleration Sensing System Based on Patch Antenna and FMCW Radar. IEEE Internet Things J. 2023, 10, 10662–10674. [Google Scholar] [CrossRef]
- Abdulkarem, M.; Samsudin, K.; Rokhani, F.Z.; A Rasid, M.F. Wireless sensor network for structural health monitoring: A contemporary review of technologies, challenges, and future direction. Struct. Health Monit. 2020, 19, 693–735. [Google Scholar] [CrossRef]
- Wang, D.F.; Fang, Y.; Gu, Z.; He, Y.; Itoh, T. A Passive Sensing-Wireless Transmitting Scheme Demonstrated by Integrating a Magnetic Cantilever With a Microstrip Patch for DC Current Monitoring. IEEE Trans. Instrum. Meas. 2023, 72, 9506509. [Google Scholar] [CrossRef]
- Ozbey, B. Wireless Surface Strain Mapping by Passive Electromagnetic Resonators. IEEE Sens. J. 2023, 23, 10370–10377. [Google Scholar] [CrossRef]
- Mohammad, I.; Gowda, V.; Zhai, H.; Huang, H. Detecting crack orientation using patch antenna sensors. Meas. Sci. Technol. 2011, 23, 015102. [Google Scholar] [CrossRef]
- Sofi, A.; Regita, J.J.; Rane, B.; Lau, H.H. Structural health monitoring using wireless smart sensor network—An overview. Mech. Syst. Signal Process. 2022, 163, 108113. [Google Scholar] [CrossRef]
- Ahmadihaji, A.; Izquierdo, R.; Shih, A. From Chip-Based to Chipless RFID Sensors: A Review. IEEE Sens. J. 2023, 23, 11356–11373. [Google Scholar] [CrossRef]
- Xue, S.; Wang, H.; Xie, L.; Li, X.; Zheng, Z.; Wan, G. Bolt loosening detection method based on double-layer slotted circular patch antenna. Struct. Heal. Monit. 2024, 23, 3371–3386. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, G.; Tam, K.-W.; Gao, Q.; Zhang, Z. A General and Effective Design Method for Compact Bandpass Filters With Extensible Orders/Channels on a Modified Patch Resonator. IEEE Trans. Microw. Theory Tech. 2024, 72, 5488–5497. [Google Scholar] [CrossRef]
- Santhanam, S.; Alagarsamy, M.; Selvan, P.T.; Rashed, A.N.Z.; Ahammad, S.H.; Hossain, A. Performance Signature and Analysis of Patterned Surfaces Trapezoidal Patch Antenna Array with Defected Ground Structure. J. Inst. Eng. India Ser. B 2024, 105, 1319–1329. [Google Scholar] [CrossRef]
- Teresa, P.M.; Umamaheswari, G. Compact slotted microstrip antenna for 5G applications operating at 28 GHz. IETE J. Res. 2020, 68, 3778–3785. [Google Scholar] [CrossRef]
- Goswami, P.K.; Goswami, G. Compact corner truncated fractal slot antenna for cognitive radio sensor network. IETE J. Res. 2020, 69, 460–471. [Google Scholar] [CrossRef]
- Singh, T.; Sehgal, S. Structural Health Monitoring of Composite Materials. Arch. Comput Method E 2022, 29, 1997–2017. [Google Scholar] [CrossRef]
- Wang, A.D.; Chen, C.F.; Qian, J.L.; Yang, F.; Wang, L.; Zhang, M. Enhanced electrical properties of PVDF thin film by addition of NaCl by near-electric-field 3D printing. J. Electron. Mater. 2021, 50, 4781–4786. [Google Scholar] [CrossRef]
- Chen, C.F.; Zhang, R.F.; Zhu, J.G.; Qian, X.; Zhu, J.; Ye, X.; Zhang, M. Direct writing polyvinylidene difluoride thin films by intercalation of nano-ZnO. Polym. Eng. Sci. 2021, 61, 1802–1809. [Google Scholar] [CrossRef]
- Raju, K.N.; Kavitha, A.; Sekhar, K.C. Design and performance analysis of miniaturized dual-band micro-strip antenna loaded with double negative meta-materials. Microsyst. Technol. 2023, 29, 1029–1038. [Google Scholar] [CrossRef]
- Prabha, K.R.; Jagadeeswari, M. High directivity microstrip patch antenna design using binary ebola search optimization for radio frequency identification application. Appl. Soft Comput. 2024, 162, 111682. [Google Scholar] [CrossRef]
- Wang, P.; Jia, Y.; Hu, W.; Liu, Y.; Lei, H.; Sun, H.; Cui, T.J. Circularly Polarized Polarization Conversion Metasurface-Inspired Antenna Array With Low RCS Over a Wide Band. IEEE Trans. Antennas Propag. 2023, 71, 5626–5636. [Google Scholar] [CrossRef]
- Niamien, C.; Collardey, S.; Sharaiha, A.; Mahdjoubi, K. Compact Expressions for Efficiency and Bandwidth of Patch Antennas Over Lossy Magneto-Dielectric Materials. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 63–66. [Google Scholar] [CrossRef]
- Huang, H. Flexible Wireless Antenna Sensor: A Review. IEEE Sens. J. 2013, 13, 3865–3872. [Google Scholar] [CrossRef]
- Ke, L.; Liu, Z.; Yu, H. Characterization of a Patch Antenna Sensor’s Resonant Frequency Response in Identifying the Notch-Shaped Cracks on Metal Structure. Sensors 2019, 19, 110. [Google Scholar] [CrossRef] [PubMed]
- Yi, Z.; Xue, S.; Xie, L.; Wan, G.; Wan, C. A Slotted-Patch Antenna Sensor With Higher Sensitivity for Detecting Setting Time of Cement Paste. IEEE Trans. Instrum. Meas. 2022, 71, 6005513. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, H.-M. Front to back ratio improvement of a micro strip patch antenna using dual-band isolated soft surface structures. Microw. Opt. Technol. Lett. 2011, 53, 2396–2400. [Google Scholar] [CrossRef]
- Li, M.; Jamal, M.Y.; Jiang, L.; Yeung, K.L. Isolation Enhancement for MIMO Patch Antennas Sharing a Common Thick Substrate: Using a Dielectric Block to Control Space-Wave Coupling to Cancel Surface-Wave Coupling. IEEE Trans. Antennas Propag. 2021, 69, 1853–1863. [Google Scholar] [CrossRef]
- Tong, C.; Song, R.; Guan, H.; Yang, Y.; He, D. Conformal metal crack detection sensor based on flexible graphene film antenna. Int. J. RF Microw. Comput. Eng. 2022, 32, 247904180. [Google Scholar] [CrossRef]
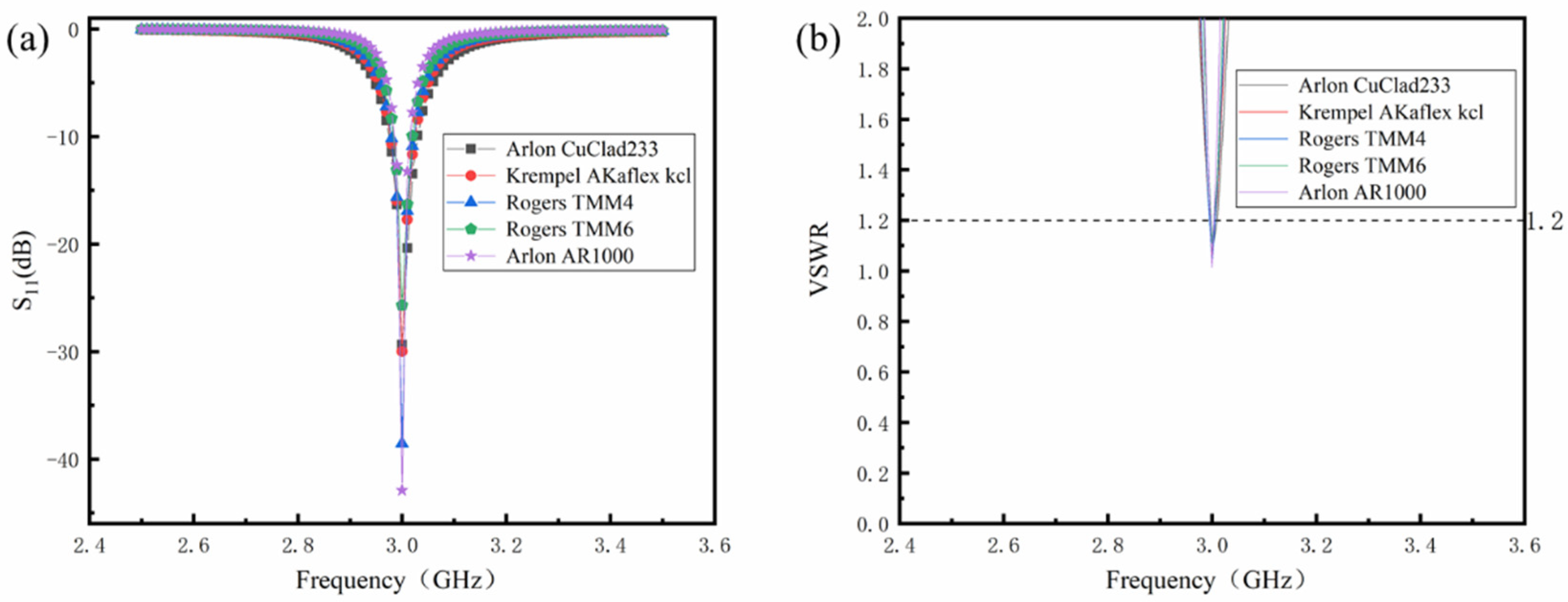


| Material | Arlon CuClad233 | Krempel AKaflex kcl | Rogers TMM4 | Rogers TMM6 | Arlon AR1000 |
|---|---|---|---|---|---|
| 2.33 | 3.40 | 4.50 | 6.00 | 10.00 | |
| tan | 0.0013 | 0.0018 | 0.0020 | 0.0023 | 0.0030 |
| Dielectric Layer Materials | Calculation | Optimization | |||||
|---|---|---|---|---|---|---|---|
| L/mm | W/mm | L/mm | W/mm | L0/mm | Antenna Area/mm2 | Radiation Efficiency/% | |
| Arlon CuClad233 | 33.16 | 38.75 | 31.00 | 38.75 | 5.5 | 1201.25 | 98.02 |
| Krempel AKaflex kcl | 27.25 | 33.71 | 25.75 | 33.71 | 4.2 | 868.03 | 94.97 |
| Rogers TMM4 | 23.88 | 30.15 | 22.40 | 30.15 | 3.6 | 675.36 | 93.14 |
| Rogers TMM6 | 21.45 | 26.73 | 19.38 | 26.73 | 2.8 | 518.03 | 90.05 |
| Arlon AR1000 | 17.11 | 21.32 | 14.95 | 21.32 | 2.0 | 318.73 | 81.57 |
| W/mm | L/mm | mm | Radiation Efficiency/% | Peak Gain/dB | ||
|---|---|---|---|---|---|---|
| 4.5 4.5 4.5 4.5 4.5 | 0.0145 0.0180 0.0210 0.0250 0.0300 | 30.15 30.15 30.15 30.15 30.15 | 22.50 22.56 22.59 22.60 22.65 | 4.6 5.0 5.1 5.5 5.8 | 59.25 53.77 49.58 45.14 40.65 | 3.39 3.08 2.84 2.59 2.34 |
| Radiation Efficiency | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 40% | 50% | 60% | |||||||
| L/mm | L0/mm | L/mm | L0/mm | L/mm | L0/mm | ||||
| 2.33 | 31.45 | 8.30 | 0.039 | 31.30 | 7.20 | 0.0270 | 31.20 | 7.00 | 0.0190 |
| 3.40 4.50 6.00 | 26.10 22.65 19.60 | 7.10 6.00 4.80 | 0.036 0.030 0.025 | 26.00 22.55 19.50 | 6.00 5.10 4.00 | 0.0240 0.0210 0.0180 | 25.90 22.50 19.50 | 5.80 4.60 3.80 | 0.0163 0.0145 0.0120 |
| 9.26 | 15.65 | 2.90 | 0.019 | 15.65 | 2.70 | 0.0130 | 15.60 | 2.60 | 0.0090 |
| 11.67 | 13.90 | 2.42 | 0.016 | 13.87 | 2.36 | 0.0110 | 13.85 | 2.10 | 0.0070 |
| 14.17 | 12.58 | 2.10 | 0.014 | 12.55 | 2.00 | 0.0095 | 12.52 | 1.70 | 0.0065 |
| 16.00 18.00 20.00 | 11.78 11.09 10.48 | 1.90 1.70 1.50 | 0.013 0.011 0.010 | 11.76 11.08 10.45 | 1.80 1.60 1.40 | 0.0083 0.0076 0.0070 | 11.75 11.05 10.45 | 1.40 1.45 1.20 | 0.0055 0.0052 0.0050 |
| Rated Radiation Efficiency/% | ||||||
|---|---|---|---|---|---|---|
| 40% | 50% | 60% | ||||
| Required tanδ | R | Required tanδ | R | Required tanδ | R | |
| 5 | 0.0298 | 39.2 | 0.0206 | 47.9 | 0.0141 | 58.1 |
| 10 | 0.0183 | 39.7 | 0.0127 | 49.1 | 0.0084 | 59.4 |
| 15 | 0.0121 | 42.3 | 0.0084 | 51.6 | 0.0056 | 62.1 |
| Layer Thickness /mm | Antenna Sensor Dimensions/mm | ||
|---|---|---|---|
| W | L | L0 | |
| 1 | 30.43 | 23.20 | 5.6 |
| 1.5 | 30.43 | 22.80 | 5.0 |
| 2 | 30.43 | 22.45 | 4.8 |
| 3 | 30.43 | 21.80 | 4.8 |
| 5 | 30.43 | 21.05 | 5.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zou, L.; Bi, C.; Wang, A. Effect of Dielectric Layer on Miniaturized Patch Antenna Sensor. Sensors 2024, 24, 7608. https://doi.org/10.3390/s24237608
Chen C, Zou L, Bi C, Wang A. Effect of Dielectric Layer on Miniaturized Patch Antenna Sensor. Sensors. 2024; 24(23):7608. https://doi.org/10.3390/s24237608
Chicago/Turabian StyleChen, Caifeng, Lei Zou, Chenglong Bi, and Andong Wang. 2024. "Effect of Dielectric Layer on Miniaturized Patch Antenna Sensor" Sensors 24, no. 23: 7608. https://doi.org/10.3390/s24237608
APA StyleChen, C., Zou, L., Bi, C., & Wang, A. (2024). Effect of Dielectric Layer on Miniaturized Patch Antenna Sensor. Sensors, 24(23), 7608. https://doi.org/10.3390/s24237608








