Response of the bGeigie Nano and CzechRad Monitors to Secondary Cosmic Radiation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Secondary Cosmic Radiation
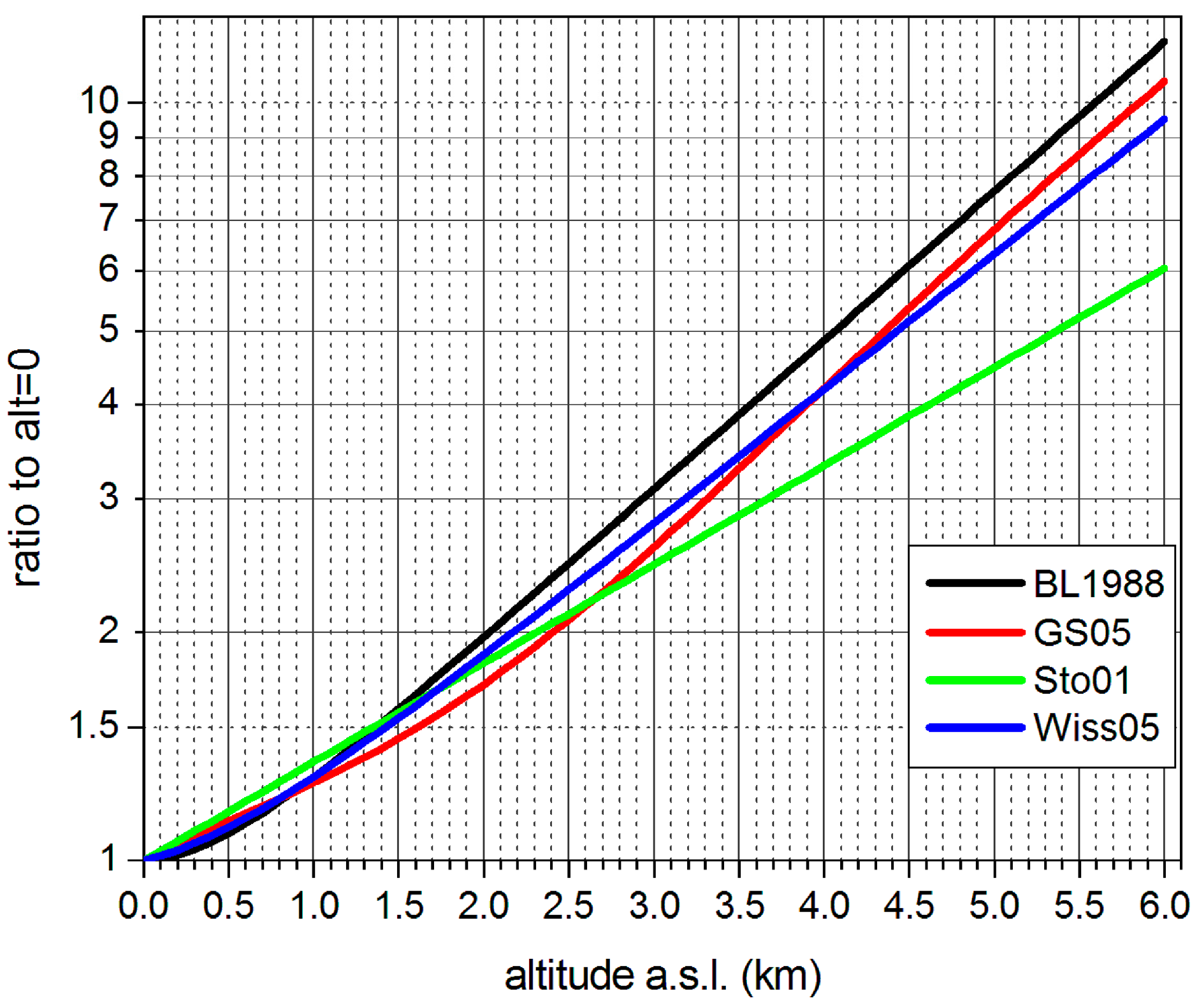
- Mass of air above the measurement point, related to air pressure, is in turn mainly controlled by altitude above sea level (a.s.l.) plus variations caused by meteorological variability. For estimating local SCR dose rate, usually altitude a.s.l. is taken as an approximate predictor. Ref. [13] gives the figure ΔADR/ADR ≈ −0.01564 Δp [kPa] for muons. For variations of 10 kPa (100 hPa; standard air pressure at sea level is 1013 hPa) due to weather variation, one thus finds about 15.6% ADR variation.
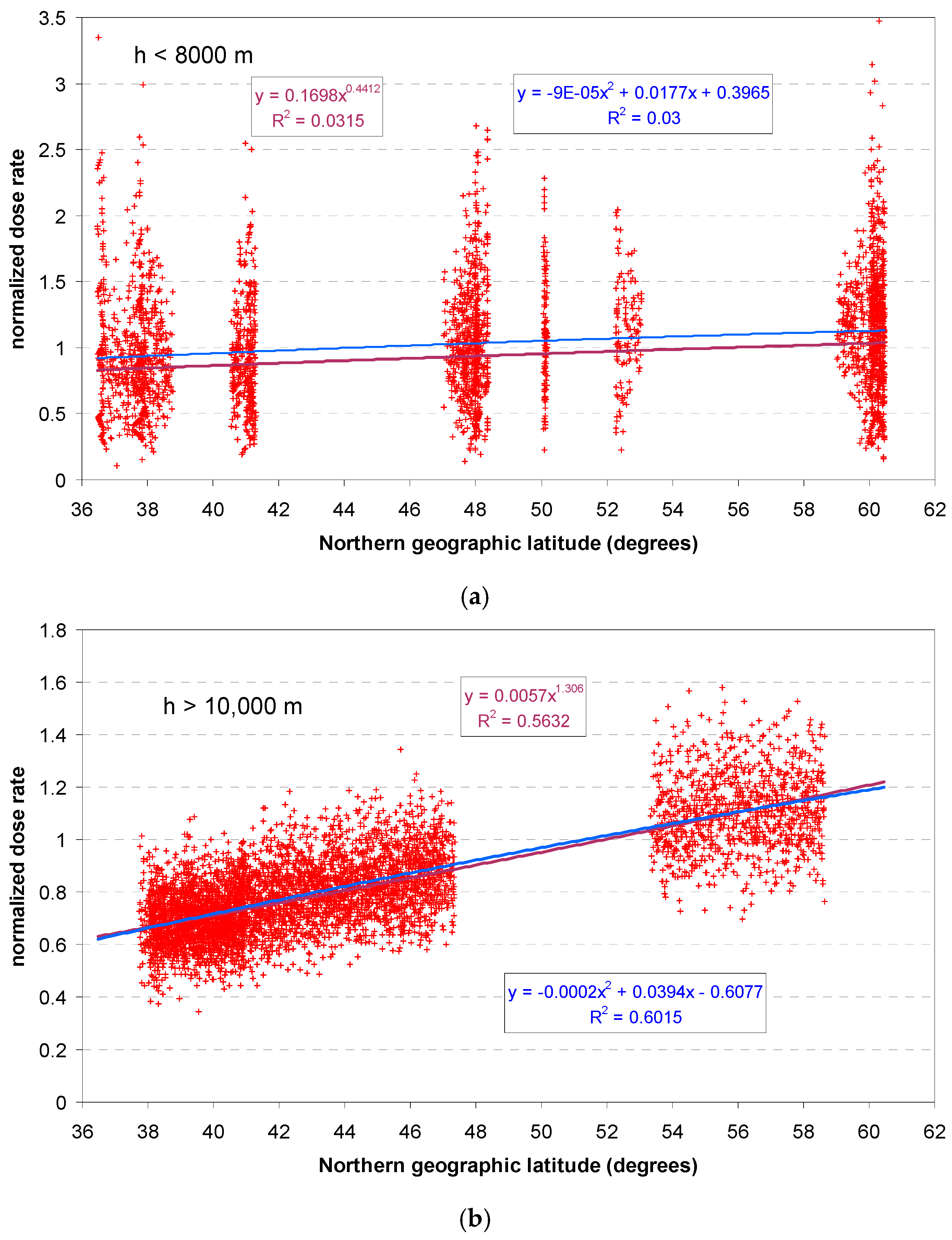
- Geomagnetic latitude: There is a latitude dependence of the SCR intensity caused by the geomagnetic shielding of primary cosmic rays before they enter the atmosphere. Therefore, the intensity of SCR at certain altitudes also depends on geomagnetic latitude. The effect origins from the fact, that to the geomagnetic field measured by the geographically variable, the so-called cut-off rigidity; e.g., Figure 2 in [14]. Geomagnetic and geographical latitudes coincide only very approximately; the lowest SCR intensity is found in the equatorial region, and the highest at high latitudes. The geomagnetic axis is the theoretical line between the geomagnetic poles, not to be confused with the magnetic poles. Both axes do not coincide with the geographical axis and moreover, the magnetic axis does not pass through the centre of the Earth. Geomagnetic coordinates are defined relative to the geomagnetic poles. The geomagnetic field appears distorted compared to the geometry of the globe (e.g., https://geomag.bgs.ac.uk/education/earthmag.html accessed on 4 November 2024). The SCR intensity difference between the equator and 60° N is about 10% at ground level [15], higher for higher altitudes. From figures given in (Table 2) in [16] one finds that the intensity in terms of dose equivalent rate is 6% and 10% higher at 55° N than 43° N at sea level and at 3 km a.s.l., respectively, during solar minimum. During solar maximum, the figures are 2% and 6%, respectively.
- Solar activity: Higher solar activity and resulting solar wind leads to repulsion of galactic cosmic rays. SCR intensity therefore follows the about 11-year solar activity cycle (which is itself modulated by longer-term cycles and overlaid by irregular variability components). During solar minima, SCR intensity at ground altitude can be up to 10% higher than during solar maxima. An irregular component is added by so-called Forbush events, which are sudden and short-term (lasting about a week) decreases in SCR due to solar coronal mass ejection. The last solar activity minimum occurred about 2019/2020 [17], and the last activity maximum in 2024, which is expected to extend to 2025. This type of solar event can produce protons with energy high enough that they generate particle cascades which can be observed at the ground level, called Ground Level Events or GLEs. These are short pulses which last about an hour, followed by a decay tail. GLEs are rare, and so far, we have made no attempt to detect them with our means.
- Seasonal effect: According to [13,18], “owing to temperature changes in the upper layer of the atmosphere, the muon production rises in summer and, thus, the mean path [length] to ground level increases”. Due to the short lifetime of muons, a longer journey to the ground in summer results in fewer muons reaching the ground. The variation amounts to about 3%. (The result is valid for northern temperate latitudes).
2.2. Response of G-M Detectors to Cosmic Radiation
2.2.1. Response to Muons
2.2.2. Response of G-M Detectors to Neutrons
2.3. Dependence of Secondary Radiation on External Factors
2.3.1. Altitude Dependence
2.3.2. Dependence on Solar Activity
2.3.3. Dependence on Geographical Latitude
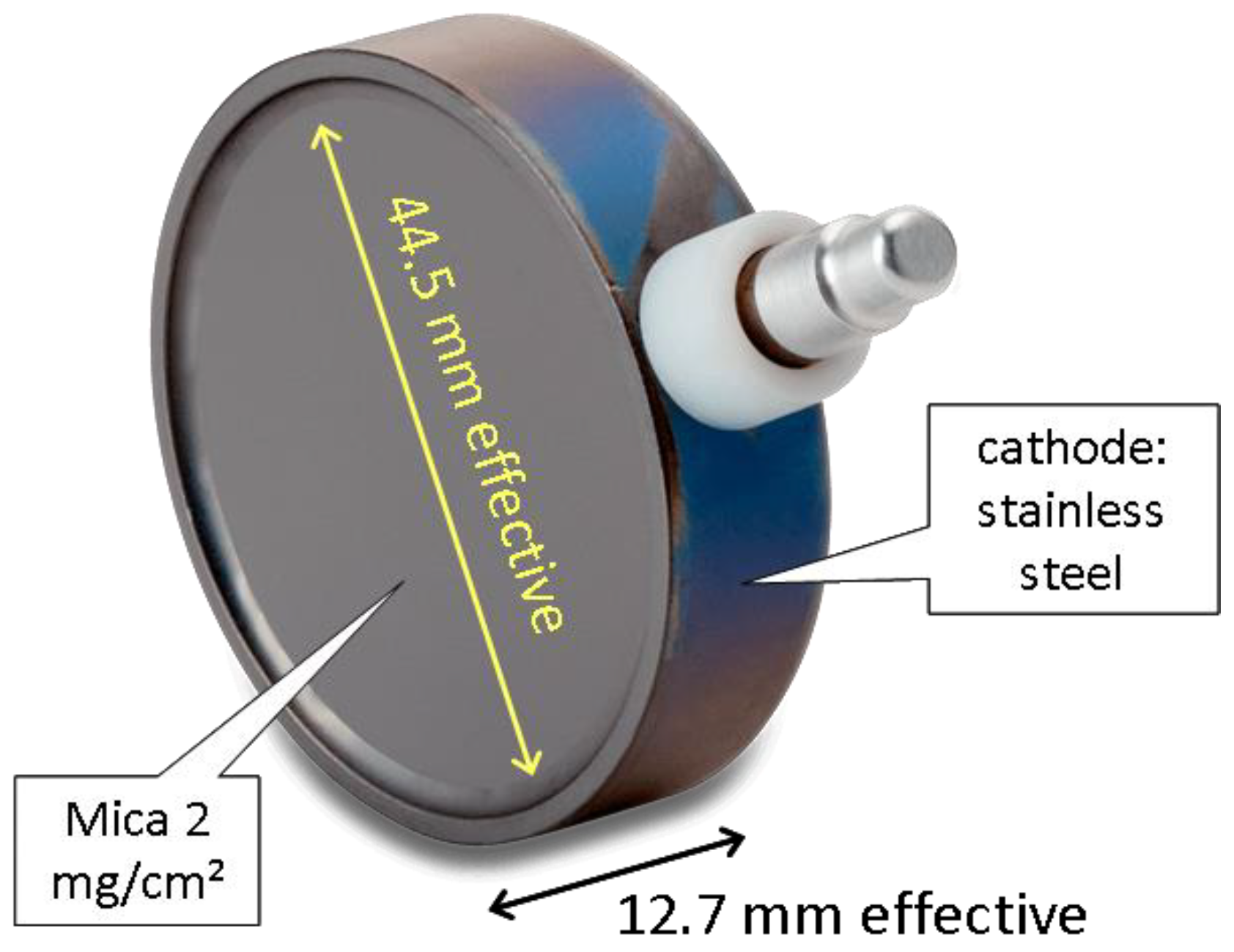
2.4. The bGeigie Nano and CzechRad Monitors
2.5. Components of Ambient Dose Rate Readings
2.5.1. Internal Background
2.5.2. Measurement in Absence of the Terrestrial Component
2.5.3. Radon Progeny
2.6. Determination of the Internal Background and Cosmic Response
2.6.1. Method I: Aircraft Ascent and Descent
2.6.2. Method II: Measurement Above Water Bodies in Different Altitudes
- All measurements were performed with detectors which have the same BG. This is not exactly true in reality, but one has to live with this uncertainty, about 10%.
- Outdoor radon concentration can be guessed approximately from experiences about mean Rn concentration in different geographical regions. The value is subject to meteorological variability (specifically, height of the atmospheric mixing layer), of which we have no control, but which we can guess to vary by factors (0.1, 5) and more. Many studies have been conducted about temporal variability in outdoor Rn concentration. References include UNSCEAR (1988) [11] (Annex A, §85ff), [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]. It would be worthwhile to further evaluate the literature to refine estimation of the ADR component due to Rn’s levels dependence on measurement season and time.
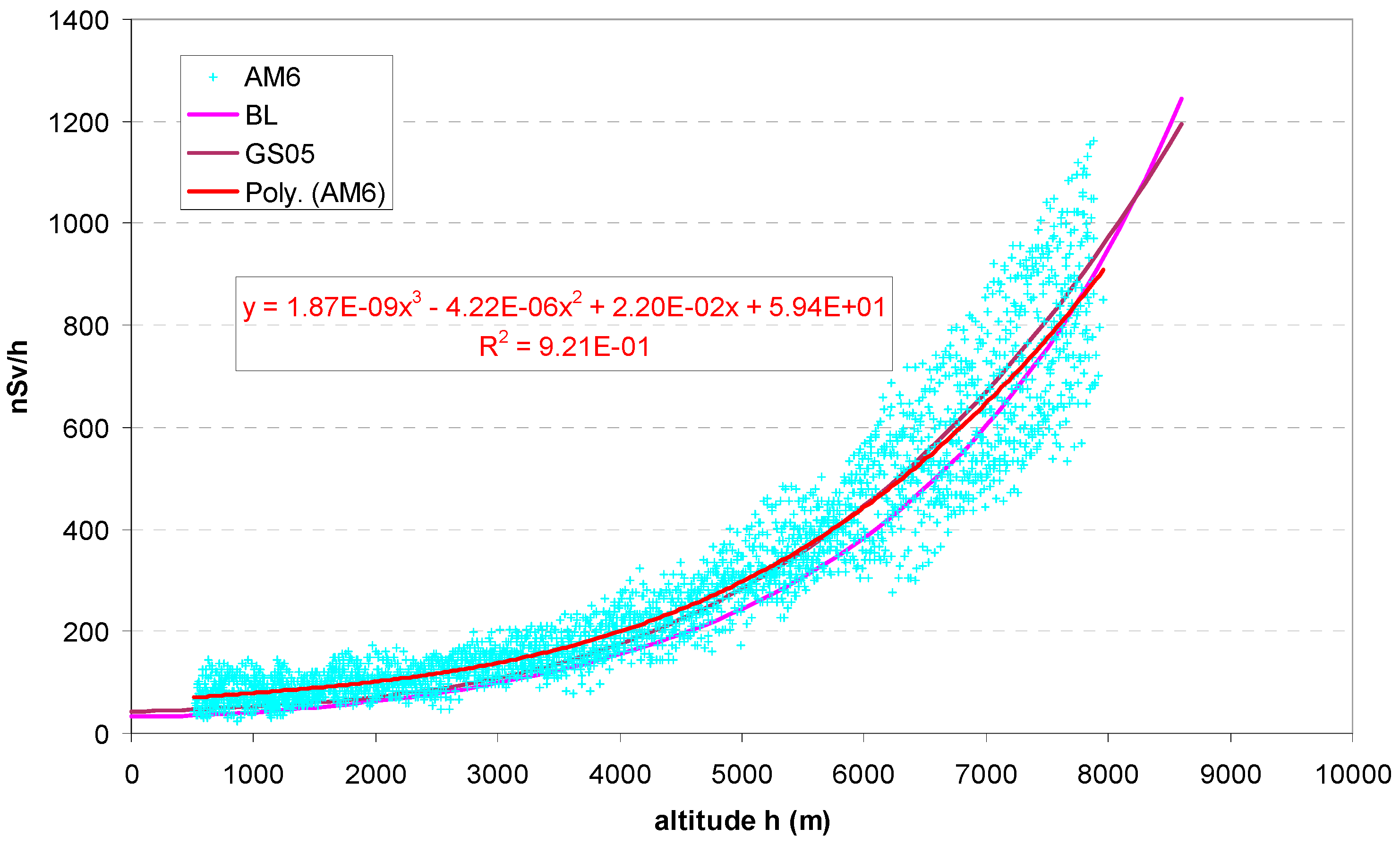
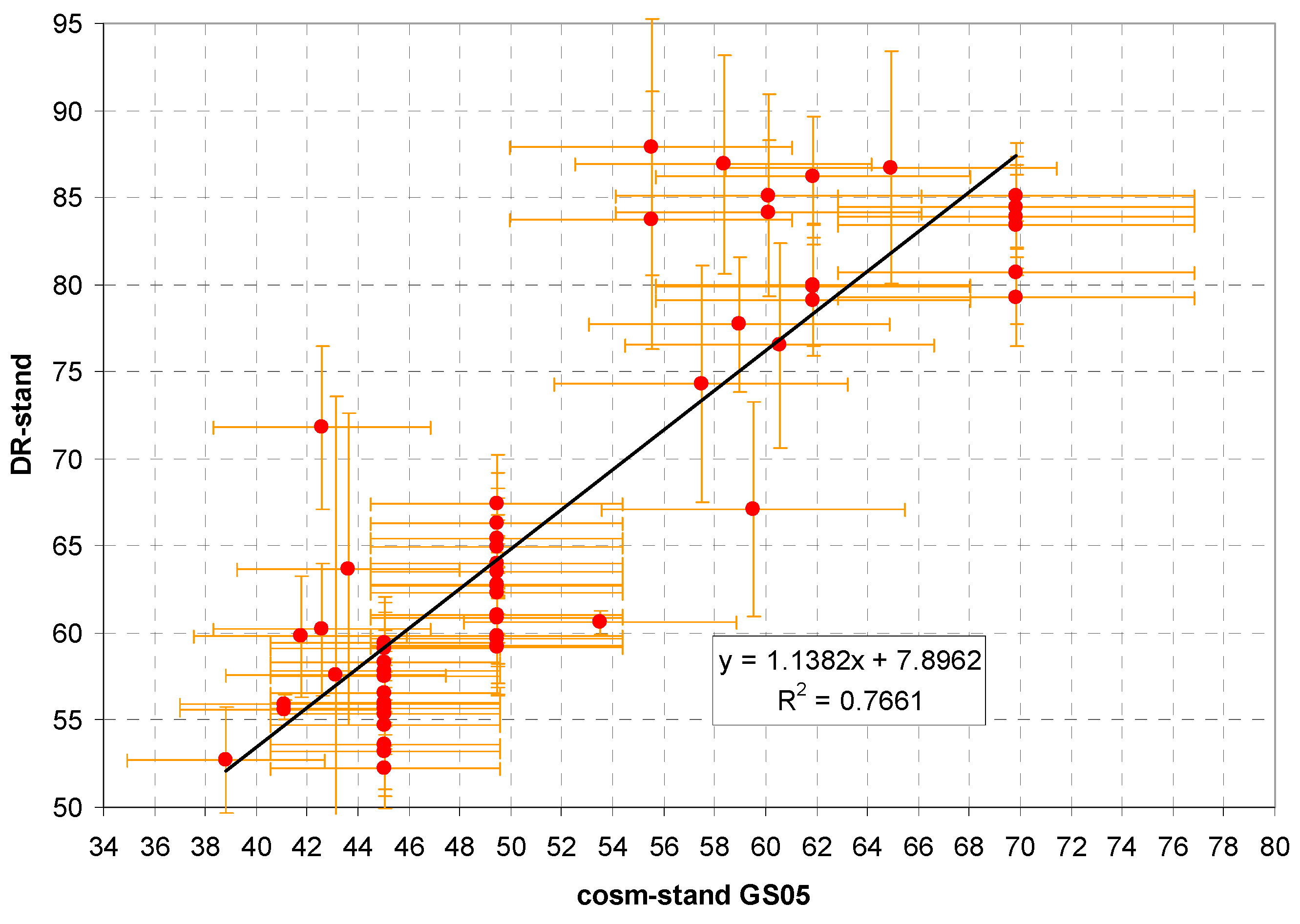
- For the cosmic component, we use the estimated value of the GS-05 G-M counter in the vertical position (used in the German Early Warning Network) in the northern temperate latitude according to the formula given in [3], Equation (2) and the Bouville–Lowder formula (Equation (1)). Factors f are applied: for low latitudes, cosmic dose rate is assumed 10% lower; if the value Y(raw) by bGeigie has been measured with the detector horizontal (axis vertical), f = 1.412 (see Section 2.3). No distinction between window facing up or down is made at this stage. The uncertainty of cosm × f is probably 10% at most.
3. Results and Discussion
3.1. Measurements in Aircraft
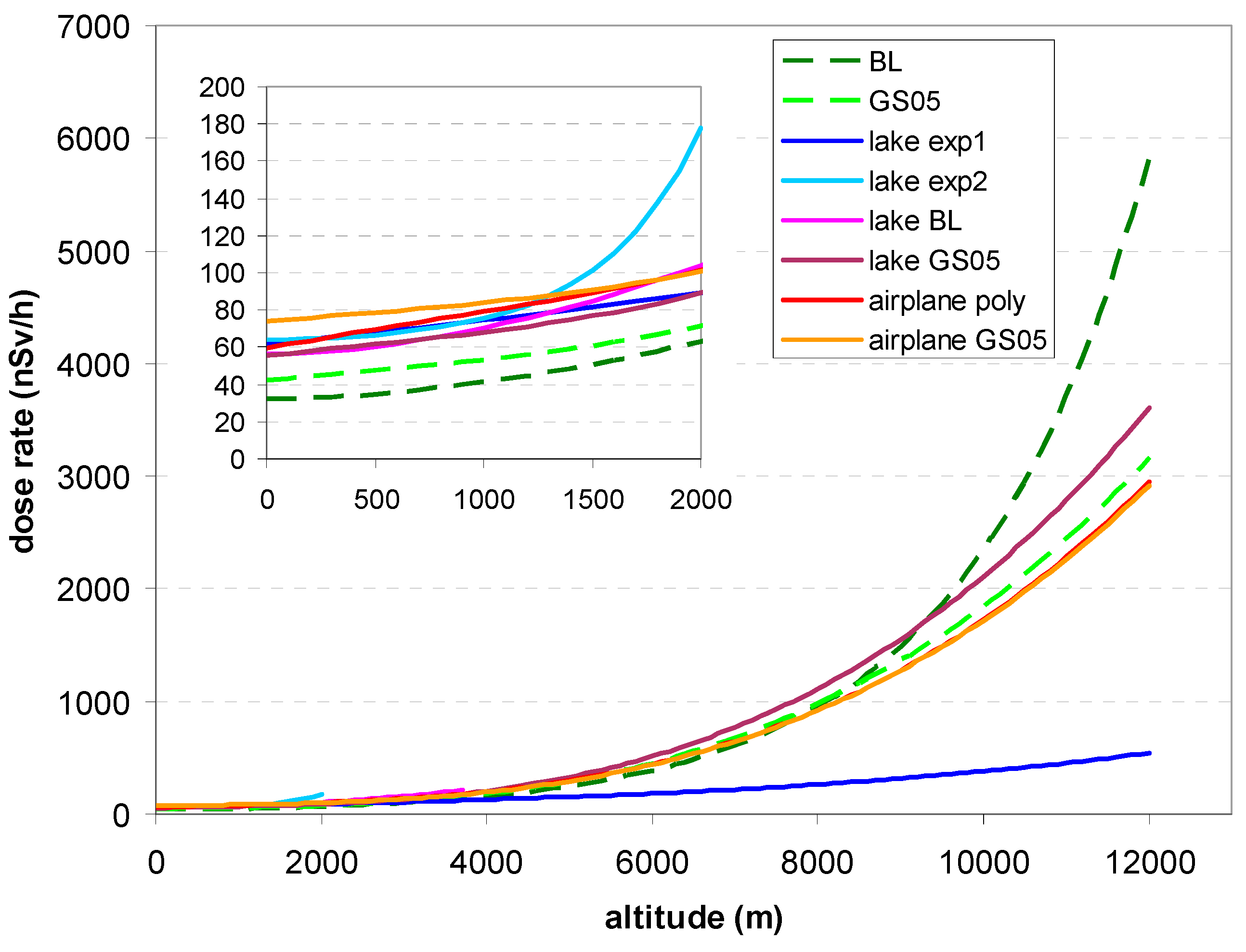
3.1.1. Dose Rate by Altitude
3.1.2. Latitude Effect
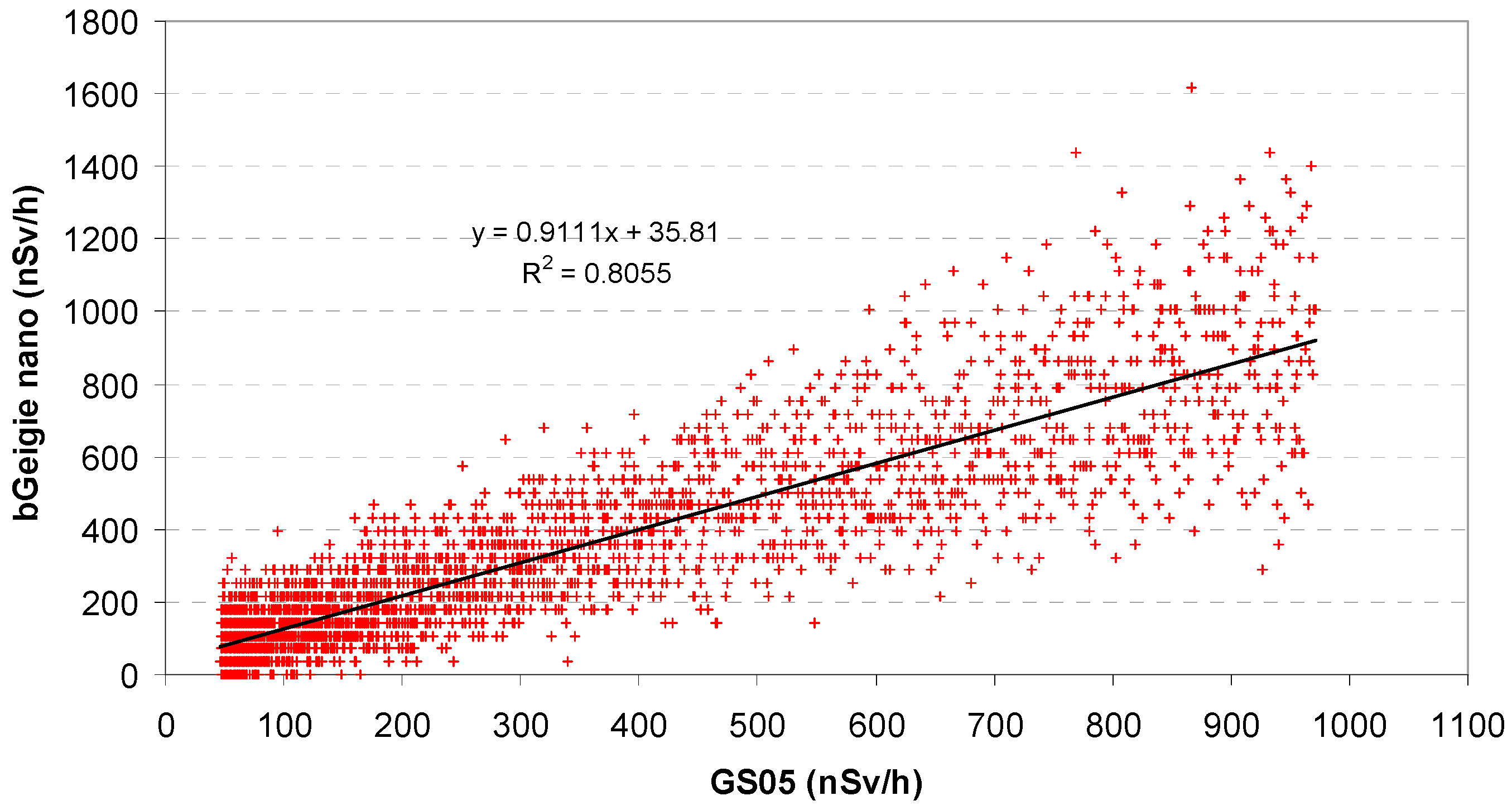
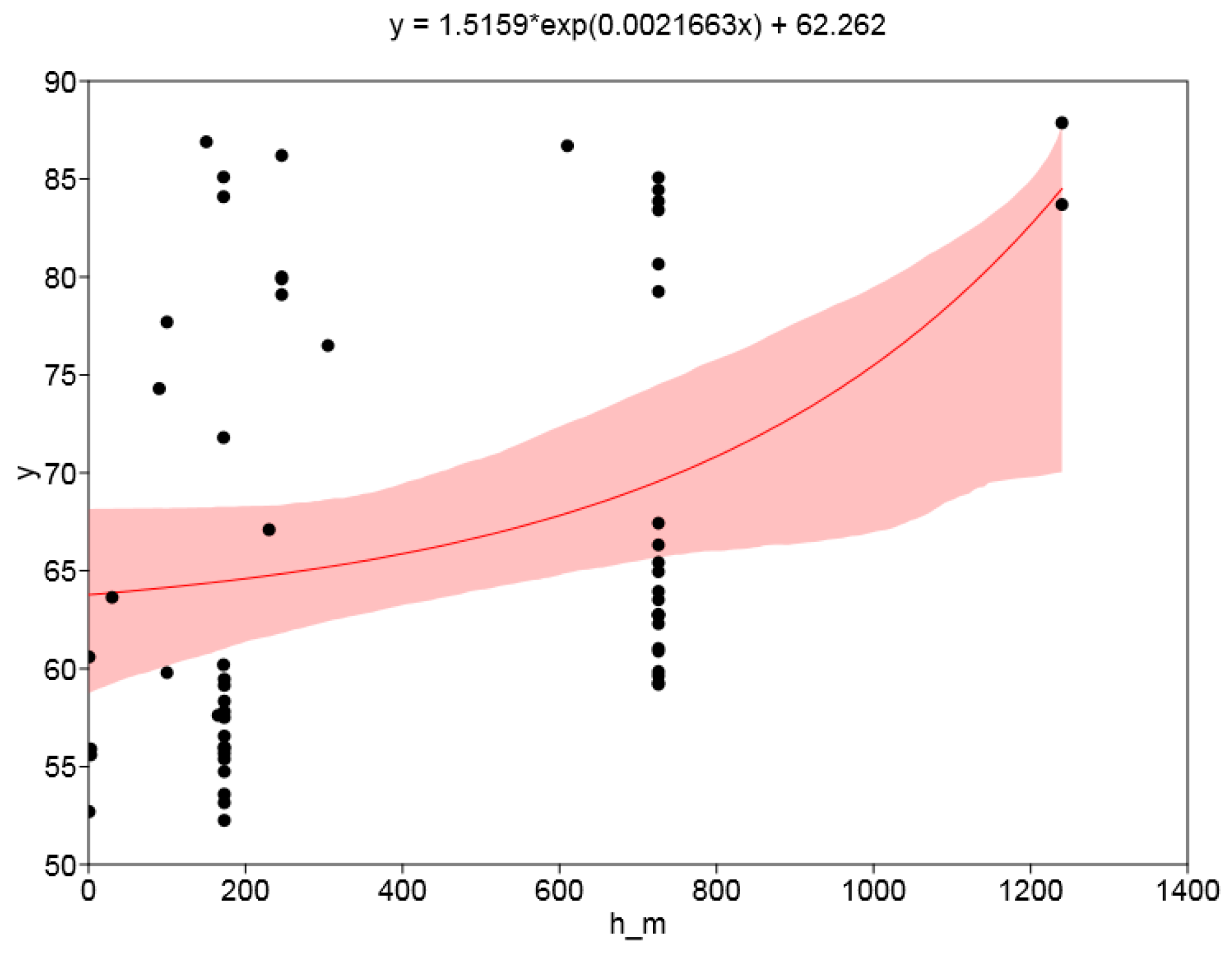
3.2. Measurements Above Water Bodies
a = 62.14 nSv/h, b = 0.000181 m−1, r2 = 0.12
a = 1.516 nSv/h, b = 0.002166 m−1; c = 62.26 nSv/h; r2 = 0.13; a + c = 63.78 nSv/h.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADR | Ambient dose rate |
| ADER | Ambient dose equivalent rate |
| AM, SD, SE | arithmetical mean, standard deviation, standard error |
| a.s.l. | above sea level |
| BG | background |
| CS, CM | Citizen Science, Monitoring |
| cpm | counts per minute |
| DCF | dose conversion factor |
| G-M counter | Geiger Müller counter |
| QA | Quality Assurance |
| SCR | Secondary cosmic radiation |
Appendix A

References
- Vohland, K.; Landzandstra, A.; Ceccaroni, L.; Lemmens, R.; Perelló, J.; Ponti, M.; Samson, R.; Wagenknecht, K. (Eds.) The Science of Citizen Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Brown, A.; Franken, P.; Bonner, S.; Dolezal, N.; Moross, J. Safecast: Successful citizen-science for radiation measurement and communication after Fukushima. J. Radiol. Prot. 2016, 36, S82–S101. [Google Scholar] [CrossRef] [PubMed]
- Bossew, P.; Kuča, P.; Helebrant, J. Mean ambient dose rate in various cities, inferred from Safecast data. J. Environ. Radioact. 2020, 225, 106363. [Google Scholar] [CrossRef] [PubMed]
- Bossew, P.; Kuča, P.; Helebrant, J. Citizen monitoring of ambient dose rate: Metrological challenges. In Proceedings of the RAD—10th International Conference on Radiation in Various Fields of Research, Herceg Novi, Montenegro, 13–17 June 2022; Available online: https://www.rad2022-spring.rad-conference.org/ (accessed on 4 November 2024).
- Bossew, P.; Kuča, P.; Helebrant, J. rue and spurious anomalies in ambient dose rate monitoring. In Proceedings of the ICHLERA, 10th International Conference on High Level Environmental Radiation Areas, Strasbourg, France, 27–30 June 2022; Available online: https://indico.in2p3.fr/event/19295/ (accessed on 4 November 2024).
- Kuča, P.; Helebrant, J.; Bossew, P. Safecast—A Citizen Science initiative for ambient dose rate mapping; Quality assurance issues. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. EGU21-1343. [Google Scholar] [CrossRef]
- Kuča, P.; Helebrant, J.; Bossew, P. Safecast—Citizen Science for radiation monitoring. RAP Conf. Proc. 2021, 6, 32–38. [Google Scholar] [CrossRef]
- Kuča, P.; Helebrant, J.; Bossew, P. Characterization of the bGeigie Nano instrument used in Citizen Science dose rate monitoring. In Proceedings of the RAP—International Conference on Radiation Applications, Thessaloniki, Greece, 6–10 June 2022; Available online: https://www.rap-conference.org/22/ (accessed on 4 November 2024).
- Kuča, P.; Helebrant, J.; Bossew, P. Citizen monitoring of ambient dose rate: The Safecast project. In Proceedings of the IRPA—6th European Congress on Radiation Protection, Budapest, Hungary, 30 May–3 June 2022. [Google Scholar]
- European Commission; Joint Research Centre; Cinelli, G.; De Cort, M.; Tollefsen, T. (Eds.) European Atlas of Natural Radiation; Publication Office of the European Union: Luxembourg, 2019; ISBN 978-92-76-08259-0. Available online: https://remon.jrc.ec.europa.eu/About/Atlas-of-Natural-Radiation/Download-page (accessed on 4 November 2024).
- UNSCEAR: United Nations Scientific Committee on the Effects of Atomic Radiation Reports to the General Assembly, with Annexes. Available online: https://www.unscear.org/unscear/en/publications/scientific-reports.html (accessed on 10 November 2022).
- Wissmann, F. Variations observed in environmental radiation at ground level. Radiat. Prot. Dosim. 2006, 118, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Spurný, F. Radiation doses at high altitudes and during space flights. Radiat. Phys. Chem. 2000, 61, 301–307. [Google Scholar] [CrossRef]
- Bouville, A.; Lowder, W.M. Human population exposure to cosmic radiation. Radiat. Prot. Dosim. 1988, 24, 293–299. [Google Scholar] [CrossRef]
- Lowder, W.M.; O’Brien, K. Cosmic-ray dose rates in the atmosphere. In HASL-254 Report; Health and Safety Laboratory, U.S. Atomic Energy Commission: New York, NY, USA, 1972. [Google Scholar]
- SpaceWeather. Solar Cycle Progression. 2022. Available online: https://www.spaceweatherlive.com/en/solar-activity/solar-cycle.html (accessed on 4 November 2024).
- Wissmann, F.; Dangendorf, V.; Schrewe, U. Radiation exposure at ground level by secondary cosmic radiation. Radiat. Meas. 2005, 39, 95–104. [Google Scholar] [CrossRef]
- Wissmann, F.; Rupp, A.; Stöhlker, U. Characterization of dose rate instruments for environmental radiation monitoring. Kerntechnik 2007, 72, 193–198. [Google Scholar] [CrossRef]
- Cinelli, G.; Bossew, P.; Hernández-Ceballos, M.A.; Tollefsen, T.; De Cort, M. Long-term variation of cosmic dose rate. In Proceedings of the ENVIRA (4th International Conference on Environmental Radioactivity), Vilnius, Lithuania, 29 May–2 June 2017; p. 124. Available online: http://envira2017.ftmc.lt/files/abstractbook20170802.pdf (accessed on 4 November 2024).
- Sato, T. Evaluation of World Population-Weighted Effective Dose due to Cosmic Ray Exposure. Sci. Rep. 2001, 6, 33932. [Google Scholar] [CrossRef]
- ICRU. ICRU Report 84, Reference Data for the Validation of Doses from Cosmic-Radiation Exposure of Aircraft Crew. J. ICRU 2010, 10. Available online: https://journals.sagepub.com/toc/crua/10/2 (accessed on 4 November 2024).
- Bossew, P.; Cinelli, G.; Hernández-Ceballos, M.; Cernohlawek, N.; Gruber, V.; Dehandschutter, B.; Menneson, F.; Bleher, M.; Stöhlker, U.; Hellmann, I.; et al. Estimating the terrestrial gamma dose rate by decomposition of the ambient dose equivalent rate. J. Environ. Radioact. 2017, 166, 296–308. [Google Scholar] [CrossRef] [PubMed]
- Spiers, F.W.; Gibson, J.A.B.; Thompson, I.M.G. A Guide to the Measurement of Environmental Gamma-Ray Dose Rate. British Committee on Radiation Units and Measurements. 1981. Available online: http://cds.cern.ch/record/1057200/files/CM-P00066948.pdf (accessed on 22 July 2020).
- Lewis, V.E.; Hunt, J.B. Fast neutron sensitivities of Geiger-Mueller counter gamma dosemeters. Phys. Med. Biol. 1978, 23, 888–893. [Google Scholar] [CrossRef] [PubMed]
- Guldbakke, S.; Jahr, R.; Lesiecki, H.; Schölermann, H. Neutron Sensitivity of Geiger-Müller Photon Dosemeters for Neutron Energies Between 100 keV and 19 MeV. 1980. Available online: https://www.irpa.net/irpa5/cdrom/VOL.2/J2_37.PDF (accessed on 4 November 2024).
- Mijnheer, B.J.; Guldbakke, S.; Lewis, V.E.; Broerse, J.J. Comparison of the fast-neutron sensitivity of a Geiger-Muller counter using different techniques. Phys. Med. Biol. 1982, 27, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Maughan, R.L.; Yudelev, M.; Kota, C. A measurement of the fast-neutron sensitivity of a Geiger-Müller detector in the pulsed neutron beam from a superconducting cyclotron. Phys. Med. Biol. 1996, 41, 1341–1351. [Google Scholar] [CrossRef]
- Nakamura, T. Cosmic-ray Neutron Spectrometry and Dosimetry. J. Nucl. Sci. Technol. 2008, 45 (Suppl. S5), 1–7. [Google Scholar] [CrossRef]
- Lowder, W.M.; Beck, H.L. Cosmic-ray ionization in the lower atmosphere. J. Geophys. Res. 1966, 71, 4661–4668. [Google Scholar] [CrossRef]
- Cinelli, G.; Gruber, V.; De Felice, L.; Bossew, P.; Hernandez-Ceballos, M.A.; Tollefsen, T.; Mundigl, S.; De Cort, M. European annual cosmic-ray dose: Estimation of population exposure. J. Maps 2017, 13, 812–821. [Google Scholar] [CrossRef]
- Hernández-Ceballos, M.A.; Cinelli, G.; Marín Ferrer, M.; Tollefsen, T.; De Felice, L.; Nweke, E.; Tognoli, P.V.; Vanzo, S.; De Cort, M. A climatology of 7Be in surface air in European Union. J. Environ. Radioact. 2015, 141, 62–70. [Google Scholar] [CrossRef]
- BGS (British Geological Survey; n.y.): The Earth’s Magnetic Field: An Overview. Available online: https://geomag.bgs.ac.uk/education/earthmag.html. Geomagnetic Coordinate Calculator. Available online: https://geomag.bgs.ac.uk/data_service/models_compass/coord_calc.html (accessed on 25 October 2024).
- World Data Center for Geomagnetism, Data Analysis Center for Geomagnetism and Space Magnetism, Graduate School of Science, Kyoto University Kyoto. Available online: https://wdc.kugi.kyoto-u.ac.jp/igrf/gggm/ (accessed on 25 October 2024).
- O’Brien, K.; Friedberg, W.; Sauer, H.H.; Smart, D.F. Atmospheric cosmic rays and solar energetic particles at aircraft altitudes. Environ. Int. 1996, 22, 9–44. [Google Scholar] [CrossRef]
- Hůlka, J.; Kuča, P.; Helebrant, J.; Rozlívka, Z. Citizens Measurements in Radiation Protection and Emergency Preparedness and Response—Its Role, Its Role, Pros and Cons. In Proceedings of the EUROSAFE, Paris, France, 6–7 November 2017. [Google Scholar]
- Kuča, P.; Helebrant, J.; Hůlka, J. Role of Citizens Measurements in Radiation Protection, Emergency Preparedness and Response—Its Pros and Cons. In Proceedings of the ICRP 4th International Symposium on the System of Radiological Protection & 2nd European Radiological Protection Week, Paris, France, 10–12 October 2017. Available online: http://www.icrp-erpw2017.com/upload/presentations/ERPW%20Communication/Session_02/Session%2002_5_KUCA_Presentation.pdf (accessed on 26 January 2019).
- Helebrant, J.; Kuča, P.; Hůlka, J. RAMESIS: Radiační měřící síť pro instituce a školy k zajištění včasné informovanosti a zvýšení bezpečnosti občanů měst a obcí. 2018. (In Czech). Available online: https://www.suro.cz/cz/vyzkum/vysledky/safecast/09Hulka.pdf (accessed on 26 January 2019).
- SÚRO. Detektor záření SAFECAST a jeho využití pro veřejnost. 2019. (In Czech). Available online: https://www.suro.cz/cz/vyzkum/vysledky/safecast (accessed on 26 January 2019).
- QGIS—A Free and Open Source Geographic Information System. Available online: https://www.qgis.org/en/site/ (accessed on 4 November 2024).
- Vanek, M.; Ďuriková, A.; Salva, J. Safecast bGeigie Nano as a Tool for Teaching Students to Understand Monitoring Environmental Radioactivity. Proc., Conference: Earth in a Trap? 2018. Analytical Methods in Fire and Environmental Science, Hodruša-Hámre, Slovak Republic. Available online: https://www.researchgate.net/publication/326031794_Safecast_bGeigie_Nano_as_a_tool_for_teaching_students_to_understand_monitoring_environmental_radioactivity (accessed on 26 January 2019).
- CzechRad. Mobile detector for radiation mapping—Similar to SAFECAST bGeigie Nano. 2021. Available online: https://github.com/juhele/CzechRad (accessed on 20 February 2021).
- Yogeshwar, R. Calibration of SAFECAST bGeigie-Nano—Radiation Detector (# 1025); Document supplied to one of the authors (PB) by Safecast; Safecast: Shibuya, Japan, 2014. [Google Scholar]
- Wagner, E.; Sorom, R.; Wiles, L. Radiation monitoring for the masses. Health Phys. 2016, 110, 37–44. [Google Scholar] [CrossRef]
- Tanji, T.; Okino, M.; Sugioka, I.; Mochizuki, S. Radon and its Daughters in the Atmosphere Over the Equatorial Pacific Ocean. Radiat. Prot. Dosim. 1992, 45, 399–401. [Google Scholar] [CrossRef]
- Čeliković, I.; Pantelić, G.; Vukanac, I.; Krneta Nikolić, J.; Živanović, M.; Cinelli, G.; Gruber, V.; Baumann, S.; Quindos Poncela, L.S.; Rabago, D. Outdoor Radon as a Tool to Estimate Radon Priority Areas—A Literature Overview. Int. J. Environ. Res. Public Health 2022, 19, 662. [Google Scholar] [CrossRef] [PubMed]
- ICRP. Dose coefficients for external exposures to environmental sources. ICRP Publication 144. Ann. ICRP 2020, 49, 111–145. [Google Scholar] [CrossRef]
- EPA. External Exposure to Radionuclides in Air, Water and Soil—Federal Guidance Report No. 5; EPA 402-R-19-002; 2019. Available online: https://www.epa.gov/sites/default/files/2019-08/documents/fgr_15_final_508_2019aug02.pdf (accessed on 4 November 2024).
- Smetsers, R.C.G.M.; Blaauboer, R.O. A Dynamic Compensation Method for Natural Ambient Dose Rate Based on 6 Years Data from the Dutch Radioactivity Monitoring Network. Radiat. Prot. Dosim. 1997, 69, 19–31. [Google Scholar] [CrossRef]
- DOE. External Dose-Rate Conversion Factors for Calculation of Dose to the Public. DOE/EH—0070. 1988. Available online: https://www.osti.gov/servlets/purl/6953527 (accessed on 4 November 2024).
- Kocher, D.C. Dose Rate Conversion Factors for External Exposure to Photons and Electrons. NUREG/CR-1918. 1981. Available online: https://digital.library.unt.edu/ark:/67531/metadc1058696/m2/1/high_res_d/5020464.pdf (accessed on 4 November 2024).
- Kümmel, M.; Dushe, C.; Müller, S.; Gehrcke, K. Outdoor 222Rn-concentrations in Germany—Part 1—Natural background. J. Environ. Radioact. 2014, 132, 123–130. [Google Scholar] [CrossRef]
- Chen, J.; Harley, N.H. A Review of Indoor and Outdoor Radon Equilibrium Factors—Part I. Health Phys. 2018, 115, 490–499. [Google Scholar] [CrossRef]
- Cuculeanu, V.; Sonoc, C.; Georgescu, M. Radioactivity of Radon and Thoron Daughters in Romania. Radiat. Prot. Dosim. 1992, 45, 83–485. [Google Scholar] [CrossRef]
- Kataoka, T.; Tsukamoto, O.; Yunoki, E.; Michihiro, K.; Sugiyama, H.; Shimizu, M.; Mori, T.; Sahashi, T.; Fujii, S. Variation of 222Rn Concentration in Outdoor Air due to Variation of the Atmospheric Boundary Layer. Radiat. Prot. Dosim. 1992, 45, 403–406. [Google Scholar] [CrossRef]
- Dueñas, C.; Pérez, M.; Fernández, M.C.; Carretero, J. Radon concentrations in surface air and vertical atmospheric stability of the lower atmosphere. J. Environ. Radioact. 1996, 31, 87–102. [Google Scholar] [CrossRef]
- Levin, I.; Born, M.; Cuntz, M.; Langendörfer, U.; Mantsch, S.; Naegler, T.; Schmidt, M.; Varlagin, A.; Verclas, S.; Wagenbach, D. Observations of atmospheric variability and soil exhalation rate of radon-222 at a Russian forest site Technical approach and deployment for boundary layer studies. Tellus 2002, 54B, 462–475. [Google Scholar] [CrossRef]
- Oikawa, S.; Kanno, N.; Sanada, T.; Ohashi, N.; Uesugi, M.; Sato, K.; Abukawa, J.; Higuchi, H. A nationwide survey of outdoor radon concentration in Japan. J. Environ. Radioact. 2003, 65, 203–213. [Google Scholar] [CrossRef] [PubMed]
- Sesana, L.; Ottobrini, B.; Polla, G.; Facchini, U. 222Rn as indicator of atmospheric turbulence: Measurements at Lake Maggiore and on the pre-Alps. J. Environ. Radioact. 2005, 86, 271–288. [Google Scholar] [CrossRef] [PubMed]
- Desideri, D.; Roselli, C.; Feduzi, L.; Assunta Meli, M. Monitoring the atmospheric stability by using radon concentration measurements: A study in a Central Italy site. J. Radioanal. Nucl. Chem. 2006, 270, 523–530. [Google Scholar] [CrossRef]
- Garbero, V.; Dellacasa, G.; Bianchi, D.; Magnoni, M.; Erbetta, L. Outdoor radon concentration measurements: Some correlation with major urban pollutants. Radiat. Prot. Dosim. 2009, 137, 332–335. [Google Scholar] [CrossRef] [PubMed]
- Omori, Y.; Tohbo, I.; Nagahama, H.; Ishikawa, Y.; Takahashi, M.; Sato, H.; Sekine, T. Variation of atmospheric radon concentration with bimodal seasonality. Radiat. Meas. 2009, 44, 1045–1050. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Guo, Q. A long-term investigation of the atmospheric radon concentration in Beijing, China. J. Radiol. Prot. 2009, 29, 263–268. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Q. Observation and analysis of atmospheric radon in Qingdao, China. J. Radiol. Prot. 2011, 31, 129–134. [Google Scholar] [CrossRef]
- Műllerová, M.; Holý, K.; Bulko, M. Results of outdoor radon monitoring in Bratislava and Nováky. Radiat. Prot. Dosim. 2011, 145, 325–328. [Google Scholar] [CrossRef]
- Weller, R.; Levin, I.; Schmithüsen, D.; Nachbar, M.; Asseng, J.; Wagenbach, D. On the variability of atmospheric 222Rn activity concentrations measured at Neumayer, coastal Antarctica. Atmos. Chem. Phys. Discuss. 2013, 13, 32817–32847. Available online: www.atmos-chem-phys-discuss.net/13/32817/2013/ (accessed on 4 November 2024).
- Hayashi, K.; Yasuoka, Y.; Nagahama, H.; Muto, J.; Ishikawa, T.; Omori, Y.; Suzuki, T.; Homma, Y.; Mukai, T. Normal seasonal variations for atmospheric radon concentration: A sinusoidal model. J. Environ. Radioact. 2015, 139, 149–153. [Google Scholar] [CrossRef]
- Holý, K.; Műllerová, M.; Bulko, M.; Holá, O.; Melicherová, T. Outdoor 222Rn behaviour in different areas of Slovakia. NUKLEONIKA 2016, 61, 281–288. [Google Scholar] [CrossRef]
- Bossew, P.; Benà, E.; Chambers, S.; Janik, M. Analysis of outdoor and indoor radon concentration time series recorded with RadonEye monitors. Atmosphere 2024. to be submitted. [Google Scholar]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 9. Available online: http://palaeo-electronica.org/2001_1/past/issue1_01.htm https://www.nhm.uio.no/english/research/resources/past/ (accessed on 2 August 2024).
- Jilek, K.; Slezákova, M.; Thomas, J. Diurnal and seasonal variability of outdoor radon concentration in te area of the NRPI Prague. Rad. Prot. Dosim. 2014, 160, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Bossew, P.; Da Silva, N.; Alberti, H.; Silva, M.A.; Navarro, F.C.; De Oliveira, T.A.; Cardoso Takahashi, L.; de Souza Filho, O.A.; Otero, U.; Kuča, P.; et al. A remarkable small local natural radiation anomaly in Poços de Caldas, Brazil. Eur. Phys. J. Spec. Topics 2024. submitted. [Google Scholar]

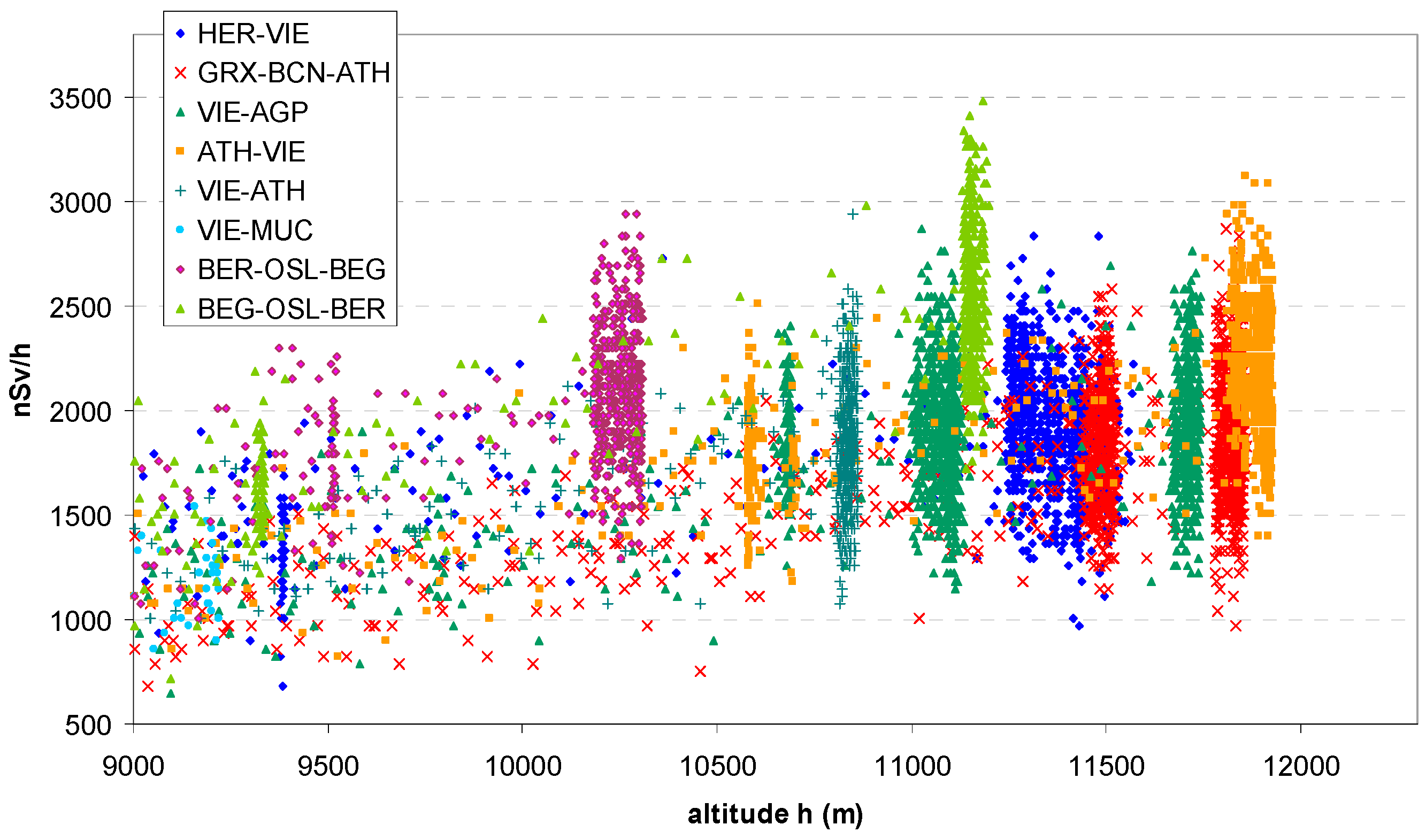
| Flights | Dates | Monitor # | Approximate Cruising Altitudes (km) |
|---|---|---|---|
| Berlin (BER) ↔ Oslo (OSL) ↔ Bergen (BEG) | September 2022 | 3273 | 9.32; 9.51; 10.18–10.30; 11.14–12 |
| Prague (PRG)–Lisbon (LIS) | October 2022 | 3281 | GPS failed at cruising alt. |
| Athens (ATH) ↔ Vienna (VIE) | May–June 2023 | 3273 | 10.80–10.87; 10.58; 11.83–11.93 |
| VIE–Munich (MUC) | November 2023 | 3273 | 9.1–9.2 |
| VIE–Malaga (AGP) | June 2024 | 3273 | 10.68–10.7; 11–11.3; 11.68–11.74 |
| Granada (GRX)–Barcelona (BCN)–ATH | June 2024 | 3273 | 11.4–11.5; 11.78–11.85 |
| Heraklion (HER)–VIE | July 2024 | 3273 | 9.38; 11.24–11.53 |
| Location | Altitude (m) | hor/ver | Remarks; Assumed Rn Concentration |
|---|---|---|---|
| Pacific Ocean, 2019 | 1 | ver | Rn: 0 |
| Helicopter ascent above Mediterranean, Southern France, 2019 | 90–610 | hor | Rn: 0; other: 2; 5 altitude steps, 1 measurement each |
| Sea off Costa Rica, 2020 | 1 | hor | Rn: 0 |
| Lake Balaton, Hungary, 2020 | 100 | both | Rn: 7; 2 measurements |
| North Sea off coast, Germany, 2020 | 3 | ver | Rn: 1; 2 measurements |
| Danube bridge, Vienna, Austria, 2020 | 172 | both | Rn: 7; other: 3; 4 measurements |
| Danube ferry crossing, near Vienna, 2020 | 165 | ver | Rn: 7 |
| Frozen lake near Prague, Czech Republic, 2021 | 246 | hor | Rn: 10; 4 measurements |
| Lipno lake, Southern Czech Republic, 2021 | 726 | both | Rn: 15; 22 measurements |
| Bridge above Hardanger Fjord, Norway, 2022 | 30 | ver | Rn: 5; other: 3; possible interference by adjacent rocks |
| Bortolan lake, Poços de Caldas, Brazil, 2023 | 1240 | both | Rn: 10; other: 2; 2 measurements |
| Lhota lake near Prague, Czech Republic, 2024 | 173 | both | Rn: 10; 14 measurements |
| Statistic | x = stand. GS05 | x = stand. B-L |
|---|---|---|
| Ordinary least square: | ||
| intercept | 7.90 ± 4.40 | 7.22 ± 4.16 |
| slope | 1.138 ± 0.083 | 1.538 ± 0.105 |
| Orthogonal (RMA): | ||
| intercept | −0.5 ± 4.4 | −0.3 ± 4.2 |
| slope | 1.300 ± 0.083 | 1.731 ± 0.105 |
| r2; p (both): | 0.77; 1.2 × 10−19 | 0.79; 6.8 × 10−21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuča, P.; Helebrant, J.; Bossew, P. Response of the bGeigie Nano and CzechRad Monitors to Secondary Cosmic Radiation. Sensors 2024, 24, 7915. https://doi.org/10.3390/s24247915
Kuča P, Helebrant J, Bossew P. Response of the bGeigie Nano and CzechRad Monitors to Secondary Cosmic Radiation. Sensors. 2024; 24(24):7915. https://doi.org/10.3390/s24247915
Chicago/Turabian StyleKuča, Petr, Jan Helebrant, and Peter Bossew. 2024. "Response of the bGeigie Nano and CzechRad Monitors to Secondary Cosmic Radiation" Sensors 24, no. 24: 7915. https://doi.org/10.3390/s24247915
APA StyleKuča, P., Helebrant, J., & Bossew, P. (2024). Response of the bGeigie Nano and CzechRad Monitors to Secondary Cosmic Radiation. Sensors, 24(24), 7915. https://doi.org/10.3390/s24247915





