High-Precision Atom Interferometer-Based Dynamic Gravimeter Measurement by Eliminating the Cross-Coupling Effect
Abstract
1. Introduction
2. Theoretical Methods
2.1. Joint Gravity Measurement Process
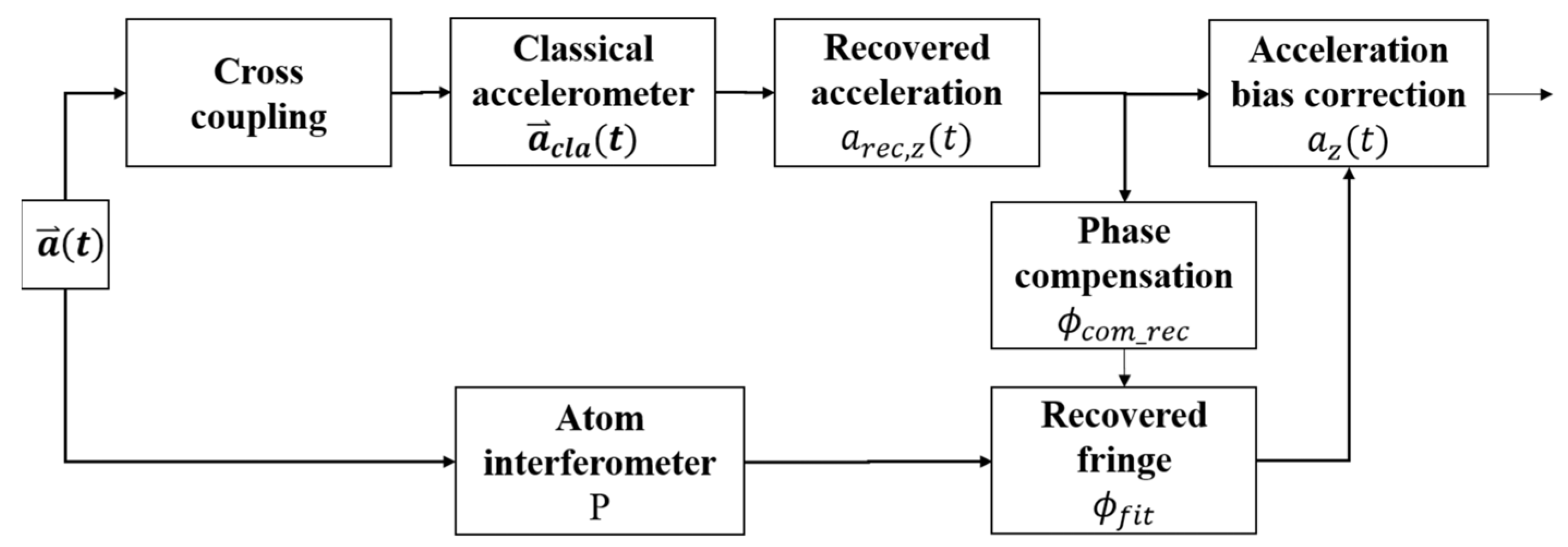
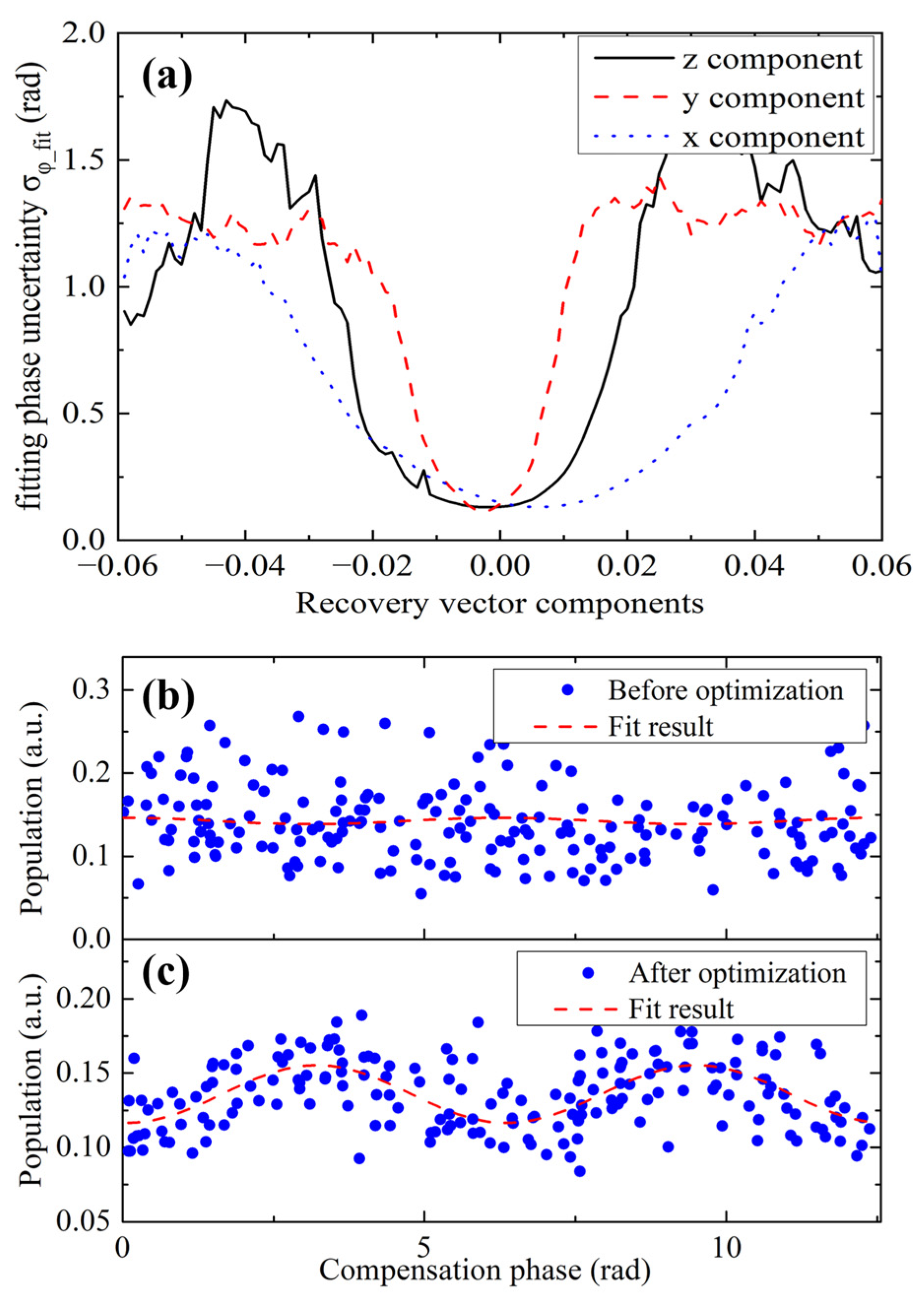
2.2. Noise Induced by the Cross-Coupling Effect and Introduction of the Recovery Vector
3. Marine Gravity Measurement Experiment
3.1. Experiment Apparatus
3.2. Systematic Error Evaluation of the AI-Based Gravimeter
3.3. Gravity Comparison under the Mooring State
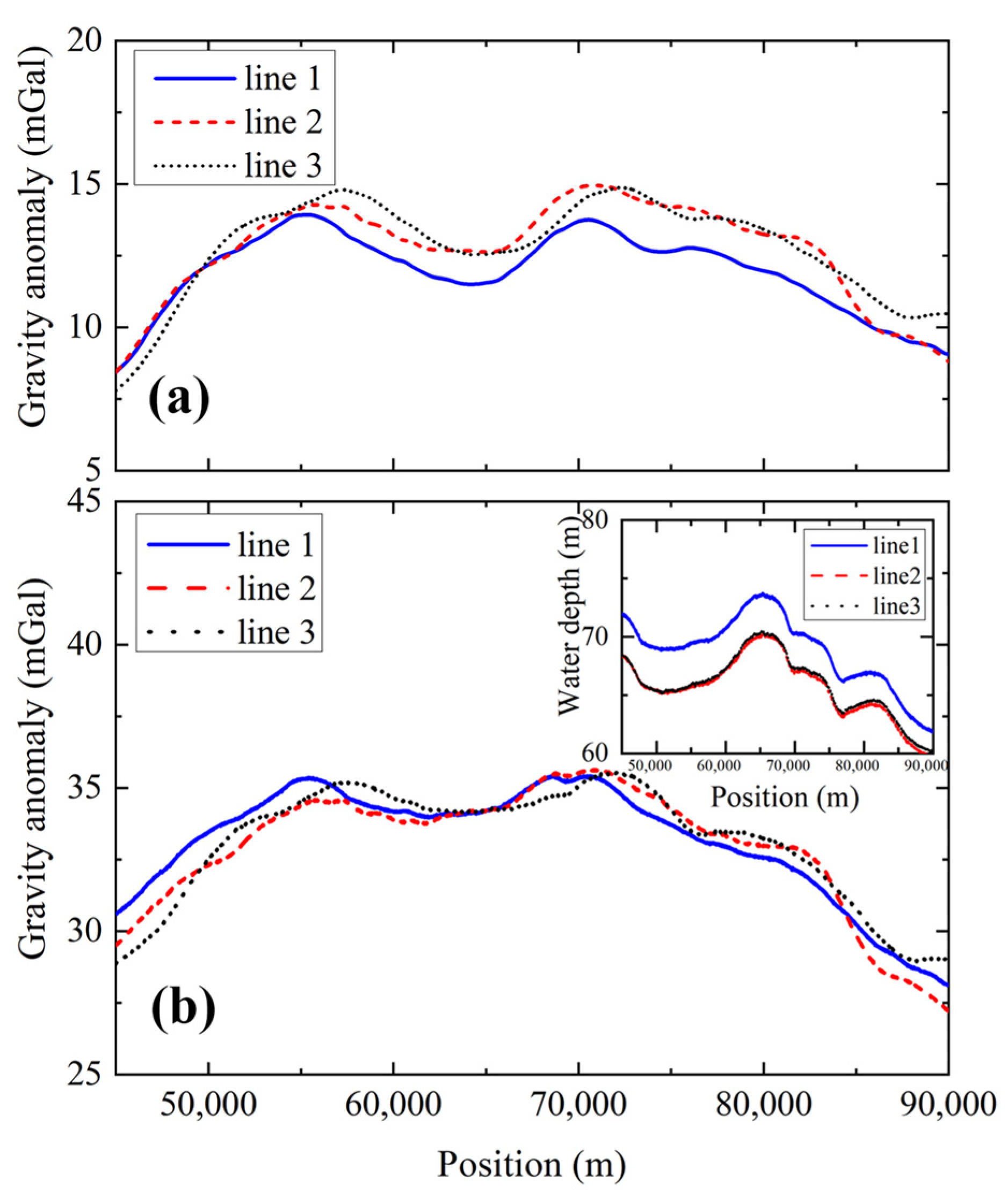
3.4. Gravity Measurement under the Sailing State
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Gravity Difference Induced by the Latitude and Height Differences
Appendix B. Definitions of the Inner and External Coincidence Accuracy
References
- Van Camp, M.; de Viron, O.; Watlet, A.; Meurers, B.; Francis, O.; Caudron, C. Geophysics from terrestrial time-variable gravity measurements. Rev. Geophys. 2017, 55, 938–992. [Google Scholar] [CrossRef]
- Wang, H.B.; Wu, L.; Chai, H.; Hsu, H.; Wang, Y. Technology of gravity aided inertial navigation system and its trial in South China Sea. IET Radar Sonar Navig. 2016, 10, 862–869. [Google Scholar] [CrossRef]
- Asenbaum, P.; Overstreet, C.; Kim, M.; Curti, J.; Kasevich, M.A. Atom-Interferometric Test of the Equivalence Principle at the 10−12 Level. Phys. Rev. Lett. 2020, 125, 191101. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Chen, X.; Fang, J.; Chen, Q.F.; Sun, H.Y.; Wang, Y.B.; Zhong, J.Q.; Zhou, L.; He, C.; Li, J.T.; et al. The space cold atom interferometer for testing the equivalence principle in the China Space Station. NPJ Microgravity 2023, 9, 58. [Google Scholar] [CrossRef] [PubMed]
- Lautier, J.; Volodimer, L.; Hardin, T.; Merlet, S.; Lours, M.; Pereira Dos Santos, F.; Landragin, A. Hybridizing matter-wave and classical accelerometers. Appl. Phys. Lett. 2014, 105, 144102. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Blanchard, C.; Bonnin, A.; Cadoret, M.; Bresson, A.; Rouxel, D.; Lequentrec-Lalancette, M.F. Absolute marine gravimetry with matter-wave interferometry. Nat. Commun. 2018, 9, 627. [Google Scholar] [CrossRef] [PubMed]
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated Raman transitions. Phys. Rev. Lett. 1991, 67, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 5–61. [Google Scholar] [CrossRef]
- Freier, C.; Hauth, M.; Schkolnik, V.; Leykauf, B.; Schilling, M.; Wziontek, H.; Scherneck, H.G.; Müller, J.; Peters, A. Mobile quantum gravity sensor with unprecedented stability. J. Phys. Conf. Ser. 2016, 723, 012050. [Google Scholar] [CrossRef]
- Merlet, S.; Bodart, Q.; Malossi, N.; Landragin, A.; Pereira Dos Santos, F.; Gitlein, O.; Timmen, L. Comparison between two mobile absolute gravimeters: Optical versus atomic interferometers. Metrologia 2010, 47, L9–L11. [Google Scholar] [CrossRef]
- Hu, Z.K.; Sun, B.L.; Duan, X.C.; Zhou, M.K.; Chen, L.L.; Zhan, S.; Zhang, Q.Z.; Luo, J. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Phys. Rev. A 2013, 88, 043610. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Z.Y.; Cheng, B.; Wang, Q.Y.; Xu, A.P.; Lin, Q. The investigation of a μGal-level cold atom gravimeter for field applications. Metrologia 2014, 51, 452–458. [Google Scholar] [CrossRef]
- Li, C.Y.; Long, J.B.; Huang, M.Q.; Chen, B.; Yang, Y.M.; Jiang, X.; Xiang, C.F.; Ma, Z.L.; He, D.Q.; Chen, L.K.; et al. Continuous gravity measurement with a portable atom gravimeter. Phys. Rev. A 2023, 108, 032811. [Google Scholar] [CrossRef]
- Wang, S.K.; Zhao, Y.; Zhuang, W.; Li, T.C.; Wu, S.Q.; Feng, J.Y.; Li, C.J. Shift evaluation of the atomic gravimeter NIM-AGRb-1 and its comparison with FG5X. Metrologia 2018, 55, 360–365. [Google Scholar] [CrossRef]
- Ge, G.G.; Chen, X.; Li, J.T.; Zhang, D.F.; He, M.; Wang, W.Z.; Zhou, Y.; Zhong, J.Q.; Tang, B.; Fang, J.; et al. Accuracy improvement of a compact 85Rb atom gravimeter by suppressing laser crosstalk and light shift. Sensors 2023, 23, 6115. [Google Scholar] [CrossRef]
- Janvier, C.; Ménoret, V.; Desruelle, B. Compact differential gravimeter at the quantum projection-noise limit. Phys. Rev. A 2022, 105, 022801. [Google Scholar] [CrossRef]
- Dutta, I.; Savoie, D.; Fang, B.; Venon, B.; Garrido Alzar, C.L.; Geiger, R.; Landragin, A. Continuous cold-atom inertial sensor with 1 nrad/sec rotation stability. Phys. Rev. Lett. 2016, 116, 183003. [Google Scholar] [CrossRef]
- Bidel, Y.; Carraz, O.; Charrière, R.; Cadoret, M.; Zahzam, N.; Bresson, A. Compact cold atom gravimeter for field applications. Appl. Phys. Lett. 2013, 102, 144107. [Google Scholar] [CrossRef]
- Wu, X.; Pagel, Z.; Malek, B.S.; Nguyen, T.H.; Zi, F.; Scheirer, D.S.; Müller, H. Gravity surveys using a mobile atom interferometer. Sci. Adv. 2019, 5, eaax0800. [Google Scholar] [CrossRef]
- Wang, H.L.; Wang, K.N.; Xu, Y.P.; Tang, Y.T.; Wu, B.; Cheng, B.; Wu, L.Y.; Zhou, Y.; Weng, K.X.; Zhu, D.; et al. A truck-borne system based on cold atom gravimeter for measuring the absolute gravity in the field. Sensors 2022, 22, 6172. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Xu, W.J.; Sun, S.D.; Shu, Y.B.; Luo, Q.; Cheng, Y.; Hu, Z.K.; Zhou, M.K. A car-based portable atom gravimeter and its application in field gravity survey. AIP Adv. 2021, 11, 115223. [Google Scholar] [CrossRef]
- Guo, J.; Ma, S.Q.; Zhou, C.; Liu, J.X.; Wang, B.; Pan, D.B.; Mao, H.C. Vibration compensation for a vehicle-mounted atom gravimeter. IEEE Sens. J. 2022, 22, 12939–12946. [Google Scholar] [CrossRef]
- Geiger, R.; Ménoret, V.; Stern, G.; Zahzam, N.; Cheinet, P.; Battelier, B.; Villing, A.; Moron, F.; Lours, M.; Bidel, Y.; et al. Detecting inertial effects with airborne matter-wave interferometry. Nat. Commun. 2011, 2, 474. [Google Scholar] [CrossRef] [PubMed]
- Bidel, Y.; Zahzam, N.; Bresson, A.; Blanchard, C.; Cadoret, M.; Olesen, A.V.; Forsberg, R. Absolute airborne gravimetry with a cold atom sensor. J. Geod. 2020, 94, 20. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Bresson, A.; Blanchard, C.; Bonnin, A.; Bernard, J.; Cadoret, M.; Jensen, T.E.; Forsberg, R.; Salaun, C.; et al. Airborne Absolute Gravimetry With a Quantum Sensor, Comparison with Classical Technologies. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025921. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, C.; Wang, K.N.; Cheng, B.; Zhu, D.; Li, R.; Wang, X.L.; Lin, Q.; Qiao, Z.K.; Zhou, Y. Marine absolute gravity field surveys based on cold atomic gravimeter. IEEE Sens. J. 2023, 23, 24292–24299. [Google Scholar] [CrossRef]
- Qiao, Z.K.; Yuan, P.; Zhang, J.J.; Zhang, Z.Y.; Li, L.L.; Zhu, D.; Jiang, M.R.; Shi, H.Y.; Hu, R.; Zhou, F.; et al. Error analysis and filtering methods for absolute ocean gravity data. IEEE Sens. J. 2023, 23, 14346–14355. [Google Scholar] [CrossRef]
- Che, H.; Li, A.; Fang, J.; Ge, G.G.; Gao, W.; Zhang, Y.; Liu, C.; Xu, J.N.; Chang, L.B.; Huang, C.F.; et al. Ship-borne dynamic absolute gravity measurement based on cold atom gravimeter. Acta Phys. Sin. 2022, 71, 113701. [Google Scholar] [CrossRef]
- Le Gouët, J.; Mehlstäubler, T.; Kim, J.; Merlet, S.; Clairon, A.; Landragin, A.; Pereira Dos Santos, F. Limits to the sensitivity of a low noise compact atomic gravimeter. Appl. Phys. B-Lasers Opt. 2008, 92, 133–144. [Google Scholar] [CrossRef]
- Merlet, S.; le Gouët, J.; Bodart, Q.; Clairon, A.; Landragin, A.; Pereira Dos Santos, F.; Rouchon, P. Operating an atom interferometer beyond its linear range. Metrologia 2009, 46, 87–94. [Google Scholar] [CrossRef]
- Cheiney, P.; Fouché, L.; Templier, S.; Napolitano, F.; Battelier, B.; Bouyer, P.; Barret, B. Navigation-compatible hybrid quantum accelerometer using a Kalman filter. Phys. Rev. Appl. 2018, 10, 034030. [Google Scholar] [CrossRef]
- Zhu, D.; Xu, H.; Zhou, Y.; Wu, B.; Cheng, B.; Wang, K.N.; Chen, P.J.; Gao, S.T.; Weng, W.K.; Wang, H.L.; et al. Data processing of shipborne absolute gravity measurement based on the extended Kalman filter algorithm. Acta Phys. Sin. 2022, 71, 133702. [Google Scholar] [CrossRef]
- Huang, C.F.; Li, A.; Qin, F.J.; Fang, J.; Chen, X. An atomic gravimeter dynamic measurement method based on Kalman filter. Meas. Sci. Technol. 2023, 34, 015013. [Google Scholar] [CrossRef]
- Fang, J.; Hu, J.G.; Chen, X.; Zhu, H.R.; Zhou, L.; Zhong, J.Q.; Wang, J.; Zhan, M.S. Realization of a compact one-seed laser system for atom interferometer-based gravimeters. Opt. Express 2018, 26, 1586–1596. [Google Scholar] [CrossRef] [PubMed]
- Titan Accelerometer. Available online: https://nanometrics.ca/products/accelerometers/titan (accessed on 1 February 2024).
- Gauguet, A.; Mehlstäubler, T.E.; Lévèque, T.; Le Gouët, J.; Chaibi, W.; Canuel, B.; Clairon, A.; Pereira Dos Santos, F.; Landragin, A. Off-resonant Raman transition impact in an atom interferometer. Phys. Rev. A 2008, 78, 4. [Google Scholar] [CrossRef]
- Carraz, O.; Charrière, R.; Cadoret, M.; Zahzam, N.; Bidel, Y. Phase shift in an atom interferometer induced by the additional laser lines of a Raman laser generated by modulation. Phys. Rev. A 2012, 86, 3. [Google Scholar] [CrossRef]
- dgShip™ Shipborne Gravimeter. Available online: http://www.hins.com.cn/show-137-142-1.html (accessed on 1 February 2024).





| Systematic Error Terms | Value (mGal) | Uncertainty (mGal) |
|---|---|---|
| Gravity gradient | −0.222 | 0.002 |
| Single photon light shift | 0.000 | 0.008 |
| Double photon light shift | 0.047 | 0.005 |
| Additional laser lines | −0.699 | 0.137 |
| Gravity calibration | −0.116 | 0.050 |
| Systematic error in total | −0.990 | 0.147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wang, W.; Ge, G.; Li, J.; Zhang, D.; He, M.; Tang, B.; Zhong, J.; Zhou, L.; Li, R.; et al. High-Precision Atom Interferometer-Based Dynamic Gravimeter Measurement by Eliminating the Cross-Coupling Effect. Sensors 2024, 24, 1016. https://doi.org/10.3390/s24031016
Zhou Y, Wang W, Ge G, Li J, Zhang D, He M, Tang B, Zhong J, Zhou L, Li R, et al. High-Precision Atom Interferometer-Based Dynamic Gravimeter Measurement by Eliminating the Cross-Coupling Effect. Sensors. 2024; 24(3):1016. https://doi.org/10.3390/s24031016
Chicago/Turabian StyleZhou, Yang, Wenzhang Wang, Guiguo Ge, Jinting Li, Danfang Zhang, Meng He, Biao Tang, Jiaqi Zhong, Lin Zhou, Runbing Li, and et al. 2024. "High-Precision Atom Interferometer-Based Dynamic Gravimeter Measurement by Eliminating the Cross-Coupling Effect" Sensors 24, no. 3: 1016. https://doi.org/10.3390/s24031016
APA StyleZhou, Y., Wang, W., Ge, G., Li, J., Zhang, D., He, M., Tang, B., Zhong, J., Zhou, L., Li, R., Mao, N., Che, H., Qian, L., Li, Y., Qin, F., Fang, J., Chen, X., Wang, J., & Zhan, M. (2024). High-Precision Atom Interferometer-Based Dynamic Gravimeter Measurement by Eliminating the Cross-Coupling Effect. Sensors, 24(3), 1016. https://doi.org/10.3390/s24031016








