A Microwave Differential Dielectric Sensor Based on Mode Splitting of Coupled Resonators
Abstract
1. Introduction
2. Avoided Mode Crossing at Microwave Regime: Theory
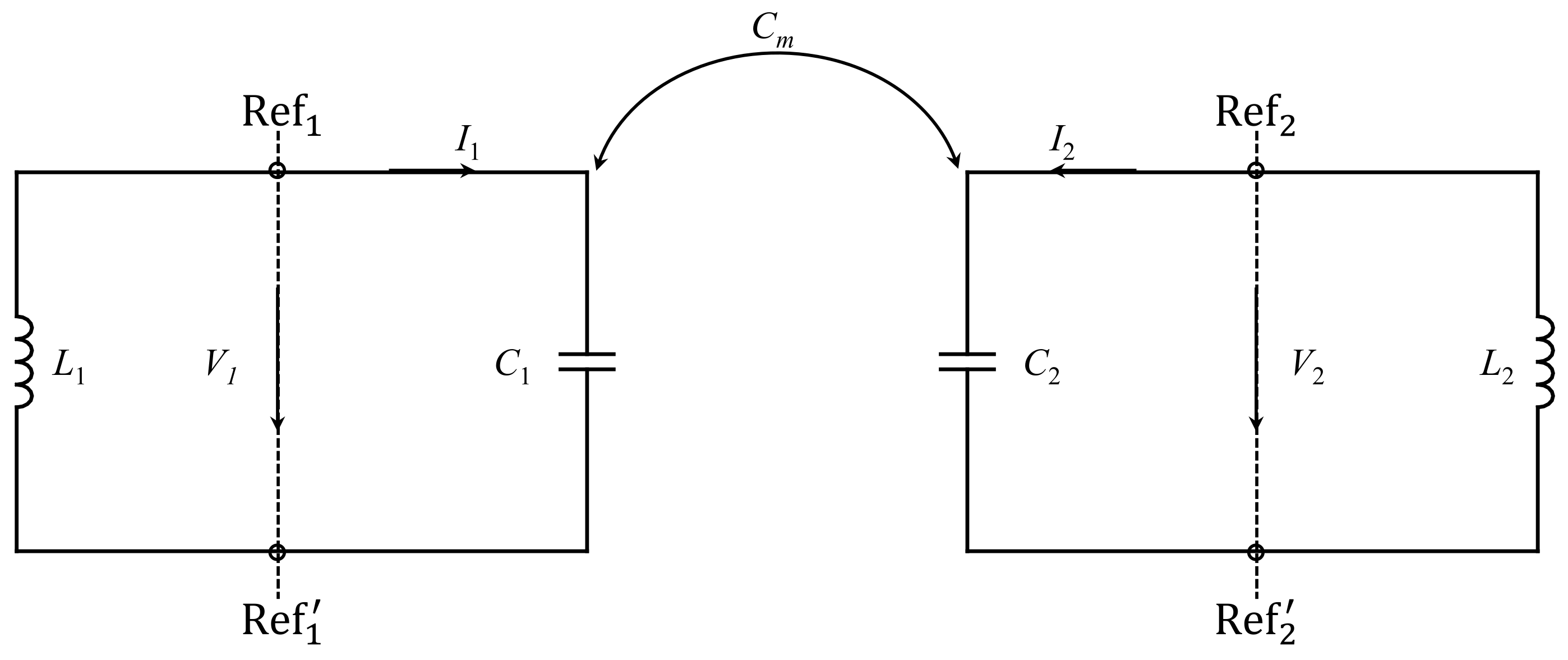
3. Case Study: A Sensor Based on Two Synchronous Split-Ring Resonators
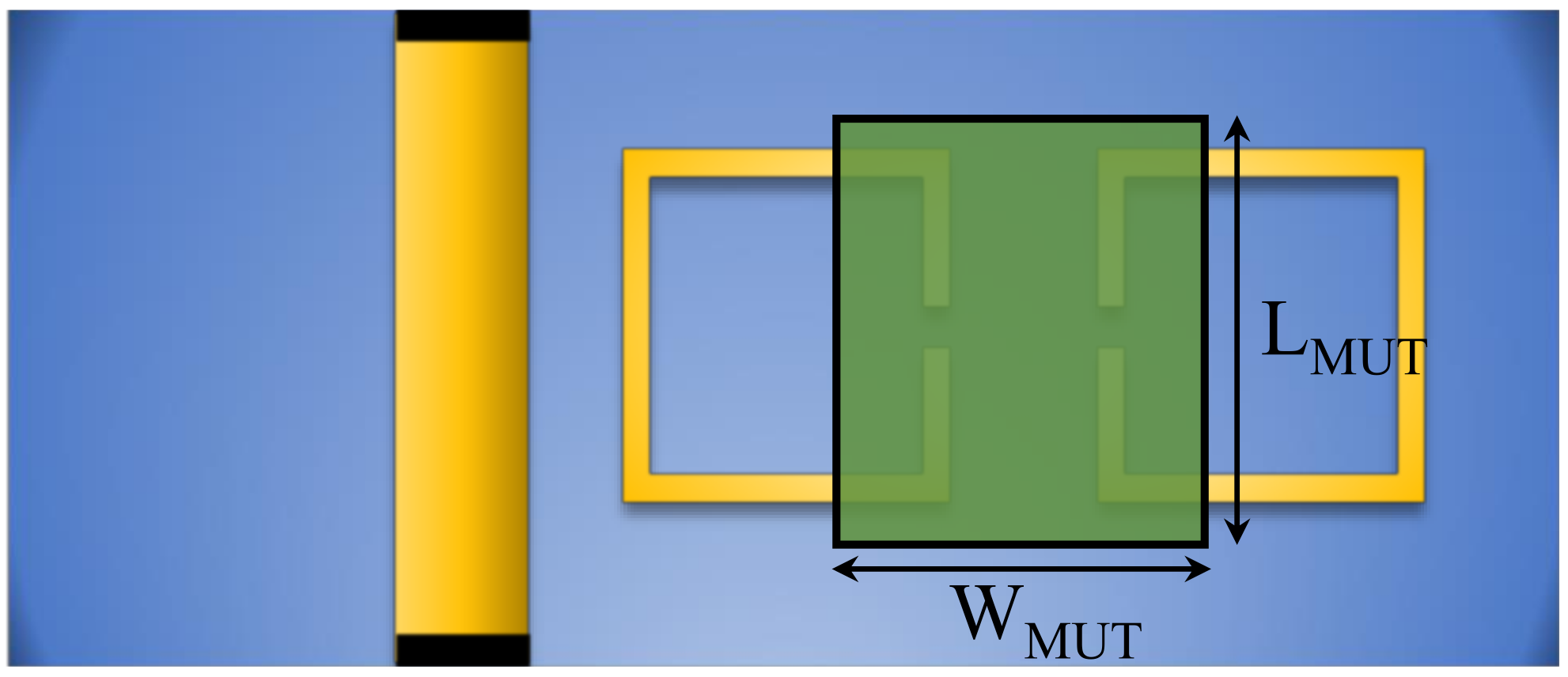
3.1. System Design
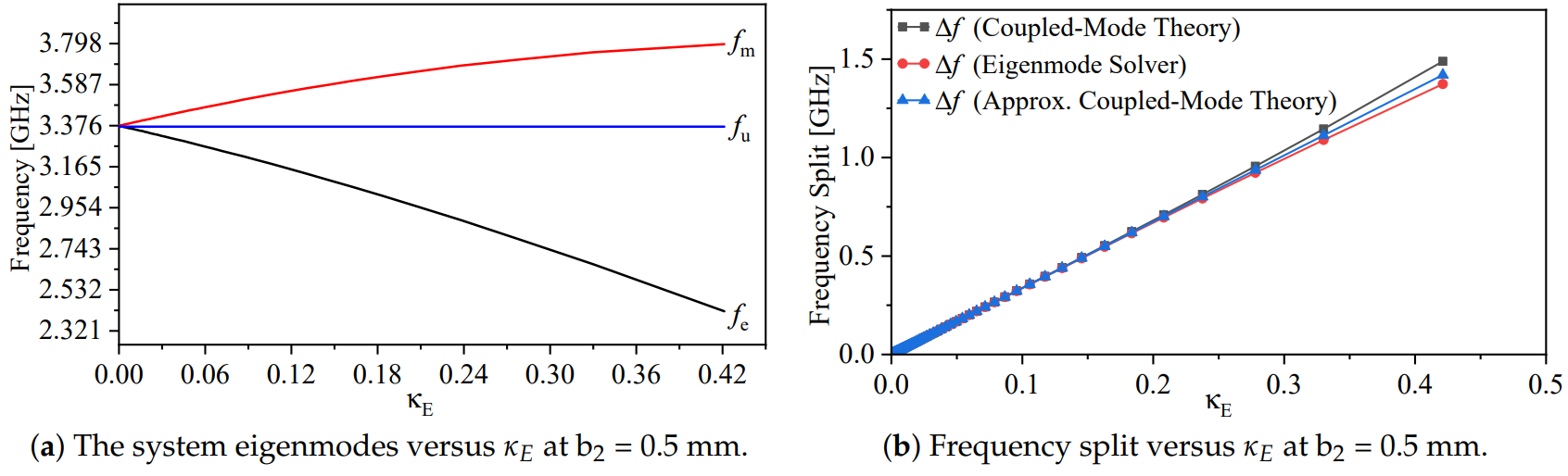
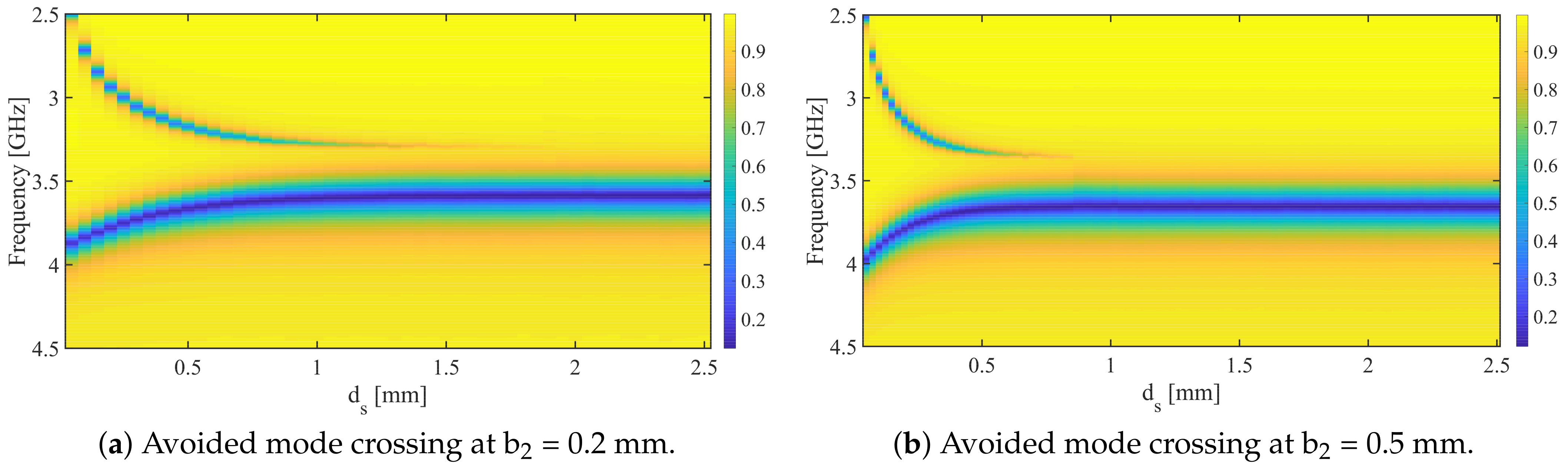
3.2. Numerical Simulation: Eigenmode-Solver-Based Analysis
- In the 3D simulation (HFSS), choose the solution type to be eigenmode;
- Design a rectangular metallic cavity where the resonance frequency of the dominant mode must be greater than the expected resonance frequencies of the resonators;
- Make the boundary of the cavity with walls made of perfect electric conductor material (PEC);
- In the eigen solution step, choose the minimum frequency to be smaller than the first resonance frequency of the intended system;
- In our case, as we are interested in extracting the resonance frequencies ( and ), choose the number of modes to be 2.
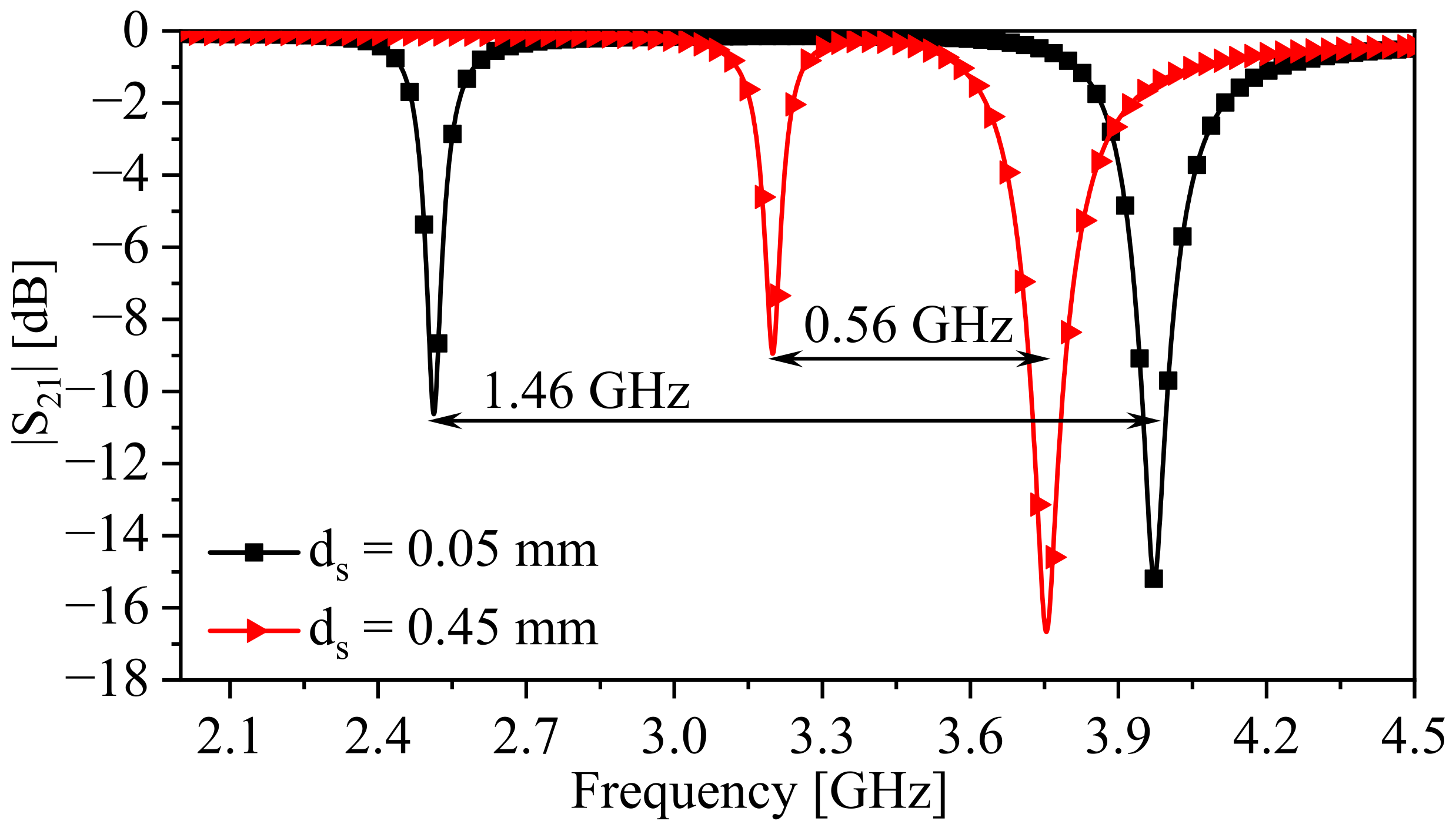
3.3. Numerical Simulation: Scattering-Parameter-Based Analysis
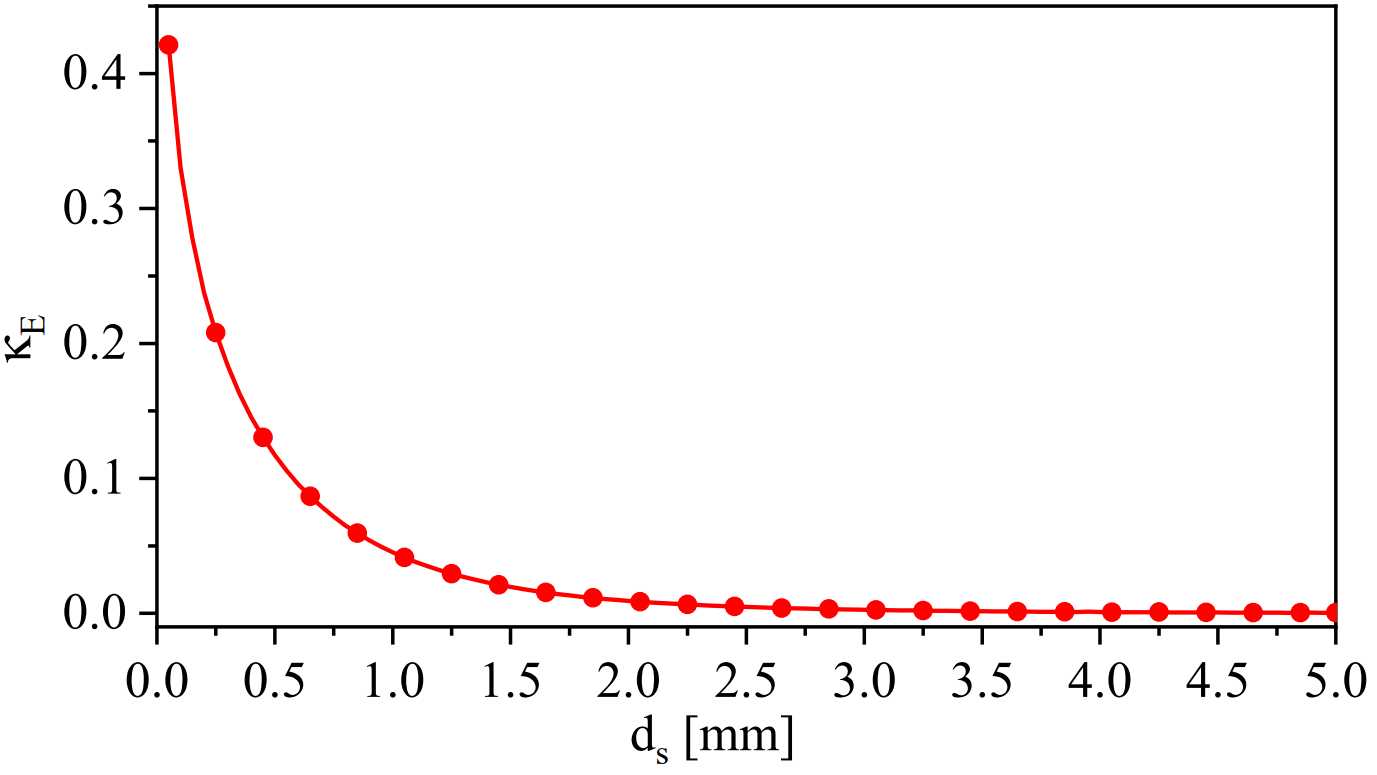
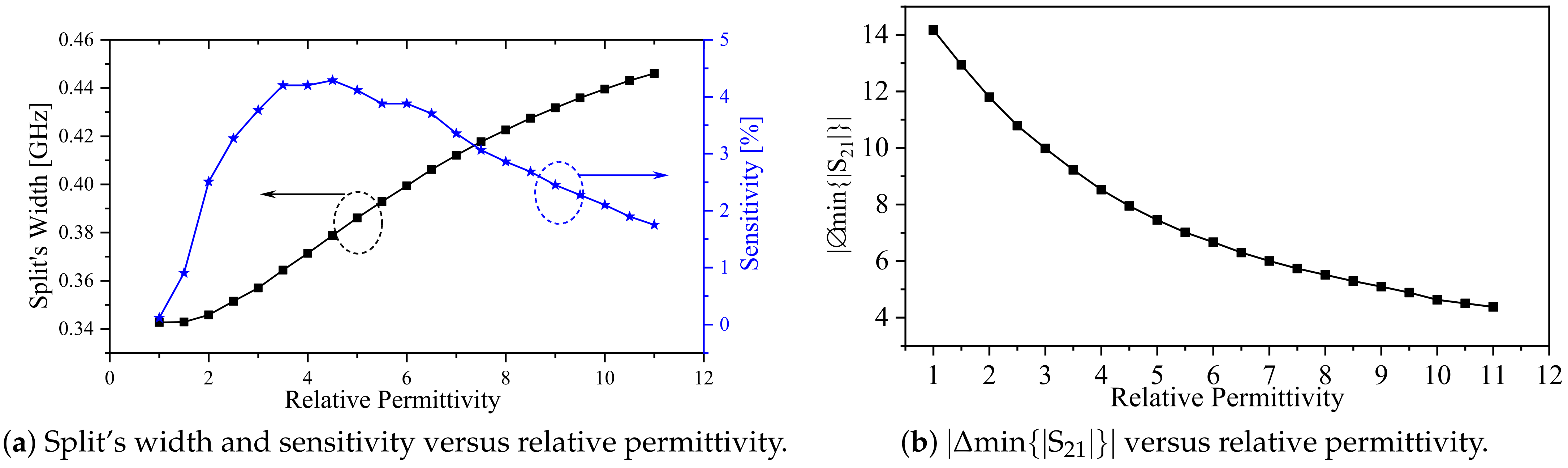
3.4. The Proposed System as a Microwave Differential Dielectric Sensor
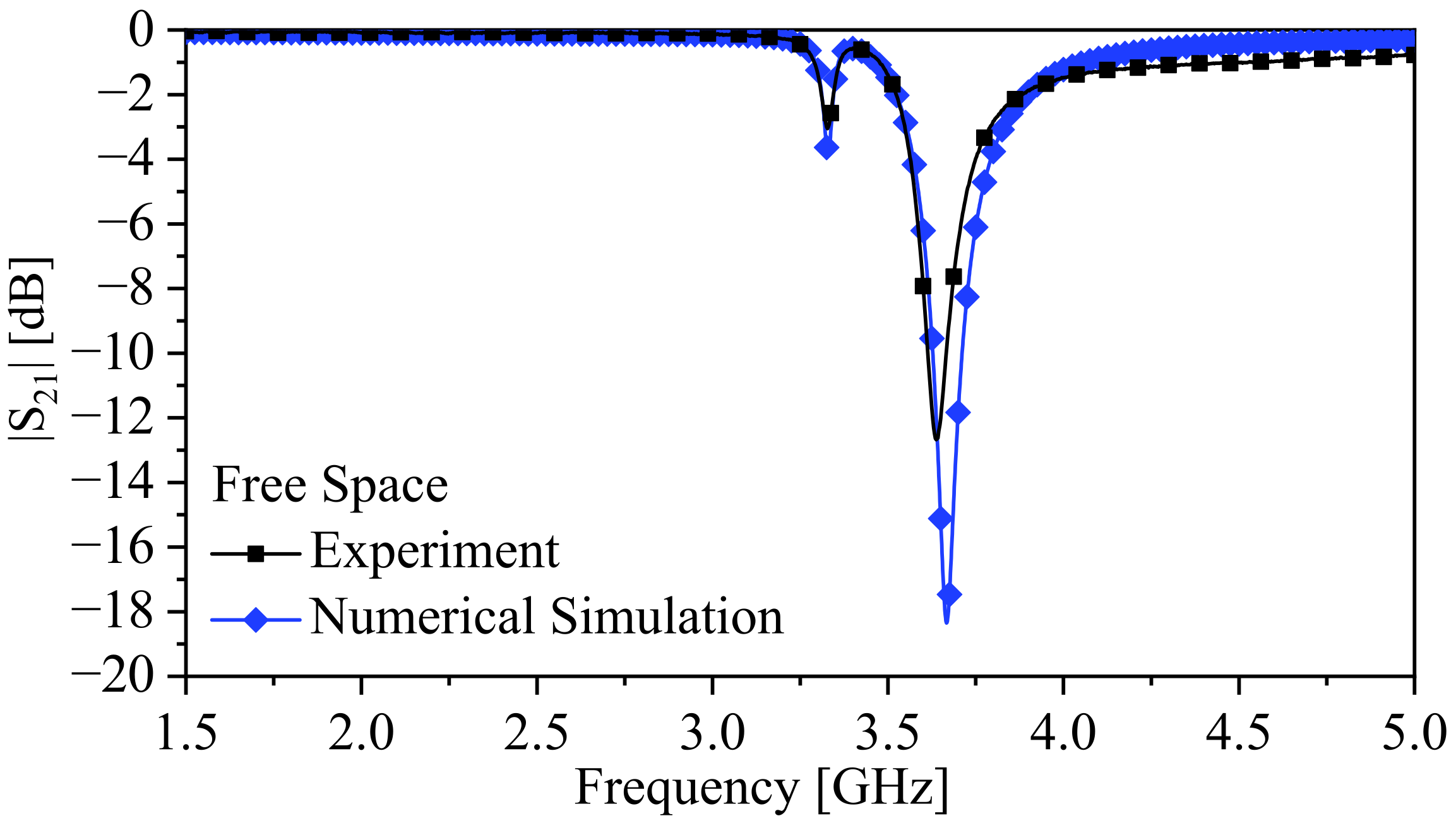
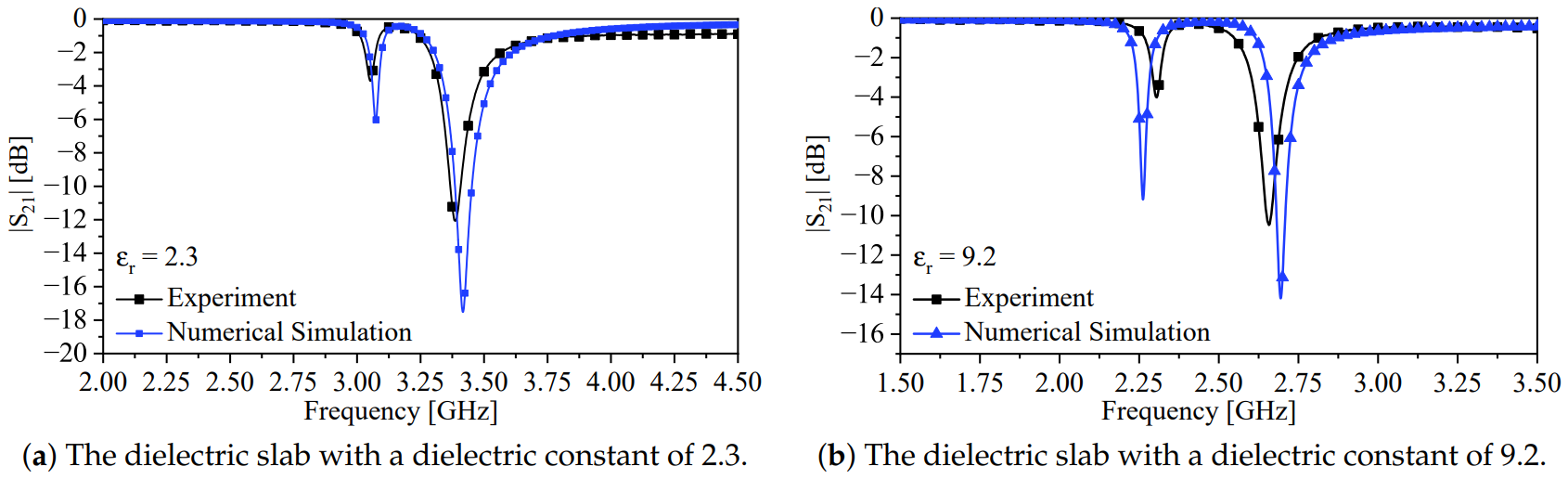
4. Fabrication and Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MUT(s) | materials under test |
| SRR(s) | split-ring resonators |
| CSRR(s) | complementary split-ring resonators |
| SIR(s) | stepped impedance resonators |
| EC | electric coupling |
References
- Schelkunoff, S.A.; Friis, H.T. Antennas: Theory and Practice; Wiley: New York, NY, USA, 1952; Volume 639. [Google Scholar]
- Pendry, J.; Holden, A.; Robbins, D.; Stewart, W. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Falcone, F.; Lopetegi, T.; Baena, J.; Marques, R.; Martin, F.; Sorolla, M. Effective negative-ϵ; stopband microstrip lines based on complementary split ring resonators. IEEE Microw. Wireless Compon. Lett. 2004, 14, 280–282. [Google Scholar] [CrossRef]
- Martín, F.; Falcone, F.; Bonache, J.; Marqués, R.; Sorolla, M. Miniaturized coplanar waveguide stop band filters based on multiple tuned split ring resonators. IEEE Microw. Wireless Compon. Lett. 2003, 13, 511–513. [Google Scholar] [CrossRef]
- García-García, J.; Martín, F.; Falcone, F.; Bonache, J.; Baena, J.D.; Gil, I.; Amat, E.; Lopetegi, T.; Laso, M.A.; Iturmendi, J.A.M.; et al. Microwave filters with improved stopband based on sub-wavelength resonators. IEEE Trans. Microw. Theory Tech. 2005, 53, 1997–2006. [Google Scholar] [CrossRef]
- Bonache, J.; Gil, I.; García-García, J.; Martín, F. Novel microstrip bandpass filters based on complementary split-ring resonators. IEEE Trans. Microw. Theory Tech. 2006, 54, 265–271. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Azpilicueta, L.; Naser-Moghadasi, M.; Akinsolu, M.O.; See, C.H.; Liu, B.; Abd-Alhameed, R.A.; Falcone, F.; Huynen, I.; et al. A Comprehensive Survey of metamaterial Transmission-Line Based Antennas: Design, challenges, and applications. IEEE Access 2020, 8, 144778–144808. [Google Scholar] [CrossRef]
- Bulu, I.; Caglayan, H.; Aydin, K.; Ozbay, E. Compact size highly directive antennas based on the SRR metamaterial medium. New J. Phys. 2005, 7, 223. [Google Scholar] [CrossRef]
- Li, B.; Zhu, P.Y.; Liang, L.; Liang, C.H. Study on high gain waveguide array antenna with SRR structure. J. Electromagn. Waves Appl. 2007, 21, 615–627. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Su, Y.; Yan, M.; Qiu, M. Coupled mode theory analysis of mode-splitting in coupled cavity system. Opt. Express 2010, 18, 8367–8382. [Google Scholar] [CrossRef] [PubMed]
- Alibakhshikenari, M.; Virdee, B.S.; See, C.H.; Abd-Alhameed, R.; Ali, A.; Falcone, F.; Limiti, E. Wideband printed monopole antenna for application in wireless communication systems. IET Microw. Antennas Propag. 2018, 12, 1222–1230. [Google Scholar] [CrossRef]
- Jang, C.; Park, J.; Lee, H.; Yun, G.; Yook, J. Non-Invasive Fluidic Glucose Detection Based on Dual Microwave Complementary Split Ring Resonators With a Switching Circuit for Environmental Effect Elimination. IEEE Sens. J. 2020, 20, 8520–8527. [Google Scholar] [CrossRef]
- Albishi, A.M.; Ramahi, O.M. Microwaves-Based High Sensitivity Sensors for Crack Detection in Metallic Materials. IEEE Trans. Microw. Theory Techn. 2017, 65, 1864–1872. [Google Scholar] [CrossRef]
- Albishi, A.M.; Alshebeili, S.A.; Ramahi, O.M. Three-Dimensional Split-Ring Resonators-Based Sensors for Fluid Detection. IEEE Sens. J. 2021, 21, 9138–9147. [Google Scholar] [CrossRef]
- Albishi, A.M. A Novel Coupling Mechanism for CSRRs as Near-Field Dielectric Sensors. Sensors 2022, 22, 3313. [Google Scholar] [CrossRef] [PubMed]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef]
- Saadat-Safa, M.; Nayyeri, V.; Ghadimi, A.; Soleimani, M.; Ramahi, O.M. A pixelated Microwave near-field Sensor for precise characterization of Dielectric Materials. Sci. Rep. 2019, 9, 13310. [Google Scholar] [CrossRef] [PubMed]
- Velez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Highly-Sensitive Microwave Sensors Based on Open Complementary Split Ring Resonators OCSRRs for Dielectric Characterization and Solute Concentration Measurement in Liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Zarifi, M.H.; Daneshmand, M. Sensitivity enhancement of split ring resonator based liquid sensors. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Yesiloz, G.; Boybay, M.S.; Ren, C.L. Effective Thermo-Capillary Mixing in Droplet Microfluidics Integrated with a Microwave Heater. Anal. Chem. 2017, 89, 1978–1984. [Google Scholar] [CrossRef]
- Boybay, M.S. Behavior of metamaterial-based microwave components for sensing and heating of nanoliter-scale volumes. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 3503–3512. [Google Scholar] [CrossRef]
- Wong, D.; Yesiloz, G.; Boybay, M.S.; Ren, C.L. Microwave temperature measurement in microfluidic devices. Lab Chip 2016, 16, 2192–2197. [Google Scholar] [CrossRef]
- Yesiloz, G.; Boybay, M.S.; Ren, C.L. Label-free high-throughput detection and content sensing of individual droplets in microfluidic systems. Lab Chip 2015, 15, 4008–4019. [Google Scholar] [CrossRef]
- Boybay, M.; Ramahi, O.M. Material Characterization Using Complementary Split-Ring Resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
- Albishi, A.M.; Ramahi, O.M. Highly Sensitive Microwaves Sensors for Fluid Concentration Measurements. IEEE Microw. Wireless Compon. Lett. 2018, 28, 287–289. [Google Scholar] [CrossRef]
- Chuma, E.L.; Iano, Y.; Fontgalland, G.; Roger, L.L.B.; Loschi, H. PCB-integrated non-destructive microwave sensor for liquid dielectric spectroscopy based on planar metamaterial resonator. Sens. Actuators Phys. 2020, 312, 112112. [Google Scholar] [CrossRef]
- Lobato-Morales, H.; Choi, J.H.; Lee, H.; Medina-Monroy, J.L. Compact Dielectric-Permittivity Sensors of Liquid Samples Based on Substrate-Integrated-Waveguide With Negative-Order-Resonance. IEEE Sens. J. 2019, 19, 8694–8699. [Google Scholar] [CrossRef]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Martín, F. Configurations of Splitter/Combiner Microstrip Sections Loaded with Stepped Impedance Resonators (SIRs) for Sensing Applications. Sensors 2016, 16, 2195. [Google Scholar] [CrossRef] [PubMed]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Mata-Contreras, J.; Martín, F. Transmission Lines Loaded with Pairs of Stepped Impedance Resonators: Modeling and Application to Differential Permittivity Measurements. IEEE Trans. Microw. Theory Tech. 2016, 64, 3864–3877. [Google Scholar] [CrossRef]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Martin, F. Splitter/Combiner Microstrip Sections Loaded With Pairs of Complementary Split Ring Resonators (CSRRs): Modeling and Optimization for Differential Sensing Applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
- Vélez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Microwave Microfluidic Sensor Based on a Microstrip Splitter/Combiner Configuration and Split Ring Resonators (SRRs) for Dielectric Characterization of Liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef]
- Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact measurement of complex permittivity and thickness by using planar resonators. IEEE Trans. Microw. Theory Tech. 2016, 64, 247–257. [Google Scholar] [CrossRef]
- Albishi, A.M.; Mirjahanmardi, S.H.; Ali, A.M.; Nayyeri, V.; Wasly, S.M.; Ramahi, O.M. Intelligent Sensing Using Multiple Sensors for Material Characterization. Sensors 2019, 19, 4766. [Google Scholar] [CrossRef] [PubMed]
- Albishi, A.M.; Badawe, M.K.E.; Nayyeri, V.; Ramahi, O.M. Enhancing the Sensitivity of Dielectric Sensors With Multiple Coupled Complementary Split-Ring Resonators. IEEE Trans. Microw. Theory Tech. 2020, 68, 4340–4347. [Google Scholar] [CrossRef]
- Novotny, L. Strong coupling, energy splitting, and level crossings: A classical perspective. Am. J. Phys. 2010, 78, 1199–1202. [Google Scholar] [CrossRef]
- Wiersig, J. Formation of long-lived, scarlike modes near avoided resonance crossings in optical microcavities. Phys. Rev. Lett. 2006, 97, 253901. [Google Scholar] [CrossRef]
- Liu, Y.; Xuan, Y.; Xue, X.; Wang, P.H.; Chen, S.; Metcalf, A.J.; Wang, J.; Leaird, D.E.; Qi, M.; Weiner, A.M. Investigation of mode coupling in normal-dispersion silicon nitride microresonators for Kerr frequency comb generation. Optica 2014, 1, 137–144. [Google Scholar] [CrossRef]
- Kim, W.; Özdemir, Ş.K.; Zhu, J.; He, L.; Yang, L. Demonstration of mode splitting in an optical microcavity in aqueous environment. Appl. Phys. Lett. 2010, 97, 071111. [Google Scholar] [CrossRef]
- Tkalčec, A.; Probst, S.; Rieger, D.; Rotzinger, H.; Wünsch, S.; Kukharchyk, N.; Wieck, A.; Siegel, M.; Ustinov, A.; Bushev, P. Strong coupling of an Er 3+-doped YAlO 3 crystal to a superconducting resonator. Phys. Rev. B 2014, 90, 075112. [Google Scholar] [CrossRef]
- Landig, A.J.; Koski, J.V.; Scarlino, P.; Müller, C.; Abadillo-Uriel, J.C.; Kratochwil, B.; Reichl, C.; Wegscheider, W.; Coppersmith, S.N.; Friesen, M.; et al. Virtual-photon-mediated spin-qubit–transmon coupling. Nat. Commun. 2019, 10, 5037. [Google Scholar] [CrossRef]
- ANSYS HFSS. Available online: http://www.ansys.com (accessed on 20 May 2023).
- Hong, J.S.G.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hong, J.S. Couplings of asynchronously tuned coupled microwave resonators. IEE Proc. Microw. Antennas Propag. 2000, 147, 354–358. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-mode theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential Sensors Using Microstrip Lines Loaded with Two Split-Ring Resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Beziuk, G.; Scott, J.; Ghorbani, K. Microwave Differential Frequency Splitting Sensor Using Magnetic-LC Resonators. Sensors 2020, 20, 1066. [Google Scholar] [CrossRef]
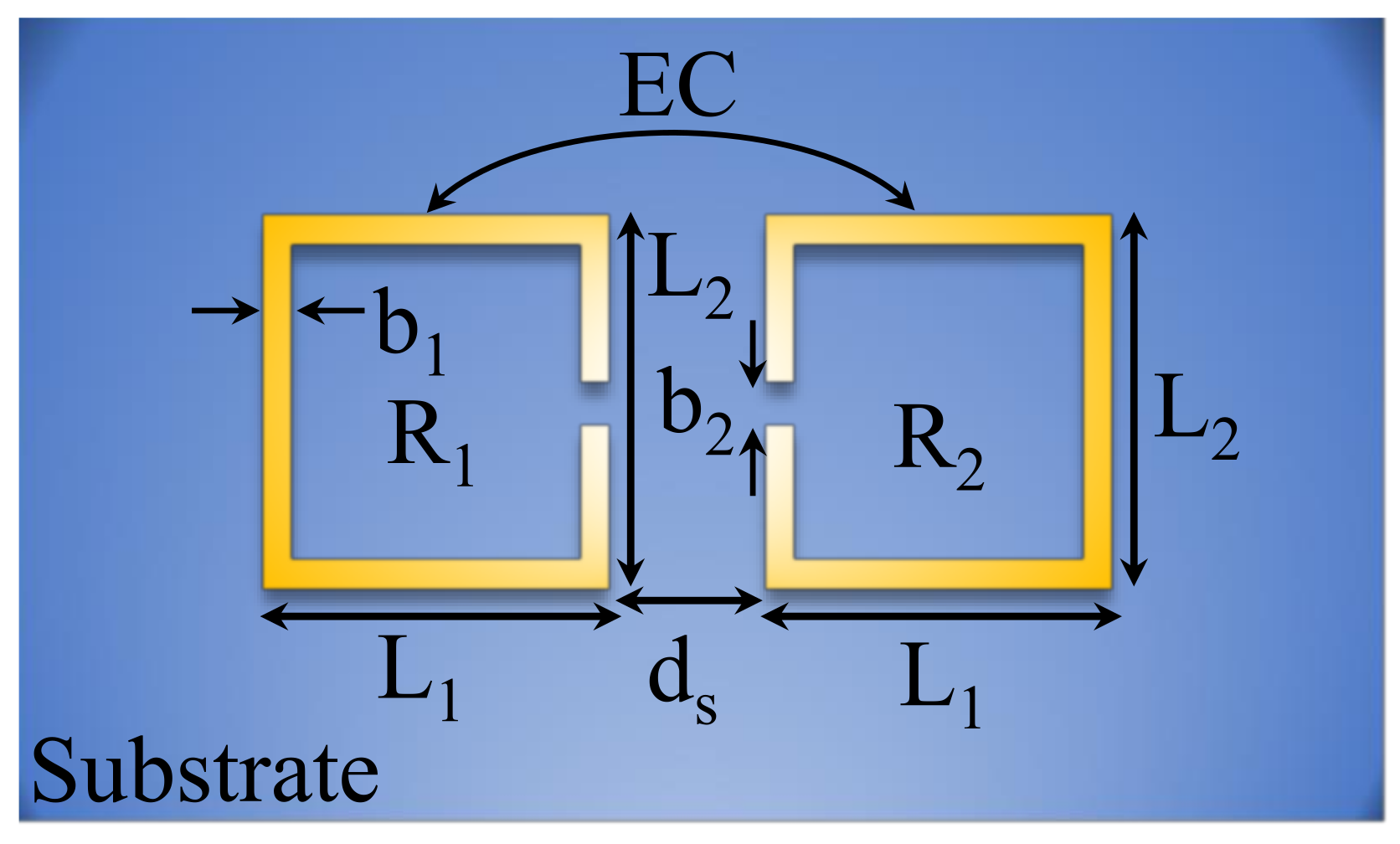
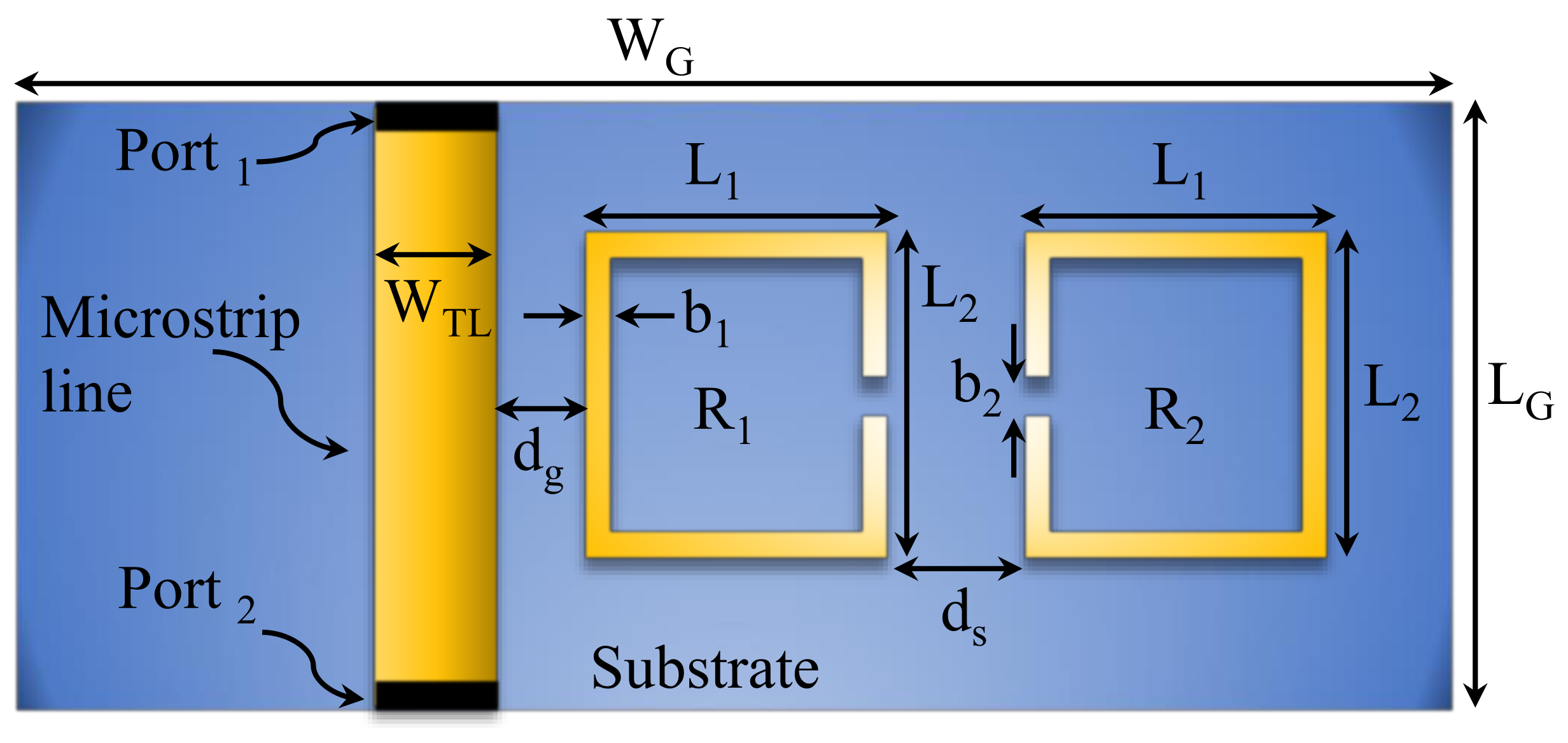




| (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|---|---|---|---|
| 1.56 | 4 | 11 | 0.2 | Vari. | Vari. | 50 | 30 | 0.1 |
| [GHz] (Simulation) | [GHz] (Simulation) | [GHz] (Experiment) | [GHz] (Experiment) | , Error (%) | , Error (%) | Width Split Error (%) | |
|---|---|---|---|---|---|---|---|
| Air | 3.667 | 3.329 | 3.64 | 3.3275 | 0.75 | 0.045 | 7.5 |
| = 2.3 | 3.416 | 3.072 | 3.3875 | 3.055 | 0.83 | 0.55 | 3.343 |
| = 9.2 | 2.693 | 2.262 | 2.6575 | 2.3025 | 1.32 | −1.8 | 7.6 |
| Ref. | Resonator Type | Frequency Splitting | Coupled Resonators | Breaking Symmetry | Mode Coupling Splitting |
|---|---|---|---|---|---|
| [28] | SIRs | Yes | No | Yes | No |
| [30] | CSRRs | Yes | No | Yes | No |
| [31] | SRRs | Yes | No | Yes | No |
| [46] | SRRs | Yes | No | Yes | No |
| [47] | Magnetic-LC Resonators | Yes | No | Yes | No |
| This Work | Coupled Synchronous SRRs | Yes | Yes | No | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuhlafi, A.M.; Alshaykh, M.S.; Alajmi, M.; Alshammari, B.; Ramahi, O.M. A Microwave Differential Dielectric Sensor Based on Mode Splitting of Coupled Resonators. Sensors 2024, 24, 1020. https://doi.org/10.3390/s24031020
Almuhlafi AM, Alshaykh MS, Alajmi M, Alshammari B, Ramahi OM. A Microwave Differential Dielectric Sensor Based on Mode Splitting of Coupled Resonators. Sensors. 2024; 24(3):1020. https://doi.org/10.3390/s24031020
Chicago/Turabian StyleAlmuhlafi, Ali M., Mohammed S. Alshaykh, Mansour Alajmi, Bassam Alshammari, and Omar M. Ramahi. 2024. "A Microwave Differential Dielectric Sensor Based on Mode Splitting of Coupled Resonators" Sensors 24, no. 3: 1020. https://doi.org/10.3390/s24031020
APA StyleAlmuhlafi, A. M., Alshaykh, M. S., Alajmi, M., Alshammari, B., & Ramahi, O. M. (2024). A Microwave Differential Dielectric Sensor Based on Mode Splitting of Coupled Resonators. Sensors, 24(3), 1020. https://doi.org/10.3390/s24031020









