Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor
Abstract
:1. Introduction
2. Principle Analysis of Line-Sweep Spectral Confocal Displacement Sensor
3. Design of Optical System for Ultra-Large-Range Line-Sweep Spectral Confocal Displacement Sensor
3.1. Dispersive Objective Lens
- (1)
- In order to address the issue of linear axial chromatic aberration, it is essential to determine the appropriate glass material. Optical design software is essential for selecting the appropriate material due to the variability of the refractive index in glass. Optical design software enables the choice of the primary glass material without compromising its optical focus. The limitations of this section are determined by Equation (1) described earlier. Upon completion of the selection process, the initial construction successfully achieves the desired level of positive axial chromatic aberration as specified in the design criteria;
- (2)
- By maintaining a constant focal length value for the center wavelength, the optical system ensures consistent optical focal length. This helps to preserve the accuracy of correcting aberrations and maintain the integrity of the axial chromatic aberration;
- (3)
- At the initial phase of addressing distortions, the optimization method entails making use of RMS (root mean square), primary ray, and barycentre. Once the primary aberration correction is nearly complete, the optimization strategy focuses on incorporating wavefront, primary ray, and barycentre to further correct any remaining aberrations. Glass replacement is ideal for surfaces that exhibit noticeable differences in aberration.
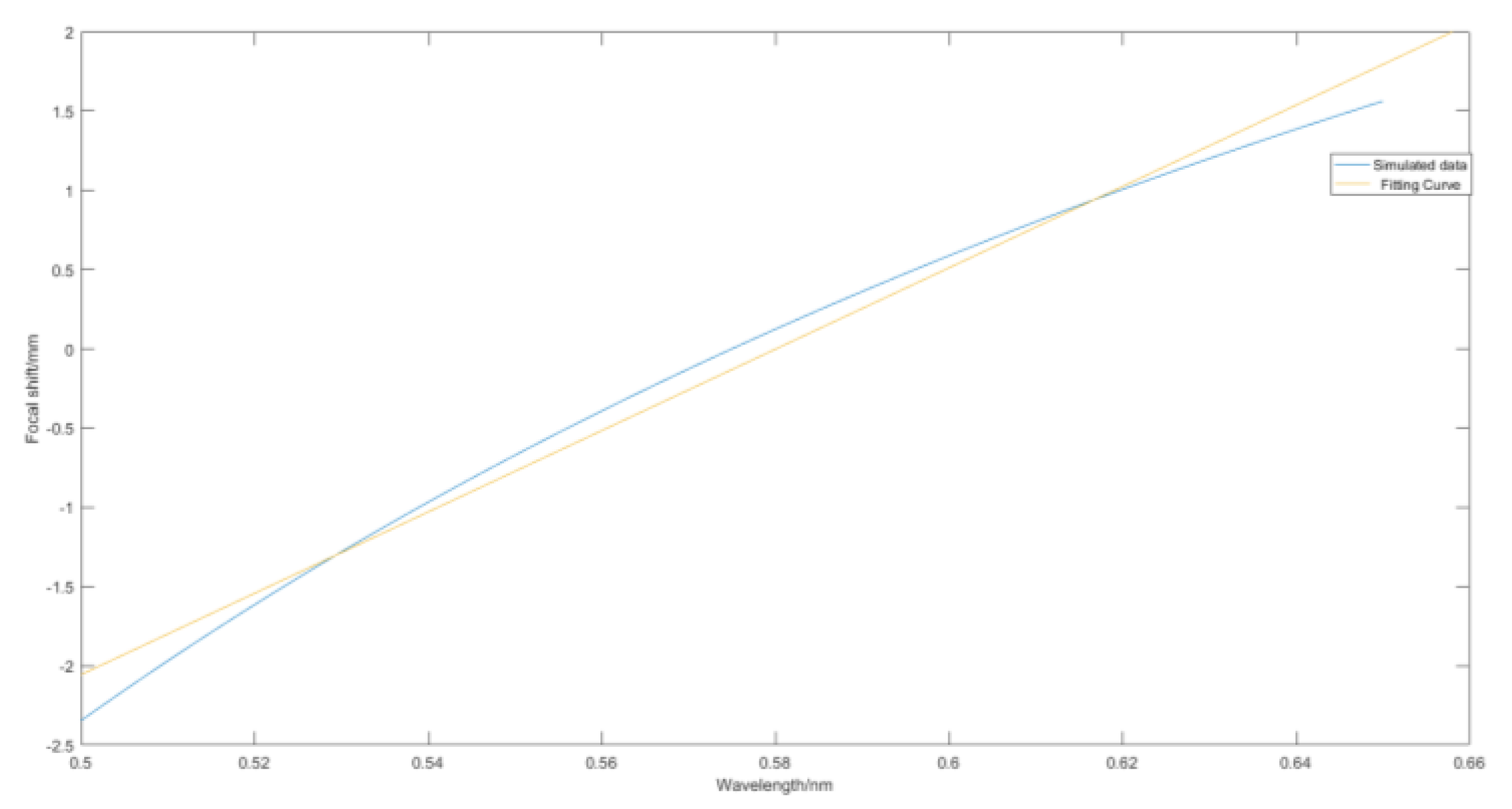
3.2. Dispersive Objective Dispersion Range and Imaging Quality Analysis
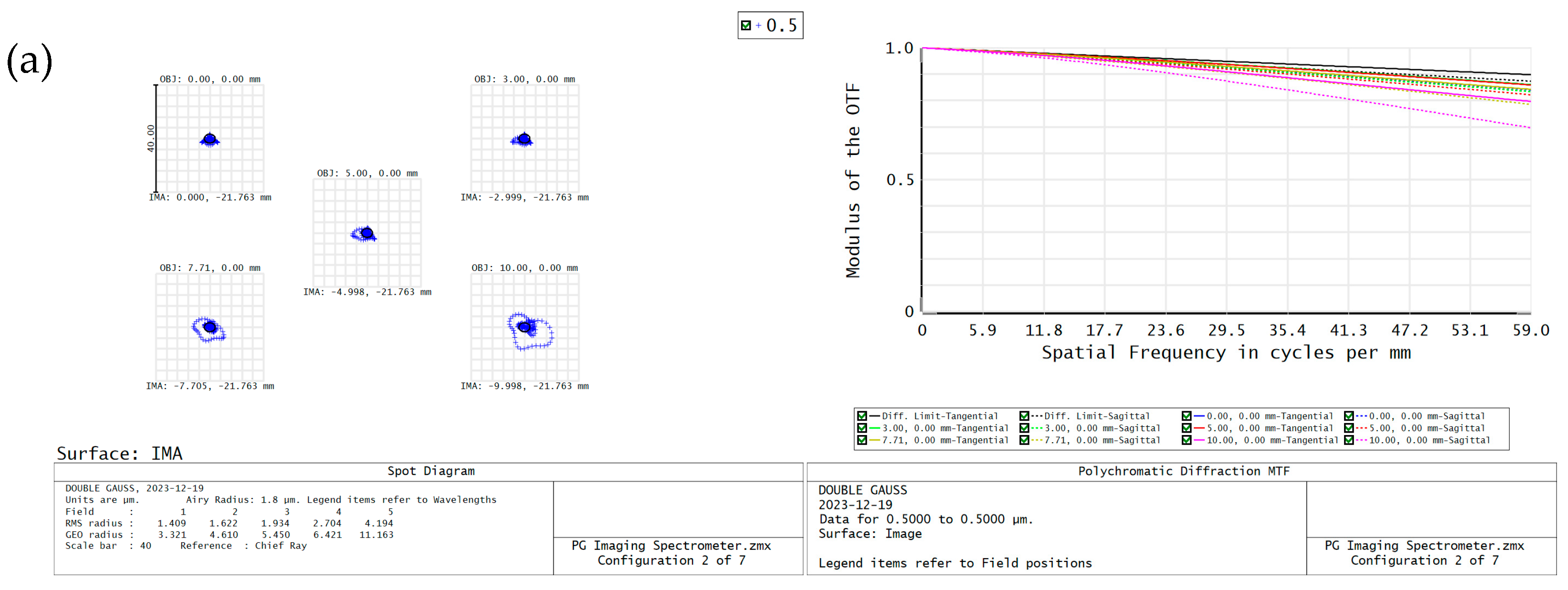
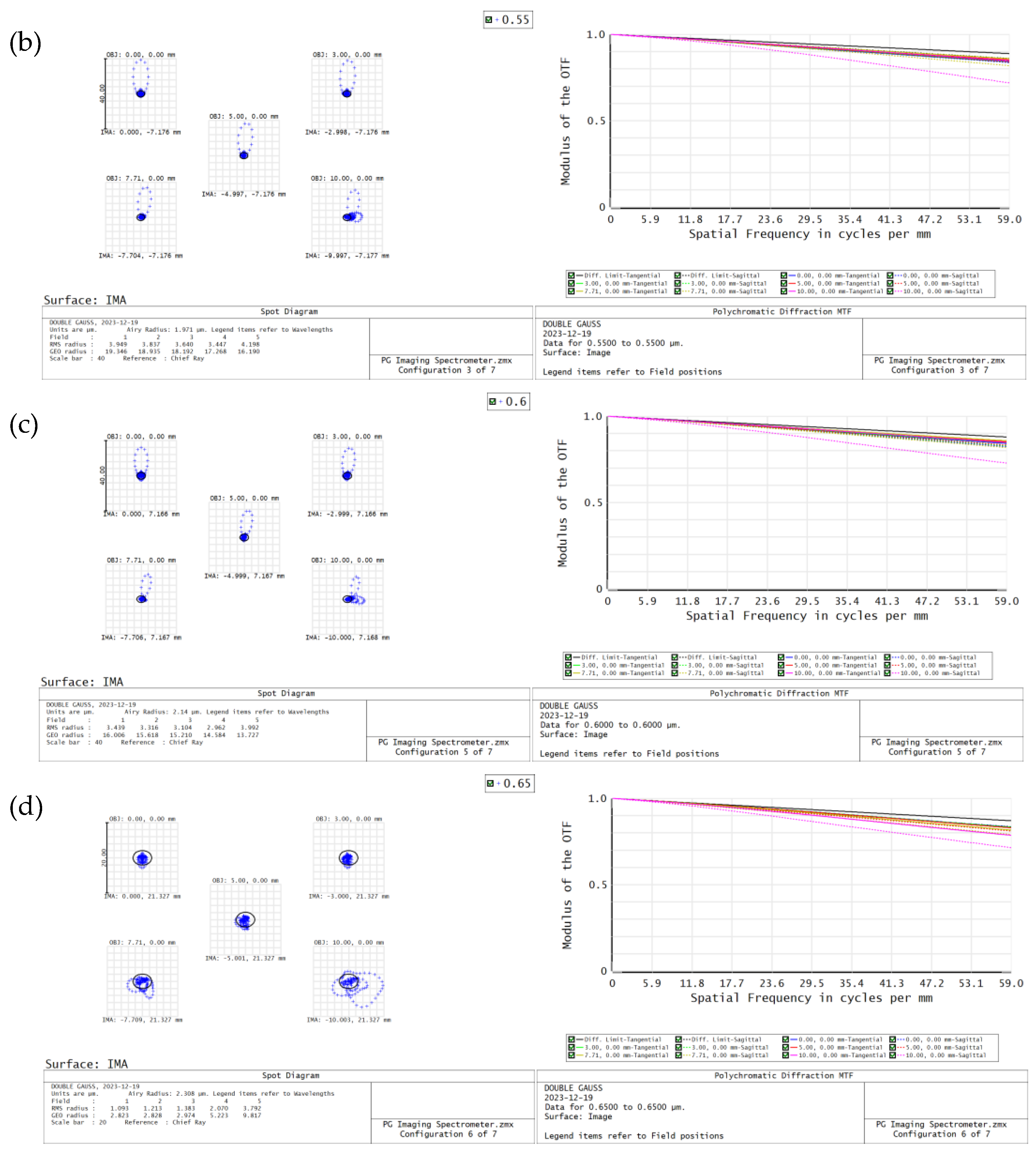
3.3. Imaging Spectrometer
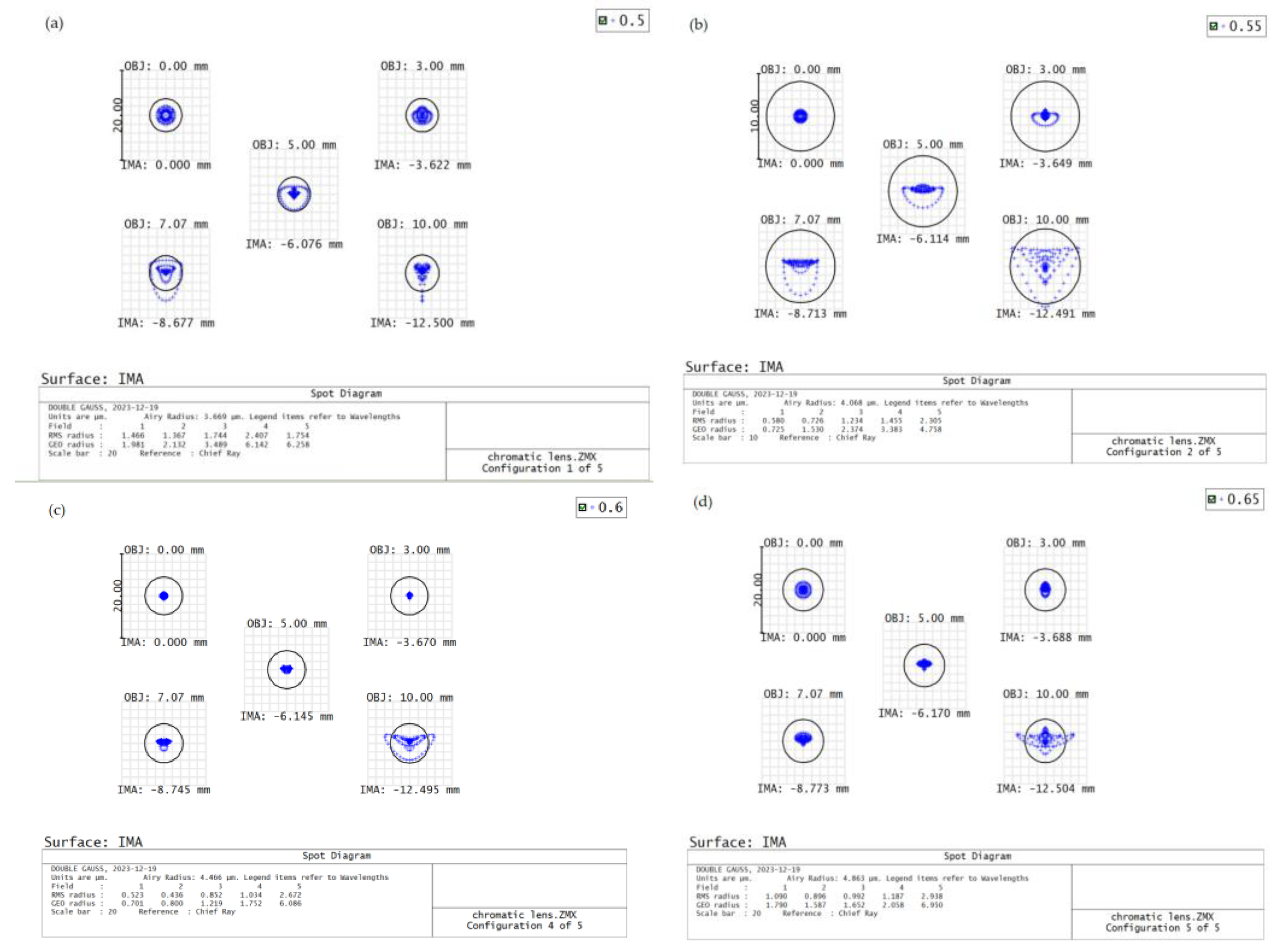
3.4. Imaging Quality Analysis
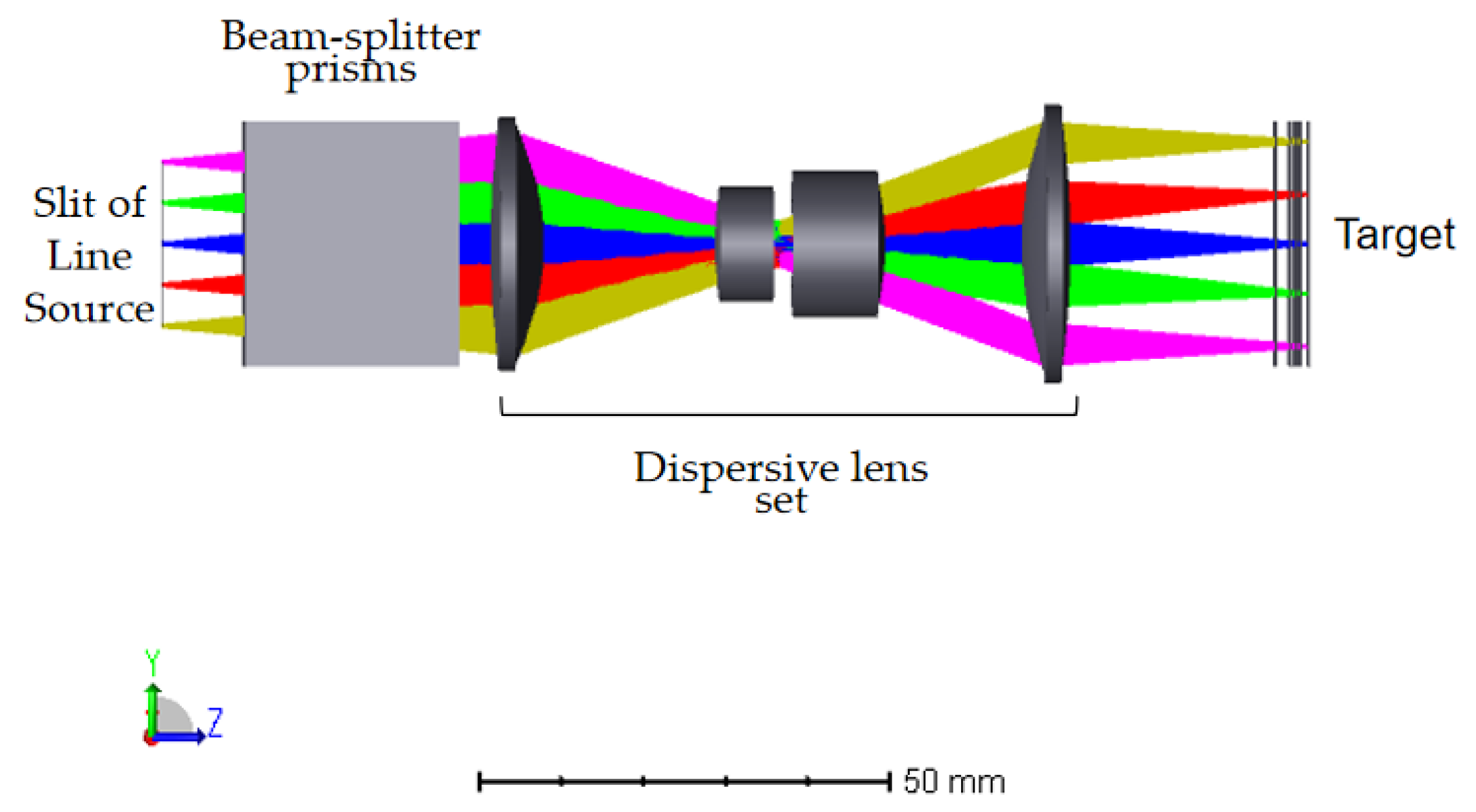
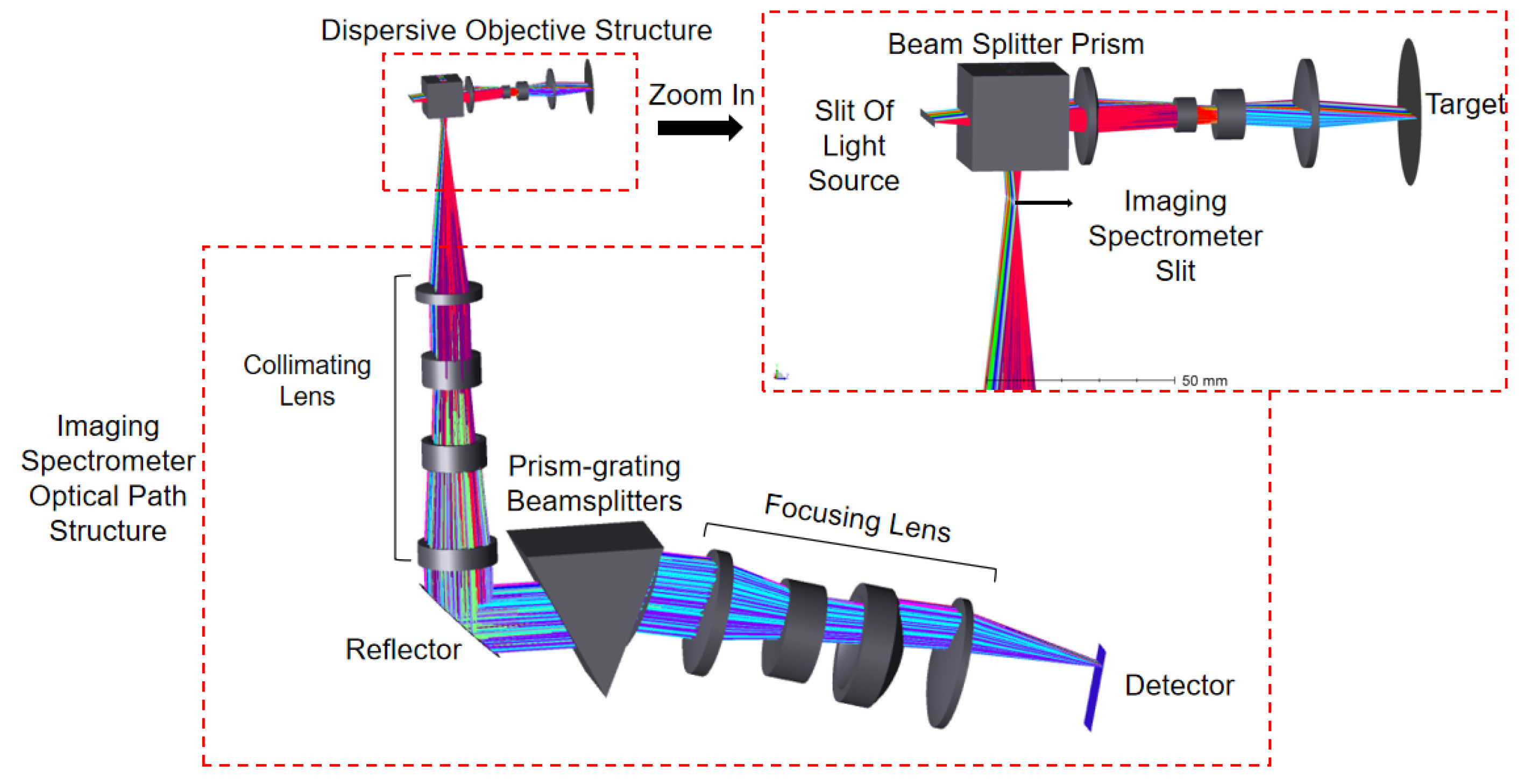
4. System-Wide Optical Path Analysis
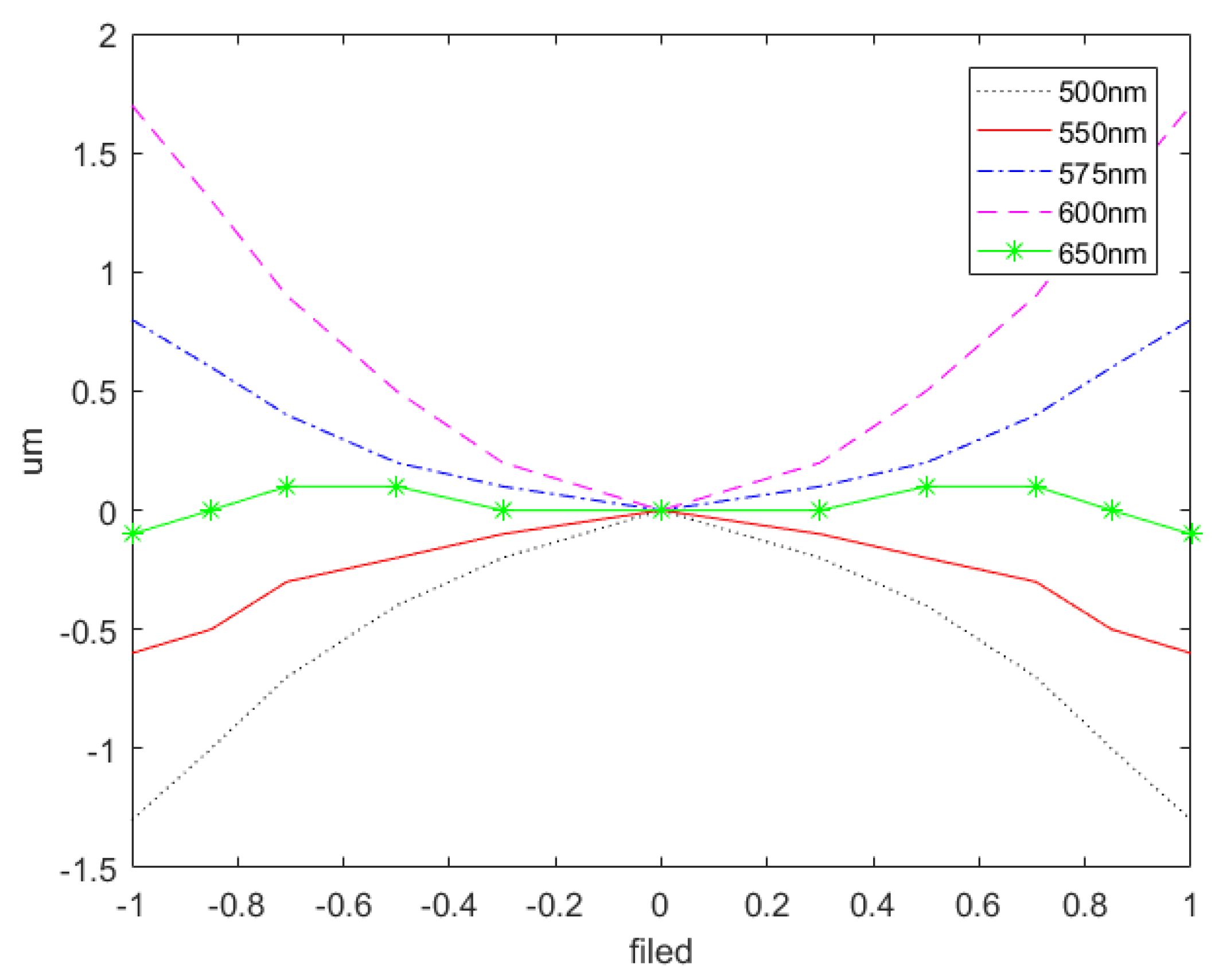
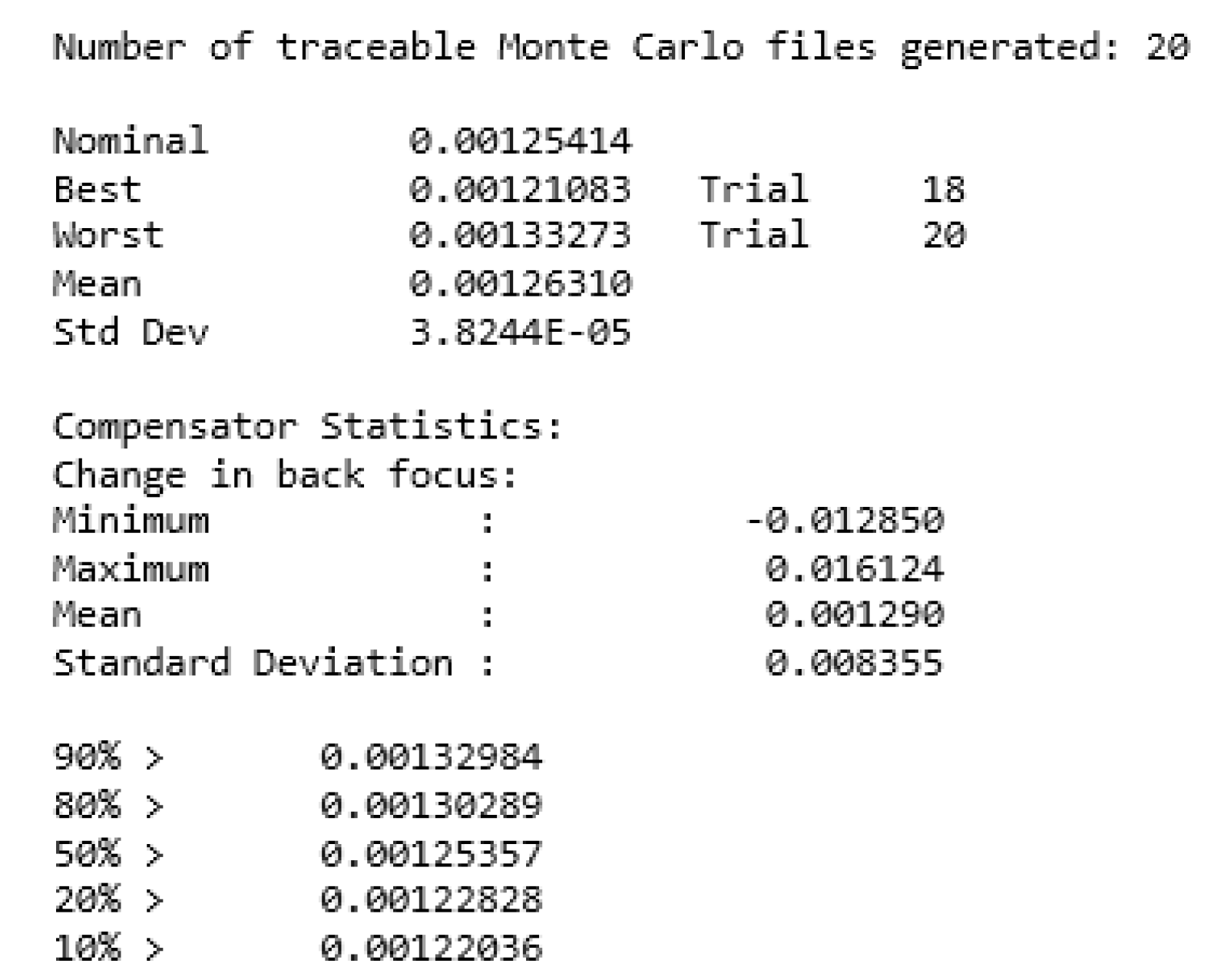
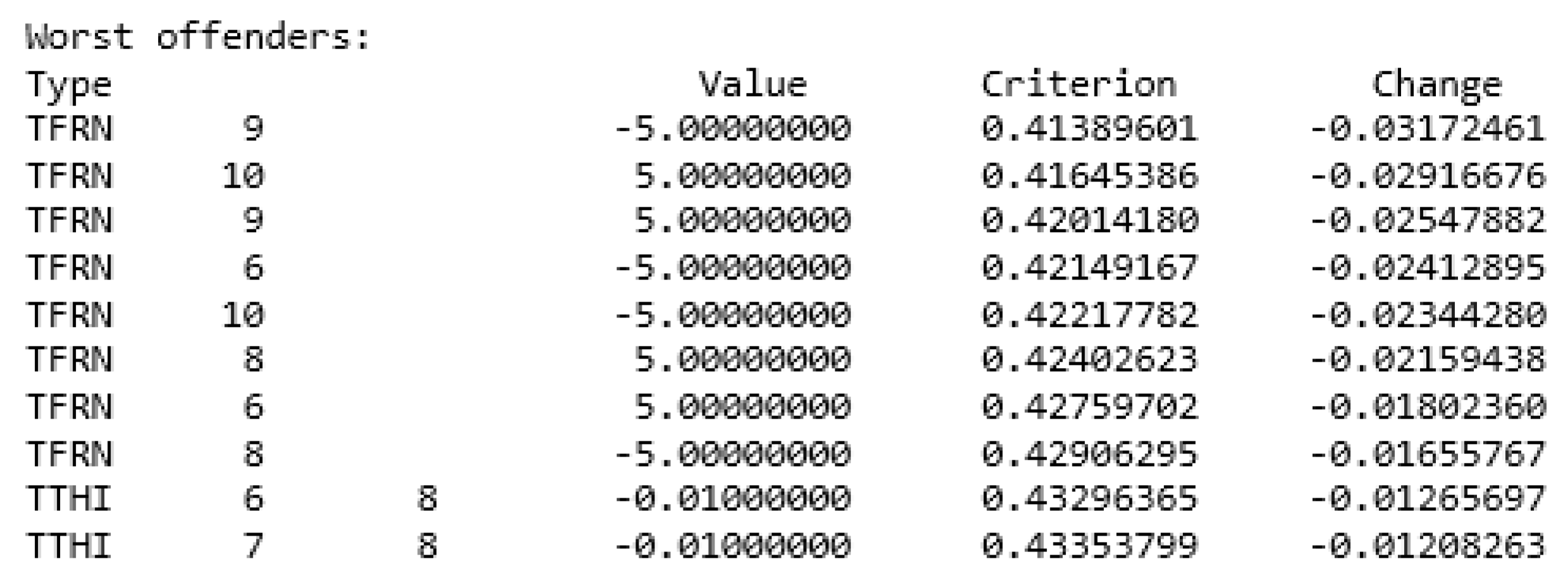
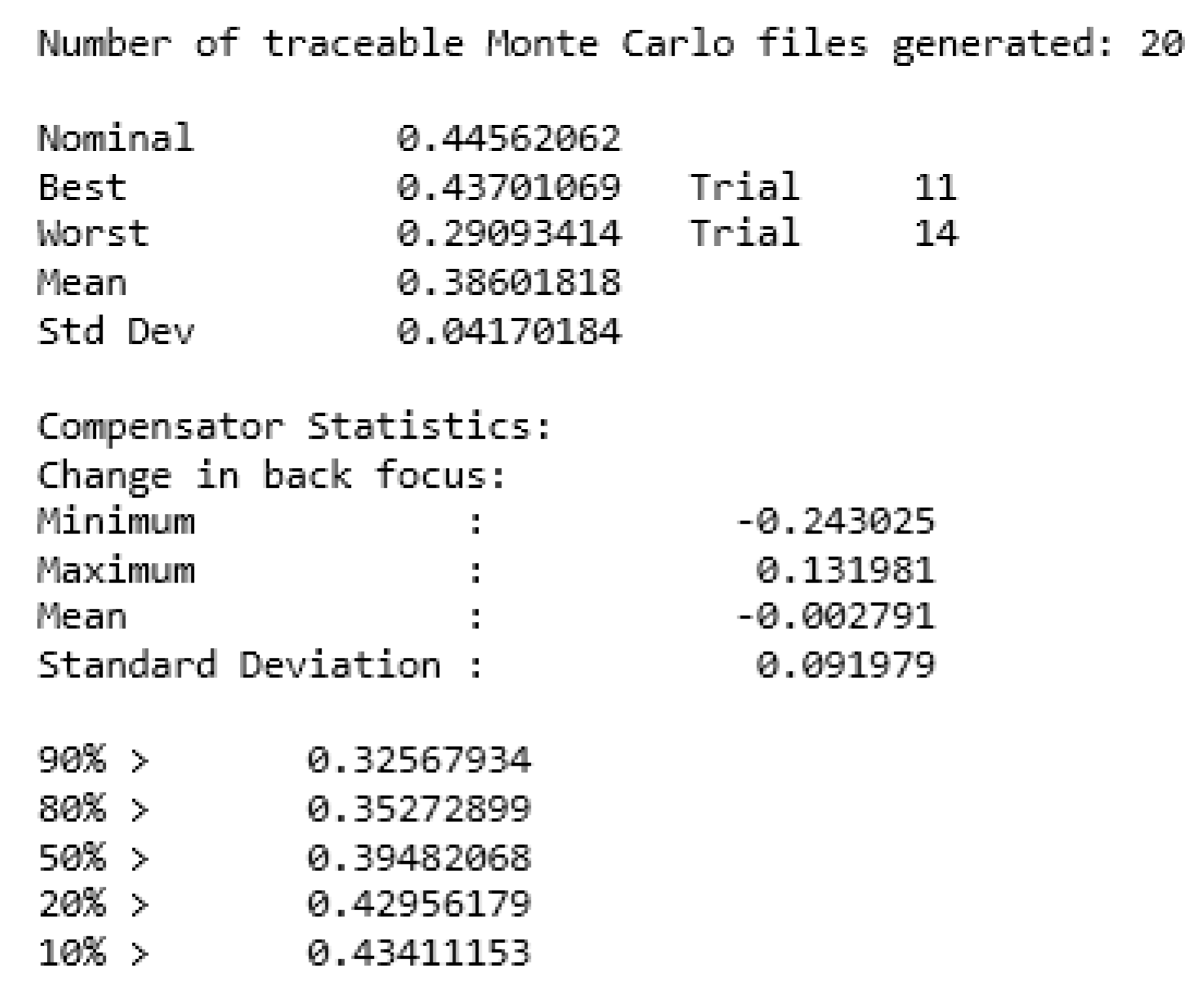
5. Tolerance Analysis
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shimizu, Y.; Matsukuma, H.; Gao, W. Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors. Sensors 2019, 19, 5289. [Google Scholar] [CrossRef] [PubMed]
- Dabrowska, S.; Ekiert, M.; Wojcik, K.; Kalemba, M.; Mlyniec, A. A 3D Scanning System for Inverse Analysis of Moist Biological Samples: Design and Validation Using Tendon Fascicle Bundles. Sensors 2020, 20, 3847. [Google Scholar] [CrossRef] [PubMed]
- Ortlepp, I.; Stauffenberg, J.; Manske, E. Processing and analysis of long-range scans with an atomic force microscope (AFM) in combination with nanopositioning and nanomeasuring technology for defect detection and quality control. Sensors 2021, 21, 5862. [Google Scholar] [CrossRef]
- Yang, H.X.; Fu, H.J.; Hu, P.C.; Yang, R.T.; Xu, X.; Liang, Y.; Di, C.; Tan, J.B. Ultra-precision and high-speed laser interferometric displacement measurement technology and instrument. Laser Optoelectron. Prog. 2022, 59, 0922018. [Google Scholar]
- Kienle, P.; Batarilo, L.; Akgül, M.; Köhler, M.H.; Wang, K.; Jakobi, M.; Koch, A.W. Optical setup for errorcompensation in a laser triangulation system. Sensors 2020, 20, 4949. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Tan, P.J.; Wu, G.W.; Lin, C.-J.; Nguyenet, D.T. High-speed chromatic confocal microscopy using multispectral sensors for submicrometer-precision microscopic surface profilometry. Meas. Sens. 2021, 18, 100165. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Yu, Q.; Shang, W.J.; Wang, C.; Liu, T.; Wang, Y.; Cheng, F. Chromatic confocal measurement system and its experimental study based on inclined illumination. Chin. Opt. 2022, 15, 514–524. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Q. L Development of an on-machine measurement system with chromatic confocal probe for measuring the profile error of off-axis biconical free-form optics in ultra-precision grinding. Measurement 2022, 202, 111825. [Google Scholar] [CrossRef]
- Ye, L.; Qian, J.; Haitjema, H.; Dominiek, R. On-machine chromatic confocal measurement for micro-EDM drilling and milling. Precis. Eng. 2022, 76, 110–123. [Google Scholar] [CrossRef]
- Agoyan, M.; Fourneau, G.; Cheymol, G.; Guy, L.; Ayoub, M.; Hicham, D.; Christophe, F.; Damien, G.; Sylvain, B.; Aziz, B. Toward confocal chromatic sensing in nuclear reactors: In situ optical refractive index measurements of bulk glass. IEEE Trans. Nucl. Sci. 2022, 69, 722–730. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, J.K.; Chen, X.M.; Jiang, X.J.; Li, G.N.; Huo, S.C.; Gao, C.; Zhu, Q.; Zhou, W.H. Chromatic confocal microscopy measurement technique: A review. Semicond. Optoelectron. 2022, 43, 752–759. [Google Scholar]
- Li, J.F.; Zhu, X.P.; Du, H.; Ji, Z.C.; Wang, K.; Zhao, M. Thickness measurement method for self-supporting film with double chromatic confocal probes. Appl. Opt. 2021, 60, 9447–9452. [Google Scholar] [CrossRef]
- Liu, T.; Wang, J.Y.; Liu, Q.; Hu, J.Q.; Wang, Z.B.; Wan, C.; Yang, S. Chromatic confocal measurement method using a phase Fresnel zone plate. Opt. Express 2022, 30, 2390–2401. [Google Scholar] [CrossRef] [PubMed]
- Shao, T.B.; Guo, W.P.; Xi, Y.H.; Liu, Z.Y.; Yang, K.C.; Xia, M. Design and performance evaluation of chromatic confocal displacement sensor with high measuring range. Chin. J. Lasers 2022, 49, 1804002. [Google Scholar]
- Park, H.M.; Kwon, U.; Joo, K.N. Vision chromatic confocal sensor based on a geometrical phase lens. Appl. Opt. 2021, 60, 2898–2901. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.H.; Wang, X.H.; Wang, J.J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.J.; Zhao, T.M.; Wang, Z.H.; Tang, S.J. Online integrated surface roughness measurement method based onspectral confocal. J. Metrol. 2021, 42, 753–758. [Google Scholar]
- Zhang, Z.L.; Lu, R.S. Initial structure of dispersion objective for chromatic confocal sensor based on doublet lens. Opt. Lasers Eng. 2021, 139, 106424. [Google Scholar] [CrossRef]
- Hu, H.; Mei, S.; Fan, L.M.; Wang, H.G. A line-scanning chromatic confocal sensor for three-dimensional profile measurement on highly reflective materials. Rev. Sci. Instrum. 2021, 92, 053707. [Google Scholar] [CrossRef]
- Novak, J.; Miks, A. Hyperchromats with linear dependence of longitudinal chromatic aberration on wavelength. Optik 2005, 116, 165–168. [Google Scholar] [CrossRef]
- Chen, H.F.; Gong, Y.; Luo, C.; Peng, J. Design of prism-grating imaging spectrometer with eliminating spectral line curvature. Acta Opt. Sin. 2014, 34, 245–252. [Google Scholar]
- Gao, Z.Y.; Fang, W.; Song, B.Q.; Jiang, M.; Wang, Y.P. Simulation of spectral response function based on Huygens point spread function. Acta Photonica Sin. 2015, 44, 65–70. [Google Scholar]
- Cao, Z.Y.; Xiang, Y. Design of a 3D zoom exoscope optical system with a long working distance. Infrared Laser Eng. 2022, 51, 20210808. [Google Scholar]





| Parameters | Value |
|---|---|
| Wavelength range | 500–650 nm |
| Scanning line length | ≥20 mm |
| Dispersion range | ≥3 mm |
| Axial resolution | ≤0.8 μm |
| Parameters | Value |
|---|---|
| Center wavelength focal length | 120 mm |
| Magnification | −1.2 |
| Scanning line length | 24 mm |
| Objective field of view | 10 mm |
| Working distance | 25 mm |
| Aperture of object | 0.1 |
| Parameters | Value |
|---|---|
| Spectral range | 490–660 nm |
| Aperture of object | 0.15 |
| Spectral resolution | 0.03 nm |
| Spatial resolution | 8.5 μm |
| Spectral line bending | Smile < 2 μm Keystone < 2 μm |
| Slit Size | 10 mm × 17 μm |
| Wave band | 500 nm | 550 nm | 600 nm | 650 nm |
| Diffuse spot radius | 6.724 μm | 6.715 μm | 6.693 μm | 6.656 μm |
| Researches | Scanning Line Length | Measurement Range | Axial Resolution | Working Distance |
|---|---|---|---|---|
| This paper | 24 mm | 3.9 mm | 0.8 μm | 25 mm |
| STIL Corporation | 12.85 mm | 2.6 mm | 1.8 μm | 16 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Du, J.; Qi, M.; Yan, J.; Cheng, M.; Zhang, Z. Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor. Sensors 2024, 24, 723. https://doi.org/10.3390/s24030723
Yang W, Du J, Qi M, Yan J, Cheng M, Zhang Z. Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor. Sensors. 2024; 24(3):723. https://doi.org/10.3390/s24030723
Chicago/Turabian StyleYang, Weiguang, Jian Du, Meijie Qi, Jiayue Yan, Mohan Cheng, and Zhoufeng Zhang. 2024. "Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor" Sensors 24, no. 3: 723. https://doi.org/10.3390/s24030723
APA StyleYang, W., Du, J., Qi, M., Yan, J., Cheng, M., & Zhang, Z. (2024). Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor. Sensors, 24(3), 723. https://doi.org/10.3390/s24030723









