Leveraging Remote Sensing Data for Yield Prediction with Deep Transfer Learning
Abstract
1. Introduction
1.1. Related Work
1.1.1. General Transfer Learning
1.1.2. Remote Sensing in Yield Prediction
1.1.3. Transfer Learning for Remote Sensing Applications
2. Materials
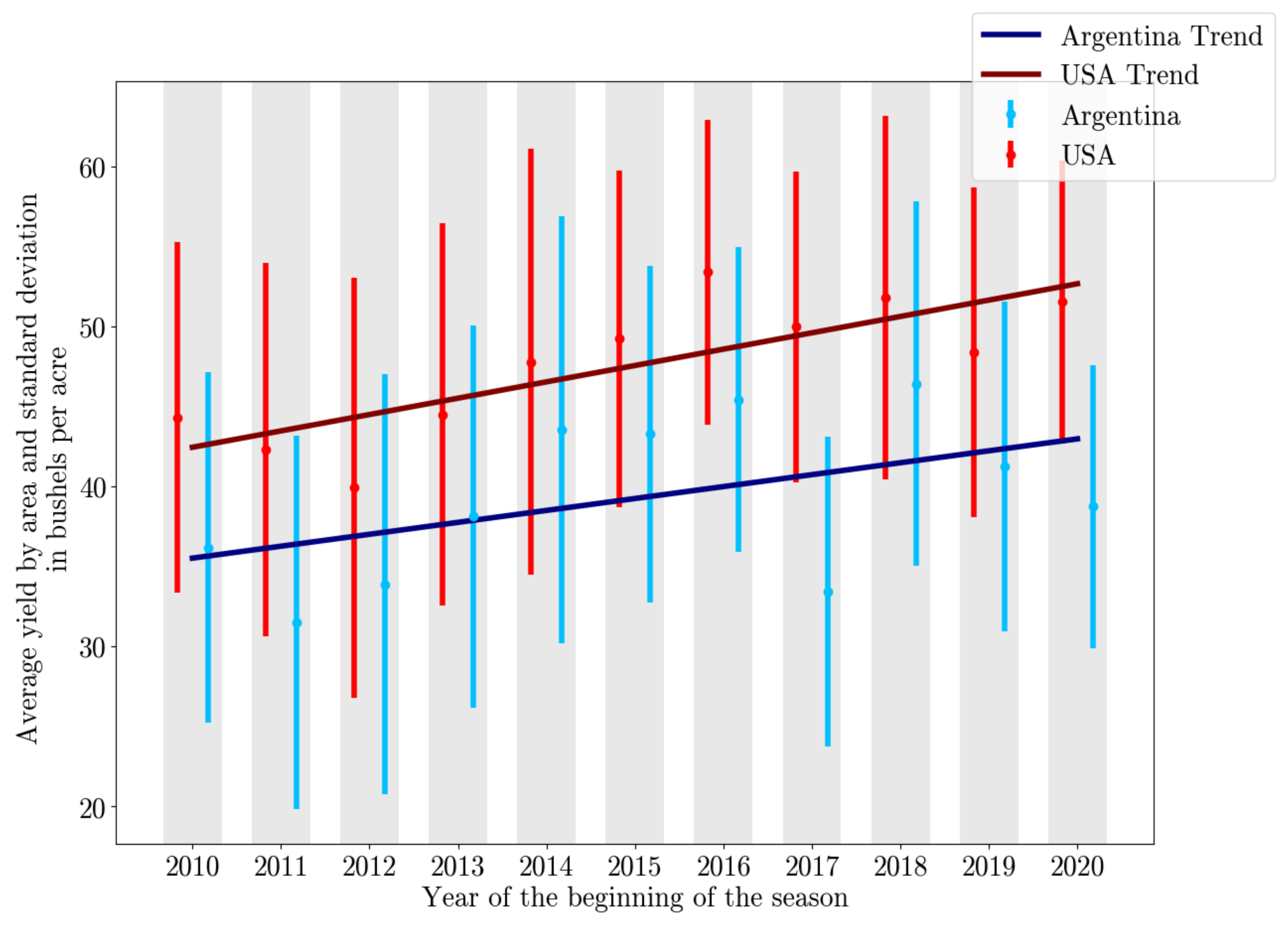
2.1. Yield Data
2.2. Remote Sensing Data
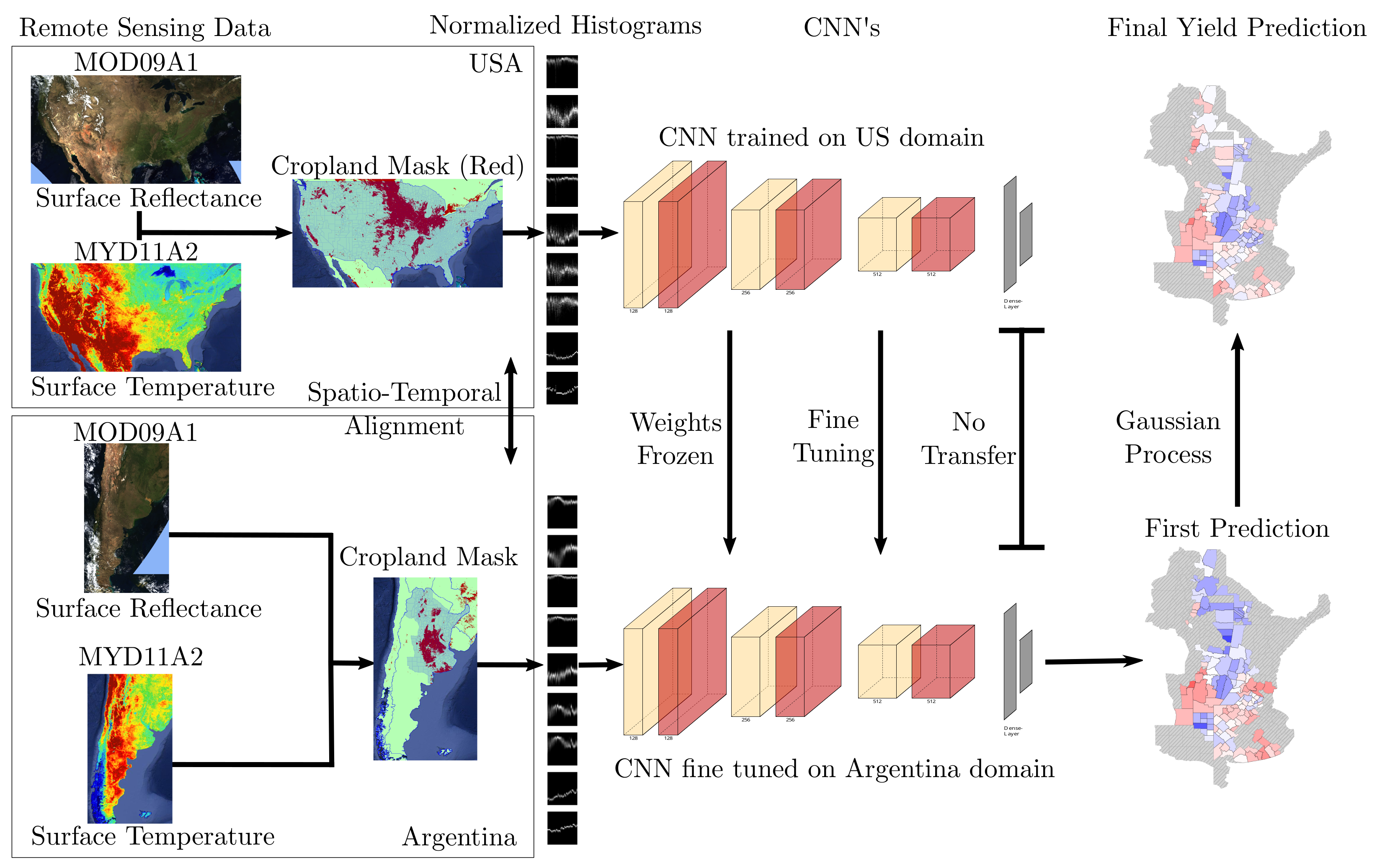
3. Methods
3.1. Spatio-Temporal Alignment
3.2. Model Design and Transfer Learning Techniques
3.3. Deep Gaussian Process
3.4. Performance Metrics and Hyperparameter Tuning
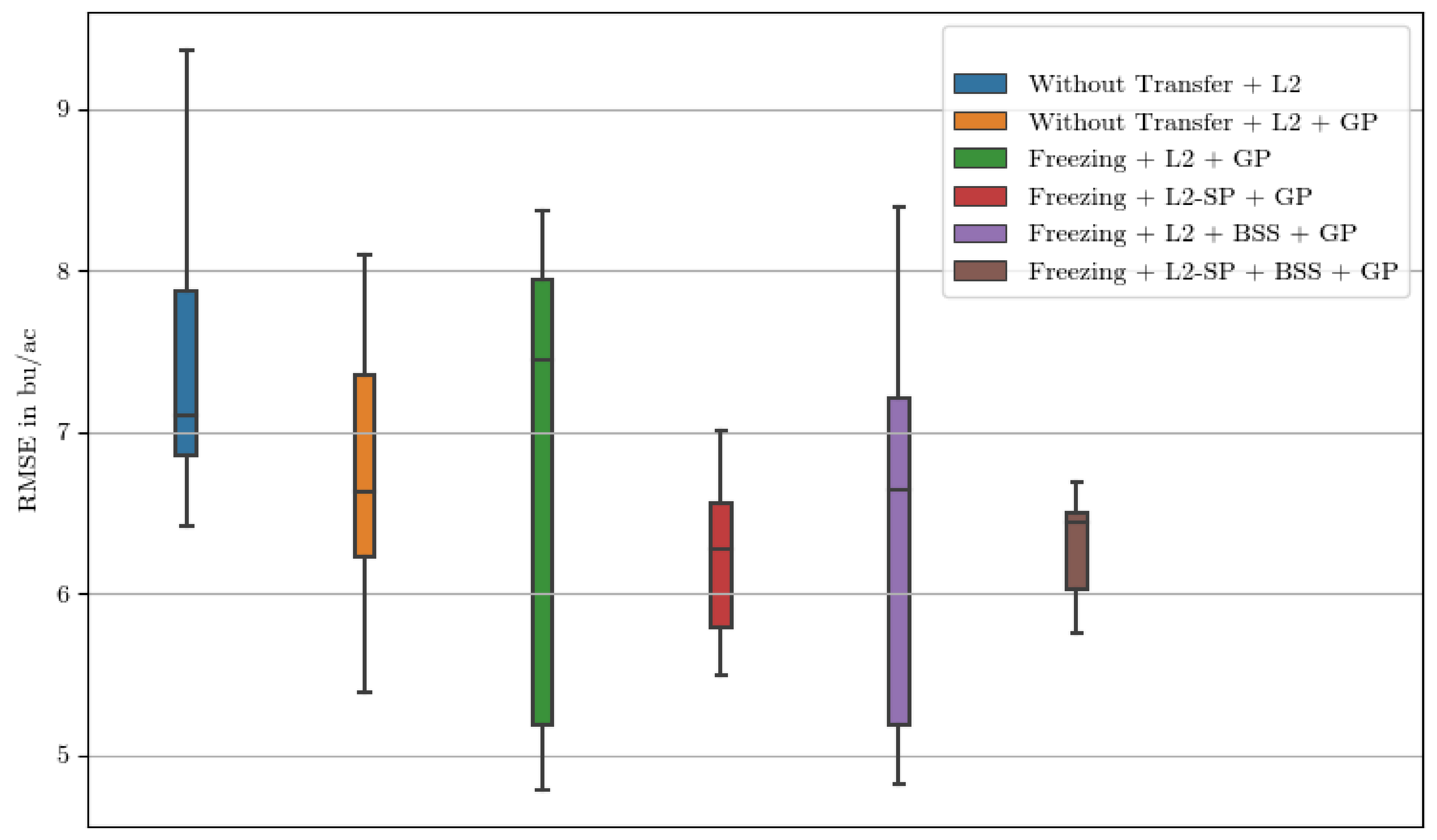
4. Results
4.1. Full Growth Cycle Prediction
4.2. In Season Prediction
5. Discussion
6. Conclusions
- Spatio-temporal alignment can be performed even between two varying remote sensing data sources to allow for transfer learning.
- The capabilities of transfer-specific regularization methods -SP and BSS together with Gaussian processes for transfer learning translate to the context of yield prediction and hyperspectral remote sensing data in the form of histograms.
- Regularized transfer learning can improve yield predictions in regions where fewer data are available and should be considered as an alternative to state-of-the-art approaches, especially for smaller study areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| USA: CNN | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2015 | 5.57 | 0.639 | 6.89 | 0.290 |
| 2016 | 6.64 | 0.375 | 8.47 | −0.071 |
| 2017 | 4.85 | 0.737 | 5.12 | 0.801 |
| 2018 | 6.77 | 0.567 | 7.04 | 0.479 |
| 2019 | 5.24 | 0.635 | 6.04 | 0.545 |
| 2020 | 6.58 | 0.545 | 7.28 | 0.480 |
| AVG | 5.94 | 0.583 | 6.81 | 0.439 |
| Argentina without Transfer | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 7.44 | 0.567 | 7.65 | 0.543 |
| 2019 | 8.15 | 0.360 | 6.70 | 0.572 |
| 2020 | 6.83 | 0.400 | 5.91 | 0.549 |
| AVG | 7.47 | 0.442 | 6.76 | 0.439 |
| Argentina + Freezing | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 7.54 | 0.557 | 8.13 | 0.487 |
| 2019 | 7.15 | 0.513 | 7.48 | 0.468 |
| 2020 | 6.13 | 0.507 | 4.95 | 0.685 |
| AVG | 6.94 | 0.526 | 6.85 | 0.547 |
| Argentina + Freezing, -SP | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 7.55 | 0.552 | 6.80 | 0.640 |
| 2019 | 7.23 | 0.503 | 6.30 | 0.623 |
| 2020 | 5.62 | 0.594 | 5.64 | 0.592 |
| AVG | 6.80 | 0.550 | 6.25 | 0.618 |
| Argentina + Freezing, and BSS | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 7.82 | 0.523 | 6.71 | 0.650 |
| 2019 | 7.83 | 0.414 | 7.62 | 0.445 |
| 2020 | 5.51 | 0.610 | 4.96 | 0.684 |
| AVG | 7.05 | 0.516 | 6.43 | 0.593 |
| Argentina + Freezing, -SP and BSS | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 7.61 | 0.548 | 6.58 | 0.664 |
| 2019 | 7.55 | 0.459 | 6.44 | 0.606 |
| 2020 | 6.06 | 0.527 | 5.90 | 0.553 |
| AVG | 7.07 | 0.511 | 6.31 | 0.608 |
Appendix B
| USA: CNN | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2015 | 6.75 | 0.471 | 6.58 | 0.541 |
| 2016 | 8.33 | 0.021 | 8.35 | 0.018 |
| 2017 | 6.15 | 0.580 | 6.02 | 0.590 |
| 2018 | 7.69 | 0.445 | 7.52 | 0.429 |
| 2019 | 7.32 | 0.289 | 7.11 | 0.381 |
| 2020 | 6.504 | 0.556 | 6.38 | 0.586 |
| AVG | 7.12 | 0.394 | 7.00 | 0.414 |
| Argentina without Transfer | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 10.73 | 0.086 | 9.08 | 0.356 |
| 2019 | 9.23 | 0.189 | 8.73 | 0.273 |
| 2020 | 8.12 | 0.146 | 7.30 | 0.312 |
| AVG | 9.36 | 0.140 | 8.37 | 0.314 |
| Argentina + Freezing, BSS and -SP | ||||
| Year | RMSE | RMSE + GP | + GP | |
| 2018 | 9.53 | 0.293 | 8.49 | 0.440 |
| 2019 | 8.43 | 0.321 | 6.45 | 0.604 |
| 2020 | 6.64 | 0.434 | 5.81 | 0.567 |
| AVG | 8.20 | 0.349 | 6.92 | 0.537 |
References
- Plested, J.; Gedeon, T. Deep transfer learning for image classification: A survey. arXiv 2022, arXiv:2205.09904. [Google Scholar]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 806–813. [Google Scholar]
- Huh, M.; Agrawal, P.; Efros, A.A. What makes ImageNet good for transfer learning? arXiv 2016, arXiv:1608.08614. [Google Scholar]
- Chu, B.; Madhavan, V.; Beijbom, O.; Hoffman, J.; Darrell, T. Best practices for fine-tuning visual classifiers to new domains. In Proceedings of the Computer Vision–ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10 and 15–16 October 2016; pp. 435–442. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Xuhong, L.; Grandvalet, Y.; Davoine, F. Explicit inductive bias for transfer learning with convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2825–2834. [Google Scholar]
- Li, X.; Xiong, H.; Wang, H.; Rao, Y.; Liu, L.; Chen, Z.; Huan, J. Delta: Deep learning transfer using feature map with attention for convolutional networks. arXiv 2019, arXiv:1901.09229. [Google Scholar]
- Chen, X.; Wang, S.; Fu, B.; Long, M.; Wang, J. Catastrophic forgetting meets negative transfer: Batch spectral shrinkage for safe transfer learning. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Muruganantham, P.; Wibowo, S.; Grandhi, S.; Samrat, N.H.; Islam, N. A systematic literature review on crop yield prediction with deep learning and remote sensing. Remote Sens. 2022, 14, 1990. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Kaneko, A.; Kennedy, T.; Mei, L.; Sintek, C.; Burke, M.; Ermon, S.; Lobell, D. Deep learning for crop yield prediction in Africa. In Proceedings of the ICML Workshop on Artificial Intelligence for Social Good, Long Beach, CA, USA, 9–15 June 2019; pp. 33–37. [Google Scholar]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep transfer learning for crop yield prediction with remote sensing data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, Menlo Park and San Jose, CA, USA, 20–22 June 2018; pp. 1–5. [Google Scholar]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous corn and soybean yield prediction from remote sensing data using deep transfer learning. Sci. Rep. 2021, 11, 11132. [Google Scholar] [CrossRef] [PubMed]
- Huber, F.; Yushchenko, A.; Stratmann, B.; Steinhage, V. Extreme Gradient Boosting for yield estimation compared with Deep Learning approaches. Comput. Electron. Agric. 2022, 202, 107346. [Google Scholar] [CrossRef]
- Desloires, J.; Ienco, D.; Botrel, A. Out-of-year corn yield prediction at field-scale using Sentinel-2 satellite imagery and machine learning methods. Comput. Electron. Agric. 2023, 209, 107807. [Google Scholar] [CrossRef]
- USDA. USDA NASS Quick Stats Database. 2022. Available online: https://quickstats.nass.usda.gov/ (accessed on 1 October 2022).
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2024, 301, 113924. [Google Scholar] [CrossRef]
- Dastour, H.; Hassan, Q.K. A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification. Sustainability 2023, 15, 7854. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of high-spatial-resolution remote sensing scenes method using transfer learning and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Alem, A.; Kumar, S. Transfer learning models for land cover and land use classification in remote sensing image. Appl. Artif. Intell. 2022, 36, 2014192. [Google Scholar] [CrossRef]
- Tseng, H.H.; Yang, M.D.; Saminathan, R.; Hsu, Y.C.; Yang, C.Y.; Wu, D.H. Rice seedling detection in UAV images using transfer learning and machine learning. Remote Sens. 2022, 14, 2837. [Google Scholar] [CrossRef]
- Chen, J.; Sun, J.; Li, Y.; Hou, C. Object detection in remote sensing images based on deep transfer learning. Multimed. Tools Appl. 2022, 81, 12093–12109. [Google Scholar] [CrossRef]
- Hilal, A.; Al-Wesabi, F.; Alzahrani, K.; Al Duhayyim, M.; Hamza, M.; Rizwanullah, M.; Díaz, V. Deep Transfer Learning based Fusion Model for Environmental Remote Sensing Image Classification Model. Eur. J. Remote. Sens. 2022, 55, 12–23. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, Z.; Huang, Q.; Zhang, Z. Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach. Remote Sens. 2023, 15, 4562. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Ministerio de Agricultura. Soja—Serie Siembra, Cosecha, Producción, Rendimiento. 2023. Available online: https://datosestimaciones.magyp.gob.ar/reportes.php?reporte=Estimaciones (accessed on 9 May 2023).
- Chambers, R.G.; Pieralli, S. The sources of measured US agricultural productivity growth: Weather, technological change, and adaptation. Am. J. Agric. Econ. 2020, 102, 1198–1226. [Google Scholar] [CrossRef]
- Vermote, E. MODIS/Terra Surface Reflectance 8-Day L3 Global 500 m SIN Grid V061 [Data Set]. NASA EOSDIS Land Processes DAAC. 2021. Available online: https://lpdaac.usgs.gov/products/mod09a1v061/ (accessed on 26 October 2022).
- Wan, Z.; Hook, S.; Hulley, G. MODIS/Aqua Land Surface Temperature/Emissivity 8-Day L3 Global 1km SIN Grid V061 [Data Set]. NASA EOSDIS Land Processes DAAC. 2021. Available online: https://lpdaac.usgs.gov/products/myd11a2v061/ (accessed on 11 November 2022).
- Friedl, M.; Sulla-Menashe, D. MCD12Q1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500 m SIN Grid V006 [Data Set]. NASA EOSDIS Land Processes DAAC. 2019. Available online: https://lpdaac.usgs.gov/products/mcd12q1v006/ (accessed on 11 November 2022).
- Bureau, U.C. Tiger: US Census Counties. 2018. Available online: https://developers.google.com/earth-engine/datasets/catalog/TIGER_2018_Counties/ (accessed on 26 October 2022).
- USDA. Country Summary. 2023. Available online: https://ipad.fas.usda.gov/countrysummary/ (accessed on 21 February 2023).
- Tseng, G. Pycrop-Yield-Prediction. 2022. Available online: https://github.com/gabrieltseng/pycrop-yield-prediction (accessed on 30 July 2022).
- Iman, M.; Rasheed, K.; Arabnia, H.R. A review of deep transfer learning and recent advancements. arXiv 2022, arXiv:2201.09679. [Google Scholar] [CrossRef]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Fernandez-Beltran, R.; Baidar, T.; Kang, J.; Pla, F. Rice-yield prediction with multi-temporal sentinel-2 data and 3D CNN: A case study in Nepal. Remote Sens. 2021, 13, 1391. [Google Scholar] [CrossRef]



| Hyperparameter | Tuning Method | Optimal Parameter |
|---|---|---|
| Number of frozen layer | Empirical | 4 ∈ [0, 6] |
| US init. of weight | Empirical | True ∈ [True, False] |
| -SP | TPE | |
| -SP | TPE | |
| BSS | TPE | |
| BSS k | Empirical | 1 |
| RMSE ↓ | ↑ | RMSE + GP ↓ | + GP ↑ | |
|---|---|---|---|---|
| USA: CNN | 5.94 | 0.583 | 6.81 | 0.439 |
| Argentina without transfer | 7.47 | 0.442 | 6.76 | 0.554 |
| Argentina + freezing | 6.94 | 0.526 | 6.85 | 0.547 |
| Argentina + freezing and -SP | 6.80 | 0.550 | 6.25 | 0.618 |
| Argentina + freezing, and BSS | 7.05 | 0.516 | 6.43 | 0.593 |
| Argentina + freezing, -SP and BSS | 7.07 | 0.511 | 6.31 | 0.608 |
| RMSE ↓ | ↑ | RMSE + GP ↓ | + GP ↑ | |
|---|---|---|---|---|
| USA: CNN | 7.12 | 0.394 | 7.00 | 0.414 |
| Argentina without transfer | 9.36 | 0.140 | 8.37 | 0.314 |
| Argentina + freezing, -SP and BSS | 8.20 | 0.349 | 6.92 | 0.537 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, F.; Inderka, A.; Steinhage, V. Leveraging Remote Sensing Data for Yield Prediction with Deep Transfer Learning. Sensors 2024, 24, 770. https://doi.org/10.3390/s24030770
Huber F, Inderka A, Steinhage V. Leveraging Remote Sensing Data for Yield Prediction with Deep Transfer Learning. Sensors. 2024; 24(3):770. https://doi.org/10.3390/s24030770
Chicago/Turabian StyleHuber, Florian, Alvin Inderka, and Volker Steinhage. 2024. "Leveraging Remote Sensing Data for Yield Prediction with Deep Transfer Learning" Sensors 24, no. 3: 770. https://doi.org/10.3390/s24030770
APA StyleHuber, F., Inderka, A., & Steinhage, V. (2024). Leveraging Remote Sensing Data for Yield Prediction with Deep Transfer Learning. Sensors, 24(3), 770. https://doi.org/10.3390/s24030770






