Integrated Simulation and Calibration Framework for Heating System Optimization
Abstract
:1. Introduction
1.1. Technical Context
1.2. Background
1.3. Focus and Contribution
1.4. Structure
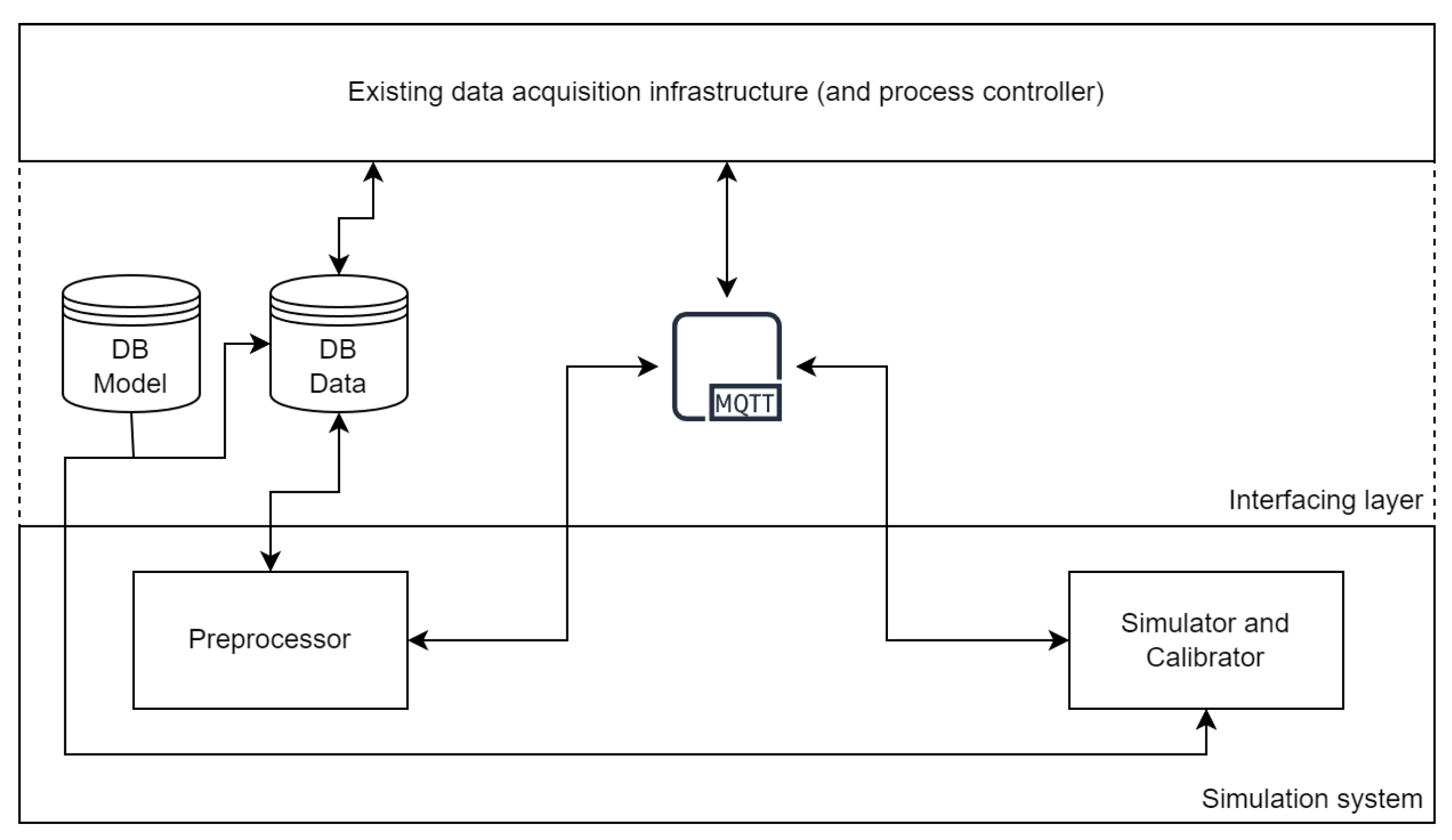
2. System Overview
2.1. Preprocessor
- Preprocessing: Raw data → Augmented data
- Reaugmentation: Augmented data → Reaugmented data
- Expansion of the timestamp to a (year, month of year, day of month, day of week, hour of day, minute of hour, minutes total) seven-tuple.
- Insertion of missing timestamps and linear interpolation of missing data.
- Extraction of training data using a quality threshold and training of the configurable LSTM network.
- Augmentation of the data with predictions from the LSTM network.
- Augmentation of the data by applying configurable preprocessing functions.
2.2. Simulator
2.3. Calibrator
| Algorithm 1: Cyclic Genetic Algorithm |
 |
| Algorithm 2: Generate Controller Parameters |
| Data: Model M and data D Parameter mapping with fixed controller parameters and calibratable free parameters Port mapping for free parameter calibration Port mapping for controller parameter calibration (with penalty-expressions) Result: Set of controller parameter values |
|

3. Materials and Methods
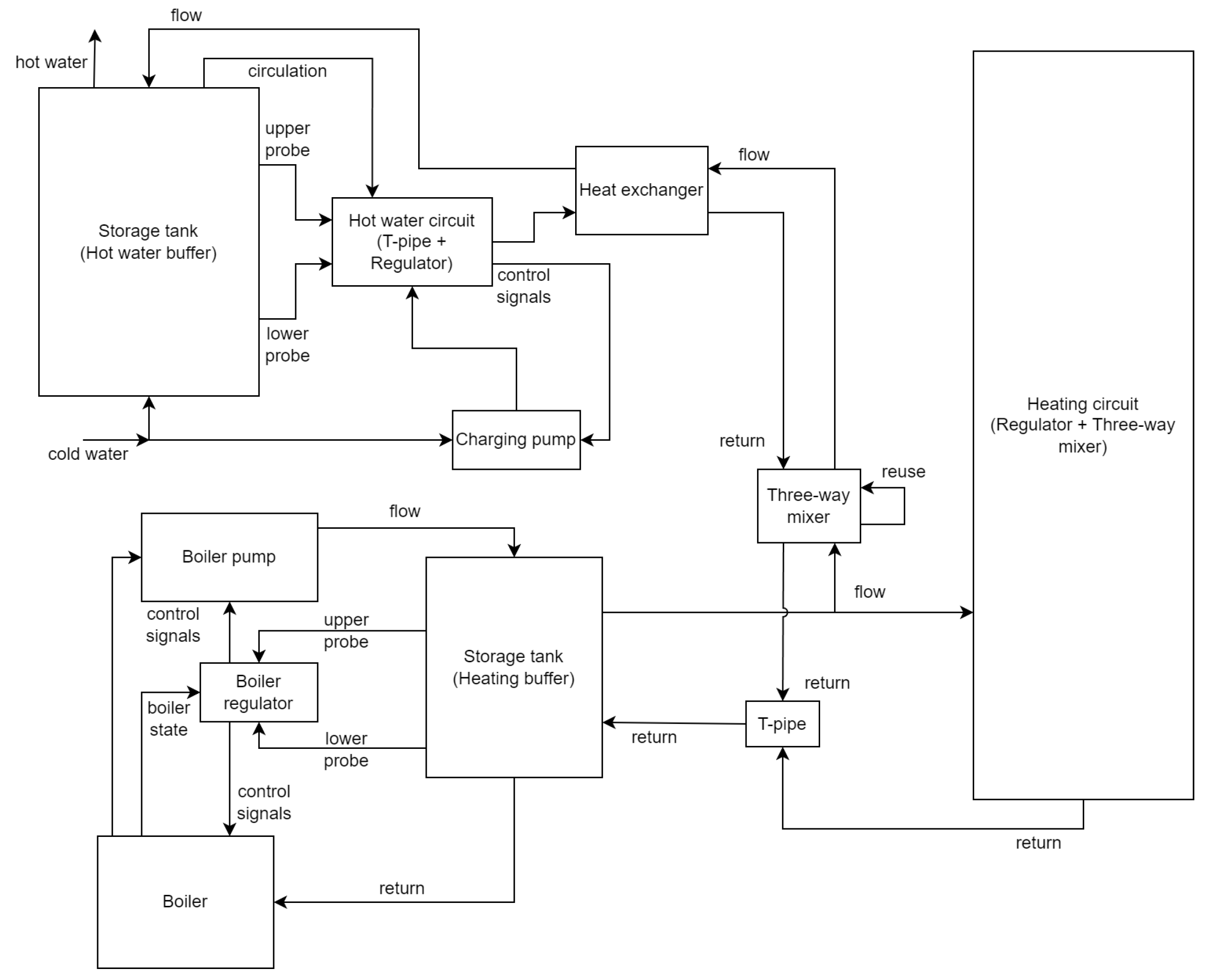
3.1. Data Acquisition
3.2. Data
3.3. Lessons Learned from Data Acquisition
3.3.1. Retrofitting Heating Systems
3.3.2. Resident Behavior Data
3.3.3. Acquisition of Controller Parameter Data
3.4. Model
4. Results
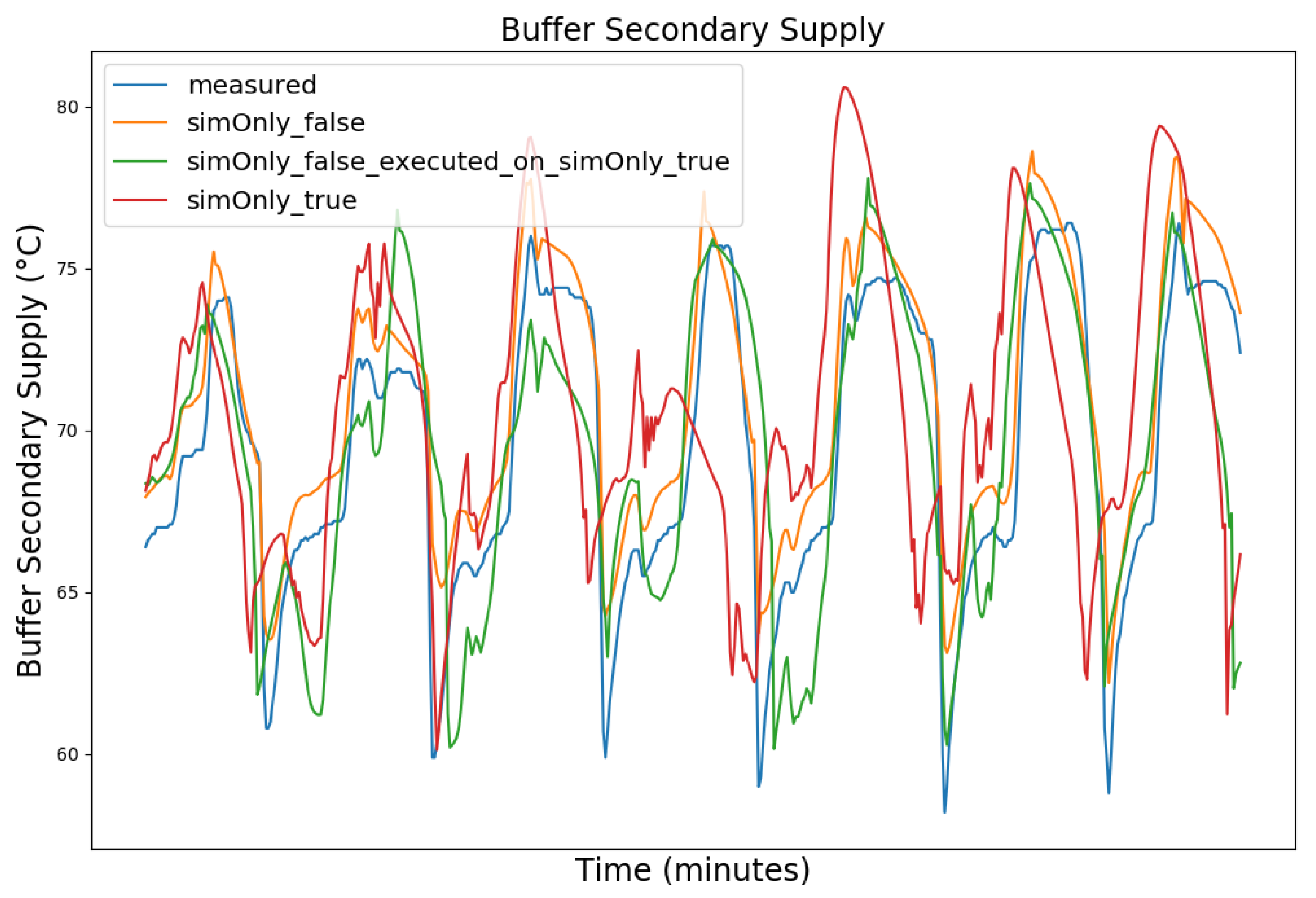
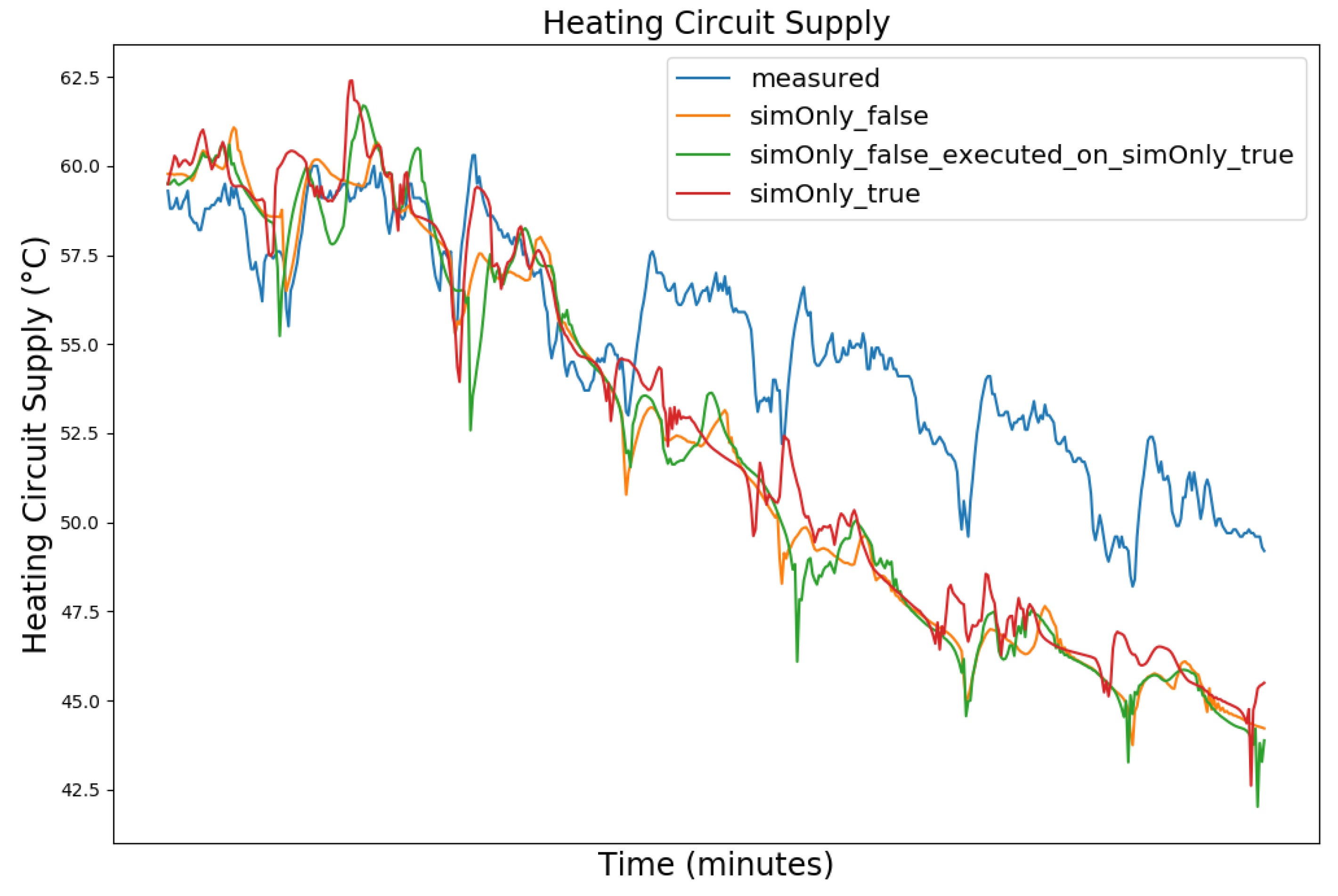
4.1. Model Calibration
4.2. Model Calibration Results
4.3. Parameter Optimization
- Simulated buffer flow temperature (secondary side) exceeding 95 °C (1.0 × 109 penalty).
- Aggregated boiler gas consumption (aggregated gas consumption · 100 as penalty).
- Boiler state switches (number of status switches as penalty).
- Loading pump status switches (number of status switches as penalty · 10).
- Average hot water temperature being below 58 °C (1.0 × 109 penalty).
- Target temperature of the three-way mixing unit (primary hot water supply to the heat exchanger) being lower than the activation temperature (1.0 × 109 penalty).
- Hot water temperature falling below 45 °C (5 × 103 penalty).
- Hot water temperature exceeding 75 °C (5 × 103 penalty).
- Small penalty every time the hot water temperature falls below 55 °C (10 penalty each).
4.4. Parameter Optimization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RMSE | Root Mean Square Error |
| GA | Genetic Algorithm |
| CGA | Cyclic Genetic Algorithm |
| LSTM | Long Short-Term Memory |
| DSS | Decision Support System |
| DIS | Decision Integration System |
| PSO | Particle Swarm Optimization |
| DE | Differential Evolution |
| BO | Bayesian Optimization |
| HVAC | Heating, Ventilation, and Air Conditioning |
| AWS | Amazon Web Services |
| MQTT | Message Queuing Telemetry Transport |
| JSON | JavaScript Object Notation |
| IoT | Internet of Things |
Appendix A. Calibratable Parameters
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 0 | HeatingBuffer.PenetrationDepthParam | 0 | 20.00 | 18.26 |
| 1 | HeatingBuffer.PenetrationDistributionParam | 1.50 | 20.00 | 4.98 |
| 2 | HeatingBuffer.PenetrationMixingFactorParam | 0 | 0.10 | 0.10 |
| 3 | HeatingBuffer.RatioScalarParam | 0.01 | 5.00 | 1.86 |
| 4 | HeatingBuffer.MixingRatioScalarParam | 0 | 0.10 | 5.5 × 10−3 |
| 5 | HeatingBuffer.DissipationParam | 5.0 × 10−4 | 5.4 × 10−4 | 5.4 × 10−4 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 6 | Boiler.KpPositiveParam | 0.05 | 0.10 | 0.05 |
| 7 | Boiler.KiPositiveParam | 0 | 2.00 | 1.51 |
| 8 | Boiler.KdPositiveParam | 0 | 2.00 | 0.52 |
| 9 | Boiler.WindupGuardPositiveParam | 0 | 100.00 | 0 |
| 10 | Boiler.MinEfficiencyParam | 0.05 | 0.75 | 0.05 |
| 11 | Boiler.EfficiencyIncreaseParam | 0.08 | 0.50 | 0.50 |
| 12 | Boiler.EfficiencyDecreaseParam | 0.95 | 0.96 | 0.95 |
| 13 | Boiler.MaxEfficiencyParam | 0.92 | 0.98 | 0.98 |
| 14 | Boiler.InertiaParam | 8.0 × 10−3 | 9.0 × 10−3 | 8.0 × 10−3 |
| 15 | Boiler.BoilerCooldownParam | 0.99 | 1.00 | 1.00 |
| 16 | Boiler.BoilerAnnealScalarParam | 1.0 × 103 | 1.0 × 109 | 1.0 × 109 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 17 | HeatingCircuit.KpParam | 0 | 2.00 | 0.38 |
| 18 | HeatingCircuit.KiParam | 0 | 2.00 | 0.65 |
| 19 | HeatingCircuit.KdParam | 0 | 2.00 | 0.56 |
| 20 | HeatingCircuit.WindupGuardParam | 0 | 100.00 | 0 |
| 21 | HeatingCircuit.BuildingInertiaParam | 3.00 | 100.00 | 29.76 |
| 22 | HeatingCircuit.TenvOffsetParam | 0 | 5.00 | 1.15 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 23 | HotWaterBuffer.PenetrationDepthParam | 0 | 20.00 | 3.89 |
| 24 | HotWaterBuffer.PenetrationDistributionParam | 1.50 | 20.00 | 20.00 |
| 25 | HotWaterBuffer.PenetrationMixingFactorParam | 0 | 0.10 | 0 |
| 26 | HotWaterBuffer.RatioScalarParam | 0.01 | 5.00 | 4.28 |
| 27 | HotWaterBuffer.MixingRatioScalarParam | 0 | 0.10 | 5.72 × 10−3 |
| 28 | HotWaterBuffer.TwzOffsetParam | 2.50 | 5.50 | 3.63 |
| 29 | HotWaterBuffer.DissipationParam | 0 | 0.01 | 3.20 × 10−3 |
| 30 | HotWaterBuffer.RequestWaterInhabitantsCutoffParam | 0 | 0.05 | 0.05 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 31 | HeatExchanger.KAParam | 1.70 | 1.90 | 1.90 |
| 32 | HeatExchanger.DefaultDtlnParam | 0.10 | 10.00 | 4.41 |
| 33 | HeatExchanger.TempAnnealScalarParam | 0.90 | 1.00 | 0.97 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 34 | ThreewayMixingUnit.KpParam | 0 | 2.00 | 2.00 |
| 35 | ThreewayMixingUnit.KiParam | 0 | 2.00 | 0 |
| 36 | ThreewayMixingUnit.KdParam | 0 | 2.00 | 0 |
| 37 | ThreewayMixingUnit.WindupGuardParam | 0 | 100.00 | 60.99 |
| Index | Portname | minValue | maxValue | Value |
|---|---|---|---|---|
| 38 | HotWaterChargingPump.KpParam | 0 | 2.00 | 0.54 |
| 39 | HotWaterChargingPump.KiParam | 0 | 2.00 | 0 |
| 40 | HotWaterChargingPump.KdParam | 0 | 2.00 | 1.36 |
| 41 | HotWaterChargingPump.WindupGuardParam | 0 | 100.00 | 100.00 |
References
- Reddy, T.A.; Maor, I.; Panjapornpon, C. Calibrating detailed building energy simulation programs with measured data—Part I: General methodology (RP-1051). Hvac&R Res. 2007, 13, 221–241. [Google Scholar]
- Eckhardt, K.; Arnold, J. Automatic calibration of a distributed catchment model. J. Hydrol. 2001, 251, 103–109. [Google Scholar] [CrossRef]
- Tun, W.; Wong, K.W.J.; Ling, S.H. Advancing Fault Detection in HVAC Systems: Unifying Gramian Angular Field and 2D Deep Convolutional Neural Networks for Enhanced Performance. Sensors 2023, 23, 7690. [Google Scholar] [CrossRef]
- Matetić, I.; Štajduhar, I.; Wolf, I.; Ljubic, S. Improving the Efficiency of Fan Coil Units in Hotel Buildings through Deep-Learning-Based Fault Detection. Sensors 2023, 23, 6717. [Google Scholar] [CrossRef]
- Kosonen, I. Microscopic freeway simulation with automatic calibration. In Proceedings of the International Symposium on Intelligence Techniques in Computer Games and Simulations, Ritsumeikan University, Shiga, Japan, 1–2 March 2007. [Google Scholar]
- Espejel-Garcia, D.; Saniger-Alba, J.A.; Wenglas-Lara, G.; Espejel-Garcia, V.V.; Villalobos-Aragon, A. A comparison among manual and automatic calibration methods in VISSIM in an Expressway (Chihuahua, Mexico). Open J. Civ. Eng. 2017, 7, 539–552. [Google Scholar] [CrossRef]
- Kim, K.O.; Rilett, L.R. Genetic-algorithm based approach for calibrating microscopic simulation models. In Proceedings of the ITSC 2001, 2001 IEEE Intelligent Transportation Systems, Proceedings (Cat. No. 01TH8585). Oakland, CA, USA, 25–29 August 2001; pp. 698–704. [Google Scholar]
- Pan, Y.; Huang, Z.; Wu, G. Calibrated building energy simulation and its application in a high-rise commercial building in Shanghai. Energy Build. 2007, 39, 651–657. [Google Scholar] [CrossRef]
- Cornaro, C.; Bosco, F.; Lauria, M.; Puggioni, V.A.; De Santoli, L. Effectiveness of automatic and manual calibration of an office building energy model. Appl. Sci. 2019, 9, 1985. [Google Scholar] [CrossRef]
- Madsen, H.; Jacobsen, T. Automatic calibration of the MIKE SHE integrated hydrological modelling system. In Proceedings of the 4th DHI Software Conference, Helsingør, Denmark, 6–8 June 2001. [Google Scholar]
- Jain, S. Calibration of conceptual models for rainfall-runoff simulation. Hydrol. Sci. J. 1993, 38, 431–441. [Google Scholar] [CrossRef]
- Eckhardt, K.; Fohrer, N.; Frede, H.G. Automatic model calibration. Hydrol. Process. Int. J. 2005, 19, 651–658. [Google Scholar] [CrossRef]
- Kuzmin, V.; Seo, D.J.; Koren, V. Fast and efficient optimization of hydrologic model parameters using a priori estimates and stepwise line search. J. Hydrol. 2008, 353, 109–128. [Google Scholar] [CrossRef]
- Khazaei, M.R.; Zahabiyoun, B.; Saghafian, B.; Ahmadi, S. Development of an automatic calibration tool using genetic algorithm for the ARNO conceptual rainfall-runoff model. Arab. J. Sci. Eng. 2014, 39, 2535–2549. [Google Scholar] [CrossRef]
- Sulianto, S.; Bisri, M.; Limantara, L.M.; Sisinggih, D. Automatic calibration and sensitivity analysis of DISPRIN model parameters: A case study on Lesti watershed in East Java, Indonesia. J. Water Land Dev. 2018, 37, 141–152. [Google Scholar] [CrossRef]
- Li, Y. An automatic parameter extraction technique for advanced CMOS device modeling using genetic algorithm. Microelectron. Eng. 2007, 84, 260–272. [Google Scholar] [CrossRef]
- Jia, M.; Tian, S.; Zheng, G. On auto-calibration algorithms for a forest growth simulation model. Open Comput. Sci. 2011, 1, 367–374. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Savaia, G.; Sohn, Y.; Formentin, S.; Panzani, G.; Corno, M.; Savaresi, S.M. Experimental automatic calibration of a semi-active suspension controller via Bayesian optimization. Control. Eng. Pract. 2021, 112, 104826. [Google Scholar] [CrossRef]
- Sha, D.; Ozbay, K.; Ding, Y. Applying Bayesian optimization for calibration of transportation simulation models. Transp. Res. Rec. 2020, 2674, 215–228. [Google Scholar] [CrossRef]
- Goswami, M.; O’Connor, K.M. Comparative assessment of six automatic optimization techniques for calibration of a conceptual rainfall—Runoff model. Hydrol. Sci. J. 2007, 52, 432–449. [Google Scholar] [CrossRef]
- Jeon, J.H.; Park, C.G.; Engel, B.A. Comparison of performance between genetic algorithm and SCE-UA for calibration of SCS-CN surface runoff simulation. Water 2014, 6, 3433–3456. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Zhao, K.; Liew, M.V. Evaluation of global optimization algorithms for parameter calibration of a computationally intensive hydrologic model. Hydrol. Process. Int. J. 2009, 23, 430–441. [Google Scholar] [CrossRef]
- Wang, Y.C.; Yu, P.S.; Yang, T.C. Comparison of genetic algorithms and shuffled complex evolution approach for calibrating distributed rainfall–runoff model. Hydrol. Process. Int. J. 2010, 24, 1015–1026. [Google Scholar] [CrossRef]
- Hadipour, S.; Harun, S.; Shahid, S. Comparison of automatic calibration techniques for simulating streamflow in tropical catchment. Malays. J. Civ. Eng. 2015, 27, 286–300. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 1551–1559. [Google Scholar]
- Acharya, R.Y.; Charlot, N.F.; Alam, M.M.; Ganji, F.; Gauthier, D.; Forte, D. Chaogate parameter optimization using bayesian optimization and genetic algorithm. In Proceedings of the 2021 22nd International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 7–9 April 2021; pp. 426–431. [Google Scholar]
- Wang, Z.L.; Ogawa, T.; Adachi, Y. Influence of algorithm parameters of Bayesian optimization, genetic algorithm, and particle swarm optimization on their optimization performance. Adv. Theory Simulations 2019, 2, 1900110. [Google Scholar] [CrossRef]
- Stanovov, V.; Brester, C.; Kolehmainen, M.; Semenkina, O. Why don’t you use Evolutionary Algorithms in Big Data? In IOP Conference Series: Materials Science and Engineering; IOP Publishing; Bristol, UK, 2017; Volume 173, p. 012020. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Ndiritu, J. A comparison of automatic and manual calibration using the Pitman model. Phys. Chem. Earth Parts A/B/C 2009, 34, 729–740. [Google Scholar] [CrossRef]
- Armesto, J.; Sánchez-Villanueva, C.; Patiño-Cambeiro, F.; Patiño-Barbeito, F. Indoor Multi-Sensor Acquisition System for Projects on Energy Renovation of Buildings. Sensors 2016, 16, 785. [Google Scholar] [CrossRef]
- Bourdeau, M.; Waeytens, J.; Aouani, N.; Basset, P.; Nefzaoui, E. A Wireless Sensor Network for Residential Building Energy and Indoor Environmental Quality Monitoring: Design, Instrumentation, Data Analysis and Feedback. Sensors 2023, 23, 5580. [Google Scholar] [CrossRef] [PubMed]
- Mayhorn, E.; Butzbaugh, J.; Meier, A. A Field Study of Nonintrusive Load Monitoring Devices and Implications for Load Disaggregation. Sensors 2023, 23, 8253. [Google Scholar] [CrossRef] [PubMed]
- Amazon Web Services. 2023. Available online: https://aws.amazon.com/ (accessed on 21 December 2023).
- Microsoft Azure. 2023. Available online: https://azure.microsoft.com/ (accessed on 21 December 2023).
- Kubernetes. 2023. Available online: https://kubernetes.io/ (accessed on 21 December 2023).
- Fan, C.; Chen, M.; Wang, X.; Wang, J.; Huang, B. A review on data preprocessing techniques toward efficient and reliable knowledge discovery from building operational data. Front. Energy Res. 2021, 9, 652801. [Google Scholar] [CrossRef]
- Wilhelmstötter, F. Jenetics: Java Genetic Algorithm Library. 2023. Available online: https://jenetics.io/ (accessed on 21 December 2023).
- ANTLR (ANother Tool for Language Recognition). 2023. Available online: https://www.antlr.org/ (accessed on 21 December 2023).
- Taconova-TacoSetter Bypass. Available online: https://www.taconova.com/en/hydronic-balancing/c/balancing-valves/v/tacosetter-bypass (accessed on 21 December 2023).
- Becker, R. Optimierung Thermischer Systeme in Dezentralen Energieversorgungsanlagen (Optimization of Thermal Systems in Decentralized Energy Supply Plants). Ph.D. Thesis, Universität Dortmund, Dortmund, Germany, 2006. [Google Scholar]


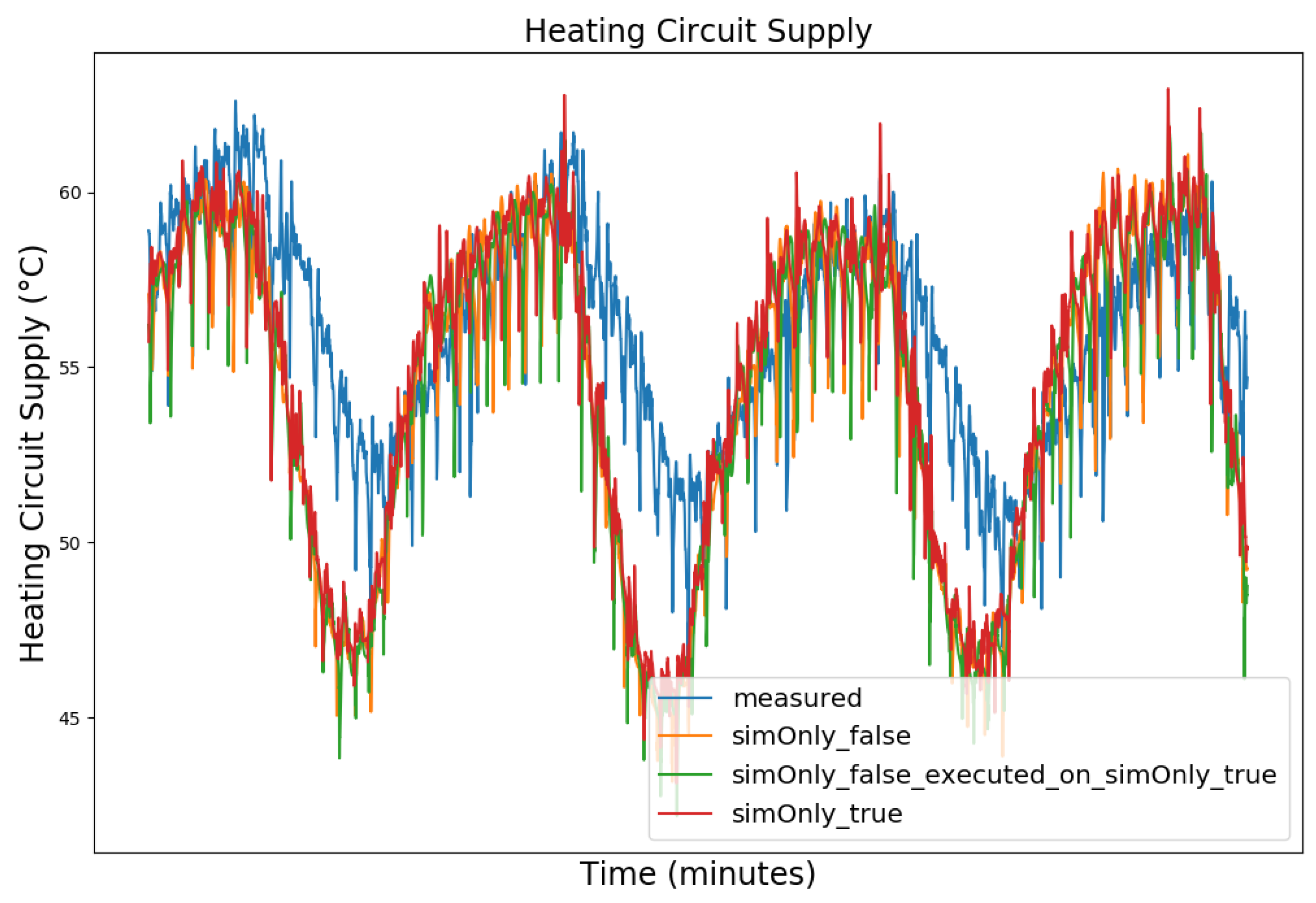
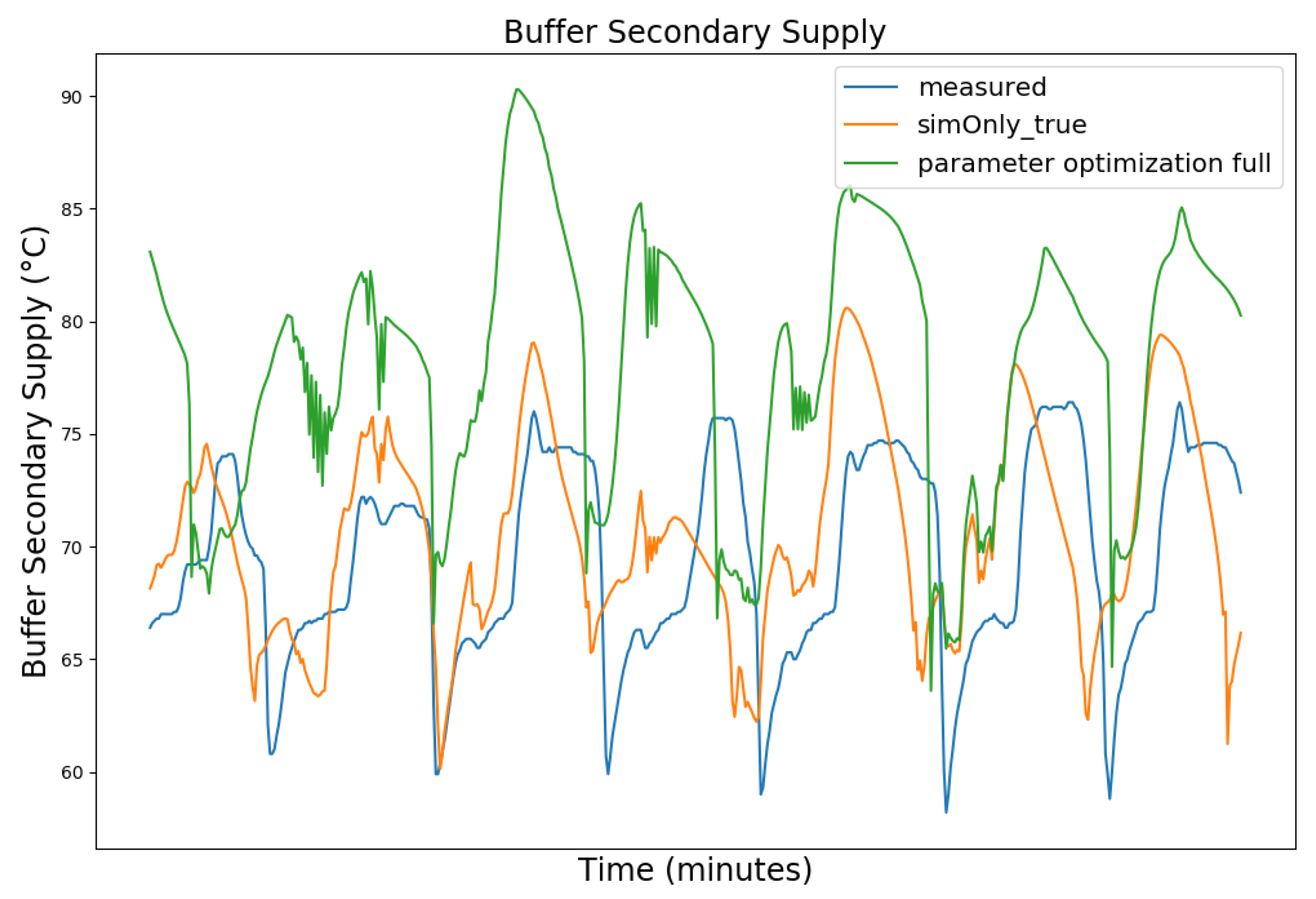
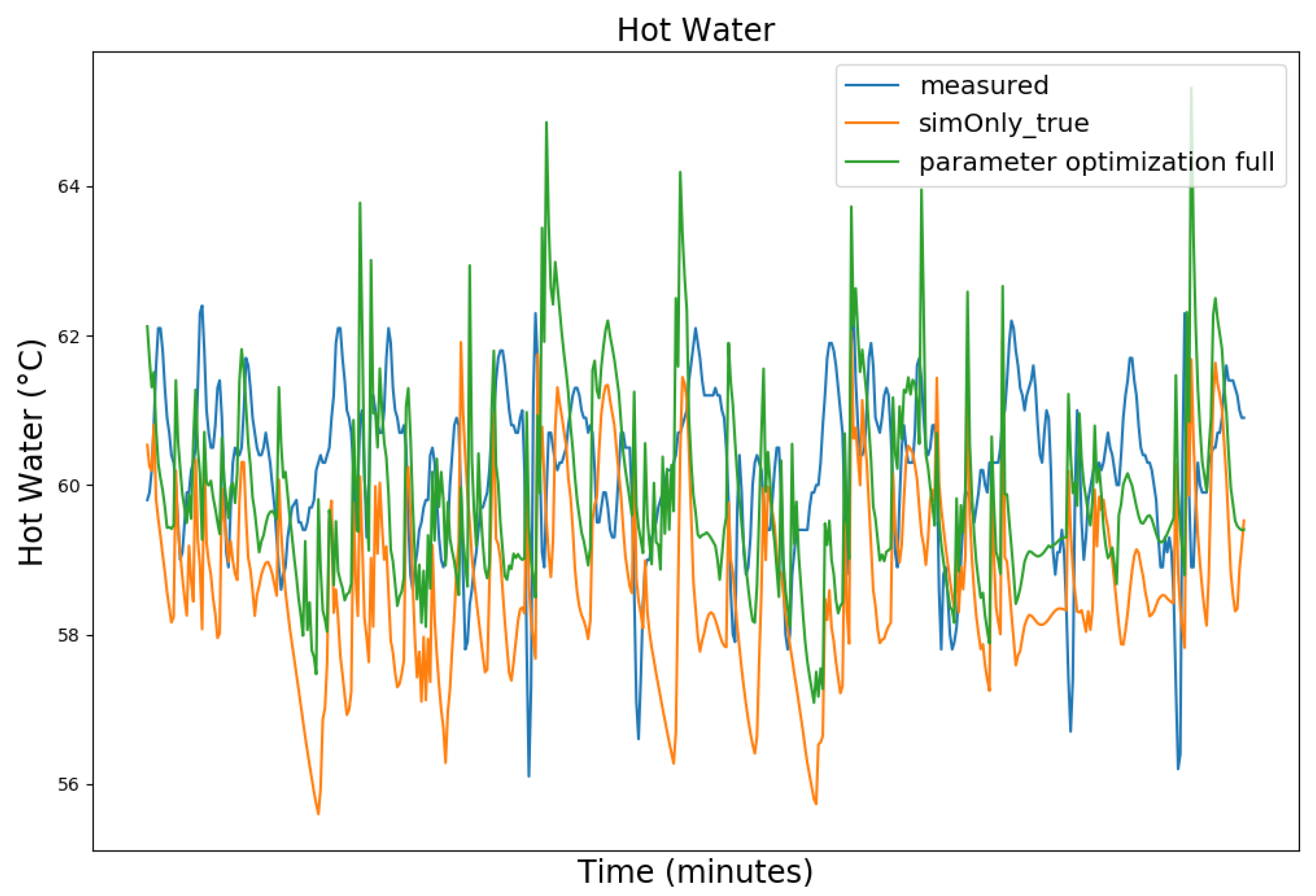
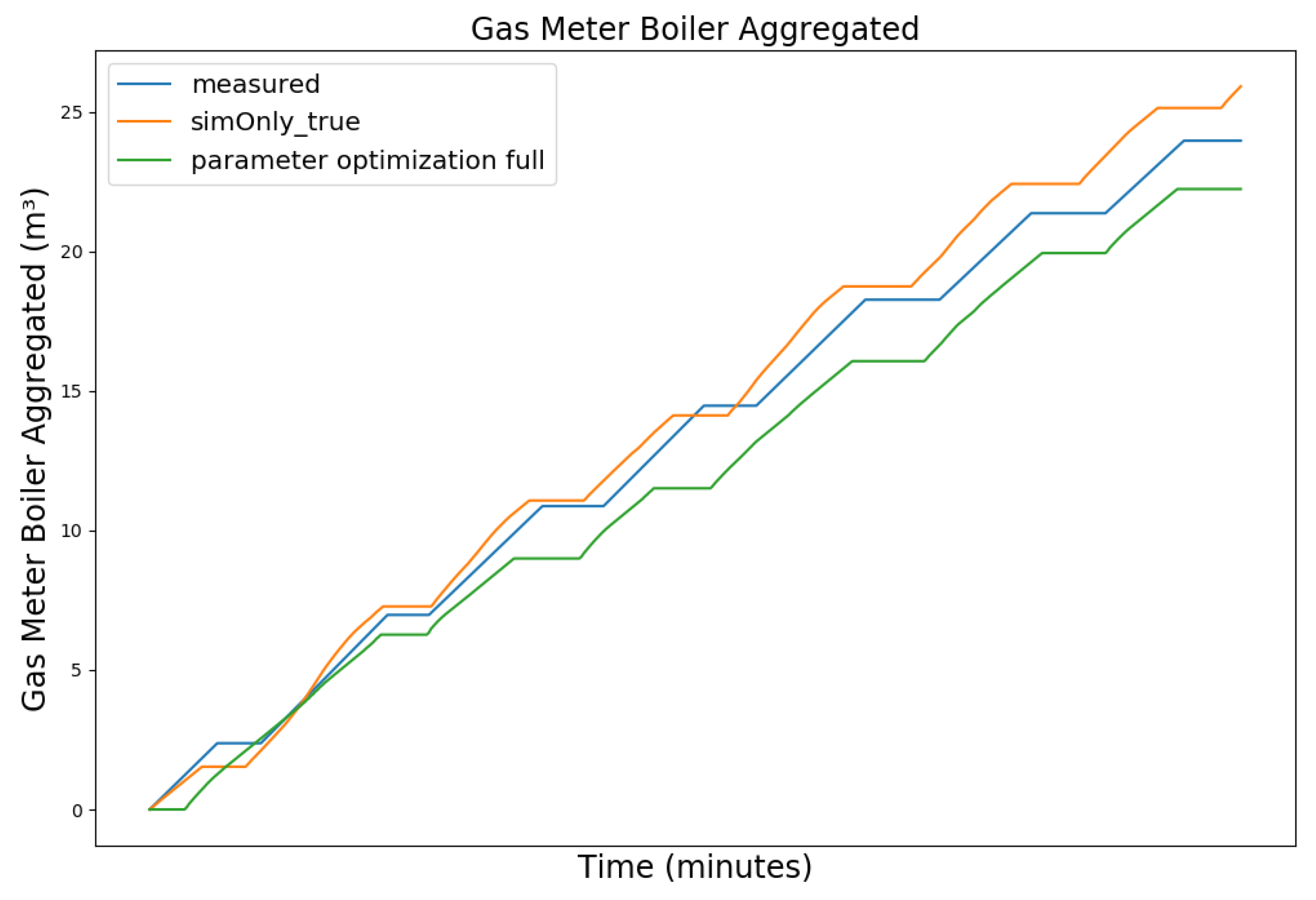
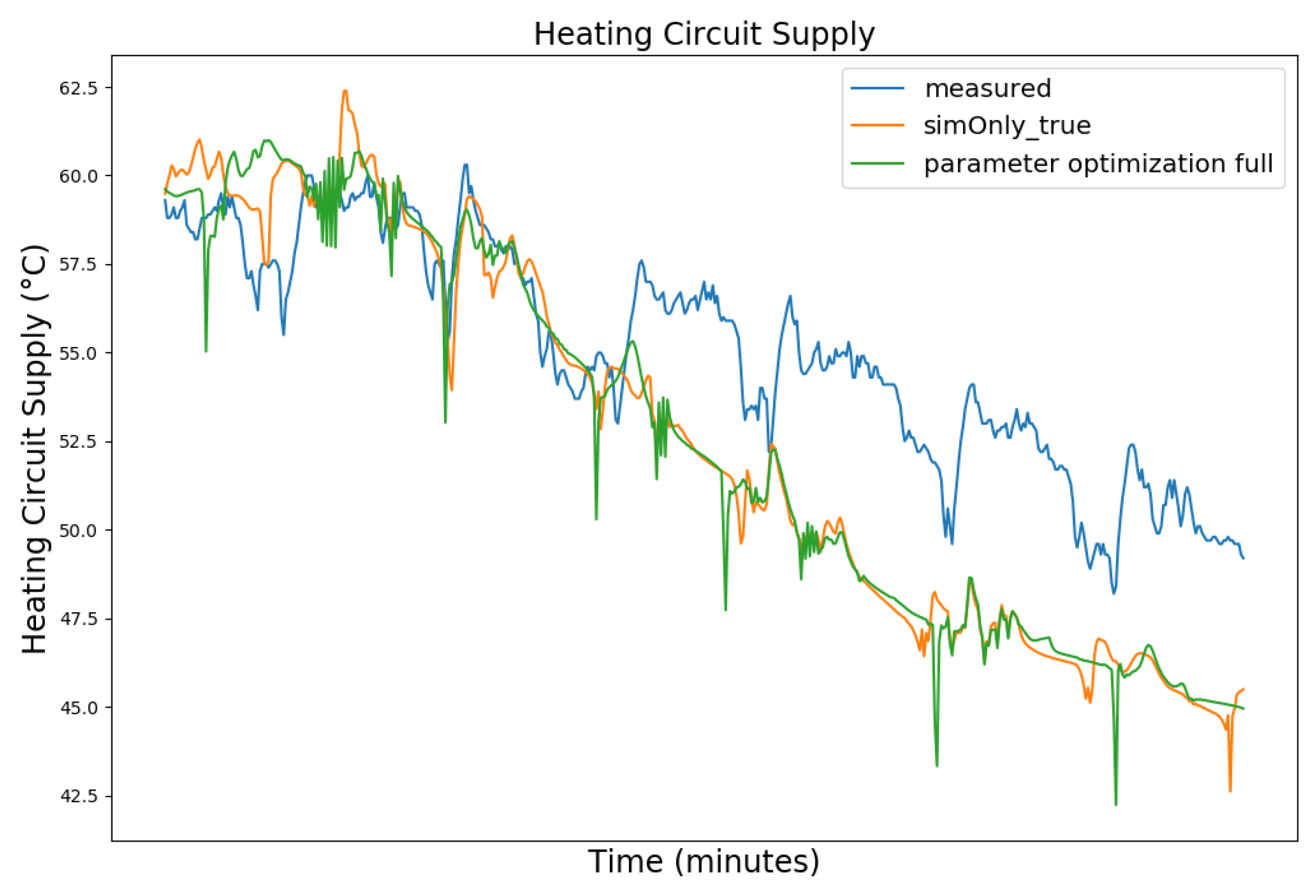
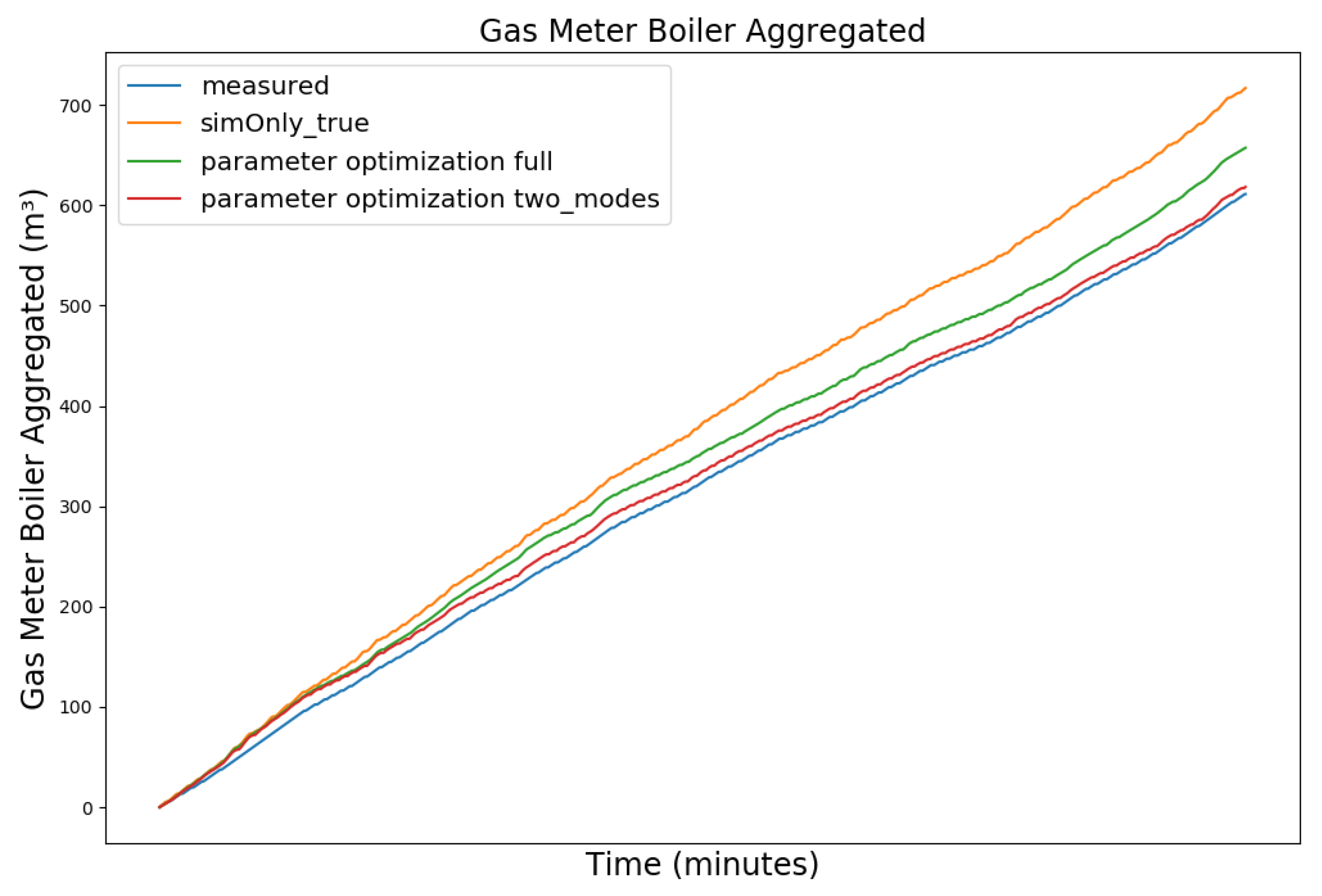
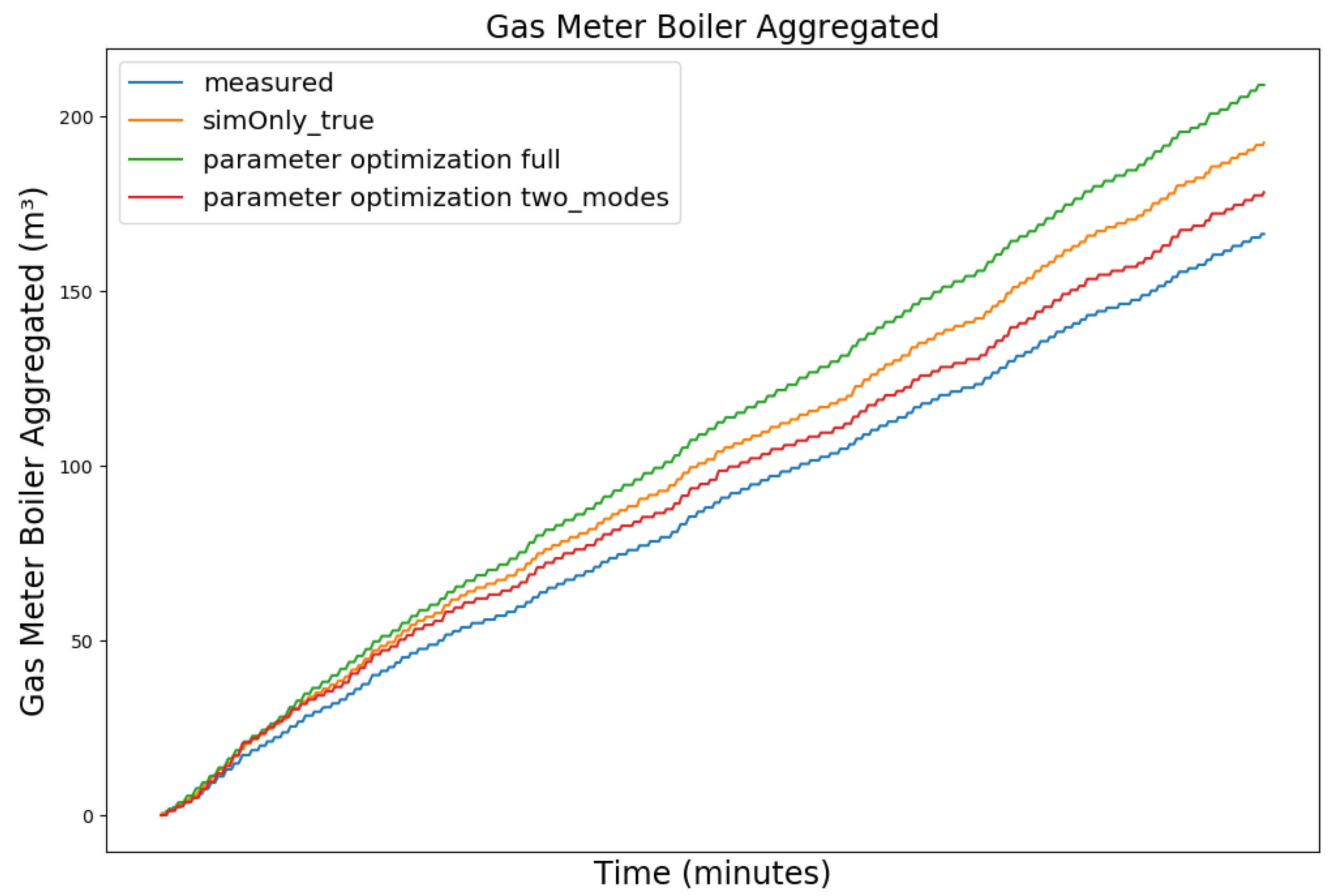
| Dataset Timeframe | No. of Missing Data Points | Availability of Controller Parameters |
|---|---|---|
| February 2019–February 2020 | 22,543 (4.29% of total dataset) | Recent controller parameters for the boiler, hot water circuit, and heating circuit available. |
| February 2020–February 2021 | 76,556 (14.53% of total dataset, one extra day due to leap year) | Boiler parameters unavailable. No recent parameters for hot water circuit and heating circuit. |
| February 2021–February 2022 | 103,818 (24.61% of total dataset) | Boiler parameters unavailable. Recent controller parameters for hot water circuit and heating circuit available. |
| Value (Measured Range) | so_False (1) | so_False (2) | so_True |
|---|---|---|---|
| Buffer Secondary Supply (49.9–77.0 °C) | 2.77 | 6.19 | 6.24 |
| Buffer Secondary Return (33.6–64.5 °C) | 2.07 | 4.62 | 4.31 |
| Boiler Supply (48.4–82.9 °C) | 4.05 | 6.33 | 6.36 |
| Boiler Return ( 37.4–71.2 °C) | 2.76 | 6.17 | 6.01 |
| Heating Circuit Supply (26.7–74.0 °C) | 2.38 | 2.53 | 2.56 |
| Heating Circuit Return (21.2–43.9 °C) | 2.50 | 2.53 | 2.47 |
| Hot Water (43.9–64.8 °C) | 1.86 | 2.57 | 2.28 |
| Circulation (32.9–58.9 °C) | 1.37 | 2.46 | 1.95 |
| Hot Water Circuit Primary Supply (42.3–75.6 °C) | 2.86 | 3.86 | 3.85 |
| Hot Water Circuit Primary Return (32.0–71.7 °C) | 4.12 | 6.27 | 5.59 |
| Hot Water Circuit Secondary Supply (47.8–68.6 °C) | 3.75 | 6.06 | 5.05 |
| Hot Water Circuit Secondary Return (8.0–57.4 °C) | 2.87 | 3.51 | 3.96 |
| Index | Portname | minValue | maxValue |
|---|---|---|---|
| 0 | BoilerRegulator.UpperLimitParam | 0 | 100 |
| 1 | BoilerRegulator.LowerLimitParam | 0 | 100 |
| 2 | Hotwatercircuit.ActivationTemperatureParam | 0 | 100 |
| 3 | Hotwatercircuit.DeactivationTemperatureParam | 0 | 100 |
| 4 | ThreewayMixingUnit.TargetTemperatureParam | 0 | 100 |
| 5 | BoilerRegulator.TargetOutputTemperatureParam | 60 | 80 |
| Portname | minValue | maxValue | Orig. | Optim. |
|---|---|---|---|---|
| BoilerRegulator.UpperLimitParam | 0.0 | 100.0 | 58.0 | 75.4 |
| BoilerRegulator.LowerLimitParam | 0.0 | 100.0 | 68.0 | 77.17 |
| Hotwatercircuit.ActivationTemperatureParam | 0.0 | 100.0 | 57.0 | 33.1 |
| Hotwatercircuit.DeactivationTemperatureParam | 0.0 | 100.0 | 58.0 | 100.0 |
| ThreewayMixingUnit.TargetTemperatureParam | 0.0 | 100.0 | 63.0 | 64.06 |
| BoilerRegulator.TargetOutputTemperatureParam | 60.0 | 80.0 | 69.0 | 66.49 |
| Feature | Measured | so_True | Optim. Full Year |
|---|---|---|---|
| Total number of state switches | 14,738 | 13,893 | 11,217 |
| Total boiler runtime (min) | 268,436 | 266,722 | 288,240 |
| Aggregated gas consumption (m3) | 19,695.04 | 22,283.78 | 20,936.15 |
| Feature | Measured | so_True | Optim. Full Year | Optim. Seasonal |
|---|---|---|---|---|
| Total number of state switches | 14,738 | 13,893 | 11,217 | 11,776 |
| Total boiler runtime (min) | 268,436 | 266,722 | 288,240 | 254,403 |
| Aggregated gas consumption (m3) | 19,695.04 | 22,283.78 | 20,936.15 | 20,078.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djebko, K.; Weidner, D.; Waleska, M.; Krey, T.; Rausch, S.; Seipel, D.; Puppe, F. Integrated Simulation and Calibration Framework for Heating System Optimization. Sensors 2024, 24, 886. https://doi.org/10.3390/s24030886
Djebko K, Weidner D, Waleska M, Krey T, Rausch S, Seipel D, Puppe F. Integrated Simulation and Calibration Framework for Heating System Optimization. Sensors. 2024; 24(3):886. https://doi.org/10.3390/s24030886
Chicago/Turabian StyleDjebko, Kirill, Daniel Weidner, Marcel Waleska, Timo Krey, Sven Rausch, Dietmar Seipel, and Frank Puppe. 2024. "Integrated Simulation and Calibration Framework for Heating System Optimization" Sensors 24, no. 3: 886. https://doi.org/10.3390/s24030886
APA StyleDjebko, K., Weidner, D., Waleska, M., Krey, T., Rausch, S., Seipel, D., & Puppe, F. (2024). Integrated Simulation and Calibration Framework for Heating System Optimization. Sensors, 24(3), 886. https://doi.org/10.3390/s24030886






