Quantum Efficiency Measurement and Modeling of Silicon Sensors Optimized for Soft X-ray Detection
Abstract
1. Introduction
2. Hybrid Detectors for X-ray Detection
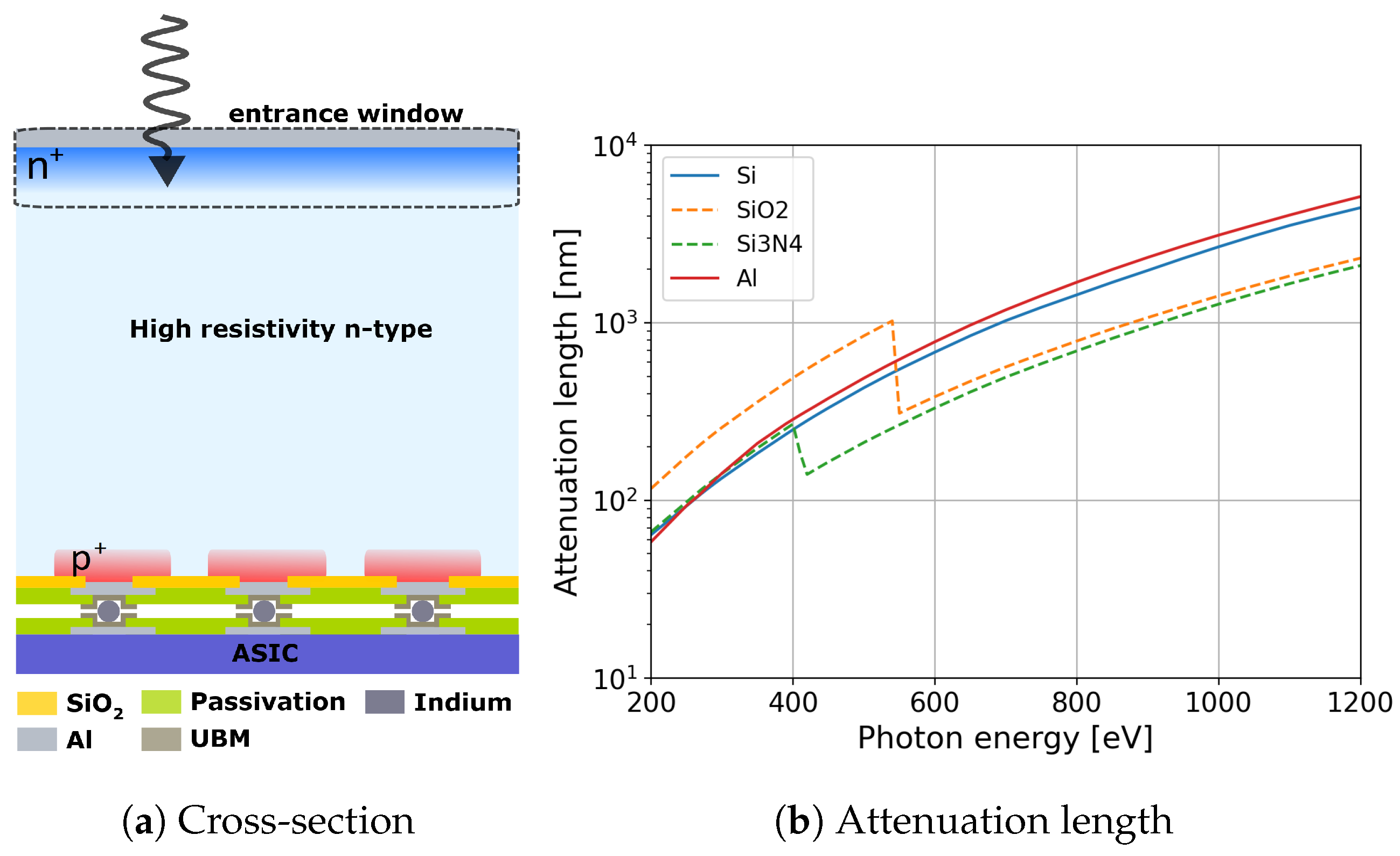
2.1. Sensors for Hybrid Detectors
2.2. Quantum Efficiency
- The IL needs to be thin and made of low-Z materials to reduce the probability of complete photon loss in the IL. The metallization thickness should be minimized in applications that require the use of this layer to avoid the detection of stray light.
- The quality of the silicon surface has to be improved by means of passivating the surface with a thermally grown oxide in order to reduce recombination near the silicon surface rather than using aluminum on bare silicon.
- The lifetime of minority carriers needs to be increased by reducing the doping concentration and the depth of the n+ region.
2.3. Signal-to-Noise Ratio
3. Materials and Methods
3.1. Optimization of the Process Technology
3.2. Experimental Setup
3.3. Quantum Efficiency Measurement
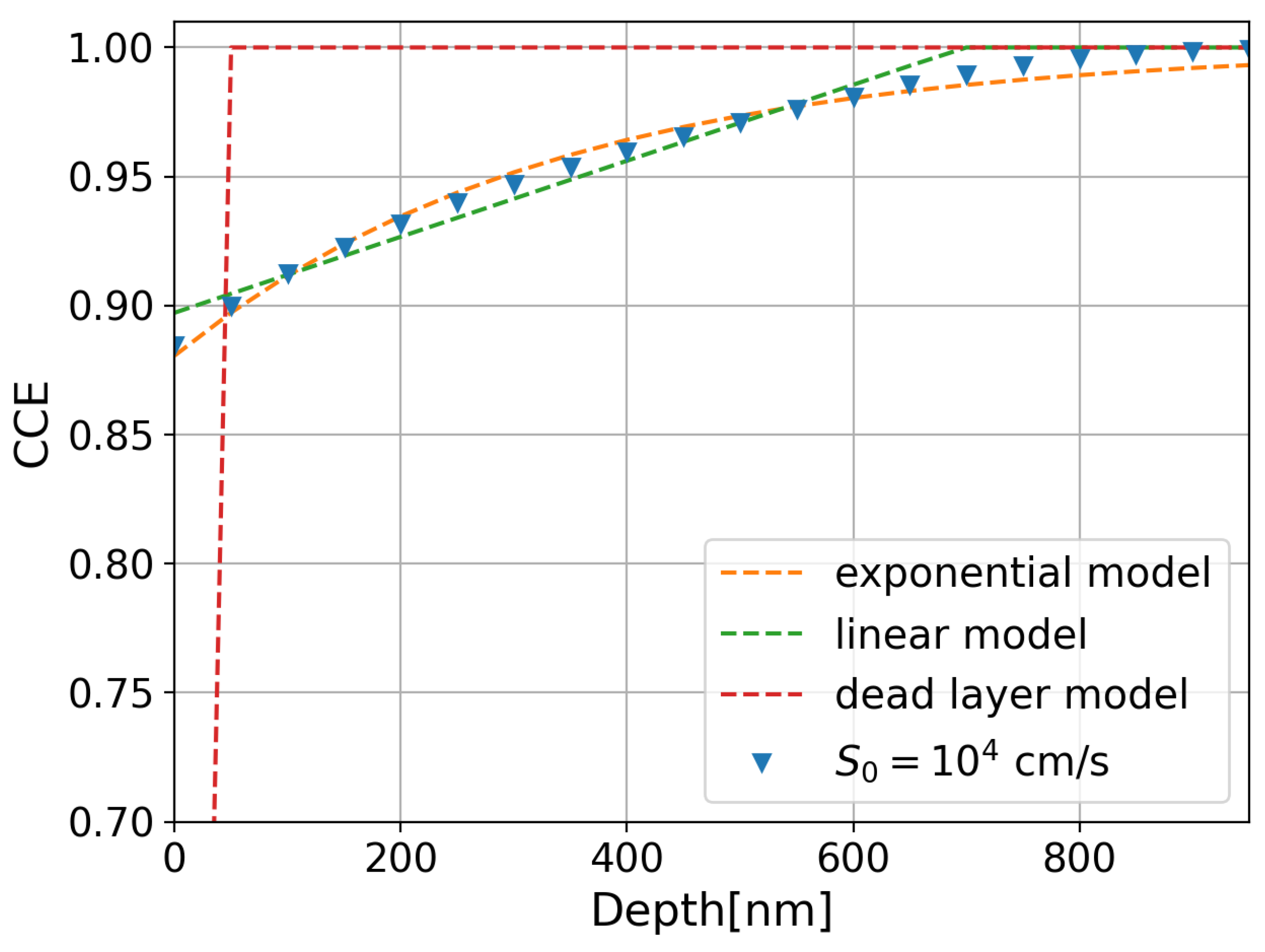
3.4. Modeling of the Quantum Efficiency
4. Results
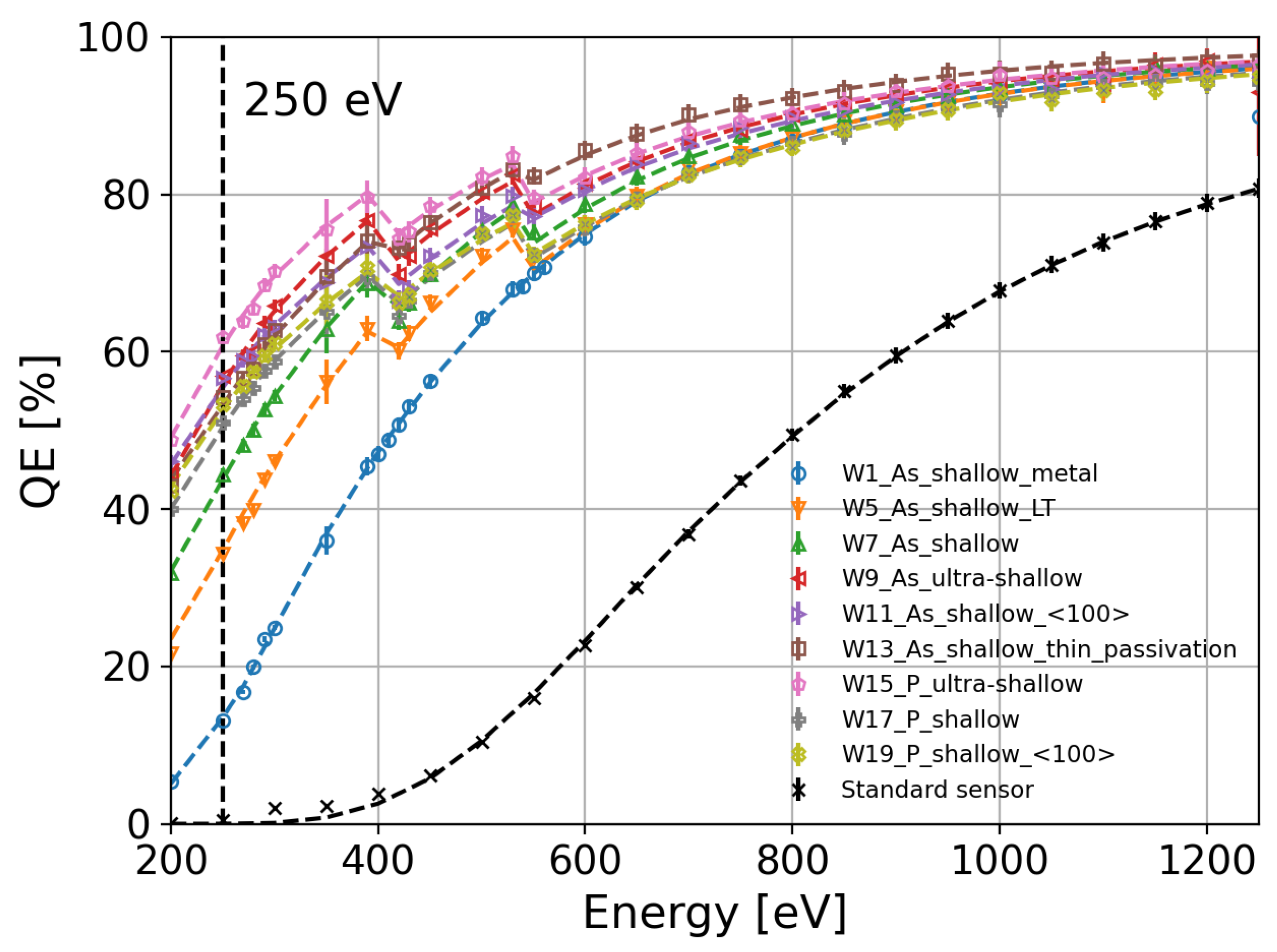
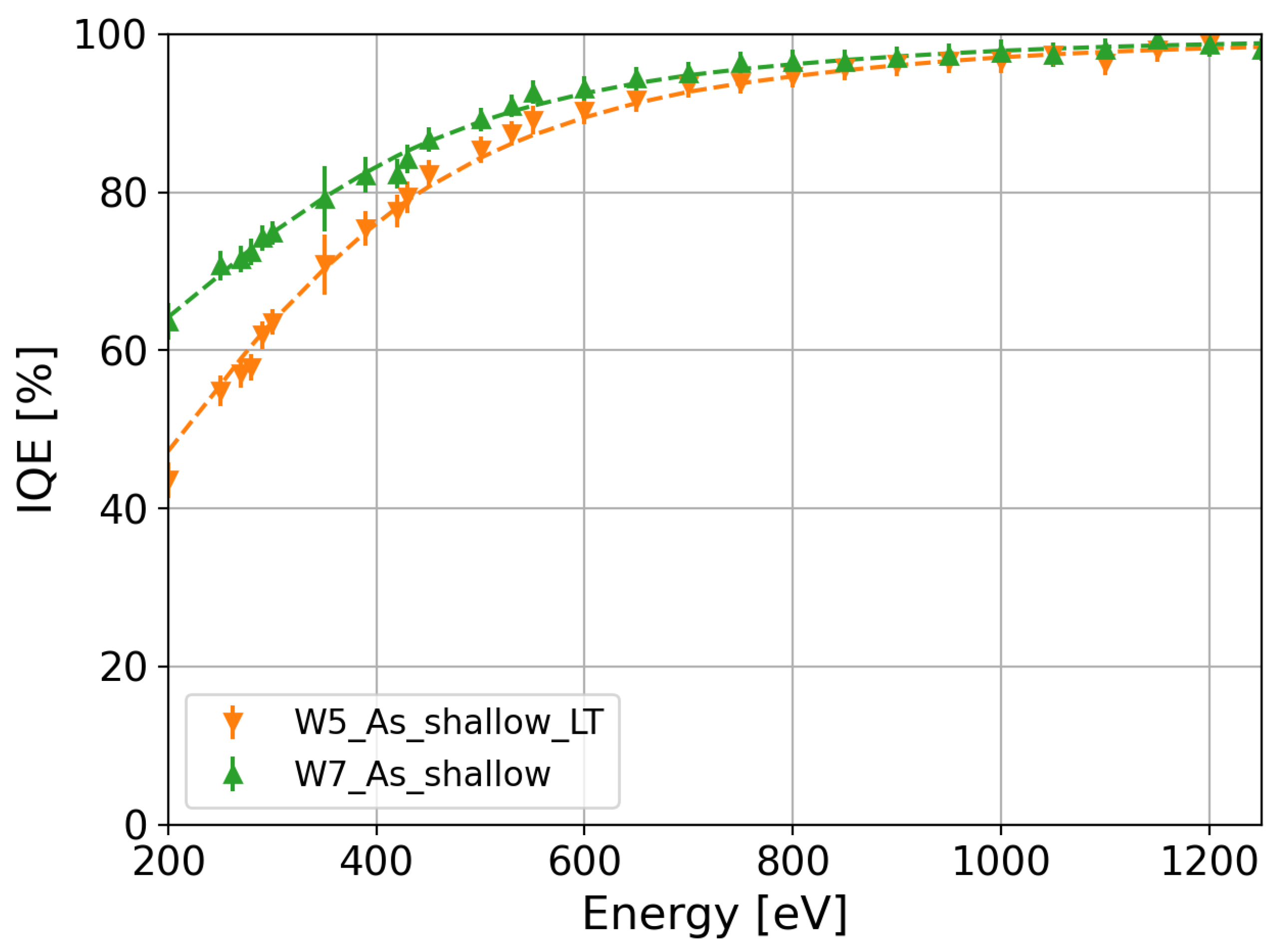
4.1. Thermal Budget
4.2. Dopant Profile
4.3. Crystal Orientation
4.4. Implantation versus Diffusion
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASIC | Application-specific integrated circuits |
| CCD | Charge-coupled device |
| CCE | Charge collection efficiency |
| CMOS | Complementary metal oxide semiconductor |
| ENC | Equivalent noise charge |
| EW | Entrance window |
| FBK | Fondazione Bruno Kessler |
| GCD | Gate-controlled diode |
| IL | Inactive layer |
| iLGAD | Inverse low-gain avalanche diodes |
| IQE | Internal quantum efficiency |
| LGAD | Low-gain avalanche diodes |
| OSA | Order-sorting aperture |
| PSI | Paul Scherrer Institut |
| PTB | Physikalish-Technische Bundesanstalt |
| QE | Quantum efficiency |
| SHR | Shockley–Read–Hall |
| SIM | Surfaces/Interfaces:Microscopy |
| SLS | Swiss Light Source |
| SNR | Signal-to-noise ratio |
| SwissFEL | Swiss X-ray Free-Electron Laser |
References
- McNeill, C.R. Resonant Tender X-ray Scattering of Organic Semiconductors. Acc. Mater. Res. 2023, 4, 16–26. [Google Scholar] [CrossRef]
- Wang, C.; Hexemer, A.; Nasiatka, J.; Chan, E.R.; Young, A.T.; Padmore, H.A.; Schlotter, W.F.; Lüning, J.; Swaraj, S.; Watts, B.; et al. Resonant Soft X-ray Scattering of Polymers with a 2D Detector: Initial Results and System Developments at the Advanced Light Source. IOP Conf. Ser. Mater. Sci. Eng. 2010, 14, 012016. [Google Scholar] [CrossRef]
- Rose, M.; Senkbeil, T.; von Gundlach, A.R.; Stuhr, S.; Rumancev, C.; Dzhigaev, D.; Besedin, I.; Skopintsev, P.; Loetgering, L.; Viefhaus, J.; et al. Quantitative ptychographic bio-imaging in the water window. Opt. Express 2018, 26, 1237–1254. [Google Scholar] [CrossRef]
- Shi, X.; Fischer, P.; Neu, V.; Elefant, D.; Lee, J.C.T.; Shapiro, D.A.; Farmand, M.; Tyliszczak, T.; Shiu, H.W.; Marchesini, S.; et al. Soft X-ray ptychography studies of nanoscale magnetic and structural correlations in thin SmCo5 films. Appl. Phys. Lett. 2016, 108, 094103. [Google Scholar] [CrossRef]
- Erny, C.; Hauri, C.P. The SwissFEL Experimental Laser facility. J. Synchrotron Radiat. 2016, 23, 1143–1150. [Google Scholar] [CrossRef]
- Streun, A.; Garvey, T.; Rivkin, L.; Schlott, V.; Schmidt, T.; Willmott, P.; Wrulich, A. SLS-2–the upgrade of the Swiss Light Source. J. Synchrotron Radiat. 2018, 25, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Barten, R.; Baruffaldi, F.; Bergamaschi, A.; Borghi, G.; Boscardin, M.; Brückner, M.; Carulla, M.; Vignali, M.C.; Dinapoli, R.; et al. Development of LGAD sensors with a thin entrance window for soft X-ray detection. J. Instrum. 2022, 17, C11011. [Google Scholar] [CrossRef]
- Hinger, V.; al Haddad, A.; Barten, R.; Bergamaschi, A.; Brückner, M.; Carulla, M.; Chiriotti-Alvarez, S.; Dinapoli, R.; Ebner, S.; Fröjdh, E.; et al. Advancing the JUNGFRAU detector toward low-energy X-ray applications. J. Instrum. 2022, 17, C09027. [Google Scholar] [CrossRef]
- Meidinger, N.; Andritschke, R.; Hartmann, R.; Herrmann, S.; Holl, P.; Lutz, G.; Strüder, L. pnCCD for photon detection from near-infrared to X-rays. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2006, 565, 251–257. [Google Scholar] [CrossRef]
- Strüder, L.; Epp, S.; Rolles, D.; Hartmann, R.; Holl, P.; Lutz, G.; Soltau, H.; Eckart, R.; Reich, C.; Heinzinger, K.; et al. Large-format, high-speed, X-ray pnCCDs combined with electron and ion imaging spectrometers in a multipurpose chamber for experiments at 4th generation light sources. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2010, 614, 483–496. [Google Scholar] [CrossRef]
- Kuster, M.; Ahmed, K.; Ballak, K.E.; Danilevski, C.; Ekmedžić, M.; Fernandes, B.; Gessler, P.; Hartmann, R.; Hauf, S.; Holl, P.; et al. The 1-Megapixel pnCCD detector for the Small Quantum Systems Instrument at the European XFEL: System and operation aspects. J. Synchrotron Radiat. 2021, 28, 576–587. [Google Scholar] [CrossRef]
- Send, S.; Abboud, A.; Hartmann, R.; Huth, M.; Leitenberger, W.; Pashniak, N.; Schmidt, J.; Strüder, L.; Pietsch, U. Characterization of a pnCCD for applications with synchrotron radiation. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2013, 711, 132–142. [Google Scholar] [CrossRef]
- Desjardins, K.; Medjoubi, K.; Sacchi, M.; Popescu, H.; Gaudemer, R.; Belkhou, R.; Stanescu, S.; Swaraj, S.; Besson, A.; Vijayakumar, J.; et al. Backside-illuminated scientific CMOS detector for soft X-ray resonant scattering and ptychography. J. Synchrotron Radiat. 2020, 27, 1577–1589. [Google Scholar] [CrossRef] [PubMed]
- Marras, A.; Correa, J.; Lange, S.; Vardanyan, V.; Gerhardt, T.; Kuhn, M.; Krivan, F.; Shevyakov, I.; Zimmer, M.; Hoesch, M.; et al. Characterization of the Percival detector with soft X-rays. J. Synchrotron Radiat. 2021, 28, 131–145. [Google Scholar] [CrossRef] [PubMed]
- Mozzanica, A.; Bergamaschi, A.; Brueckner, M.; Cartier, S.; Dinapoli, R.; Greiffenberg, D.; Jungmann-Smith, J.; Maliakal, D.; Mezza, D.; Ramilli, M.; et al. Characterization results of the JUNGFRAU full scale readout ASIC. J. Instrum. 2016, 11, C02047. [Google Scholar] [CrossRef]
- Dullin, C.; Albers, J.; Tromba, G.; Andrä, M.; Ramilli, M.; Bergamaschi, A. MÖNCH detector enables fast and low-dose free-propagation phase-contrast computed tomography of in situ mouse lungs. J. Synchrotron Radiat. 2018, 25, 565–569. [Google Scholar] [CrossRef] [PubMed]
- Greiffenberg, D.; Andrä, M.; Barten, R.; Bergamaschi, A.; Brückner, M.; Busca, P.; Chiriotti, S.; Chsherbakov, I.; Dinapoli, R.; Fajardo, P.; et al. Characterization of Chromium Compensated GaAs Sensors with the Charge-Integrating JUNGFRAU Readout Chip by Means of a Highly Collimated Pencil Beam. Sensors 2021, 21, 1550. [Google Scholar] [CrossRef] [PubMed]
- Chantler, C.; Olsen, K.; Dragoset, R.; Chang, J.; Kishore, A.; Kotochigova, S.; Zucker, D. X-ray Form Factor, Attenuation and Scattering Tables (Version 2.1). National Institute of Standards and Technology, Gaithersburg, MD. Originally published as Chantler, C.T., J. Phys. Chem. Ref. Data 2000, 29, 597–1048; and Chantler, C.T., J. Phys. Chem. Ref. Data. 1995, 24, 71–643. Available online: http://physics.nist.gov/ffast (accessed on 25 June 2023).
- Richter, A.; Werner, F.; Cuevas, A.; Schmidt, J.; Glunz, S. Improved Parameterization of Auger Recombination in Silicon. Energy Procedia 2012, 27, 88–94. [Google Scholar] [CrossRef]
- Sproul, A.B. Dimensionless solution of the equation describing the effect of surface recombination on carrier decay in semiconductors. J. Appl. Phys. 1994, 76, 2851–2854. [Google Scholar] [CrossRef]
- Andrä, M.; Zhang, J.; Bergamaschi, A.; Barten, R.; Borca, C.; Borghi, G.; Boscardin, M.; Busca, P.; Brückner, M.; Cartiglia, N.; et al. Development of low-energy X-ray detectors using LGAD sensors. J. Synchrotron Radiat. 2019, 26, 1226–1237. [Google Scholar] [CrossRef]
- Pellegrini, G.; Fernández-Martínez, P.; Baselga, M.; Fleta, C.; Flores, D.; Greco, V.; Hidalgo, S.; Mandić, I.; Kramberger, G.; Quirion, D.; et al. Technology developments and first measurements of Low Gain Avalanche Detectors (LGAD) for high energy physics applications. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2014, 765, 12–16. [Google Scholar] [CrossRef]
- Dalla Betta, G.F.; Pancheri, L.; Boscardin, M.; Paternoster, G.; Piemonte, C.; Cartiglia, N.; Cenna, F.; Bruzzi, M. Design and TCAD simulation of double-sided pixelated low gain avalanche detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2015, 796, 154–157. [Google Scholar] [CrossRef]
- Liguori, A.; Barten, R.; Baruffaldi, F.; Bergamaschi, A.; Borghi, G.; Boscardin, M.; Brückner, M.; Butcher, T.A.; Carulla, M.; Vignali, M.C.; et al. Characterization of iLGADs using soft X-rays. J. Instrum. 2023, 18, P12006. [Google Scholar] [CrossRef]
- Quitmann, C.; Flechsig, U.; Patthey, L.; Schmidt, T.; Ingold, G.; Howells, M.; Janousch, M.; Abela, R. A beamline for time resolved photoelectron microscopy on magnetic materials at the Swiss light source. Surf. Sci. 2001, 480, 173–179. [Google Scholar] [CrossRef]
- Stern, R.A.; Shing, L.; Blouke, M.M. Quantum efficiency measurements and modeling of ion-implanted, laser-annealed charge-coupled devices: X-ray, extreme-ultraviolet, ultraviolet, and optical data. Appl. Opt. 1994, 33, 2521–2533. [Google Scholar] [CrossRef]
- Cuevas, A.; Balbuena, M. Review of analytical models for the study of highly doped regions of silicon devices. IEEE Trans. Electron Devices 1989, 36, 553–560. [Google Scholar] [CrossRef]
- Razouk, R.R.; Deal, B.E. Dependence of Interface State Density on Silicon Thermal Oxidation Process Variables. J. Electrochem. Soc. 1979, 126, 1573. [Google Scholar] [CrossRef]
- Goetzberger, A.; Klausmann, E.; Schulz, M.J. Interface states on semiconductor/insulator surfaces. CRC Crit. Rev. Solid State Sci. 1976, 6, 1–43. [Google Scholar] [CrossRef]
- Deal, B.E. The Current Understanding of Charges in the Thermally Oxidized Silicon Structure. J. Electrochem. Soc. 1974, 121, 198C. [Google Scholar] [CrossRef]
- Zhang, J. X-ray Radiation Damage Studies and Design of a Silicon Pixel Sensor. Ph.D. Thesis, Hamburg University, Hamburg, Germany, 2013. Available online: https://bib-pubdb1.desy.de/record/152137/files/DESY-2013-00115.pdf (accessed on 23 March 2022).
- Lu, H.; Gauthier, A.; Hepting, M.; Tremsin, A.S.; Reid, A.H.; Kirchmann, P.S.; Shen, Z.X.; Devereaux, T.P.; Shao, Y.C.; Feng, X.; et al. Time-resolved RIXS experiment with pulse-by-pulse parallel readout data collection using X-ray free electron laser. Sci. Rep. 2020, 10, 22226. [Google Scholar] [CrossRef]
- Abela, R.; Alarcon, A.; Alex, J.; Arrell, C.; Arsov, V.; Bettoni, S.; Bopp, M.; Bostedt, C.; Braun, H.H.; Calvi, M.; et al. The SwissFEL soft X-ray free-electron laser beamline: Athos. J. Synchrotron Radiat. 2019, 26, 1073–1084. [Google Scholar] [CrossRef] [PubMed]
- Ansuinelli, P.; Coene, W.M.J.; Urbach, H.P. Improved ptychographic inspection of EUV reticles via inclusion of prior information. Appl. Opt. 2020, 59, 5937–5947. [Google Scholar] [CrossRef] [PubMed]
- Tinti, G.; Marchetto, H.; Vaz, C.A.F.; Kleibert, A.; Andrä, M.; Barten, R.; Bergamaschi, A.; Brückner, M.; Cartier, S.; Dinapoli, R.; et al. The EIGER detector for low-energy electron microscopy and photoemission electron microscopy. J. Synchrotron Radiat. 2017, 24, 963–974. [Google Scholar] [CrossRef] [PubMed]




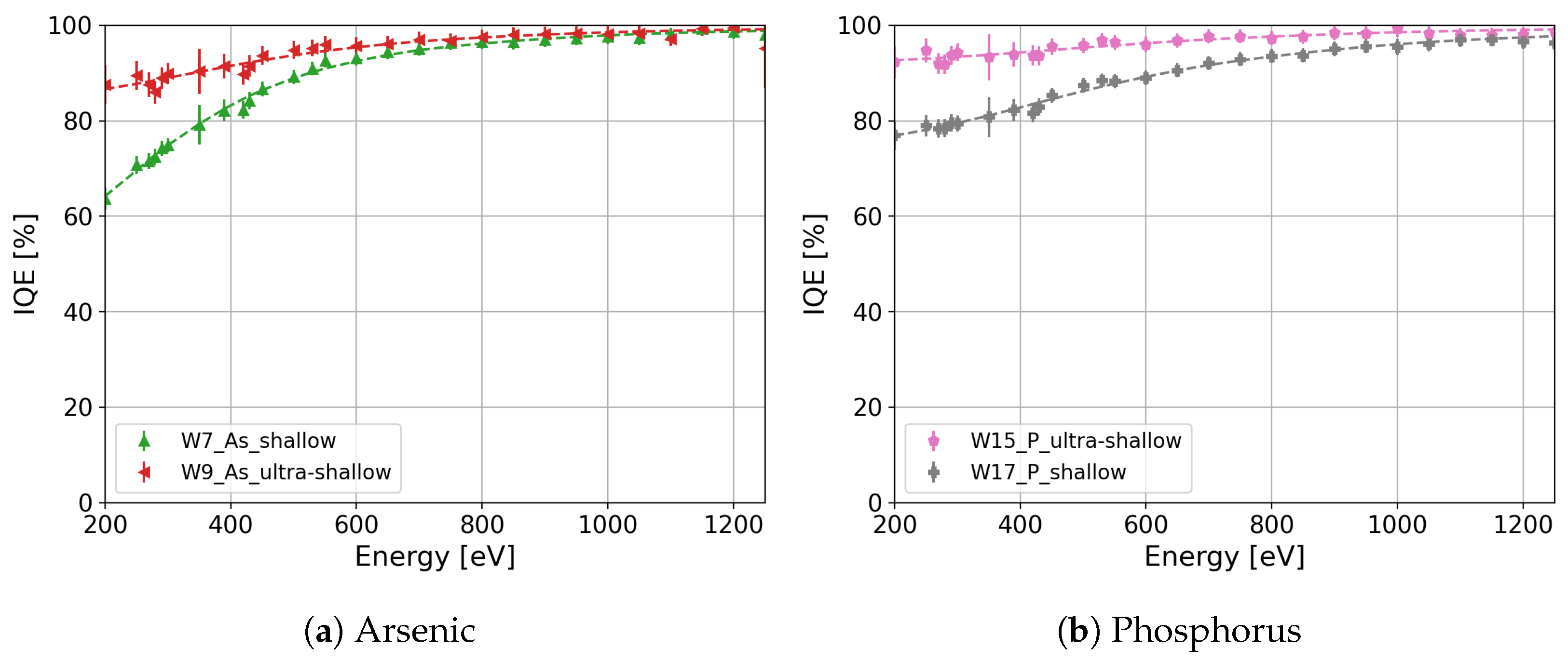


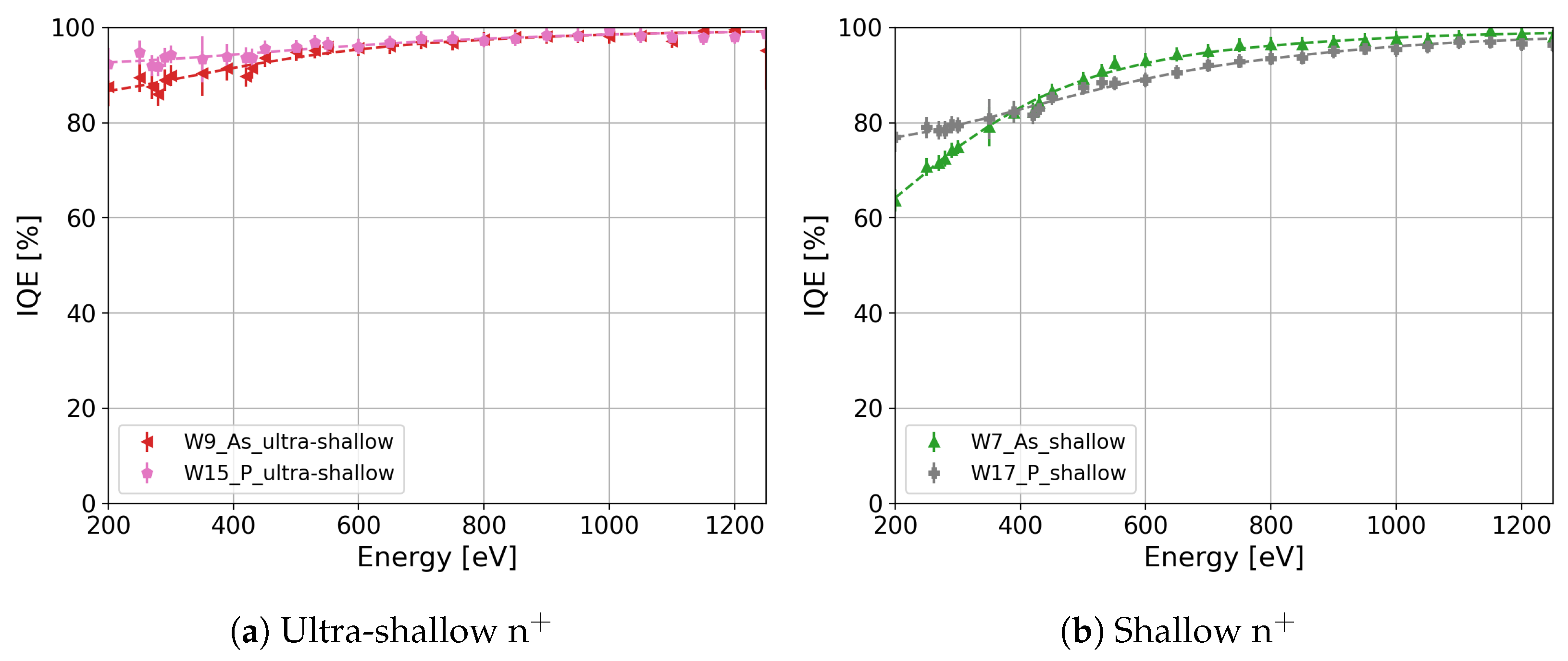
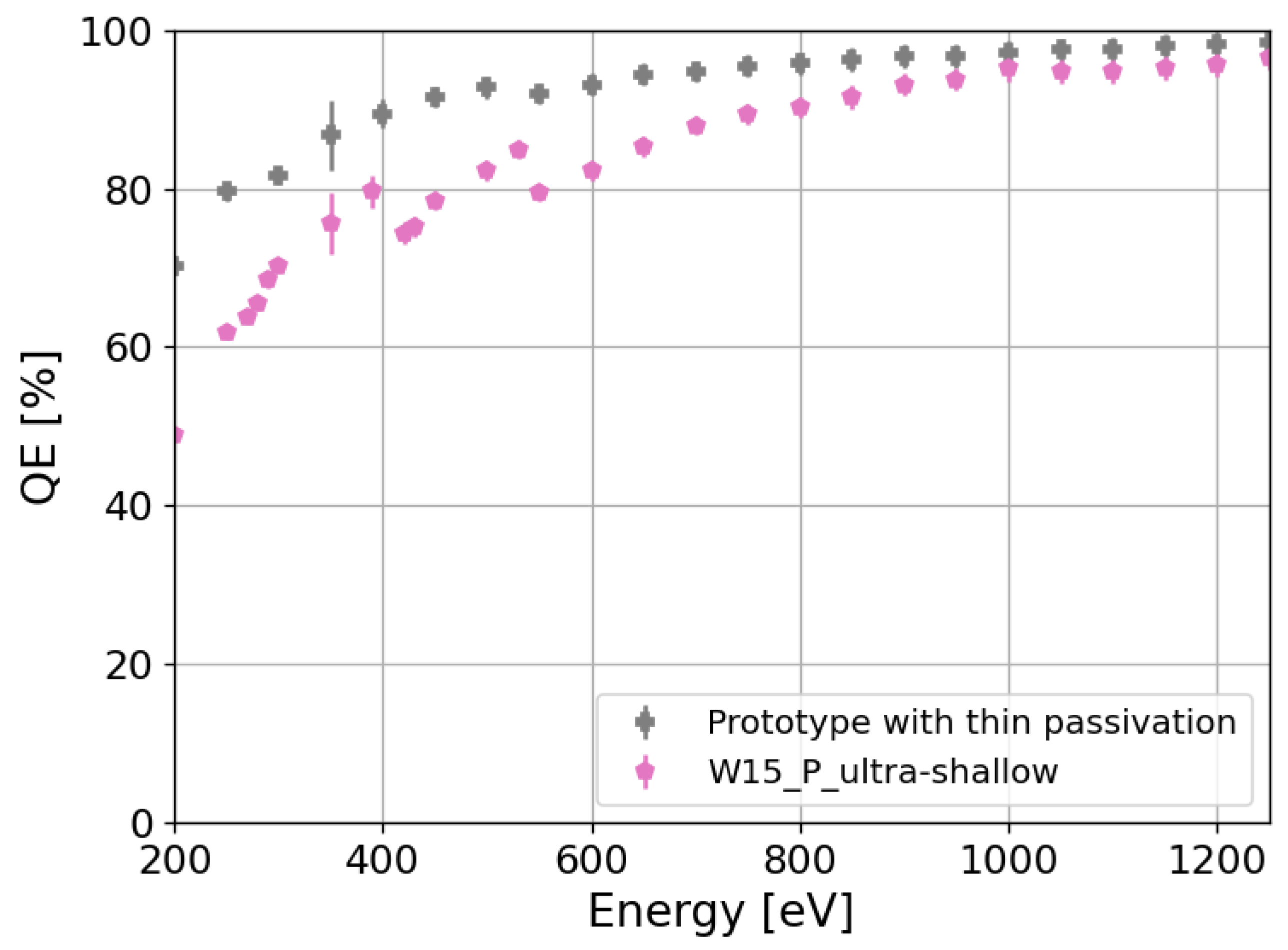
| Wafer | Si Orientation | n+ Dopant | Dopant Profile | Annealing Temperature | Surface Layer |
|---|---|---|---|---|---|
| W1 | As | Shallow | High | Aluminum | |
| W5 | As | Shallow | Low | SiO2 and Si3N4 | |
| W7 | As | Shallow | High | SiO2 and Si3N4 | |
| W9 | As | Ultra-shallow | Low | SiO2 and Si3N4 | |
| W11 | As | Shallow | High | SiO2 and Si3N4 | |
| W13 | As | Shallow | High | Thin SiO2 and Si3N4 | |
| W15 | P | Ultra-shallow | Low | SiO2 and Si3N4 | |
| W17 | P | Shallow | High | SiO2 and Si3N4 | |
| W19 | P | Shallow | High | SiO2 and Si3N4 |
| Wafer | Volume Leakage Current Density (µA/cm3) | Surface Recombination Velocity (cm/s) (Pixel Side) |
|---|---|---|
| W1 | ||
| W5 | ||
| W7 | ||
| W9 | ||
| W11 | - | |
| W13 | ||
| W15 | ||
| W17 | ||
| W19 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carulla, M.; Barten, R.; Baruffaldi, F.; Bergamaschi, A.; Borghi, G.; Boscardin, M.; Brückner, M.; Butcher, T.A.; Centis Vignali, M.; Dinapoli, R.; et al. Quantum Efficiency Measurement and Modeling of Silicon Sensors Optimized for Soft X-ray Detection. Sensors 2024, 24, 942. https://doi.org/10.3390/s24030942
Carulla M, Barten R, Baruffaldi F, Bergamaschi A, Borghi G, Boscardin M, Brückner M, Butcher TA, Centis Vignali M, Dinapoli R, et al. Quantum Efficiency Measurement and Modeling of Silicon Sensors Optimized for Soft X-ray Detection. Sensors. 2024; 24(3):942. https://doi.org/10.3390/s24030942
Chicago/Turabian StyleCarulla, Maria, Rebecca Barten, Filippo Baruffaldi, Anna Bergamaschi, Giacomo Borghi, Maurizio Boscardin, Martin Brückner, Tim A. Butcher, Matteo Centis Vignali, Roberto Dinapoli, and et al. 2024. "Quantum Efficiency Measurement and Modeling of Silicon Sensors Optimized for Soft X-ray Detection" Sensors 24, no. 3: 942. https://doi.org/10.3390/s24030942
APA StyleCarulla, M., Barten, R., Baruffaldi, F., Bergamaschi, A., Borghi, G., Boscardin, M., Brückner, M., Butcher, T. A., Centis Vignali, M., Dinapoli, R., Ebner, S., Ficorella, F., Fröjdh, E., Greiffenberg, D., Hammad Ali, O., Hasanaj, S., Heymes, J., Hinger, V., King, T., ... Zhang, J. (2024). Quantum Efficiency Measurement and Modeling of Silicon Sensors Optimized for Soft X-ray Detection. Sensors, 24(3), 942. https://doi.org/10.3390/s24030942






