Suppression of Railway Catenary Galloping Based on Structural Parameters’ Optimization
Abstract
:1. Introduction
1.1. Problem Description
1.2. Literature Review
1.3. Contribution of This Paper
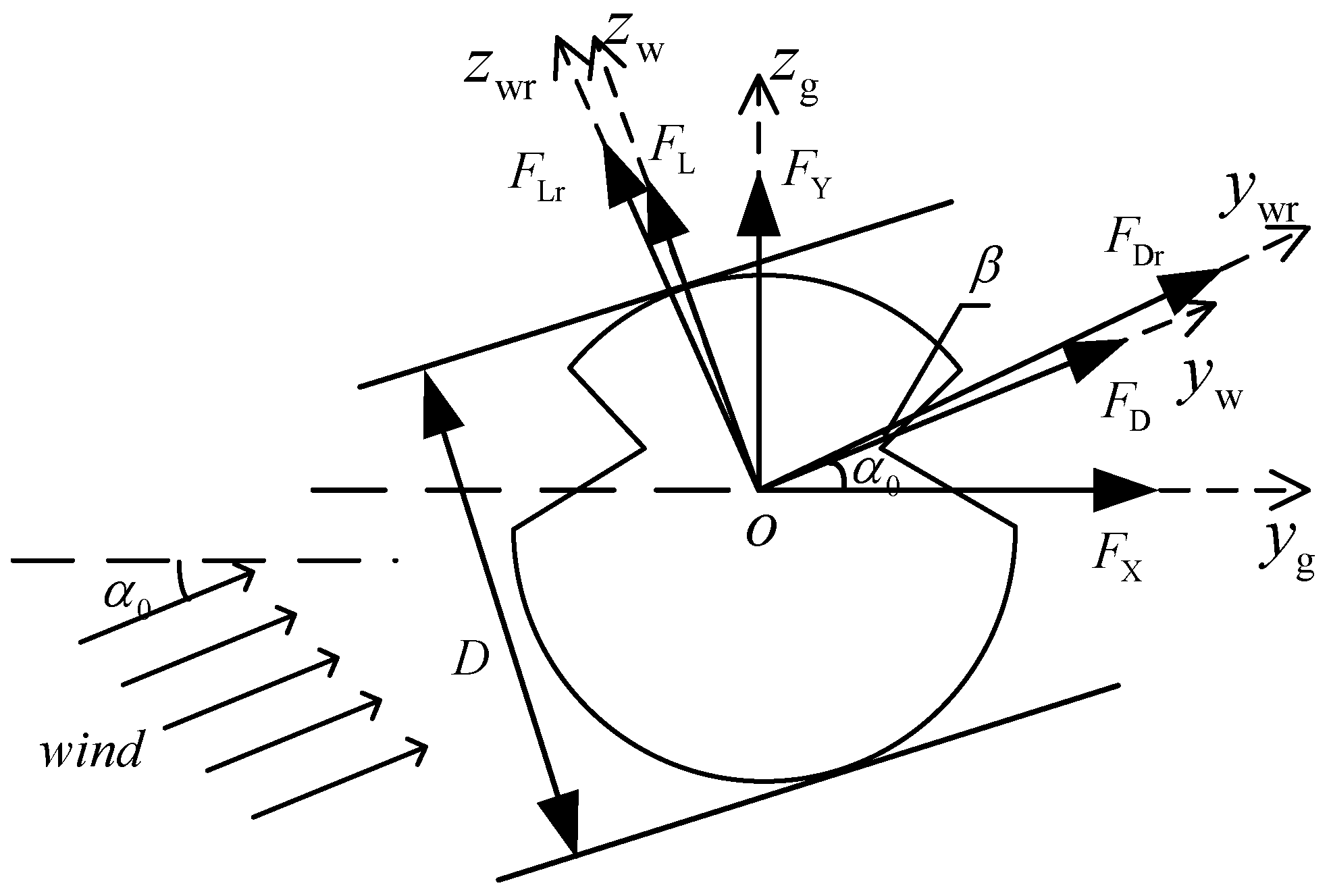
2. Modeling of Catenary Galloping
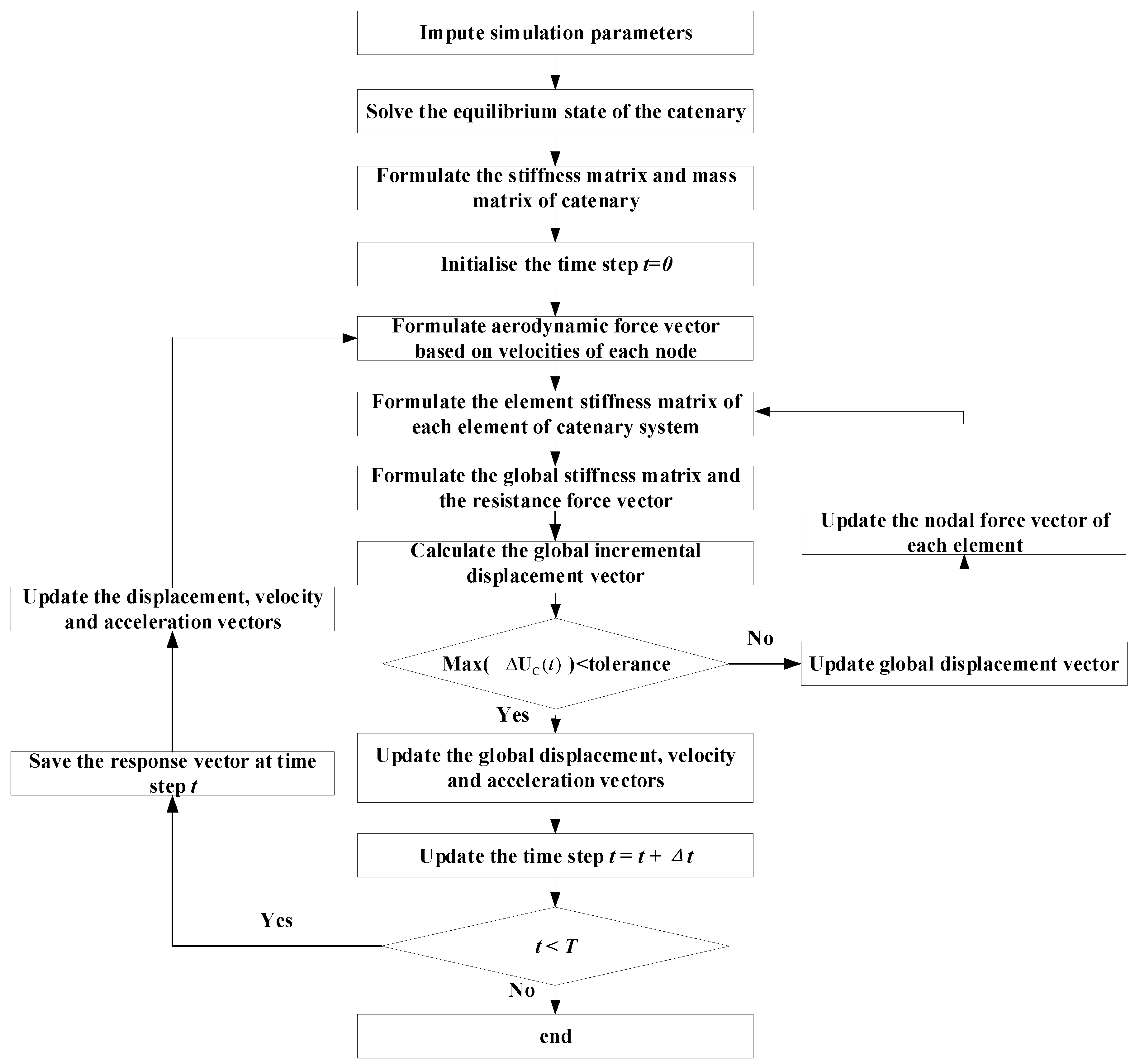
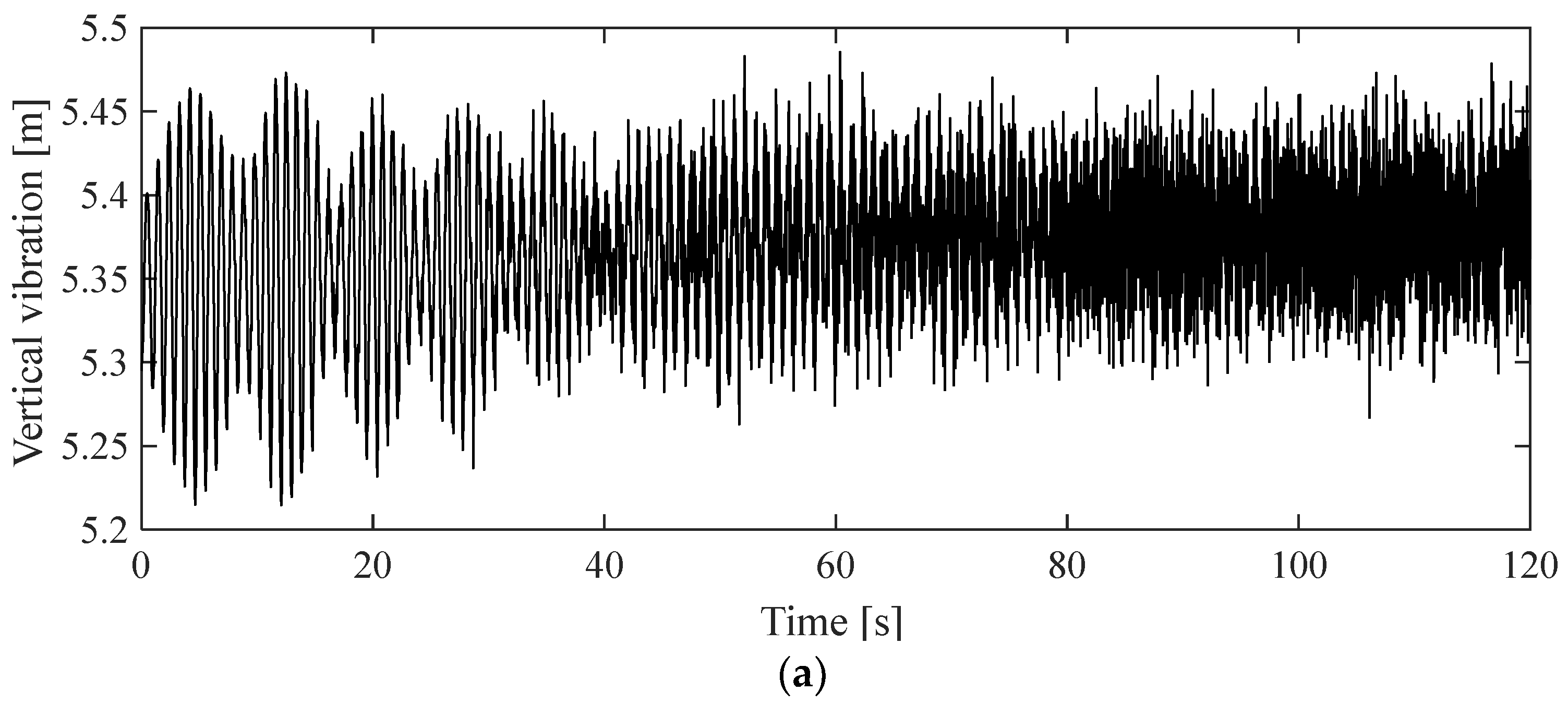
3. Preliminary Analysis of Catenary Galloping Response
4. Effect of Geometry Parameters on Catenary Galloping Response
4.1. Sobol Sequence
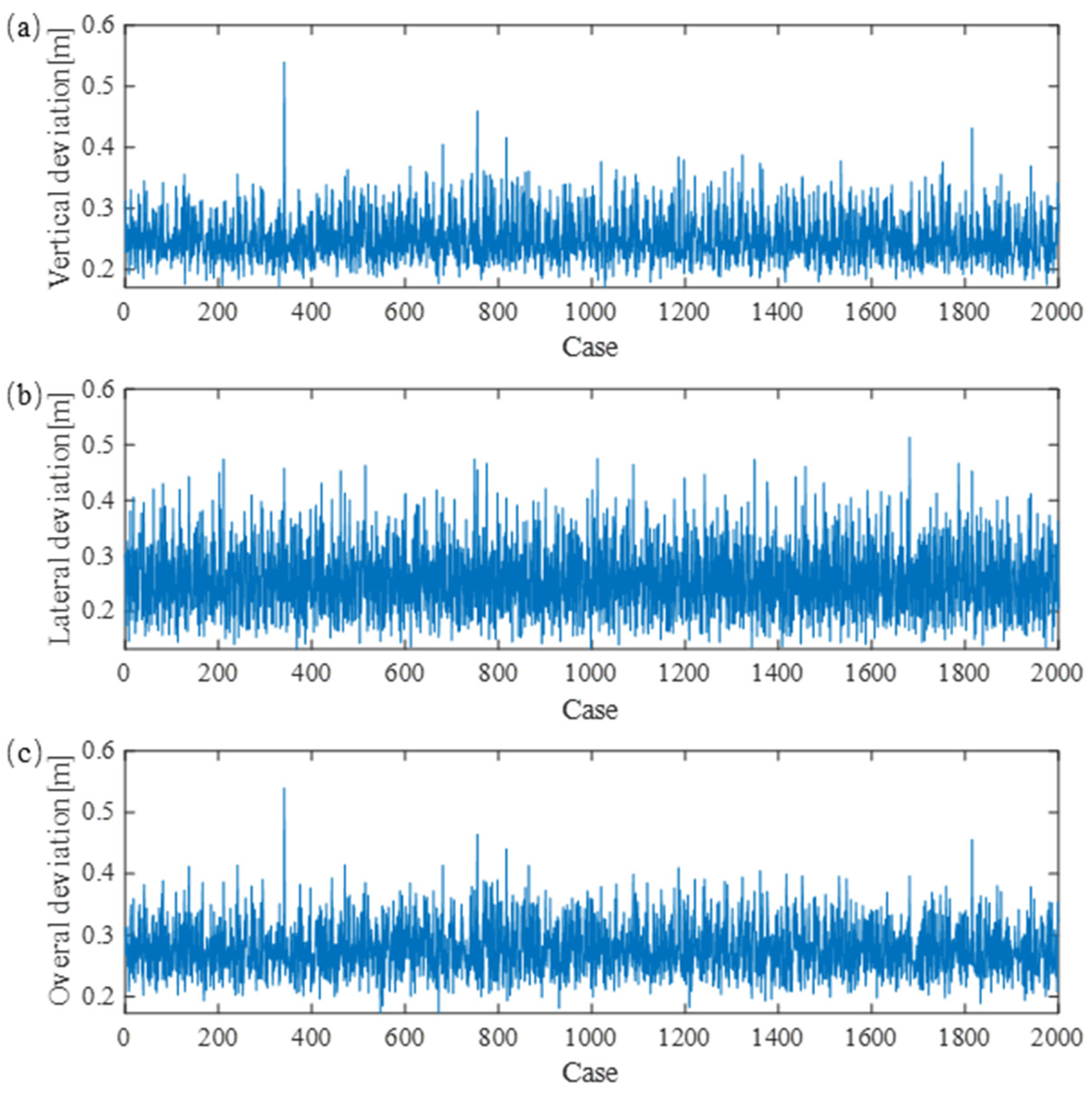
4.2. Simulation Results with Random Parameters
- Worst Case (Case 341):
- Best Case (Case 1126):
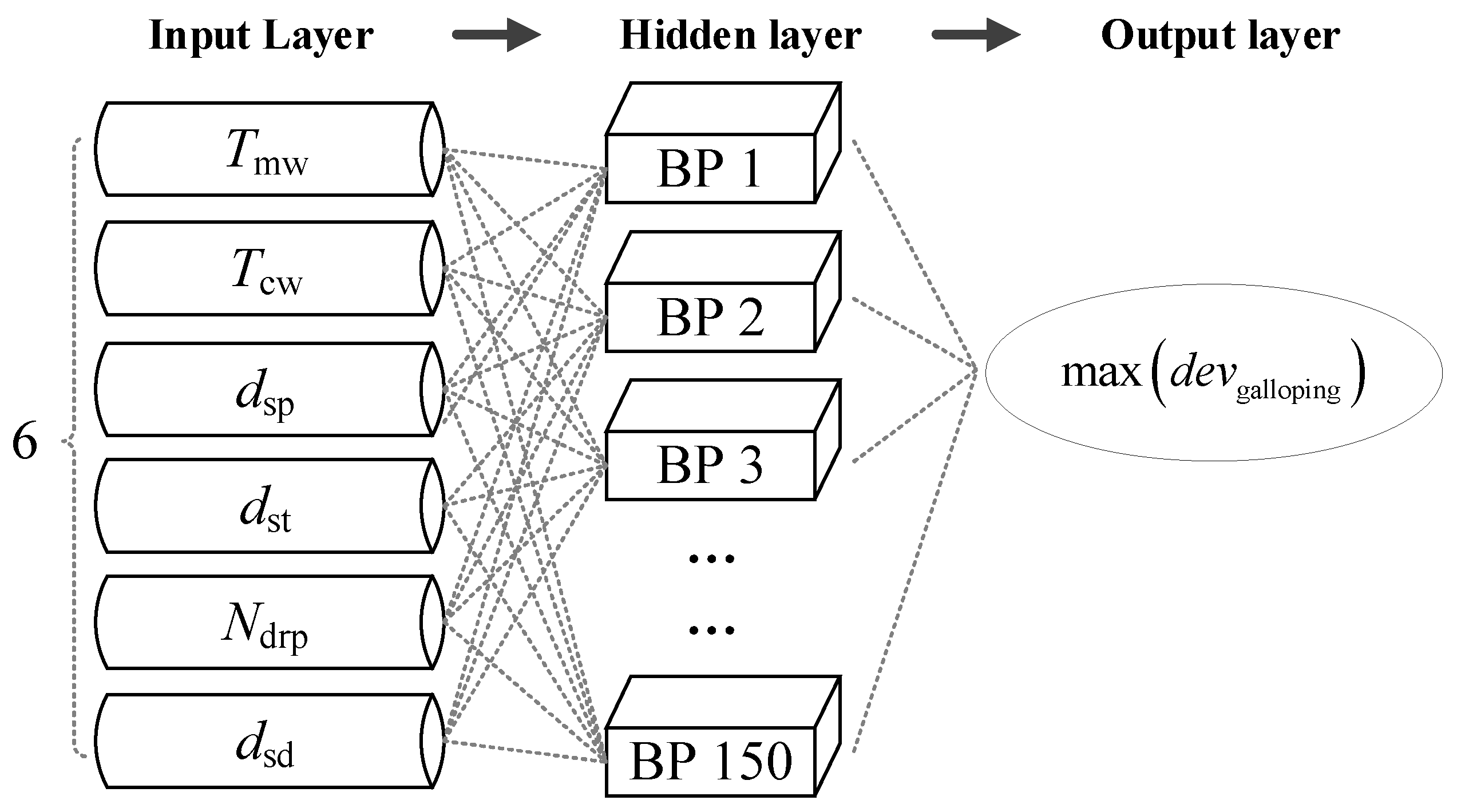
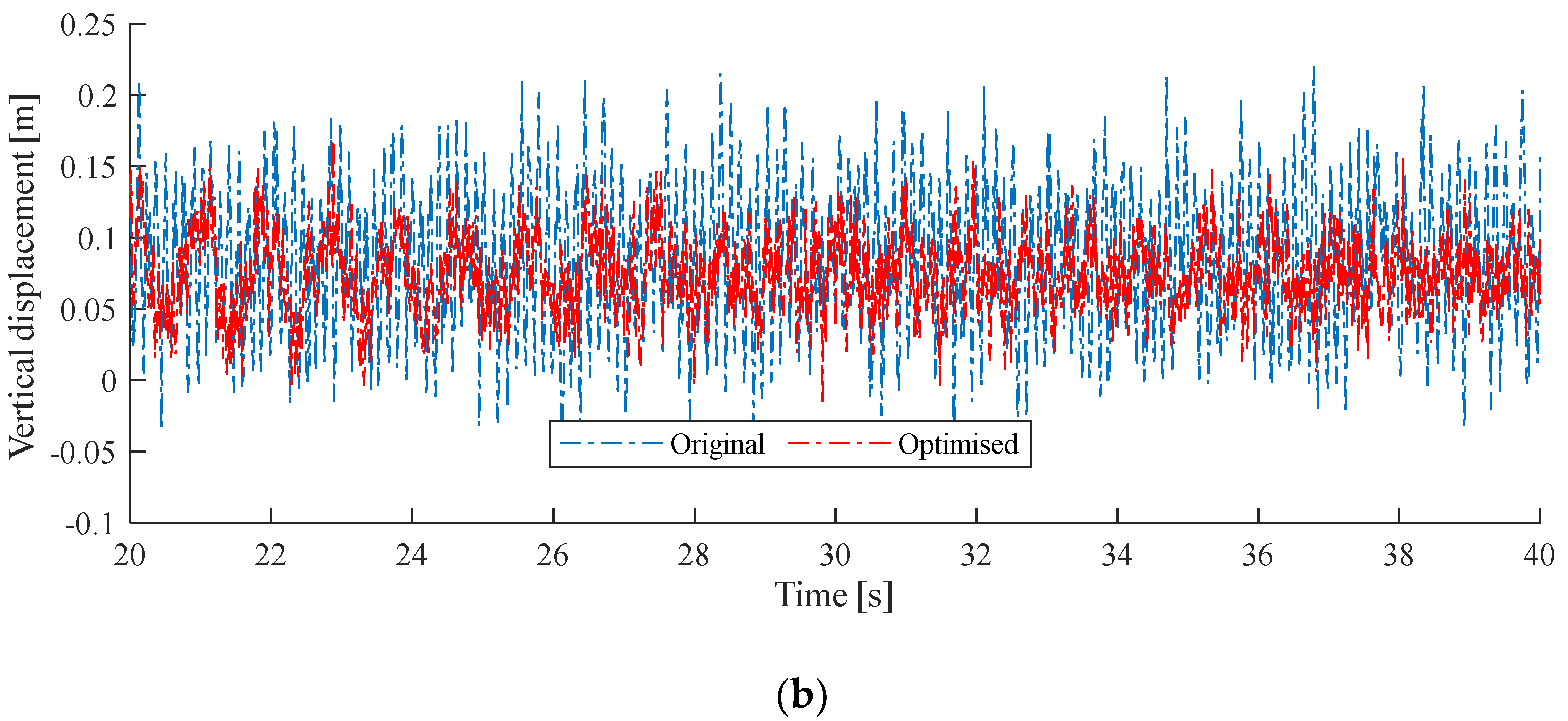
5. Optimization Based on Neural Networks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Kiessling, F.; Puschmann, R.; Schmieder, A.; Schneider, E. Contact Lines for Electric Railways, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Scanlan, R.H. The action of flexible bridges under wind, II: Buffeting theory. J. Sound. Vib. 1978, 60, 201–211. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrosio, J. Environmental and track perturbations on multiple pantograph interaction with catenaries in high-speed trains. Comput. Struct. 2013, 124, 88–101. [Google Scholar] [CrossRef]
- Novak, M. Galloping oscillations of prismatic structures. ASCE J. Eng. Mech. Div. 1972, 98, 27–46. [Google Scholar] [CrossRef]
- Duan, F.; Song, Y.; Gao, S.; Liu, Y.; Chu, W.; Lu, X.; Liu, Z. Study on Aerodynamic Instability and Galloping Response of Rail Overhead Contact Line Based on Wind Tunnel Tests. IEEE Trans. Veh. Technol. 2023. [CrossRef]
- Stickland, M.T.; Scanlon, T.J.; Craighead, I.A.; Fernandez, J. An investigation into the mechanical damping characteristics of catenary contact wires and their. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2001, 217, 63–72. [Google Scholar] [CrossRef]
- Scanion, T.J.; Stickland, M.T.; Oldroyd, A.B. An investigation into the attenuation of wind speed by the use of windbreaks in the vicinity of overhead wires. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2000, 214, 173–182. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Wang, Q.; Mo, J.; Feng, J.; Wang, K. The effect of wheel polygonal wear on temperature and vibration characteristics of a high-speed train braking system. Mech. Syst. Signal Process 2023, 186, 109864. [Google Scholar] [CrossRef]
- Ye, Y.; Zhu, B.; Huang, P.; Peng, B. OORNet: A deep learning model for on-board condition monitoring and fault diagnosis of out-of-round wheels of high-speed trains. Measurement 2022, 199, 111268. [Google Scholar] [CrossRef]
- Zhang, W.; Zou, D.; Tan, M.; Zhou, N.; Li, R.; Mei, G. Review of pantograph and catenary interaction. Front. Mech. Eng. 2018, 13, 311–322. [Google Scholar] [CrossRef]
- Pombo, J.; Antunes, P.; Ambrósio, J. A study on multiple pantograph operations for high-speed catenary contact. In Proceedings of the Eleventh International Conference on Computational Structures Technology, Dubrovnik, Croatia, 4–7 September 2012; Topping, B.H.V., Ed.; Civil-Comp Press: Stirlingshire, UK, 2012; Volume 99, p. 139. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Jiang, T.; Nåvik, P. Railway pantograph-catenary interaction performance in an overlap section: Modelling, validation and analysis. J. Sound. Vib. 2023, 548, 117506. [Google Scholar] [CrossRef]
- Filograno, M.L.; Corredera, P.; González-Herráez, M. Field testing of a low-cost, self-referenced all-fibre polarimetric current sensor for the monitoring of current in the high-speed railway catenary. Opt. Sens. Detect. II 2012, 8439, 475–482. [Google Scholar] [CrossRef]
- Bruni, S.; Bucca, G.; Carnevale, M.; Collina, A.; Facchinetti, A. Pantograph–catenary interaction: Recent achievements and future research challenges. Int. J. Rail Transp. 2018, 6, 57–82. [Google Scholar] [CrossRef]
- Su, K.; Zhang, J.; Zhang, J.; Yan, T.; Mei, G. Optimisation of current collection quality of high-speed pantograph-catenary system using the combination of artificial neural network and genetic algorithm. Veh. Syst. Dyn. 2022, 61, 260–285. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact force control In multibody pantograph/catenary systems. Proc. Inst. Mech. Eng. Part K J. Multi.-Body Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Karakose, E.; Gencoglu, M.T. Adaptive fuzzy control approach for dynamic pantograph-catenary interaction. In Proceedings of the 15th International Conference on MECHATRONICS, Prague, Czech Republic, 5–7 December 2012; pp. 1–5. [Google Scholar]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process 2021, 151, 107336. [Google Scholar] [CrossRef]
- Zhang, W.; Mei, G.; Zeng, J. A study of pantograph/catenary system dynamics with influence of presag and irregularity of contact wire. Veh. Syst. Dyn. 2003, 37, 593–604. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F.; Wu, F.; Liu, Z.; Gao, S. Assessment of the Current Collection Quality of Pantograph-Catenary with Contact Line Height Variability in Electric Railways. IEEE Trans. Transp. Electrif. 2021, 8, 788–798. [Google Scholar] [CrossRef]
- Van, O.V.; Massat, J.P.; Laurent, C.; Balmes, E. Introduction of variability into pantograph-catenary dynamic simulations. Veh. Syst. Dyn. 2014, 52, 1254–1269. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Ronnquist, A.; Navik, P.; Liu, Z. Contact wire irregularity stochastics and effect on high-speed railway pantograph-catenary interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrosio, J.; Pereira, M.; Rauter, F.; Collina, A.; Facchinetti, A. Influence of the aerodynamic forces on the pantograph-catenary system for high-speed trains. Veh. Syst. Dyn. 2009, 47, 1327–1347. [Google Scholar] [CrossRef]
- Luo, Q.; Mei, G.; Chen, G.; Zhang, W. Study of pantograph-catenary system dynamic in crosswind environments. Veh. Syst. Dyn. 2023. [Google Scholar] [CrossRef]
- Xie, Q.; Zhi, X. Wind tunnel test of an aeroelastic model of a catenary system for a high-speed railway in China. J. Wind. Eng. Ind. Aerodyn. 2019, 184, 23–33. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Avila-Sanchez, S.; Lopez-Garcia, O.; Cuerva, A.; Meseguer, J. Assesment of the transverse galloping stability of a railway overhead located above a railway bridge. Int. J. Mech. Sci. 2017, 131–132, 649–662. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Zhang, J.; Lu, X.; Duan, F. Analysis of the galloping behaviour of an electrified railway overhead contact line using the non-linear finite element method. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2018, 232, 2339–2352. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, L.; Li, H.; Gao, J.; Yu, C.; Domel, R.; Yang, Y.; Tang, S.; Liu, W.K. Hierarchical deep-learning neural networks: Finite elements and beyond. Comput. Mech. 2021, 67, 207–230. [Google Scholar] [CrossRef]
- Bolandi, H.; Li, X.; Salem, T.; Boddeti, V.N.; Lajnef, N. Bridging finite element and deep learning: High-resolution stress distribution prediction in structural components. Front. Struct. Civil. Eng. 2022, 16, 1365–1377. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, H.; Xing, C.; Tao, T.; Mao, J.; Liu, Y. Physics guided wavelet convolutional neural network for wind-induced vibration modeling with application to structural dynamic reliability analysis. Eng. Struct. 2023, 297, 117027. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, B. Optimal PV array reconfiguration under partial shading condition through dynamic leader based collective intelligence. Prot. Control. Mod. Power Syst. 2023, 8, 40. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Q.; Ai, Y.; Chen, W.; Benbouzid, M.; Liu, S.; Gao, F. Two-stage distributionally robust optimization-based coordinated scheduling of integrated energy system with electricity-hydrogen hybrid energy storage. Prot. Control. Mod. Power Syst. 2023, 8, 33. [Google Scholar] [CrossRef]
- Wu, F.; Xie, X.; Ye, W. Rail Internal Defect Detection Method Based on Enhanced Network Structure and Module Design Using Ultrasonic Images. Chin. J. Mech. Eng. 2023, 36, 151. [Google Scholar] [CrossRef]
- Zhu, T.; Ding, H.; Wang, C.; Liu, Y.; Xiao, S.; Yang, G.; Yang, B. Parameters Calibration of the GISSMO Failure Model for SUS301L-MT. Chin. J. Mech. Eng. 2023, 36, 20. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Chen, C.; Hu, W. Reinforcement learning-based optimal tracking control for levitation system of maglev vehicle with input time delay. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. Available online: https://ieeexplore.ieee.org/abstract/document/9693414/ (accessed on 17 October 2023). [CrossRef]
- Sun, Y.; Xu, J.; Lin, G.; Ji, W.; Wang, L. RBF neural network-based supervisor control for maglev vehicles on an elastic track with network time delay. IEEE Trans. Ind. Inform. 2020, 18, 509–519. Available online: https://ieeexplore.ieee.org/abstract/document/9229504/ (accessed on 17 October 2023). [CrossRef]
- Kuang, Y.; Wang, S.; Peng, Z.; Fan, F.; Xie, J. Research and analysis of electrothermally actuated heating rates of smart concrete beam embedded with Shape Memory Alloy. J. Railw. Sci. Eng. 2023, 20, 1858–1870. [Google Scholar]
- GU, Z.; JIANG, R.; LIU, D.; SUN, H. Optimization design of the control arm of CFRP–aluminum foam sandwich structure. Chin. J. Eng. 2023, 45, 446–453. [Google Scholar]
- Zhao, L.; Yuan, Y.; Xing, L.; Bao, Y. Effect of electromagnetic stirring in extra-large billet on the flow field and temperature field. Chin. J. Eng. 2023, 45, 64–71. [Google Scholar]
- Dai, G.; Chen, Y. Research on nonlinear additional force algorithm of continuously welded rails on integral bridges. J. Railw. Sci. Eng. 2023, 20, 1304–1315. [Google Scholar]
- Zemljarič, B.; Ažbe, V. Analytically derived matrix end-form elastic-forces equations for a low-order cable element using the absolute nodal coordinate formulation. J. Sound. Vib. 2019, 446, 263–272. [Google Scholar] [CrossRef]
- Tur, M.; García, E.; Baeza, L.; Fuenmayor, F.J. A 3D absolute nodal coordinate finite element model to compute the initial configuration of a railway catenary. Eng. Struct. 2014, 71, 234–243. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F. Performance assessment of pantograph and overhead system based on a vertical coupling dynamics model of the railway system. Complex. Eng. Syst. 2022, 2, 9. [Google Scholar] [CrossRef]
- Sobol’, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Mendelson, E. Introduction to Mathematical Logic. 2009. Available online: https://books.google.com/books?hl=en&lr=&id=NJ7SBQAAQBAJ&oi=fnd&pg=PP1&dq=Introduction+to+Mathematical+Logic&ots=zaimWFaerk&sig=LktnnNnwvN2fU3YcbCGm-Mc9wWA (accessed on 19 January 2024).
- Nåvik, P.; Rønnquist, A.; Stichel, S. Identification of system damping in railway catenary wire systems from full-scale measurements. Eng. Struct. 2016, 113, 71–78. [Google Scholar] [CrossRef]
- Paul, R.J.; Chanev, T.S. Simulation optimisation using a genetic algorithm. 1998. [Google Scholar]
- Wu, Q.; Cole, C.; McSweeney, T. Applications of particle swarm optimization in the railway domain. Int. J. Rail Transp. 2016, 4, 167–190. [Google Scholar] [CrossRef]
- Song, Y.; Lu, X.; Yin, Y.; Liu, Y.; Liu, Z. Optimisation of Railway Pantograph-catenary Systems for over 350 km/h Based on an Experimentally Validated Model. IEEE Trans. Ind. Inform. 2024. [Google Scholar] [CrossRef]
- Ampazis, N.; Perantonis, S.J. Levenberg-Marquardt algorithm with adaptive momentum for the efficient training of feedforward networks. Proc. Int. Jt. Conf. Neural Netw. 2000, 1, 126–131. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Zhang, Z. Sensitivity analysis and research on optimisation methods of design parameters of high-speed railway catenary. IET Electr. Syst. Transp. 2019, 9, 150–156. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, R. Intelligent Feature Selection Using GA and Neural Network Optimization for Real-Time Driving Pattern Recognition. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12665–12674. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Y.; Gao, S.; Wang, H. Review of Perspectives on Pantograph-Catenary Interaction Research for High-Speed Railways Operating at 400 km/h and above. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
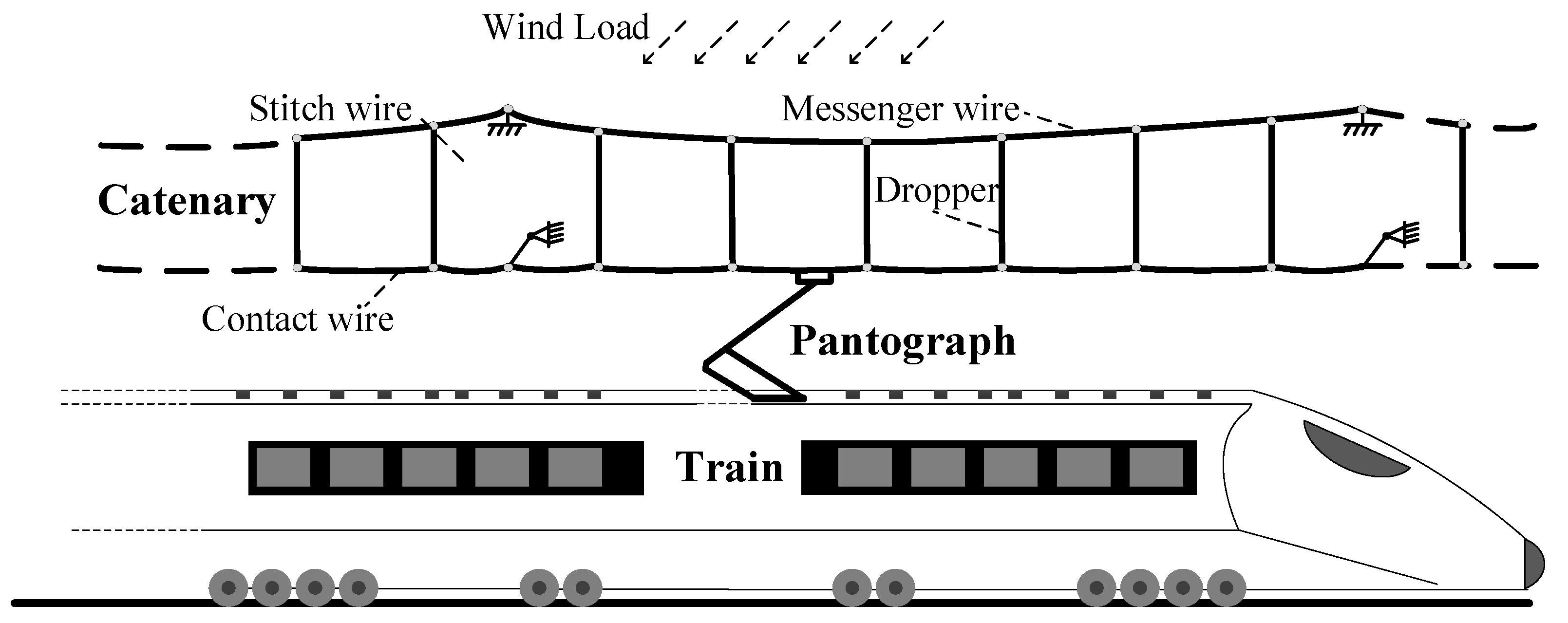

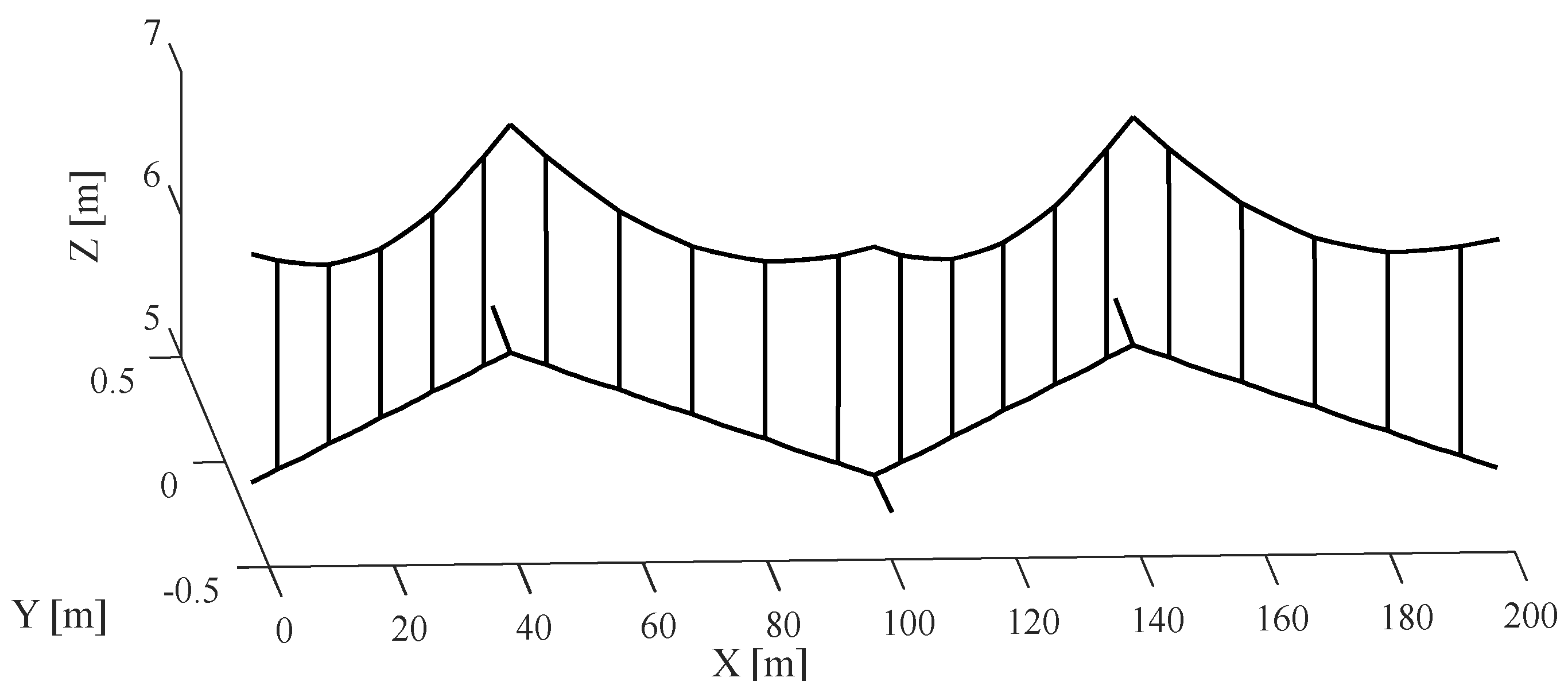




| OCL Geometrical Property | |
| Encumbrance: 1.6 m; Interval of droppers: 10 m; Span: 50 m; Number of droppers: 5 | |
| Material property | |
| Contact line | Line density: 1.082 kg/m; Cross-section area: 120 mm2; Tensile rigidity: 106 N/m; Tension: 15 kN |
| Messenger line | Line density: 1.068 kg/m; Cross-section area: 120 mm2; Tensile rigidity: 106 N/m; Tension: 15 kN |
| Dropper | Line density: 0.14 kg/m; Tensile rigidity: 105 N/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Song, Y.; Duan, F.; Liu, Z. Suppression of Railway Catenary Galloping Based on Structural Parameters’ Optimization. Sensors 2024, 24, 976. https://doi.org/10.3390/s24030976
Liu Y, Song Y, Duan F, Liu Z. Suppression of Railway Catenary Galloping Based on Structural Parameters’ Optimization. Sensors. 2024; 24(3):976. https://doi.org/10.3390/s24030976
Chicago/Turabian StyleLiu, Yuhui, Yang Song, Fuchuan Duan, and Zhigang Liu. 2024. "Suppression of Railway Catenary Galloping Based on Structural Parameters’ Optimization" Sensors 24, no. 3: 976. https://doi.org/10.3390/s24030976








