Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data
Abstract
1. Introduction
2. Basis Theory
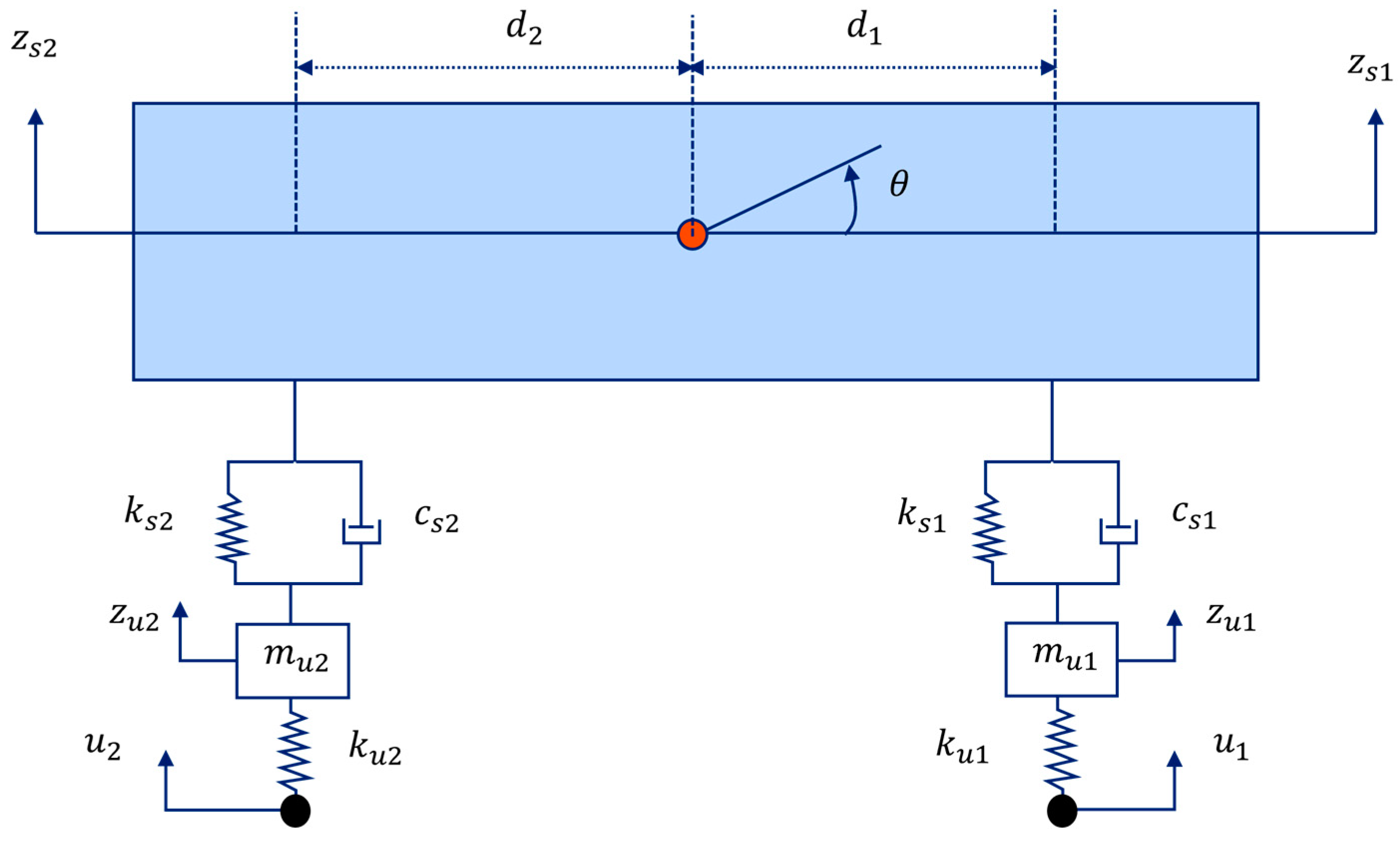
2.1. Vehicle Bridge Interaction System
2.1.1. Bridge System
2.1.2. Vehicle System
2.1.3. Interactions
- (a)
- Contact forces
- (b)
- Input profiles
3. The Proposed Method
3.1. The Basic Theory of the Proposed Method
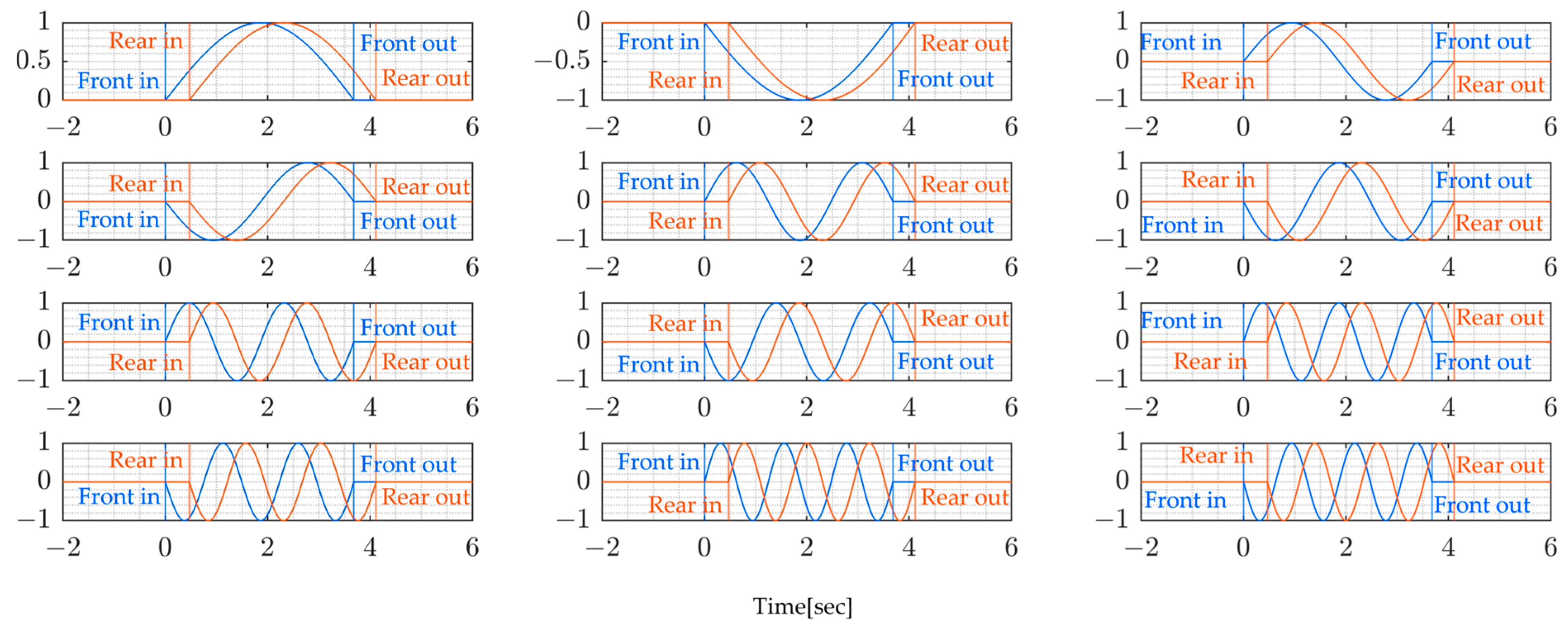
3.2. Window Functions and Modal Loads
3.3. Procedure of the Proposed Method
4. Numerical Simulation
4.1. VBI Simulation
4.2. VBI Models
4.3. Simulated Signals
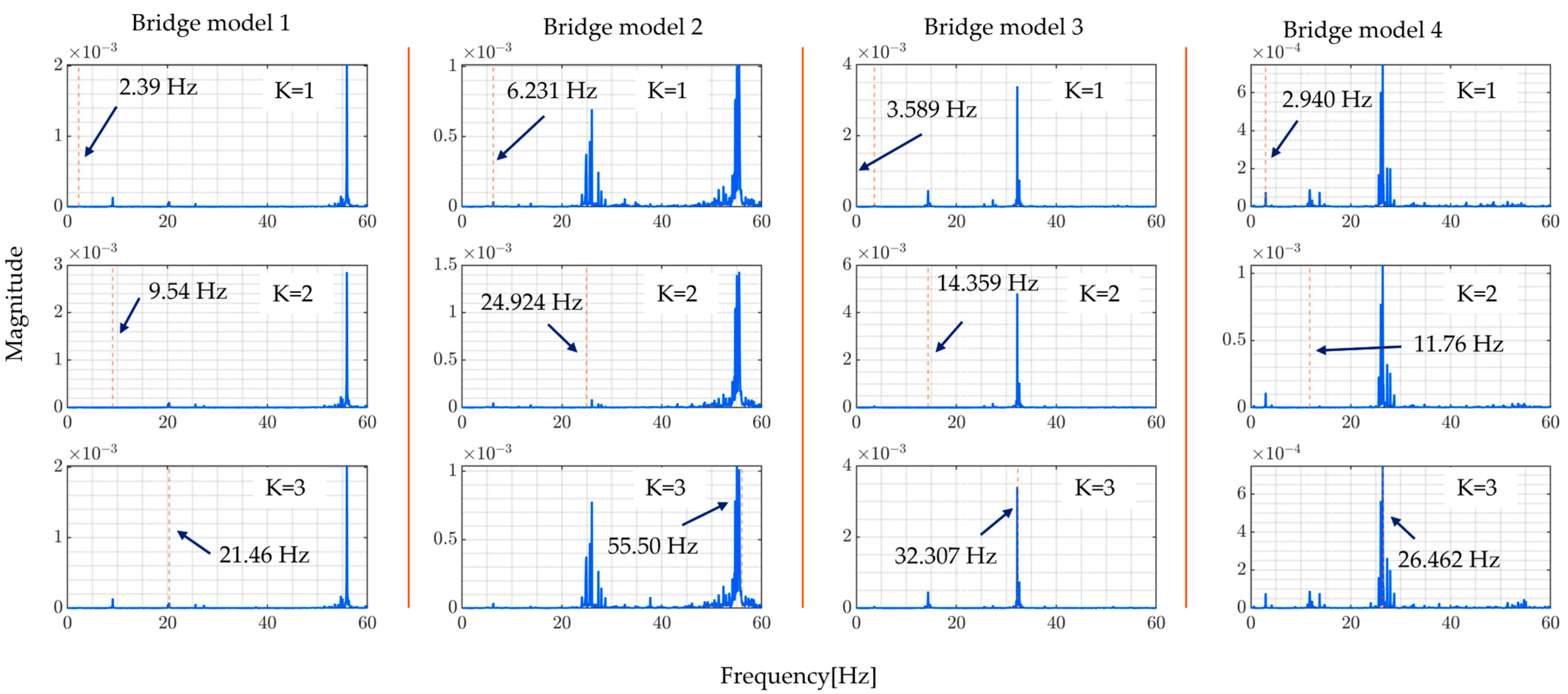
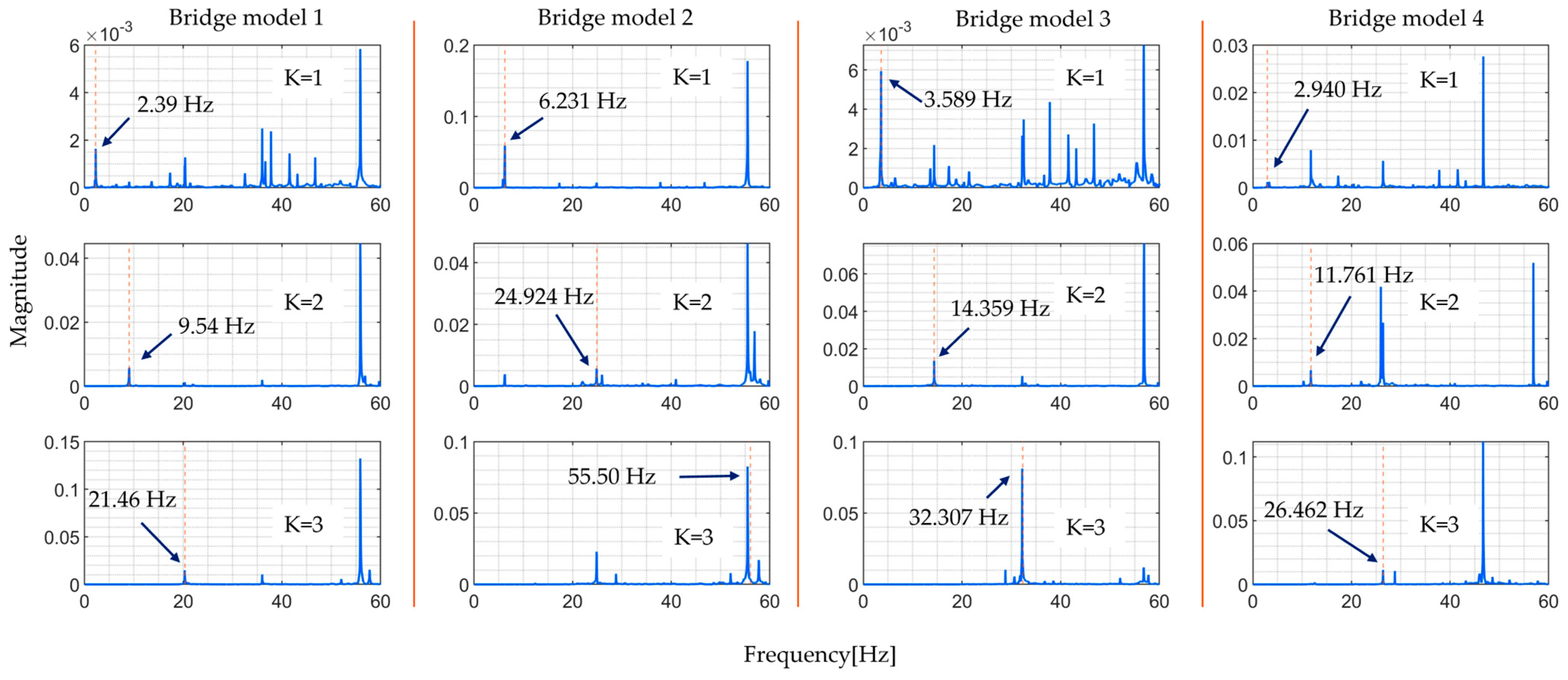
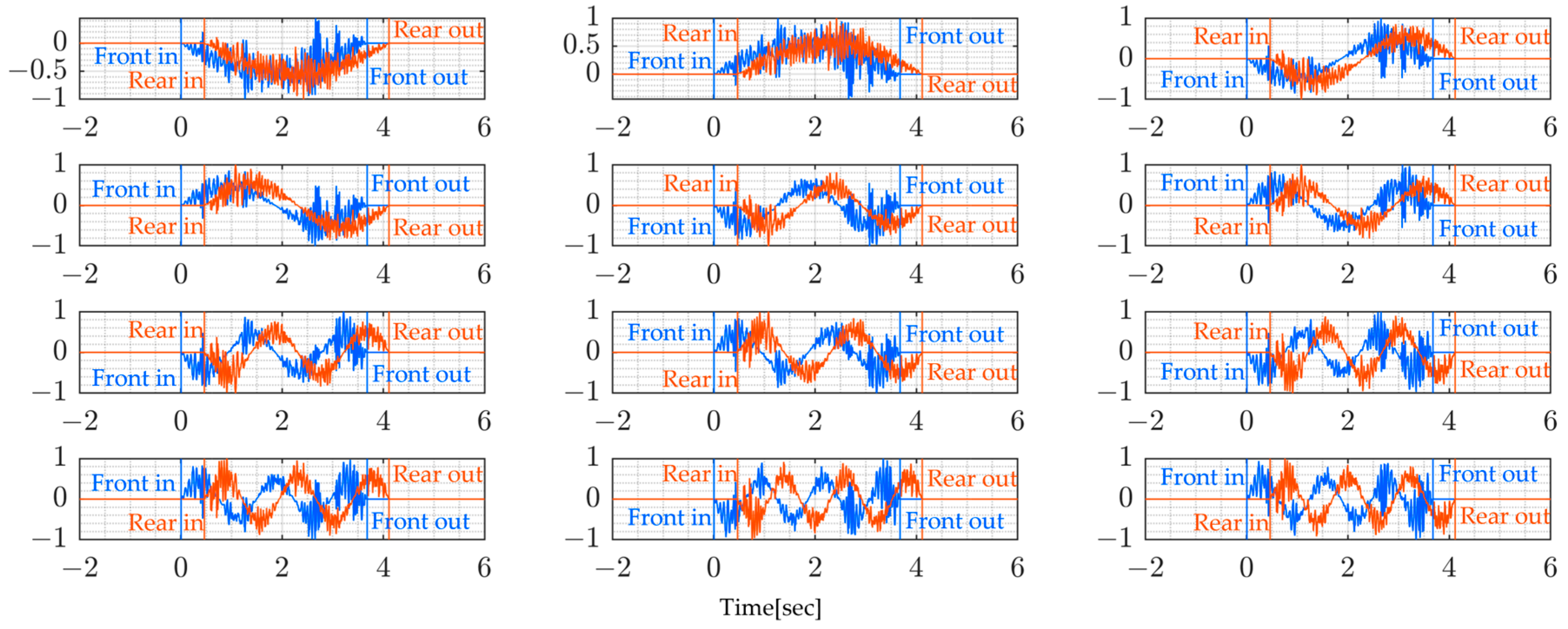
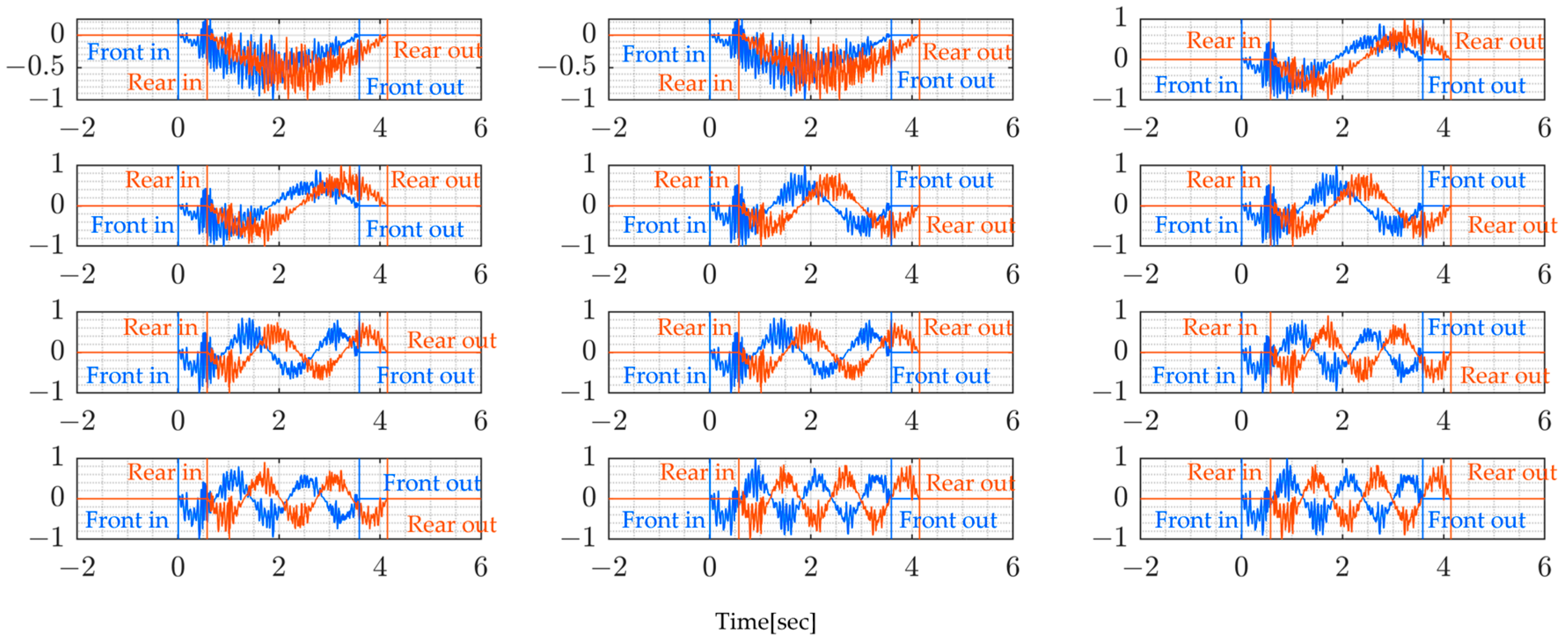
4.4. Numerical Results and Discussion
5. Field Experiment
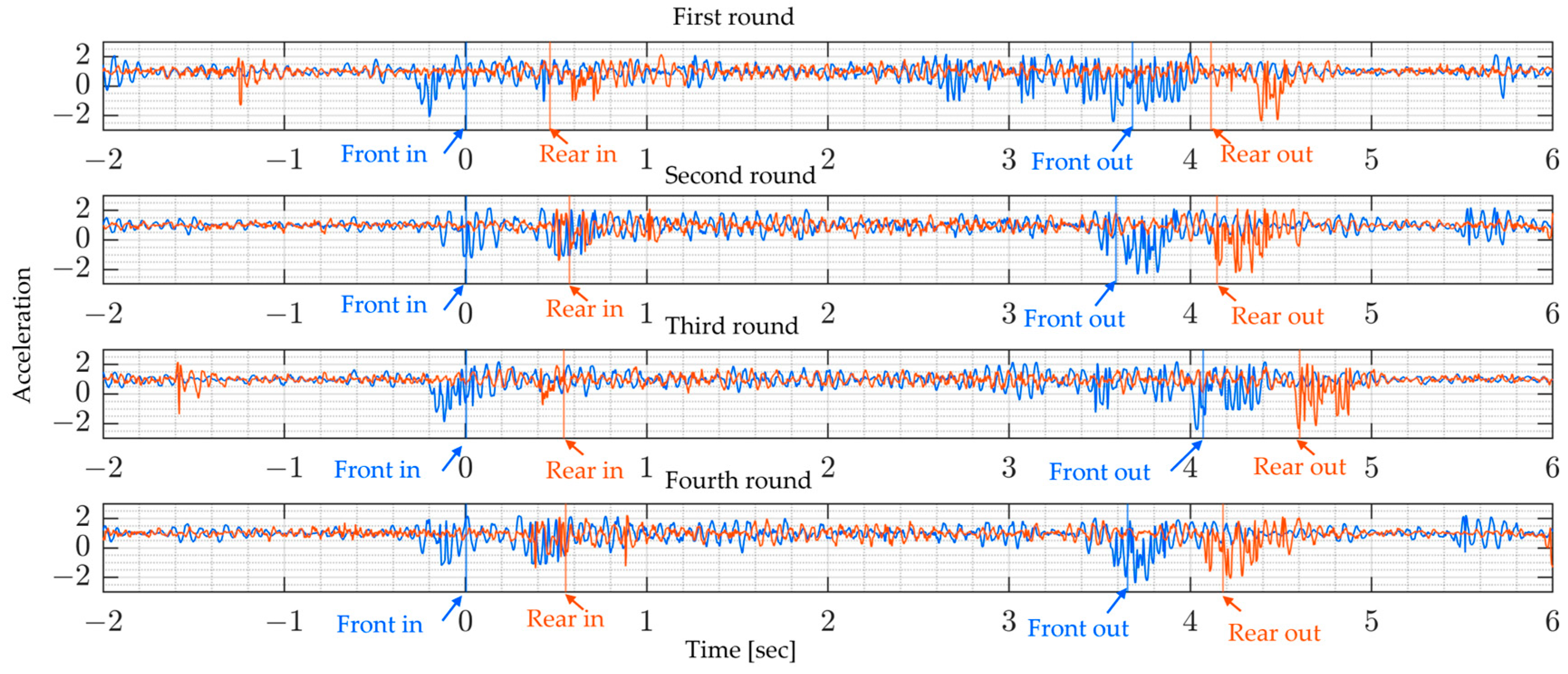
5.1. Experimental Preparation and Setting
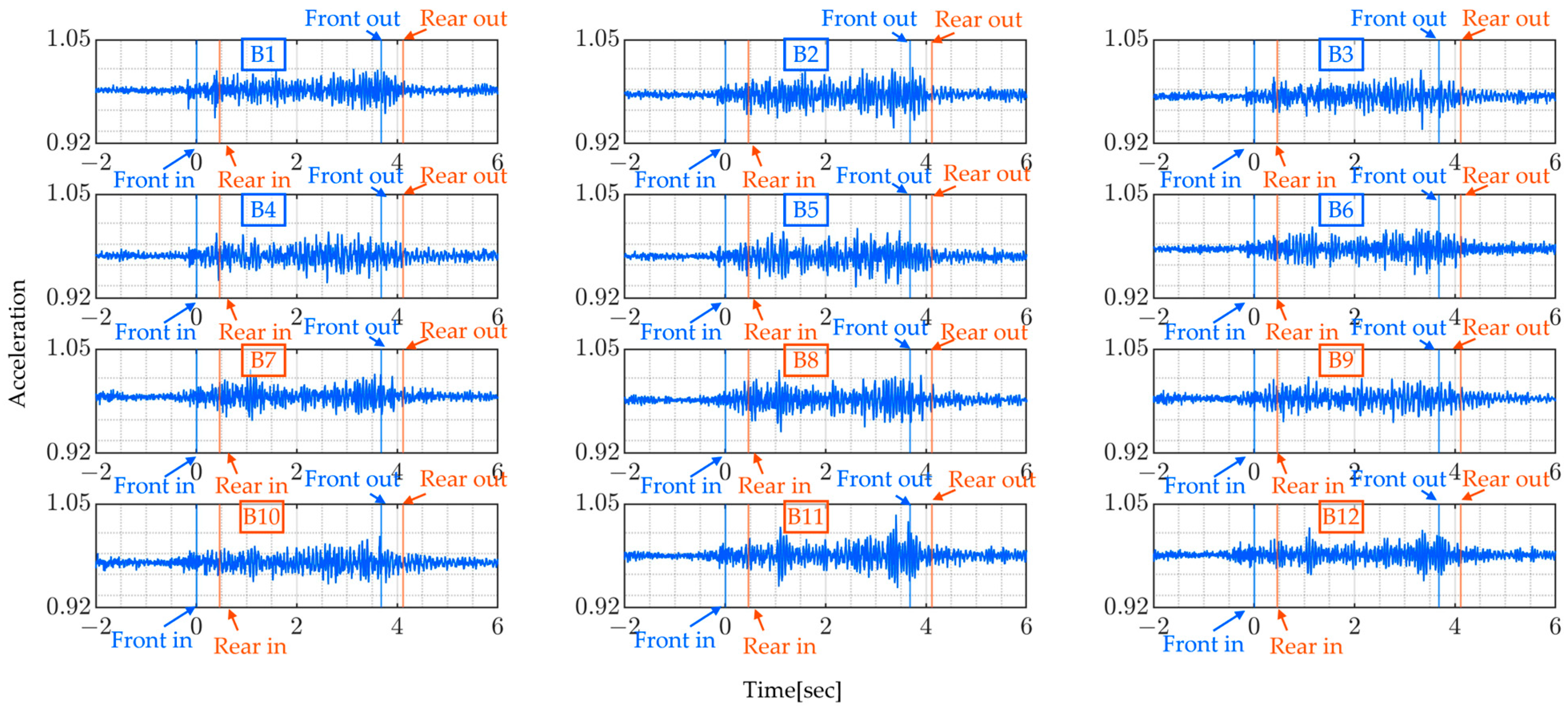
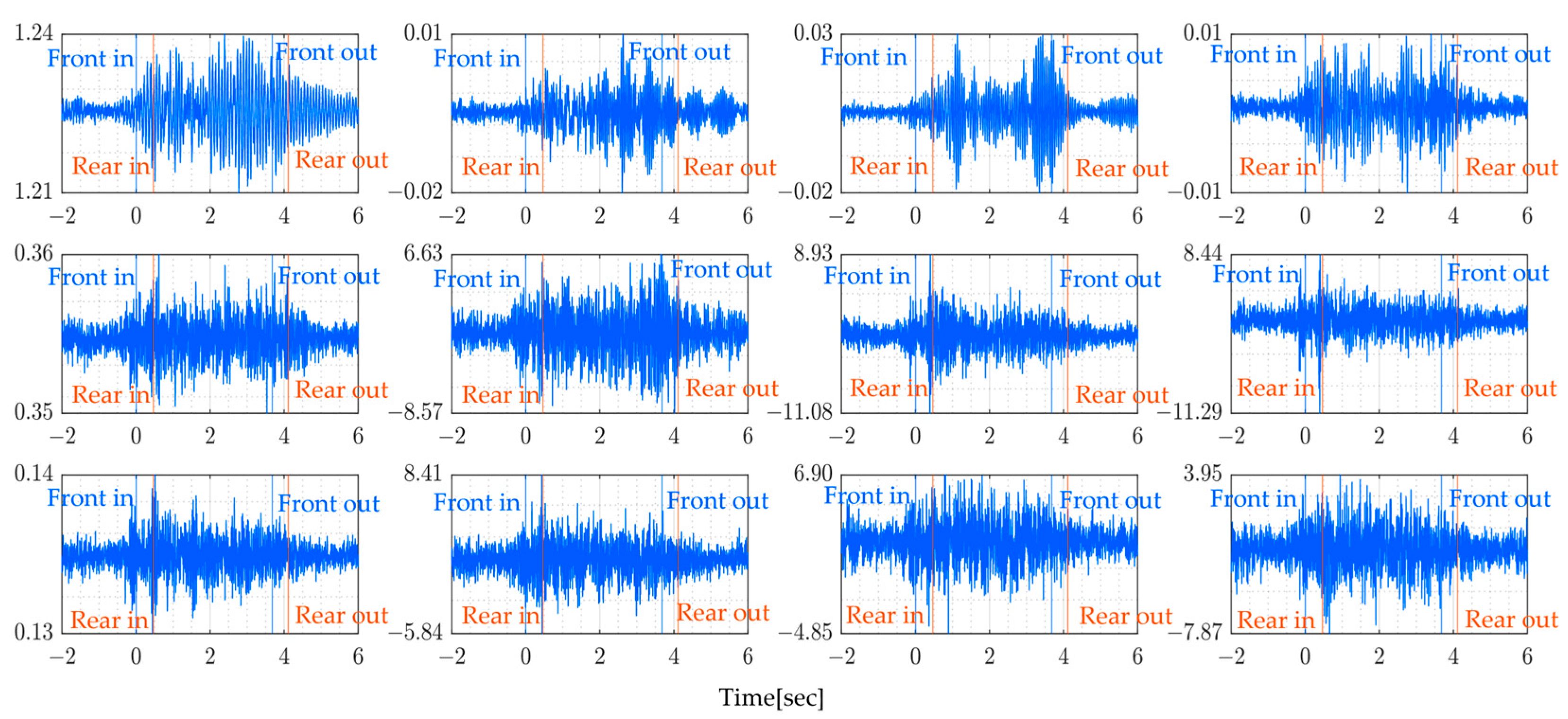
5.2. Obtained Data
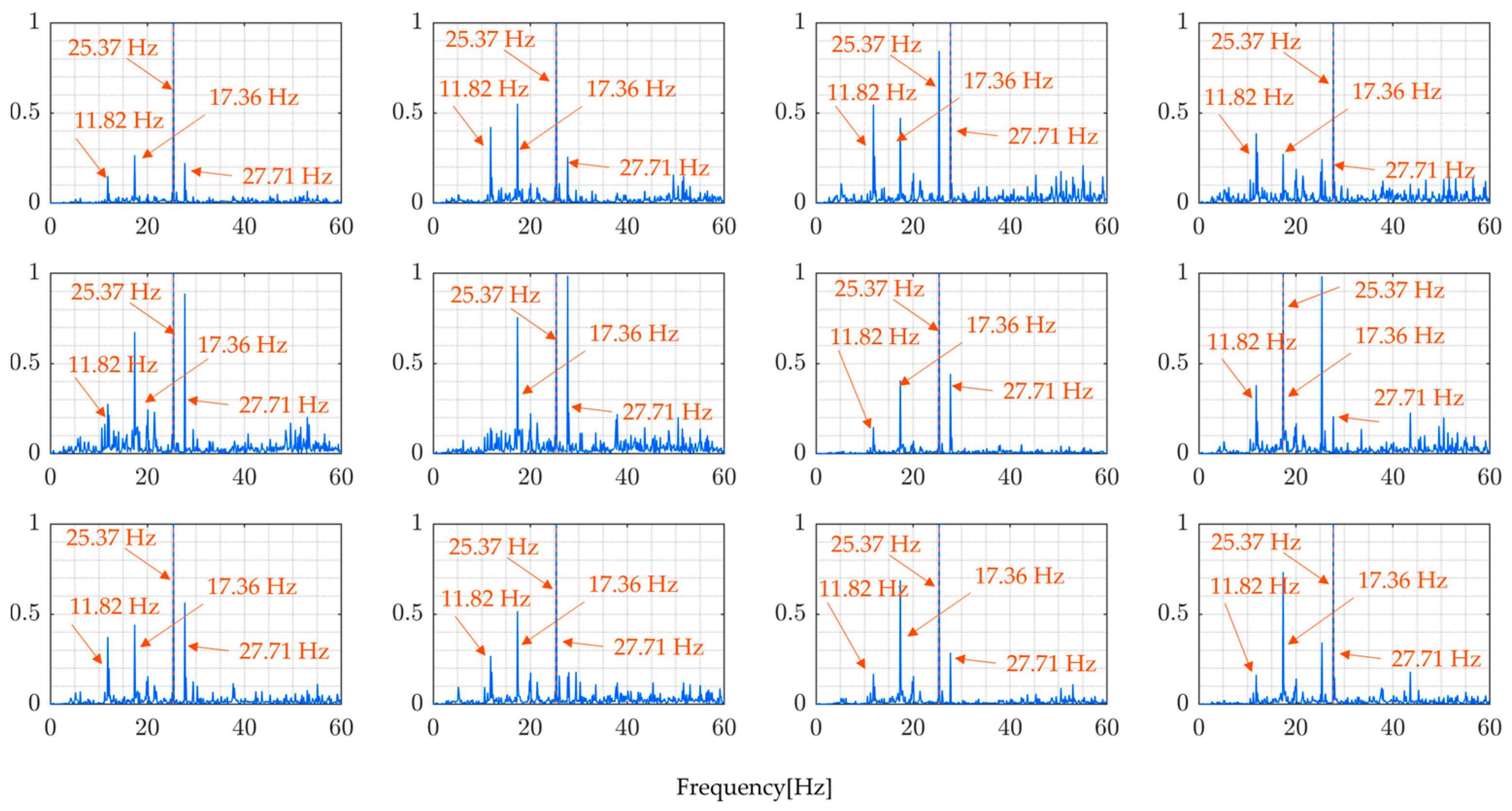
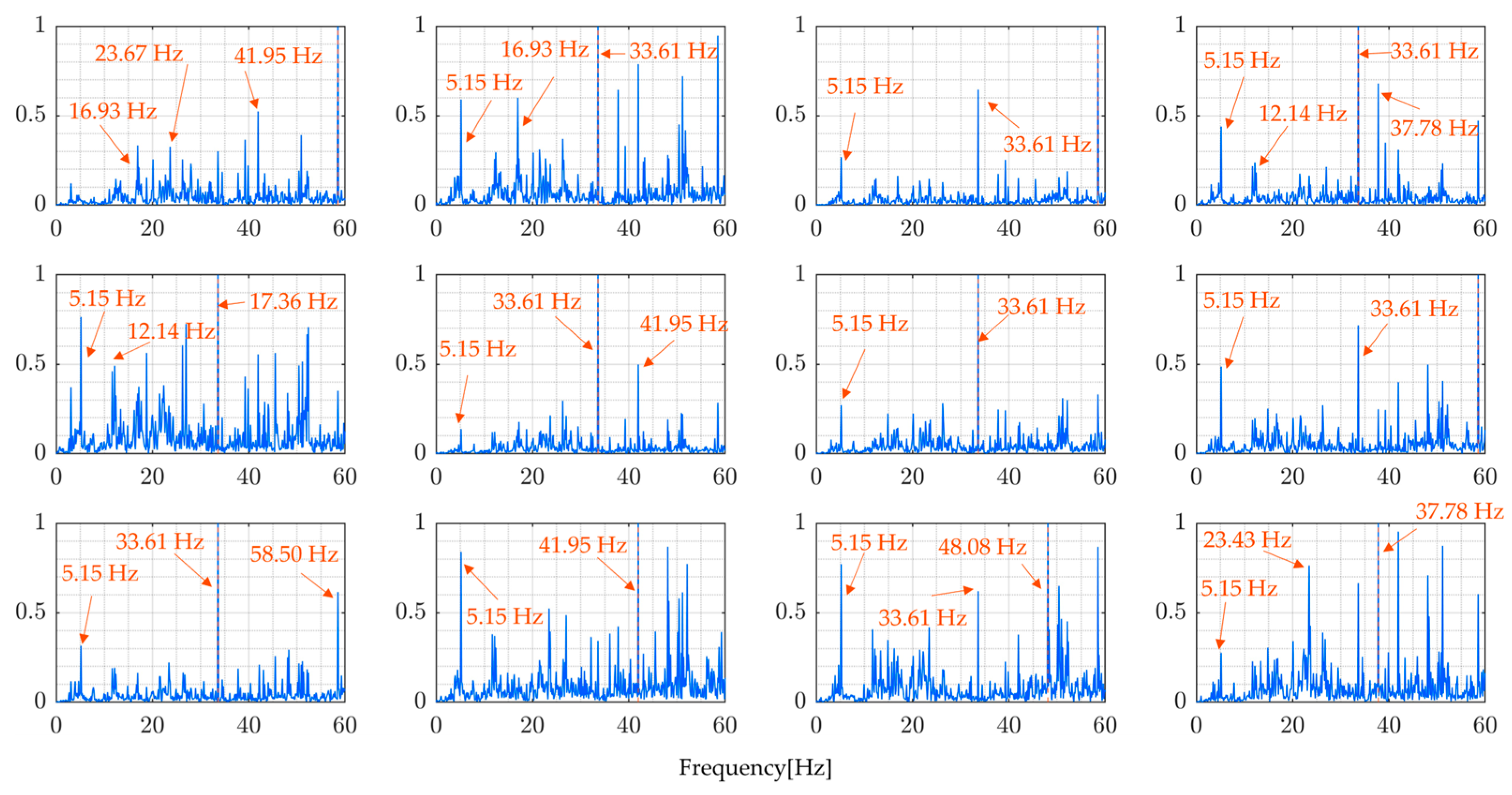
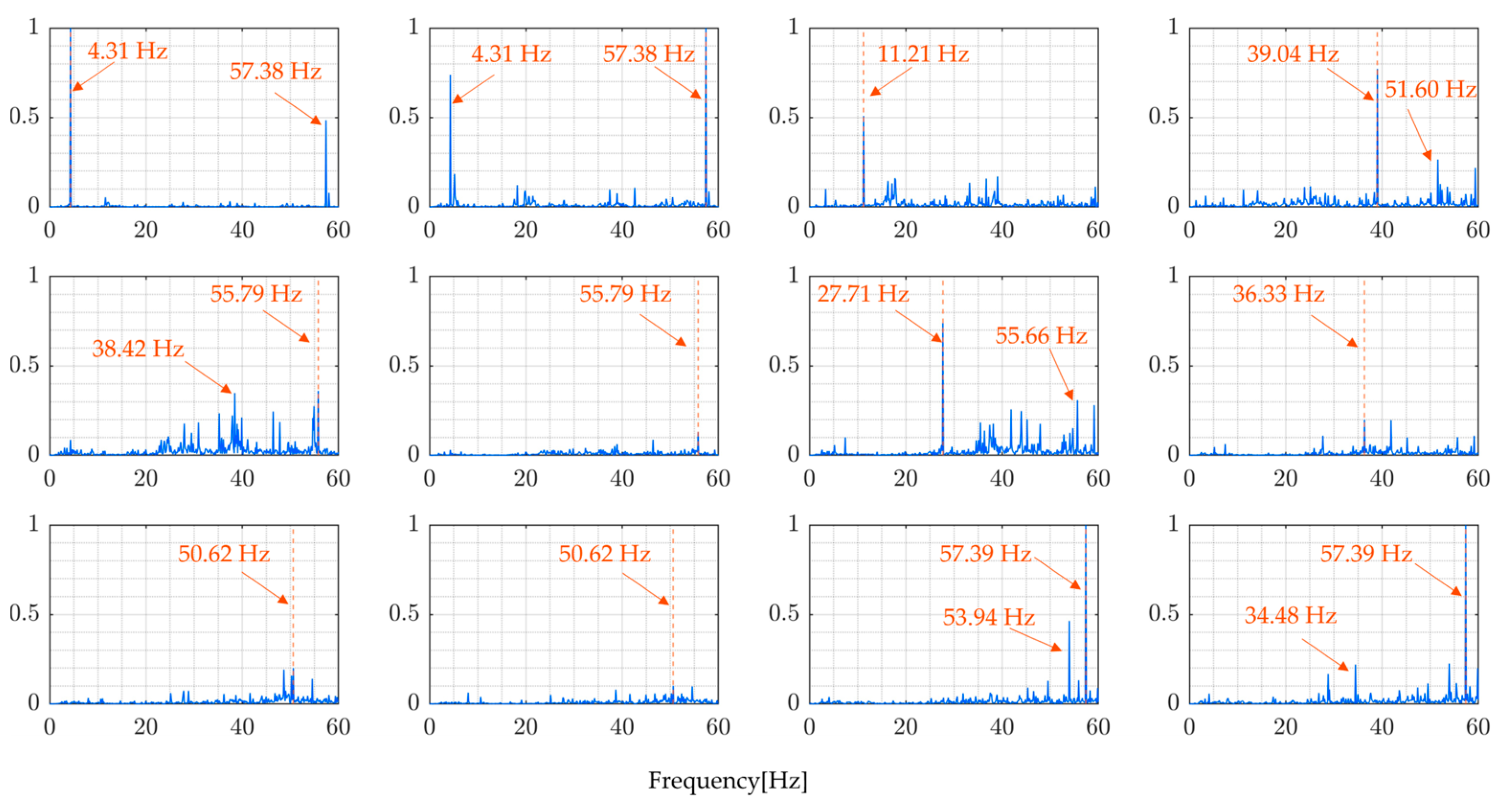
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Azhar, A.S.; Kudus, S.A.; Jamadin, A.; Mustaffa, N.K.; Sugiura, K. Recent vibration-based structural health monitoring on steel bridges: Systematic literature review. Ain Shams Eng. J. 2023, 15, 102501. [Google Scholar] [CrossRef]
- Fawad, M.; Salamak, M.; Poprawa, G.; Koris, K.; Jasinski, M.; Lazinski, P.; Piotrowski, D.; Hasnain, M.; Gerges, M. Automation of structural health monitoring (SHM) system of a bridge using BIMification approach and BIM-based finite element model development. Sci. Rep. 2023, 13, 13215. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Saidin, S.S.; Jamadin, A.; Abdul Kudus, S.; Mohd Amin, N.; Anuar, M.A. An overview: The application of vibration-based techniques in bridge structural health monitoring. Int. J. Concr. Struct. Mater. 2022, 16, 69. [Google Scholar] [CrossRef]
- Nagayama, T.; Reksowardojo, A.P.; Su, D.; Mizutani, T. Bridge natural frequency estimation by extracting the common vibration component from the responses of two vehicles. Eng. Struct. 2017, 150, 821–829. [Google Scholar] [CrossRef]
- Mazzeo, M.; De Domenico, D.; Quaranta, G.; Santoro, R. An efficient automatic modal identification method based on free vibration response and enhanced Empirical Fourier Decomposition technique. Eng. Struct. 2024, 298, 117046. [Google Scholar] [CrossRef]
- Magalhães, F.; Caetano, E.; Cunha, Á.; Flamand, O.; Grillaud, G. Ambient and free vibration tests of the Millau Viaduct: Evaluation of alternative processing strategies. Eng. Struct. 2012, 45, 372–384. [Google Scholar] [CrossRef]
- Lorenzoni, F.; De Conto, N.; da Porto, F.; Modena, C. Ambient and free-vibration tests to improve the quantification and estimation of modal parameters in existing bridges. J. Civ. Struct. Health Monit. 2019, 9, 617–637. [Google Scholar] [CrossRef]
- Casas, J.R.; Moughty, J.J. Bridge damage detection based on vibration data: Past and new developments. Front. Built Environ. 2017, 3, 4. [Google Scholar] [CrossRef]
- Talebinejad, I.; Fischer, C.; Ansari, F. Numerical evaluation of vibration-based methods for damage assessment of cable-stayed bridges. Comput. Aided Civ. Infrastruct. Eng. 2011, 26, 239–251. [Google Scholar] [CrossRef]
- Hearn, G.; Testa, R.B. Modal analysis for damage detection in structures. J. Struct. Eng. 1991, 117, 3042–3063. [Google Scholar] [CrossRef]
- Laory, I.; Trinh, T.N.; Smith, I.F.; Brownjohn, J.M. Methodologies for predicting natural frequency variation of a suspension bridge. Eng. Struct. 2014, 80, 211–221. [Google Scholar] [CrossRef]
- Cho, K.; Cho, J.R. Effect of Temperature on the Modal Variability in Short-Span Concrete Bridges. Appl. Sci. 2022, 12, 9757. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, K.; Ye, Z.; Liu, C.; Lu, K.; Wang, L. Influence of Temperature on the Natural Vibration Characteristics of Simply Supported Reinforced Concrete Beam. Sensors 2021, 21, 4242. [Google Scholar] [CrossRef]
- Whitlow, R.D.; Haskins, R.; McComas, S.L.; Crane, C.K.; Howard, I.L.; McKenna, M.H. Remote bridge monitoring using infrasound. J. Bridge Eng. 2019, 24, 04019023. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef]
- Sakai, M.; Kaneko, N.; Shin, R.; Yamamoto, K. The Application of the SVD-FDD Hybrid Method to Bridge Mode Shape Estimation. In European Workshop on Structural Health Monitoring; Springer International Publishing: Cham, Switzerland, 2022; pp. 575–585. [Google Scholar]
- Yang, Y.Y.; Leu, L.J.; Yamamoto, K. Numerical Verification on Optimal Sensor Placements for Building Structure before and after the Stiffness Decrease. Int. J. Struct. Stab. Dyn. 2023, 23, 2350104. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chang, K.C. Extraction of bridge frequencies from the dynamic response of a passing vehicle enhanced by the EMD technique. J. Sound. Vib. 2009, 322, 718–739. [Google Scholar] [CrossRef]
- Cantero, D.; Hester, D.; Brownjohn, J. Evolution of bridge frequencies and modes of vibration during truck passage. Eng. Struct. 2017, 152, 452–464. [Google Scholar] [CrossRef]
- Giunta, F.; Muscolino, G.; Sofi, A.; Elishakoff, I. Dynamic analysis of Bernoulli-Euler beams with interval uncertainties under moving loads. Procedia Eng. 2017, 199, 2591–2596. [Google Scholar] [CrossRef]
- Van Do, V.N.; Ong, T.H.; Thai, C.H. Dynamic responses of Euler–Bernoulli beam subjected to moving vehicles using isogeometric approach. Appl. Math. Model. 2017, 51, 405–428. [Google Scholar] [CrossRef]
- Colmenares, D.; Andersson, A.; Karoumi, R. Closed-form solution for mode superposition analysis of continuous beams on flexible supports under moving harmonic loads. J. Sound. Vib. 2022, 520, 116587. [Google Scholar] [CrossRef]
- Nagayama, T.; Spencer, B.F., Jr. Structural Health Monitoring Using Smart Sensors; Report Series 001; Newmark Structural Engineering Laboratory: Champaign, IL, USA, 2007. [Google Scholar]
- Yamamoto, K.; Shin, R.; Sakuma, K.; Ono, M.; Okada, Y. Practical application of drive-by monitoring technology to road roughness estimation using buses in service. Sensors 2023, 23, 2004. [Google Scholar] [CrossRef] [PubMed]
- Hasan, K.-F.; Feng, Y.; Tian, Y.-C. Precise GNSS Time Synchronization with Experimental Validation in Vehicular Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 3289–3301. [Google Scholar] [CrossRef]
- Hasan, K.F.; Wang, C.; Feng, Y.; Tian, Y.C. Time synchronization in vehicular ad-hoc networks: A survey on theory and practice. Veh. Commun. 2018, 14, 39–51. [Google Scholar] [CrossRef]
- Yang, Y.B.; Zhang, B.; Wang, T.; Xu, H.; Wu, Y. Two-axle test vehicle for bridges: Theory and applications. Int. J. Mech. Sci. 2019, 152, 51–62. [Google Scholar] [CrossRef]
- Yang, Y.B.; Zhang, B.; Qian, Y.; Wu, Y. Contact-point response for modal identification of bridges by a moving test vehicle. Int. J. Struct. Stab. Dyn. 2018, 18, 1850073. [Google Scholar] [CrossRef]
- Yamamoto, K.; Shin, R.; Mudahemuka, E. Numerical Verification of the Drive-By Monitoring Method for Identifying Vehicle and Bridge Mechanical Parameters. Appl. Sci. 2023, 13, 3049. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Law, S.S.; Samali, B. Indirect bridge modal parameters identification with one stationary and one moving sensors and stochastic subspace identification. J. Sound Vib. 2019, 446, 1–21. [Google Scholar] [CrossRef]
- Yang, F.; Fonder, G.A. An iterative solution method for dynamic response of bridge–vehicles systems. Earthq. Eng. Struct. Dyn. 1996, 25, 195–215. [Google Scholar] [CrossRef]
- González, A. Vehicle-Bridge Dynamic Interaction Using Finite Element Modelling; Intech Open Access Publisher: London, UK, 2010. [Google Scholar]
- Cebon, D. Handbook of Vehicle-Road Interaction; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- González, A.; O’brien, E.J.; Li, Y.Y.; Cashell, K. The use of vehicle acceleration measurements to estimate road roughness. Veh. Syst. Dyn. 2008, 46, 483–499. [Google Scholar] [CrossRef]
- Okabayashi, T.; Yamaguchi, Z. Mean square response analysis of highway bridges under a series of moving vehicles. In Proceedings of the Japan Society of Civil Engineers, Tokyo, Japan, 20 June 1983; Volume 1983, pp. 1–11. [Google Scholar]











| Parameter Name | Symbol | Value | SI Unit |
|---|---|---|---|
| Body mass | 13,560 | kg | |
| Unsprung mass (front) | 751 | kg | |
| Unsprung mass (rear) | 469 | kg | |
| Suspension stiffness (front) | 456 × 103 | N/m | |
| Suspension stiffness (rear) | 41.0 × 104 | N/m | |
| Suspension damping (front) | 29.0 × 103 | Ns/m | |
| Suspension damping (rear) | 24.2 × 103 | Ns/m | |
| Tire stiffness (front) | 431 × 104 | N/m | |
| Tire stiffness (rear) | 431 × 104 | N/m | |
| Distance from the front axle to the center of gravity | 2.00 | m | |
| Distance from the rear axle to the center of gravity | 2.40 | m | |
| Velocity | 10.0 | m/s |
| Bridge Model | Flexural Rigidity [N/m2] | Mass Per Unit Length [kg/m] | Span Length [m] | Damping Coefficient 1 | Damping Coefficient 2 |
|---|---|---|---|---|---|
| Model 1 | 12.369 × 109 | 6624 | 30 | 1.2 × 10−1 | 1.0 × 10−6 |
| Model 2 | 6.0850 × 109 | 2417 | 20 | 1.2 × 10−1 | 1.0 × 10−6 |
| Model 3 | 12.170 × 109 | 2583 | 30 | 1.2 × 10−1 | 1.0 × 10−6 |
| Model 4 | 23.920 × 109 | 2667 | 40 | 1.2 × 10−1 | 1.0 × 10−6 |
| First Mode (Hz) | Second Mode (Hz) | Third Mode (Hz) | Fourth Mode (Hz) | |
|---|---|---|---|---|
| Vehicle | 1.210 | 2.549 | 12.694 | 15.980 |
| Bridge Model 1 | 2.259 | 9.039 | 20.338 | 36.156 |
| Bridge Model 2 | 6.231 | 24.924 | 56.078 | 99.695 |
| Bridge Model 3 | 3.589 | 14.359 | 32.307 | 57.435 |
| Bridge Model 4 | 2.940 | 11.761 | 26.462 | 47.044 |
| Axle | Dominant Frequency Order | Bridge Model 1 | Bridge Model 2 | Bridge Model 3 | Bridge Model 4 |
|---|---|---|---|---|---|
| Front Axle | First | 3.4 | 3.4 | 3.4 | 3.4 |
| Second | 8.15 | 8.15 | 8.15 | 8.15 | |
| Third | 15.15 | 15.15 | 15.15 | 15.15 | |
| Forth | 20.75 | 20.75 | 20.75 | 20.75 | |
| Rear Axle | First | 2.25 | 2.25 | 2.25 | 2.25 |
| Second | 8.15 | 8.15 | 8.15 | 8.15 | |
| Third | 15.15 | 15.15 | 15.15 | 15.15 | |
| Forth | 20.75 | 20.75 | 20.75 | 20.75 |
| Axle | Dominant Frequency Order | Bridge Model 1 | Bridge Model 2 | Bridge Model 3 | Bridge Model 4 |
|---|---|---|---|---|---|
| Front Axle | First | 10.65 | 10.65 | 10.65 | 10.65 |
| Second | 11.85 | 11.85 | 11.85 | 11.85 | |
| Third | 13.37 | 13.37 | 13.37 | 13.37 | |
| Forth | - | - | - | - | |
| Rear Axle | First | 15.15 | 15.15 | 15.15 | 15.15 |
| Second | 16.65 | 16.65 | 16.65 | 16.65 | |
| Third | 17.25 | 17.25 | 17.25 | 17.25 | |
| Forth | - | - | - | - |
| Round | Sensor Number | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | |
| 1 | 17.36 | 12.07 | 12.07 | 12.07 | 12.07 | 17.00 | 17.36 | 17.36 | 12.07 | 12.07 | 17.36 | 17.36 |
| 2 | 13.12 | 13.12 | 12.26 | 12.26 | 12.26 | 12.26 | 16.80 | 16.68 | 12.26 | 12.14 | 12.26 | 16.80 |
| 3 | 17.41 | 17.41 | 12.07 | 12.07 | 17.41 | 17.07 | 17.41 | 17.41 | 11.96 | 12.07 | - | 17.41 |
| 4 | 16.98 | 16.98 | 16.98 | 11.97 | 16.98 | 16.98 | 16.98 | 16.98 | 11.97 | 11.97 | - | 16.98 |
| Round | Modal Order | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 11.82 | 17.36 | 25.37 | 27.71 | 12.07 | - | - | - | - | - | - | - |
| 2 | 3.07 | 12.39 | 16.93 | 23.67 | 33.61 | - | - | - | - | - | - | - |
| 3 | 3.02 | 13.58 | 26.35 | - | - | - | - | - | - | - | - | - |
| 4 | 7.57 | 12.34 | 17.34 | 21.62 | 23.70 | - | - | - | - | - | - | - |
| Round | Modal Order | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 4.31 | 5.17 | 11.21 | 14.16 | 38.42 | 41.87 | 49.51 | - | - | - | - | - |
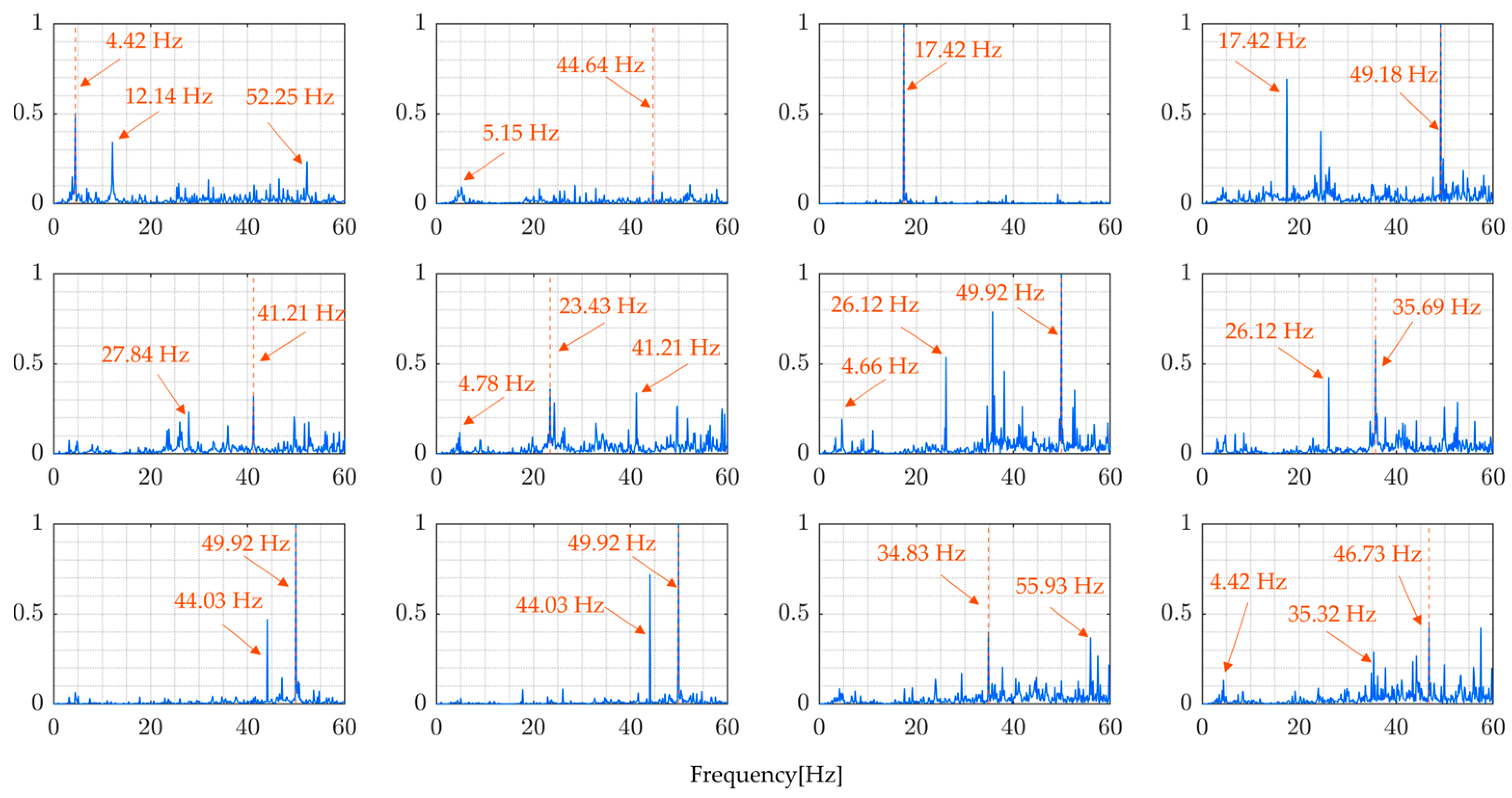
| 2 | 4.42 | 5.15 | 11.65 | 17.42 | 26.12 | 35.69 | 49.92 | - | - | - | - | - |
| 3 | 3.02 | 5.11 | 11.84 | 16.95 | 37.96 | 36.80 | 48.76 | - | - | - | - | - |
| 4 | 4.28 | 5.01 | 11.84 | 17.34 | 25.16 | 38.11 | 46.78 | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mudahemuka, E.; Miyagi, M.; Shin, R.; Kaneko, N.; Okada, Y.; Yamamoto, K. Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data. Sensors 2024, 24, 1060. https://doi.org/10.3390/s24041060
Mudahemuka E, Miyagi M, Shin R, Kaneko N, Okada Y, Yamamoto K. Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data. Sensors. 2024; 24(4):1060. https://doi.org/10.3390/s24041060
Chicago/Turabian StyleMudahemuka, Eugene, Masatatsu Miyagi, Ryota Shin, Naoki Kaneko, Yukihiko Okada, and Kyosuke Yamamoto. 2024. "Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data" Sensors 24, no. 4: 1060. https://doi.org/10.3390/s24041060
APA StyleMudahemuka, E., Miyagi, M., Shin, R., Kaneko, N., Okada, Y., & Yamamoto, K. (2024). Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data. Sensors, 24(4), 1060. https://doi.org/10.3390/s24041060






