Adaptive Ant Colony Optimization with Sub-Population and Fuzzy Logic for 3D Laser Scanning Path Planning
Abstract
1. Introduction
1.1. Background
1.2. Ant Colony Optimization
1.3. Contributions of This Manuscript
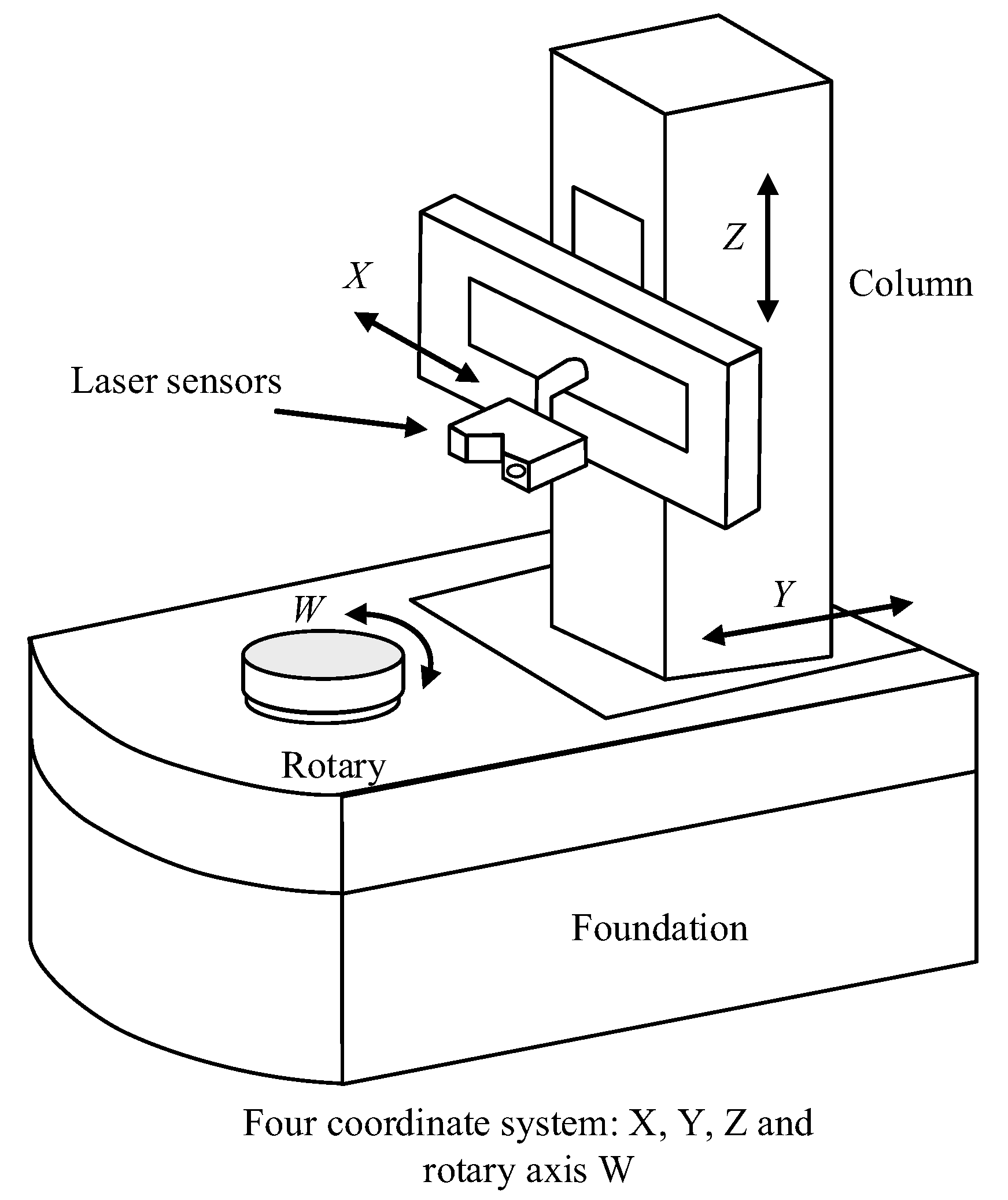
- This manuscript establishes three coordinate systems based on a laser scanning four-coordinate measuring machine. Moreover, it inversely solves the machine readings of each axis of the object to be measured in normal measuring attitude according to the conversion between coordinate systems. Furthermore, we constructed the nominal distance matrix by utilizing the machine readings of each axis of all the points to be measured on the object to be measured in the optimal measuring attitude.
- An adaptive ant colony with sub-population algorithm was designed. Ant colonies can simulate human social learning through sub-population and adaptive parameter strategies, as well as improve the convergence performance of ant populations by the guidance of transcendental knowledge.
- A 3-opt neighborhood structure was implemented to alter the course of the ant colony in order to enhance the variety of the population. The algorithm’s guidance for optimizing the next-generation population was enhanced by applying a fuzzy logic strategy to dynamically adjust pheromone volatilization parameters. The TSP benchmark test confirmed the effectiveness of the proposed SFACO algorithm.
- The proposed SFACO algorithm is utilized to identify the most efficient planning path for the intricate 3D laser scanning path planning problem.
2. The Design of the Laser Measurement Attitude
2.1. Establishing and Converting the Coordinate System
2.2. Normal Measurement Attitude Establishment
2.3. Nominal Distance Matrix Construction
3. Adaptive Ant Colony with Sub-Population and Fuzzy Logic (SFACO) Algorithm
3.1. Population Diversity
3.2. Sub-Population Strategies
3.3. Adaptive Heuristic Factor
3.4. Dynamic Neighborhood Structures
3.5. Fuzzy Logic Control
3.6. SFACO Algorithm Steps
4. Simulation Experiment Verification
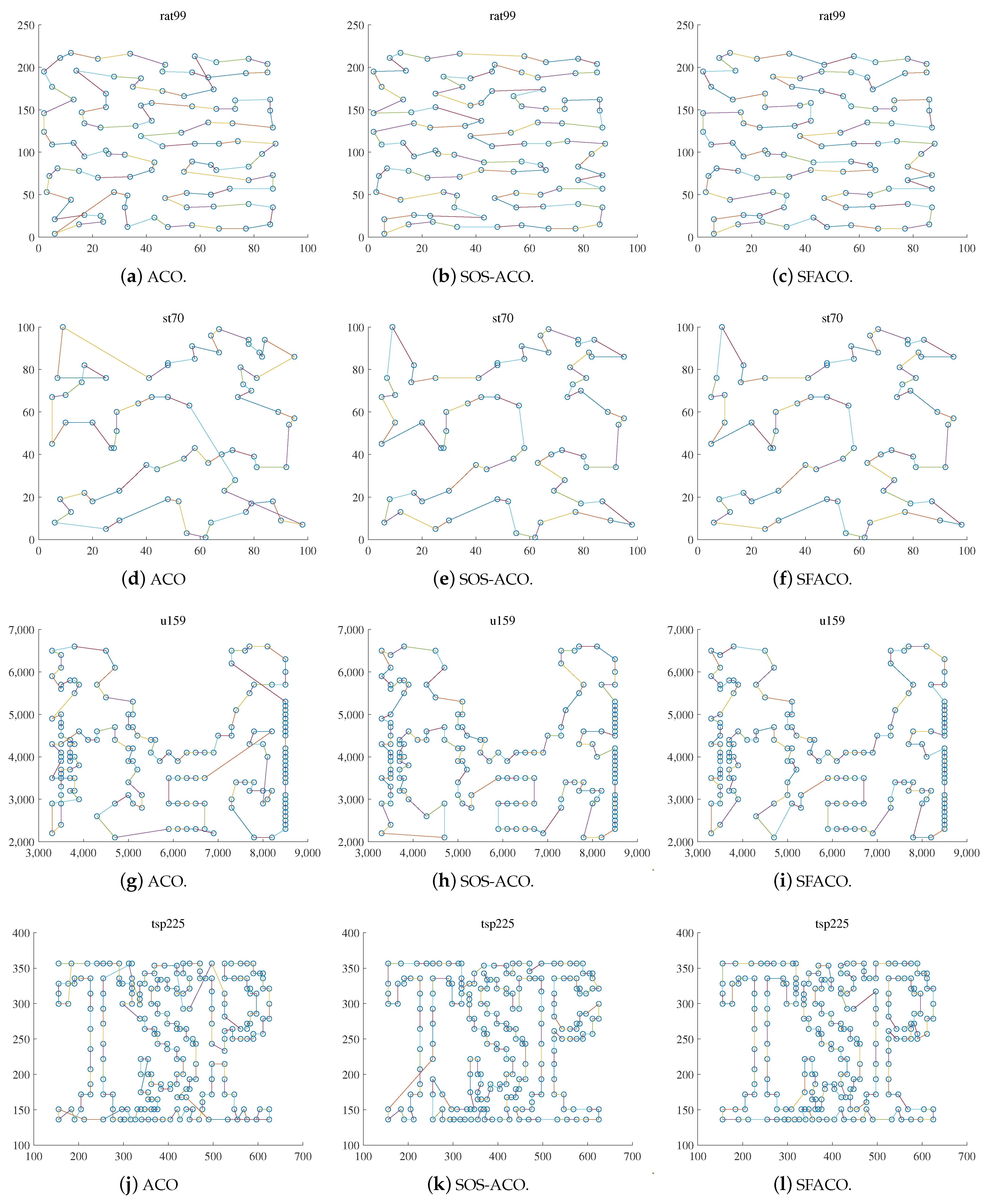
4.1. TSP Simulation Experiment Based on the SFACO Approach
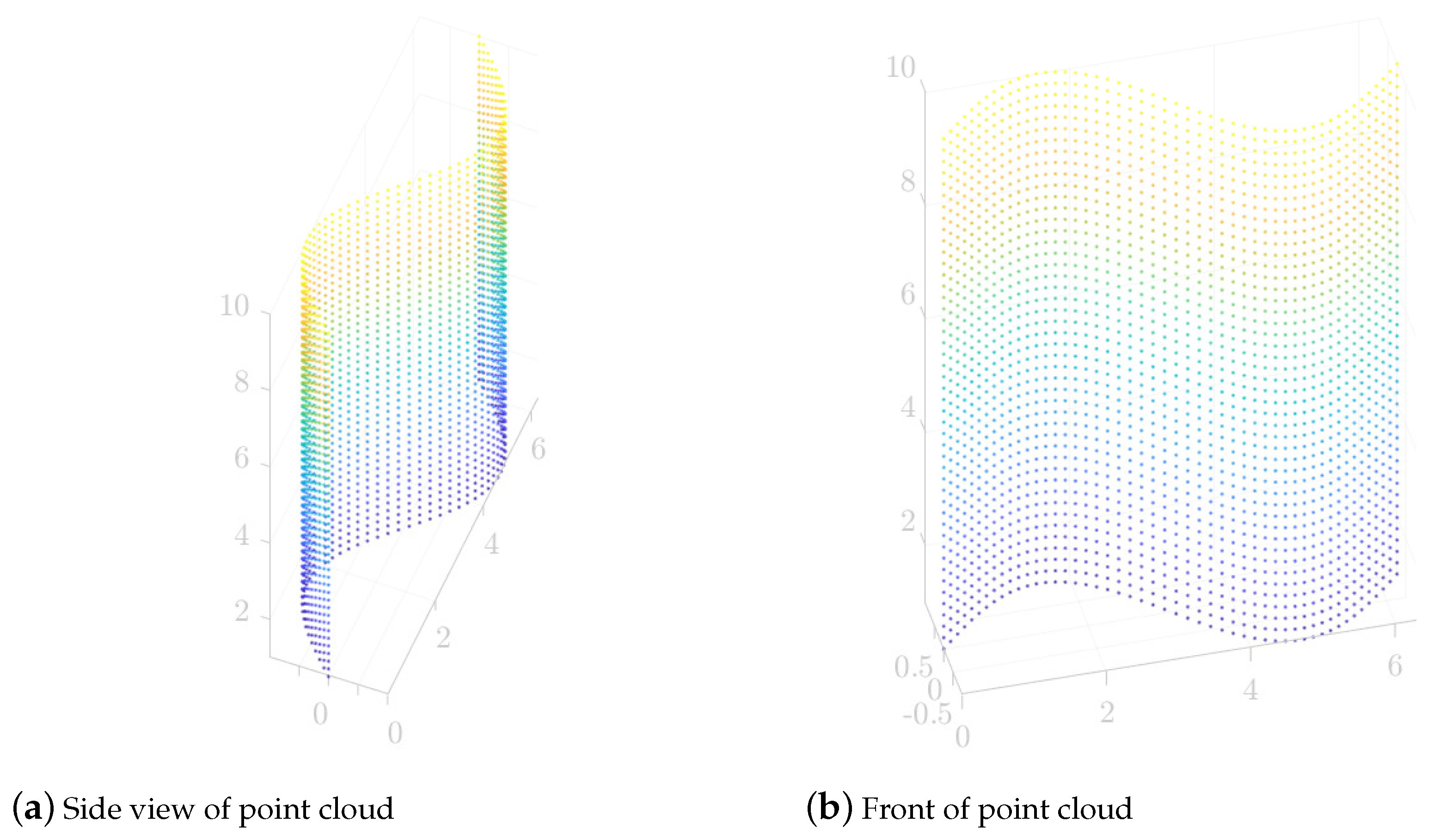
4.2. Simulation Application of Sliced Surface Laser Scanning When Based on the SFACO Algorithm
4.3. Analysis of the SFACO Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Chen, Z.; Yang, P.; Huang, X.; Guo, Z.; Chang, Z.; Wang, X.; Zhang, P. Design optical surface as the measurement datum in measuring gear tooth flank by symmetrical laser interferometer. Opt. Laser Technol. 2024, 169, 110034. [Google Scholar] [CrossRef]
- Zolfaghari, P.; Khodapanahandeh, M.; Urey, H.; Ferhanoglu, O. Cascaded laser scanning towards high-resolution LiDAR. Opt. Laser Technol. 2024, 168, 109906. [Google Scholar] [CrossRef]
- Ding, L.J.; Dai, S.G.; Mu, P.A. CAD-Based Path Planning for 3D Laser Scanning of Complex Surface. Procedia Comput. Sci. 2016, 92, 526–535. [Google Scholar] [CrossRef]
- Sedao, X.; Steinlin, S.; Becker, J.M.; Fournel, T. Ultrafast Laser Surface Functionalization and Route to Industrial Applications: Computer-Vision-Based Path Planning. In Proceedings of the 2023 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 26–30 June 2023; p. cm_p_15. [Google Scholar]
- Diao, S.; Yang, Y.; Cui, G.; Chen, Y. Complex parts machining path planning through cross-source point cloud processing. Comput. Commun. 2023, 203, 48–59. [Google Scholar] [CrossRef]
- Zong, Y.; Liang, J.; Pai, W.; Ye, M.; Ren, M.; Zhao, J.; Tang, Z.; Zhang, J. A high-efficiency and high-precision automatic 3D scanning system for industrial parts based on a scanning path planning algorithm. Opt. Lasers Eng. 2022, 158, 107176. [Google Scholar] [CrossRef]
- Huang, P.; Lin, L.; Xu, K.; Huang, H. Autonomous Outdoor Scanning via Online Topological and Geometric Path Optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3682–3695. [Google Scholar] [CrossRef]
- Yan, Y.; He, G.; Sang, Y.; Yao, C.; Wang, S.; Chen, F. A two-module automated scanning inspection planning methodology for complex surfaces on coordinate measuring machine. Measurement 2022, 202, 111827. [Google Scholar] [CrossRef]
- Pop, P.C.; Cosma, O.; Sabo, C.; Sitar, C.P. A comprehensive survey on the generalized traveling salesman problem. Eur. J. Oper. Res. 2023, 314, 819–835. [Google Scholar] [CrossRef]
- Thong-ia, S.; Champrasert, P. Gene-Ants: Ant Colony Optimization with Genetic Algorithm for Traveling Salesman Problem Solving. In Proceedings of the 2023 International Technical Conference on Circuits/Systems, Computers, and Communications (ITC-CSCC), Jeju, Republic of Korea, 25–28 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, H.; Gu, J.; Chen, H.; Deng, W. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism. Eng. Appl. Artif. Intell. 2022, 114, 105139. [Google Scholar] [CrossRef]
- Cui, Y.; Zhong, J.; Yang, F.; Li, S.; Li, P. Multi-Subdomain Grouping-Based Particle Swarm Optimization for the Traveling Salesman Problem. IEEE Access 2020, 8, 227497–227510. [Google Scholar] [CrossRef]
- Wu, M.; Ou, X.; Lu, Y.; Li, W.; Yu, D.; Liu, Z.; Ji, C. Heterogeneous Cuckoo Search-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2023, 62, 1–16. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W.; Wang, X.; Qiu, Y.; Shen, W. Adaptive gradient descent enabled ant colony optimization for routing problems. Swarm Evol. Comput. 2022, 70, 101046. [Google Scholar] [CrossRef]
- Reda, M.; Onsy, A.; Elhosseini, M.A.; Haikal, A.Y.; Badawy, M. A discrete variant of cuckoo search algorithm to solve the Travelling Salesman Problem and path planning for autonomous trolley inside warehouse. Knowl.-Based Syst. 2022, 252, 109290. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J. A discrete cuckoo search algorithm for traveling salesman problem and its application in cutting path optimization. Comput. Ind. Eng. 2022, 169, 108157. [Google Scholar] [CrossRef]
- Pal, K.; Sachan, S.; Gholian-Jouybari, F.; Hajiaghaei-Keshteli, M. An analysis of the security of multi-area power transmission lines using fuzzy-ACO. Expert Syst. Appl. 2023, 224, 120070. [Google Scholar] [CrossRef]
- Sui, F.; Tang, X.; Dong, Z.; Gan, X.; Luo, P.; Sun, J. ACO+PSO+A∗: A bi-layer hybrid algorithm for multi-task path planning of an AUV. Comput. Ind. Eng. 2023, 175, 108905. [Google Scholar] [CrossRef]
- Chuang, Y.T.; Hung, Y.T. A real-time and ACO-based offloading algorithm in edge computing. J. Parallel Distrib. Comput. 2023, 179, 104703. [Google Scholar] [CrossRef]
- Rivera, G.; Cruz-Reyes, L.; Fernandez, E.; Gomez-Santillan, C.; Rangel-Valdez, N.; Coello Coello, C.A. An ACO-based Hyper-heuristic for Sequencing Many-objective Evolutionary Algorithms that Consider Different Ways to Incorporate the DM’s Preferences. Swarm Evol. Comput. 2023, 76, 101211. [Google Scholar] [CrossRef]
- Das, M.; Roy, A.; Maity, S.; Kar, S. A Quantum-inspired Ant Colony Optimization for solving a sustainable four-dimensional traveling salesman problem under type-2 fuzzy variable. Adv. Eng. Inform. 2023, 55, 101816. [Google Scholar] [CrossRef]
- Liu, C.; Wu, L.; Xiao, W.; Li, G.; Xu, D.; Guo, J.; Li, W. An improved heuristic mechanism ant colony optimization algorithm for solving path planning. Knowl.-Based Syst. 2023, 271, 110540. [Google Scholar] [CrossRef]
- Ren, T.; Luo, T.; Jia, B.; Yang, B.; Wang, L.; Xing, L. Improved ant colony optimization for the vehicle routing problem with split pickup and split delivery. Swarm Evol. Comput. 2023, 77, 101228. [Google Scholar] [CrossRef]
- Pu, Y.F.; Siarry, P.; Zhu, W.Y.; Wang, J.; Zhang, N. Fractional-Order Ant Colony Algorithm: A Fractional Long Term Memory Based Cooperative Learning Approach. Swarm Evol. Comput. 2022, 69, 101014. [Google Scholar] [CrossRef]
- Pu, Y.; Song, J.; Wu, M.; Xu, X.; Wu, W. Node location using cuckoo search algorithm with grouping and drift strategy for WSN. Phys. Commun. 2023, 59, 102088. [Google Scholar] [CrossRef]
- E, J.; Liu, J.; Wan, Z. A novel adaptive algorithm of particle swarm optimization based on the human social learning intelligence. Swarm Evol. Comput. 2023, 80, 101336. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.; Zhang, X. Adaptive dynamic neighborhood hybrid cuckoo search algorithm for solving traveling salesman problems. Comput. Eng. Appl. 2018, 54, 42–50. [Google Scholar]
- Ou, X.; Wu, M.; Pu, Y.; Tu, B.; Zhang, G.; Xu, Z. Cuckoo search algorithm with fuzzy logic and Gauss–Cauchy for minimizing localization error of WSN. Appl. Soft Comput. 2022, 125, 109211. [Google Scholar] [CrossRef]
- TSPLIB. TSPLIB Standard Test Set for TSP Problem of Universität Heidelberg 2013. Available online: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95 (accessed on 23 July 2023).
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Boston, MA, USA, 1975. [Google Scholar]
- Yip, P.; Pao, Y.H. Combinatorial optimization with use of guided evolutionary simulated annealing. IEEE Trans. Neural Netw. 1995, 6, 290–295. [Google Scholar] [CrossRef]
- Couceiro, M.; Sivasundaram, S. Novel fractional order particle swarm optimization. Appl. Math. Comput. 2016, 283, 36–54. [Google Scholar] [CrossRef]
- Osaba, E.; Yang, X.S.; Diaz, F.; Lopez-Garcia, P.; Carballedo, R. An improved discrete bat algorithm for symmetric and asymmetric Traveling Salesman Problems. Eng. Appl. Artif. Intell. 2016, 48, 59–71. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant colony optimization for traveling salesman problem based on parameters optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Stutzle, T.; Hoos, H. MAX-MIN Ant System and local search for the traveling salesman problem. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC ’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 309–314. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Population size | |
| Initial value of the pheromone importance factor | |
| Initial value of the heuristic function importance factor | |
| Initial value of the pheromone volatilization factor |
| GA | ESA | FPSO | IBA | MMAS | ACO | SOS-ACO | SFACO | ||
|---|---|---|---|---|---|---|---|---|---|
| avg. | - | - | 33,585.70 | - | 33,576.40 | 35,834.32 | 33,539.49 | 33,528.40 | |
| att48 | best | - | - | 33,522.00 | - | 33,522.00 | 34,845.64 | 33,523.71 | 33,522.00 |
| std | - | - | - | - | - | 481.26 | 15.78 | 12.80 | |
| avg. | 7542.00 | 7542.00 | 7542.00 | 7542.00 | 7596.00 | 8141.72 | 7544.37 | 7542.00 | |
| berlin52 | best | 7542.00 | 7542.00 | 7542.00 | 7542.00 | 7542.00 | 7933.38 | 7544.37 | 7542.00 |
| std | 0.00 | 0.00 | 0.00 | 0.00 | 54.39 | 94.50 | 0.00 | 0.00 | |
| avg. | - | - | 6545.40 | - | 6552.00 | 6908.25 | 6589.38 | 6568.30 | |
| ch150 | best | - | - | 6528.00 | - | 6528.00 | 6852.33 | 6582.31 | 6544.00 |
| std | - | - | 17.45 | - | 24.09 | 61.35 | 7.73 | 13.11 | |
| avg. | 673.80 | 658.40 | 636.50 | 646.40 | 636.10 | 705.52 | 648.80 | 638.50 | |
| eil101 | best | 655.00 | 650.00 | 630.00 | 634.00 | 629.00 | 692.07 | 644.95 | 629.00 |
| std | 12.50 | 4.40 | 7.60 | - | 7.18 | 9.16 | 3.38 | 2.20 | |
| avg. | 21,510.40 | 21,170.40 | 20,812.40 | 21,050.00 | 20,812.70 | 22,115.20 | 20,798.85 | 20,789.30 | |
| kroC100 | best | 20,861.00 | 20,749.00 | 20,749.00 | 20,749.00 | 20,749.00 | 21,864.01 | 20,780.22 | 20749.00 |
| std | 390.20 | 188.70 | 63.59 | - | 63.90 | 146.73 | 20.76 | 14.21 | |
| avg. | - | - | 14,454.40 | - | 14,458.60 | 16,022.69 | 14,423.45 | 14,404.00 | |
| lin105 | best | - | - | 14,379.00 | - | 14,379.00 | 15,754.01 | 14,406.12 | 14,379.00 |
| std | - | - | 73.77 | - | 80.04 | 174.09 | 17.35 | 26.92 | |
| avg. | - | - | 109,470.50 | - | 109,646.00 | 123,569.31 | 108,326.58 | 108,295.40 | |
| pr76 | best | - | - | 108,159.00 | - | 108,159.00 | 121,710.56 | 108,304.51 | 108,159.00 |
| std | - | - | 1327.40 | - | 1507.44 | 1162.73 | 34.36 | 50.85 | |
| avg. | 60,591.40 | 58,807.30 | 58,679.30 | 58,537.00 | 58,560.30 | 61,315.75 | 58,615.95 | 58,602.10 | |
| pr144 | best | 58,599.00 | 58,574.00 | 58,537.00 | 58,537.00 | 58,537.00 | 60,877.45 | 58,602.32 | 58,537.00 |
| std | 2342.80 | 220.90 | 142.65 | - | 23.31 | 203.68 | 22.13 | 16.72 | |
| avg. | - | - | 1215.20 | - | 1214.50 | 1333.32 | 1231.54 | 1218.70 | |
| rat99 | best | - | - | 1211.00 | - | 1212.00 | 1311.34 | 1223.12 | 1211.00 |
| std | - | - | 4.21 | - | 3.51 | 11.30 | 6.32 | 6.31 | |
| avg. | 709.80 | 682.10 | 682.30 | 679.00 | 682.60 | 742.58 | 677.53 | 676.00 | |
| st70 | best | 675.00 | 675.00 | 675.00 | 675.00 | 675.00 | 727.32 | 677.11 | 675.00 |
| std | 5.70 | 3.90 | 7.38 | - | 7.69 | 8.63 | 0.63 | 0.77 | |
| avg. | - | - | 42,202.50 | - | 42,159.50 | 46,244.16 | 42,246.48 | 42,187.80 | |
| u159 | best | - | - | 42,080.00 | - | 42,080.00 | 45,793.52 | 42,193.08 | 42,080.00 |
| std | - | - | 122.86 | - | 79.65 | 294.47 | 44.64 | 55.64 | |
| avg. | - | - | 3972.10 | - | 3971.00 | 4291.19 | 3987.72 | 4026.85 | |
| tsp225 | best | - | - | 3916.00 | - | 3919.00 | 4246.60 | 3970.64 | 3985.00 |
| std | - | - | 56.90 | - | 55.77 | 30.42 | 10.49 | 16.69 |
| Before | After | |||||
|---|---|---|---|---|---|---|
| 0.000000 | 0.000000 | 1 | −0.18109 | 14.99851 | 1 | 0.775792 |
| 0.128228 | 0.127877 | 1 | −0.36066 | 14.99310 | 1 | 0.760739 |
| 0.256457 | 0.253655 | 1 | −0.53710 | 14.98055 | 1 | 0.736746 |
| 0.384685 | 0.375267 | 1 | −0.70865 | 14.95735 | 1 | 0.703068 |
| 0.512913 | 0.490718 | 1 | −0.87329 | 14.91959 | 1 | 0.658720 |
| 0.641141 | 0.598111 | 1 | −1.02846 | 14.86301 | 1 | 0.602535 |
| 0.769370 | 0.695683 | 1 | −1.17090 | 14.78324 | 1 | 0.533310 |
| 0.897598 | 0.781831 | 1 | −1.29637 | 14.67644 | 1 | 0.450083 |
| 1.025826 | 0.855143 | 1 | −1.39973 | 14.54039 | 1 | 0.352579 |
| 1.154054 | 0.914413 | 1 | −1.47562 | 14.37610 | 1 | 0.241807 |
| 1.282283 | 0.958668 | 1 | −1.52020 | 14.18923 | 1 | 0.120598 |
| 1.410511 | 0.987182 | 1 | −1.53354 | 13.99009 | 1 | 3.147889 |
| 1.538739 | 0.999486 | 1 | −1.60814 | 13.90959 | 1 | 3.199096 |
| 1.666968 | 0.995379 | 1 | −1.58971 | 13.71474 | 1 | 3.323844 |
| 1.795196 | 0.974928 | 1 | −1.56275 | 13.53582 | 1 | 3.440314 |
| Avg. | Best | Std. | |
|---|---|---|---|
| ACO | 444.6934 | 441.4736 | 2.5467 |
| SOS-ACO | 407.2981 | 407.1513 | 0.1304 |
| SFACO | 406.3894 | 405.9972 | 0.2838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Pu, Y.; Xu, X. Adaptive Ant Colony Optimization with Sub-Population and Fuzzy Logic for 3D Laser Scanning Path Planning. Sensors 2024, 24, 1098. https://doi.org/10.3390/s24041098
Song J, Pu Y, Xu X. Adaptive Ant Colony Optimization with Sub-Population and Fuzzy Logic for 3D Laser Scanning Path Planning. Sensors. 2024; 24(4):1098. https://doi.org/10.3390/s24041098
Chicago/Turabian StyleSong, Junfang, Yuanyuan Pu, and Xiaoyu Xu. 2024. "Adaptive Ant Colony Optimization with Sub-Population and Fuzzy Logic for 3D Laser Scanning Path Planning" Sensors 24, no. 4: 1098. https://doi.org/10.3390/s24041098
APA StyleSong, J., Pu, Y., & Xu, X. (2024). Adaptive Ant Colony Optimization with Sub-Population and Fuzzy Logic for 3D Laser Scanning Path Planning. Sensors, 24(4), 1098. https://doi.org/10.3390/s24041098





