Enhanced Robot Motion Block of A-Star Algorithm for Robotic Path Planning
Abstract
1. Introduction
- This paper proposes an adaptive cost function for robot movement, which keeps track of the goal node, adaptively calculates the movement costs for quickly getting to the goal node, and reduces the number of search nodes.
- An optimal RMB with an adaptive cost function is proposed to improve the performance of robot navigation by significantly reducing the searches of less impactful and redundant nodes. The reduced number of search nodes significantly improves the time complexity and the overall performance of the A* algorithm.
- In this paper, a comprehensive experiment is conducted by customizing a large open-source dataset, including various types of grid maps, various map sizes, and several sets of source-to-destination nodes. This experiment validates the proposed model in terms of efficiency, robustness, and scalability.
- Also, conducting experiments using the ROS platform and Gazebo simulator, this paper adds empirical evidence, strengthening the contributions and demonstrating the generalizability of the proposed model in real-world scenarios.
- The quantifiable results, revealing substantial improvements in the number of search nodes and time complexity, distinctly position the proposed model as an advancement over conventional A* and other state-of-the-art algorithms.
2. Related Work
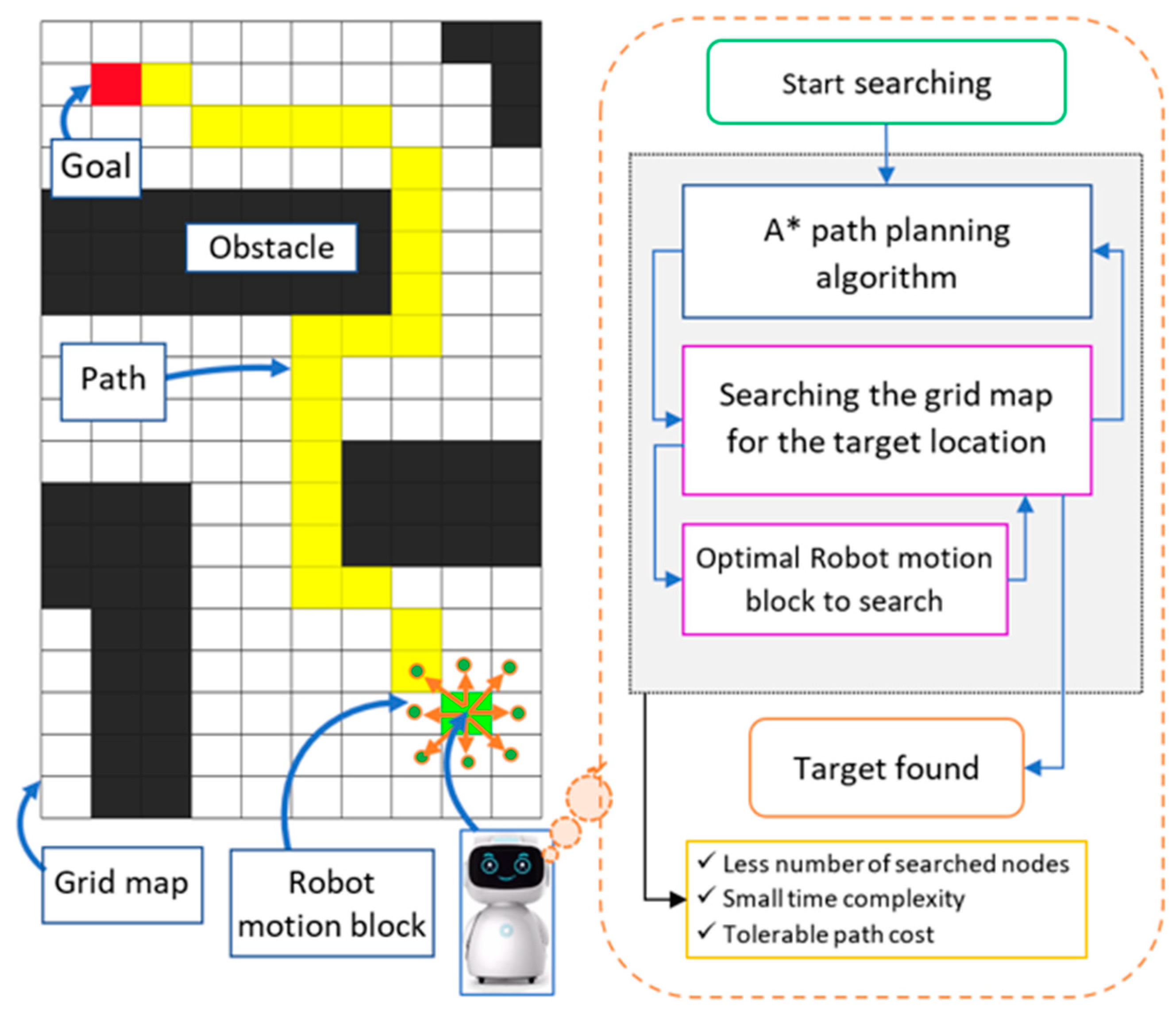
3. Proposed Model
3.1. A* Path-Planning Algorithm with Proposed RMB
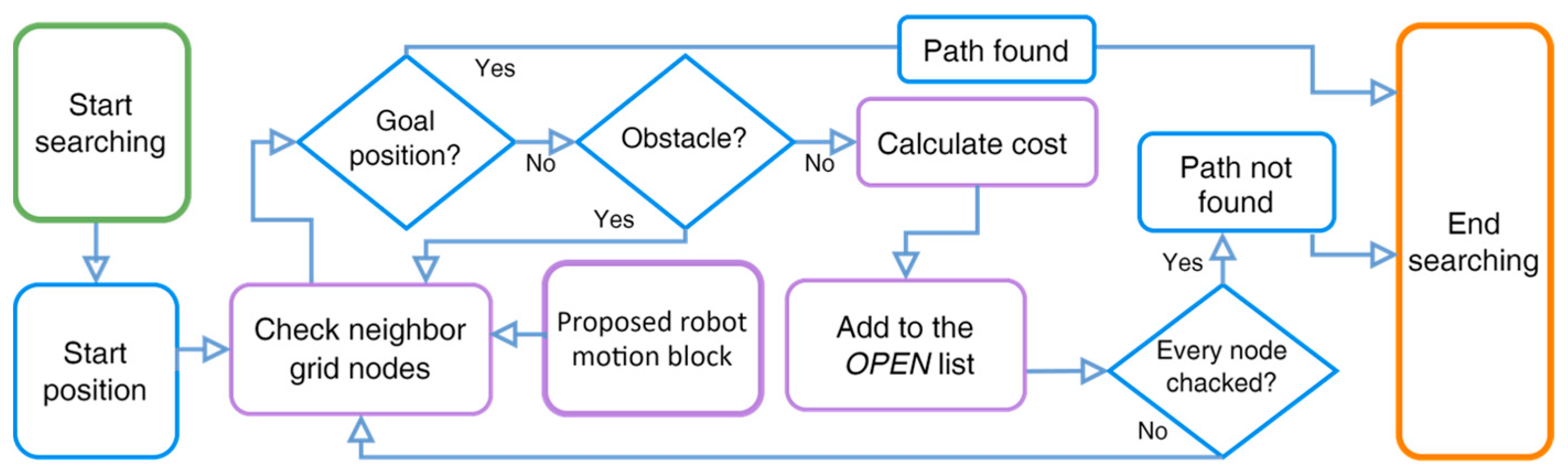
- To begin the A* algorithm with the proposed robot motion block, initialize the start node with a cost of 0 and add it to an list of nodes to be considered for expansion.
- Check the neighboring grid nodes for the goal node with the proposed robot motion block explained in Section 3.2. If the current node is an obstacle node , ignore it, and add only the end nodes in the list. While the list is not empty, select the node with the lowest total cost, and remove it from the list.
- Here, denotes an heuristic function that uses Euclidean distance,
- If the selected node is the goal node, stop the search and return the optimal path. Generate all possible successors of the selected node and calculate their costs and heuristic values.
- For each successor node, update its cost and heuristic value if it has not already been visited or has a higher cost. Add each updated successor node to the list if it is not already in the list.
- If a successor node is already in the list, update its cost and heuristic value if the new values are lower than the previous values. If a successor node is already in the visited list (i.e., has already been expanded), ignore it.
- If all nodes in the motion block cells have been checked, return to step II and repeat the steps until every node on the grid map has been checked.
- Terminate the algorithm when the goal node is found or the list is empty.
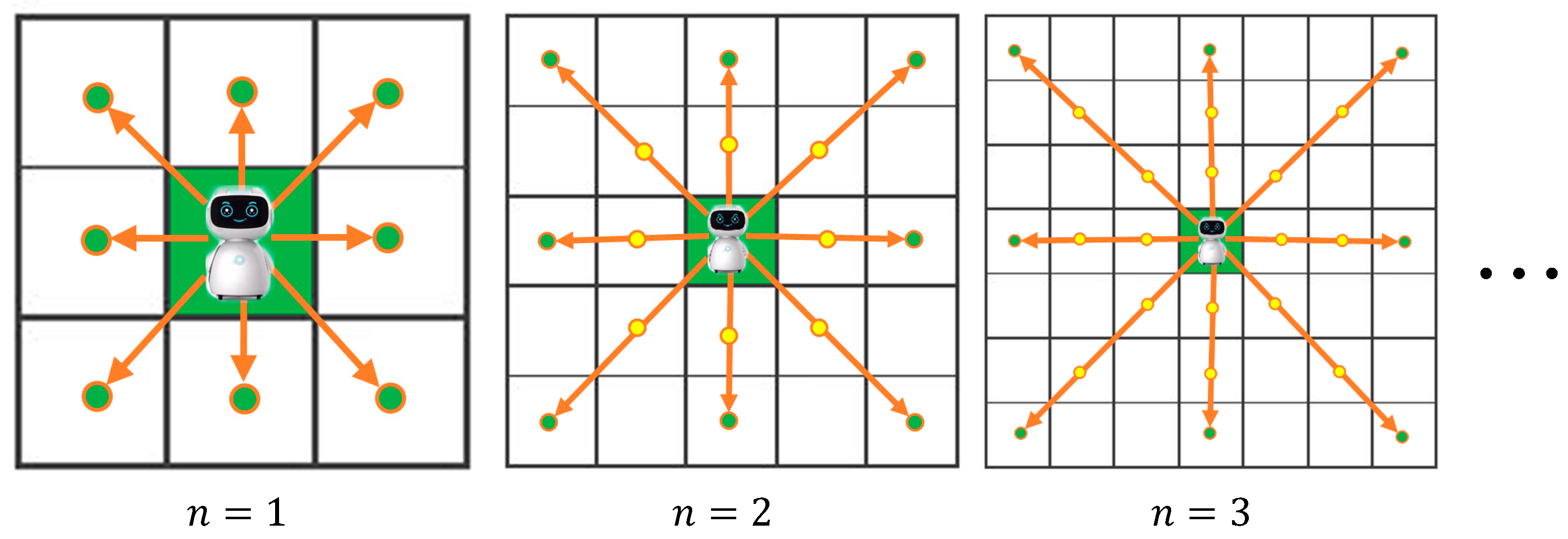
3.2. Proposed Robot Motion Block with an Adaptive Cost-Function
- = Cardinal movement cost.
- = Diagonal movement cost.
- = The cost associated with cardinal movements.
- = The cost associated with diagonal movements.
- = Adaptive cost.
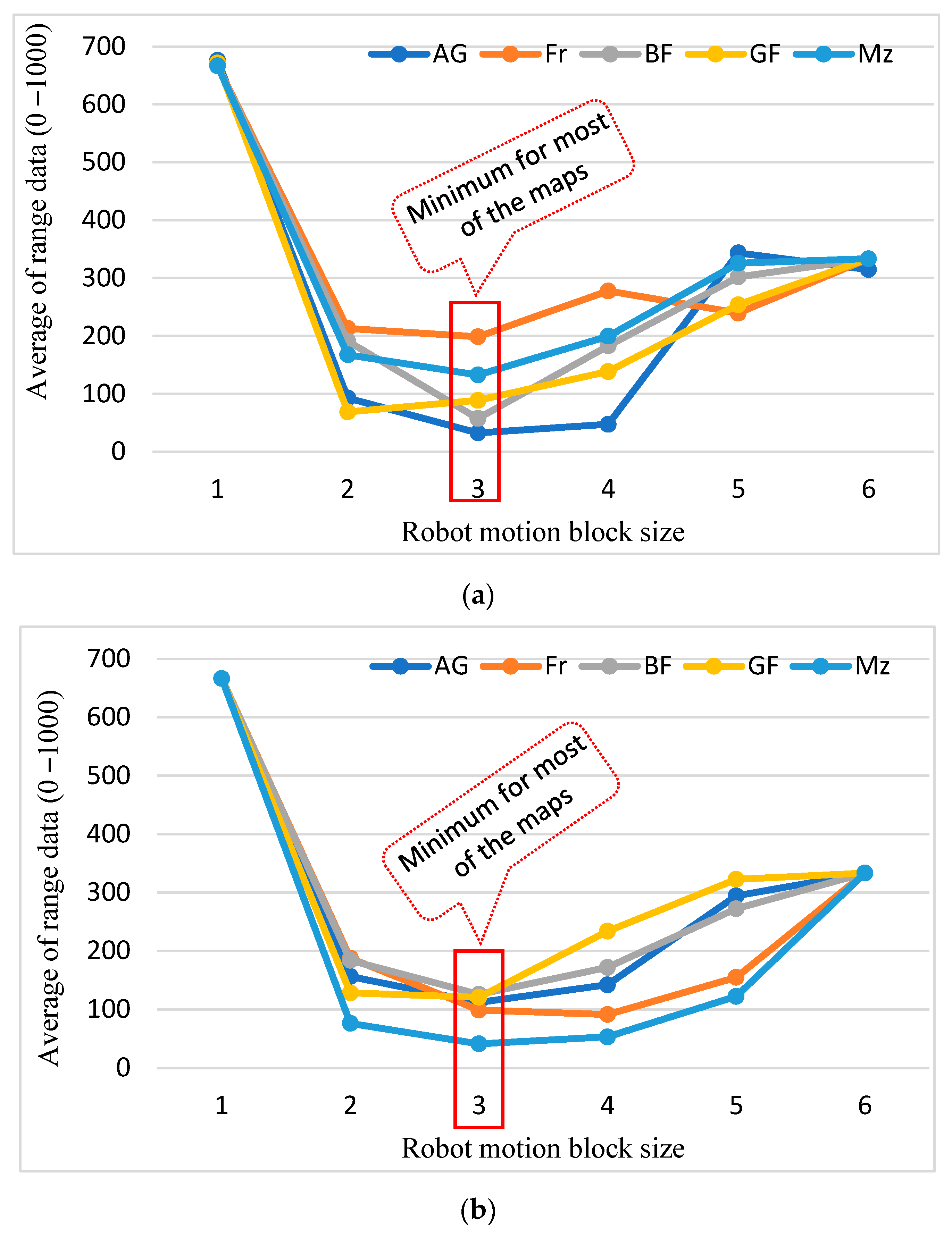
3.3. Optimal Robot Motion Block Selection
4. Experimental Results and Discussion
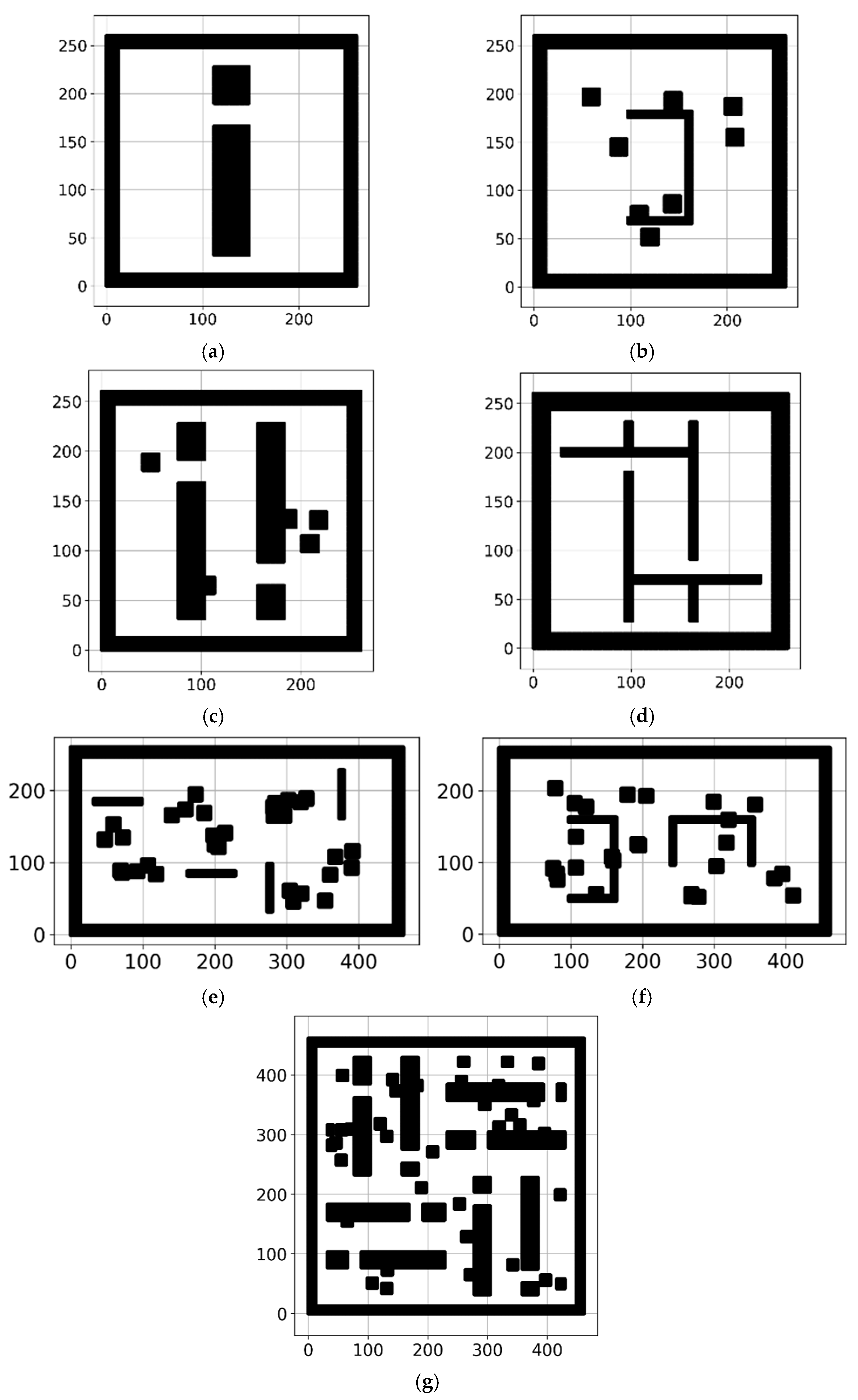
4.1. Grid Map Preparations Using the Dataset
4.1.1. Dataset
4.1.2. Grid-Map Preparation
4.1.3. Source and Destination Selection
4.2. Experimental Results of the Proposed Model
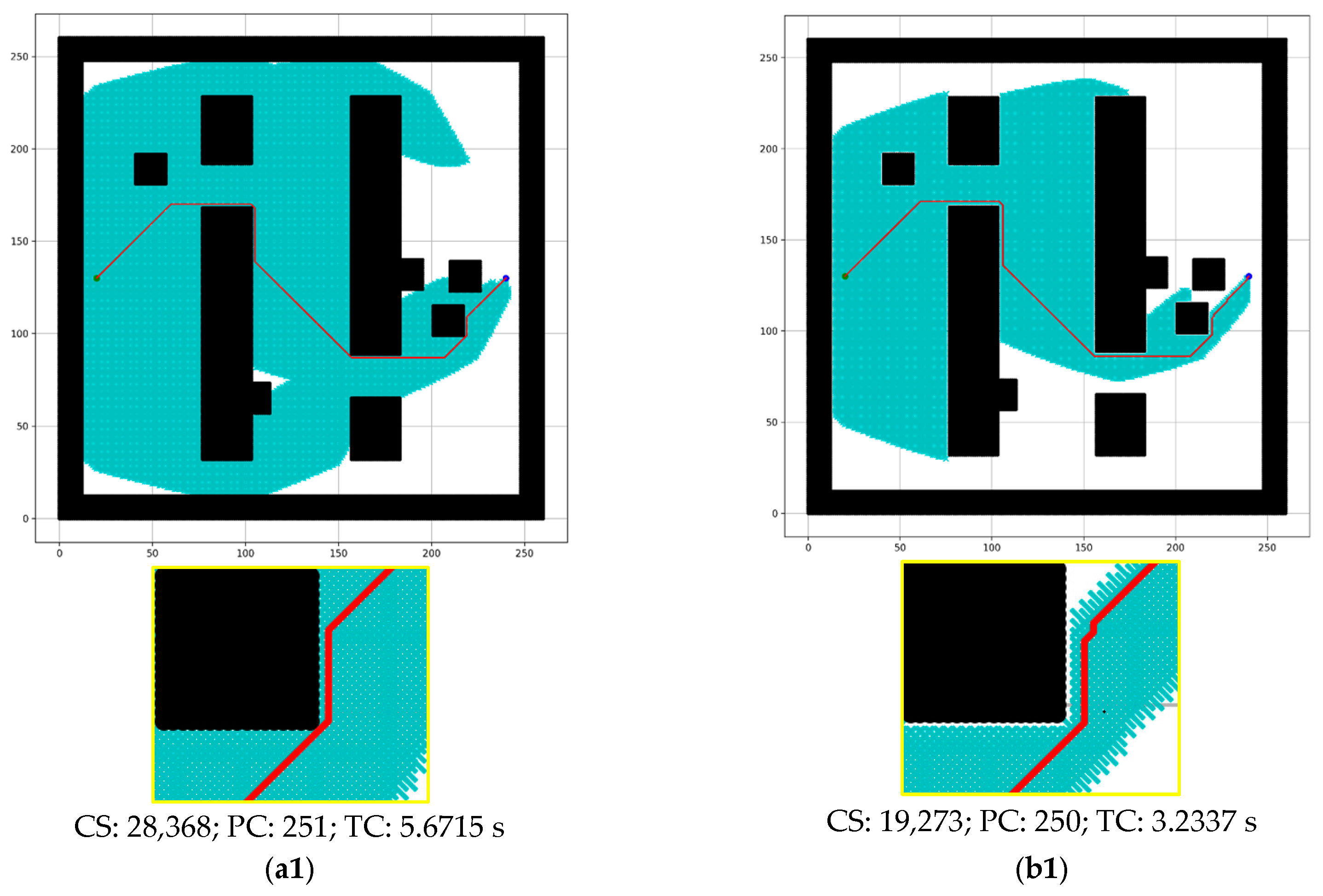
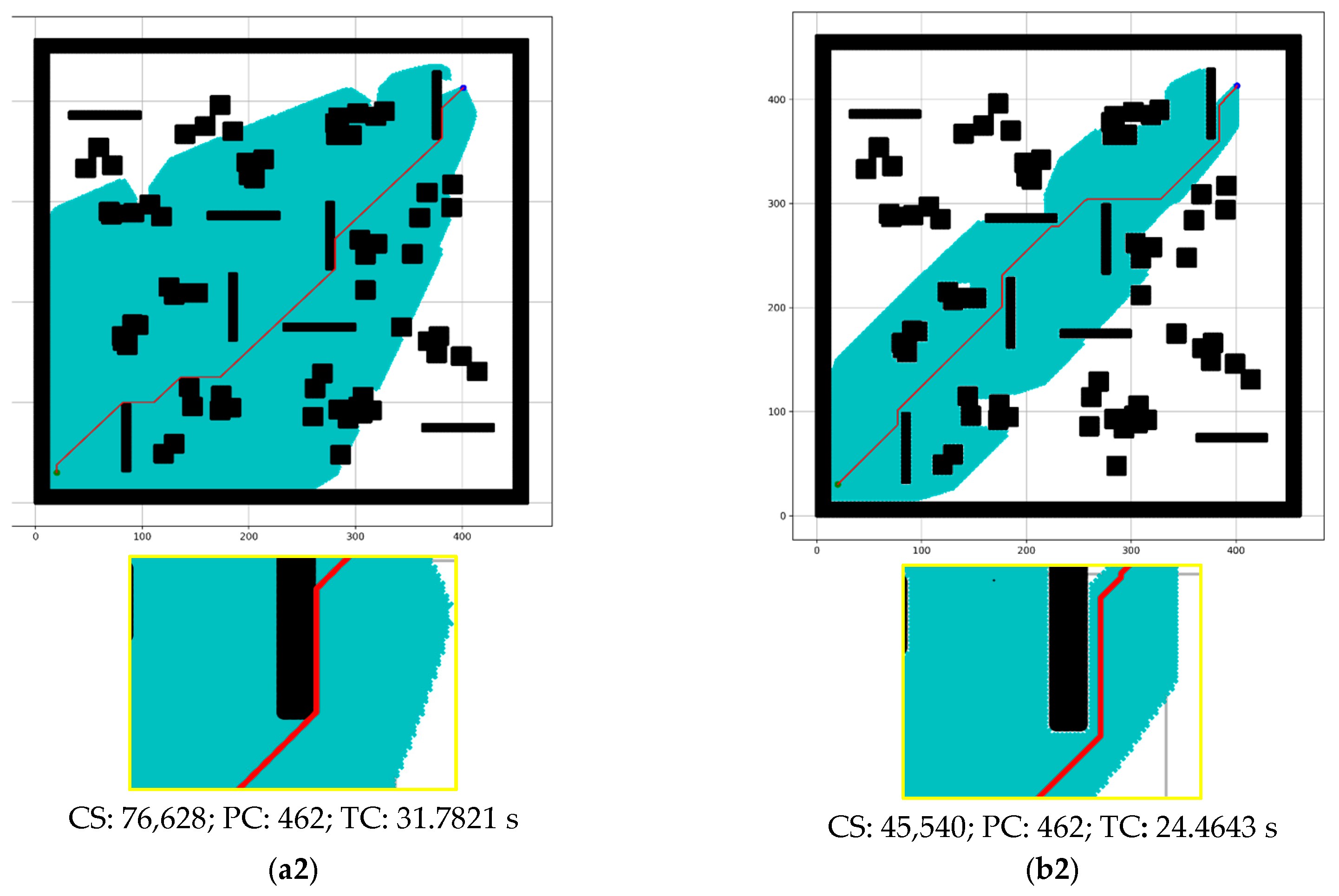
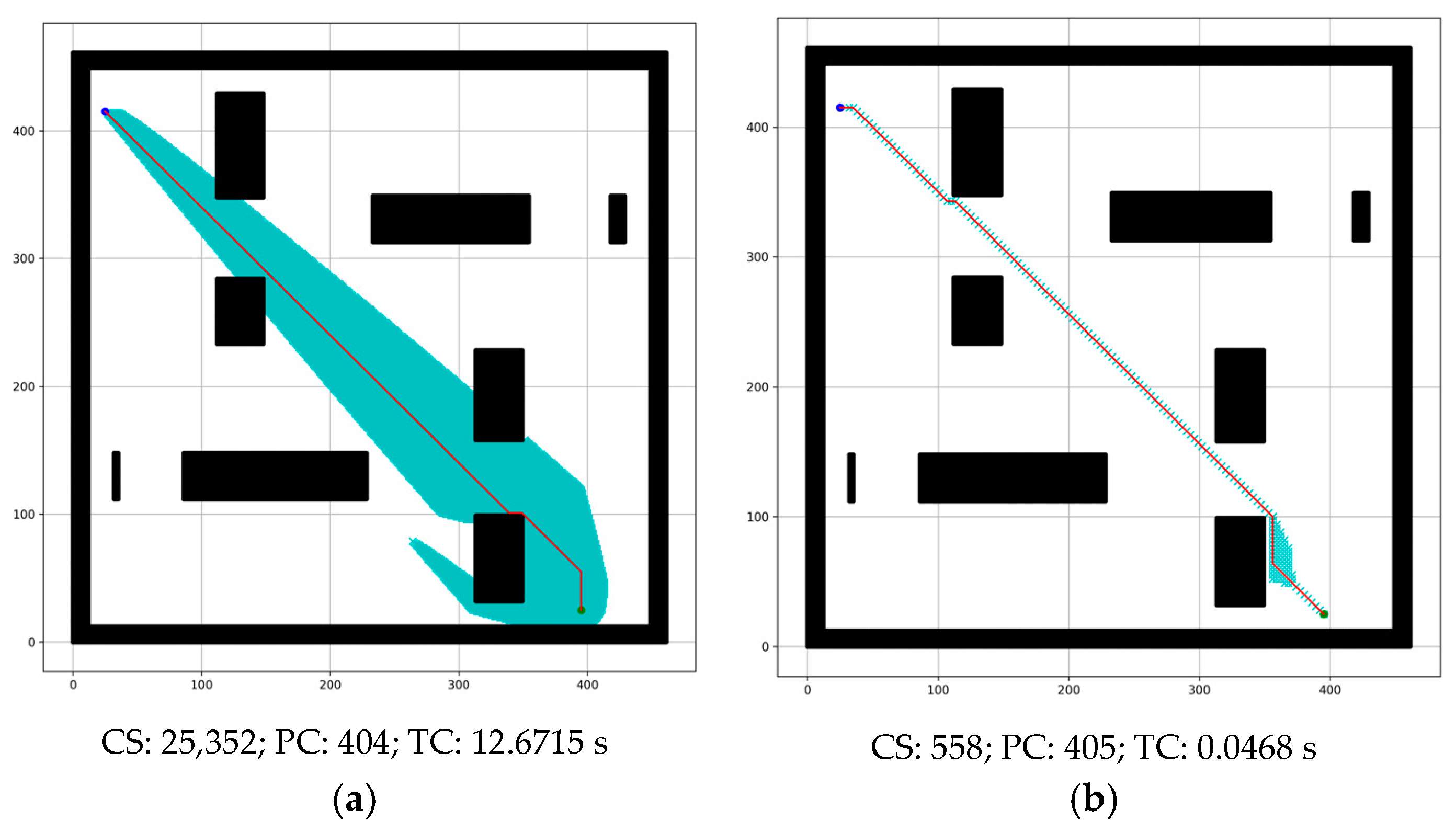
4.2.1. Comparison between Conventional A* and the Proposed Method
- Impact Evaluation
- = Value of conventional A*
- = Value of proposed model
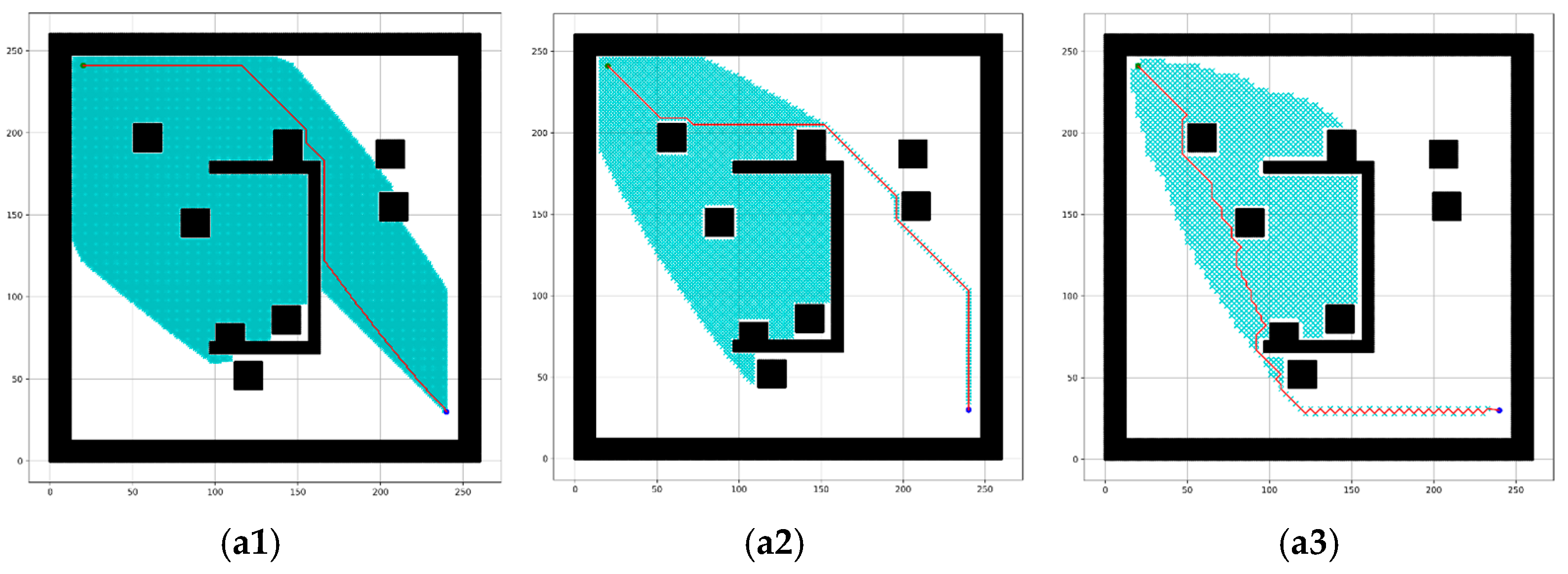
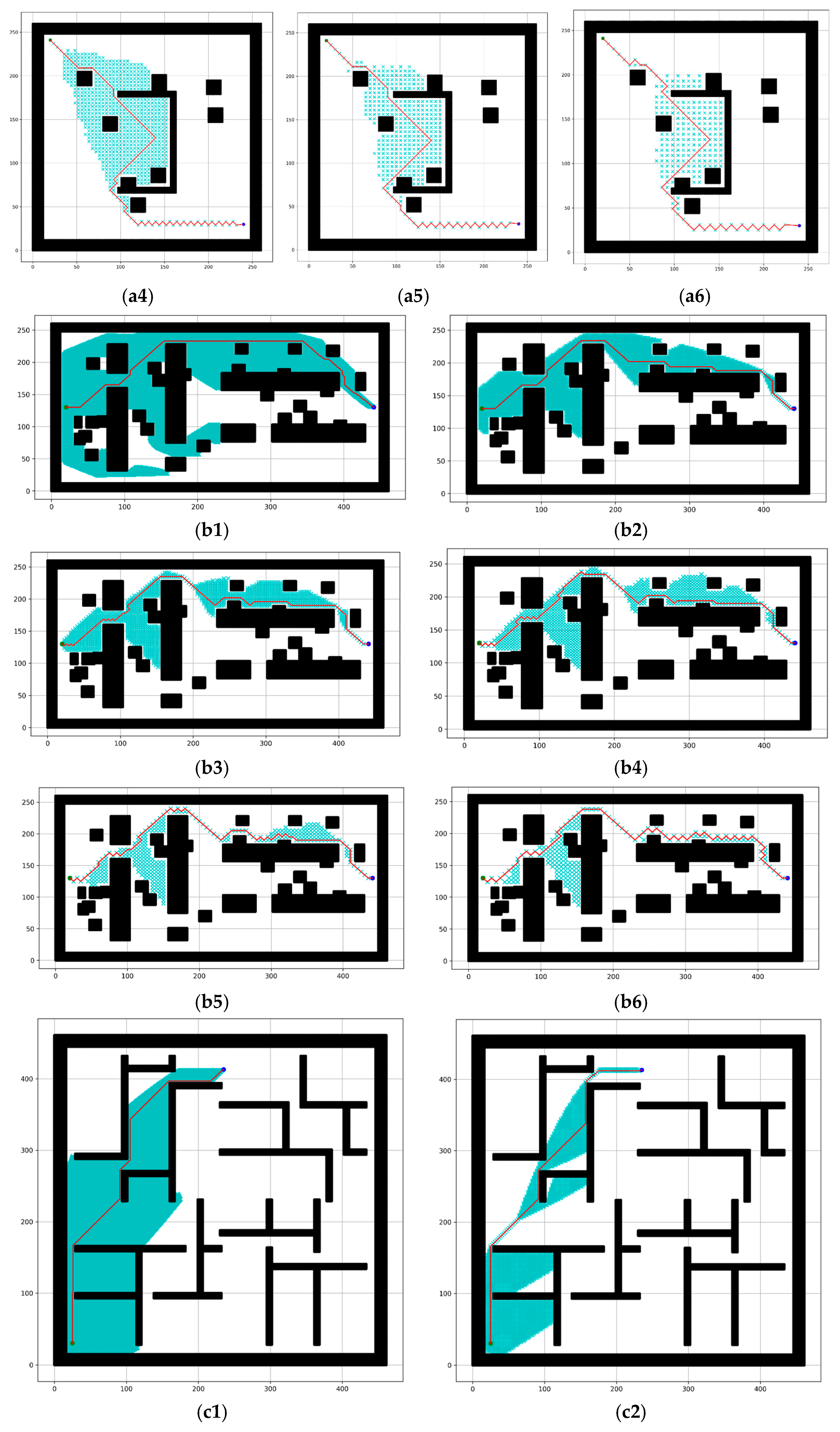
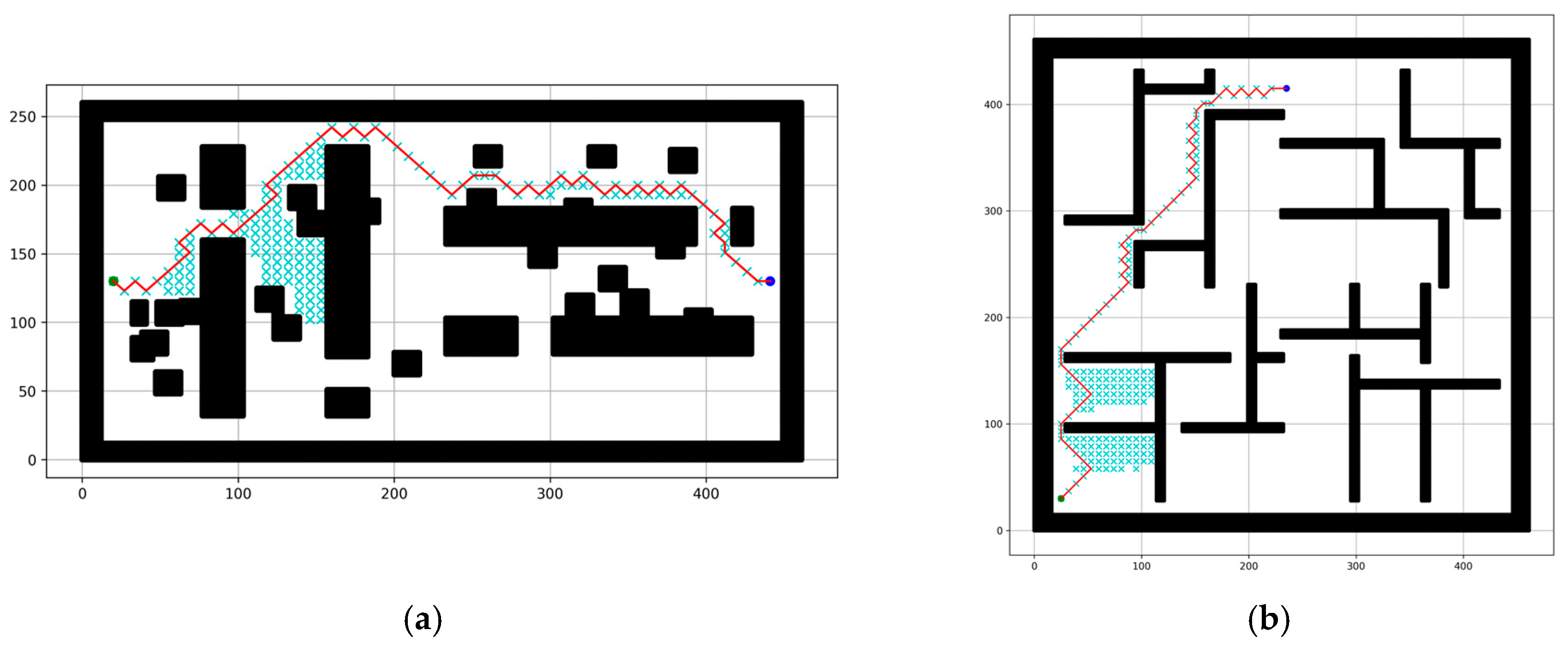
4.2.2. Experimental Results Using Different Sizes (n) of the Robot Motion Block
4.2.3. Results for Optimal Robot Motion Block Selection
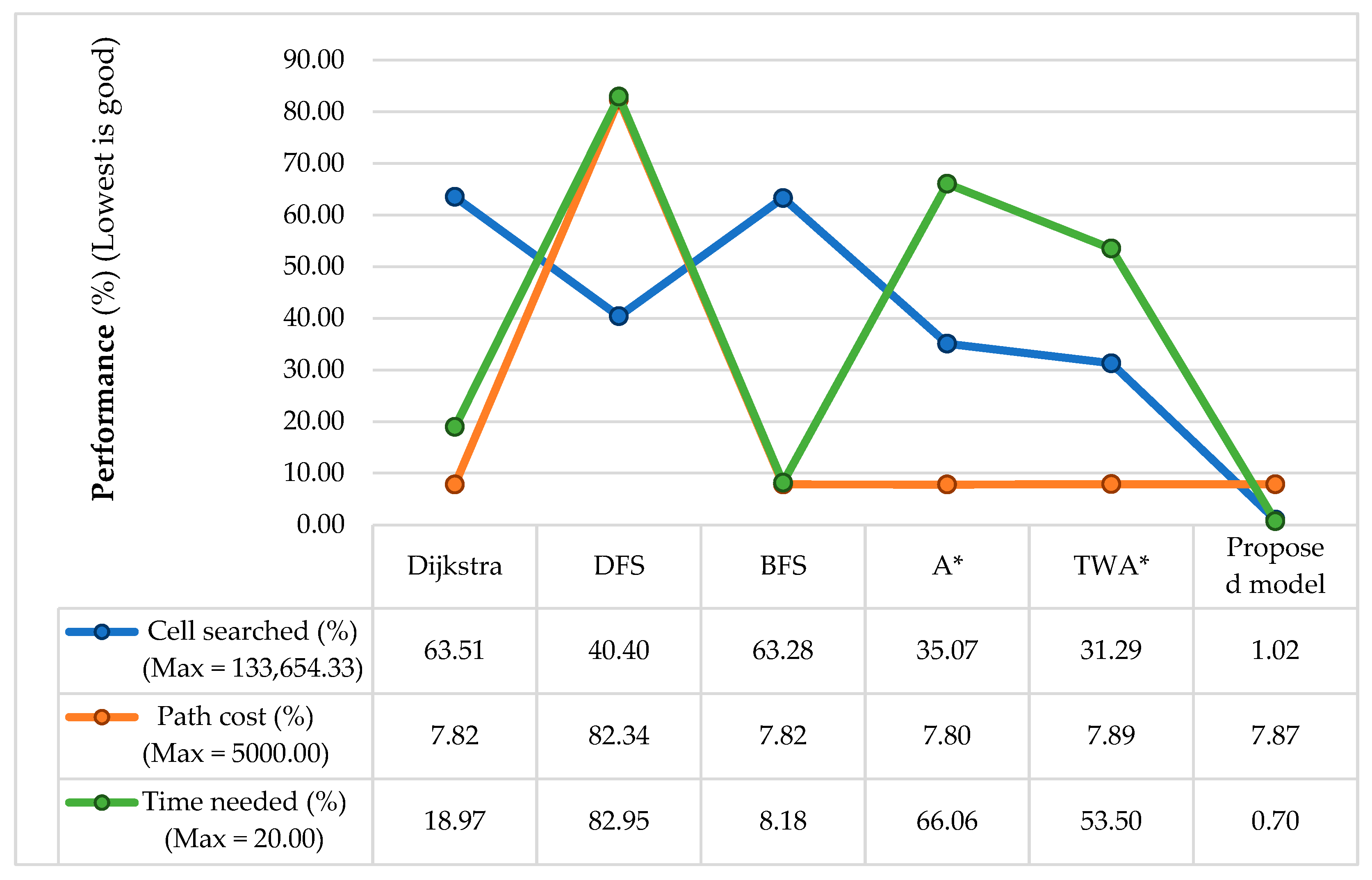
4.2.4. Comparison of the Proposed Method with the State-of-the-Art Algorithms
- Performance calculation.
- = mean of from (map dimensions).
- Maximum value of each parameter.
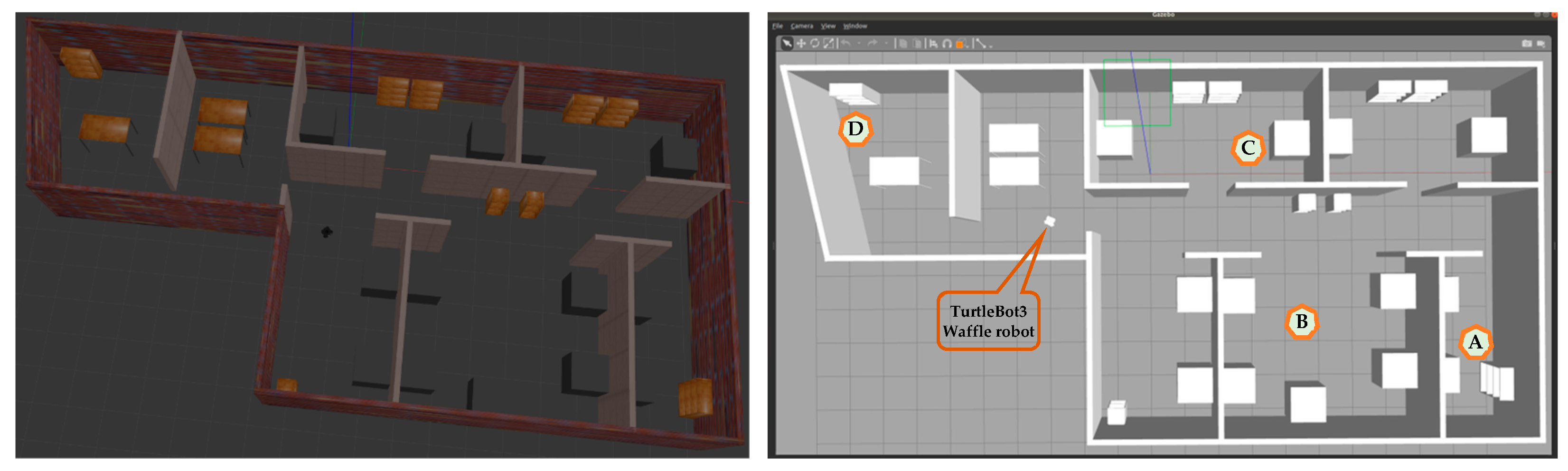
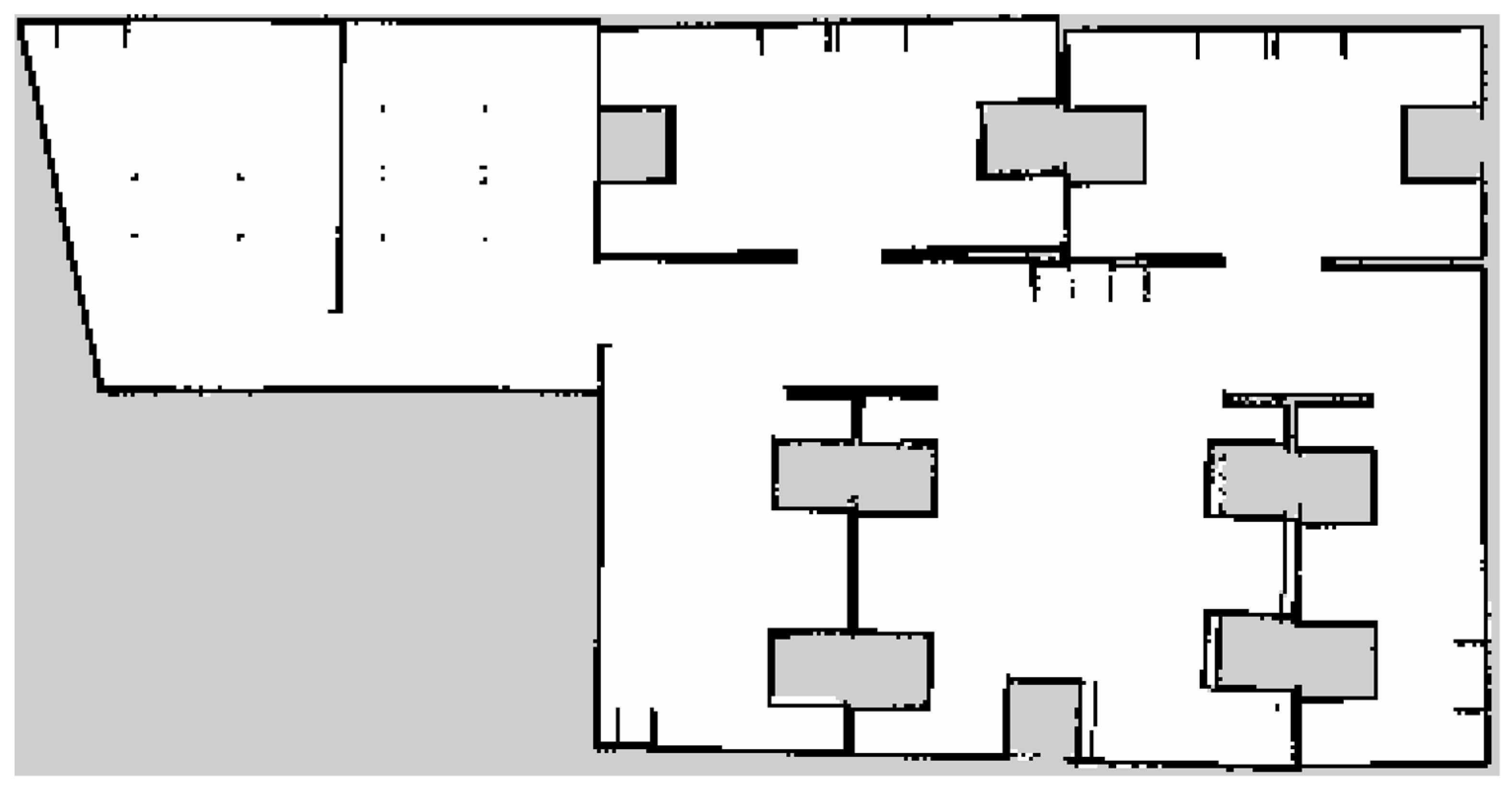
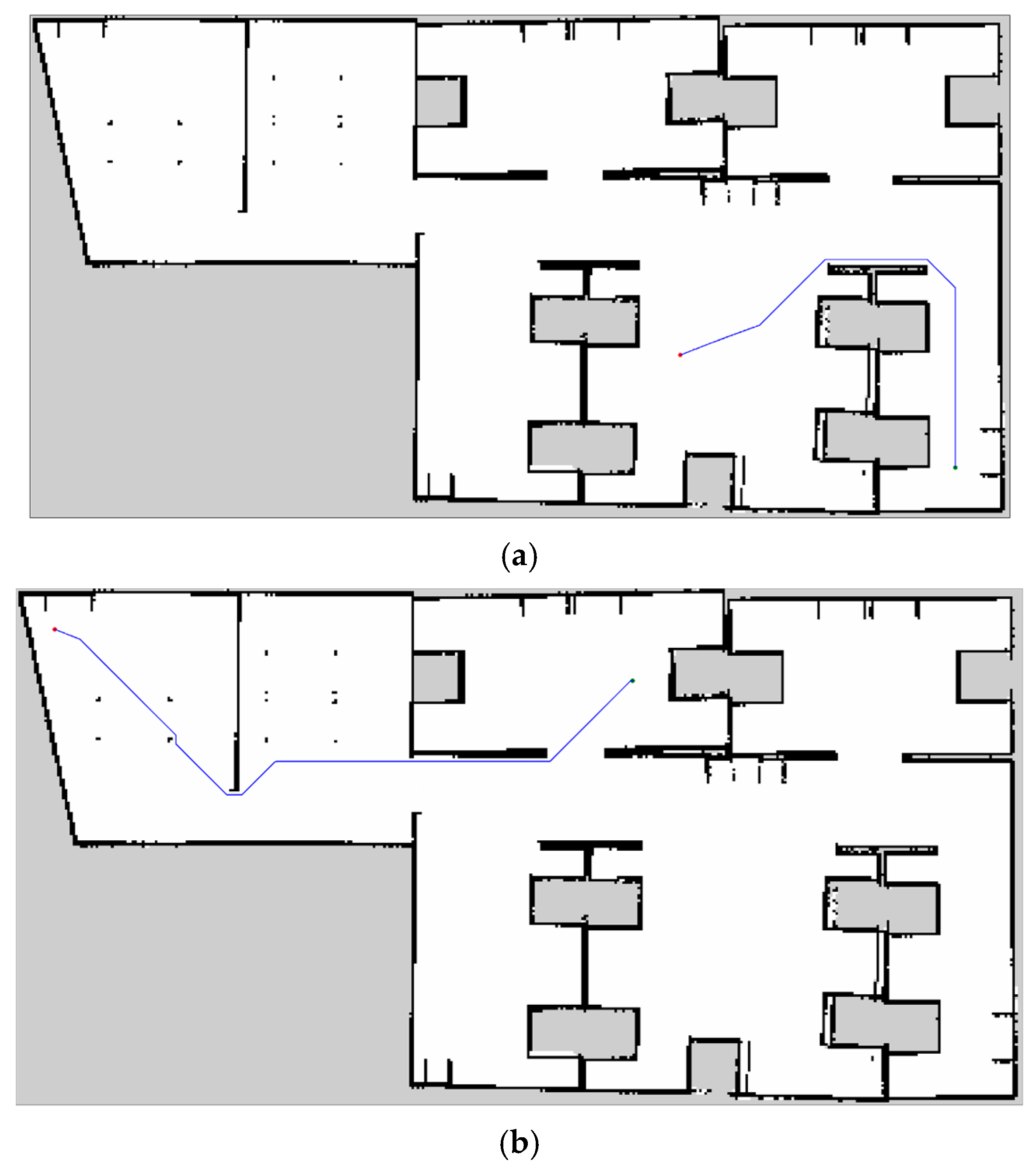
4.2.5. ROS Experiments
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.-Y.; Lin, W.-M.; Chen, A.-X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Kabir, R.; Watanobe, Y.; Islam, R.; Naruse, K.; Rahman, M. Unknown Object Detection Using a One-Class Support Vector Machine for a Cloud–Robot System. Sensors 2022, 22, 1352. [Google Scholar] [CrossRef]
- Wang, N.; Xu, H. Dynamics-Constrained Global-Local Hybrid Path Planning of an Autonomous Surface Vehicle. IEEE Trans. Veh. Technol. 2020, 69, 6928–6942. [Google Scholar] [CrossRef]
- Liu, H. Robot Systems for Rail Transit Applications; Elsevier BV: Amsterdam, The Netherlands, 2020; ISBN 9780128229682. [Google Scholar]
- Karur, K.; Sharma, N.; Dharmatti, C.; Siegel, J.E. A Survey of Path Planning Algorithms for Mobile Robots. Vehicles 2021, 3, 448–468. [Google Scholar] [CrossRef]
- Cai, K.; Wang, C.; Cheng, J.; de Silva, C.W.; Meng, M.Q.-H. Mobile Robot Path Planning in Dynamic Environments: A Survey. arXiv 2020, arXiv:2006.14195. [Google Scholar]
- Karaoguz, H.; Jensfelt, P. Object Detection Approach for Robot Grasp Detection. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4953–4959. [Google Scholar]
- Kabir, R.; Watanobe, Y.; Islam, R.; Naruse, K. Service Point Searching for Disabled People using Wheelchair based Robotic Path Planning and ArUco Markers. In Proceedings of the 2022 IEEE 8th World Forum on Internet of Things (WF-IoT), Yokohama, Japan, 26 October–11 November 2022; pp. 1–7. [Google Scholar]
- Udugama, B. Mini bot 3D: A ROS based Gazebo Simulation. arXiv 2023, arXiv:2302.06368. [Google Scholar]
- Matveev, A.S. Survey of algorithms for safe navigation of mobile robots in complex environments. In Safe Robot Navigation Among Moving and Steady Obstacles; Butterworth-Heinemann: Oxford, UK, 2016; pp. 21–49. [Google Scholar]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-Star Algorithm: An Improved A-Star Algorithm for AGV Path Planning in a Port Environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Kabir, R.; Watanobe, Y.; Naruse, K.; Islam, M.R. Effectiveness of Robot Motion Block on A-Star Algorithm for Robotic Path Planning. SoMeT 2022, 337, 85–96. [Google Scholar]
- Li, C.; Huang, X.; Ding, J.; Song, K.; Lu, S. Global path planning based on a bidirectional alternating search A* algorithm for mobile robots. Comput. Ind. Eng. 2022, 168, 108123. [Google Scholar] [CrossRef]
- BiBi, S.; Abbas, M.; Misro, M.Y.; Hu, G. A Novel Approach of Hybrid Trigonometric Bézier Curve to the Modeling of Symmetric Revolutionary Curves and Symmetric Rotation Surfaces. IEEE Access 2019, 7, 165779–165792. [Google Scholar] [CrossRef]
- de Assis Brasil, P.M.; Pereira, F.U.; de Souza Leite Cuadros, M.A.; Cukla, A.R.; Tello Gamarra, D.F. A Study on Global Path Planners Algorithms for the Simulated TurtleBot 3 Robot in ROS. In Proceedings of the 2020 Latin American Robotics Symposium (LARS), 2020 Brazilian Symposium on Robotics (SBR) and 2020 Workshop on Robotics in Education (WRE), Natal, Brazil, 10–13 November 2020; pp. 1–6. [Google Scholar]
- Szczepanski, R.; Tarczewski, T. Global path planning for mobile robot based on Artificial Bee Colony and Dijkstra’s algorithms. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference, Gliwice, Poland, 25–29 April 2021; pp. 724–730. [Google Scholar]
- Wang, H.; Wang, W.; Xiao, S.; Cui, Z.; Xu, M.; Zhou, X. Improving artificial Bee colony algorithm using a new neighborhood selection mechanism. Inf. Sci. 2020, 527, 227–240. [Google Scholar] [CrossRef]
- Gunawan, R.D.; Napianto, R.; Borman, R.I.; Hanifah, I. Implementation Of Dijkstra’s Algorithm In Determining The Shortest Path Case Study: Specialist Doctor Search In Bandar Lampung. Int. J. Inf. Syst. Comput. Sci. 2019, 3, 98–106. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-Del-Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Patle, B.K.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A.J.D.T. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Tripathy, H.K.; Mishra, S.; Thakkar, H.K.; Rai, D. CARE: A Collision-Aware Mobile Robot Navigation in Grid Environment using Improved Breadth First Search. Comput. Electr. Eng. 2021, 94, 107327. [Google Scholar] [CrossRef]
- Panigrahi, P.K.; Bisoy, S.K. Localization strategies for autonomous mobile robots: A review. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6019–6039. [Google Scholar] [CrossRef]
- Zhong, X.; Tian, J.; Hu, H.; Peng, X. Hybrid path planning based on safe A* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment. J. Intell. Robot. Syst. 2020, 99, 65–77. [Google Scholar] [CrossRef]
- Ali, H.; Gong, D.; Wang, M.; Dai, X. Path Planning of mobile robot with improved ant colony algorithm and MDP to produce smooth trajectory in grid-based environment. Front. Neurorobot. 2020, 14, 44. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, Y.; Zhang, X.; Lin, Y.; Yang, W. Improved A* Path Planning Method Based on the Grid Map. Sensors 2022, 22, 6198. [Google Scholar] [CrossRef]
- Abbyasov, B.; Gamberov, T.; Zhukova, V.; Tsoy, T.; Martínez-García, E.A.; Magid, E. A Tutorial on Modelling a Real Office Environment in Gazebo Simulator. J. Robot. Netw. Artif. Life 2023, 10, 166–169. [Google Scholar]
- Chen, J.; Tan, C.; Mo, R.; Zhang, H.; Cai, G.; Li, H. Research on path planning of three-neighbor search A* algorithm combined with artificial potential field. Int. J. Adv. Robot. Syst. 2021, 18. [Google Scholar] [CrossRef]
- Raheem, F.A.; Abdulkareem, M.I. Development of A* algorithm for robot path planning based on modified probabilistic road map and artificial potential field. J. Eng. Sci. Technol. 2020, 15, 3034–3054. [Google Scholar]
- Saeed, R.; Recupero, D. Path Planning of a Mobile Robot in Grid Space using Boundary Node Method. In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics, Prague, Czech Republic, 29–31 July 2019. [Google Scholar]
- Ichter, B.; Pavone, M. Robot Motion Planning in Learned Latent Spaces. IEEE Robot. Autom. Lett. 2019, 4, 2407–2414. [Google Scholar] [CrossRef]
- Gammell, J.D.; Strub, M.P. Asymptotically optimal sampling-based motion planning methods. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 295–318. [Google Scholar] [CrossRef]
- Cao, X.; Zou, X.; Jia, C.; Chen, M.; Zeng, Z. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths in graphs. IEEE Trans. Syst. Sci. Cybern. 1968, 2, 100–107. [Google Scholar] [CrossRef]
- Bhardwaj, M. Motion Planning Datasets. 2017. Available online: https://github.com/mohakbhardwaj/motion_planning_datasets (accessed on 21 May 2023).
- Bhardwaj, M.; Choudhury, S.; Scherer, S. Learning heuristic search via imitation. In Proceedings of the Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 271–280. [Google Scholar]










| Article | Test Environment with Obstacles | Cost Function Optimization | RMB Improvement | Test on Robots with Sensors | ROS Experiment | Test on Different Map Sizes | Test on Large Numbers of Maps |
|---|---|---|---|---|---|---|---|
| [13] | √ | - | - | √ | √ | - | - |
| [16] | √ | - | - | - | - | - | - |
| [21] | √ | √ | - | - | - | √ | - |
| [25] | √ | √ | - | √ | √ | - | - |
| [27] | √ | - | √ | √ | √ | - | - |
| Proposed method | √ | √ | √ | √ | √ | √ | √ |
| Algorithms | # Search Nodes | Path Cost | Time Required (s) |
|---|---|---|---|
| Conventional A* | 46,878.88 | 390.10 | 13.2112 |
| Proposed model | 31,604.34 | 389.94 | 9.3736 |
| Map Type | Map Dimension | Parameters | RMB | |||||
|---|---|---|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | |||
| alternating_gaps | 261 × 261 | # search nodes | 11,903.92 | 2838.90 | 1198.65 | 903.76 | 786.34 | 502.14 |
| Path cost | 246.26 | 245.78 | 246.01 | 247.32 | 262.92 | 261.95 | ||
| Time required (s) | 2.5259 | 0.2006 | 0.0735 | 0.0585 | 0.0296 | 0.0166 | ||
| 462 × 261 | # search nodes | 38,132.17 | 8351.43 | 2789.37 | 1702.49 | 1076.50 | 888.37 | |
| Path cost | 431.22 | 433.96 | 435.06 | 436.84 | 443.55 | 445.29 | ||
| Time required (s) | 11.0979 | 0.8327 | 0.1473 | 0.0712 | 0.0383 | 0.0221 | ||
| 462 × 462 | # search nodes | 38,069.77 | 3958.41 | 1522.72 | 1266.83 | 811.02 | 632.05 | |
| Path cost | 437.09 | 436.52 | 437.20 | 438.33 | 439.89 | 445.18 | ||
| Time required (s) | 13.3132 | 0.7858 | 0.1109 | 0.0383 | 0.0245 | 0.0202 | ||
| forest | 261 × 261 | # search nodes | 8181.34 | 1809.13 | 1142.62 | 869.21 | 629.31 | 482.98 |
| Path cost | 235.69 | 241.27 | 242.17 | 245.92 | 244.84 | 248.83 | ||
| Time required (s) | 1.9034 | 0.0982 | 0.0521 | 0.0256 | 0.0245 | 0.0195 | ||
| 462 × 261 | # search nodes | 22,056.06 | 3855.53 | 1764.34 | 1356.10 | 1175.00 | 936.63 | |
| Path cost | 417.87 | 419.61 | 419.07 | 419.09 | 420.10 | 422.81 | ||
| Time required (s) | 5.8014 | 0.4410 | 0.1067 | 0.0617 | 0.0336 | 0.0200 | ||
| 462 × 462 | # search nodes | 41,497.96 | 1098.45 | 759.14 | 632.76 | 567.44 | 495.21 | |
| Path cost | 423.38 | 425.47 | 425.23 | 427.45 | 429.58 | 428.90 | ||
| Time required (s) | 19.1736 | 0.1115 | 0.0405 | 0.0245 | 0.0186 | 0.0156 | ||
| bugtrap_forest | 261 × 261 | # search nodes | 18,436.83 | 5909.82 | 2731.87 | 1533.71 | 1105.00 | 892.15 |
| Path cost | 260.13 | 261.72 | 260.52 | 264.59 | 268.00 | 268.97 | ||
| Time required (s) | 3.9576 | 0.4435 | 0.1137 | 0.0500 | 0.0383 | 0.0245 | ||
| 462 × 261 | # search nodes | 41,725.85 | 9255.84 | 4571.77 | 2855.64 | 2372.93 | 1382.53 | |
| Path cost | 436.70 | 440.48 | 440.36 | 442.83 | 446.93 | 449.65 | ||
| Time required (s) | 12.5779 | 0.8432 | 0.2342 | 0.1087 | 0.0692 | 0.0383 | ||
| 462 × 462 | # search nodes | 46,582.38 | 5011.74 | 1913.54 | 1509.35 | 1339.76 | 1121.14 | |
| Path cost | 460.24 | 465.91 | 467.55 | 474.02 | 479.76 | 481.96 | ||
| Time required (s) | 15.7666 | 0.8953 | 0.1778 | 0.0861 | 0.0588 | 0.0291 | ||
| gaps_and_forest | 261 × 261 | # search nodes | 9260.30 | 1858.17 | 938.19 | 761.81 | 558.93 | 380.48 |
| Path cost | 251.04 | 250.87 | 253.21 | 255.33 | 259.90 | 263.07 | ||
| Time required (s) | 2.3573 | 0.1129 | 0.0455 | 0.0334 | 0.0206 | 0.0186 | ||
| 462 × 261 | # search nodes | 31,361.01 | 7935.98 | 3511.17 | 2356.03 | 1336.57 | 991.89 | |
| Path cost | 448.15 | 449.54 | 453.95 | 462.83 | 469.79 | 470.84 | ||
| Time required (s) | 6.6211 | 0.6473 | 0.1781 | 0.0847 | 0.0411 | 0.0245 | ||
| 462 × 462 | # search nodes | 41,334.98 | 5584.34 | 2427.80 | 1517.65 | 1124.17 | 759.52 | |
| Path cost | 485.89 | 486.88 | 488.99 | 493.71 | 497.64 | 496.01 | ||
| Time required (s) | 11.3063 | 0.9169 | 0.1356 | 0.0595 | 0.0393 | 0.0208 | ||
| mazes | 261 × 261 | # search nodes | 26,045.38 | 10,176.25 | 5986.73 | 3896.61 | 2564.64 | 2008.82 |
| Path cost | 320.51 | 320.78 | 322.35 | 325.45 | 329.83 | 330.33 | ||
| Time required (s) | 4.7198 | 0.6722 | 0.2536 | 0.1198 | 0.0658 | 0.0435 | ||
| 462 × 261 | # search nodes | 49,235.53 | 8426.30 | 3654.47 | 2122.42 | 1590.48 | 1247.94 | |
| Path cost | 471.47 | 472.21 | 473.32 | 475.49 | 481.91 | 500.58 | ||
| Time required (s) | 13.6747 | 0.7576 | 0.1655 | 0.0679 | 0.0479 | 0.0346 | ||
| 462 × 462 | # search nodes | 58,241.65 | 17,939.49 | 7454.32 | 4472.24 | 3274.23 | 2194.61 | |
| Path cost | 522.04 | 524.76 | 527.02 | 530.56 | 532.45 | 536.13 | ||
| Time required (s) | 17.9080 | 1.8732 | 0.3839 | 0.1729 | 0.1012 | 0.0563 | ||
| Map Type | Map Dimension | Parameters | RMB | |||||
|---|---|---|---|---|---|---|---|---|
| = 1 | = 2 | = 3 | = 4 | = 5 | = 6 | |||
| alternating_gaps | 261 × 261 | # search nodes | 1000.00 | 204.95 | 61.09 | 35.22 | 24.93 | 0.00 |
| Path cost | 28.30 | 0.00 | 13.42 | 89.74 | 1000.00 | 943.69 | ||
| Time required | 1000.00 | 73.30 | 22.66 | 16.67 | 5.16 | 0.00 | ||
| Average | 676.10 | 92.75 | 32.39 | 47.21 | 343.36 | 314.56 | ||
| 462 × 261 | # search nodes | 1000.00 | 200.38 | 51.04 | 21.86 | 5.05 | 0.00 | |
| Path cost | 0.00 | 194.97 | 273.07 | 399.64 | 876.12 | 1000.00 | ||
| Time required | 1000.00 | 73.18 | 11.31 | 4.44 | 1.46 | 0.00 | ||
| Average | 666.67 | 156.18 | 111.80 | 141.98 | 294.21 | 333.33 | ||
| 462 × 462 | # search nodes | 1000.00 | 88.85 | 23.79 | 16.96 | 4.78 | 0.00 | |
| Path cost | 66.33 | 0.00 | 79.17 | 208.90 | 389.30 | 1000.00 | ||
| Time required | 1000.00 | 57.59 | 6.82 | 1.36 | 0.32 | 0.00 | ||
| Average | 688.78 | 48.81 | 36.59 | 75.74 | 131.47 | 333.33 | ||
| forest | 261 × 261 | # search nodes | 1000.00 | 172.27 | 85.69 | 50.17 | 19.01 | 0.00 |
| Path cost | 0.00 | 424.75 | 493.11 | 779.07 | 696.73 | 1000.00 | ||
| Time required | 1000.00 | 41.75 | 17.29 | 3.24 | 2.65 | 0.00 | ||
| Average | 666.67 | 212.92 | 198.70 | 277.49 | 239.46 | 333.33 | ||
| 462 × 261 | # search nodes | 1000.00 | 138.21 | 39.19 | 19.86 | 11.29 | 0.00 | |
| Path cost | 0.00 | 351.94 | 241.79 | 246.73 | 450.17 | 1000.00 | ||
| Time required | 1000.00 | 72.83 | 15.00 | 7.21 | 2.35 | 0.00 | ||
| Average | 666.67 | 187.66 | 98.66 | 91.27 | 154.61 | 333.33 | ||
| 462 × 462 | # search nodes | 1000.00 | 14.71 | 6.44 | 3.35 | 1.76 | 0.00 | |
| Path cost | 0.00 | 337.47 | 298.24 | 656.74 | 1000.00 | 890.39 | ||
| Time required | 1000.00 | 5.00 | 1.30 | 0.46 | 0.15 | 0.00 | ||
| Average | 666.67 | 119.06 | 101.99 | 220.18 | 333.97 | 296.80 | ||
| bugtrap_forest | 261 × 261 | # search nodes | 1000.00 | 285.99 | 104.86 | 36.57 | 12.13 | 0.00 |
| Path cost | 0.00 | 180.21 | 44.58 | 504.79 | 890.38 | 1000.00 | ||
| Time required | 1000.00 | 106.54 | 22.70 | 6.50 | 3.51 | 0.00 | ||
| Average | 666.67 | 190.91 | 57.38 | 182.62 | 302.01 | 333.33 | ||
| 462 × 261 | # search nodes | 1000.00 | 195.16 | 79.05 | 36.51 | 24.55 | 0.00 | |
| Path cost | 0.00 | 291.88 | 282.17 | 472.96 | 789.82 | 1000.00 | ||
| Time required | 1000.00 | 64.19 | 15.63 | 5.61 | 2.46 | 0.00 | ||
| Average | 666.67 | 183.74 | 125.62 | 171.70 | 272.28 | 333.33 | ||
| 462 × 462 | # search nodes | 1000.00 | 85.58 | 17.43 | 8.54 | 4.81 | 0.00 | |
| Path cost | 0.00 | 260.96 | 336.57 | 634.61 | 898.72 | 1000.00 | ||
| Time required | 1000.00 | 55.04 | 9.45 | 3.63 | 1.89 | 0.00 | ||
| Average | 666.67 | 133.86 | 121.15 | 215.59 | 301.80 | 333.33 | ||
| gaps_and_forest | 261 × 261 | # search nodes | 1000.00 | 166.41 | 62.81 | 42.94 | 20.10 | 0.00 |
| Path cost | 14.27 | 0.00 | 191.82 | 365.81 | 740.76 | 1000.00 | ||
| Time required | 1000.00 | 40.32 | 11.52 | 6.36 | 0.85 | 0.00 | ||
| Average | 671.42 | 68.91 | 88.72 | 138.37 | 253.90 | 333.33 | ||
| 462 × 261 | # search nodes | 1000.00 | 228.66 | 82.96 | 44.92 | 11.35 | 0.00 | |
| Path cost | 0.00 | 60.99 | 255.46 | 647.02 | 953.69 | 1000.00 | ||
| Time required | 1000.00 | 94.41 | 23.30 | 9.13 | 2.53 | 0.00 | ||
| Average | 666.67 | 128.02 | 120.57 | 233.69 | 322.52 | 333.33 | ||
| 462 × 462 | # search nodes | 1000.00 | 118.91 | 41.12 | 18.68 | 8.99 | 0.00 | |
| Path cost | 0.00 | 83.76 | 264.05 | 665.66 | 1000.00 | 860.81 | ||
| Time required | 1000.00 | 79.40 | 10.17 | 3.43 | 1.64 | 0.00 | ||
| Average | 666.67 | 94.02 | 105.11 | 229.26 | 336.87 | 286.94 | ||
| mazes | 261 × 261 | # search nodes | 1000.00 | 339.79 | 165.49 | 78.54 | 23.12 | 0.00 |
| Path cost | 0.00 | 27.82 | 187.67 | 503.39 | 949.12 | 1000.00 | ||
| Time required | 1000.00 | 134.45 | 44.93 | 16.32 | 4.78 | 0.00 | ||
| Average | 666.67 | 167.35 | 132.70 | 199.42 | 325.67 | 333.33 | ||
| 462 × 261 | # search nodes | 1000.00 | 149.59 | 50.15 | 18.22 | 7.14 | 0.00 | |
| Path cost | 0.00 | 25.29 | 63.31 | 138.00 | 358.44 | 1000.00 | ||
| Time required | 1000.00 | 53.01 | 9.60 | 2.44 | 0.97 | 0.00 | ||
| Average | 666.67 | 75.96 | 41.02 | 52.89 | 122.18 | 333.33 | ||
| 462 × 462 | # search nodes | 1000.00 | 280.92 | 93.84 | 40.64 | 19.26 | 0.00 | |
| Path cost | 0.00 | 192.96 | 353.21 | 604.99 | 739.05 | 1000.00 | ||
| Time required | 1000.00 | 101.78 | 18.35 | 6.53 | 2.52 | 0.00 | ||
| Average | 666.67 | 191.89 | 155.14 | 217.39 | 253.61 | 333.33 | ||
| Algorithms | Map Dimension | Number of Search Nodes | Path Cost | Time Required (s) |
|---|---|---|---|---|
| Dijkstra | 261 × 261 | 43,440.25 | 258.95 | 1.5023 |
| 462 × 261 | 73,496.51 | 436.65 | 2.4945 | |
| 462 × 462 | 137,696.72 | 477.27 | 7.3836 | |
| Average | 84,877.83 | 390.96 | 3.7935 | |
| DFS | 261 × 261 | 36,553.30 | 1342.70 | 4.5641 |
| 462 × 261 | 48,019.90 | 5644.20 | 9.5305 | |
| 462 × 462 | 77,399.00 | 5363.70 | 35.6750 | |
| Average | 53,990.73 | 4116.87 | 16.5898 | |
| BFS | 261 × 261 | 43,874.00 | 258.40 | 1.0516 |
| 462 × 261 | 72,871.50 | 436.65 | 1.2953 | |
| 462 × 462 | 136,987.80 | 477.70 | 2.5602 | |
| Average | 84,577.77 | 390.92 | 1.6357 | |
| A* | 261 × 261 | 22,587.45 | 257.95 | 4.5156 |
| 462 × 261 | 49,740.21 | 435.65 | 12.8063 | |
| 462 × 462 | 68,308.97 | 476.70 | 22.3117 | |
| Average | 46,878.88 | 390.10 | 13.2112 | |
| TWA* | 261 × 261 | 19,218.59 | 262.32 | 3.9392 |
| 462 × 261 | 44,035.81 | 442.96 | 9.8472 | |
| 462 × 462 | 62,199.15 | 478.47 | 18.3117 | |
| Average | 41,817.85 | 394.58 | 10.6993 | |
| Proposed model (ORMBA*) | 261 × 261 | 2219.61 | 264.85 | 0.0957 |
| 462 × 261 | 3258.22 | 444.35 | 0.1664 | |
| 462 × 462 | 2995.51 | 470.80 | 0.1597 | |
| Average | 2824.45 | 393.33 | 0.1406 |
| Parameters | Source to Destination | A to B | B to C | C to D | Average | |
|---|---|---|---|---|---|---|
| Algorithms | ||||||
| Path length (m) | A* | 42.95 | 24.15 | 54.80 | 40.63 | |
| TWA* | 43.10 | 24.25 | 54.93 | 40.75 | ||
| ORMBA* | 43.08 | 24.23 | 54.90 | 40.74 | ||
| Search time (s) | A* | 18.7923 | 2.9738 | 114.5114 | 45.4258 | |
| TWA* | 17.0025 | 2.7609 | 102.3118 | 40.6917 | ||
| ORMBA* | 3.9341 | 0.5793 | 20.5904 | 8.3679 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabir, R.; Watanobe, Y.; Islam, M.R.; Naruse, K. Enhanced Robot Motion Block of A-Star Algorithm for Robotic Path Planning. Sensors 2024, 24, 1422. https://doi.org/10.3390/s24051422
Kabir R, Watanobe Y, Islam MR, Naruse K. Enhanced Robot Motion Block of A-Star Algorithm for Robotic Path Planning. Sensors. 2024; 24(5):1422. https://doi.org/10.3390/s24051422
Chicago/Turabian StyleKabir, Raihan, Yutaka Watanobe, Md Rashedul Islam, and Keitaro Naruse. 2024. "Enhanced Robot Motion Block of A-Star Algorithm for Robotic Path Planning" Sensors 24, no. 5: 1422. https://doi.org/10.3390/s24051422
APA StyleKabir, R., Watanobe, Y., Islam, M. R., & Naruse, K. (2024). Enhanced Robot Motion Block of A-Star Algorithm for Robotic Path Planning. Sensors, 24(5), 1422. https://doi.org/10.3390/s24051422







