Modelling and Thermographic Measurements of LED Optical Power
Abstract
1. Introduction
2. Materials and Methods
2.1. Thermal Modelling
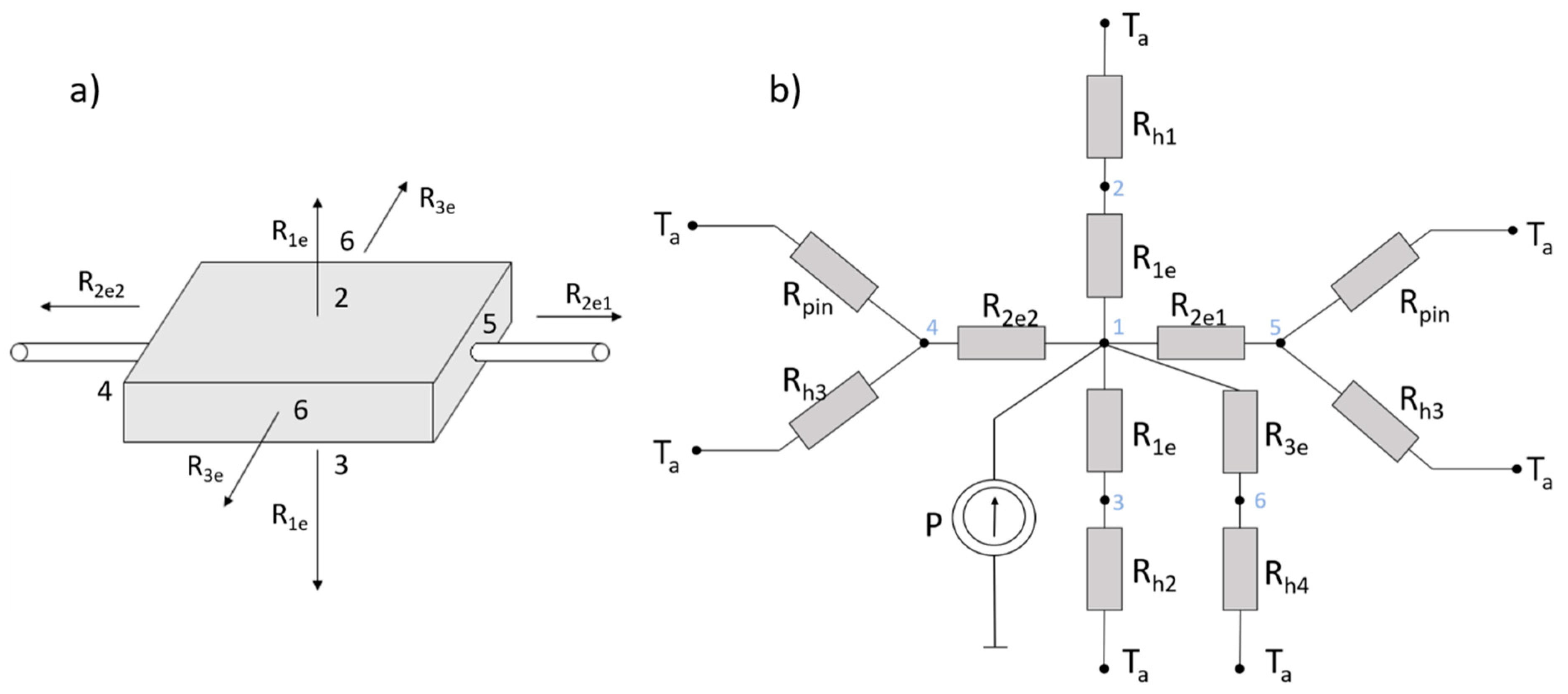
2.1.1. Rth Network—Compact Thermal LED Model
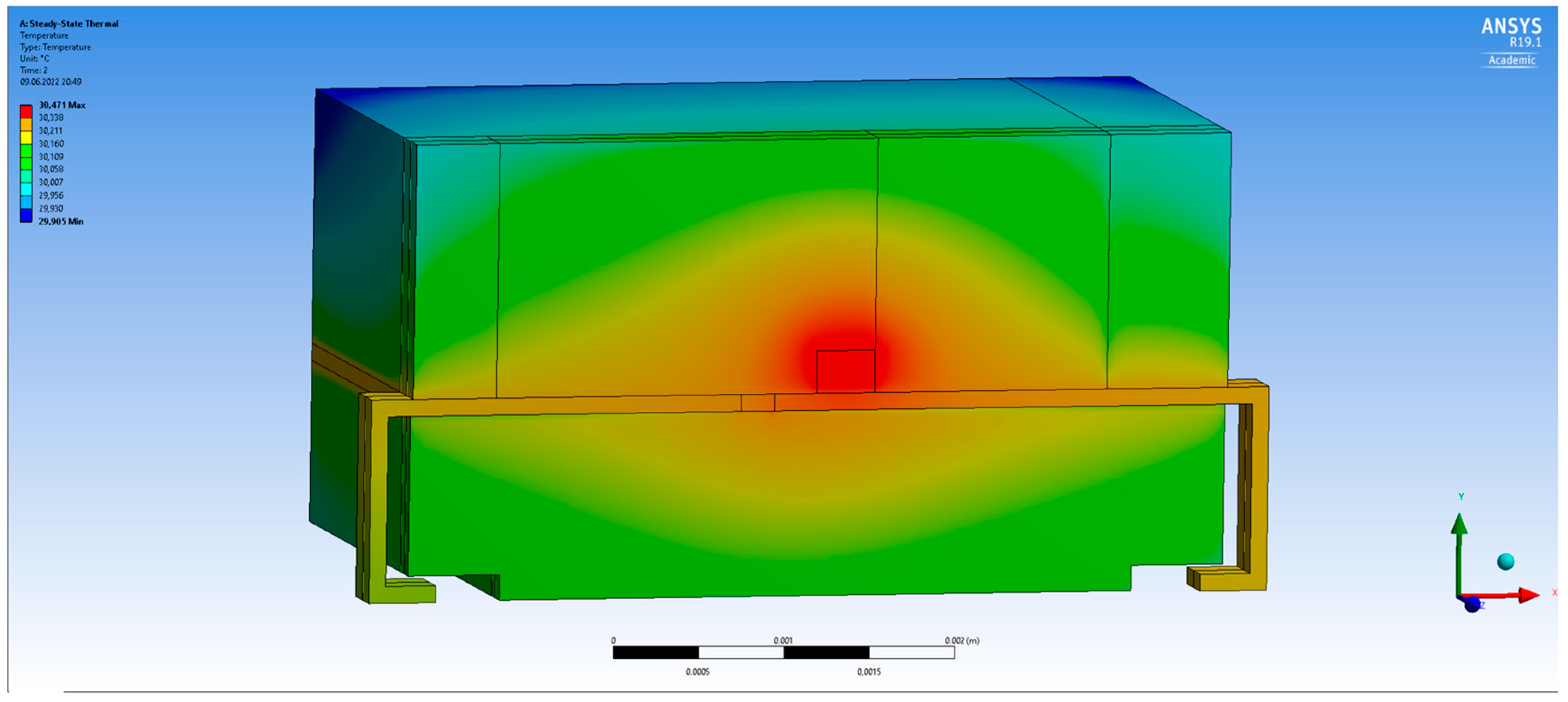
2.1.2. Three-Dimensional FEM Model
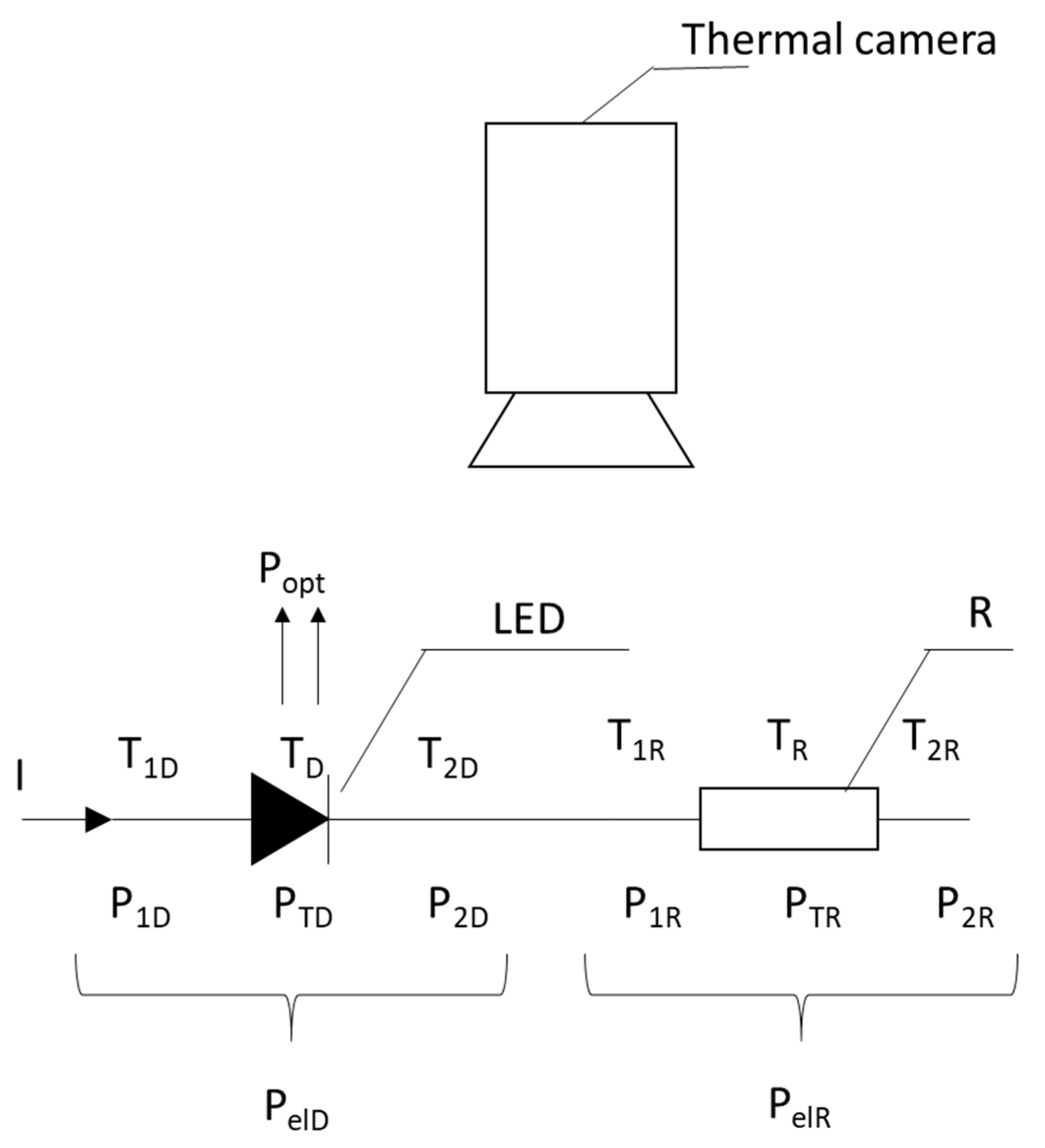
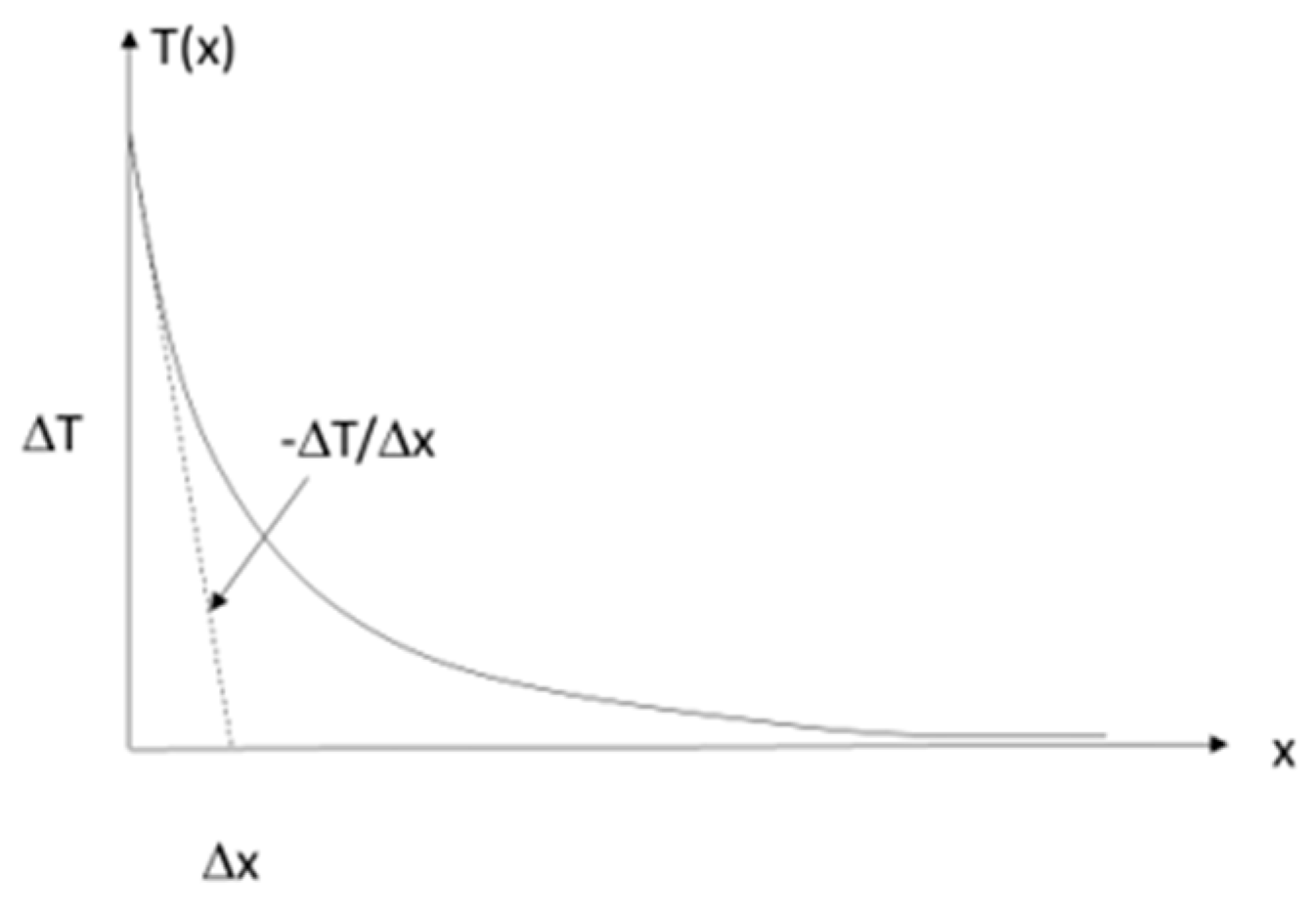
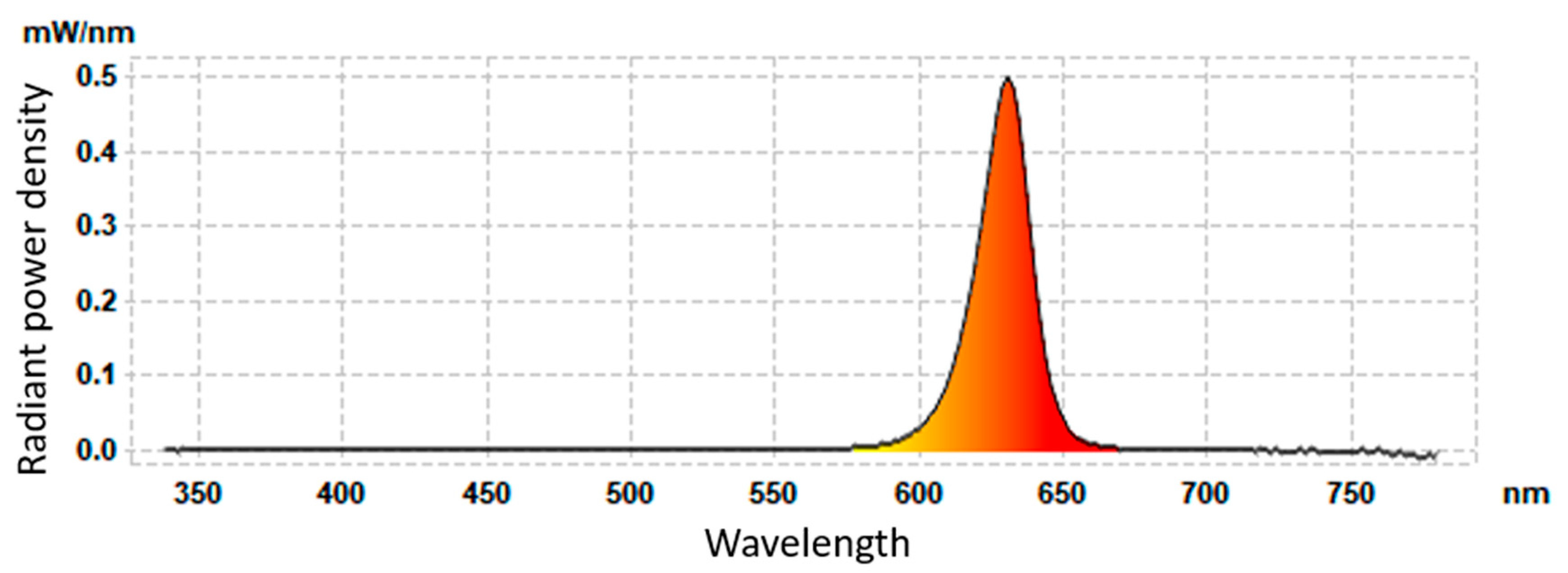
2.2. Thermographic Method of LED Optical Power Evaluation
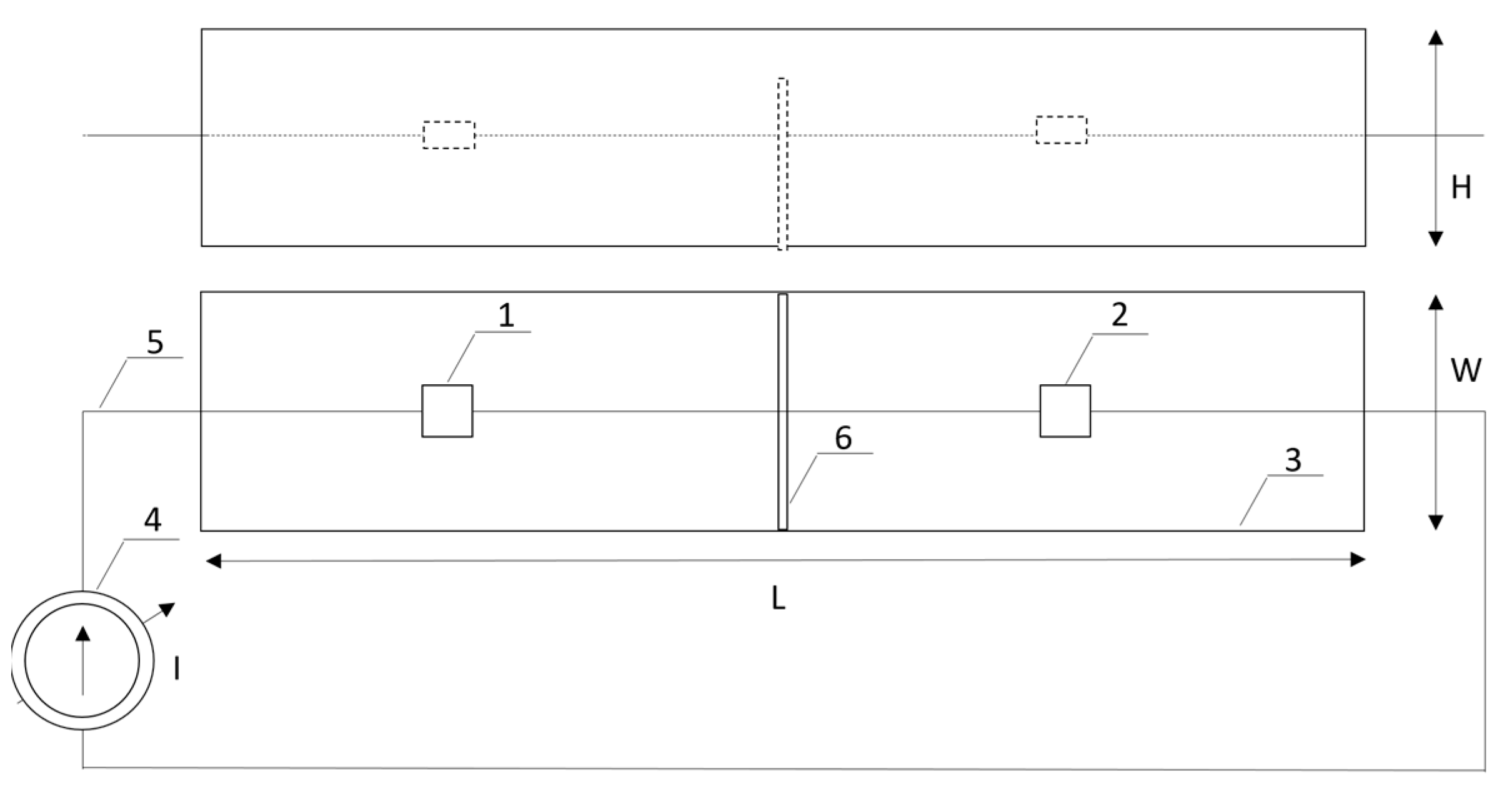
2.3. Measurement Setup
3. Results and Discussion
3.1. Modelling Results
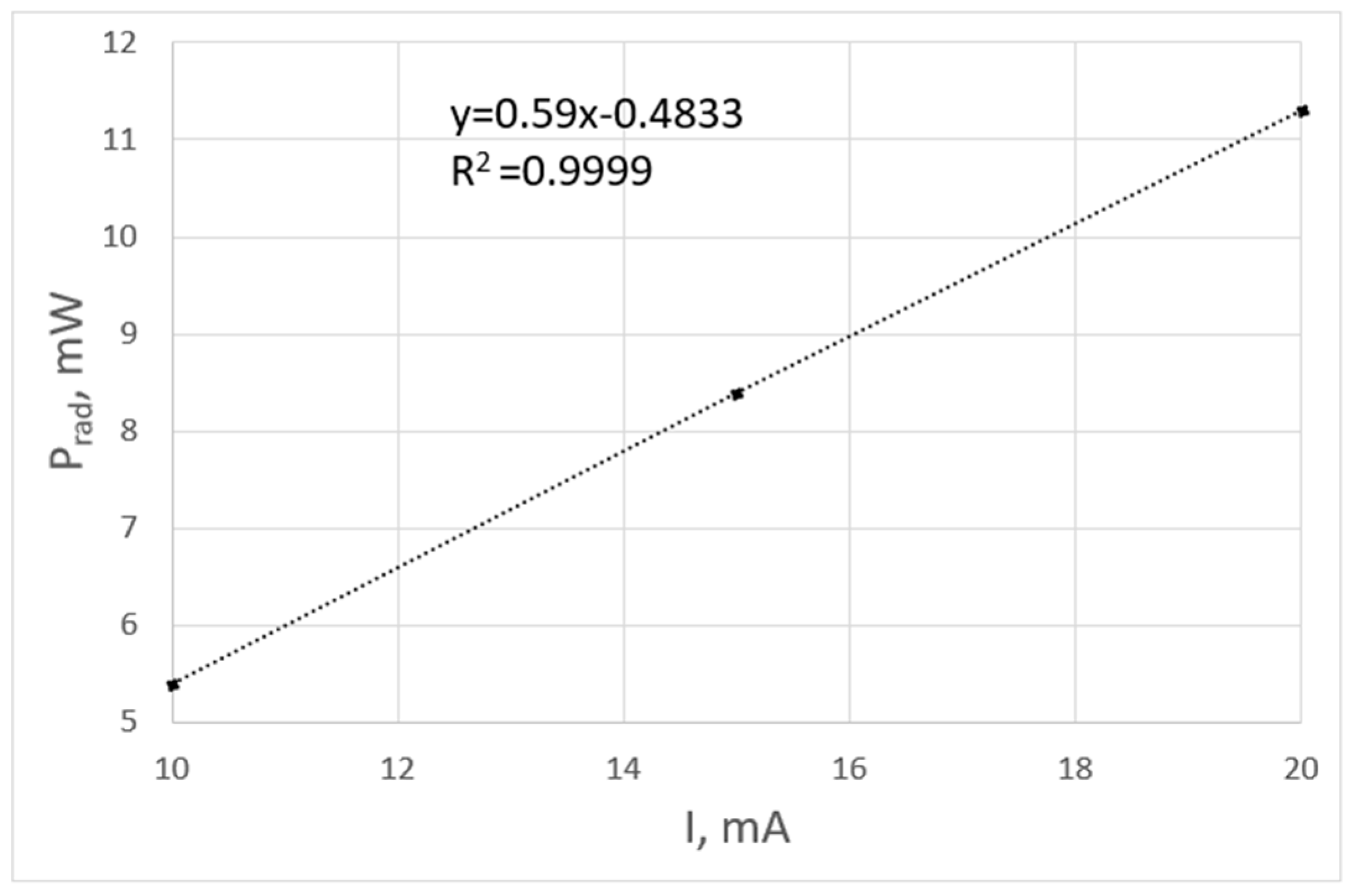
3.2. Optical Power Evaluation
3.3. Uncertainty Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mujahid, M.A.; Panatarani, C.; Maulana, D.W.; Wibawa, B.M.; Joni, I. Integrating sphere design for characterization of LED efficacy. AIP Conf. Proc. 2016, 1712, 030010. [Google Scholar]
- Kong, D.-J.; Kang, C.-M.; Lee, J.-Y.; Kim, J.; Lee, D.-S. Color tunable monolithic InGaN/GaN LED having a multi-junction structure. Opt. Express 2016, 24, A667–A673. [Google Scholar] [CrossRef] [PubMed]
- Horng, R.-H.; Shen, K.-C.; Kuo, Y.-W.; Wuu, D.-S. GaN light emitting diodes with wing-type imbedded contacts. Optics Express 2013, 21, A1–A6. [Google Scholar] [CrossRef] [PubMed]
- Janicki, M.; Ptak, P.; Torzewicz, T.; Górecki, K. Compact Thermal Modeling of Color LEDs—A Comparative Study. IEEE Trans. Electron Devices 2020, 67, 3186–3190. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies 2021, 14, 1286. [Google Scholar] [CrossRef]
- Zwinkels, J.C.; Ikonen, E.; Fox, N.P.; Ulm, G.; Rastello, M.L. Photometry, radiometry and ‘the candela’: Evolution in the classical and quantum world. Metrologia 2010, 47, 5. [Google Scholar] [CrossRef]
- Kasikowski, R.; Więcek, B. Fringing-Effect Losses in Inductors by Thermal Modeling and Thermographic Measurements. IEEE Trans. Power Electron. 2021, 36, 9772–9786. [Google Scholar] [CrossRef]
- Kopeć, M.; Więcek, B. Low-cost IR system for thermal characterization of electronic devices. Meas. Automat. Monitor. 2018, 64, 103–107. [Google Scholar]
- Poppe, A.A. Multi-domain compact modeling of LEDs: An overview of models and experimental data. Microelectron. J. 2015, 46, 1138–1151. [Google Scholar] [CrossRef]
- Ptak, P.; Górecki, K.; Heleniak, J.; Orlikowski, M. Investigations of Electrical and Optical Parameters of Some LED Luminaires—A Study Case. Energies 2021, 14, 1612. [Google Scholar] [CrossRef]
- Kim, Y.-Y.; Joo, J.-Y.; Kim, J.-M.; Lee, S.-K. Compact Measurement of the Optical Power in High-Power LED Using a Light-Absorbent Thermal Sensor. Sensors 2021, 21, 4690. [Google Scholar] [CrossRef] [PubMed]
- Rongier, C.; Gilblas, R.; Le Maoult, Y.; Belkessam, S.; Schmidt, F. Infrared thermography applied to the validation of thermal simulation of high luminance LED used in automotive front lighting. Infrared Phys. Technol. 2022, 120, 103980. [Google Scholar] [CrossRef]
- Chang, C.-H.; Teng, T.-P.; Teng, T.-C. Influence of Ambient Temperature on Optical Characteristics and Power Consumption of LED Lamp for Automotive Headlamp. Appl. Sci. 2022, 12, 11443. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. JCGM 100: Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, Technical Report; Joint Committee for Guides in Metrology: Paris, France, 2008. [Google Scholar]
- Minkina, W.; Dudzik, S. Infrared Thermography: Errors and Uncertainties; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-74718-6. [Google Scholar]
- Minkina, W.; Dudzik, S. Simulation analysis of uncertainty of infrared camera measurement and processing path. Measurement 2006, 39, 758–763. [Google Scholar] [CrossRef]
- EFSA Scientific Committee. Guidance on Uncertainty Analysis in Scientific Assessments. EFSA J. 2018, 16, 1. [Google Scholar]
- Fotowicz, P. A method of approximation of the coverage factor in calibration. Measurement 2004, 35, 251–256. [Google Scholar] [CrossRef]






| Parameter | Value | Description |
|---|---|---|
| kepoxy | 2 W/(m·K) | Thermal conductivity of epoxy resin |
| kCu | 300 W/(m·K) | Thermal conductivity of metal contacts containing mainly copper (wire) |
| Sd | 4.92 × 4.92 × 10−6 m2 | Diode top and bottom surface |
| S1e | 3 × 3 × 10−6 m2 | Epoxy resin replaced cross-section surface |
| S2e | 4.92 × 2.7 × 10−6 m2 | Left and right diode surface |
| S3e | 4.92 × 3 × 10−6 m2 | Side surfaces of the diode |
| r | 300 × 10−6 m | Connecting wire radius |
| d1 | 1.5 × 10−3 m | Half the thickness of the epoxy layer |
| d2 | 2 × 10−3 m | The length of the inner connector to the outer conductor |
| dCu | 2.5 × 10−3 m | The length of the copper pad on which the diode is placed |
| h1 | 10.61 W/m2K | Heat transfer coefficient for the top surface |
| h2 | 5.96 W/m2K | Heat transfer coefficient for the bottom surface |
| h3 | 13.33 W/m2K | Heat transfer coefficient for the side’s surfaces |
| h | 12.09 W/m2K | Heat transfer coefficient for the connecting wire |
| Node No | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| ΔT, °C | 7.07 | 6.93 | 6.99 | 7.07 | 7.07 | 6.98 |
| Measuring Point | Heat Source | Top Surface | Bottom Surface | Electrical Contact 1 | Electrical Contact 2 | Side Surfaces |
|---|---|---|---|---|---|---|
| ΔT°C | 7.46 | 6.95 | 7.02 | 7.26 | 7.24 | 7.11 |
| PelD mW | PelR mW | Tamb °C | Td °C | Tr °C | ΔTd = TD °C | ΔTr = TR °C | P12D mW | P12R mW | Prad mW | η % |
|---|---|---|---|---|---|---|---|---|---|---|
| 38.7 | 87.3 | 26.3 | 33.8 | 47.7 | 7.05 | 20.95 | 1.5 | 11 | 11.55 | 29.80 |
| 38.7 | 87.3 | 26.7 | 33.77 | 47.6 | 7.02 | 20.85 | 1.6 | 9 | 10.77 | 27.79 |
| 38.8 | 87.6 | 27.3 | 33.73 | 47.72 | 6.98 | 20.97 | 1.5 | 9 | 11.15 | 28.77 |
| 38.7 | 87.3 | 26.9 | 33.67 | 47.70 | 6.92 | 20.95 | 1 | 9 | 11.88 | 30.66 |
| 38.7 | 87.2 | 26.8 | 33.47 | 47.52 | 6.72 | 20.77 | 3 | 10 | 10.72 | 27.66 |
| 38.8 | 87.5 | 26.5 | 33.62 | 47.7 | 6.87 | 20.95 | 3 | 10 | 10.39 | 26.82 |
| 38.8 | 87.4 | 26.75 | 33.68 | 47.66 | 6.93 | 20.91 | 1.93 | 9.67 | 11.08 | 28.58 |
| Parameter | Mean Value | uA | uB | uc |
|---|---|---|---|---|
| TD (°C) | 6.93 | 0.05 | 0.08 | 0.09 |
| TR (°C) | 20.91 | 0.03 | 0.24 | 0.24 |
| P12D (mW) | 1.93 | 0.35 | 0.00 | 0.35 |
| P12R (mW) | 9.67 | 0.33 | 0.00 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strąkowska, M.; Urbaś, S.; Felczak, M.; Torzyk, B.; Shatarah, I.S.M.; Kasikowski, R.; Tabaka, P.; Więcek, B. Modelling and Thermographic Measurements of LED Optical Power. Sensors 2024, 24, 1471. https://doi.org/10.3390/s24051471
Strąkowska M, Urbaś S, Felczak M, Torzyk B, Shatarah ISM, Kasikowski R, Tabaka P, Więcek B. Modelling and Thermographic Measurements of LED Optical Power. Sensors. 2024; 24(5):1471. https://doi.org/10.3390/s24051471
Chicago/Turabian StyleStrąkowska, Maria, Sebastian Urbaś, Mariusz Felczak, Błażej Torzyk, Iyad S. M. Shatarah, Rafał Kasikowski, Przemysław Tabaka, and Bogusław Więcek. 2024. "Modelling and Thermographic Measurements of LED Optical Power" Sensors 24, no. 5: 1471. https://doi.org/10.3390/s24051471
APA StyleStrąkowska, M., Urbaś, S., Felczak, M., Torzyk, B., Shatarah, I. S. M., Kasikowski, R., Tabaka, P., & Więcek, B. (2024). Modelling and Thermographic Measurements of LED Optical Power. Sensors, 24(5), 1471. https://doi.org/10.3390/s24051471








