Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm
Abstract
:1. Introduction
- The PMR-Dueling DQN method for mobile robot path planning in complex and dynamic situations is used to address the problems of instability and slow convergence seen in the DQN algorithm. To achieve superior performance in terms of convergence speed, stability, and path planning performance, the algorithm integrates deep neural networks, dueling architecture, Prioritized Experience Replay, and shaped Rewards.
- A more realistic Gazebo simulation setting is used in addition to the traditional grid map. The physical simulation platform, called Gazebo, bridges the gap between the real and virtual environments by offering a simplified model of the environment that is quite similar to the real one. This method guarantees the agent’s learned methods apply to actual robotic environments.
- To address the influence of obstacles, a shaped Reward function is built for each environment model, contributing to the enhancement of the planning path and a boost in the convergence speed of the algorithm by incorporating obstacle avoidance and the distance metrics to the target position. This improvement aims to strike a balance between steering clear of obstacles and progressing toward the target, enabling the robot to devise a path that avoids the area of obstacles which addresses challenges associated with sparse reward problems.
- A comparative analysis is conducted, wherein we evaluate the efficiency of our proposed method by comparing it with traditional Q-learning and other deep reinforcement learning (DRL) algorithms.
2. Related Work
3. Theoretical Foundations
3.1. Deep Q-Network (DQN)
3.2. Deep Dueling Neural Network (Dueling DQN)
3.3. Prioritized Experience Replay
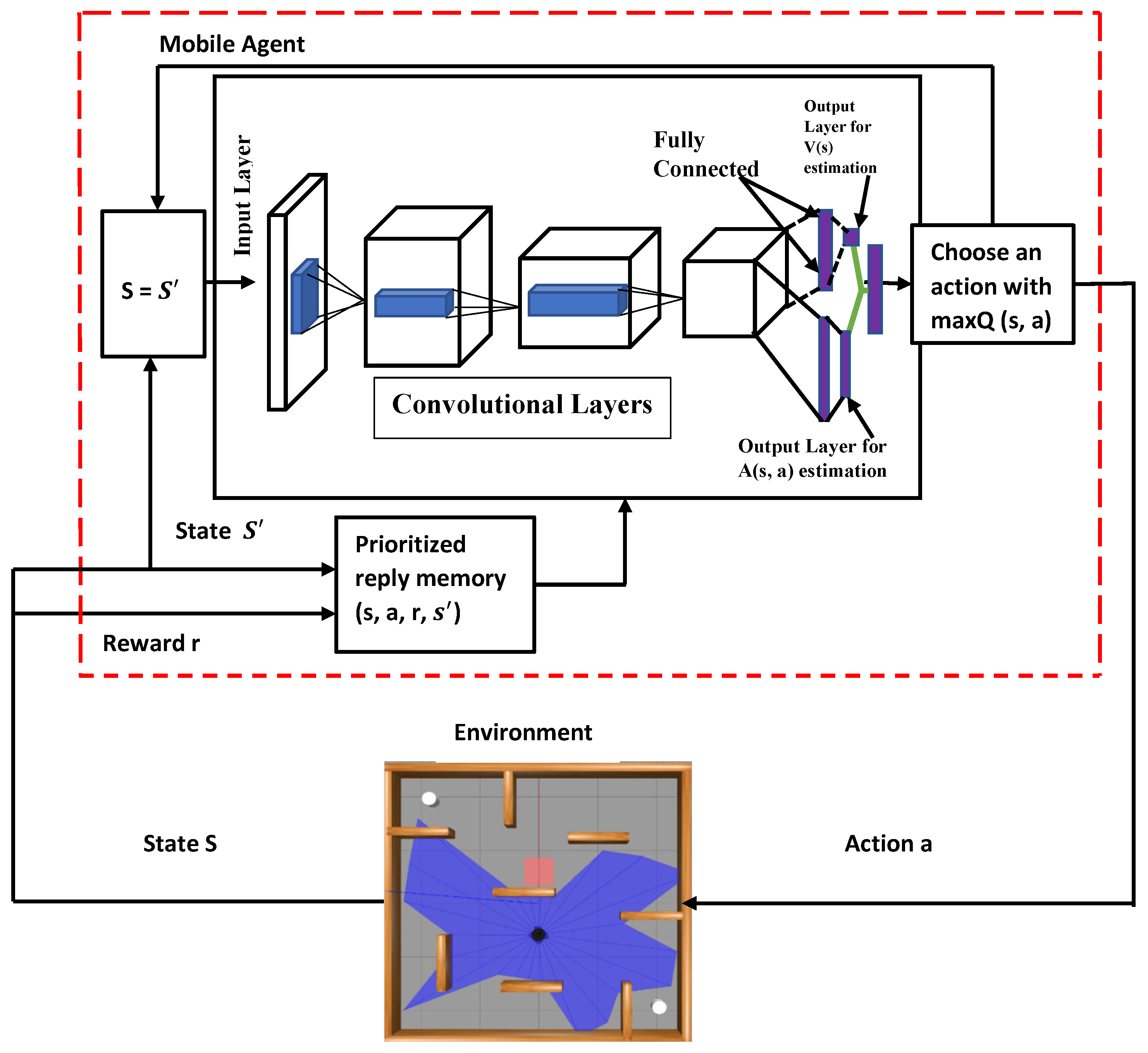
4. Methodology
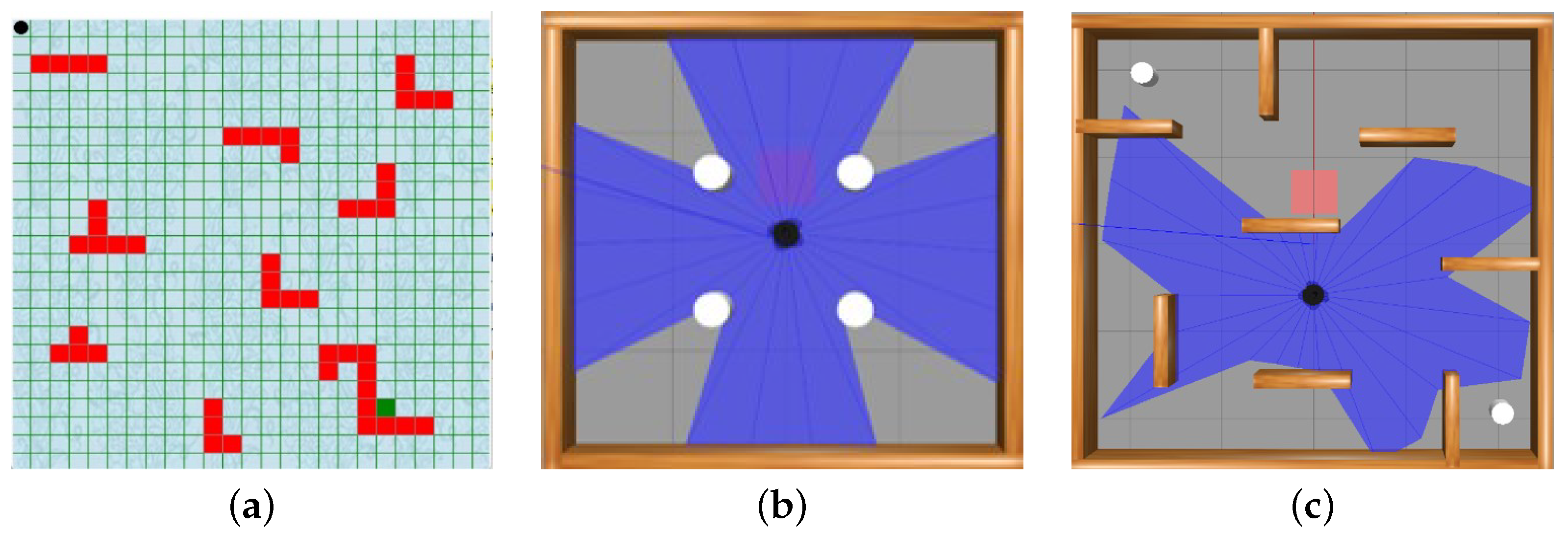
4.1. Simulation Environments and Setup
4.2. State of the Environment
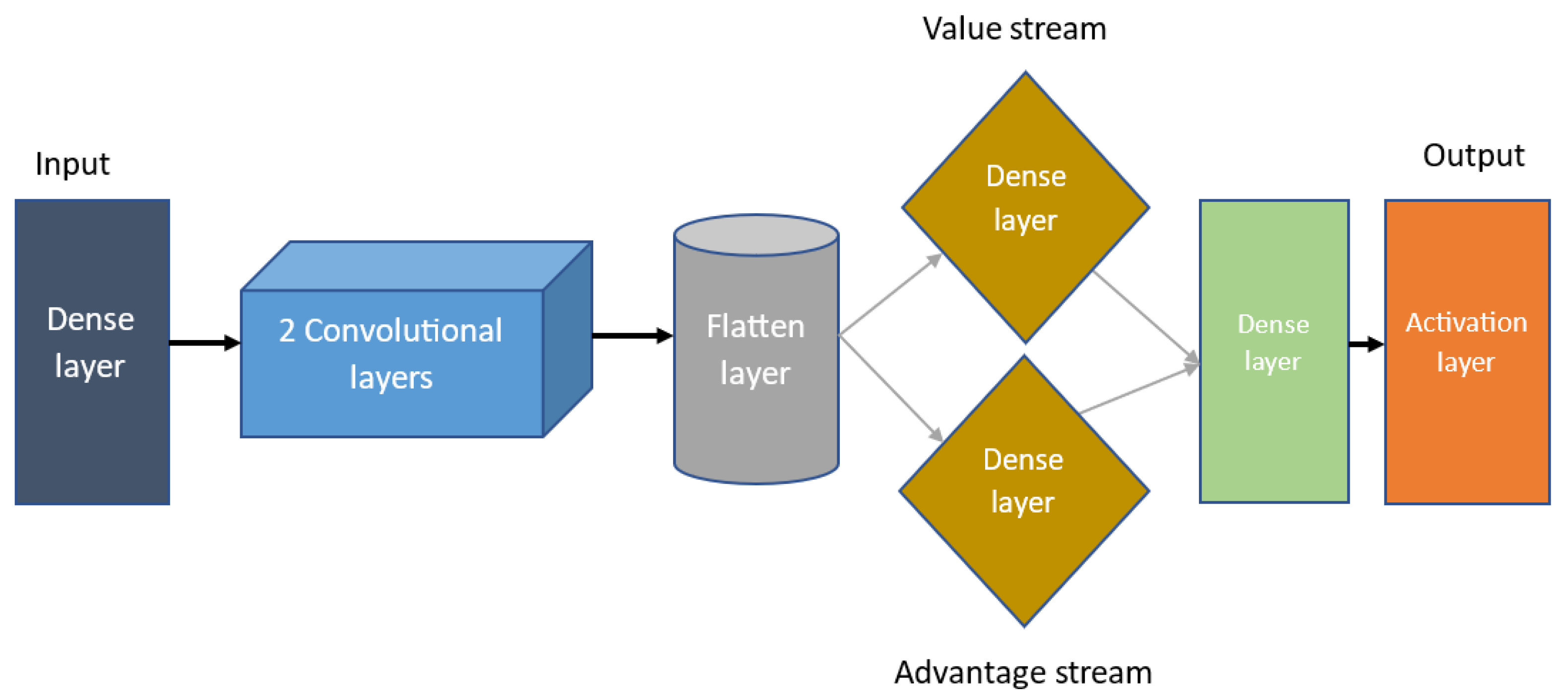
4.3. Network Structure
4.4. Design of Shaped Reward Function
5. Performance Evaluation
5.1. Parameter Settings
| Algorithm 1 Dueling Deep Q-Network with shaped Rewards and Prioritized Experience Replay (PMR-Dueling DQN). |
|
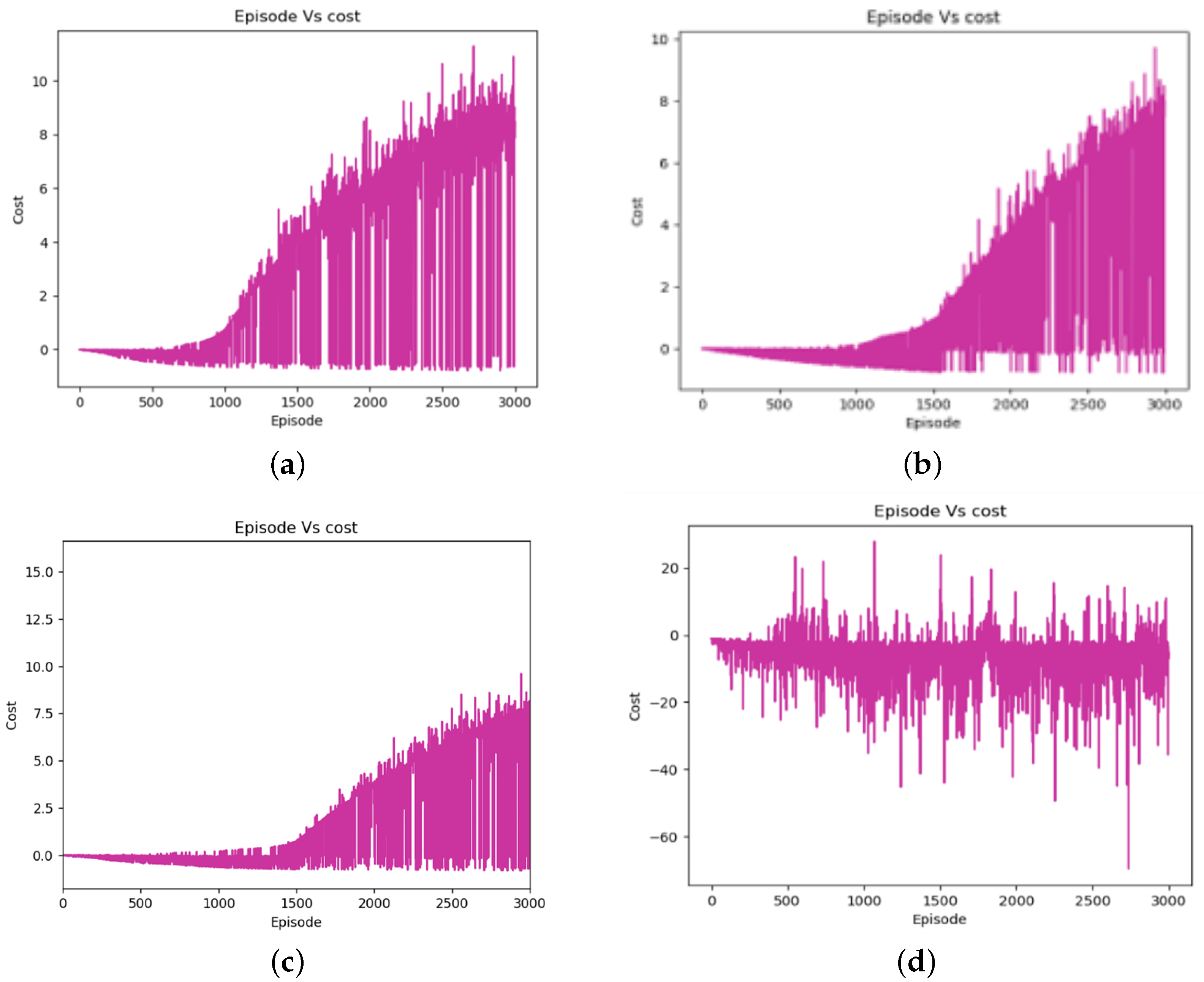
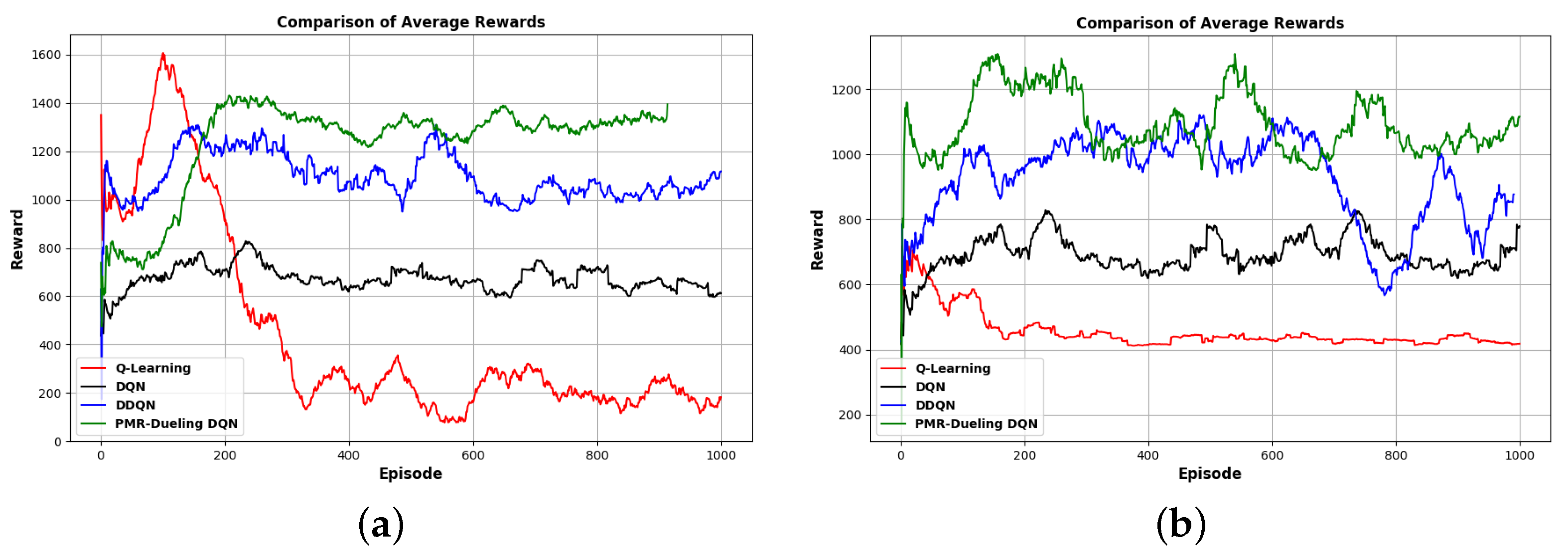
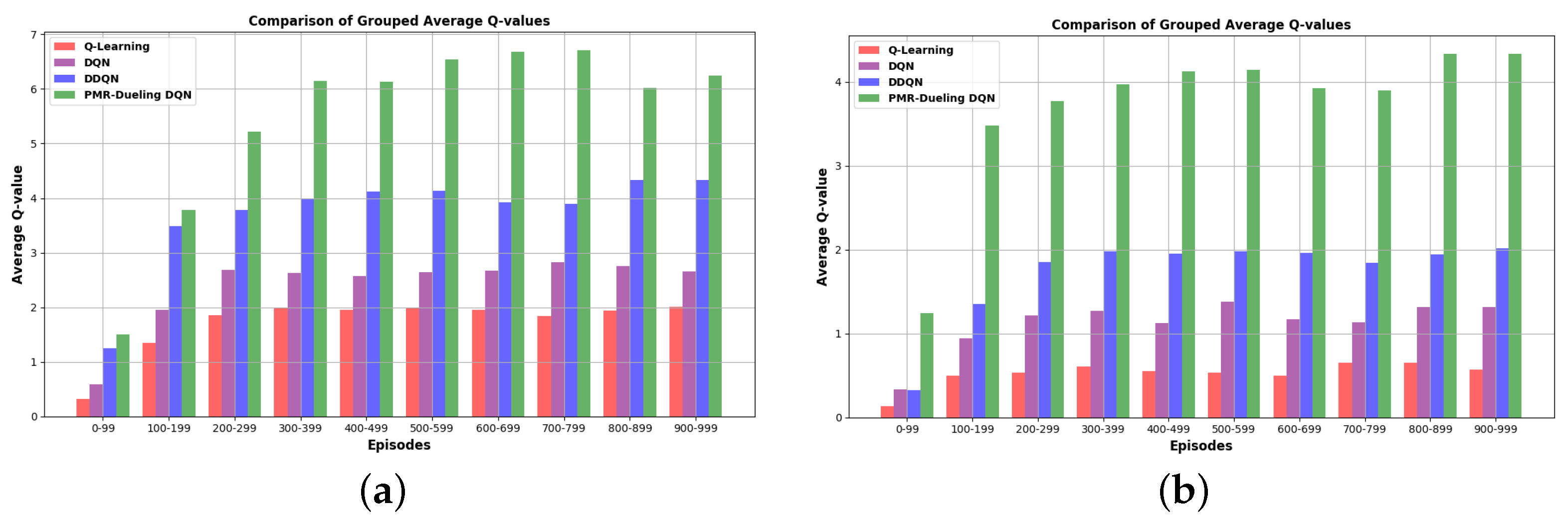
5.2. Simulation Results and Performance Analysis
5.2.1. For the Grid Map Environment (E-1)
5.2.2. For the Gazebo Simulation Environments (E-2 and E-3)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Zafar, M.N.; Mohanta, J. Methodology for path planning and optimization of mobile robots: A review. Procedia Comput. Sci. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Tian, S.; Lei, S.; Huang, Q.; Huang, A. The application of path planning algorithm based on deep reinforcement learning for mobile robots. In Proceedings of the 2022 International Conference on Culture-Oriented Science and Technology (CoST), Lanzhou, China, 18–21 August 2022; IEEE: New York, NY, USA, 2022; pp. 381–384. [Google Scholar] [CrossRef]
- Patle, B.; Babu, L.G.; Pandey, A.; Parhi, D.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Guo, X.; Peng, G.; Meng, Y. A modified Q-learning algorithm for robot path planning in a digital twin assembly system. Int. J. Adv. Manuf. Technol. 2022, 119, 3951–3961. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Holen, M.; Saha, R.; Goodwin, M.; Omlin, C.W.; Sandsmark, K.E. Road detection for reinforcement learning based autonomous car. In Proceedings of the 3rd International Conference on Information Science and Systems, Cambridge, UK, 19–22 March 2020; pp. 67–71. [Google Scholar] [CrossRef]
- Xu, J.; Tian, Y.; Ma, P.; Rus, D.; Sueda, S.; Matusik, W. Prediction-guided multi-objective reinforcement learning for continuous robot control. In Proceedings of the 37th International Conference on Machine Learning PMLR, Virtual, 13–18 July 2020; pp. 10607–10616. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Glimcher, P.W. Understanding dopamine and reinforcement learning: The dopamine reward prediction error hypothesis. Proc. Natl. Acad. Sci. USA 2011, 108, 15647–15654. [Google Scholar] [CrossRef] [PubMed]
- Manju, S.; Punithavalli, M. An analysis of Q-learning algorithms with strategies of reward function. Int. J. Comput. Sci. Eng. 2011, 3, 814–820. [Google Scholar]
- Rupprecht, T.; Wang, Y. A survey for deep reinforcement learning in markovian cyber–physical systems: Common problems and solutions. Neural Netw. 2022, 153, 13–36. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning PMLR, New York, NY, USA, 20–22 June 2016; pp. 1995–2003. [Google Scholar]
- Felner, A. Position paper: Dijkstra’s algorithm versus uniform cost search or a case against dijkstra’s algorithm. In Proceedings of the International Symposium on Combinatorial Search, Barcelona, Spain, 15–16 July 2011; Volume 2, pp. 47–51. [Google Scholar] [CrossRef]
- Nannicini, G.; Delling, D.; Liberti, L.; Schultes, D. Bidirectional A∗ search for time-dependent fast paths. In Proceedings of the Experimental Algorithms: 7th International Workshop, WEA 2008, Provincetown, MA, USA, 30 May–1 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 334–346. [Google Scholar]
- Boor, V.; Overmars, M.H.; Van Der Stappen, A.F. The Gaussian sampling strategy for probabilistic roadmap planners. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; IEEE: New York, NY, USA, 1999; Volume 2, pp. 1018–1023. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-exploring random trees: A new tool for path planning. In Research Report 9811; Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Panov, A.I.; Yakovlev, K.S.; Suvorov, R. Grid path planning with deep reinforcement learning: Preliminary results. Procedia Comput. Sci. 2018, 123, 347–353. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, M.; Wang, X.; Zhang, Y. Reinforcement Learning in Robot Path Optimization. J. Softw. 2012, 7, 657–662. [Google Scholar] [CrossRef]
- Arin, A.; Rabadi, G. Integrating estimation of distribution algorithms versus Q-learning into Meta-RaPS for solving the 0-1 multidimensional knapsack problem. Comput. Ind. Eng. 2017, 112, 706–720. [Google Scholar] [CrossRef]
- Fang, M.; Li, H. Heuristically accelerated state backtracking Q-learning based on cost analysis. Int. J. Pattern Recognit. Artif. Intell. 2013, 35, 838–844. [Google Scholar]
- Wang, Y.H.; Li, T.H.S.; Lin, C.J. Backward Q-learning: The combination of Sarsa algorithm and Q-learning. Eng. Appl. Artif. Intell. 2013, 26, 2184–2193. [Google Scholar] [CrossRef]
- Duguleana, M.; Mogan, G. Neural networks based reinforcement learning for mobile robots obstacle avoidance. Expert Syst. Appl. 2016, 62, 104–115. [Google Scholar] [CrossRef]
- Rakshit, P.; Konar, A.; Bhowmik, P.; Goswami, I.; Das, S.; Jain, L.C.; Nagar, A.K. Realization of an adaptive memetic algorithm using differential evolution and Q-learning: A case study in multirobot path planning. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 814–831. [Google Scholar] [CrossRef]
- Carlucho, I.; De Paula, M.; Wang, S.; Petillot, Y.; Acosta, G.G. Adaptive low-level control of autonomous underwater vehicles using deep reinforcement learning. Robot. Auton. Syst. 2018, 107, 71–86. [Google Scholar] [CrossRef]
- Kayakoku, H.; Guzel, M.S.; Bostanci, E.; Medeni, I.T.; Mishra, D. A novel behavioral strategy for RoboCode platform based on deep Q-learning. Complexity 2021, 2021, 9963018. [Google Scholar] [CrossRef]
- Gao, X.; Luo, H.; Ning, B.; Zhao, F.; Bao, L.; Gong, Y.; Xiao, Y.; Jiang, J. RL-AKF: An adaptive kalman filter navigation algorithm based on reinforcement learning for ground vehicles. Remote. Sens. 2020, 12, 1704. [Google Scholar] [CrossRef]
- You, C.; Lu, J.; Filev, D.; Tsiotras, P. Advanced planning for autonomous vehicles using reinforcement learning and deep inverse reinforcement learning. Robot. Auton. Syst. 2019, 114, 1–18. [Google Scholar] [CrossRef]
- Maeda, Y.; Watanabe, T.; Moriyama, Y. View-based programming with reinforcement learning for robotic manipulation. In Proceedings of the 2011 IEEE International Symposium on Assembly and Manufacturing (ISAM), Tampere, Finland, 25–27 May 2011; IEEE: New York, NY, USA, 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, Z. Application of optimized q learning algorithm in reinforcement learning. Bull. Sci. Technol. 2018, 34, 74–76. [Google Scholar]
- Wu, Z.; Yin, Y.; Liu, J.; Zhang, D.; Chen, J.; Jiang, W. A Novel Path Planning Approach for Mobile Robot in Radioactive Environment Based on Improved Deep Q Network Algorithm. Symmetry 2023, 15, 2048. [Google Scholar] [CrossRef]
- Escobar-Naranjo, J.; Caiza, G.; Ayala, P.; Jordan, E.; Garcia, C.A.; Garcia, M.V. Autonomous Navigation of Robots: Optimization with DQN. Appl. Sci. 2023, 13, 7202. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar] [CrossRef]
- Quan, L.; Yan, Y.; Fei, Z. A Deep Recurrent Q Network with Exploratory Noise. Chin. J. Comput. 2019, 42, 1588–1604. [Google Scholar]
- Xia, Z.; Qin, J. An improved algorithm for deep Q-network. J. Comput. Appl. Res. 2019, 36, 3661–3665. [Google Scholar]
- Kim, K.S.; Kim, D.E.; Lee, J.M. Deep learning based on smooth driving for autonomous navigation. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: New York, NY, USA, 2018; pp. 616–621. [Google Scholar] [CrossRef]
- Ruan, X.; Ren, D.; Zhu, X.; Huang, J. Mobile robot navigation based on deep reinforcement learning. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; IEEE: New York, NY, USA, 2019; pp. 6174–6178. [Google Scholar] [CrossRef]
- Chen, G.; Pan, L.; Chen, Y.; Xu, P.; Wang, Z.; Wu, P.; Ji, J.; Chen, X. Deep Reinforcement Learning of Map-Based Obstacle Avoidance for Mobile Robot Navigation. SN Comput. Sci. 2021, 2, 417. [Google Scholar] [CrossRef]
- Zhou, F.Y.; Jin, L.P.; Dong, J. Review of convolutional neural network. J. Comput. 2017, 40, 1229–1251. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar] [CrossRef]








| Software | Hardware |
|---|---|
| Python 3.7 | 16 GB RAM memory |
| TensorFlow (backend for Keras) https://www.tensorflow.org/ | Nvidia GeForce GTX 1050 GPU |
| Robot Operating System (ros melodic) | Intel Core i5-9300H CPU |
| Gazebo 9 | - |
| Parameter | For E-1 | For E-2 and E-3 |
|---|---|---|
| Number of episodes | 3000 | 1000 |
| Learning rate | 0.01 | 0.00025 |
| Discount factor | 0.9 | 0.99 |
| Minibatch size | 32 | 128 |
| Replay memory size | 10,000 | 10,000 |
| 0.5 | 0.6 | |
| 0.5 | 0.4 |
| Status | Action to Up | Action to Down | Action to Right | Action to Left |
|---|---|---|---|---|
| Performance Parameters | PMR-DQN | DDQN | DQN | Q-Learning |
|---|---|---|---|---|
| Episodes | 3000 | 3000 | 3000 | 3000 |
| Shortest path steps | 40 | 43 | 72 | 103 |
| Longest path steps | 1577 | 1798 | 3579 | 5909 |
| Success rate (%) | 94.3 | 83.7 | 62.84 | 37.43 |
| Method | Success Rate | Convergence Time/min |
|---|---|---|
| Algorithm comparisons on environment E-2 | ||
| Q-learning | 26.7 | 268 |
| DQN | 49.3 | 139 |
| DDQN | 56.4 | 116 |
| PMR-Dueling DQN | ||
| Algorithm comparisons on environment E-3 | ||
| Q-learning | 21.4 | 276 |
| DQN | 32.6 | 161 |
| DDQN | 41.5 | 143 |
| PMR-Dueling DQN | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deguale, D.A.; Yu, L.; Sinishaw, M.L.; Li, K. Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm. Sensors 2024, 24, 1523. https://doi.org/10.3390/s24051523
Deguale DA, Yu L, Sinishaw ML, Li K. Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm. Sensors. 2024; 24(5):1523. https://doi.org/10.3390/s24051523
Chicago/Turabian StyleDeguale, Demelash Abiye, Lingli Yu, Melikamu Liyih Sinishaw, and Keyi Li. 2024. "Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm" Sensors 24, no. 5: 1523. https://doi.org/10.3390/s24051523
APA StyleDeguale, D. A., Yu, L., Sinishaw, M. L., & Li, K. (2024). Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm. Sensors, 24(5), 1523. https://doi.org/10.3390/s24051523





