1 V Electronically Tunable Differential Difference Current Conveyors Using Multiple-Input Operational Transconductance Amplifiers
Abstract
:1. Introduction
2. Proposed Electronically Tunable Current Conveyors
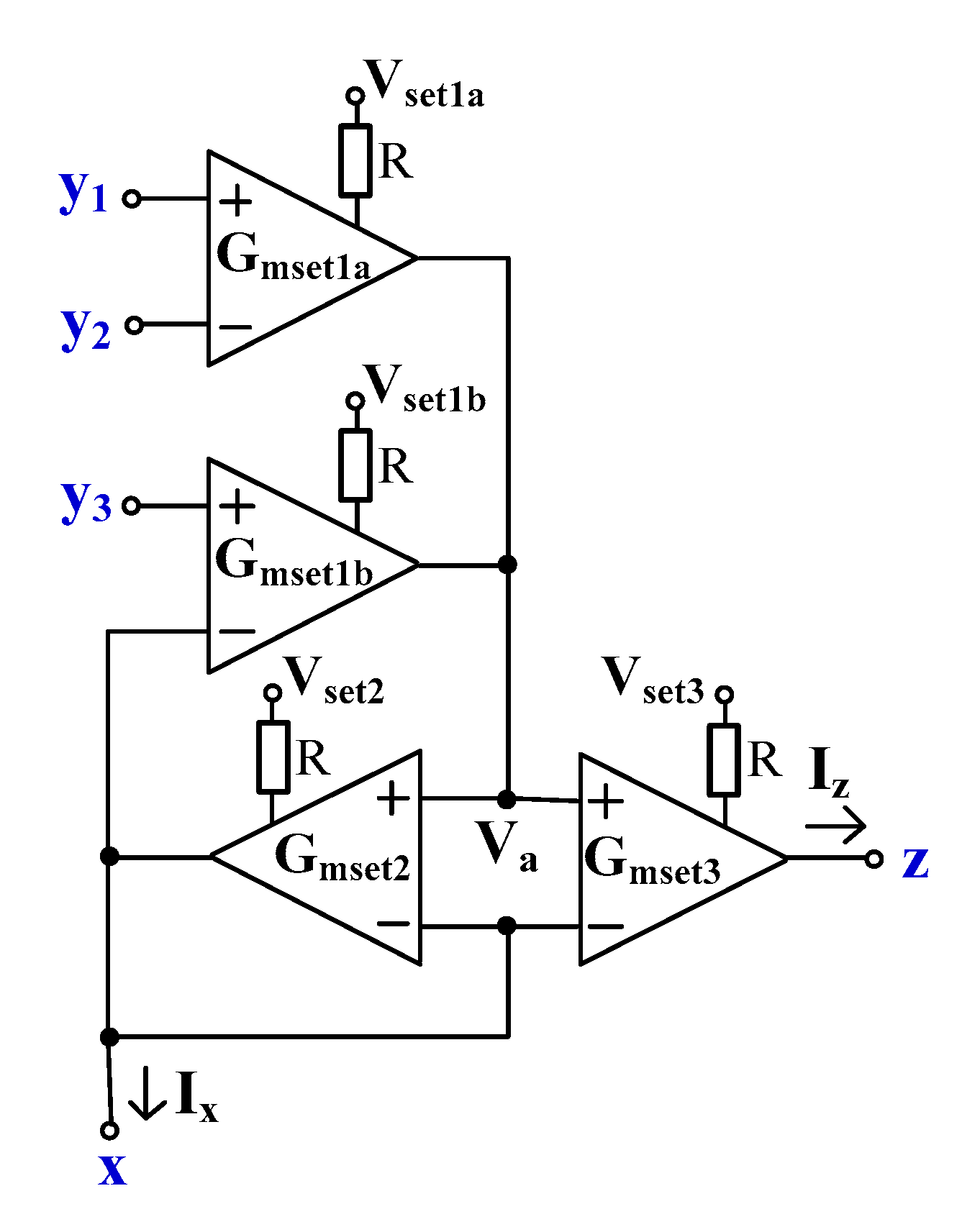
2.1. The Multiple-Input Operational Transconductance Amplifier
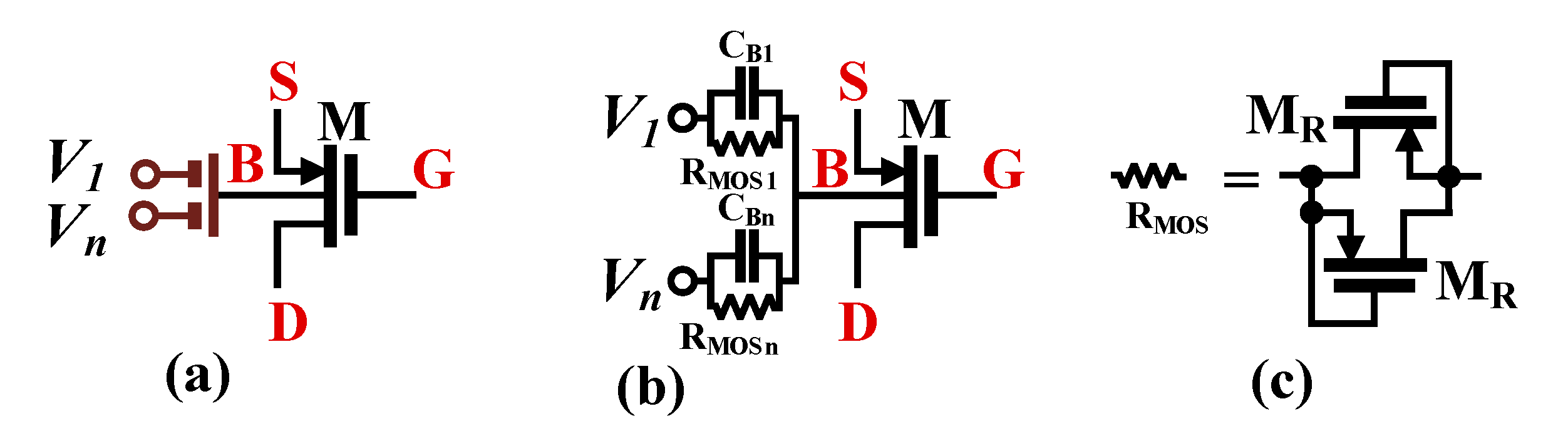
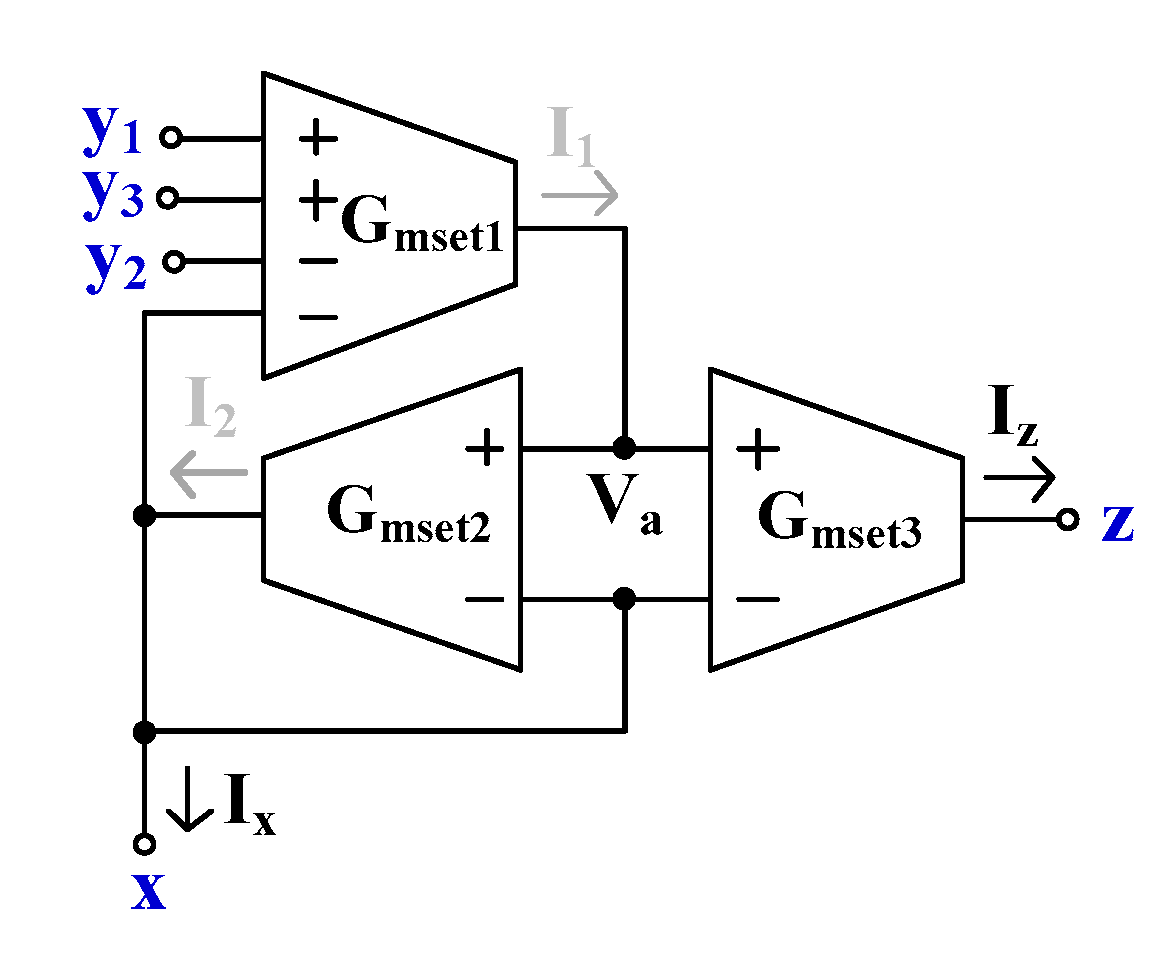
2.2. Proposed Electronically Tunable Current Conveyors

3. Applications of the EDDCC
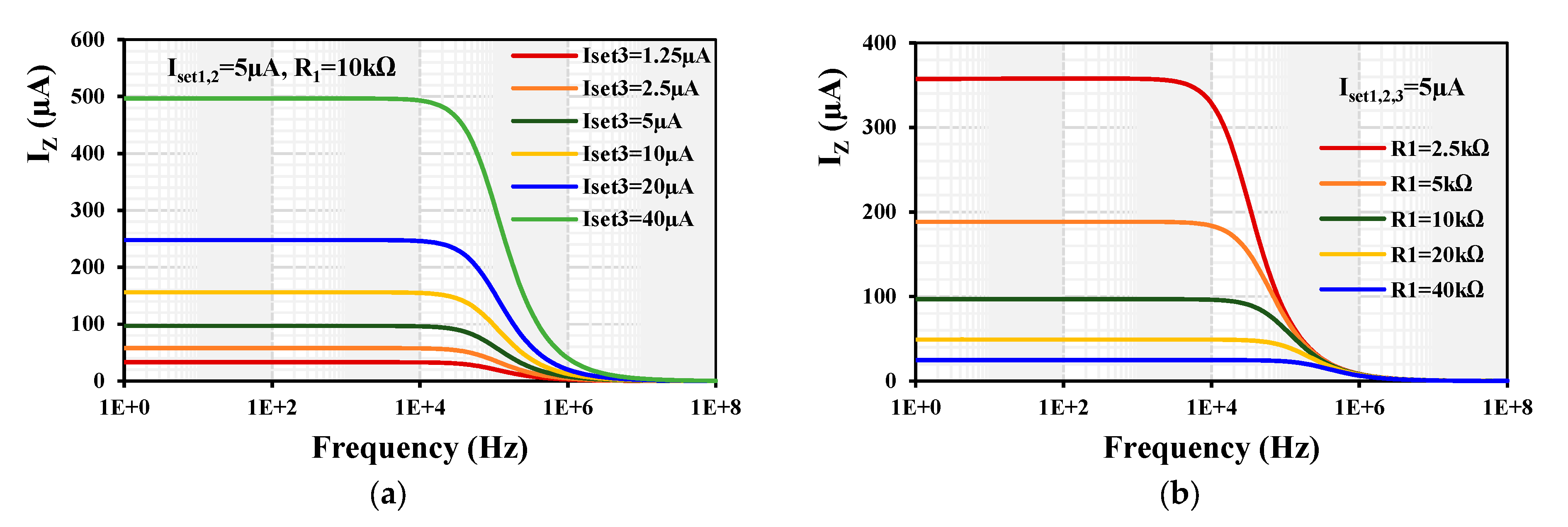
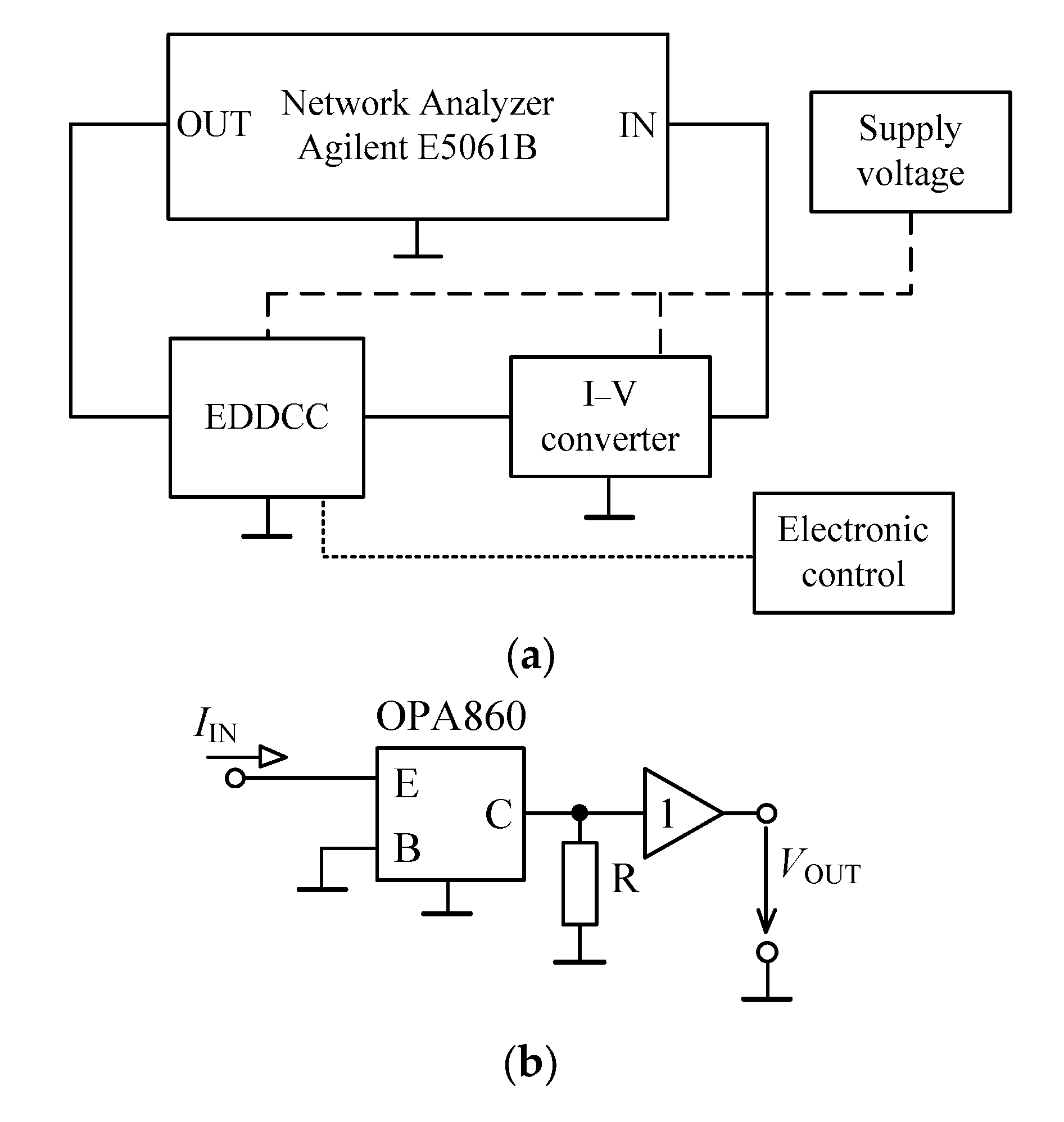
3.1. V-to-I Converter Using EDDCC
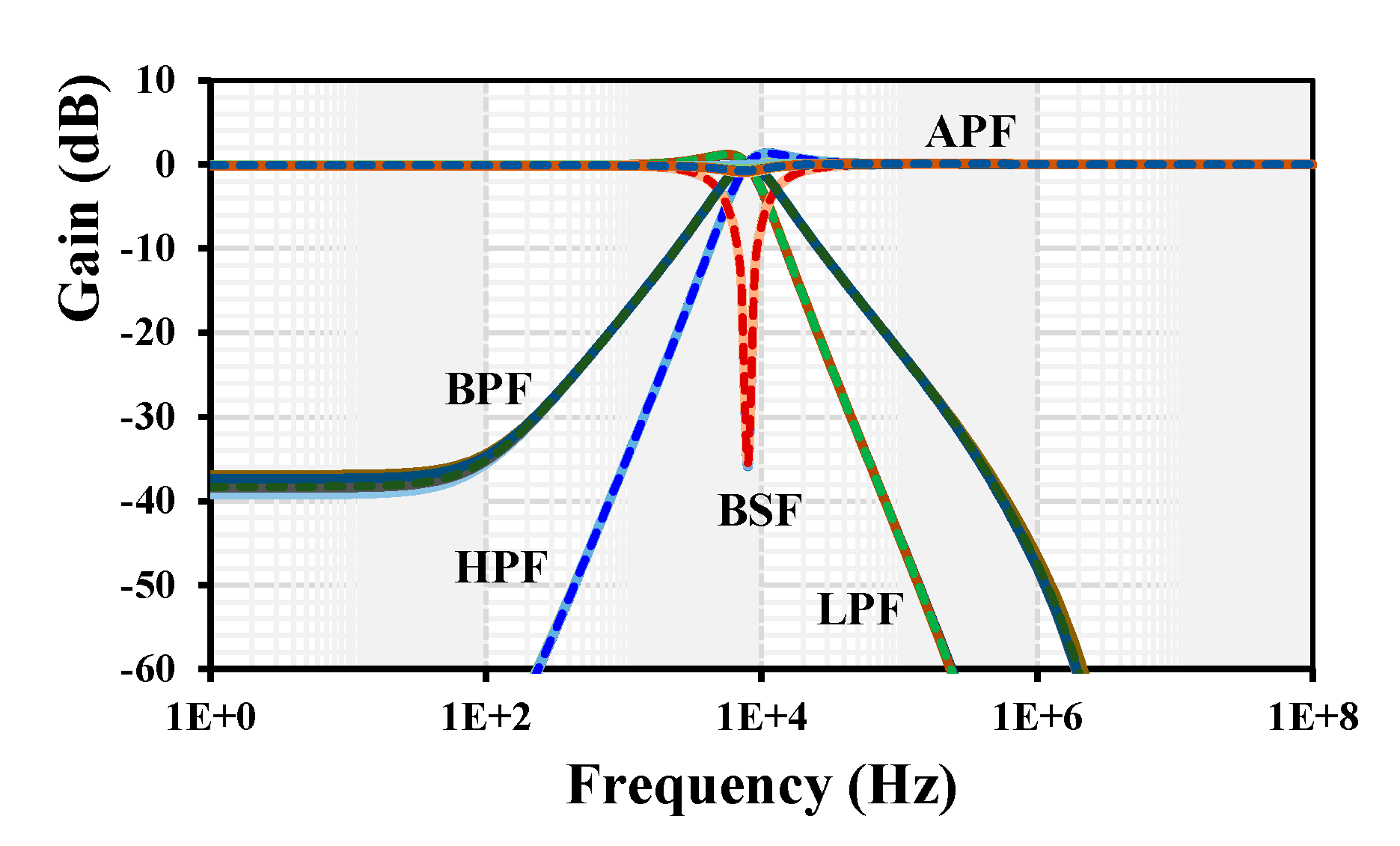
3.2. Current-Mode Universal Filter Using EDDCCs
3.3. Non-Ideal Analysis
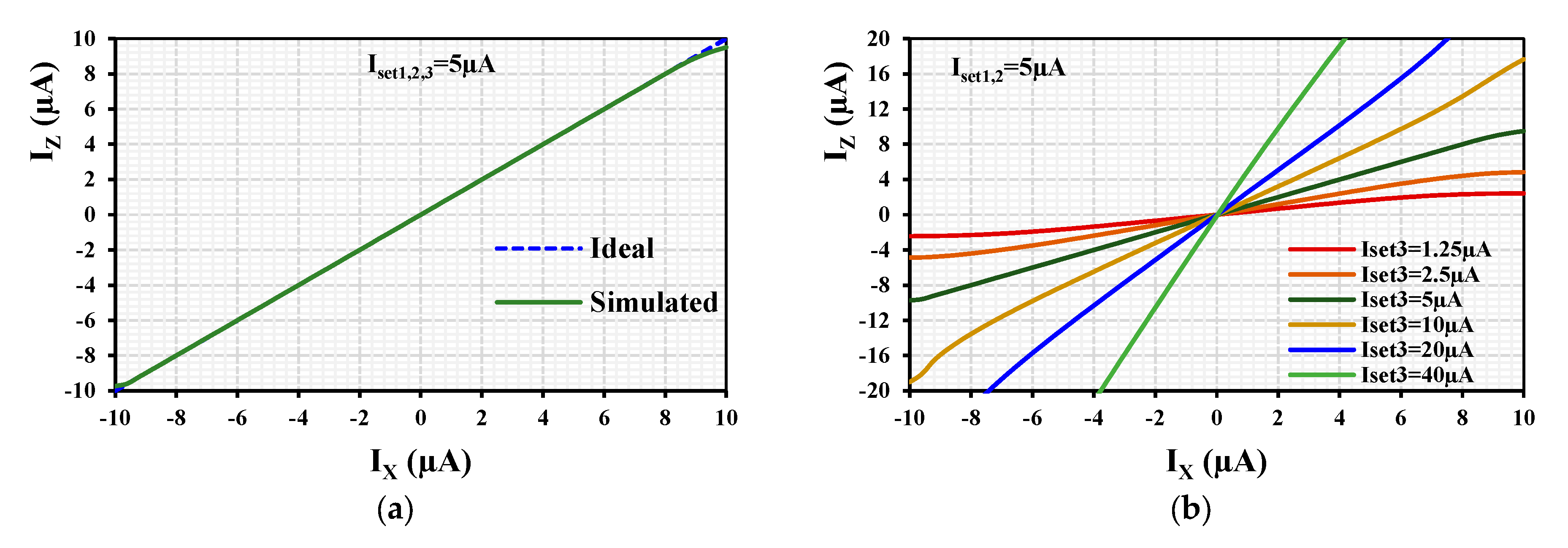
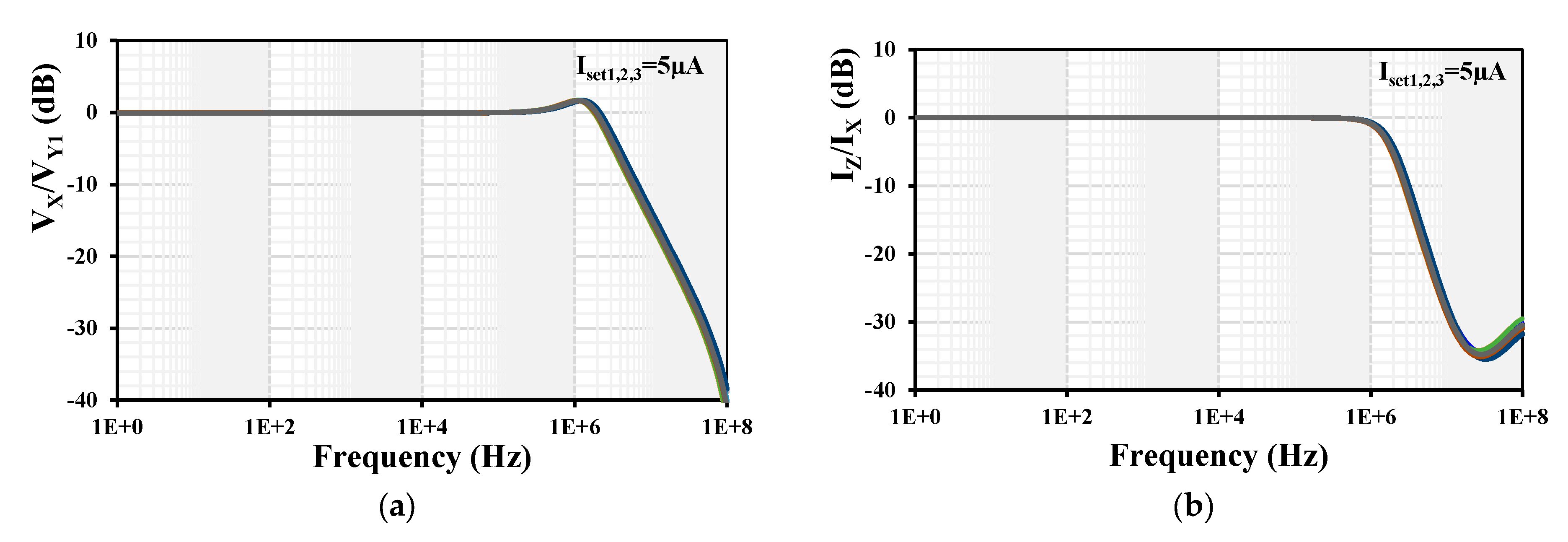
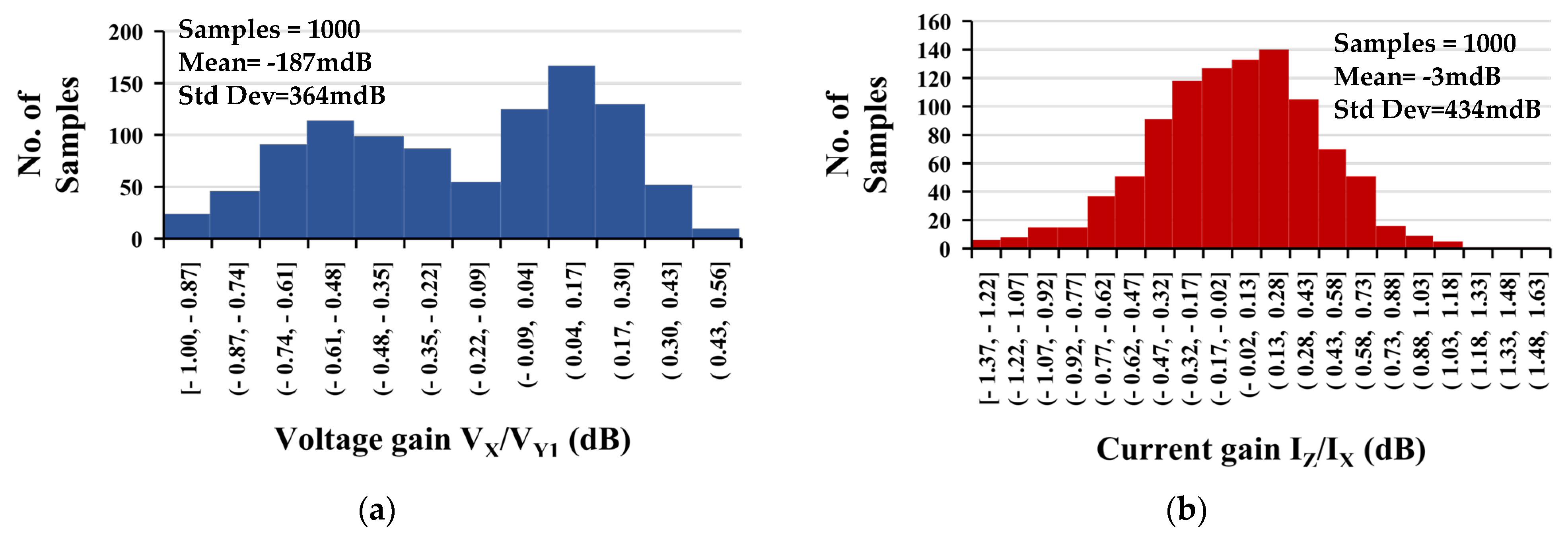
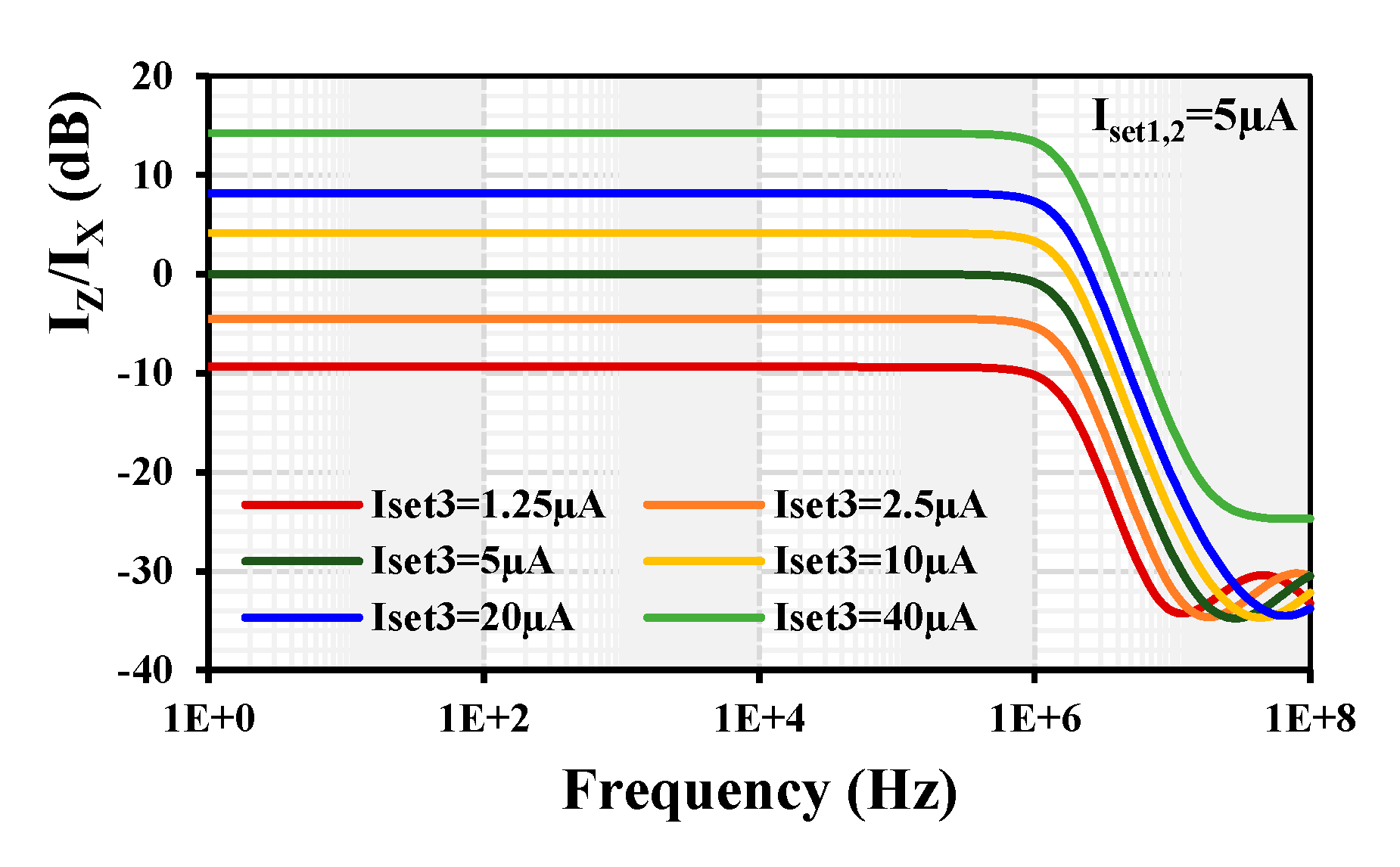
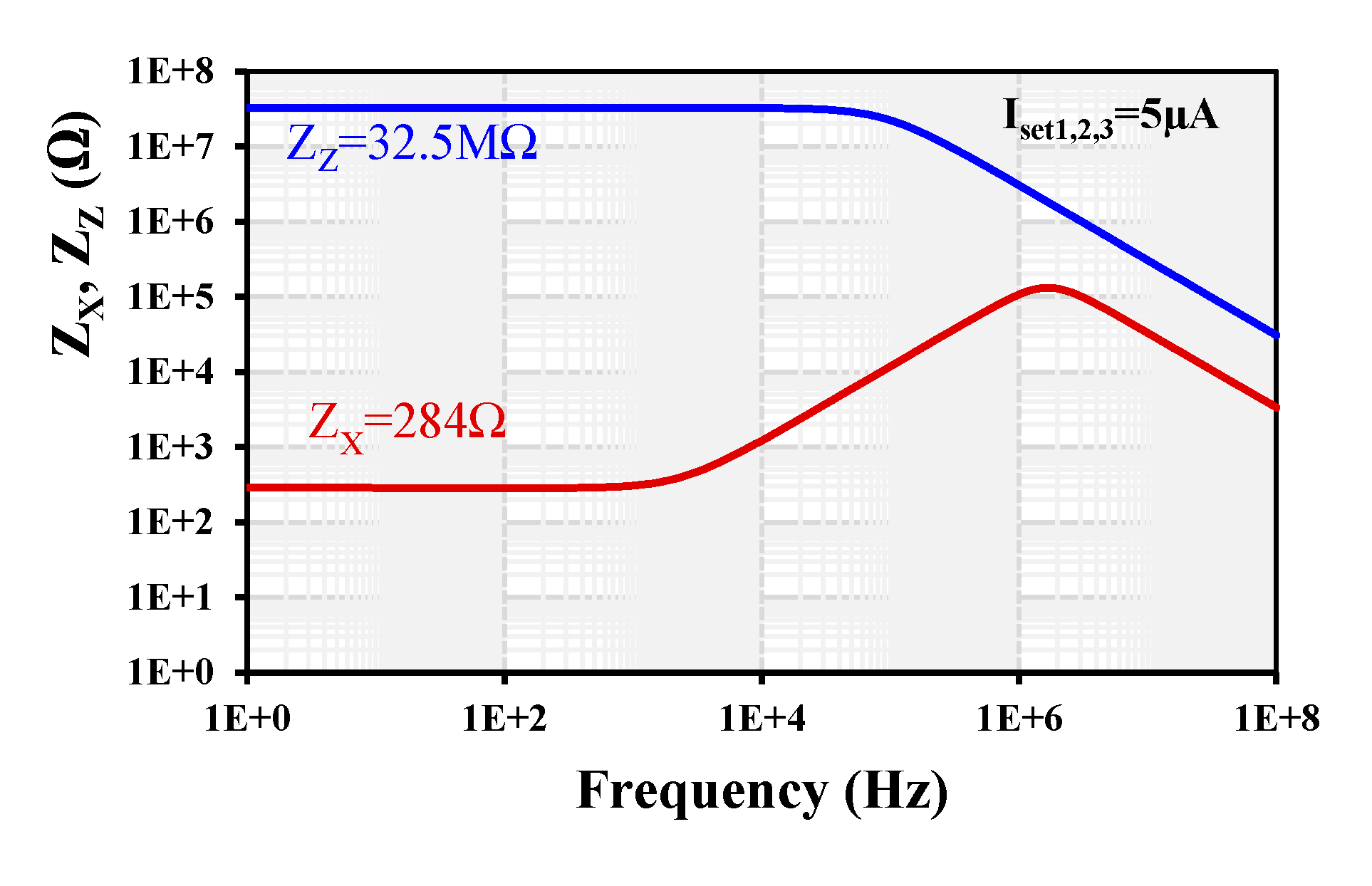
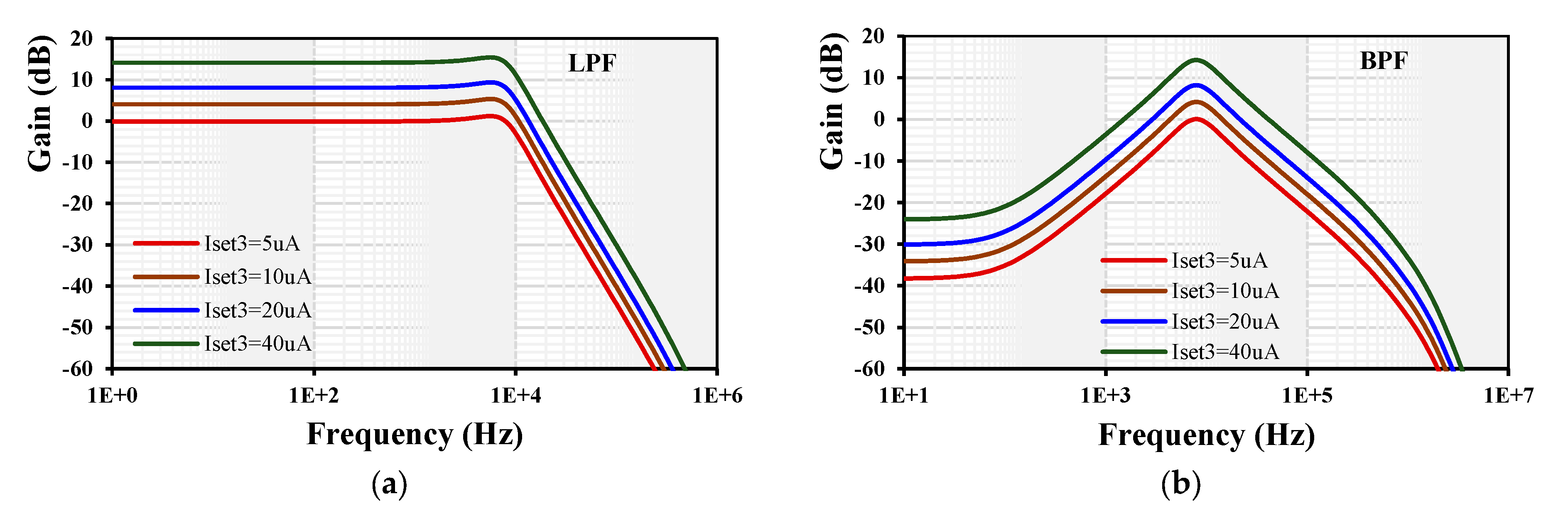
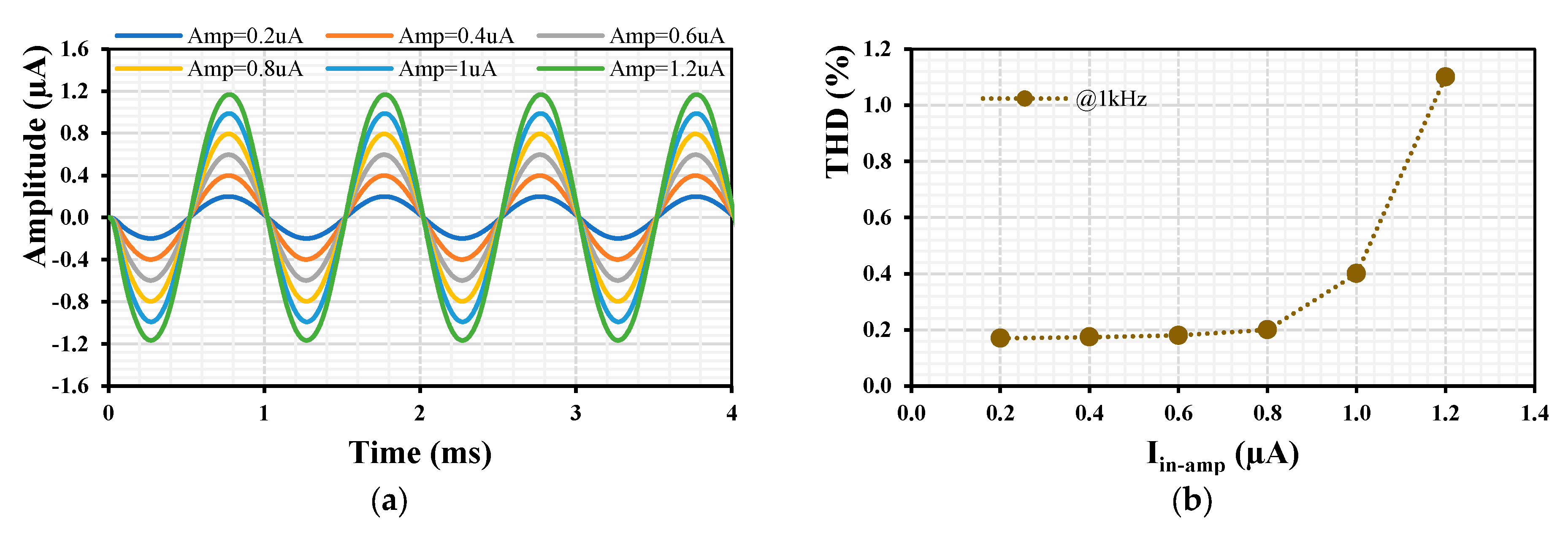
4. Simulation Results
5. Experimental Measurements
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kennedy, E.J. Operational Amplifier Circuits: Theory and Applications; Holt, Rinehart, and Winston: Austin, TX, USA, 1988. [Google Scholar]
- Sedra, A.; Smith, K.C. A second-generation current conveyor and its applications. IEEE Trans. Circuit Theory 1970, 17, 132–134. [Google Scholar] [CrossRef]
- Soliman, A.M. Current-mode universal filters using current conveyors: Classification and review. Circuits Syst. Signal Process. 2008, 27, 405–427. [Google Scholar] [CrossRef]
- Yucel, F.; Yuce, E. Grounded capacitor based fully cascadable electronically tunable current-mode universal filter. AEU-Int. J. Electron. Commun. 2017, 79, 116–123. [Google Scholar] [CrossRef]
- Yucehan, T.; Yuce, E. CCII-based voltage-mode and current-mode high-order filters with gains and grounded passive elements only. AEU-Int. J. Electron. Commun. 2022, 155, 154346. [Google Scholar] [CrossRef]
- Signh, D.; Paul, S.K. Improved current mode biquadratic shadow universal filter. Inf. MIDEM 2022, 52, 51–66. [Google Scholar] [CrossRef]
- Soliman, A.M. New grounded-capacitor current-mode oscillators using single-output CCIIs. J. Circuits Syst. Comput. 1998, 8, 363–378. [Google Scholar] [CrossRef]
- Horng, J.-W. A sinusoidal oscillator using current-controlled conveyors. Int. J. Electron. 2001, 88, 659–664. [Google Scholar] [CrossRef]
- Soliman, A.M. Current mode CCII oscillators using grounded capacitors and resistors. Int. J. Circuit Theory Appl. 1998, 26, 431–438. [Google Scholar] [CrossRef]
- Bajer, J.; Lahiri, A.; Biolek, D. Current-mode CCII+ based oscillator circuits using a conventional and a modified Wien-bridge with all capacitors grounded. Radioengineering 2011, 20, 245–250. [Google Scholar]
- Koton, J.; Herencsar, N.; Vrba, K. Current and voltage conveyors in current- and voltage-mode precision full-wave rectifiers. Radioengineering 2011, 20, 19–24. [Google Scholar]
- Monpapassorn, A. Low output impedance dual CCII full-wave rectifier. Int. J. Electron. 2013, 100, 648–654. [Google Scholar] [CrossRef]
- Petrovic, P.B. Current/voltage mode full-wave rectifier based on a single CCCII. Int. J. Circuit Theory Appl. 2020, 48, 1140–1153. [Google Scholar] [CrossRef]
- Chiu, W.; Liu, S.-I.; Tsao, H.-W.; Chen, J.-J. CMOS differential difference current conveyors and their applications. IEE Proceeding Circuits Devices Syst. 1996, 143, 91–96. [Google Scholar] [CrossRef]
- Elwan, H.O.; Soliman, A.M. Novel CMOS differential voltage current conveyor and its application. IEE Proc.-Circuits Devices Syst. 1997, 144, 195–200. [Google Scholar] [CrossRef]
- El-Adawy, A.A.; Soliman, A.M.; Elwan, H.O. A novel fully differential current conveyor and applications for analog VLSI. IEEE Trans. Circuits Syst.-II 2000, 47, 306–313. [Google Scholar] [CrossRef]
- Alzaher, H.A.; Elwan, H.; Ismail, M. A CMOS fully balanced second-generation current conveyor. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2003, 50, 278–287. [Google Scholar] [CrossRef]
- Reda, A.; Ibrahim, M.F.; Farag, F. Input–output Rail-to-Rail CMOS CCII for low voltage–low power applications. Microelectron. J. 2016, 48, 60–75. [Google Scholar] [CrossRef]
- Stornelli, V.; Pantoli, L.; Ferri, G.; Liberati, L.; Centurelli, F.; Monsurrò, P. Trifiletti. The AB-CCII, a novel adaptive biasing LV-LP current conveyor architecture. AEU-Int. J. Electron. Commun. 2017, 79, 301–306. [Google Scholar] [CrossRef]
- El Beqal, A.; Benhala, B.; Zorkani, I. Design of low-voltage low-power CMOS second generation current conveyor by using the genetic algorithm. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 3–4 March 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Khateb, F.; Kumngern, M.; Spyridon, V.; Psychalinos, C. Differential difference current conveyor using bulk-driven technique for ultra-low-voltage applications. Circuits Syst. Signal Process. 2014, 33, 159–176. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. 0.3 V differential difference current conveyor using multiple-input bulk-driven technique. Circuits Syst. Signal Process. 2020, 39, 3189–3205. [Google Scholar] [CrossRef]
- Fani, R.; Farshidi, E. A FG-MOS based fully differential current controlled conveyor and its applications. Circuits Syst. Signal Process. 2013, 32, 993–1011. [Google Scholar] [CrossRef]
- Suwansawang, S.; Thongleam, T. A 1-V bulk-driven CMOS fully differential second-generation current conveyor. In Proceedings of the 2013 International Symposium on Intelligent Signal Processing and Communication Systems, Naha, Japan, 12–15 November 2013; pp. 662–665. [Google Scholar] [CrossRef]
- Veerendranath, P.S.; Singh, S. 0.5 V, 10.94 μW, 36.89 μVrms IRN, 3rd order bulk-driven quadrature filter using fully differential current conveyor for bluetooth applications. Analog Integr. Circuits Signal Process. 2021, 109, 57–67. [Google Scholar] [CrossRef]
- Chunhua, W.; Qiujing, Z.; Haiguang, L. CMOS current controlled fully balanced current conveyor. J. Semicond. 2009, 30, 075009. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. Bulk-driven fully balanced second-generation current conveyor in 0.18 µm CMOS. AEU-Int. J. Electron. Commun. 2019, 104, 66–75. [Google Scholar] [CrossRef]
- Veerendranath, P.S.; Sharma, V.; Vasantha, M.H.; Kumar, Y.B.N. ±0.5 V, 254 μW second-order tunable biquad low-pass filter with 7.3 fJ FOM using a novel low-voltage fully balanced current-mode circuit. Circuits Syst. Signal Process. 2021, 40, 2114–2134. [Google Scholar] [CrossRef]
- Senani, R. Novel circuit implementation of current conveyors using an OA and an OTA. Electron. Lett. 1980, 16, 2–3. [Google Scholar] [CrossRef]
- Surakampontorn, W.; Thitimajshima, P. Integrable electronically tunable current conveyors. IEE Proc. G (Electron. Circuits Syst.) 1988, 135, 71–77. [Google Scholar] [CrossRef]
- Fabre, A.; Mimeche, N. Class A/AB second generation current conveyor with controlled current gain. Electron. Lett. 1996, 43, 82–91. [Google Scholar] [CrossRef]
- Surakampontorn, W.; Kumwachara, K. CMOS-based electronically tunable current conveyor. Electron. Lett. 1992, 28, 1316–1317. [Google Scholar] [CrossRef]
- Mimaei, S.; Sayin, O.K.; Kuntman, H. A New CMOS electronically tunable current conveyor and its application to current-mode filters. IEEE Trans. Circuits Syst.–I Regul. Pap. 2006, 53, 1448–1458. [Google Scholar] [CrossRef]
- Song, S.-X.; Xie, H.-G.; Huang, S.-L. A new CMOS electronically tunable current conveyor based on programmable current amplifier. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 23–25 September 2011; pp. 1043–1046. [Google Scholar] [CrossRef]
- Yamacli, S.; Ozcan, S.; Kuntman, H. A novel active circuit building block: Electronically tunable differential difference current conveyor (EDDCC) and its application to KEN filter design. In Proceedings of the 2006 International Conference on Applied Electronics, Pilsen, Czech Republic, 6–7 September 2006; pp. 237–240. [Google Scholar] [CrossRef]
- Knobnob, B. Electronically tunable differential difference current conveyor using commercially available OTAS. J. Circuits Syst. Comput. 2023, 32, 2350295. [Google Scholar] [CrossRef]
- Altun, M.; Kuntman, H.; Minaei, S.; Sayin, O.K. Realisation of nth-order current transfer function employing ECCIIs and application examples. Int. J. Electron. 2009, 96, 1115–1126. [Google Scholar] [CrossRef]
- Jaroslav, K.; Norbert, H.; Oguzhan, C.; Kamil, V. Current-mode KHN equivalent frequency filter using ECCIIs. In Proceedings of the 33rd International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 17–20 August 2010; pp. 27–30. [Google Scholar]
- Hassan, T.M.; Mahmoud, S.A. Fully programmable universal filter with independent gain-ωo-Q control based on new digitally programmable CMOS CCII. J. Circuits Syst. Comput. 2009, 18, 875–897. [Google Scholar] [CrossRef]
- Sayin, O.K.; Kuntman, H.H. Design of high-order active filters employing CMOS ECCIIs. In Proceedings of the IEEE 12th Signal Processing and Communications Applications Conference, Kusadasi, Turkey, 30 April 2004; pp. 375–378. [Google Scholar] [CrossRef]
- Kumngern, M.; Wareechol, E.; Phasukkit, P. Quadrature oscillator and universal filter based on translinear current conveyors. AEU-Int. J. Electron. Commun. 2018, 94, 69–78. [Google Scholar] [CrossRef]
- Sotner, R.; Lahiri, A.; Kartci, A.; Herencsar, N.; Jerabek, J.; Vrba, K. Design of novel precise quadrature oscillators employing ECCIIs with electronic control. Adv. Electr. Comput. Eng. 2013, 13, 65–72. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Horng, J.-W.; Vrba, K.; Dostal, T. Simple oscillator with enlarged tunability range based on ECCII and VGA utilizing commercially available analog multiplier. Meas. Sci. Rev. 2016, 16, 35–41. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Dostal, T.; Vrba, K. Design of Z-copy controlled-gain voltage differencing current conveyor based adjustable functional generator. Microelectron. J. 2015, 46, 143–152. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Langhammer, L.; Polak, J.; Herencsar, N.; Prokop, R.; Petrzela, J.; Jaikla, W. Comparison of two solutions of quadrature oscillators with linear control of frequency of oscillation employing modern commercially available devices. Circuits Syst. Signal Process. 2015, 34, 3449–3469. [Google Scholar] [CrossRef]
- Sotner, R.; Herencsar, N.; Jerabek, J.; Langhammer, L.; Polak, J. On practical construction of electronically controllable compact current amplifier based on commercially available elements and its application. AEU-Int. J. Electron. Commun. 2017, 81, 56–66. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Langhammer, L.; Dvorak, J. Design and analysis of CCII-based oscillator with amplitude stabilization employing optocouplers for linear voltage control of the output frequency. Electronics 2018, 7, 157. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Psychalinos, C. Multiple-input bulk-driven MOS transistor for low-voltage low-frequency applications. Circuits Syst. Signal Process. 2019, 38, 2829–2845. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Tang, K.-T. A 0.5-V multiple-input bulk-driven OTA in 0.18-μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1739–1747. [Google Scholar] [CrossRef]
- Krummenacher, F.; Joehl, N. A 4-MHz CMOS continuous-time filter with on-chip automatic tuning. IEEE J. Solid-State Circuits 1988, 23, 750–758. [Google Scholar] [CrossRef]
- Furth, P.M.; Andreou, A.G. Linearised differential transconductors in subthreshold CMOS. Electron. Lett. 1995, 31, 545–547. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; Baswa, S.; Ramirez-Angulo, J.; Carvajal, R.G. Low-voltage super class AB CMOS OTA cells with very high slew rate and power efficiency. IEEE J. Solid-State Circuits 2005, 40, 1068–1077. [Google Scholar] [CrossRef]
- Surakampontorn, W.; Riewruja, V.; Kumwachara, K.; Surawatpunya, C.; Anuntahirunrat, K. Temperature-insensitive voltage-to-current converter and its applications. IEEE Trans. Instrum. Meas. 1999, 48, 1270–1277. [Google Scholar] [CrossRef]
- Rai, M.; Senani, R.; Singh, A.K. New CMOS linear transconductors and their applications. J. Circuits Syst. Comput. 2023, 32, 2350211. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Aminzadeh, H.; Ballo, A. Ladder-type Gm-C filters with improved linearity. IEEE Access 2023, 11, 41503–41513. [Google Scholar] [CrossRef]
- Corbacho, I.; Carrillo, J.M.; Ausín, J.L.; Domínguez, M.Á.; Pérez-Aloe, R.; Duque-Carrillo, J.F. Compact CMOS Wideband Instrumentation Amplifiers for Multi-Frequency Bioimpedance Measurement: A Design Procedure. Electronics 2022, 11, 1668. [Google Scholar] [CrossRef]
- Texas Instruments—LM13700—Dual Operational Transconductance Amplifiers with Linearizing Diodes and Buffers (Datasheet). Available online: https://www.ti.com/lit/ds/symlink/lm13700.pdf (accessed on 1 January 2023).
- Texas Instruments—OPA860—Wide Bandwidth Operational Transconductance Amplifier (Datasheet). Available online: http://www.ti.com/lit/ds/symlink/opa860.pdf (accessed on 1 January 2023).













| Filtering Function | Input | Output | Condition | Gain | |
|---|---|---|---|---|---|
| LP | Inverting | - | |||
| Non-Inverting | - | ||||
| HP | Inverting | 1 | |||
| BP | Non-inverting | - | |||
| Non-inverting | - | ||||
| BS | Inverting | 1 | |||
| AP | Inverting | 1 | |||
| Transistor | W/L (µm/µm) |
|---|---|
| M1–M4, M13–M18 | 10/0.5 |
| M1s, M2s | 5/0.5 |
| M5–M12 | 20/0.5 |
| MR | 4/5 |
| CB = 0.5 pF | |
| VB1 = −300 mV, VB2 = 200 mV | |
| Parameters | Unit | This Work | [18] | [21] | [23] | [33] | [41] |
|---|---|---|---|---|---|---|---|
| EDDCC | CCII | DDCC | FDCCII | CCII | CCCII | ||
| Technique | - | BD | BD | BD | FG | GD | - |
| Technology | - | 0.18 μm CMOS | 0.18 μm CMOS | 0.18 μm CMOS | 0.18 μm CMOS | 0.35 μm CMOS | BJT ALA400-CBIC-R |
| Power supply | V | ±0.5 | ±0.4 | ±0.3 | ±0.8 | ±1.5 | ±1.5 |
| Power consumption | mW | 0.09 (90 µW) | 0.064 | 0.0186 | <3 | 6.6 | 2.2 |
| Voltage gains: | |||||||
| Vx/Vy1, | - | 0.996 | 1 | 1 | 0.94 | 1 | 0.99 |
| Vx/Vy2, | - | 0.995 | - | 1 | - | - | - |
| Vx/Vy3 | - | 0.996 | - | 1 | - | - | - |
| Current gain | - | k | 1 | 1 | 1 | k | k |
| DC voltage range | mV | −200 to 200 | −380 to 380 | −150 to 150 | −1000 to 1000 | −500 to 600 | −700 to 700 |
| Voltage offset | μV | ~90 | −0.4 to 0.5 | <93 | - | - | 1.29 to −1.72 |
| DC current range | μA | −10 to 10 | −7 to 7 | −8 to 8 | −300 to 300 | −50 to 50 | −200 to 200 |
| Current offset | nA | ~−2.3 | −0.9 to 0.4 | <3 | - | - | 0.0596 to −0.0497 |
| −3 dB bandwidth: | [CL = 0.1 pF] | ||||||
| Vx/Vy1, | MHz | 3.16 | 14 | 27 | - | 107 | 70 |
| Iz/Ix | MHz | 1.58 | 13 | 27 | >1000 | 77 | 19 |
| Parasitic parameters: | |||||||
| Rx/Lx | Ω/mH | 284/18.5 | 27/860 | 2.6 k/270 | 300 | 46/240 | 275/0.119 |
| Ry1/Cy1 | GΩ/fF | 42/252 | 272/117 | 119/5 | - | ∞/2.7 | 748 × 10−3/491 |
| Rz/Cz | MΩ/fF | 32.5/52 | 0.89/40 | 10.38/0.13 | - | 73/0.35 | 814 × 10−3/916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumngern, M.; Khateb, F.; Kulej, T.; Langhammer, L. 1 V Electronically Tunable Differential Difference Current Conveyors Using Multiple-Input Operational Transconductance Amplifiers. Sensors 2024, 24, 1558. https://doi.org/10.3390/s24051558
Kumngern M, Khateb F, Kulej T, Langhammer L. 1 V Electronically Tunable Differential Difference Current Conveyors Using Multiple-Input Operational Transconductance Amplifiers. Sensors. 2024; 24(5):1558. https://doi.org/10.3390/s24051558
Chicago/Turabian StyleKumngern, Montree, Fabian Khateb, Tomasz Kulej, and Lukas Langhammer. 2024. "1 V Electronically Tunable Differential Difference Current Conveyors Using Multiple-Input Operational Transconductance Amplifiers" Sensors 24, no. 5: 1558. https://doi.org/10.3390/s24051558
APA StyleKumngern, M., Khateb, F., Kulej, T., & Langhammer, L. (2024). 1 V Electronically Tunable Differential Difference Current Conveyors Using Multiple-Input Operational Transconductance Amplifiers. Sensors, 24(5), 1558. https://doi.org/10.3390/s24051558







