Fixed-Time-Convergent Sliding Mode Control with Sliding Mode Observer for PMSM Speed Regulation
Abstract
:1. Introduction
- An FSMC is proposed for the PMSM speed loop to achieve the fixed-time convergence property, thereby improving the convergence speed and robustness of the CSMC;
- An FSMO is designed to observe the unknown nonlinear lumped disturbance including mode uncertainties and external load torque. Meanwhile, the observed lumped disturbance is used to compensate the FSMC to further improve the robustness of the PMSM speed control system and effectively attenuate high-frequency sliding mode chattering;
- The stability and fixed-time convergence property of the proposed method are proofed by the Lyapunov method, and the feasibility and effectiveness are verified by the simulation and experimental results.
2. Mathematical Model and Theoretical Foundations
2.1. Mathematical Model of the Permanent Magnet Synchronous Motor
2.2. A New Fixed-Time Stable System
3. Design of Speed Controller Based on the Fixed-Time-Convergent Sliding Mode Control with a Fixed-Time-Convergent Sliding Mode Observer Method
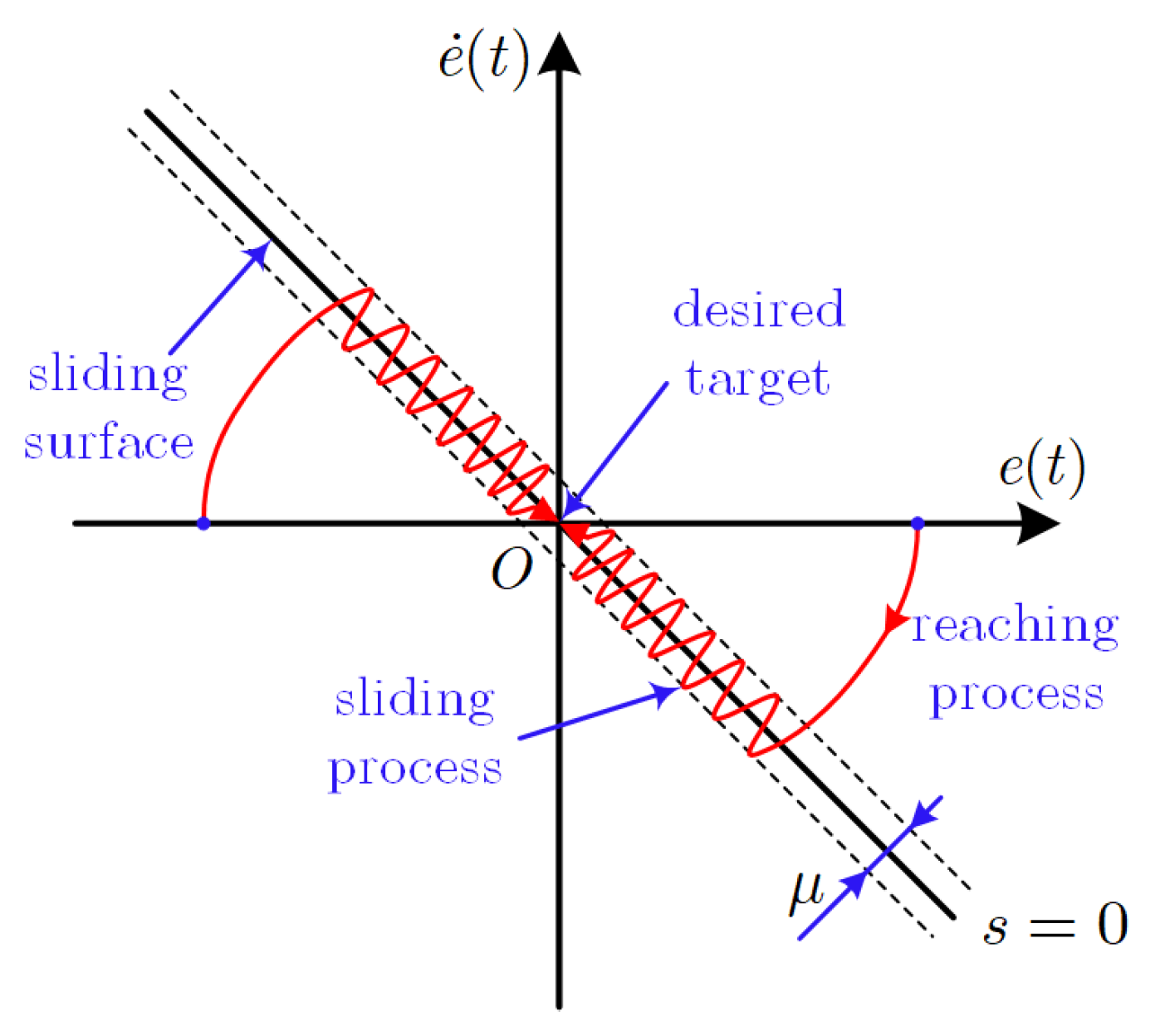
3.1. Design of the Conventional Sliding Mode Control
3.2. Design of the Fixed-Time-Convergent Sliding Mode Controller
3.3. Design of the Fixed-Time-Convergent Sliding Mode Observer
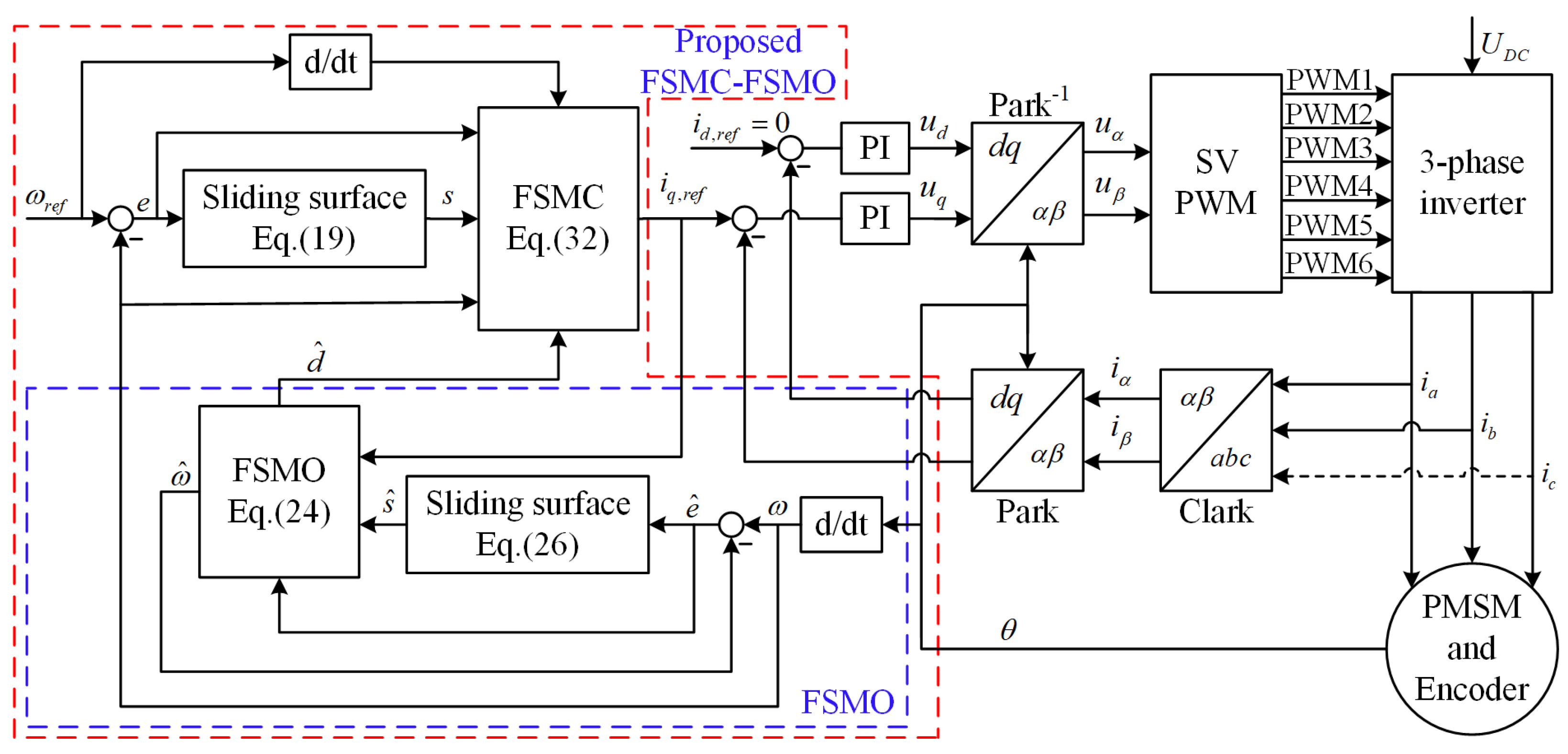
3.4. The Proposed Fixed-Time-Convergent Sliding Mode Control with a Fixed-Time-Convergent Sliding Mode Observer
4. Simulation and Experimental Results
4.1. Simulation Results and Analysis
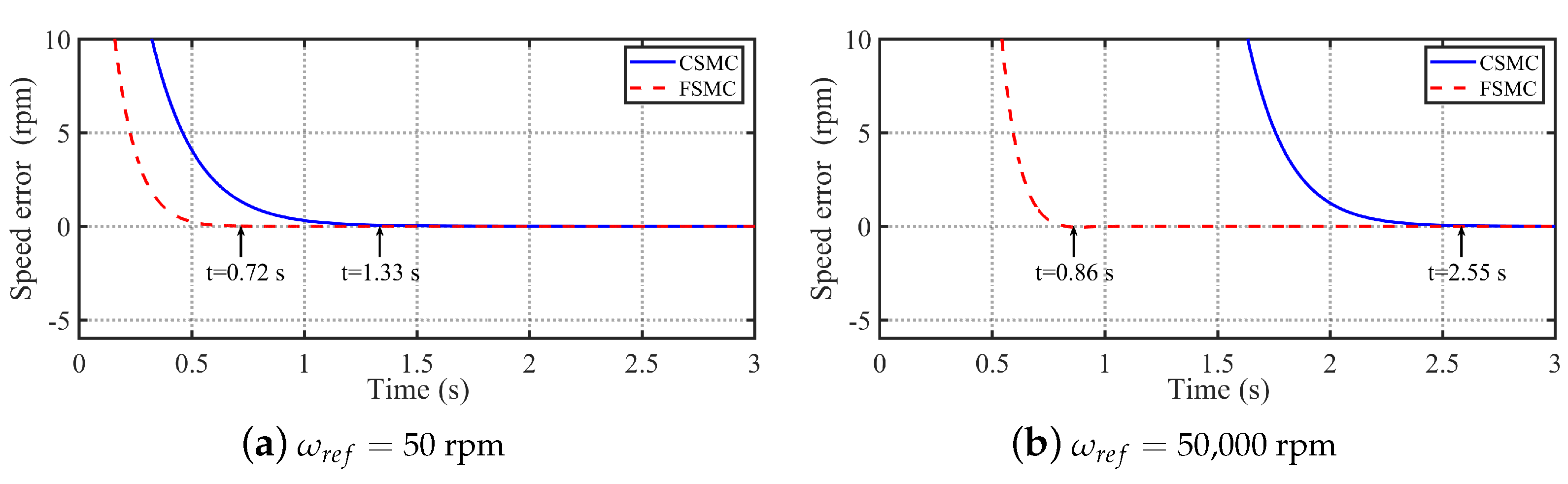
4.1.1. The Fixed-Time Convergence Property Analysis
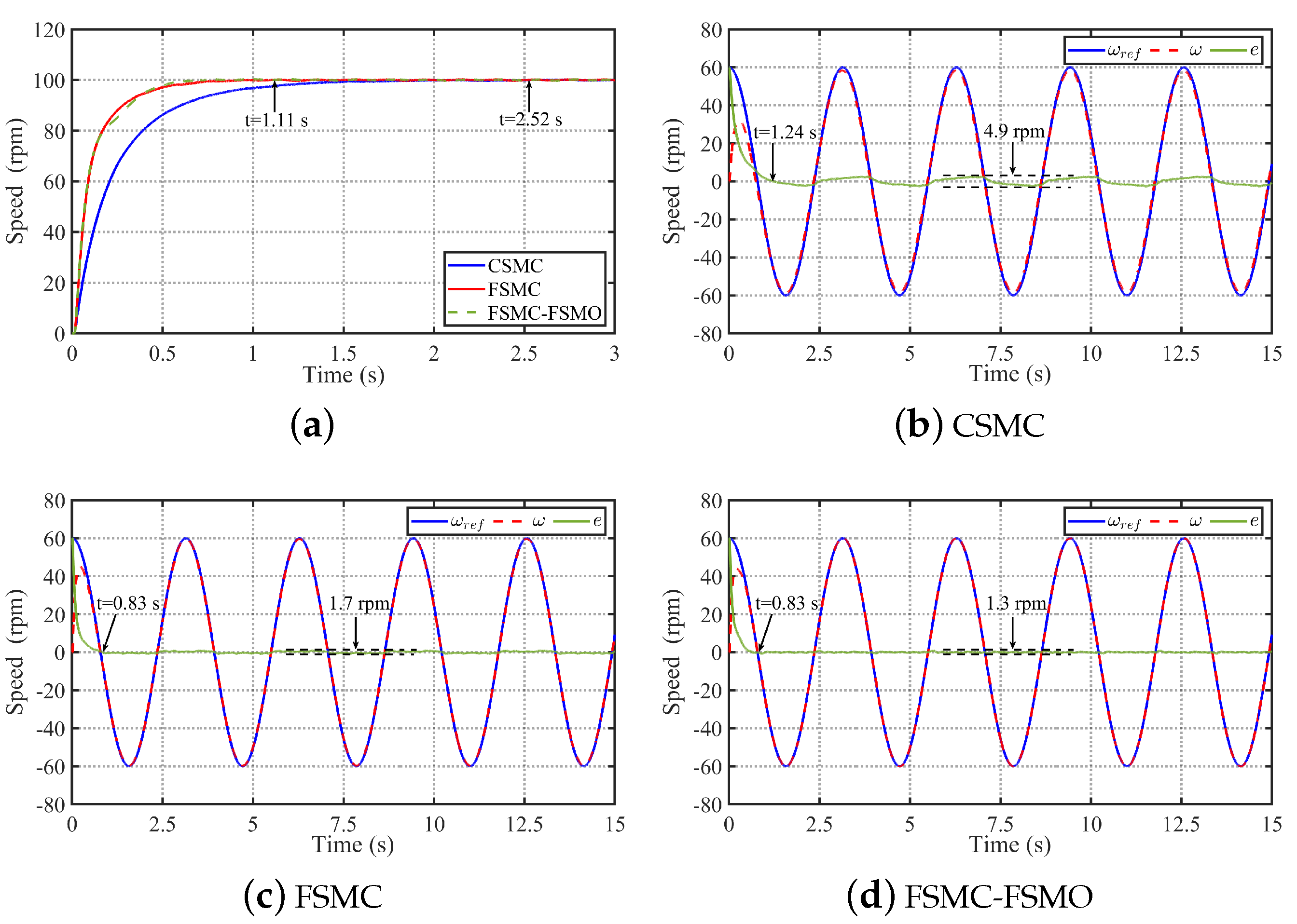
4.1.2. Speed Response Performance and Robustness Analysis
4.1.3. Analysis of Robustness to Mode Uncertainties
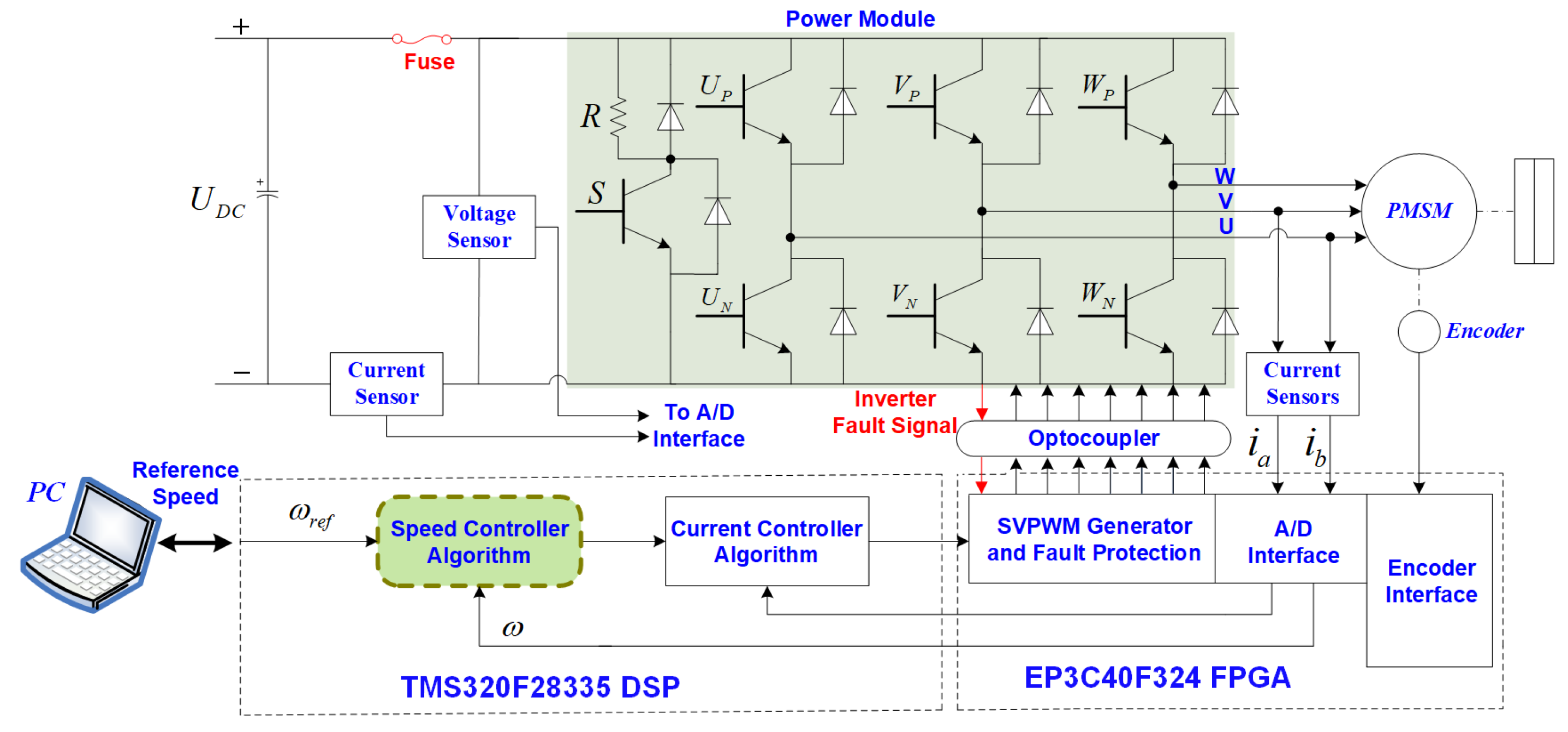
4.2. Experimental Results and Analysis
4.2.1. Speed Tracking Performance Verification
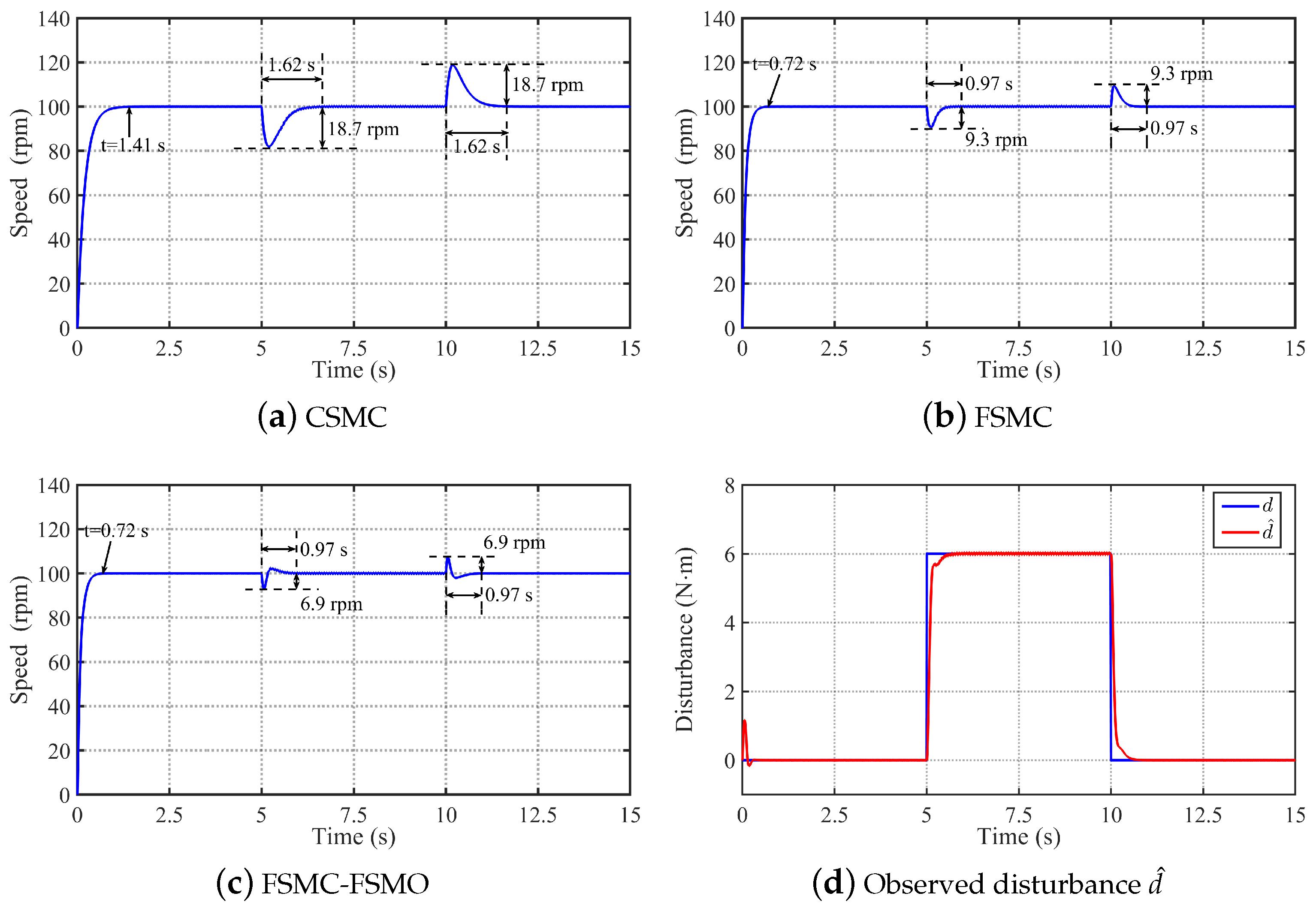
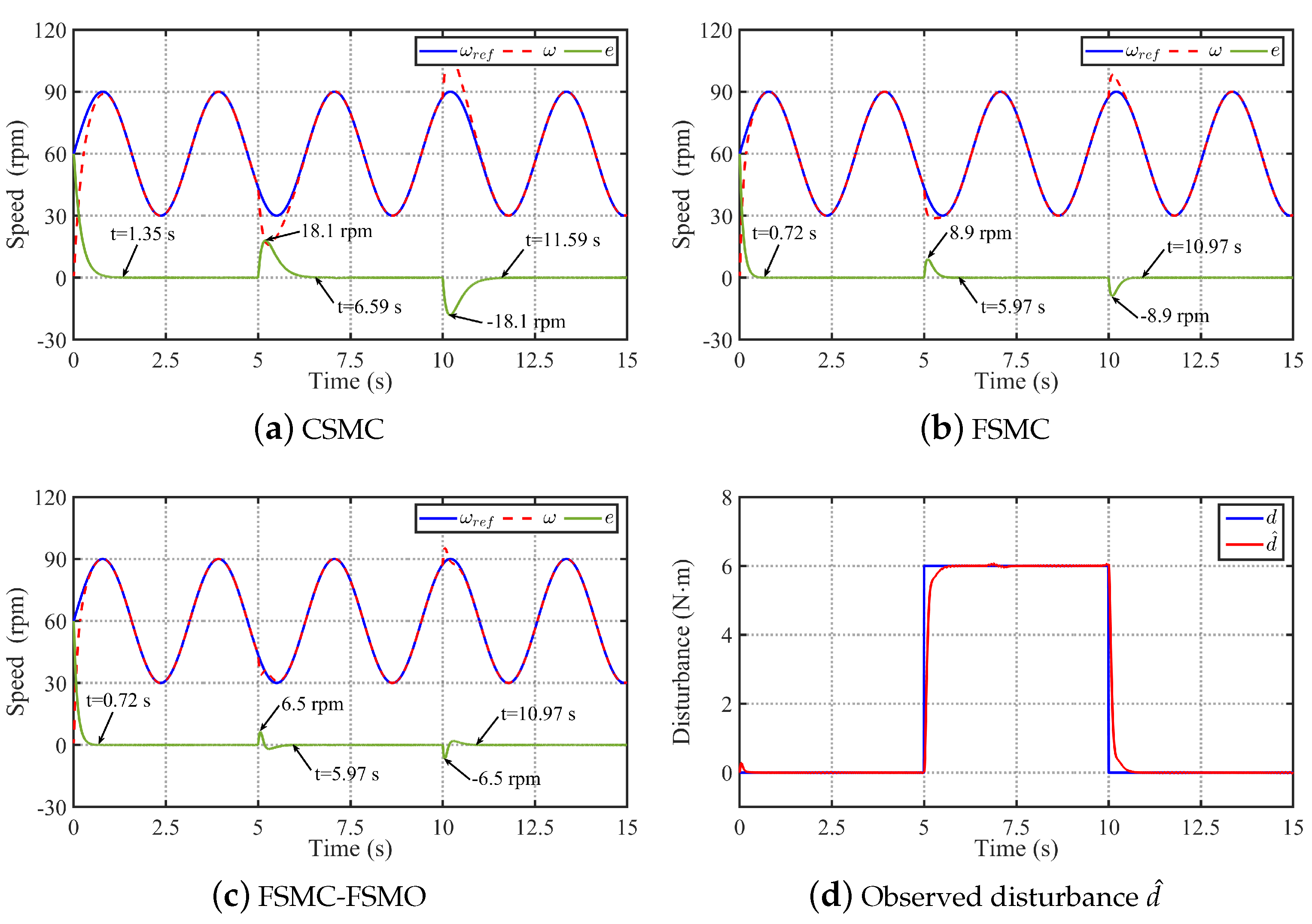
4.2.2. Anti-Disturbance Performance Verification
4.2.3. Parameter Robustness Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H. Improved ADRC with a Cascade Extended State Observer Based on Quasi-Generalized Integrator for PMSM Current Disturbances Attenuation. IEEE Trans. Transp. Electr. 2023. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Li, H.; Wang, J.; Wang, D. Precise and Efficient Pointing Control of a 2.5-m-Wide Field Survey Telescope Using ADRC and Nonlinear Disturbance Observer. Sensors 2023, 23, 6068. [Google Scholar] [CrossRef]
- Hu, F.; Luo, D.; Luo, C.; Long, Z.; Wu, G. Cascaded robust fault-tolerant predictive control for PMSM drives. Energies 2018, 11, 3087. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Li, K.; Zhang, Q. Robust current control-based generalized predictive control with sliding mode disturbance compensation for PMSM drives. ISA Trans. 2017, 71, 542–552. [Google Scholar] [CrossRef]
- Rabiei, A.; Thiringer, T.; Alatalo, M. Improved maximum-torque per-ampere algorithm accounting for core saturation, cross-coupling effect, and tempera ture for a PMSM intended for vehicular applications. IEEE Trans. Transp. Electr. 2016, 2, 150–159. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, B.; Nan, N.; Li, M.; Chen, Y. An adaptive PID-type sliding mode learning compensation of torque ripple in pmsm position servo systems towards energy efficiency. ISA Trans. 2021, 110, 258–270. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Li, H.; Wang, J.; Liu, X.; Sun, Z.; Yang, T. Generalized active disturbance rejection with reduced-order vector resonant control for PMSM current disturbances suppression. IEEE Trans. Power Electron. 2023, 38, 6407–6421. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H. Unified Interpretation of Active Disturbance Rejection Control for Electrical Drives. IEEE Trans. Circuits Syst. II 2024. [Google Scholar] [CrossRef]
- Sun, Z.; Deng, Y.; Wang, J.; Yang, T.; Wei, Z.; Cao, H. Finite Control Set Model-Free Predictive Current Control of PMSM with Two Voltage Vectors Based on Ultralocal Model. IEEE Trans. Power Electron. 2023, 38, 776–788. [Google Scholar] [CrossRef]
- Ping, Z.; Wang, T.; Huang, Y.; Wang, H.; Lu, J.-G.; Li, Y. Internal model control of pmsm position servo system: Theory and experimental results. IEEE Trans. Industr. Inform. 2019, 16, 2202–2211. [Google Scholar] [CrossRef]
- Yang, T.; Deng, Y.; Li, H.; Sun, Z.; Cao, H.; Wei, Z. Fast integral terminal sliding mode control with a novel disturbance observer based on iterative learning for speed control of PMSM. ISA Trans. 2023, 134, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Yu, X.; Han, F. High-order terminal sliding-mode observer for parameter estimation of a permanent-magnet synchronous motor. IEEE Trans. Ind. Electron. 2013, 60, 4272–4280. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2018, 88, 113–126. [Google Scholar] [CrossRef]
- Huang, M.; Deng, Y.; Li, H.; Shao, M.; Liu, J. Integrated Uncertainty/Disturbance Suppression Based on Improved Adaptive Sliding Mode Controller for PMSM Drives. Energies 2021, 14, 6538. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Disturbance Observer for PMSM Drives. IEEE Trans. Transp. Electr. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Contr. 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Cao, S.; Sun, L.; Jiang, J.; Zuo, Z. Reinforcement Learning-Based Fixed-Time Trajectory Tracking Control for Uncertain Robotic Manipulators with Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4584–4595. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast Fixed-Time Nonsingular Terminal Sliding Mode Control and Its Application to Chaos Suppression in Power System. IEEE Trans. Circuits Syst. II 2016, 64, 151–155. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z. Terminal sliding mode control—An overview. IEEE Open J. Ind. Electr. Soc. 2020, 2, 36–52. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Ren, J.; Ye, Y.; Xu, G.; Zhao, Q.; Zhu, M. Uncertainty-and-disturbance-estimator-based current control scheme for PMSM drives with a simple parameter tuning algorithm. IEEE Trans. Power Electron. 2017, 32, 5712–5722. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.-H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty estimation and attenuation techniques in PMSM Drives—A survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, C.P.; Zheng, G.; Wang, Y. On sliding mode observers for non-infinitely observable descriptor systems. Automatica 2022, 147, 110676. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Tan, C.P.; Trinh, H. Sliding mode observer for estimating states and faults of linear time-delay systems with outputs subject to delays. Automatica 2020, 124, 109274. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Lee, T.H.; Tan, C.P. Secure Communication Through a Chaotic System and a Sliding-Mode Observer. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1869–1881. [Google Scholar] [CrossRef]
- Ooi, J.H.T.; Tan, C.P.; Nurzaman, S.G.; Ng, K.Y. A Sliding Mode Observer for Infinitely Unobservable Descriptor Systems. IEEE Trans. Autom. Control 2017, 62, 3580–3587. [Google Scholar] [CrossRef]
- Jin, N.; Wang, X.; Wu, X. Current sliding mode control with a load sliding mode observer for permanent magnet synchronous machines. J. Power. Electron. 2014, 14, 105–114. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, B.; Mao, D. Robust Sliding Mode Control of PMSM Based on Rapid Nonlinear Tracking Differentiator and Disturbance Observer. Sensors 2018, 18, 1031. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Wang, L.; Li, M.; Hu, Y. Combined vector resonant and active disturbance rejection control for PMSLM current harmonic suppression. IEEE Trans. Ind. Inform. 2020, 16, 5691–5702. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]




| Symbols | Characteristics | Values |
|---|---|---|
| DC-bus-rated voltage | 100 V | |
| Rated current | 5 A | |
| Rated torque | 6 N·m | |
| Number of pole pairs | 3 | |
| Rotor flux linkage | 0.29 Wb | |
| Stator resistance | 0.675 | |
| -axis inductance | 0.0065 H |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, H.; Shao, M. Fixed-Time-Convergent Sliding Mode Control with Sliding Mode Observer for PMSM Speed Regulation. Sensors 2024, 24, 1561. https://doi.org/10.3390/s24051561
Zhang X, Li H, Shao M. Fixed-Time-Convergent Sliding Mode Control with Sliding Mode Observer for PMSM Speed Regulation. Sensors. 2024; 24(5):1561. https://doi.org/10.3390/s24051561
Chicago/Turabian StyleZhang, Xin, Hongwen Li, and Meng Shao. 2024. "Fixed-Time-Convergent Sliding Mode Control with Sliding Mode Observer for PMSM Speed Regulation" Sensors 24, no. 5: 1561. https://doi.org/10.3390/s24051561




