Transversal Displacement Detection of an Arched Bridge with a Multimonostatic Multiple-Input Multiple-Output Radar
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Processing Methods
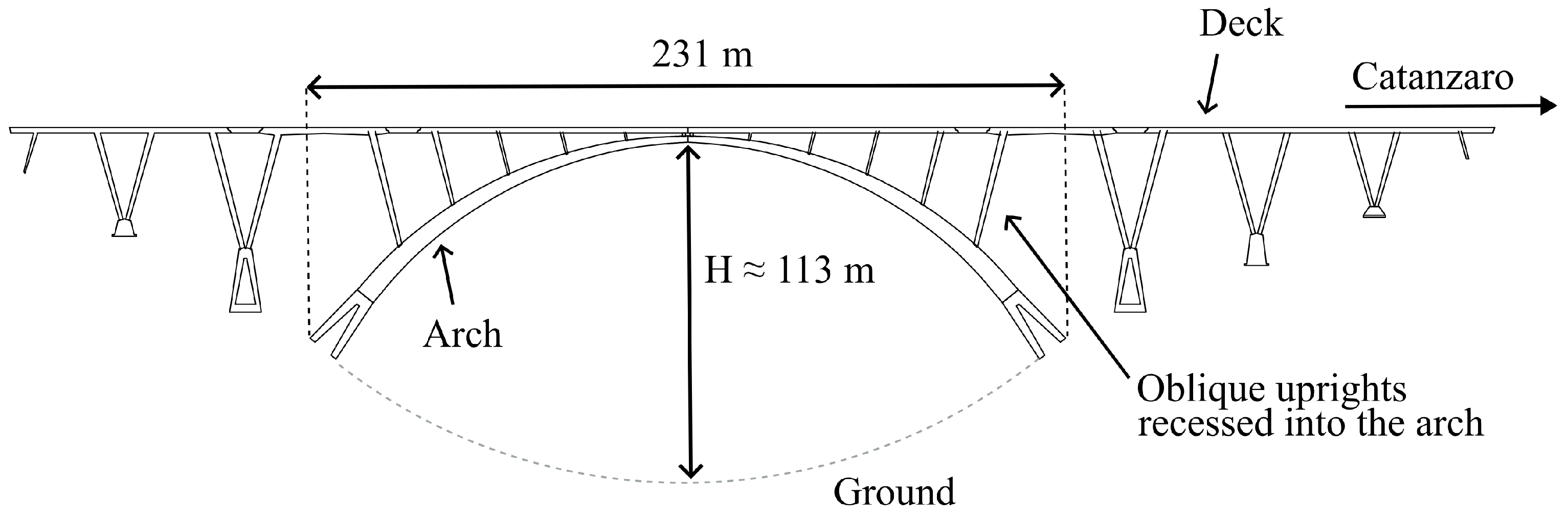
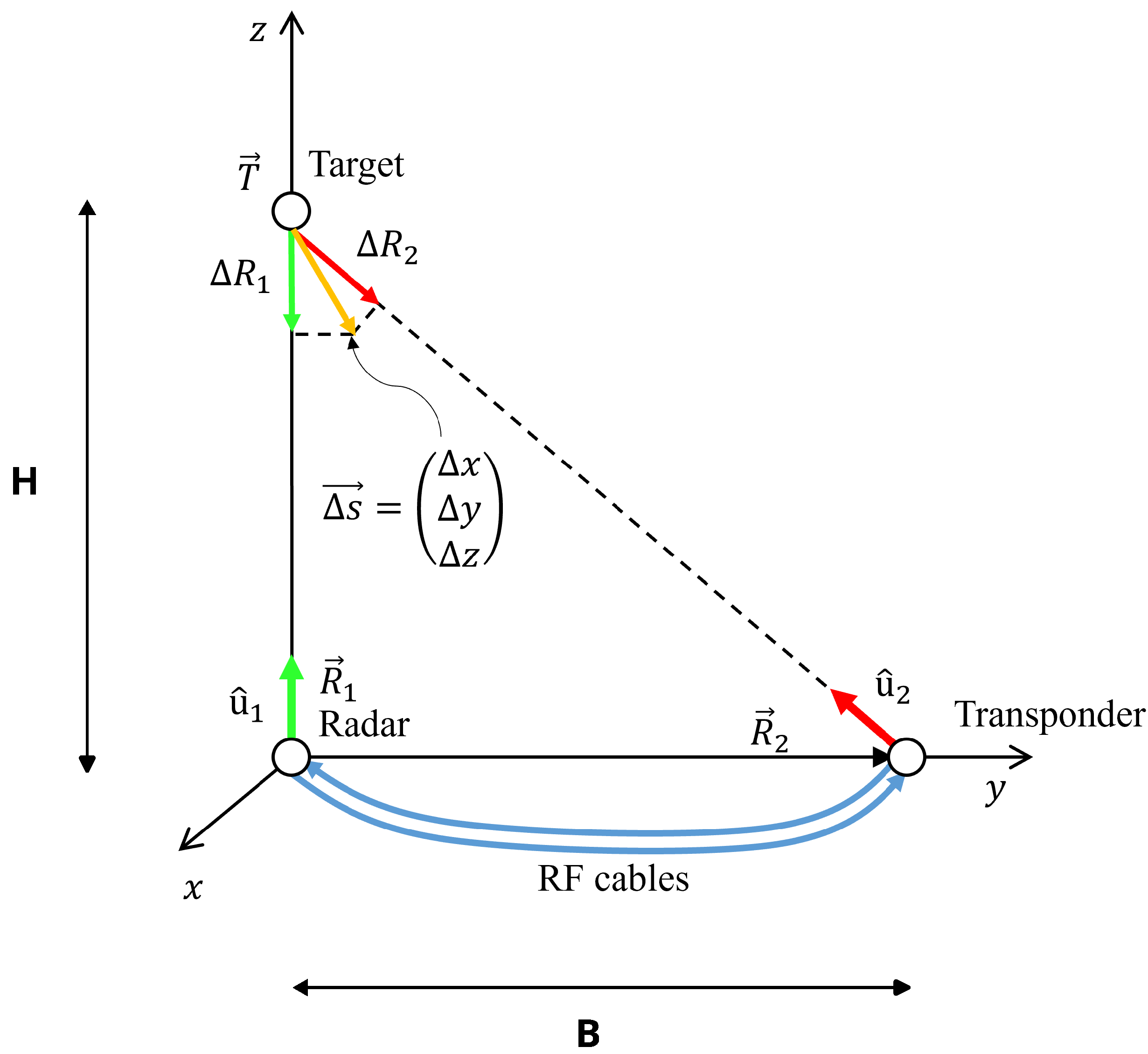
2.2. Geometry Description
2.3. Uncertainty Evaluation
2.4. Radar Equipment
3. Results
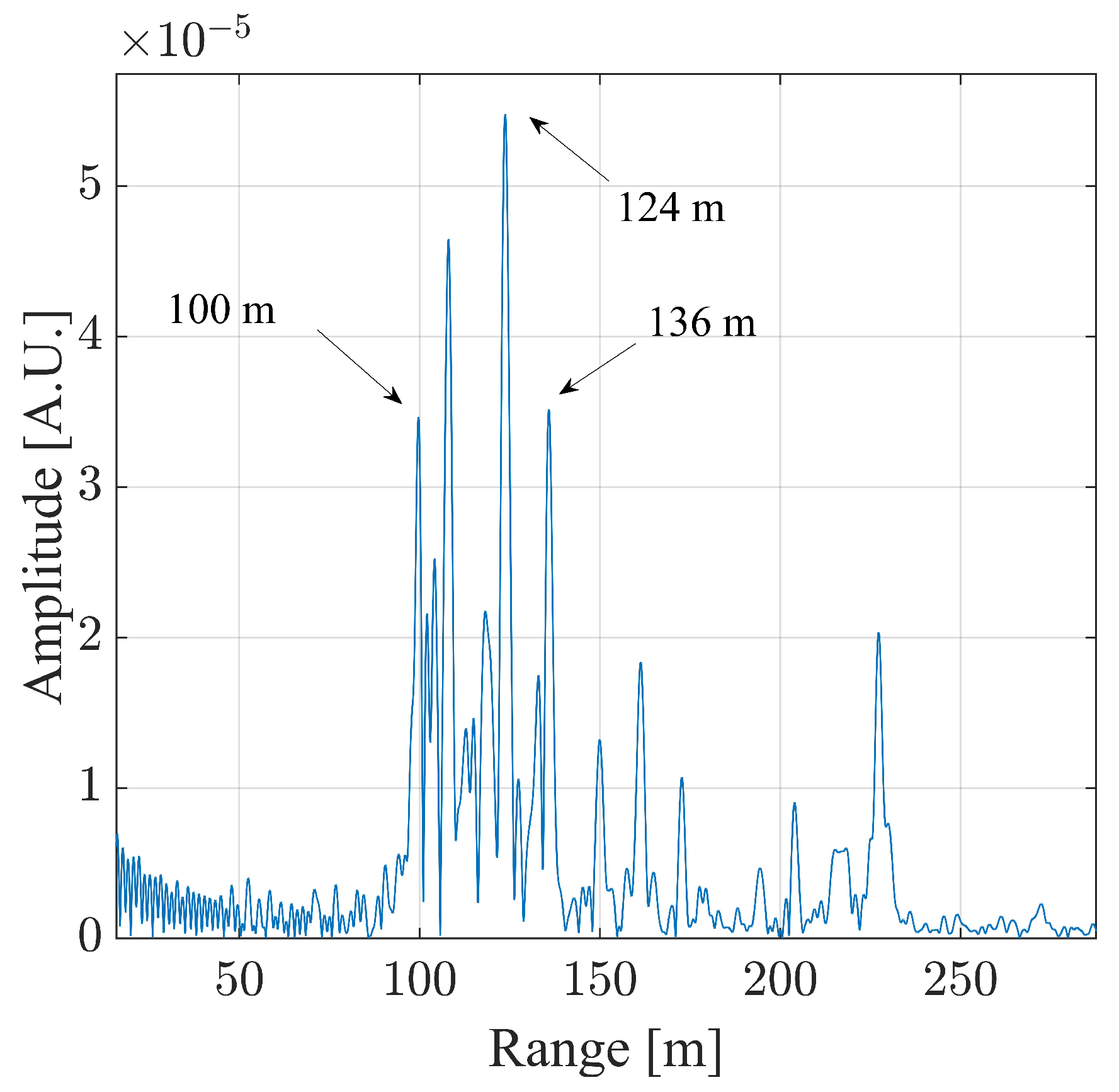
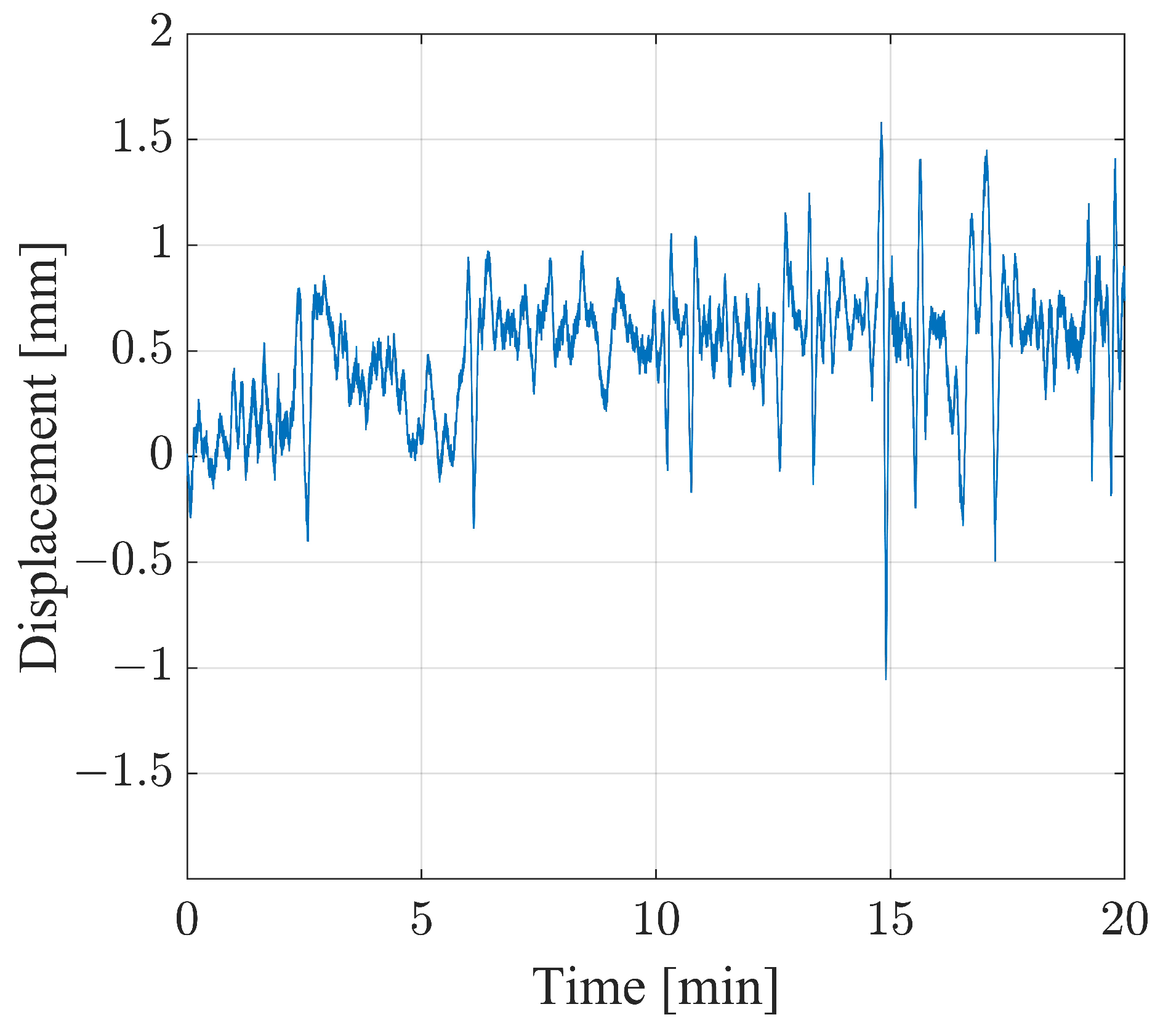
3.1. Monostatic Measurement
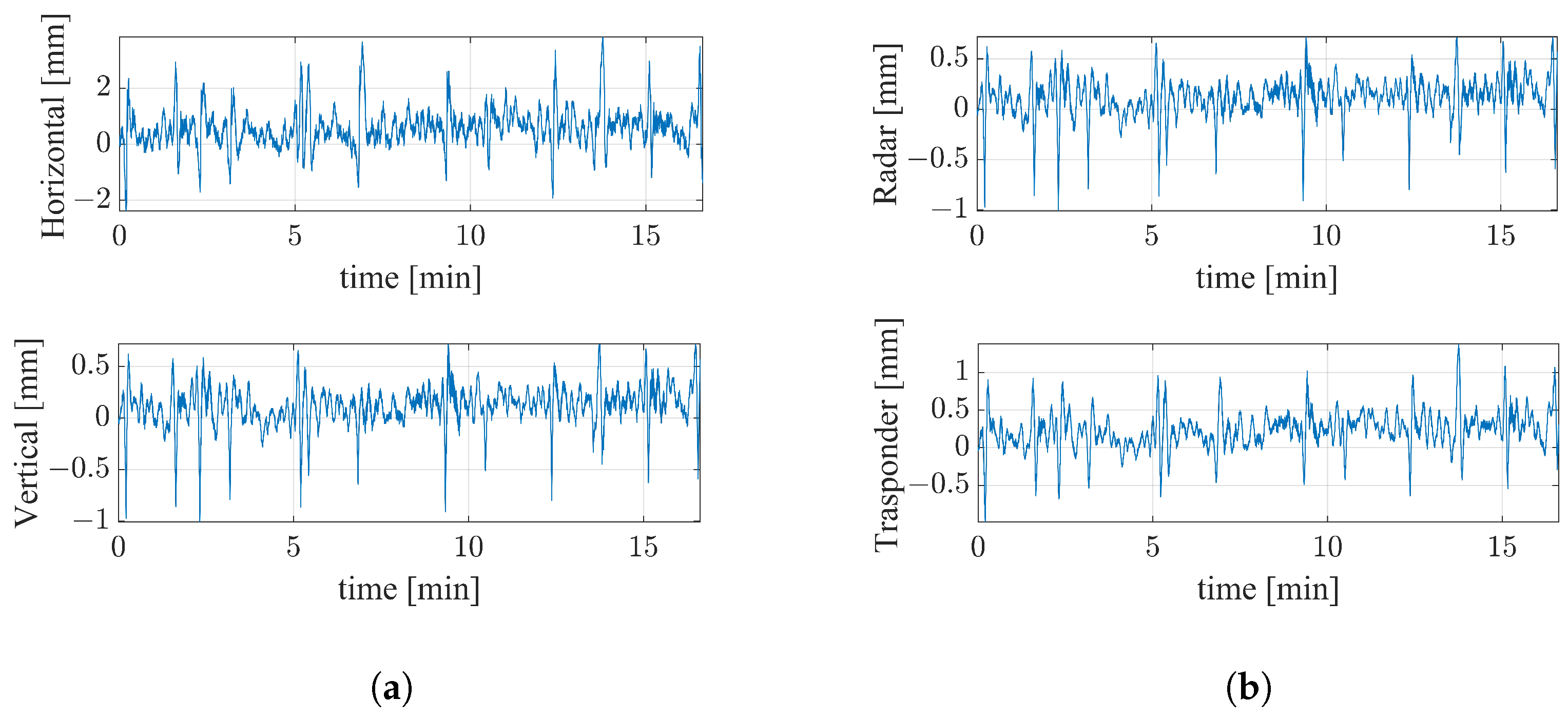
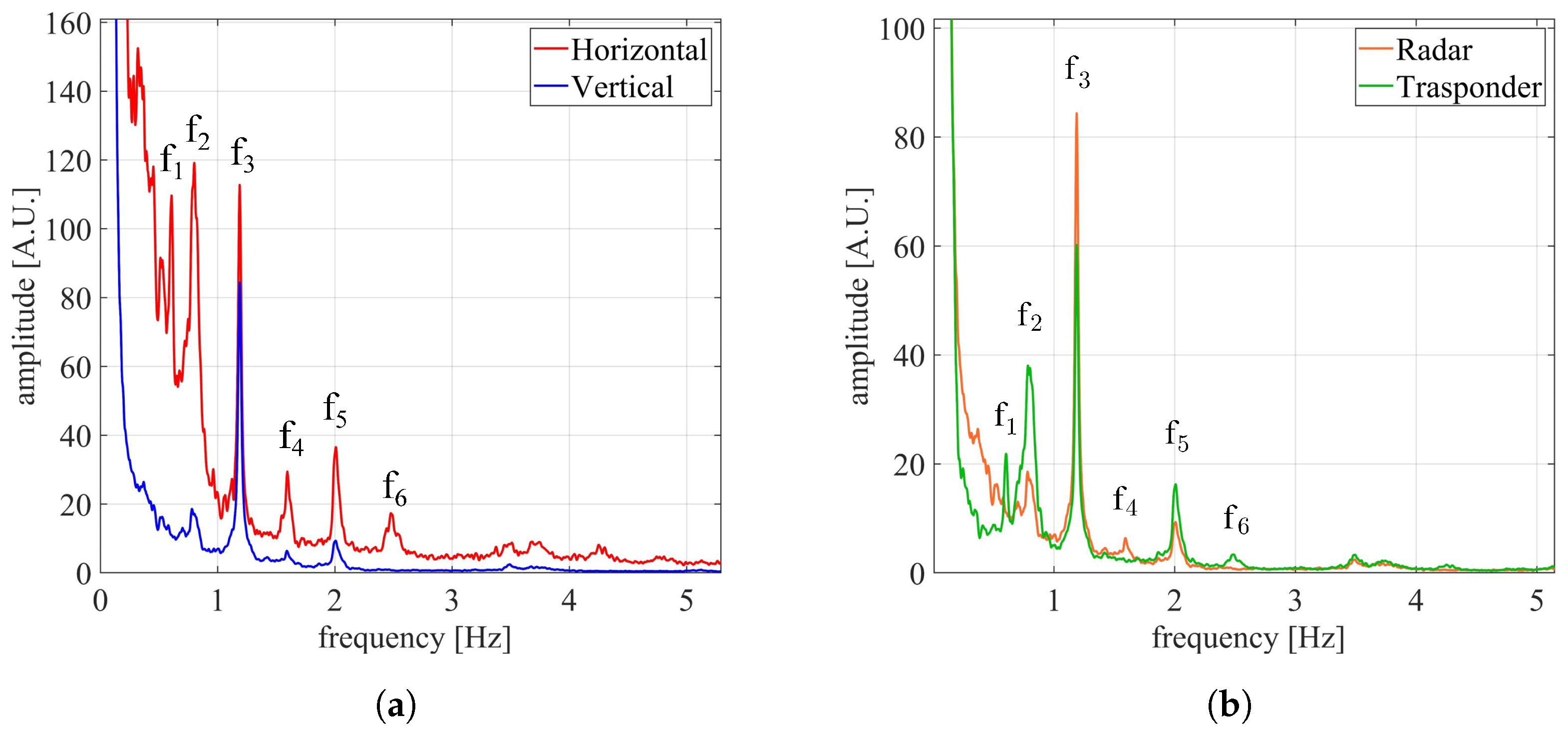
3.2. Multimonostatic Measurement
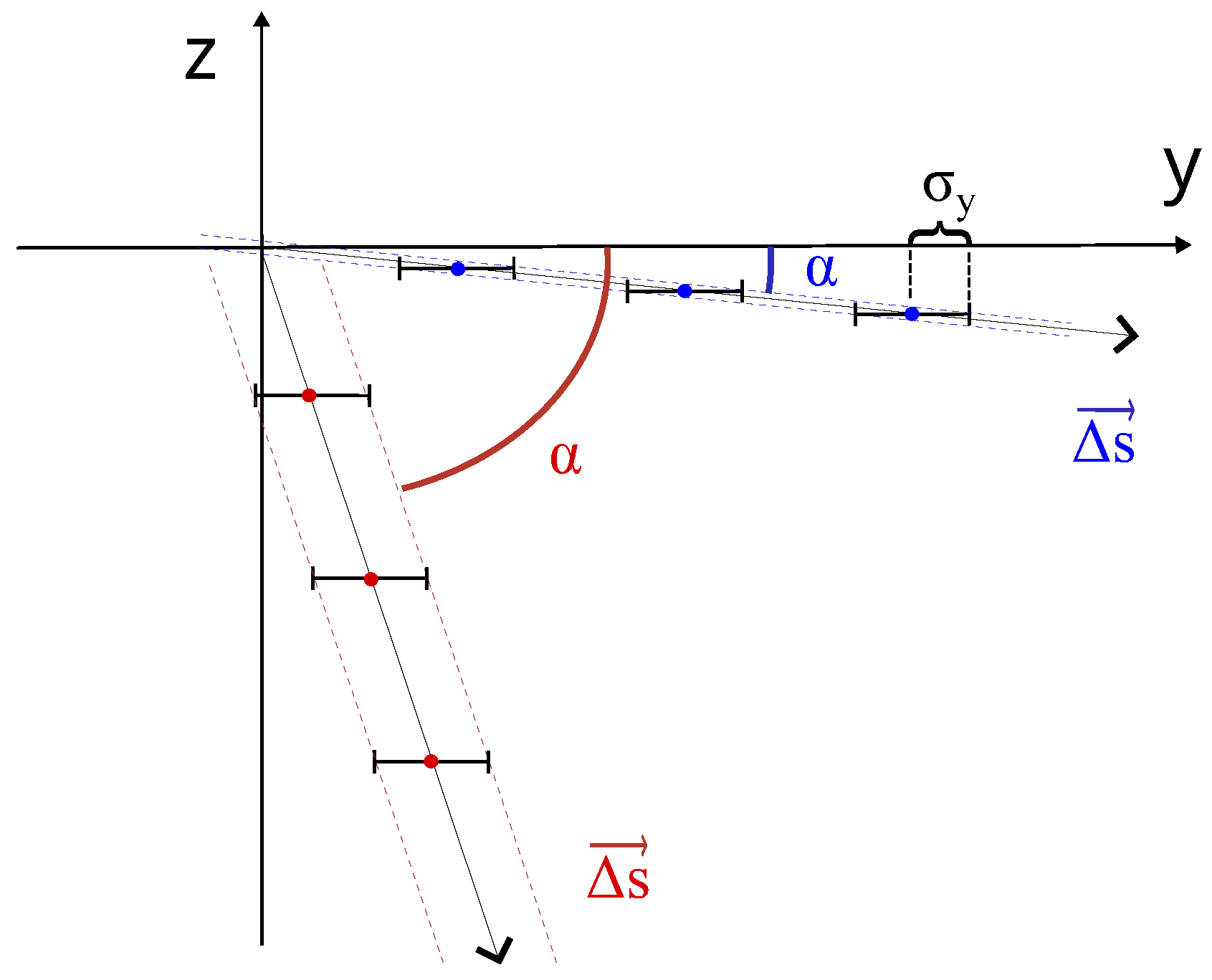
3.3. Displacement Direction Retrievement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garnica, G.I.Z.; Lantsoght, E.O.L.; Yang, Y. Monitoring structural responses during load testing of reinforced concrete bridges: A review. Struct. Infrastruct. Eng. 2022, 18, 1558–1580. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Catbas, N.; Avci, O. A review of latest trends in bridge health monitoring. Proc. Inst. Civ. Eng. Bridge Eng. 2023, 176, 76–91. [Google Scholar] [CrossRef]
- An, Y.; Chatzi, E.; Sim, S.H.; Laflamme, S.; Blachowski, B.; Ou, J. Recent progress and future trends on damage identification methods for bridge structures. Struct. Control Health Monit. 2019, 26, e2416. [Google Scholar] [CrossRef]
- Vardanega, P.; Webb, G.; Fidler, P.; Huseynov, F.; Kariyawasam, K.; Middleton, C. 32—Bridge monitoring. In Innovative Bridge Design Handbook, 2nd ed.; Pipinato, A., Ed.; Butterworth-Heinemann: Oxford, UK, 2022; pp. 893–932. [Google Scholar]
- Veilleux, S.; Abedi, A.; Wilkerson, C.; Wilkerson, D.; Boyd, D. Wireless Linear Variable Differential Transformer Design and Structural Performance Analysis. In Proceedings of the 2018 6th IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Huntsville, AL, USA, 11–13 December 2018; pp. 152–157. [Google Scholar]
- Mutlib, N.K.; Baharom, S.B.; El-Shafie, A.; Nuawi, M.Z. Ultrasonic health monitoring in structural engineering: Buildings and bridges. Struct. Control Health Monit. 2016, 23, 409–422. [Google Scholar] [CrossRef]
- Sun, A.; Wu, Z.; Fang, D.; Zhang, J.; Wang, W. Multimode Interference-Based Fiber-Optic Ultrasonic Sensor for Non-Contact Displacement Measurement. IEEE Sens. J. 2016, 16, 5632–5635. [Google Scholar] [CrossRef]
- Liu, Y.; Bao, Y. Real-time remote measurement of distance using ultra-wideband (UWB) sensors. Autom. Constr. 2023, 150, 104849. [Google Scholar] [CrossRef]
- Jeong, S.H.; Jang, W.S.; Nam, J.W.; An, H.; Kim, D.J. Development of a Structural Monitoring System for Cable Bridges by Using Seismic Accelerometers. Appl. Sci. 2020, 10, 716. [Google Scholar] [CrossRef]
- Morichika, S.; Sekiya, H.; Zhu, Y.; Hirano, S.; Maruyama, O. Estimation of Displacement Response in Steel Plate Girder Bridge Using a Single MEMS Accelerometer. IEEE Sens. J. 2021, 21, 8204–8208. [Google Scholar] [CrossRef]
- Ma, Z.; Chung, J.; Liu, P.; Sohn, H. Bridge displacement estimation by fusing accelerometer and strain gauge measurements. Struct. Control Health Monit. 2021, 28, e2733. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Sohn, H. Development and full-scale dynamic test of a combined system of heterogeneous laser sensors for structural displacement measurement. Smart Mater. Struct. 2016, 25, 065015. [Google Scholar] [CrossRef]
- Nasimi, R.; Moreu, F. A methodology for measuring the total displacements of structures using a laser–camera system. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 421–437. [Google Scholar] [CrossRef]
- Maksymenko, O.P.; Sakharuk, O.M.; Ivanytskyi, Y.L.; Kun, P.S. Multilaser spot tracking technology for bridge structure displacement measuring. Struct. Control Health Monit. 2021, 28, e2675. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, P.; Yan, X.; Zhao, X. Middle displacement monitoring of medium–small span bridges based on laser technology. Struct. Control Health Monit. 2020, 27, e2509. [Google Scholar] [CrossRef]
- Pramudita, A.A.; Lin, D.B.; Dhiyani, A.A.; Ryanu, H.H.; Adiprabowo, T.; Yudha, E.A. FMCW Radar for Noncontact Bridge Structure Displacement Estimation. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Stabile, T.A.; Perrone, A.; Gallipoli, M.R.; Ditommaso, R.; Ponzo, F.C. Dynamic Survey of the Musmeci Bridge by Joint Application of Ground-Based Microwave Radar Interferometry and Ambient Noise Standard Spectral Ratio Techniques. IEEE Geosci. Remote Sens. Lett. 2013, 10, 870–874. [Google Scholar] [CrossRef]
- Placidi, S.; Meta, A.; Testa, L.; Rödelsperger, S. Monitoring structures with FastGBSAR. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 435–439. [Google Scholar]
- Zhang, B.; Ding, X.; Werner, C.; Tan, K.; Zhang, B.; Jiang, M.; Zhao, J.; Xu, Y. Dynamic displacement monitoring of long-span bridges with a microwave radar interferometer. ISPRS J. Photogramm. Remote Sens. 2018, 138, 252–264. [Google Scholar] [CrossRef]
- Pagnini, L.; Collodi, G.; Cidronali, A. A GaN-HEMT Active Drain-Pumped Mixer for S-Band FMCW Radar Front-End Applications. Sensors 2023, 23, 4479. [Google Scholar] [CrossRef]
- Dei, D.; Mecatti, D.; Pieraccini, M. Static Testing of a Bridge Using an Interferometric Radar: The Case Study of “Ponte degli Alpini,” Belluno, Italy. Sci. World J. 2013, 2013, e504958. [Google Scholar] [CrossRef]
- Li, C.; Chen, W.; Liu, G.; Yan, R.; Xu, H.; Qi, Y. A Noncontact FMCW Radar Sensor for Displacement Measurement in Structural Health Monitoring. Sensors 2015, 15, 7412–7433. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.; Falcone, P.; D’Aria, D.; Giunta, G. 3D Vibration Estimation from Ground-Based Radar. Remote Sens. 2018, 10, 1670. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, C.; Tian, W.; Zhao, Z. 3-D Deformation Measurement Based on Three GB-MIMO Radar Systems: Experimental Verification and Accuracy Analysis. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2092–2096. [Google Scholar] [CrossRef]
- Olaszek, P.; Świercz, A.; Boscagli, F. The Integration of Two Interferometric Radars for Measuring Dynamic Displacement of Bridges. Remote Sens. 2021, 13, 3668. [Google Scholar] [CrossRef]
- Michel, C.; Keller, S. Advancing Ground-Based Radar Processing for Bridge Infrastructure Monitoring. Sensors 2021, 21, 2172. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.; Keller, S. Assessing Important Uncertainty Influences of Ground-Based Radar for Bridge Monitoring. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.Y.; Liang, X.D.; Ding, C.b.; Li, K. Implementation of the OFDM Chirp Waveform on MIMO SAR Systems. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5218–5228. [Google Scholar] [CrossRef]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO Radar and Ground-Based SAR Imaging Systems: Equivalent Approaches for Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 425–435. [Google Scholar] [CrossRef]
- Michelini, A.; Coppi, F.; Bicci, A.; Alli, G. SPARX, a MIMO Array for Ground-Based Radar Interferometry. Sensors 2019, 19, 252. [Google Scholar] [CrossRef]
- Hu, C.; Wang, J.; Tian, W.; Zeng, T.; Wang, R. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays. Sensors 2017, 17, 598. [Google Scholar] [CrossRef]
- Cardillo, E.; Caddemi, A. A Review on Biomedical MIMO Radars for Vital Sign Detection and Human Localization. Electronics 2020, 9, 1497. [Google Scholar] [CrossRef]
- Miccinesi, L.; Beni, A.; Pieraccini, M. Multi-Monostatic Interferometric Radar for Bridge Monitoring. Electronics 2021, 10, 247. [Google Scholar] [CrossRef]
- Miccinesi, L.; Pieraccini, M.; Beni, A.; Andries, O.; Consumi, T. Multi-Monostatic Interferometric Radar with Radar Link for Bridge Monitoring. Electronics 2021, 10, 2777. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sens. 2019, 11, 1403. [Google Scholar] [CrossRef]
- Lanari, R.; Reale, D.; Bonano, M.; Verde, S.; Muhammad, Y.; Fornaro, G.; Casu, F.; Manunta, M. Comment on “Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy” by Milillo et al. (2019). Remote Sens. 2020, 12, 4011. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Reply to Lanari, R., et al. Comment on “Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy” by Milillo et al. (2019). Remote Sens. 2020, 12, 4016. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Ullo, S.L.; Clemente, C.; Orlando, D. Perspectives on the Structural Health Monitoring of Bridges by Synthetic Aperture Radar. Remote Sens. 2020, 12, 3852. [Google Scholar] [CrossRef]
- Pieraccini, M.; Luzi, G.; Noferini, L.; Mecatti, D.; Atzeni, C. Joint time-frequency analysis for investigation of layered masonry structures using penetrating radar. IEEE Trans. Geosci. Remote Sens. 2004, 42, 309–317. [Google Scholar] [CrossRef]
- IBIS-ArcSAR Lite/Performance|IDS GeoRadar. Available online: https://idsgeoradar.com/products/interferometric-radar/ibis-arcsar-lite-or–performance (accessed on 1 March 2024).
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C.; Bartoli, G. Interferometric radar vs. accelerometer for dynamic monitoring of large structures: An experimental comparison. NDT E Int. 2008, 41, 258–264. [Google Scholar] [CrossRef]












| [Hz] | |
|---|---|
| 2 | |
| Multimonostatic (Horizontal) [Hz] | Multimonostatic (Vertical) [Hz] | Monostatic [Hz] | |
|---|---|---|---|
| 0.60 | - | - | |
| 0.80 | 0.80 | 0.80 | |
| 1.19 | 1.19 | 1.19 | |
| 1.59 | 1.59 | - | |
| 2.00 | 2.00 | 2.00 | |
| 2.48 | - | - | |
| - | - | 3.26 | |
| - | - | 3.80 | |
| - | - | 6.42 | |
| - | - | 6.86 | |
| - | - | 10.27 |
| [DEG] | |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pagnini, L.; Miccinesi, L.; Beni, A.; Pieraccini, M. Transversal Displacement Detection of an Arched Bridge with a Multimonostatic Multiple-Input Multiple-Output Radar. Sensors 2024, 24, 1839. https://doi.org/10.3390/s24061839
Pagnini L, Miccinesi L, Beni A, Pieraccini M. Transversal Displacement Detection of an Arched Bridge with a Multimonostatic Multiple-Input Multiple-Output Radar. Sensors. 2024; 24(6):1839. https://doi.org/10.3390/s24061839
Chicago/Turabian StylePagnini, Lorenzo, Lapo Miccinesi, Alessandra Beni, and Massimiliano Pieraccini. 2024. "Transversal Displacement Detection of an Arched Bridge with a Multimonostatic Multiple-Input Multiple-Output Radar" Sensors 24, no. 6: 1839. https://doi.org/10.3390/s24061839
APA StylePagnini, L., Miccinesi, L., Beni, A., & Pieraccini, M. (2024). Transversal Displacement Detection of an Arched Bridge with a Multimonostatic Multiple-Input Multiple-Output Radar. Sensors, 24(6), 1839. https://doi.org/10.3390/s24061839









