Time-Efficient SNR Optimization of WMS-Based Gas Sensor Using a Genetic Algorithm
Abstract
:1. Introduction
2. Materials and Methods
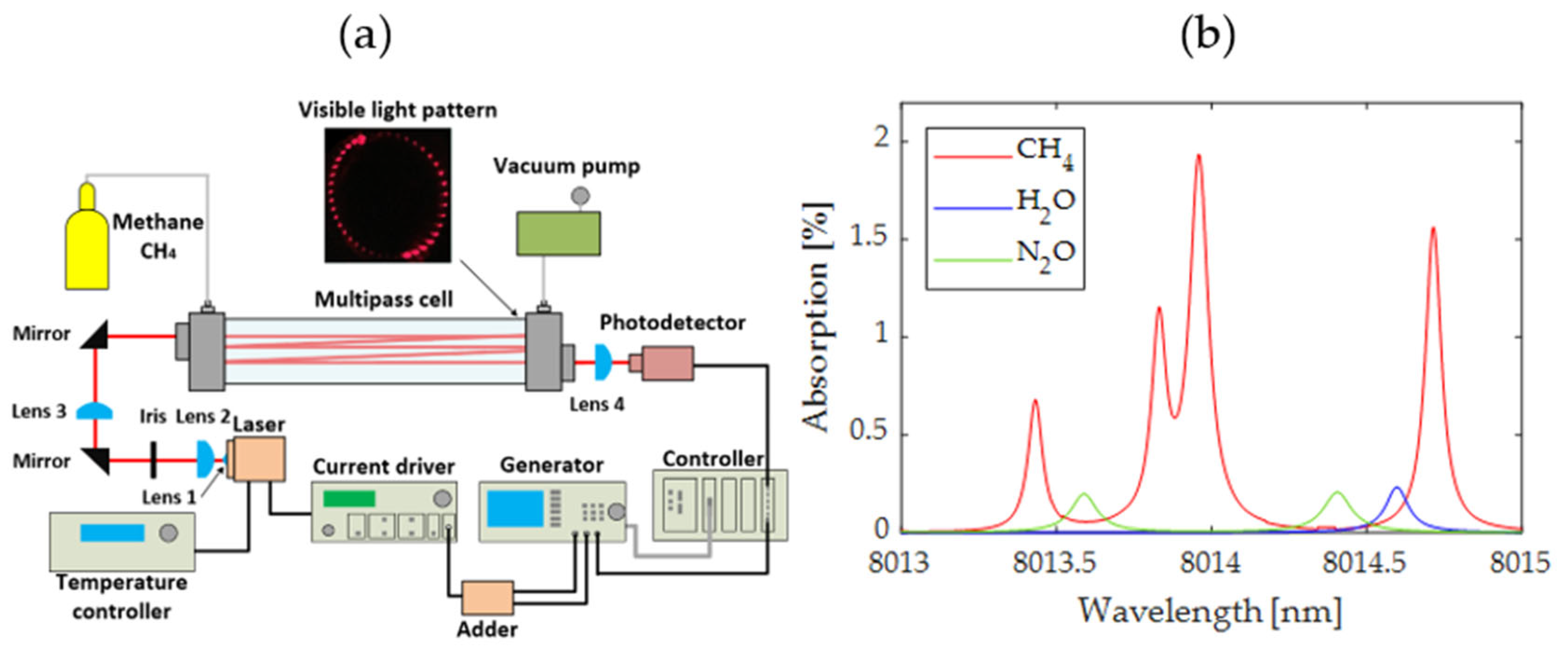
2.1. Experimental Setup
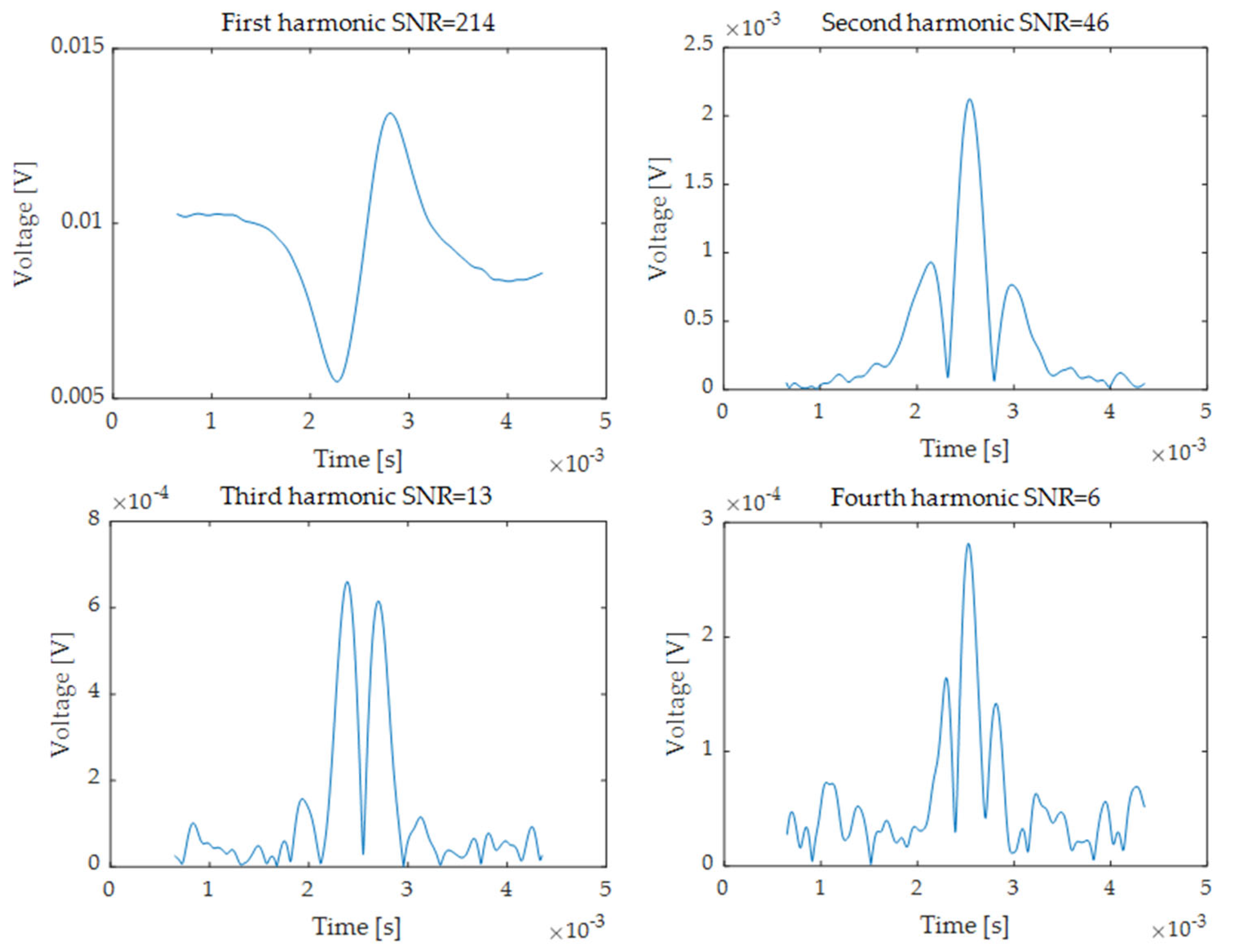
2.2. Test the Sensor Operation with Initial Settings
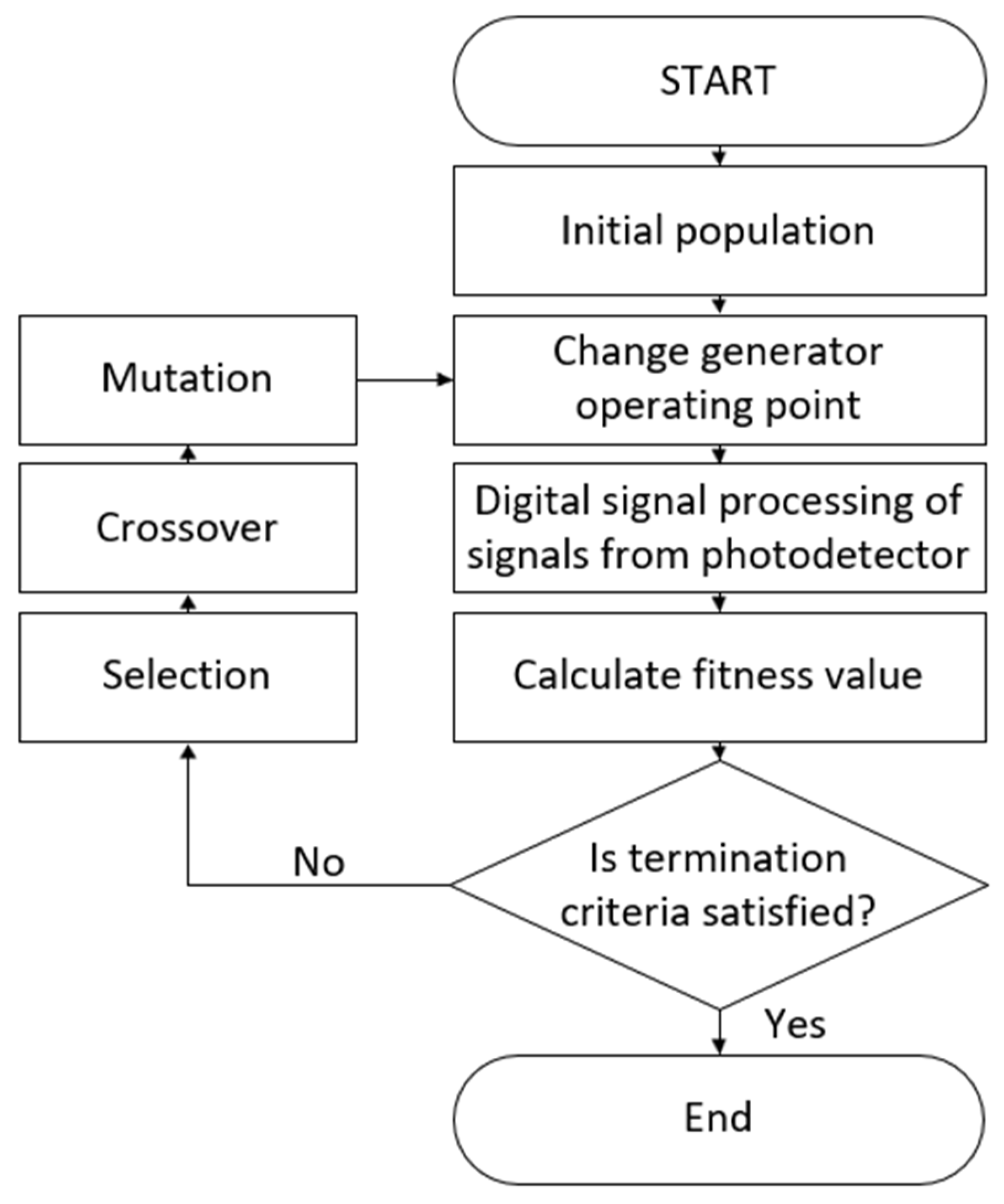
2.3. Optimization Procedure
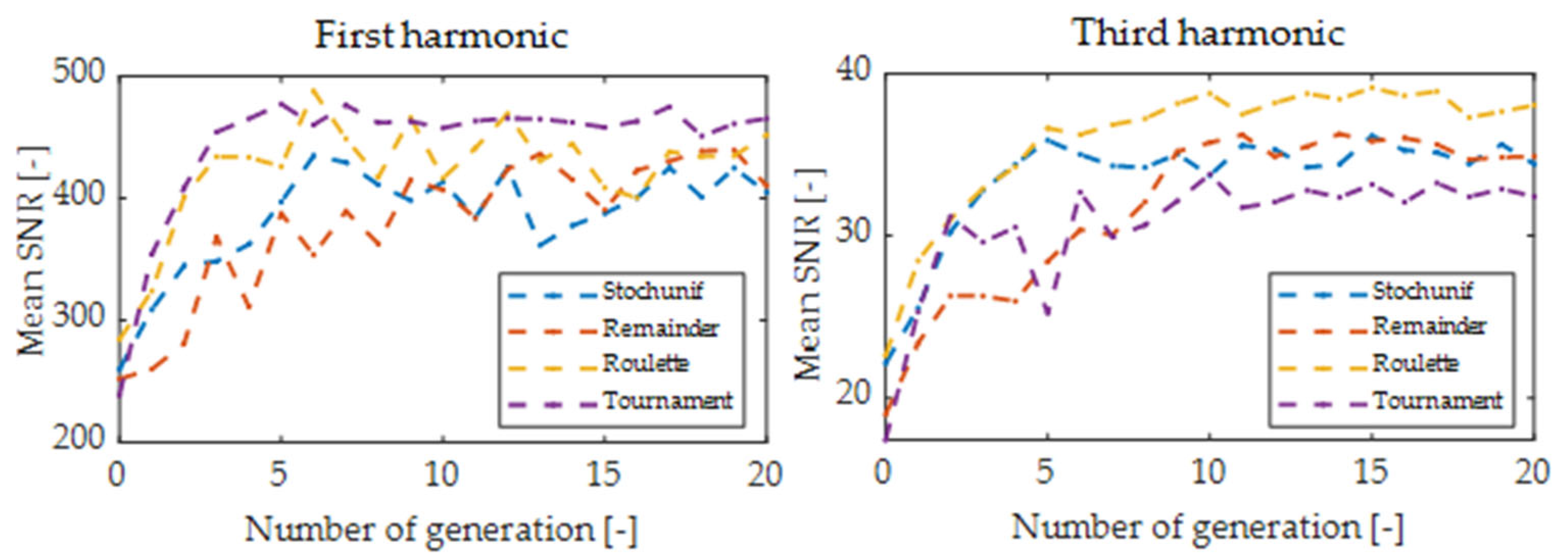
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baudelet, M. Laser Spectroscopy for Sensing; Woodhead Publishing: Cambridge, UK, 2014. [Google Scholar]
- Hodgkinson, J.; Tatam, R.P. Optical Gas Sensing: A Review. Meas. Sci. Technol. 2013, 24, 012004. [Google Scholar] [CrossRef]
- Wojtas, J.; Mikolajczyk, J.; Nowakowski, M.; Rutecka, B.; Medrzycki, R.; Bielecki, Z. Applying CEAS Method to UV, VIS, and IR Spectroscopy Sensors. Bull. Polish Acad. Sci. Tech. Sci. 2011, 59, 415–418. [Google Scholar] [CrossRef]
- Goldenstein, C.S.; Spearrin, R.M.; Jeffries, J.B.; Hanson, R.K. Infrared Laser-Absorption Sensing for Combustion Gases. Prog. Energy Combust. Sci. 2017, 60, 132–176. [Google Scholar] [CrossRef]
- Klapec, D.J.; Czarnopys, G.; Pannuto, J. Interpol review of the analysis and detection of explosives and explosives residues. Forensic Sci. Int. Synerg. 2023, 6, 100298. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, R.; Schmidt, F.M. ICL-Based TDLAS Sensor for Real-Time Breath Gas Analysis of Carbon Monoxide Isotopes. Opt. Express 2017, 25, 12743. [Google Scholar] [CrossRef]
- Wang, C.; Sahay, P. Breath Analysis Using Laser Spectroscopic Techniques: Breath Biomarkers, Spectral Fingerprints, and Detection Limits. Sensors 2009, 9, 8230–8262. [Google Scholar] [CrossRef]
- Wojtas, J.; Bielecki, Z. Signal processing system in cavity enhanced spectroscopy. Opto-Electron. Rev. 2008, 16, 420–427. [Google Scholar] [CrossRef]
- Werle, P. A Review of Recent Advances in Semiconductor Laser Based Gas Monitors. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1998, 54, 197–236. [Google Scholar] [CrossRef]
- Kluczynski, P.; Lindberg, Å.M.; Axner, O. Characterization of Background Signals in Wavelength-Modulation Spectrometry in Terms of a Fourier Based Theoretical Formalism. Appl. Opt. 2001, 40, 770–782. [Google Scholar] [CrossRef]
- Kluczynski, P.; Gustafsson, J.; Lindberg, Å.M.; Axner, O. Wavelength Modulation Absorption Spectrometry—An Extensive Scrutiny of the Generation of Signals. Spectrochim. Acta Part B At. Spectrosc. 2001, 56, 1277–1354. [Google Scholar] [CrossRef]
- Sun, K. Utilization of Multiple Harmonics of Wavelength Modulation Absorption Spectroscopy for Practical Gas Sensing. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Schilt, S.; Thévenaz, L.; Robert, P. Wavelength Modulation Spectroscopy: Combined Frequency and Intensity Laser Modulation. Appl. Opt. 2003, 42, 6728. [Google Scholar] [CrossRef]
- Rieker, G.B.; Jeffries, J.B.; Hanson, R.K. Calibration-Free Wavelength-Modulation Spectroscopy for Measurements of Gas Temperature and Concentration in Harsh Environments. Appl. Opt. 2009, 48, 5546–5560. [Google Scholar] [CrossRef] [PubMed]
- Silver, J.A. Frequency-Modulation Spectroscopy for Trace Species Detection: Theory and Comparison among Experimental Methods. Appl. Opt. 1992, 31, 707–717. [Google Scholar] [CrossRef] [PubMed]
- Xiong, B.; Du, Z.; Li, J. Modulation Index Optimization for Optical Fringe Suppression in Wavelength Modulation Spectroscopy. Rev. Sci. Instrum. 2015, 86, 113104. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Fu, P.; Chao, X. Laser Absorption Sensing Systems: Challenges, Modeling, and Design Optimization. Appl. Sci. 2019, 9, 2723. [Google Scholar] [CrossRef]
- Liang, W.; Wei, G.; He, A.; Shen, H. A Novel Wavelength Modulation Spectroscopy in TDLAS. Infrared Phys. Technol. 2021, 114, 103661. [Google Scholar] [CrossRef]
- Mohammadi, M.J.; Khorsandi, A.; Ghavami, S.S. Modulation Index Optimization for Wavelength Modulation Spectroscopy. Opt. Appl. 2016, 46, 630–650. [Google Scholar] [CrossRef]
- Röder, L.L.; Fischer, H. Theoretical Investigation of Applicability and Limitations of Advanced Noise Reduction Methods for Wavelength Modulation Spectroscopy. Appl. Phys. B 2021, 128, 10. [Google Scholar] [CrossRef]
- Wojtas, J. Towards the Highest Sensitivity and Selectivity of the Earth’s and Space’s Laser-Based Methane Sensors. Measurement 2023, 225, 114064. [Google Scholar] [CrossRef]
- Inczedy, J.; Lengyel, T.; Ure, A. Compendium of Analytical Nomenclature. IUPAC Orange Book; Blackwell Sci: Oxford, UK, 1997. [Google Scholar]
- Thomsen, V.; Schatzlein, D.; Mercuro, D. Limits of Detection in Spectroscopy. Spectroscopy 2003, 18, 112–114. Available online: https://www.spectroscopyonline.com (accessed on 23 February 2024).
- Du, Z.; Yan, Y.; Li, J.; Zhang, S.; Yang, X.; Xiao, Y. In situ, multiparameter optical sensor for monitoring the selective catalytic reduction process of diesel engines. Sens. Actuators B Chem. 2018, 267, 255–264. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975; Volume 1. [Google Scholar]
- Hudzikowski, A.J.; Głuszek, A.K.; Sotor, J.; Abramski, K.M. Multipass Cells and Optical Cavities Design Using Ray Tracing and Genetic Algorithm. In Proceedings of the SPIE 10974, Laser Technology 2018: Progress and Applications of Lasers, Thirteenth Symposium on Laser Technology, Jastarnia, Poland, 4 December 2018; p. 37. [Google Scholar]
- Vié, A. Qualities, Challenges and Future of Genetic Algorithms. SSRN Electron. J. 2021. [Google Scholar] [CrossRef]


| Device | Parameter | Accuracy | Resolution | Range of Research | Number of Points | Remarks |
|---|---|---|---|---|---|---|
| LDX 3232 | Laser current | ±0.15% of setpoint ± 2 mA | 40 µA | 245–525 mA | 7k | Laser wavelength tuning: 0.065 nm/mA |
| TEC 3210 | Laser temperature | 0.05 °C | 0.01 °C | 14–45 °C | 3k | Laser wavelength tuning: 0.638 nm/°C |
| AFG 3252 | Modulation frequency | ±1 ppm ± 1 μHz | 1 μHz | 5–60 kHz | 55M | - |
| Modulation amplitude | ±(1% of setting + 1 mV) | 0.1 mVpp | 100–500 mVpp | 4k | Laser current driver conversion: 200 mA/V | |
| Scanning frequency | ±1 ppm ± 1 μHz | 1 μHz | 5–5000 Hz | 4M | - | |
| Scanning Amplitude | ±(1% of setting + 1 mV) | 0.1 mVpp | 250–1000 mVpp | 7.5M | Laser current driver conversion: 200 mA/V |
| Parameter | Value |
|---|---|
| Population size | 20 |
| Number of generations | 20 |
| Creation function | Gacreationlinearfeasible |
| Crossover function | Crossoverintermediate |
| Mutation function | Mutationpower |
| Sine-wave amplitude constraints | 100 mVpp–500 mVpp |
| Modulation frequency constraints | 5 kHz–60 kHz |
| Ramp amplitude constraints | 250 mVpp–1000 mVpp |
| Ramp frequency constraints | 5 Hz–5000 Hz |
| Selection Function | Modulation Amplitude [mVpp] | Modulation Frequency [kHz] | Ramp Amplitude [mVpp] | Ramp Frequency [Hz] | SNR [v/v] | SNR Improvement [%] |
|---|---|---|---|---|---|---|
| The first harmonic | ||||||
| Stochunif | 376 | 47,272 | 530 | 467 | 770 | 360 |
| Remainder | 393 | 58,031 | 539 | 777 | 750 | 350 |
| Roulette | 344 | 48,323 | 339 | 252 | 700 | 327 |
| Tournament | 393 | 33,930 | 492 | 161 | 580 | 271 |
| The second harmonic | ||||||
| Stochunif | 349 | 53,599 | 664 | 48 | 77 | 167 |
| Remainder | 260 | 36,821 | 544 | 96 | 73 | 159 |
| Roulette | 268 | 44,631 | 585 | 513 | 74 | 161 |
| Tournament | 359 | 58,036 | 445 | 216 | 75 | 163 |
| The third harmonic | ||||||
| Stochunif | 385 | 36,927 | 329 | 276 | 45 | 346 |
| Remainder | 376 | 55,205 | 326 | 163 | 44 | 338 |
| Roulette | 388 | 46,617 | 576 | 75 | 45 | 346 |
| Tournament | 320 | 33,965 | 265 | 188 | 44 | 338 |
| The fourth harmonic | ||||||
| Stochunif | 367 | 32,844 | 446 | 206 | 34 | 567 |
| Remainder | 386 | 32,296 | 483 | 398 | 37 | 617 |
| Roulette | 400 | 24,768 | 252 | 442 | 39 | 650 |
| Tournament | 375 | 27,819 | 448 | 225 | 34 | 567 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musiałek, F.; Szabra, D.; Wojtas, J. Time-Efficient SNR Optimization of WMS-Based Gas Sensor Using a Genetic Algorithm. Sensors 2024, 24, 1842. https://doi.org/10.3390/s24061842
Musiałek F, Szabra D, Wojtas J. Time-Efficient SNR Optimization of WMS-Based Gas Sensor Using a Genetic Algorithm. Sensors. 2024; 24(6):1842. https://doi.org/10.3390/s24061842
Chicago/Turabian StyleMusiałek, Filip, Dariusz Szabra, and Jacek Wojtas. 2024. "Time-Efficient SNR Optimization of WMS-Based Gas Sensor Using a Genetic Algorithm" Sensors 24, no. 6: 1842. https://doi.org/10.3390/s24061842
APA StyleMusiałek, F., Szabra, D., & Wojtas, J. (2024). Time-Efficient SNR Optimization of WMS-Based Gas Sensor Using a Genetic Algorithm. Sensors, 24(6), 1842. https://doi.org/10.3390/s24061842







