Playing Flappy Bird Based on Motion Recognition Using a Transformer Model and LIDAR Sensor
Abstract
:1. Introduction
- Improved performance: Our transformer model with a distance sensor significantly outperformed existing methods (an increase of over 50 times in both average and maximum scores). This suggests that real robots equipped with similar sensors can potentially achieve considerably higher accuracy when processing long sequences of sensor data.
- Sensor-focused learning: Unlike previous approaches, our agent solely relies on sensor data (not on the full game image) to learn from past experiences, identify obstacles, and navigate the environment. This suggests that focusing on relevant sensor data can be an efficient strategy for controlling robots.
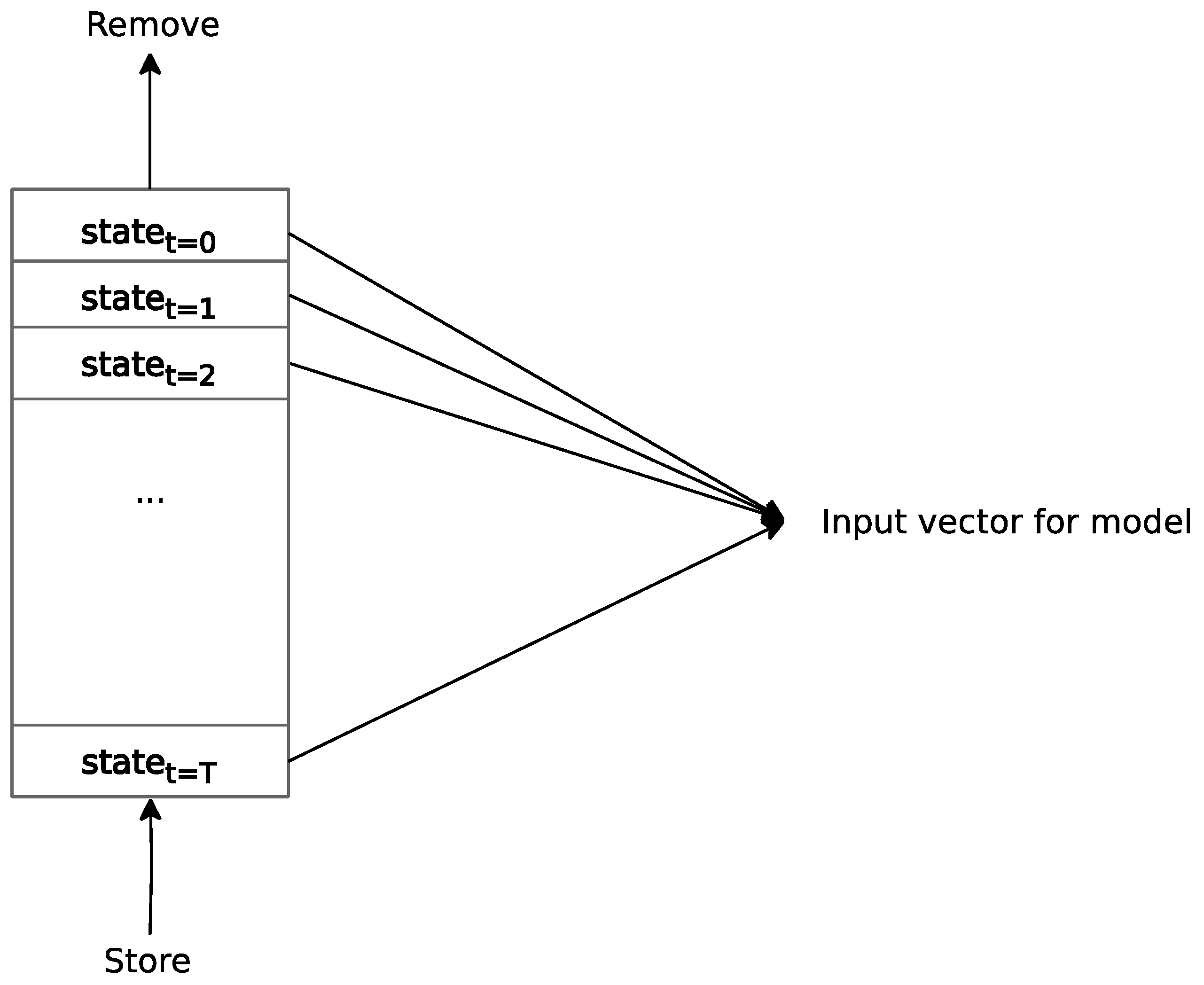
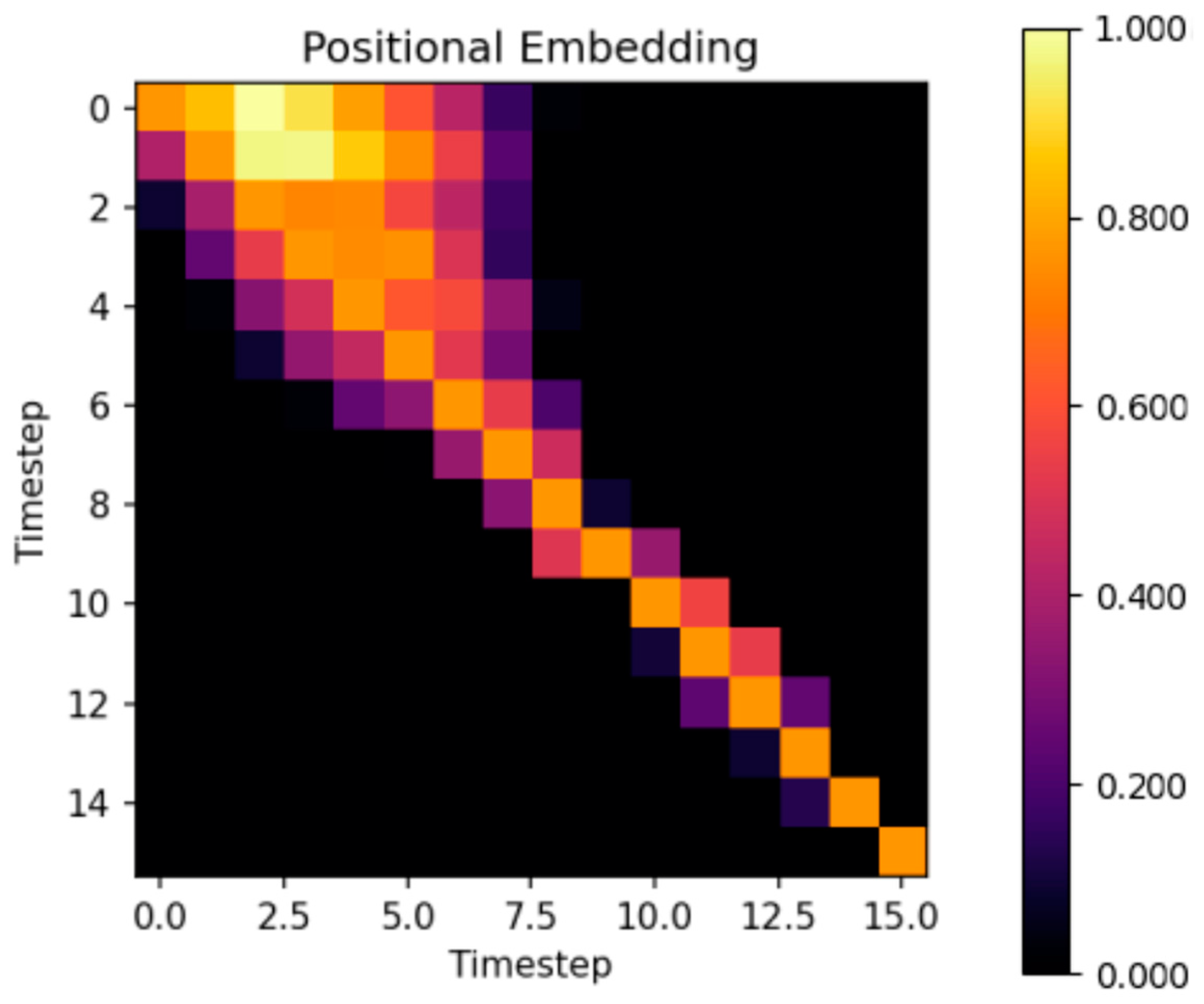
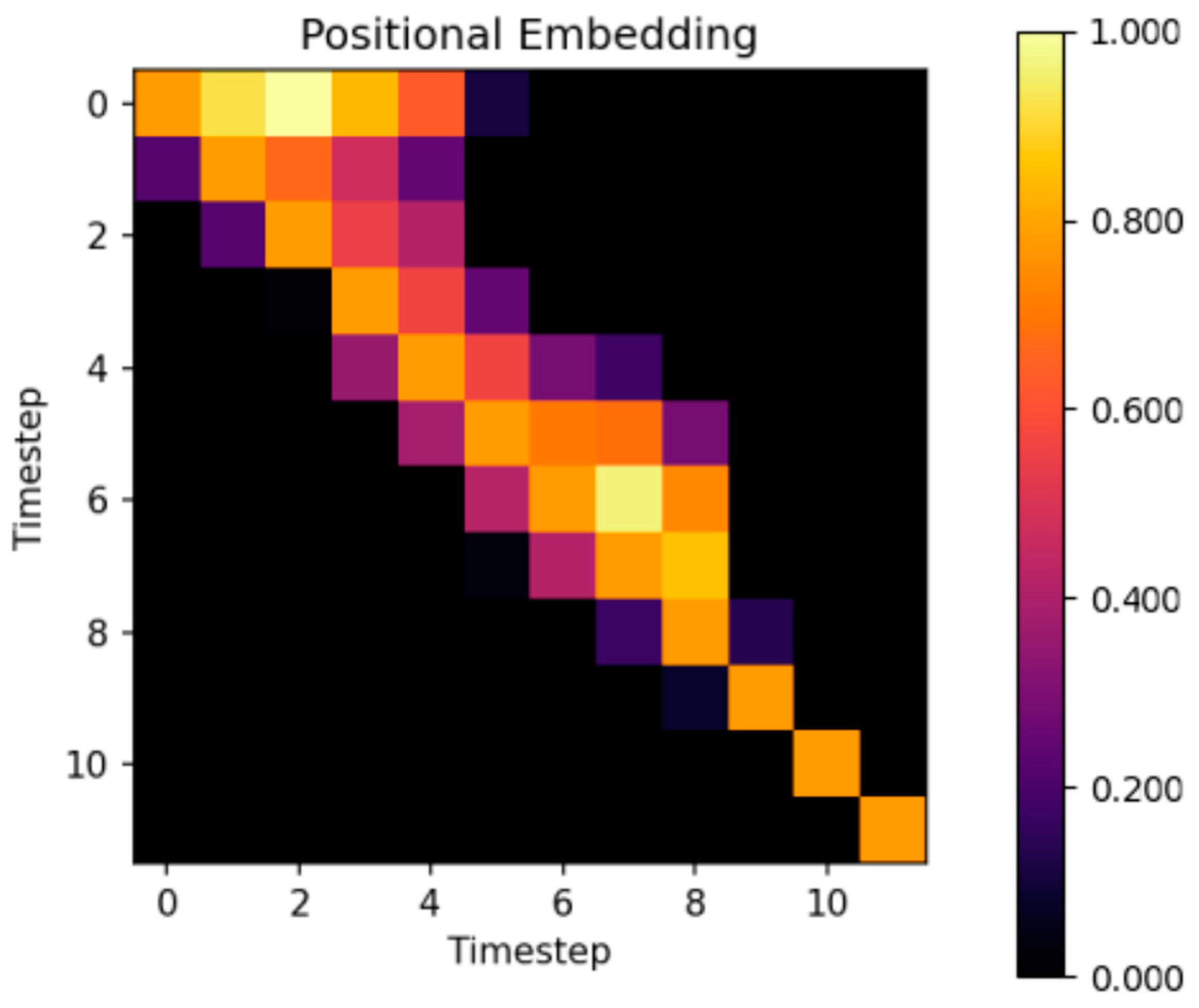
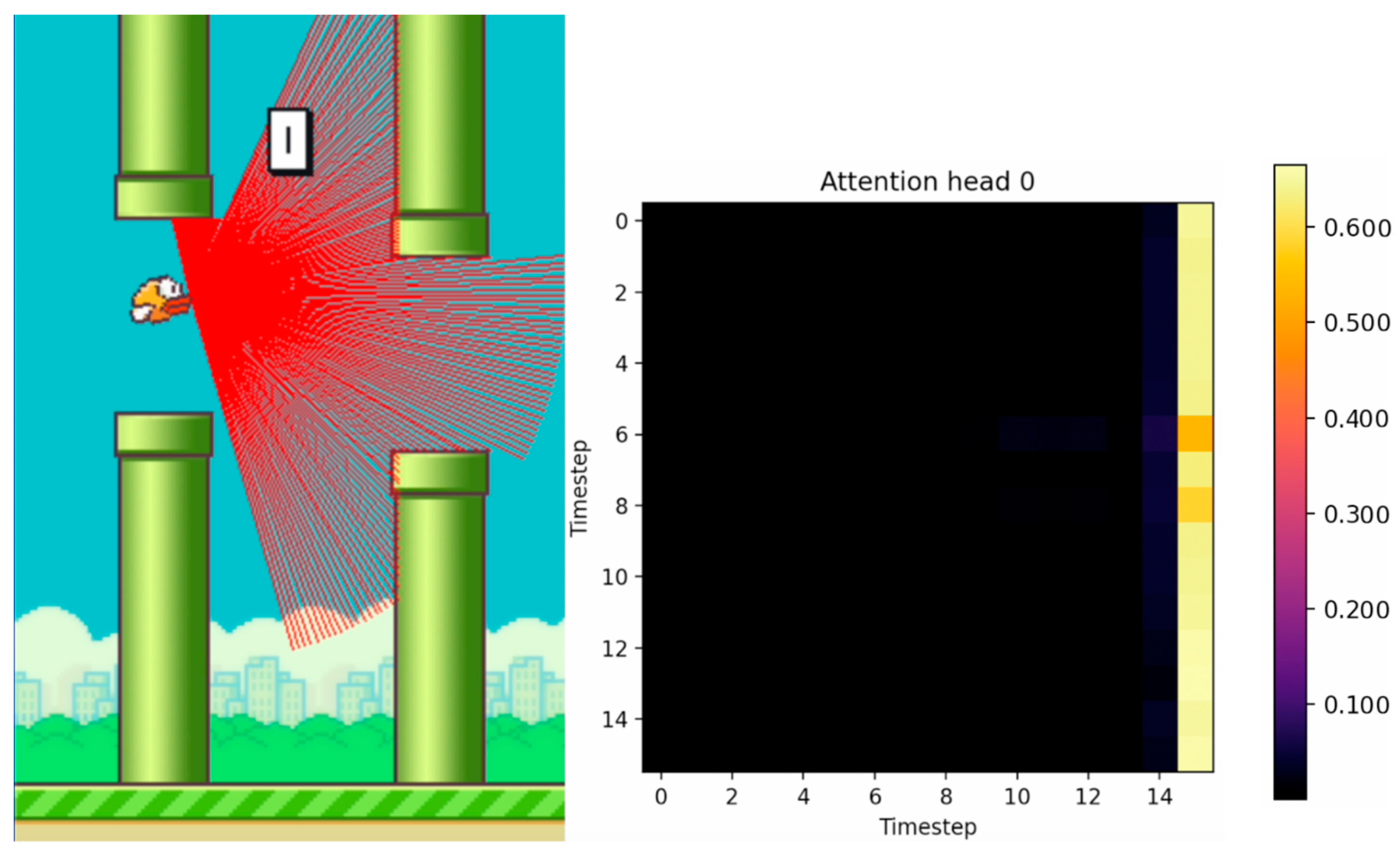
- Visualizing and tracking the temporal similarity of sensor data: This research introduces a visualization technique to track similarities within sensor data sequences during a transformer’s model training. This technique helps adjust the model to focus on the crucial measurements that impact the game’s strategy and ultimate outcome, effectively discarding non-critical information. This approach was developed to reduce training times and lower memory requirements for the agent.
- Real-world applicability: Our findings have the potential to be applied to real robots operating in hazardous environments (comparable to the Flappy Bird simulation, where the agent can crash). By incorporating a “private zone” concept and deep learning guidance, robots could potentially navigate complex tasks while minimizing collisions and extending their operational lifespan.
2. Materials and Methods
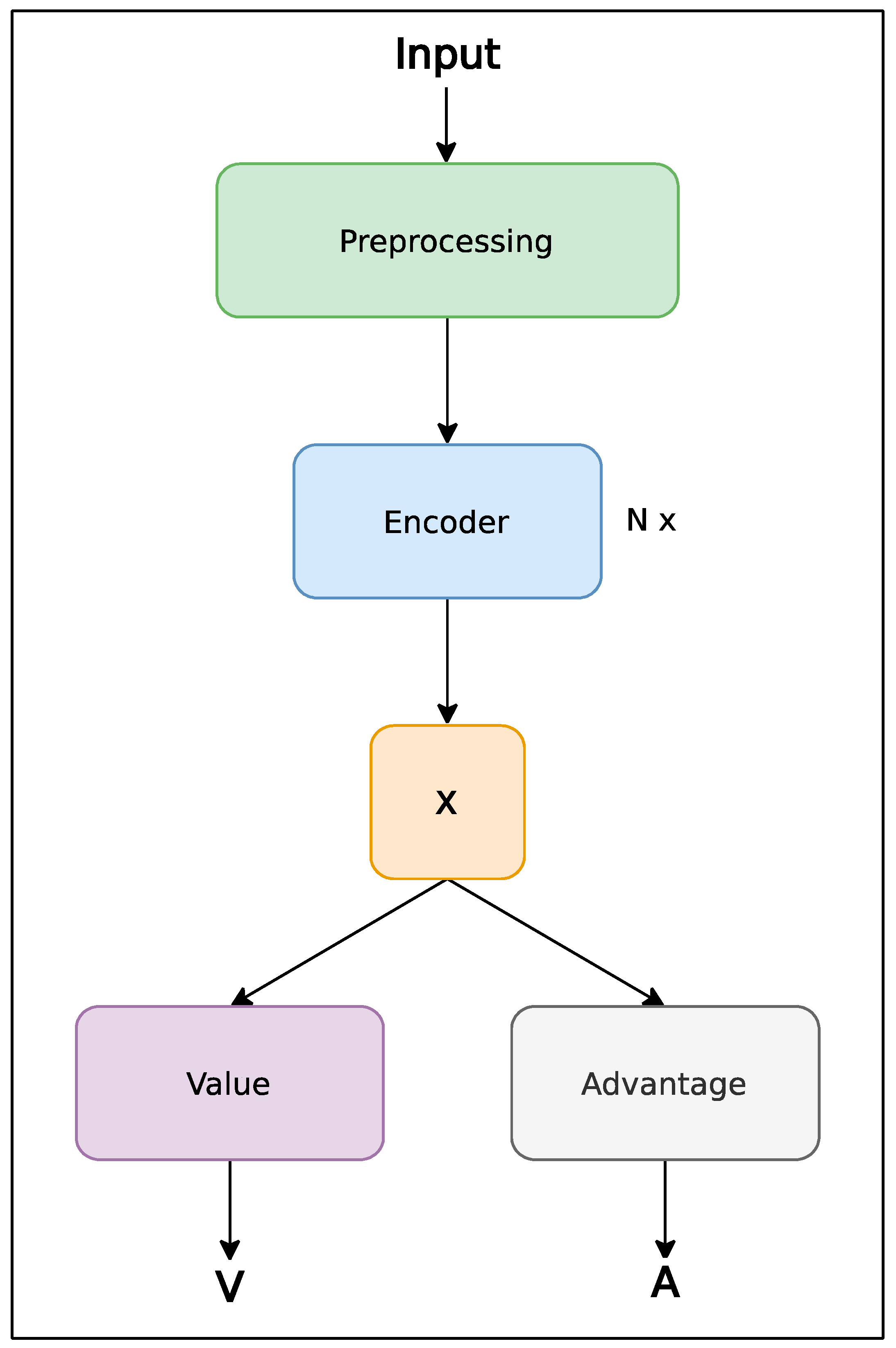
2.1. Dueling Deep Q Network
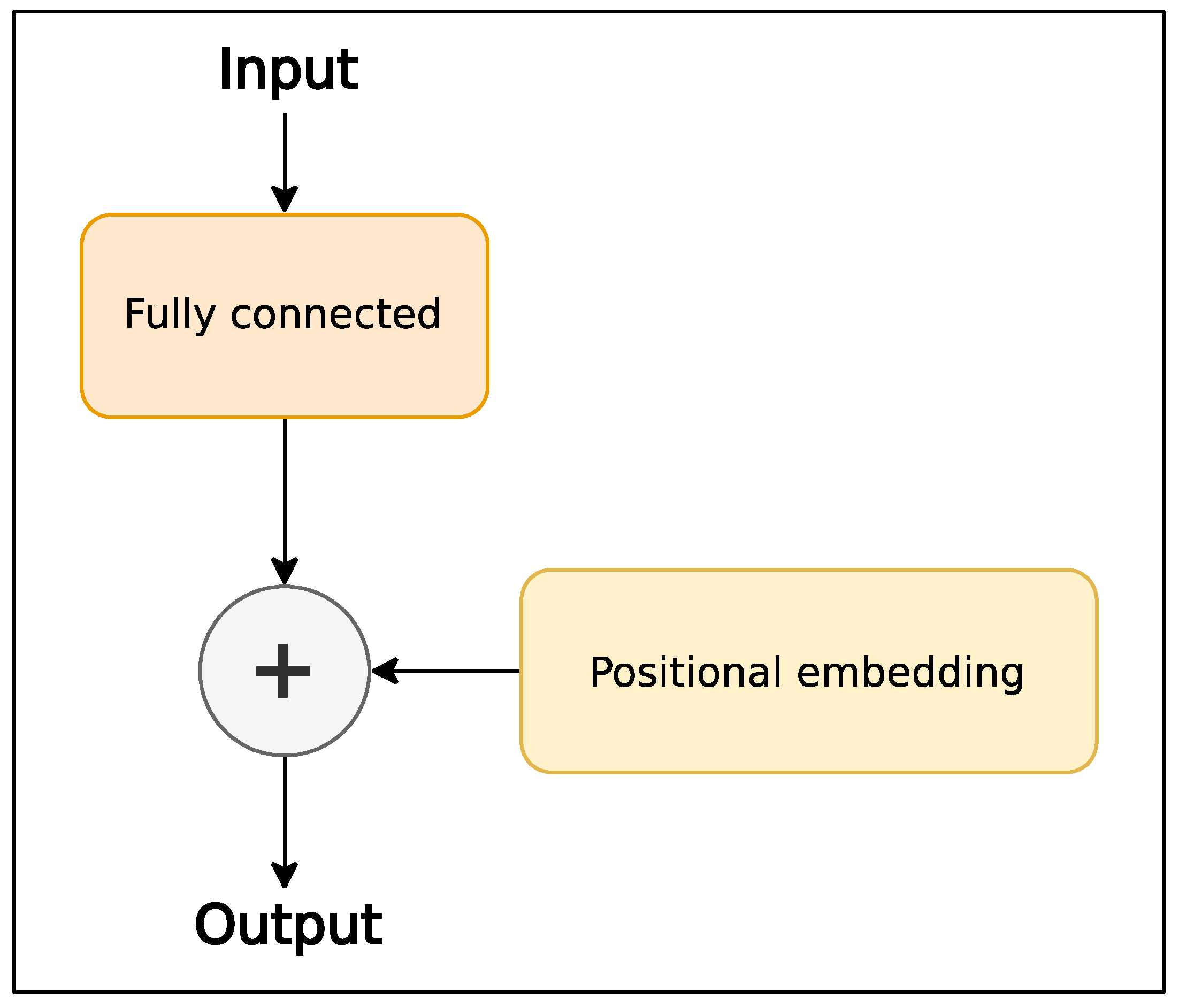
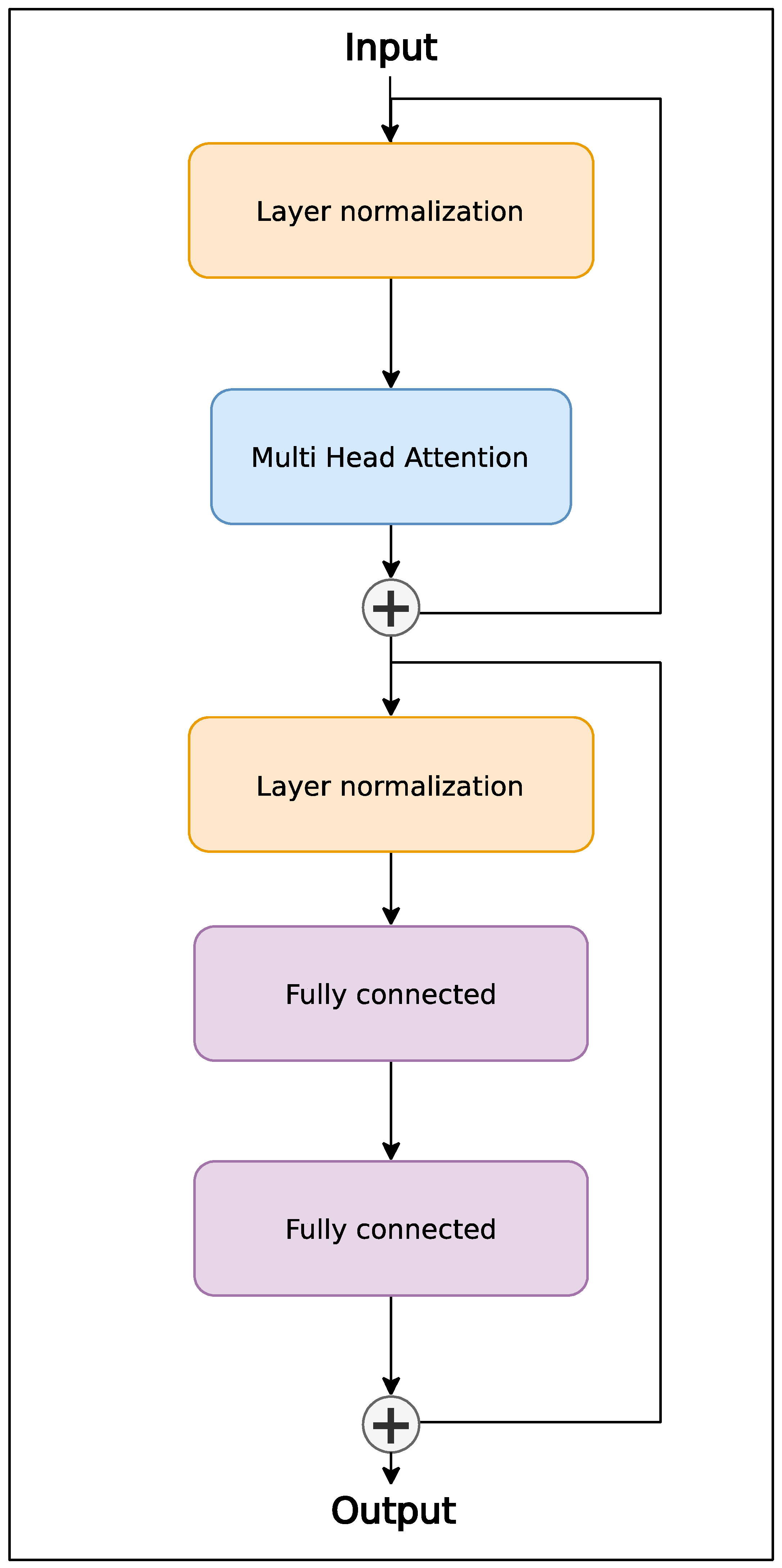
2.2. Motion Transformer
2.3. Database Reverb
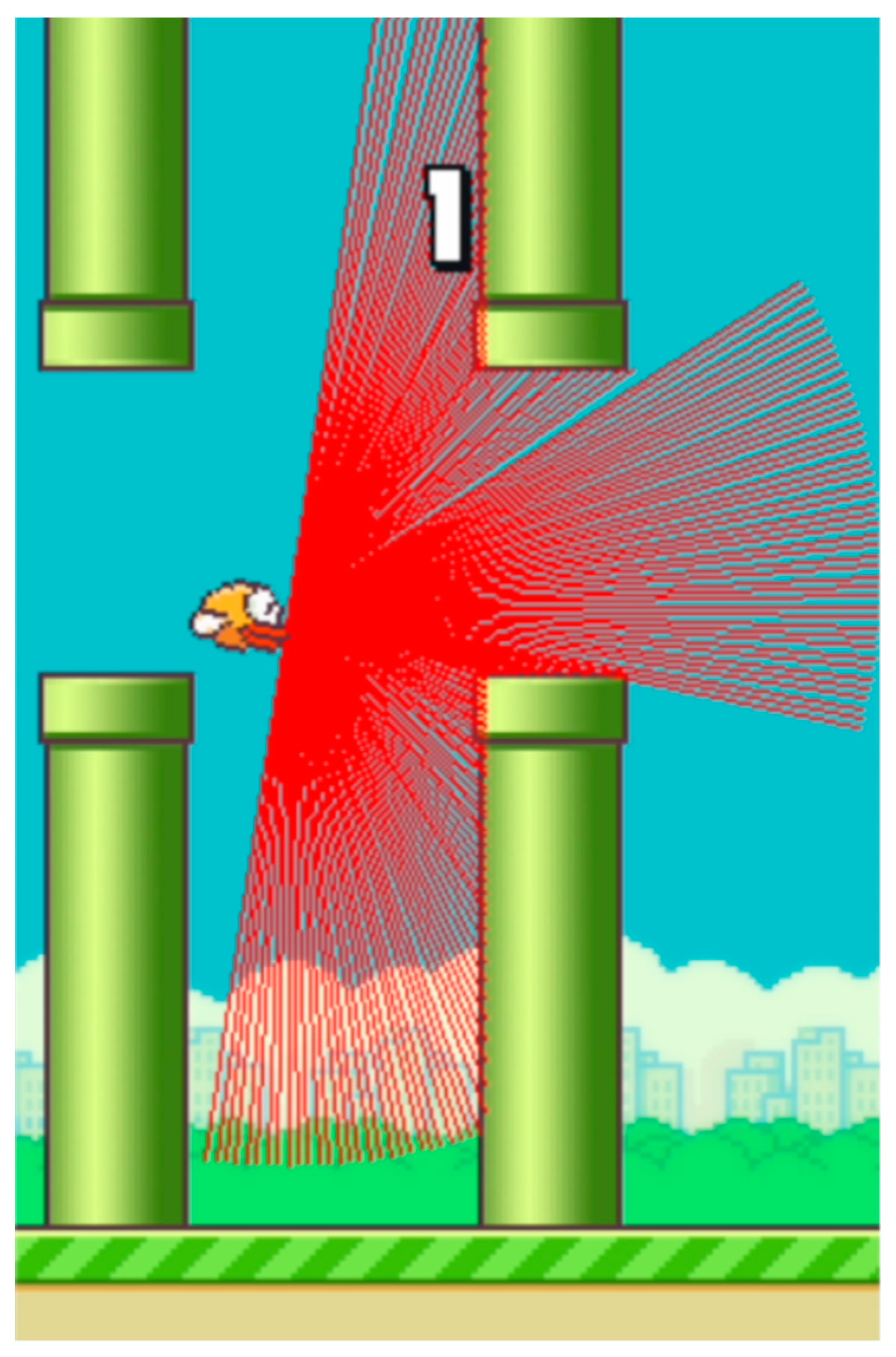
2.4. LIDAR
2.5. Episodic Memory
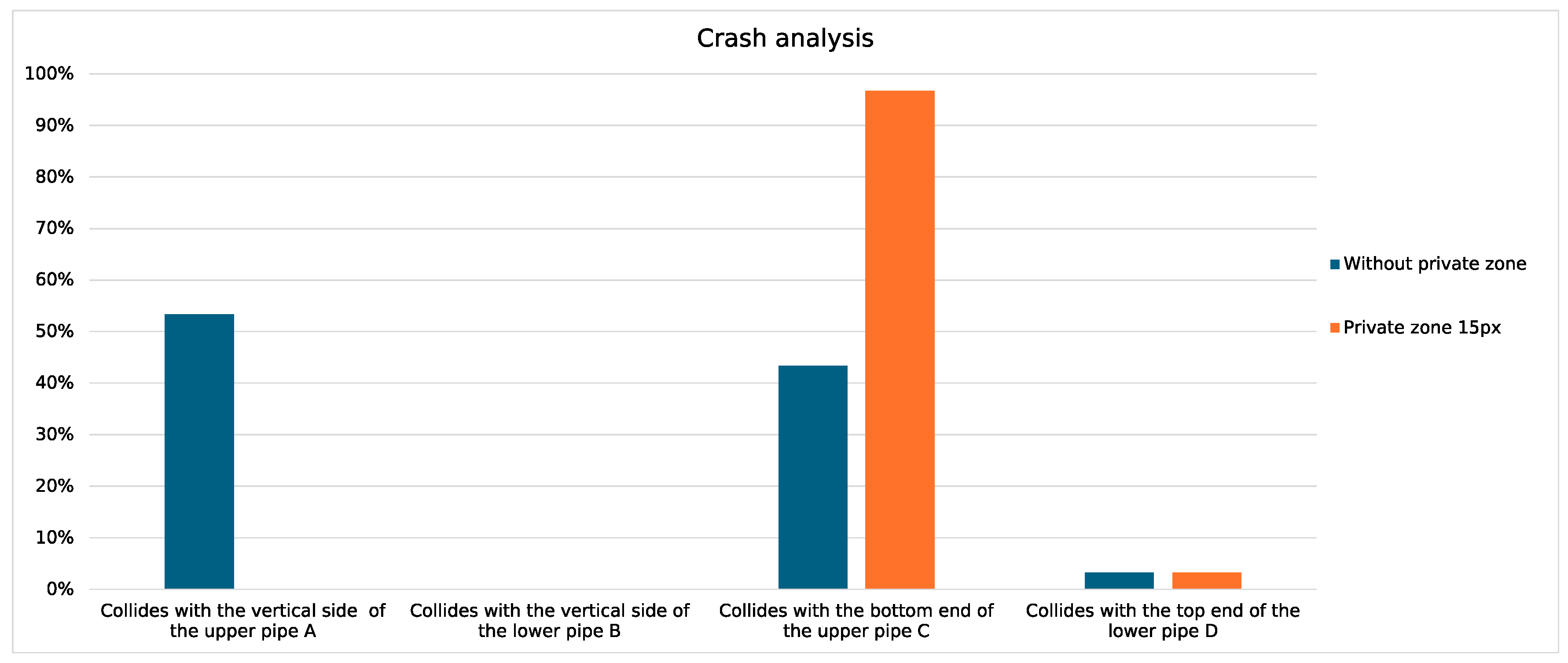
2.6. Private Zone around the Agent
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 10 December 2023).
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 11121–11128. Available online: https://ojs.aaai.org/index.php/AAAI/article/view/26317/26089 (accessed on 10 December 2023). [CrossRef]
- Wei, S. Reinforcement Learning for Improving Flappy Bird Game. Highlights Sci. Eng. Technol. 2023, 34, 244–249. Available online: https://drpress.org/ojs/index.php/HSET/article/download/5479/5298 (accessed on 10 December 2023). [CrossRef]
- Pilcer, L.S.; Hoorelbeke, A.; Andigne, A.D. Playing Flappy Bird with Deep Reinforcement Learning. IEEE Trans. Neural Netw. 2015, 16, 285–286. Available online: https://www.researchgate.net/profile/Louis-Samuel-Pilcer/publication/324066514_Playing_Flappy_Bird_with_Deep_Reinforcement_Learning/links/5abbc2230f7e9bfc045592df/Playing-Flappy-Bird-with-Deep-Reinforcement-Learning.pdf (accessed on 10 December 2023).
- Yang, K. Using DQN and Double DQN to Play Flappy Bird. In Proceedings of the 2022 International Conference on Artificial Intelligence, Internet and Digital Economy (ICAID 2022), Xi’an, China, 15–17 April 2022; Atlantis Press: Amsterdam, The Netherlands, 2022; pp. 1166–1174. Available online: https://www.atlantis-press.com/article/125977189.pdf (accessed on 10 December 2023).
- Chen, K. Deep Reinforcement Learning for Flappy Bird. CS 229 Machine-Learning Final Projects. 2015. Available online: https://cs229.stanford.edu/proj2015/362_report.pdf (accessed on 10 December 2023).
- Vu, T.; Tran, L. FlapAI Bird: Training an Agent to Play Flappy Bird Using Reinforcement Learning Techniques. arXiv 2020, arXiv:2003.09579. [Google Scholar]
- Li, J.; Yin, Y.; Chu, H.; Zhou, Y.; Wang, T.; Fidler, S.; Li, H. Learning to generate diverse dance motions with transformer. arXiv 2020, arXiv:2008.08171. [Google Scholar]
- Shi, S.; Jiang, L.; Dai, D.; Schiele, B. Motion transformer with global intention localization and local movement refinement. Adv. Neural Inf. Process. Syst. 2022, 35, 6531–6543. Available online: https://proceedings.neurips.cc/paper_files/paper/2022/file/2ab47c960bfee4f86dfc362f26ad066a-Paper-Conference.pdf (accessed on 10 December 2023).
- Hu, M.; Zhu, X.; Wang, H.; Cao, S.; Liu, C.; Song, Q. STDFormer: Spatial-Temporal Motion Transformer for Multiple Object Tracking. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6571–6594. Available online: https://ieeexplore.ieee.org/iel7/76/4358651/10091152.pdf (accessed on 10 December 2023). [CrossRef]
- Esslinger, K.; Platt, R.; Amato, C. Deep Transformer Q-Networks for Partially Observable Reinforcement Learning. arXiv 2022, arXiv:2206.01078. [Google Scholar]
- Meng, L.; Goodwin, M.; Yazidi, A.; Engelstad, P. Deep Reinforcement Learning with Swin Transformer. arXiv 2022, arXiv:2206.15269. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. Adv. Neural Inf. Process. Syst. 2021, 34, 15084–15097. Available online: https://proceedings.neurips.cc/paper_files/paper/2021/file/7f489f642a0ddb10272b5c31057f0663-Paper.pdf (accessed on 10 December 2023).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, R.; Ji, C.; Niu, J.; Guo, B. Research on intrusion detection method based on 1D-ICNN-BiGRU. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2347, p. 012001. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/2347/1/012001/pdf (accessed on 10 December 2023).
- Crocioni, G.; Pau, D.; Delorme, J.M.; Gruosso, G. Li-ion batteries parameter estimation with tiny neural networks embedded on intelligent IoT microcontrollers. IEEE Access 2020, 8, 122135–122146. Available online: https://ieeexplore.ieee.org/iel7/6287639/6514899/09133084.pdf (accessed on 10 December 2023). [CrossRef]
- Gholamalinezhad, H.; Khosravi, H. Pooling Methods in Deep Neural Networks, a Review. arXiv 2020, arXiv:2009.07485. [Google Scholar]
- Anders, K.; Winiwarter, L.; Lindenbergh, R.; Williams, J.G.; Vos, S.E.; Höfle, B. 4D objects-by-change: Spatiotemporal segmentation of geomorphic surface change from LiDAR time series. ISPRS J. Photogramm. Remote Sens. 2020, 159, 352–363. Available online: https://www.sciencedirect.com/science/article/pii/S0924271619302850 (accessed on 10 December 2023). [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York City, NY, USA, 19–24 June 2016; pp. 1995–2003. Available online: http://proceedings.mlr.press/v48/wangf16.pdf (accessed on 10 December 2023).
- Haarnoja, T.; Tang, H.; Abbeel, P.; Levine, S. Reinforcement learning with deep energy-based policies. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1352–1361. Available online: http://proceedings.mlr.press/v70/haarnoja17a/haarnoja17a.pdf (accessed on 10 December 2023).
- Peng, B.; Sun, Q.; Li, S.E.; Kum, D.; Yin, Y.; Wei, J.; Gu, T. End-to-end autonomous driving through dueling double deep Q-network. Automot. Innov. 2021, 4, 328–337. Available online: https://link.springer.com/content/pdf/10.1007/s42154-021-00151-3.pdf (accessed on 10 December 2023). [CrossRef]
- Liu, F.; Li, S.; Zhang, L.; Zhou, C.; Ye, R.; Wang, Y.; Lu, J. 3DCNN-DQN-RNN: A deep reinforcement learning framework for semantic parsing of large-scale 3D point clouds. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5678–5687. Available online: https://openaccess.thecvf.com/content_ICCV_2017/papers/Liu_3DCNN-DQN-RNN_A_Deep_ICCV_2017_paper.pdf (accessed on 10 December 2023).
- Saleh, R.A.; Saleh, A.K. Statistical Properties of the Log-Cosh Loss Function Used in Machine Learning. arXiv 2022, arXiv:2208.04564. [Google Scholar]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. Adv. Neural Inf. Process. Syst. 2017, 30, 1195–1204. Available online: https://proceedings.neurips.cc/paper/2017/file/68053af2923e00204c3ca7c6a3150cf7-Paper.pdf (accessed on 10 December 2023).
- Tummala, S.; Kadry, S.; Bukhari, S.A.C.; Rauf, H.T. Classification of brain tumor from magnetic resonance imaging using vision transformers ensembling. Curr. Oncol. 2022, 29, 7498–7511. Available online: https://www.mdpi.com/1718-7729/29/10/590/htm (accessed on 10 December 2023). [CrossRef]
- Wang, X.; Yang, Z.; Chen, G.; Liu, Y. A Reinforcement Learning Method of Solving Markov Decision Processes: An Adaptive Exploration Model Based on Temporal Difference Error. Electronics 2023, 12, 4176. Available online: https://www.mdpi.com/2079-9292/12/19/4176 (accessed on 10 December 2023). [CrossRef]
- Feng, H.; Yang, B.; Wang, J.; Liu, M.; Yin, L.; Zheng, W.; Yin, Z.; Liu, C. Identifying malignant breast ultrasound images using ViT-patch. Appl. Sci. 2023, 13, 3489. Available online: https://www.mdpi.com/2076-3417/13/6/3489 (accessed on 10 December 2023). [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-Training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. Available online: https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf (accessed on 10 December 2023).
- Hasan, F.; Huang, H. MALS-Net: A multi-head attention-based LSTM sequence-to-sequence network for socio-temporal interaction modelling and trajectory prediction. Sensors 2023, 23, 530. Available online: https://www.mdpi.com/1424-8220/23/1/530/pdf (accessed on 10 December 2023). [CrossRef]
- Mogan, J.N.; Lee, C.P.; Lim, K.M.; Muthu, K.S. Gait-ViT: Gait Recognition with Vision Transformer. Sensors 2022, 22, 7362. Available online: https://www.mdpi.com/1424-8220/22/19/7362/pdf (accessed on 10 December 2023). [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (Gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Sun, W.; Wang, H.; Xu, J.; Yang, Y.; Yan, R. Effective Convolutional Transformer for Highly Accurate Planetary Gearbox Fault Diagnosis. IEEE Open J. Instrum. Meas. 2022, 1, 1–9. Available online: https://ieeexplore.ieee.org/iel7/9552935/9775186/09828477.pdf (accessed on 10 December 2023). [CrossRef]
- Cassirer, A.; Barth-Maron, G.; Brevdo, E.; Ramos, S.; Boyd, T.; Sottiaux, T.; Kroiss, M. Reverb: A Framework for Experience Replay. arXiv 2021, arXiv:2102.04736. [Google Scholar]
- Hoffman, M.W.; Shahriari, B.; Aslanides, J.; Barth-Maron, G.; Momchev, N.; Sinopalnikov, D.; Stańczyk, P.; Ramos, S.; Raichuk, A.; Vincent, D.; et al. Acme: A Research Framework for Distributed Reinforcement Learning. arXiv 2020, arXiv:2006.00979. [Google Scholar]
- Lapan, M. Deep Reinforcement Learning Hands-On: Apply Modern RL Methods, with Deep Q-Networks, Value Iteration, Policy Gradients, TRPO, AlphaGo Zero and More; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Singh, A.; Yang, L.; Hartikainen, K.; Finn, C.; Levine, S. End-to-End Robotic Reinforcement Learning without Reward Engineering. arXiv 2019, arXiv:1904.07854. [Google Scholar]
- Capellier, E.; Davoine, F.; Cherfaoui, V.; Li, Y. Evidential deep learning for arbitrary LIDAR object classification in the context of autonomous driving. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1304–1311. Available online: https://hal.science/hal-02322434/file/IV19-Edouard.pdf (accessed on 10 December 2023).
- Skrinárová, J.; Huraj, L.; Siládi, V. A neural tree model for classification of computing grid resources using PSO tasks scheduling. Neural Netw. World 2013, 23, 223. Available online: https://www.proquest.com/docview/1418215646/fulltextPDF/AF8F42E64A49412CPQ/1?accountid=49441&sourcetype=Scholarly%20Journals (accessed on 10 December 2023). [CrossRef]
- Sualeh, M.; Kim, G.W. Dynamic multi-lidar based multiple object detection and tracking. Sensors 2019, 19, 1474. Available online: https://www.mdpi.com/1424-8220/19/6/1474/pdf (accessed on 10 December 2023). [CrossRef]
- Kyselica, D.; Šilha, J.; Ďurikovič, R.; Bartková, D.; Tóth, J. Towards image processing of reentry event. J. Appl. Math. Stat. Inform. 2023, 19, 47–60. Available online: https://sciendo.com/article/10.2478/jamsi-2023-0003 (accessed on 10 December 2023). [CrossRef]
- Orkphol, K.; Yang, W. Word sense disambiguation using cosine similarity collaborates with Word2vec and WordNet. Future Internet 2019, 11, 114. Available online: https://www.mdpi.com/1999-5903/11/5/114/pdf (accessed on 10 December 2023). [CrossRef]
- Appiah, N.; Vare, S. Playing Flappy Bird with Deep Reinforcement Learning. 2018. Available online: http://vision.stanford.edu/teaching/cs231n/reports/2016/pdfs/111_Report.pdf (accessed on 10 December 2023).
- Li, L.; Jiang, Z.; Yang, Z. Playing Modified Flappy Bird with Deep Reinforcement Learning. 2023. Available online: https://github.com/SeVEnMY/DeepLearningFinal (accessed on 10 December 2023).
- Hasselt, H. Double Q-Learning. Adv. Neural Inf. Process. Syst. 2010, 23, 2613–2621. Available online: https://proceedings.neurips.cc/paper_files/paper/2010/file/091d584fced301b442654dd8c23b3fc9-Paper.pdf (accessed on 10 December 2023).
- Al Rahhal, M.M.; Bazi, Y.; Jomaa, R.M.; AlShibli, A.; Alajlan, N.; Mekhalfi, M.L.; Melgani, F. COVID-19 detection in Ct/X-ray imagery using vision transformers. J. Pers. Med. 2022, 12, 310. Available online: https://www.mdpi.com/2075-4426/12/2/310 (accessed on 10 December 2023). [CrossRef] [PubMed]
- Passricha, V.; Aggarwal, R.K. A comparative analysis of pooling strategies for convolutional neural network based Hindi ASR. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 675–691. Available online: https://link.springer.com/article/10.1007/s12652-019-01325-y (accessed on 10 December 2023). [CrossRef]
- Mazumder, S.; Liu, B.; Wang, S.; Zhu, Y.; Yin, X.; Liu, L.; Li, J.; Huang, Y. Guided Exploration in Deep Reinforcement Learning. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019; Available online: https://openreview.net/forum?id=SJMeTo09YQ (accessed on 10 December 2023).
- Hessel, M.; Modayil, J.; Van Hasselt, H.; Schaul, T.; Ostrovski, G.; Dabney, W.; Horgan, D.; Piot, B.; Azar, M.; Silver, D. Rainbow: Combining improvements in deep reinforcement learning. AAAI Conf. Artif. Intell. 2018, 32, 1. Available online: https://ojs.aaai.org/index.php/AAAI/article/download/11796/11655 (accessed on 10 December 2023). [CrossRef]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. Beit: Bert Pre-Training of Image Transformers. arXiv 2021, arXiv:2106.08254. [Google Scholar]





| Architecture | Timesteps | Highest Score | Average Score |
|---|---|---|---|
| Global average pooling | 16 | 2970 | 324.198 |
| Last timestep | 16 | 2809 | 286.394 |
| Global maximum pooling | 16 | 1948 | 329.194 |
| Global average pooling | 12 | 2348 | 380.284 |
| Last timestep | 12 | 1922 | 335.114 |
| Global maximum pooling | 12 | 1128 | 152.858 |
| Paper | Highest Score | Average Score |
|---|---|---|
| [43] | 15 | 3.300 |
| [4] | 80 | 16.400 |
| [6] | 215 | 82.200 |
| [5] | - | 102.170 |
| [7] | 1491 | 209.298 |
| This paper without a private zone | 2970 | 380.284 |
| This paper with a private zone | 74,755 | 13,156.590 |
| Private Zone | Highest Score | Average Score |
|---|---|---|
| None | 2970 | 380.284 |
| 0 | 10,250 | 2138.858 |
| 15 | 74,755 | 13,156.590 |
| 30 | 11,383 | 1645.654 |
| Hyperparameter | Description | Value |
|---|---|---|
| port | Database server port | 8000 |
| max_replay_size | Maximum database memory | 1,000,000 |
| samples_per_insert | Samples per insert ratio for reverb | 32 |
| temp_init | Initial Boltzmann temperature for exploration | 0.500 |
| temp_min | Minimal Boltzmann temperature | 0.010 |
| temp_decay | Decay of Boltzmann temperature | 0.999999 |
| warmup_steps | Warmup steps for learning rate cosine scheduler | 1000 |
| train_steps | Training steps | 1,000,000 |
| batch_size | Batch size | 256 |
| gamma | Discount factor | 0.990 |
| tau | Tau factor (for EMA model) | 0.005 |
| num_layers | Num. of encoder blocks | 2 |
| embed_dim | Embedding dimension | 128 |
| ff_mult | Multiplier of MLP block dimension | 4 |
| num_heads | Num. of attention heads | 6 |
| learning_rate | Learning rate | 3 × 10−4 |
| global_clipnorm | Globally normalized clipping of gradient | 1 |
| weight_decay | Weight decay for AdamW optimizer | 1 × 10−4 |
| frame_stack | Size of short-term (episodic) memory | 16 or 12 |
| player_private_zone | Size of agent’s private zone | None, 0, 15 or 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dirgová Luptáková, I.; Kubovčík, M.; Pospíchal, J. Playing Flappy Bird Based on Motion Recognition Using a Transformer Model and LIDAR Sensor. Sensors 2024, 24, 1905. https://doi.org/10.3390/s24061905
Dirgová Luptáková I, Kubovčík M, Pospíchal J. Playing Flappy Bird Based on Motion Recognition Using a Transformer Model and LIDAR Sensor. Sensors. 2024; 24(6):1905. https://doi.org/10.3390/s24061905
Chicago/Turabian StyleDirgová Luptáková, Iveta, Martin Kubovčík, and Jiří Pospíchal. 2024. "Playing Flappy Bird Based on Motion Recognition Using a Transformer Model and LIDAR Sensor" Sensors 24, no. 6: 1905. https://doi.org/10.3390/s24061905
APA StyleDirgová Luptáková, I., Kubovčík, M., & Pospíchal, J. (2024). Playing Flappy Bird Based on Motion Recognition Using a Transformer Model and LIDAR Sensor. Sensors, 24(6), 1905. https://doi.org/10.3390/s24061905









