Enhancing View Synthesis with Depth-Guided Neural Radiance Fields and Improved Depth Completion
Abstract
:1. Introduction
- Introducing depth completion to NeRF to provide dense and accurate depth maps.
- Enhancing the sampling efficiency by utilizing dense depth information.
- Proposing a mechanism for generating depth rays in NeRF to enhance rendering quality, improve accuracy, and ensure consistent scene depth.
2. Related Work
2.1. Neural Volume Rendering
2.2. Neural Radiance Field with Depth
2.3. NeRF Training Acceleration
2.4. Limitation of Existing Methods
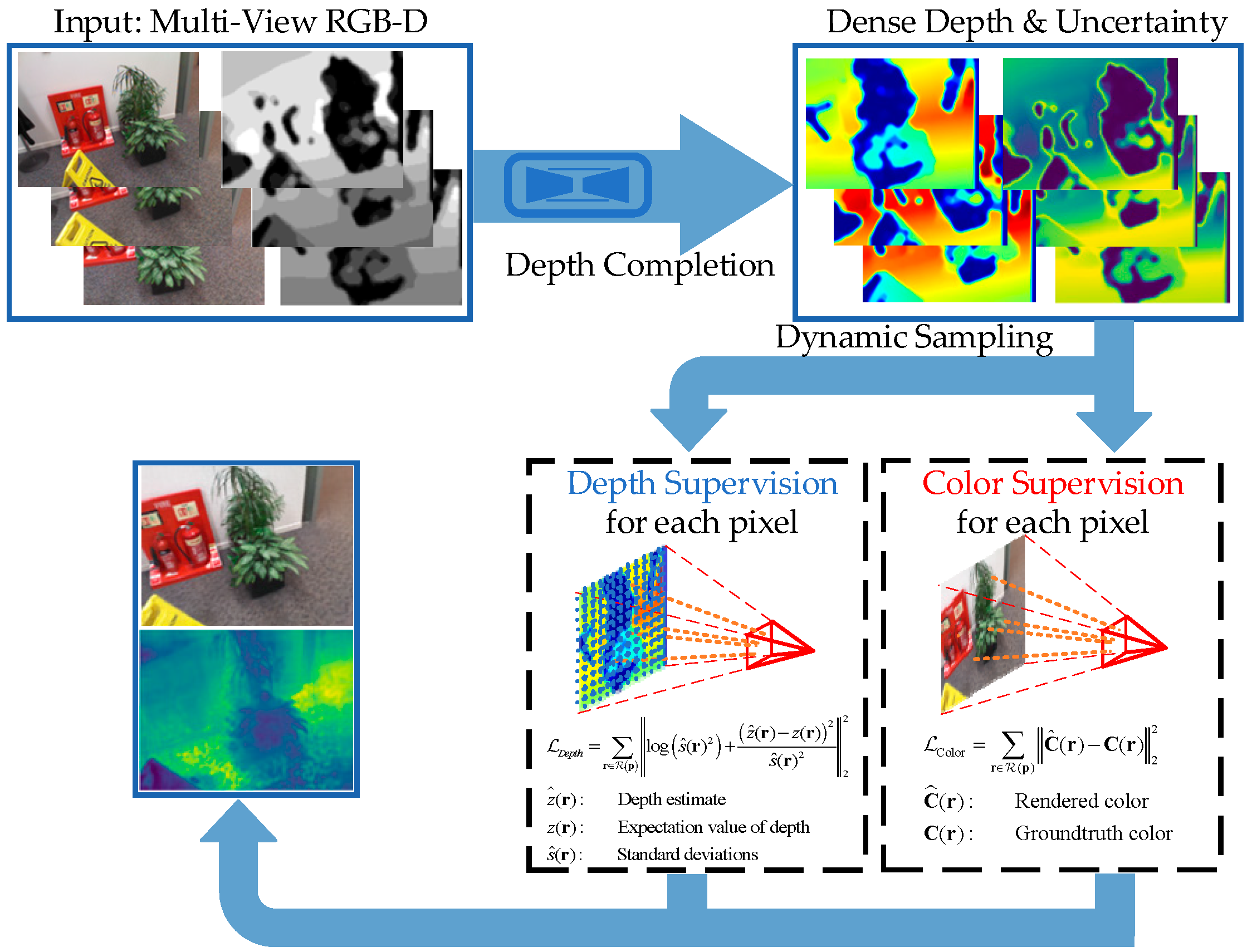
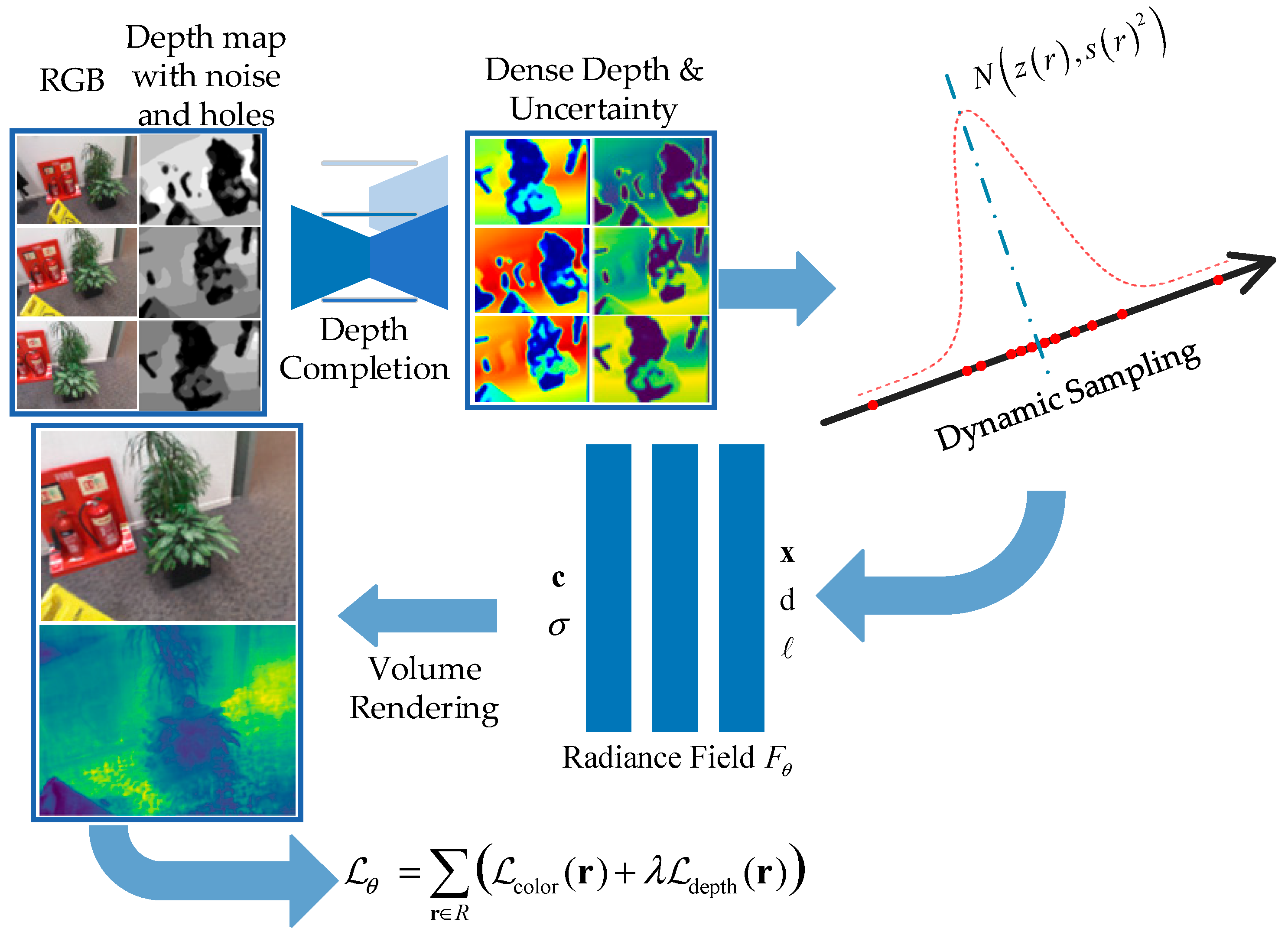
3. Method
- a.
- Volume Rendering with Radiance Fields
- b.
- Depth Completion with Uncertainty
- c.
- Depth-Guided Sampling
- d.
- Optimization with Depth Constrain
4. Experiments
4.1. Experimental Setup
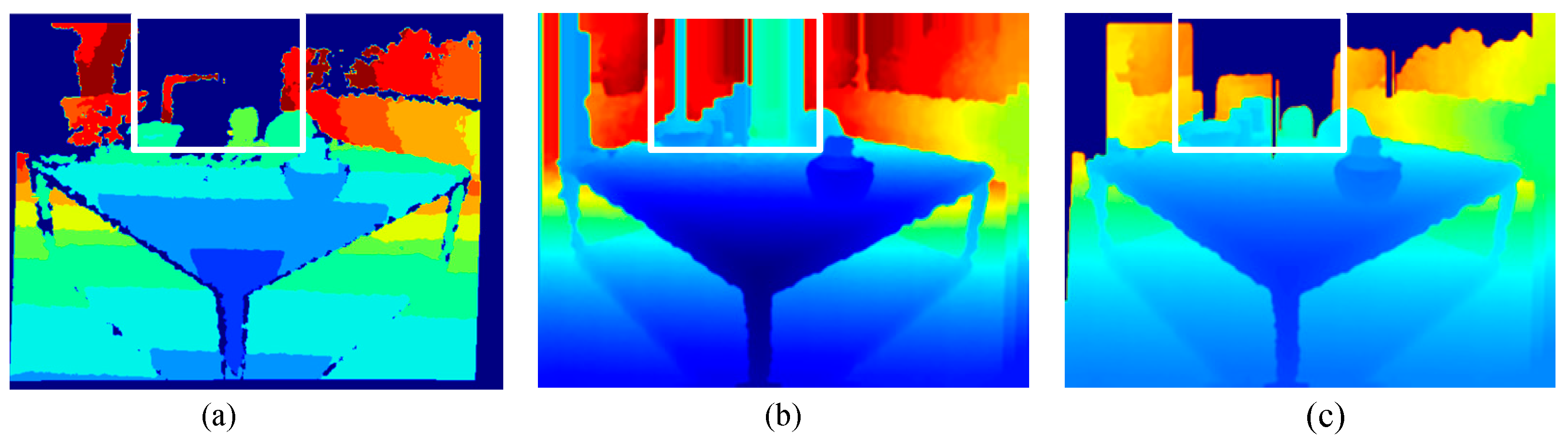
4.2. Basic Comparison
4.3. Ablation Study
4.4. Training Speed
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neff, T.; Stadlbauer, P.; Parger, M.; Kurz, A.; Mueller, J.H.; Chaitanya, C.R.A.; Kaplanyan, A.; Steinberger, M. DONeRF: Towards Real-Time Rendering of Compact Neural Radiance Fields using Depth Oracle Networks. Comput. Graph. Forum 2021, 40, 45–59. [Google Scholar] [CrossRef]
- Hu, T.; Liu, S.; Chen, Y.; Shen, T.; Jia, J. EfficientNeRF: Efficient Neural Radiance Fields. arXiv 2022, arXiv:2206.00878. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. arXiv 2020, arXiv:2003.08934. [Google Scholar] [CrossRef]
- Gafni, G.; Thies, J.; Zollhofer, M.; Niesner, M. Dynamic Neural Radiance Fields for Monocular 4D Facial Avatar Reconstruction. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8645–8654. [Google Scholar]
- Tretschk, E.; Tewari, A.; Golyanik, V.; Zollhofer, M.; Lassner, C.; Theobalt, C. Non-Rigid Neural Radiance Fields: Reconstruction and Novel View Synthesis of a Dynamic Scene From Monocular Video. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 12939–12950. [Google Scholar]
- Pumarola, A.; Corona, E.; Pons-Moll, G.; Moreno-Noguer, F. D-NeRF: Neural Radiance Fields for Dynamic Scenes. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10313–10322. [Google Scholar]
- Tancik, M.; Mildenhall, B.; Wang, T.; Schmidt, D.; Srinivasan, P.P.; Barron, J.T.; Ng, R. Learned Initializations for Optimizing Coordinate-Based Neural Representations. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 2845–2854. [Google Scholar]
- Chan, E.R.; Monteiro, M.; Kellnhofer, P.; Wu, J.; Wetzstein, G. pi-GAN: Periodic Implicit Generative Adversarial Networks for 3D-Aware Image Synthesis. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 5795–5805. [Google Scholar]
- Yu, A.; Ye, V.; Tancik, M.; Kanazawa, A. pixelNeRF: Neural Radiance Fields from One or Few Images. arXiv 2021, arXiv:2012.02190. [Google Scholar] [CrossRef]
- Schwarz, K.; Liao, Y.; Niemeyer, M.; Geiger, A. GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis. arXiv 2021, arXiv:2007.02442. [Google Scholar] [CrossRef]
- Lombardi, S.; Simon, T.; Saragih, J.; Schwartz, G.; Lehrmann, A.; Sheikh, Y. Neural volumes: Learning dynamic renderable volumes from images. ACM Trans. Graph. 2019, 38, 1–14. [Google Scholar] [CrossRef]
- Henzler, P.; Rasche, V.; Ropinski, T.; Ritschel, T. Single-image Tomography: 3D Volumes from 2D Cranial X-rays. Comput. Graph. Forum 2018, 37, 377–388. [Google Scholar] [CrossRef]
- Sitzmann, V.; Thies, J.; Heide, F.; NieBner, M.; Wetzstein, G.; Zollhofer, M. DeepVoxels: Learning Persistent 3D Feature Embeddings. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2432–2441. [Google Scholar]
- Martin-Brualla, R.; Pandey, R.; Yang, S.; Pidlypenskyi, P.; Taylor, J.; Valentin, J.; Khamis, S.; Davidson, P.; Tkach, A.; Lincoln, P.; et al. LookinGood: Enhancing Performance Capture with Real-time Neural Re-Rendering. arXiv 2018, arXiv:1811.05029. [Google Scholar] [CrossRef]
- Yariv, L.; Hedman, P.; Reiser, C.; Verbin, D.; Srinivasan, P.P.; Szeliski, R.; Barron, J.T.; Mildenhall, B. BakedSDF: Meshing Neural SDFs for Real-Time View Synthesis. In Proceedings of the ACM SIGGRAPH 2023 Conference Proceedings, Los Angeles, CA, USA, 6–10 August 2023. [Google Scholar]
- Yu, Z.; Peng, S.; Niemeyer, M.; Sattler, T.; Geiger, A. MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction. Adv. Neural Inf. Process. Syst. 2022, 35, 25018–25032. [Google Scholar]
- Li, Z.; Müller, T.; Evans, A.; Taylor, R.H.; Unberath, M.; Liu, M.-Y.; Lin, C.-H. Neuralangelo: High-Fidelity Neural Surface Reconstruction. arXiv 2023, arXiv:2306.03092. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, S.; Rao, Y.; Zhao, W.; Lu, J.; Zhou, J. NerfingMVS: Guided Optimization of Neural Radiance Fields for Indoor Multi-view Stereo. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 5590–5599. [Google Scholar]
- Deng, K.; Liu, A.; Zhu, J.-Y.; Ramanan, D. Depth-supervised NeRF: Fewer Views and Faster Training for Free. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12872–12881. [Google Scholar]
- Dey, A.; Ahmine, Y.; Comport, A.I. Mip-NeRF RGB-D: Depth Assisted Fast Neural Radiance Fields. J. WSCG 2022, 30, 34–43. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 5835–5844. [Google Scholar]
- Azinovic, D.; Martin-Brualla, R.; Goldman, D.B.; Niebner, M.; Thies, J. Neural RGB-D Surface Reconstruction. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6280–6291. [Google Scholar]
- Garbin, S.J.; Kowalski, M.; Johnson, M.; Shotton, J.; Valentin, J. FastNeRF: High-Fidelity Neural Rendering at 200FPS. arXiv 2021, arXiv:2103.10380. [Google Scholar] [CrossRef]
- Reiser, C.; Peng, S.; Liao, Y.; Geiger, A. KiloNeRF: Speeding up Neural Radiance Fields with Thousands of Tiny MLPs. arXiv 2021, arXiv:2103.13744. [Google Scholar] [CrossRef]
- Yu, A.; Li, R.; Tancik, M.; Li, H.; Ng, R.; Kanazawa, A. PlenOctrees for Real-time Rendering of Neural Radiance Fields. arXiv 2021, arXiv:2103.14024. [Google Scholar] [CrossRef]
- Liu, L.; Gu, J.; Lin, K.Z.; Chua, T.-S.; Theobalt, C. Neural Sparse Voxel Fields. arXiv 2021, arXiv:2007.11571. [Google Scholar] [CrossRef]
- Hedman, P.; Srinivasan, P.P.; Mildenhall, B.; Barron, J.T.; Debevec, P. Baking Neural Radiance Fields for Real-Time View Synthesis. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 5855–5864. [Google Scholar]
- Chen, A.; Xu, Z.; Zhao, F.; Zhang, X.; Xiang, F.; Yu, J.; Su, H. MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 14104–14113. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-view Stereo. In Computer Vision—ECCV 2018, Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 785–801. [Google Scholar]
- Schonberger, J.L.; Frahm, J.-M. Structure-from-Motion Revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Ku, J.; Harakeh, A.; Waslander, S.L. In Defense of Classical Image Processing: Fast Depth Completion on the CPU. arXiv 2018, arXiv:1802.00036. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Niessner, M. ScanNet: Richly-Annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2432–2443. [Google Scholar]
- Zeng, A.; Song, S.; Niessner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 199–208. [Google Scholar]
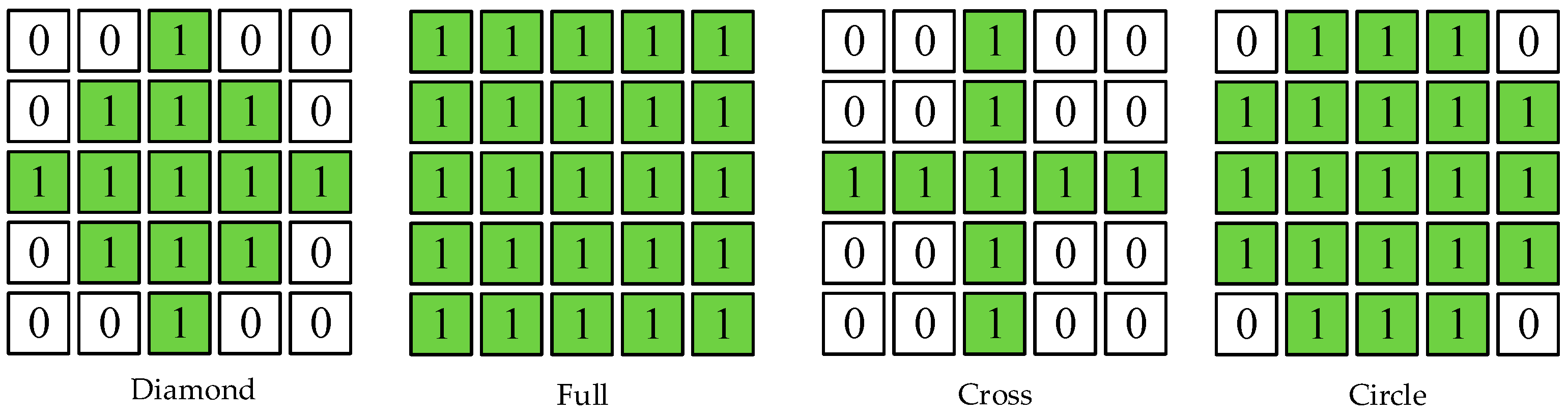





| Kernel Size | RMSE (mm) | MAE (mm) |
|---|---|---|
| 3 × 3 | 1649.97 | 367.06 |
| 4 × 4 | 1427.74 | 335.67 |
| 5 × 5 | 1545.85 | 349.45 |
| Full | 1545.85 | 349.45 |
| Circle | 1528.45 | 342.49 |
| Cross | 1521.95 | 333.94 |
| Diamond | 1512.18 | 333.67 |
| 3DMatch Rgbd-Scenes-v2-Scene_01 | ScanNet Scene0002_00 | 3DMatch 7-Scenes-Pumpkin | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | LPIPS↓ | Depth-RMSE↓ | PSNR↑ | SSIM↑ | LPIPS↓ | Depth-RMSE↓ | PSNR↑ | SSIM↑ | LPIPS↓ | Depth-RMSE↓ | |
| NeRF | 29.44 | 0.613 | 0.046 | 0.485 | 30.03 | 0.527 | 0.190 | 0.092 | 30.11 | 0.691 | 0.122 | 0.198 |
| DS-NeRF | 31.55 | 0.854 | 0.080 | 1.113 | 30.02 | 0.535 | 0.208 | 1.347 | 30.21 | 0.810 | 0.075 | 1.124 |
| NerfingMVS | 29.39 | 0.537 | 0.274 | 1.098 | 29.23 | 0.546 | 0.266 | 0.989 | 29.62 | 0.759 | 0.094 | 1.163 |
| Mip-NeRF RGB-D | 28.740 | 0.198 | 0.332 | 0.846 | 28.18 | 0.219 | 0.436 | 0.723 | 28.42 | 0.798 | 0.070 | 0.542 |
| Instant-NGP | 30.12 | 0.768 | 0.196 | 0.727 | 29.84 | 0.482 | 0.367 | 0.535 | 30.73 | 0.887 | 0.182 | 0.194 |
| Depth-NeRF | 32.47 | 0.883 | 0.077 | 0.462 | 30.10 | 0.534 | 0.186 | 0.116 | 31.66 | 0.836 | 0.067 | 0.151 |
| 3DMatch 7-Scenes-Fire | ScanNet Scene0002_00 | |||||||
|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | LPIPS↓ | Depth-RMSE↓ | PSNR↑ | SSIM↑ | LPIPS↓ | Depth-RMSE↓ | |
| Depth-NeRF w/o completion | 29.78 | 0.549 | 0.038 | 0.173 | 28.55 | 0.496 | 0.278 | 0.204 |
| Depth-NeRF w/o depth loss | 30.31 | 0.572 | 0.099 | 1.115 | 29.59 | 0.534 | 0.320 | 0.524 |
| Depth-NeRF w/o dynamic sampling | 30.40 | 0.564 | 0.128 | 0.498 | 29.48 | 0.531 | 0.231 | 0.489 |
| Depth-NeRF | 30.41 | 0.592 | 0.026 | 0.152 | 30.03 | 0.566 | 0.186 | 0.201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhang, D.; Su, Y.; Zhang, H. Enhancing View Synthesis with Depth-Guided Neural Radiance Fields and Improved Depth Completion. Sensors 2024, 24, 1919. https://doi.org/10.3390/s24061919
Wang B, Zhang D, Su Y, Zhang H. Enhancing View Synthesis with Depth-Guided Neural Radiance Fields and Improved Depth Completion. Sensors. 2024; 24(6):1919. https://doi.org/10.3390/s24061919
Chicago/Turabian StyleWang, Bojun, Danhong Zhang, Yixin Su, and Huajun Zhang. 2024. "Enhancing View Synthesis with Depth-Guided Neural Radiance Fields and Improved Depth Completion" Sensors 24, no. 6: 1919. https://doi.org/10.3390/s24061919
APA StyleWang, B., Zhang, D., Su, Y., & Zhang, H. (2024). Enhancing View Synthesis with Depth-Guided Neural Radiance Fields and Improved Depth Completion. Sensors, 24(6), 1919. https://doi.org/10.3390/s24061919





