Quantitative Prediction of Surface Hardness in Cr12MoV Steel and S136 Steel with Two Magnetic Barkhausen Noise Feature Extraction Methods
Abstract
1. Introduction
2. Experimental Device and Preparation of Samples
2.1. Experimental Device
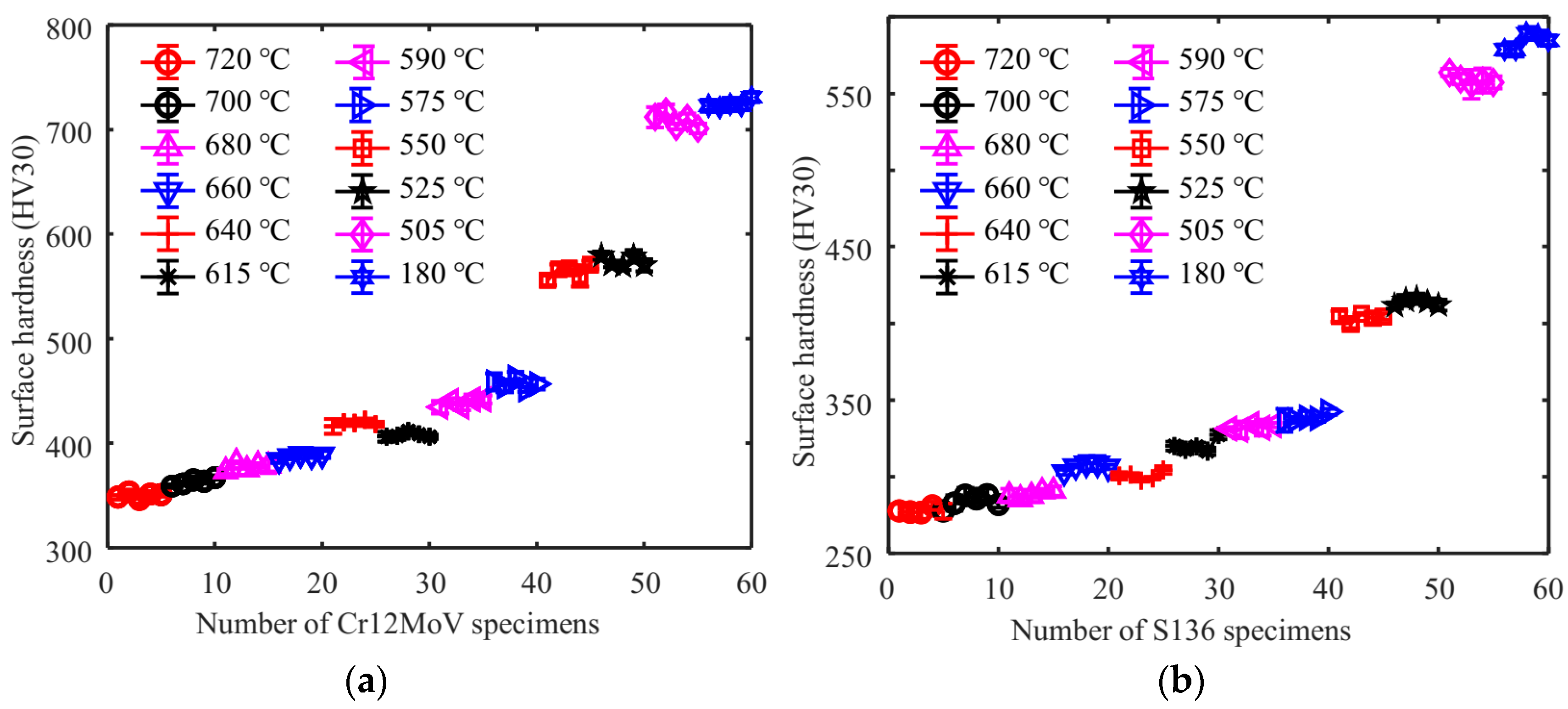
2.2. Sample Preparation
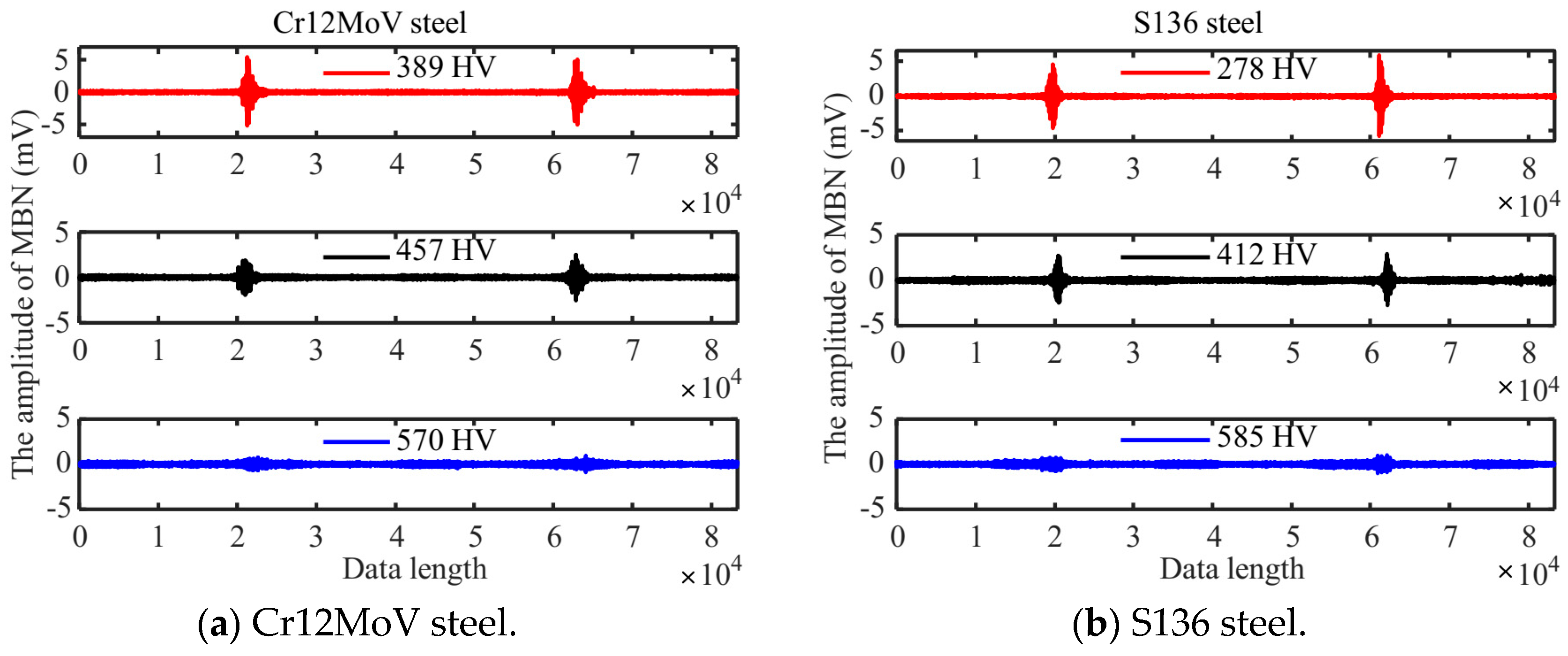
2.3. MBN Detection Experiments
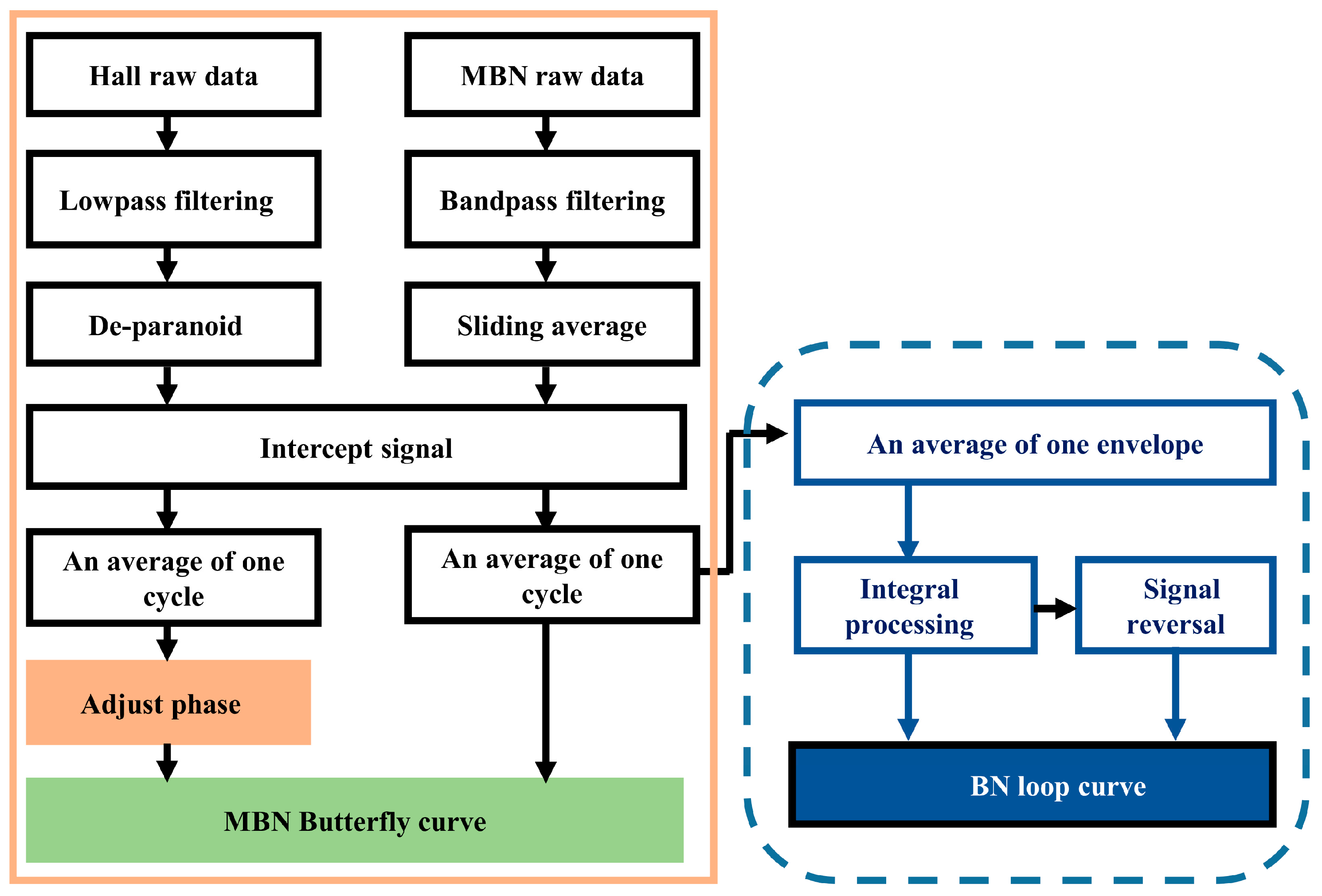
3. Processing Methods of MBN Signals
3.1. MBN Butterfly Curve
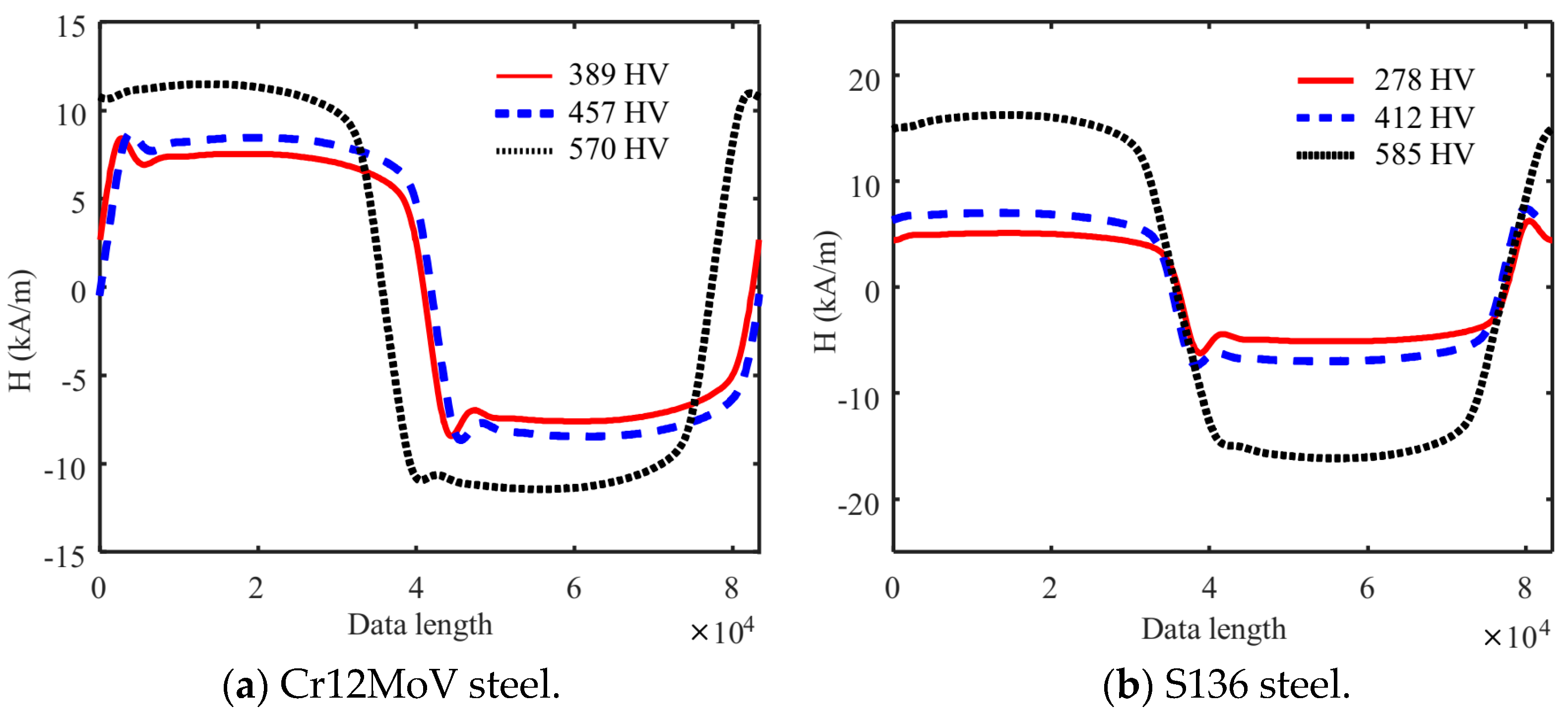
3.2. Calculation of MBN Hysteretic Curve
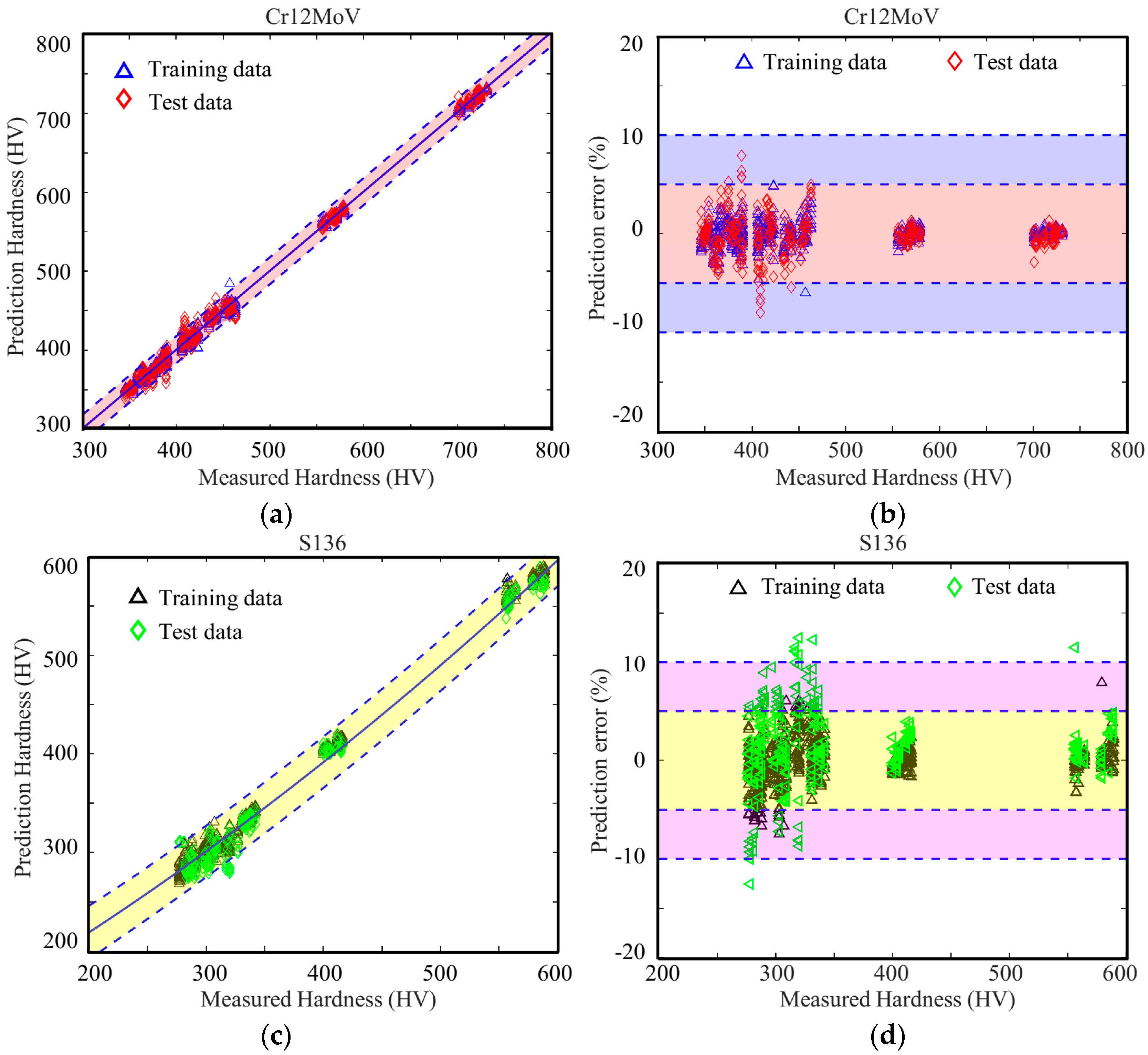
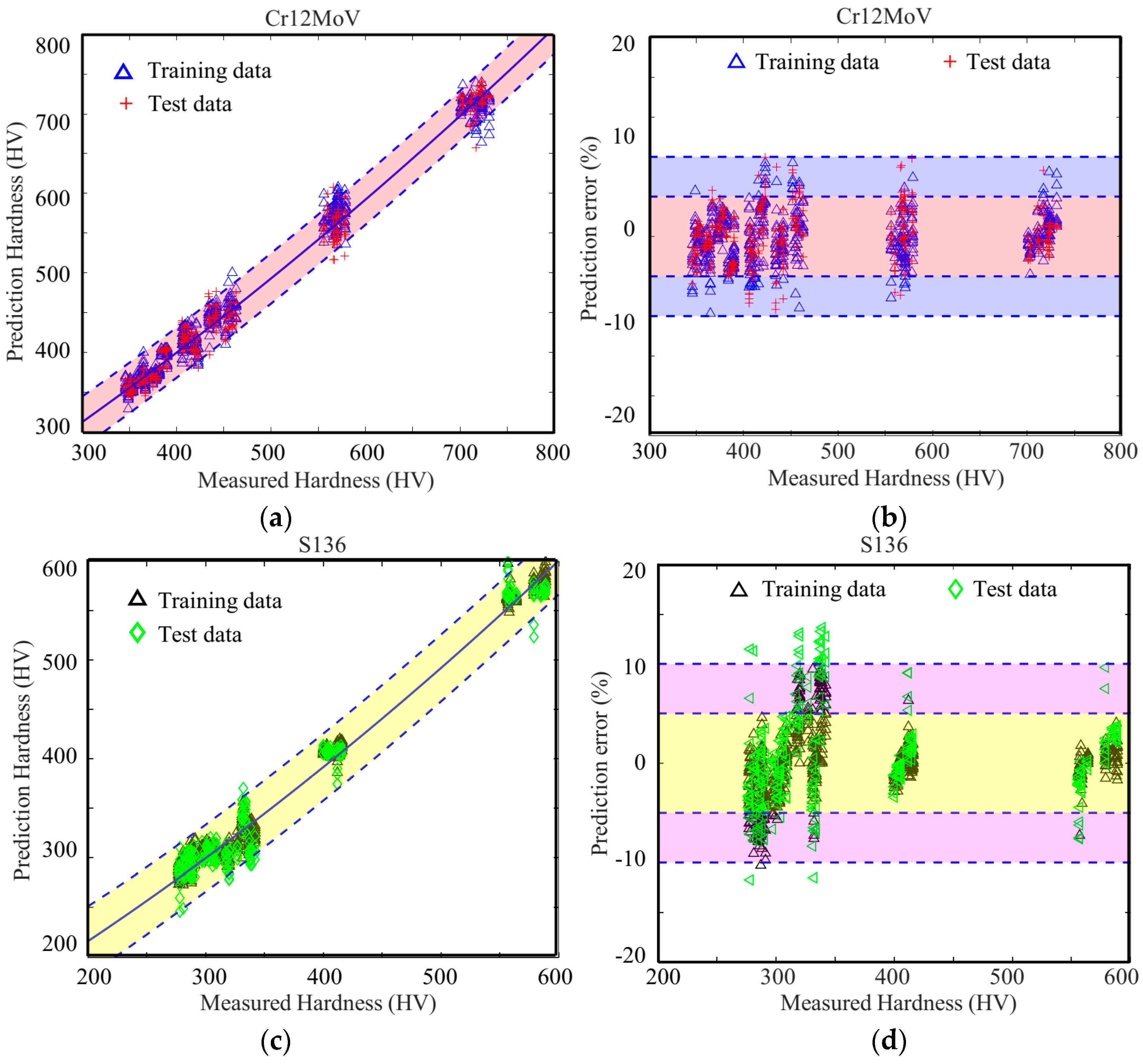
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hanke, R. Fraunhofer institute for non-destructive testing IZFP—Expanding the potential of NDT across the entire product life cycle. In Proceedings of the 55th Annual Conference of the British Institute of Non-Destructive Testing, NDT 2016, Nottingham, UK, 12–14 September 2016; pp. 305–308. [Google Scholar]
- Dobmann, G. Physical basics and industrial applications of 3MA—Micromagnetic multiparameter microstructure and stress analysis. In Proceedings of the 10th European Conference on Nondestructive Testing, ECNDT 2010, Moscow, Russia, 7–11 June 2010; pp. 7–11. [Google Scholar]
- Wolter, B.; Gabi, Y.; Conrad, C. Nondestructive Testing with 3MA—An Overview of Principles and Applications. Appl. Sci. 2019, 9, 1068. [Google Scholar] [CrossRef]
- Sorsa, A.; Santa-Aho, S.; Aylott, C. Case Depth Prediction of Nitrided Samples with Barkhausen Noise Measurement. Metals 2019, 9, 325. [Google Scholar] [CrossRef]
- Stupakov, A.; Perevertov, A.; Neslusan, M. Reading depth of the magnetic Barkhausen noise. i.one-phase semi-hard ribbons. J. Magn. Magn. Mater. 2020, 513, 167086. [Google Scholar] [CrossRef]
- Stashkov, A.N.; Schapova, E.A.; Nichipuruk, A.P. Magnetic incremental permeability as indicator of compression stress in low-carbon steel. NDT E Int. 2021, 118, 102398. [Google Scholar] [CrossRef]
- Golling, S.; Frómeta, D.; Casellas, D. Influence of microstructure on the fracture toughness of hot stamped boron steel. Mater. Eng. A 2019, 743, 529–539. [Google Scholar] [CrossRef]
- Qiu, F.; Ren, W.; Tian, G.Y. Characterization of applied tensile stress using domain wall dynamic behavior of grain-oriented electrical steel. J. Magn. Magn. Mater. 2017, 432, 250–259. [Google Scholar] [CrossRef]
- Ghanel, S.; Kashefi, M.; Mazinani, M. Comparative study of eddy current and Barkhausennoise nondestructive testing methods in microstructural examination of ferrite–martensitedual-phase steel. J. Magn. Magn. Mater. 2014, 356, 103–110. [Google Scholar] [CrossRef]
- Liu, X.C.; Shang, W.L.; He, C.F. Simultaneous quantitative prediction of tensile stress, surface hardness and case depth in medium carbon steel rods based on multifunctional magnetic testing techniques. Measurement 2018, 128, 455–463. [Google Scholar] [CrossRef]
- Ding, S.; Tian, G. Non-destructive hardness prediction for 18CrNiMo7-6 steel based on feature selection and fusion of Magnetic Barkhausen Noise. NDT E Int. 2019, 107, 102138. [Google Scholar] [CrossRef]
- Jedamski, R.; Epp, J. Non-Destructive Micromagnetic Determination of Hardness and Case Hardening Depth Using Linear Regression Analysis and Artificial Neural Networks. Metals 2020, 11, 18. [Google Scholar] [CrossRef]
- Yan, Z.X.; Sun, G.M.; Liu, X.C. FilterNet: A deep convolutional neural network for measuring plastic deformation from raw Barkhausen noise waveform. J. Magn. Magn. Mater. 2022, 555, 169330. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.; Wang, K.; Zhang, Y. Nondestructive evaluation of hot stamping boron steel with martensite/bainite mixed microstructures based on magnetic Barkhausen noise detection. J. Magn. Magn. Mater. 2020, 503, 166598. [Google Scholar] [CrossRef]
- Krause, A.K.; Underhill, P.R.; Krause, T.W.; Clapham, L. Magnetic Flux Density Superposition in Nonlinear Anisotropic Ferromagnetic Material and Resulting Magnetic Barkhausen Noise. IEEE Trans. Magn. 2021, 57, 6101007. [Google Scholar] [CrossRef]
- Nahak, B.; Srivastava, A. Non-destructive monitoring of electro-discharge machined die steel. Arab. J. Sci. Eng. 2022, 47, 15153–15160. [Google Scholar] [CrossRef]
- Franco, F.A.; González, M.F.R. Relation Between Magnetic Barkhausen Noise and Hardness for Jominy Quench Tests in SAE 4140 and 6150 Steels. J. Nondestruct. Eval. 2013, 32, 93–103. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, R. Quantitative Prediction of Surface Hardness in 12CrMoV Steel Plate Based on Magnetic Barkhausen Noise and Tangential Magnetic Field Measurements. J. Nondestruct. Eval. 2018, 37, 38. [Google Scholar]
- Akhlaghi, I.A.; Kahrobaee, S.; Nezhad, K.K. An accurate non-destructive method for determining mechanical properties of plain carbon steel parts using MHL and GRNN. Nondestruct. Test. Eval. 2020, 36, 278–296. [Google Scholar] [CrossRef]
- Wang, X.X.; He, C.F.; Li, P. Micromagnetic and quantitative prediction of surface hardness in carbon steels based on a joint classification-regression method. J. Nondestruct. Eval. 2022, 41, 62. [Google Scholar] [CrossRef]
- Dong, H.; Liu, X.; Song, Y. Quantitative Evaluation of Residual Stress and Surface Hardness in Deep Drawn Parts Based on Magnetic Barkhausen Noise Technology. Measurement 2021, 168, 108473. [Google Scholar] [CrossRef]
- Vashista, M.; Paul, S. Novel processing of Barkhausen noise signal for assessment of residual stress in surface ground components exhibiting poor magnetic response. J. Magn. Magn. Mater. 2011, 323, 2579–2584. [Google Scholar] [CrossRef]
- Stefanita, C.G.; Atherton, D.L.; Clapham, L. Plastic versus elastic deformation on magnetic Barkhausen noise in steel. Acta Mater. 2000, 48, 3545–3551. [Google Scholar] [CrossRef]
- Ding, S.; Tian, G.Y.; Moorthy, V. New feature extraction for applied stress detection on ferromagnetic material using magnetic Barkhausen noise. Measurement 2015, 73, 515–519. [Google Scholar] [CrossRef]
- Xing, Z.X.; Wang, X.X.; Ning, N.M. Micromagnetic and robust evaluation of surface hardness in Cr12MoV steel considering repeatability of the instrument. Sensors 2023, 23, 1273. [Google Scholar] [CrossRef]
- Qiu, F.; Jovičević-Klug, M.; Tian, G.; Wu, G.; McCord, J. Correlation of magnetic field and stress-induced magnetic domain reorientation with Barkhausen Noise. J. Magn. Magn. Mater. 2021, 523, 167588. [Google Scholar] [CrossRef]
- Takács, J. Mathematics of Hysteretic Phenomena: The T(x) Model for the Description of Hysteresis; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]



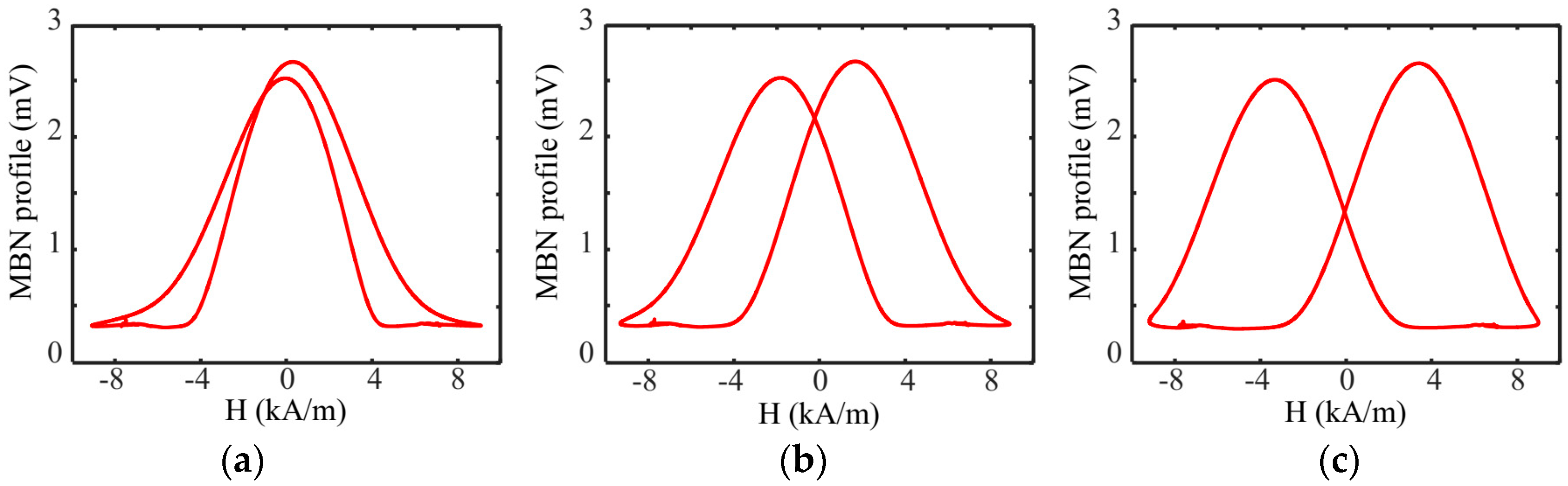
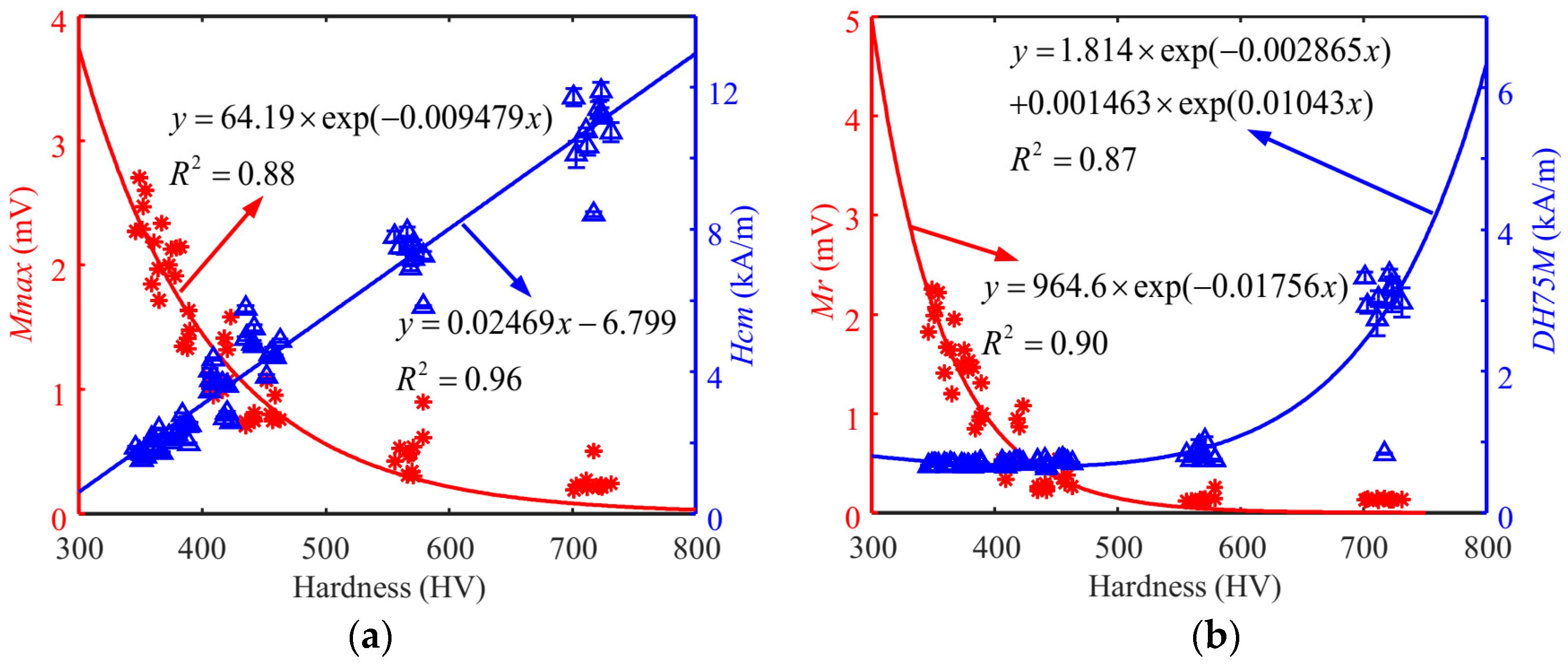
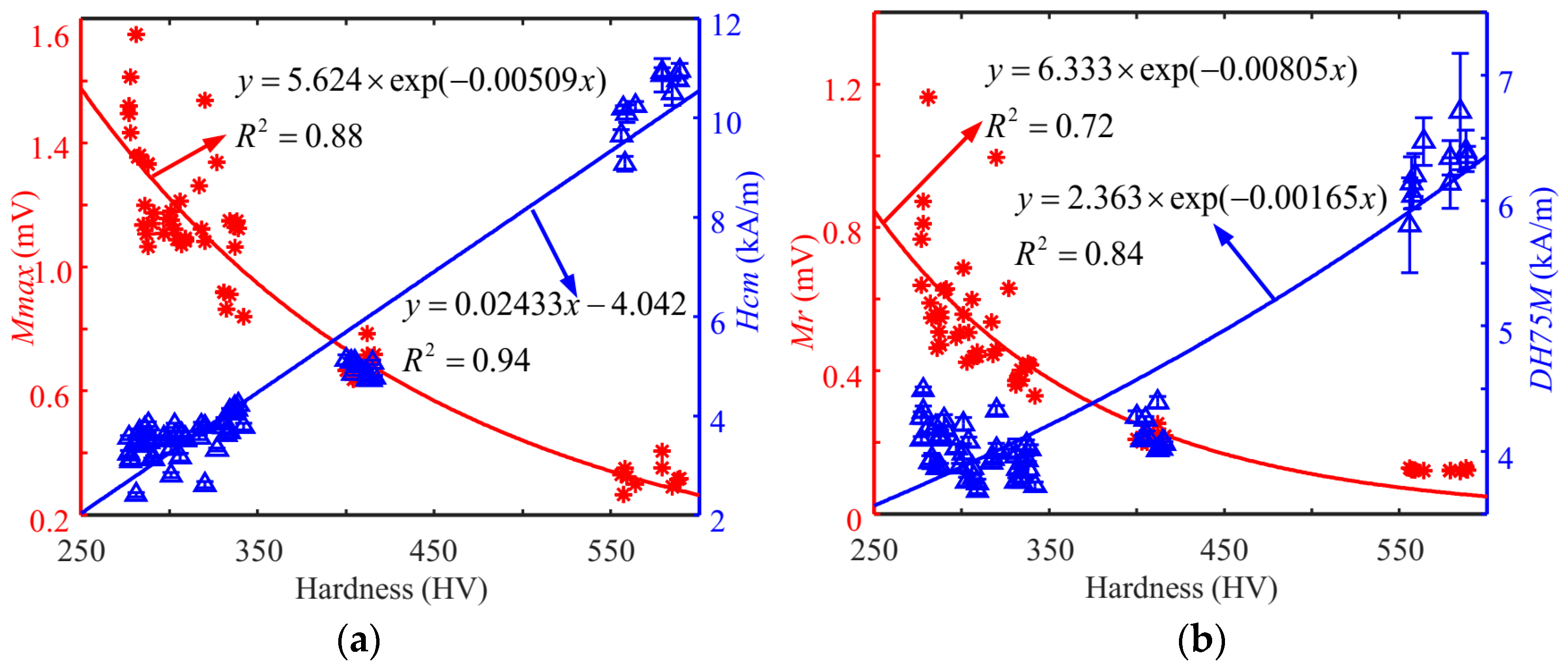

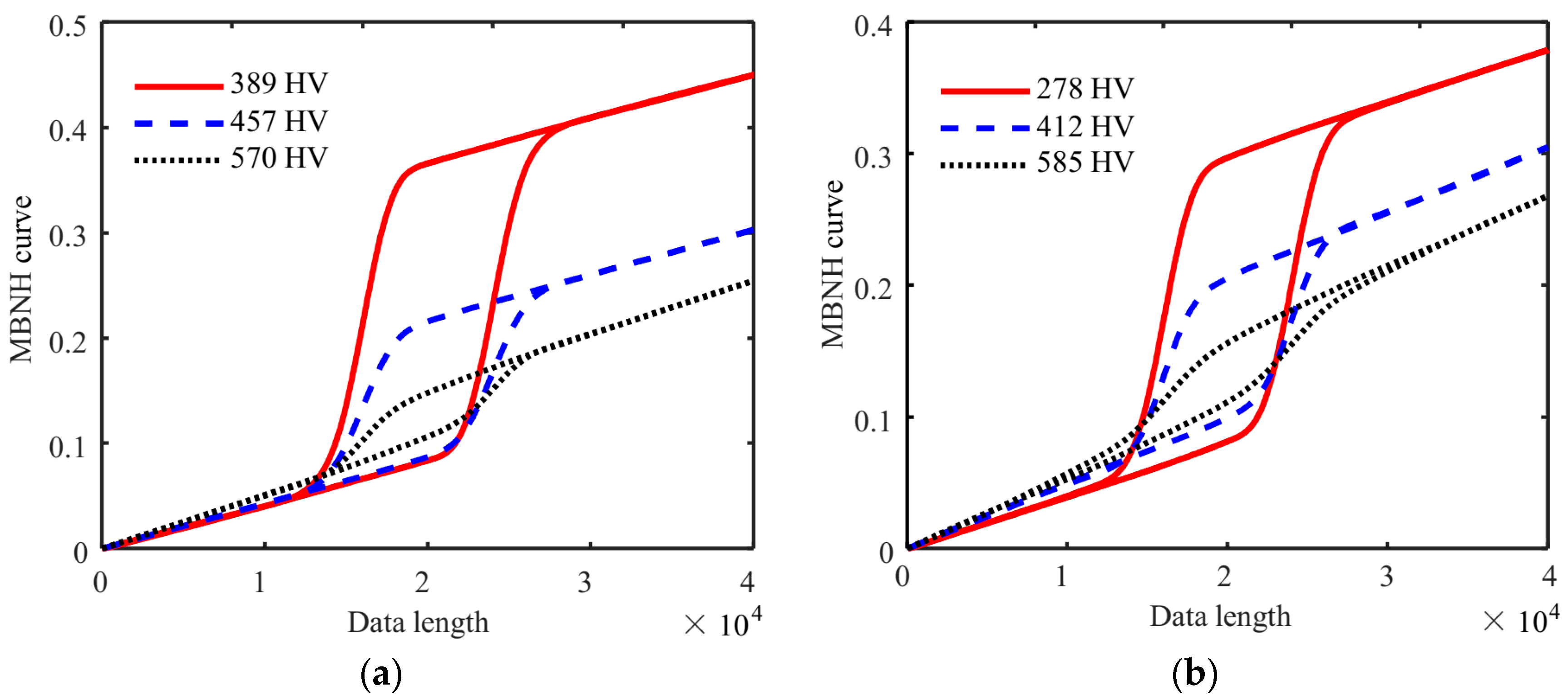
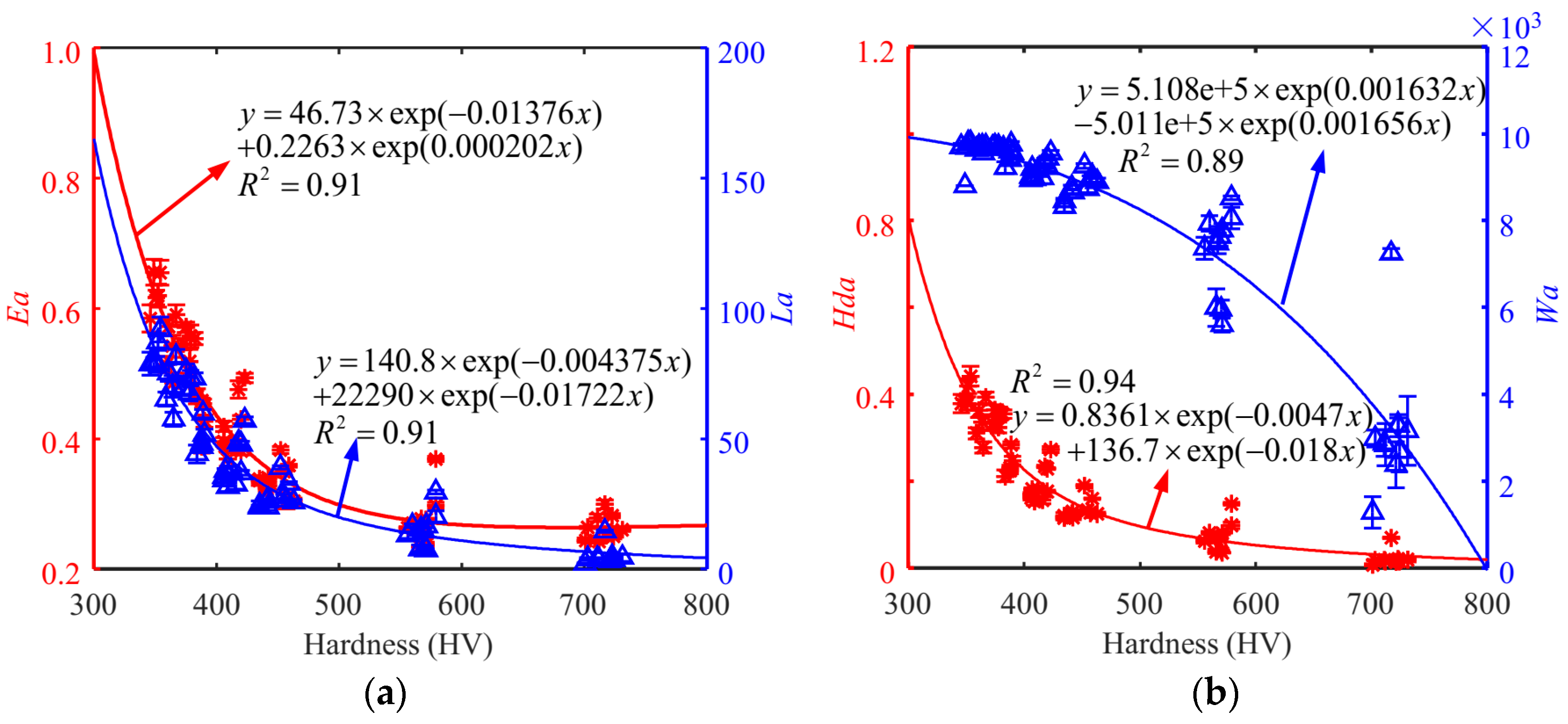
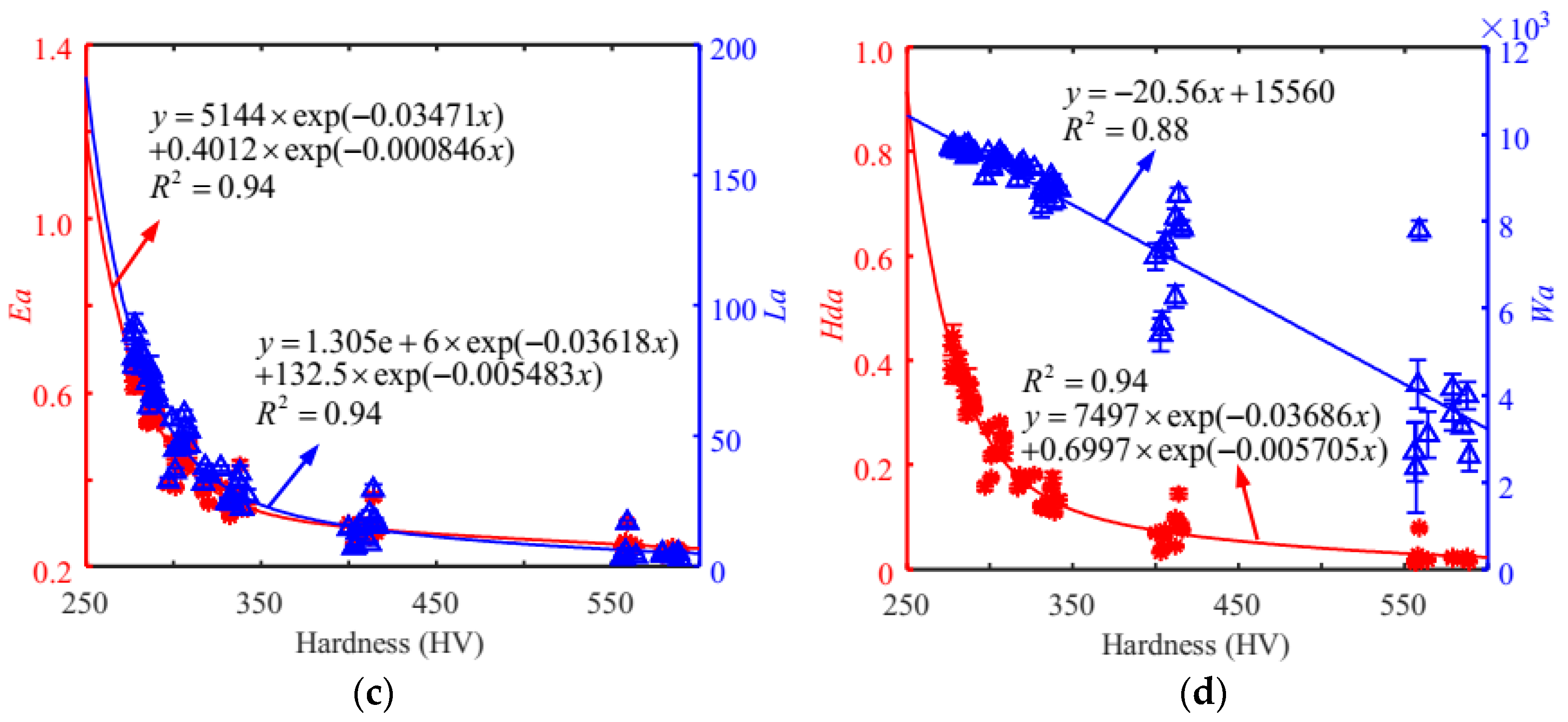
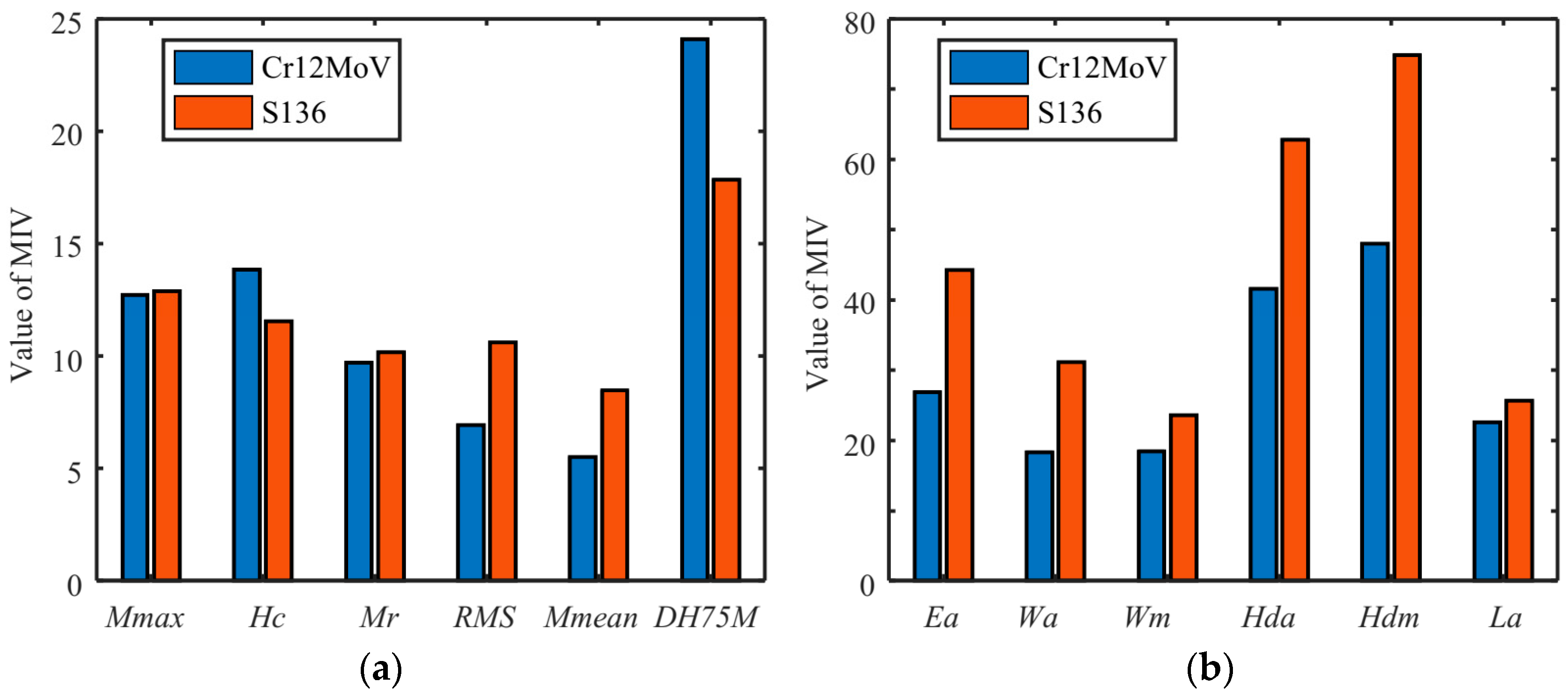
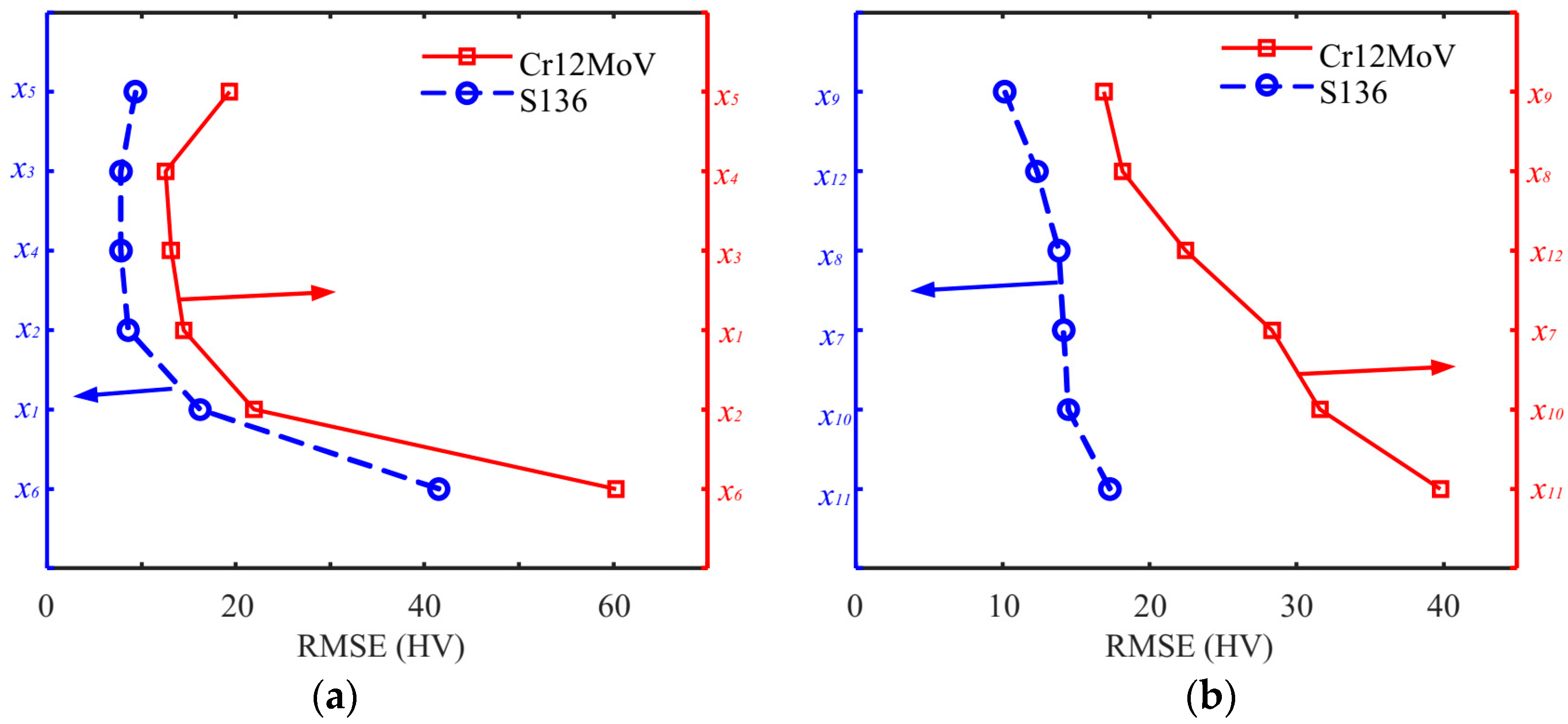
| Features | MBN Signals | 0 | 1/160 | 1/80 | Cr12MoV | S136 |
|---|---|---|---|---|---|---|
| x1 | Peak height of the MBN butterfly curve, Mmax | 3.9% | 3.9% | 3.9% | 3.1% | 3.5% |
| x2 | Peak position of the MBN butterfly curve, Hcm | 38.8% | 3.7% | 1.5% | 1.3% | 2.1% |
| x3 | Intercept of MBN envelope at the vertical axis, Mr | 3.9% | 3.9% | 4.1% | 3.9% | 3.4% |
| x4 | Mean value of MBN envelope, Mmean | 3.9% | 3.9% | 3.8% | 3.1% | 2.9% |
| x5 | Full width at 75% of maxima of MBN butterfly curve, DH75M | 23.1% | 3.5% | 1.9% | 2.0% | 2.4% |
| x6 | Full width at 50% of maxima of MBN butterfly curve, DH50M | 14.6% | 3.1% | 1.5% | 15.4% | 9.1% |
| Features | MBNHL Curve Explanation | Coefficient of Variation (%) | |
|---|---|---|---|
| Cr12MoV | S136 | ||
| x7 | Maximum point on the integration curve, Ea | 1.9 | 1.5 |
| x8 | Time difference between two points on the integration curve corresponding to Ea/2, Wa | 1.1 | 1.1 |
| x9 | Maximum time difference for the same integral value on the integration curve, Wm | 1.6 | 1.2 |
| x10 | Height difference between the two integration curve at Ts/4, Hda | 3.5 | 3.5 |
| x11 | Maximum difference between two integration curves at the same time, Hdm | 3.2 | 3.2 |
| x12 | The area of the closed curve, La | 3.6 | 3.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cai, Y.; Liu, X.; He, C. Quantitative Prediction of Surface Hardness in Cr12MoV Steel and S136 Steel with Two Magnetic Barkhausen Noise Feature Extraction Methods. Sensors 2024, 24, 2051. https://doi.org/10.3390/s24072051
Wang X, Cai Y, Liu X, He C. Quantitative Prediction of Surface Hardness in Cr12MoV Steel and S136 Steel with Two Magnetic Barkhausen Noise Feature Extraction Methods. Sensors. 2024; 24(7):2051. https://doi.org/10.3390/s24072051
Chicago/Turabian StyleWang, Xianxian, Yanchao Cai, Xiucheng Liu, and Cunfu He. 2024. "Quantitative Prediction of Surface Hardness in Cr12MoV Steel and S136 Steel with Two Magnetic Barkhausen Noise Feature Extraction Methods" Sensors 24, no. 7: 2051. https://doi.org/10.3390/s24072051
APA StyleWang, X., Cai, Y., Liu, X., & He, C. (2024). Quantitative Prediction of Surface Hardness in Cr12MoV Steel and S136 Steel with Two Magnetic Barkhausen Noise Feature Extraction Methods. Sensors, 24(7), 2051. https://doi.org/10.3390/s24072051







