Error Analysis of Normal Surface Measurements Based on Multiple Laser Displacement Sensors
Abstract
:1. Introduction
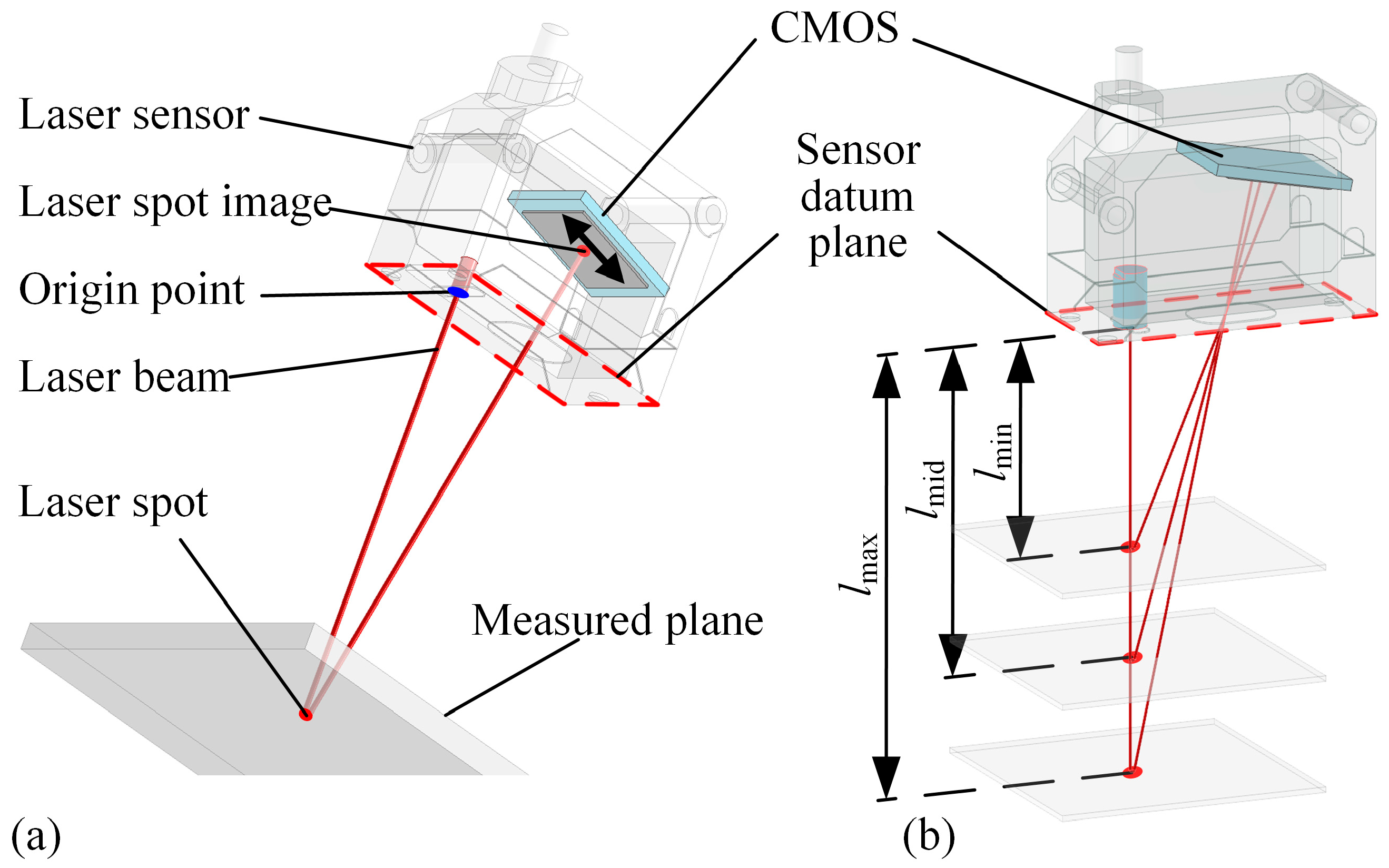
2. Normal Measurement Principle of Rotationally Symmetric Multi-Sensor Measurements
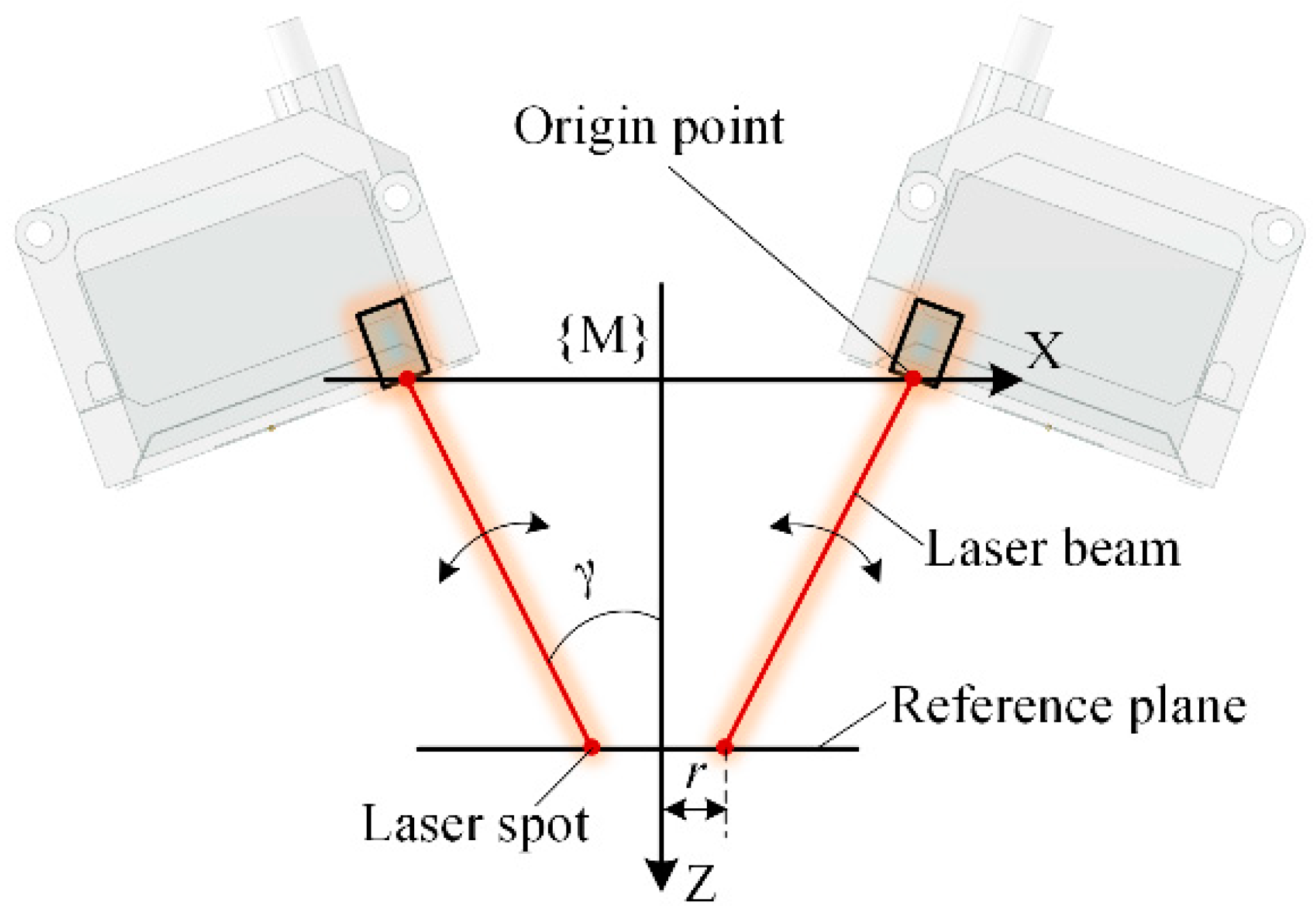
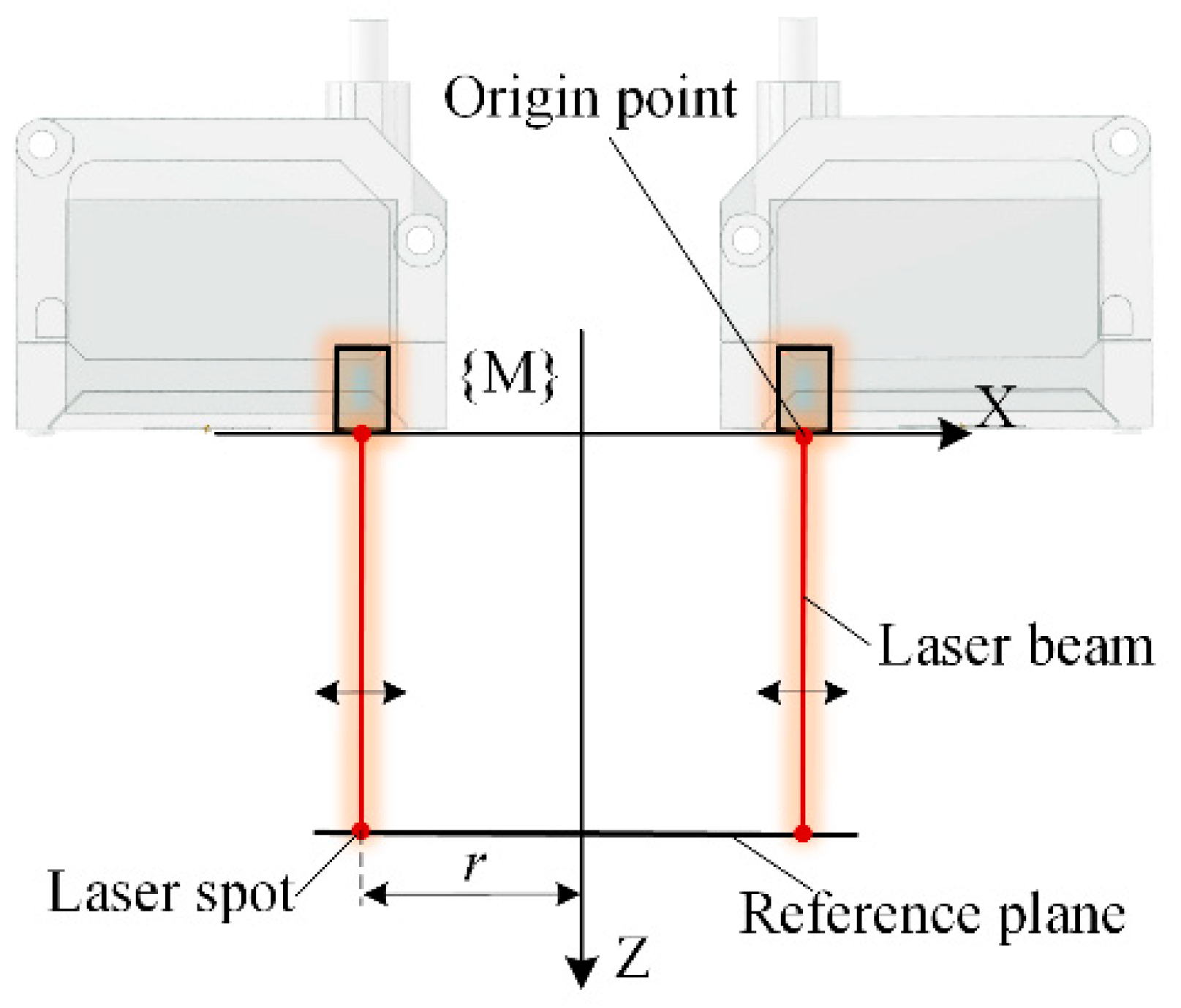
2.1. Normal Measurement Based on Multiple Laser Sensors with Rotationally Symmetric Layout
2.2. Normal Calculation Based on Parameter-Matrix Eigen-Decomposition
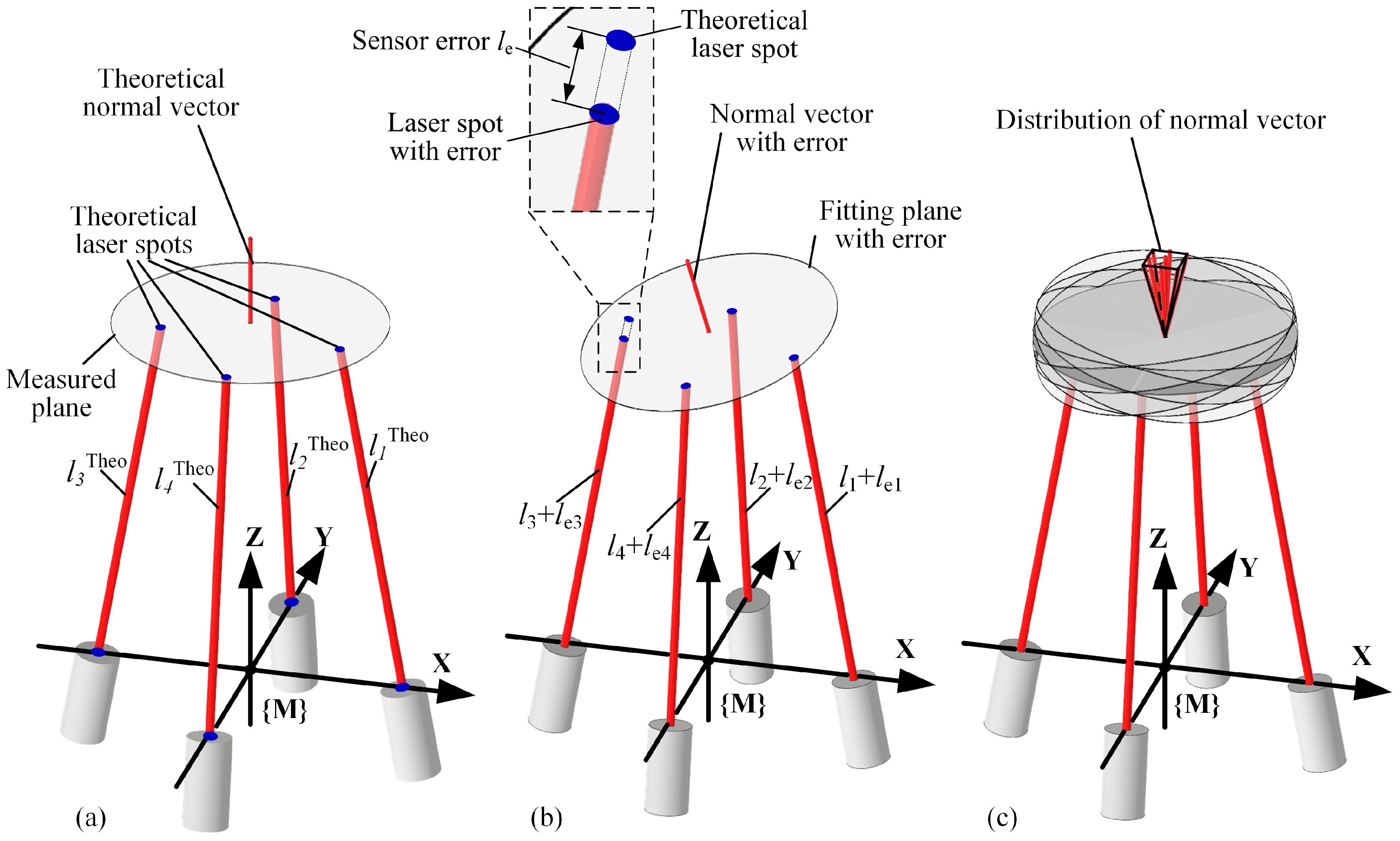
2.3. Error Propagation of Sensor Measurements for Normal Calculation
3. Normal Measurement Error Estimation
3.1. Normal Measurement Error Estimation Method Based on Random Sampling
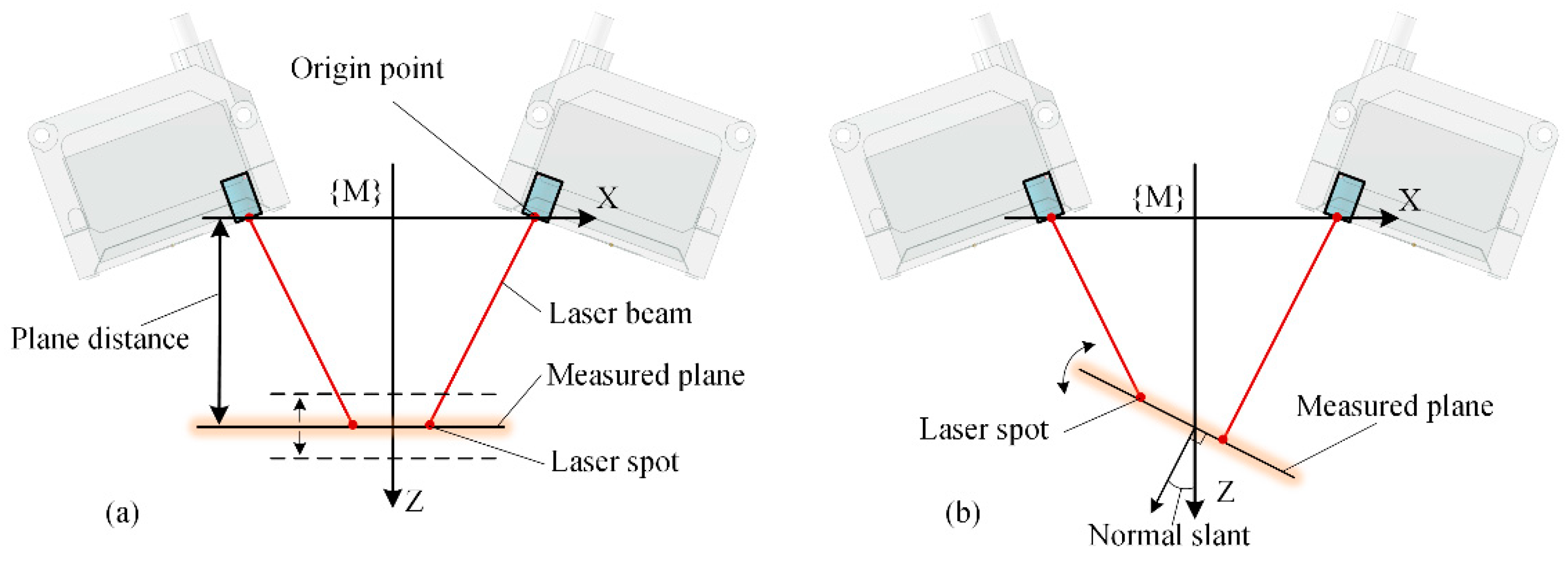
3.2. Normal Measurement Accuracy Influenced by the Measurement Plane Position
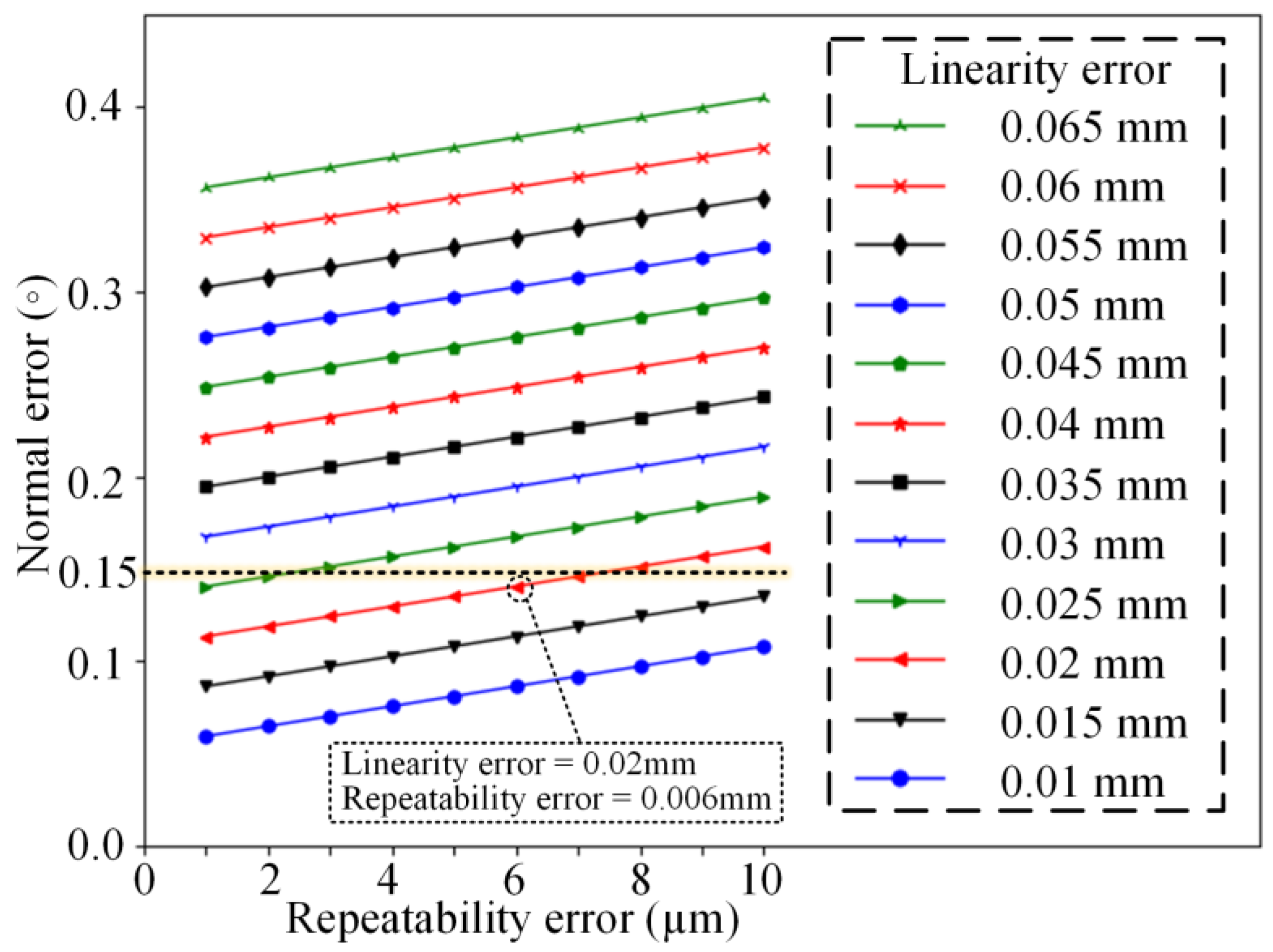
3.3. Normal Measurement Error Influenced by Sensor Accuracy
3.4. Normal Error Influenced by Normal Measurement Device
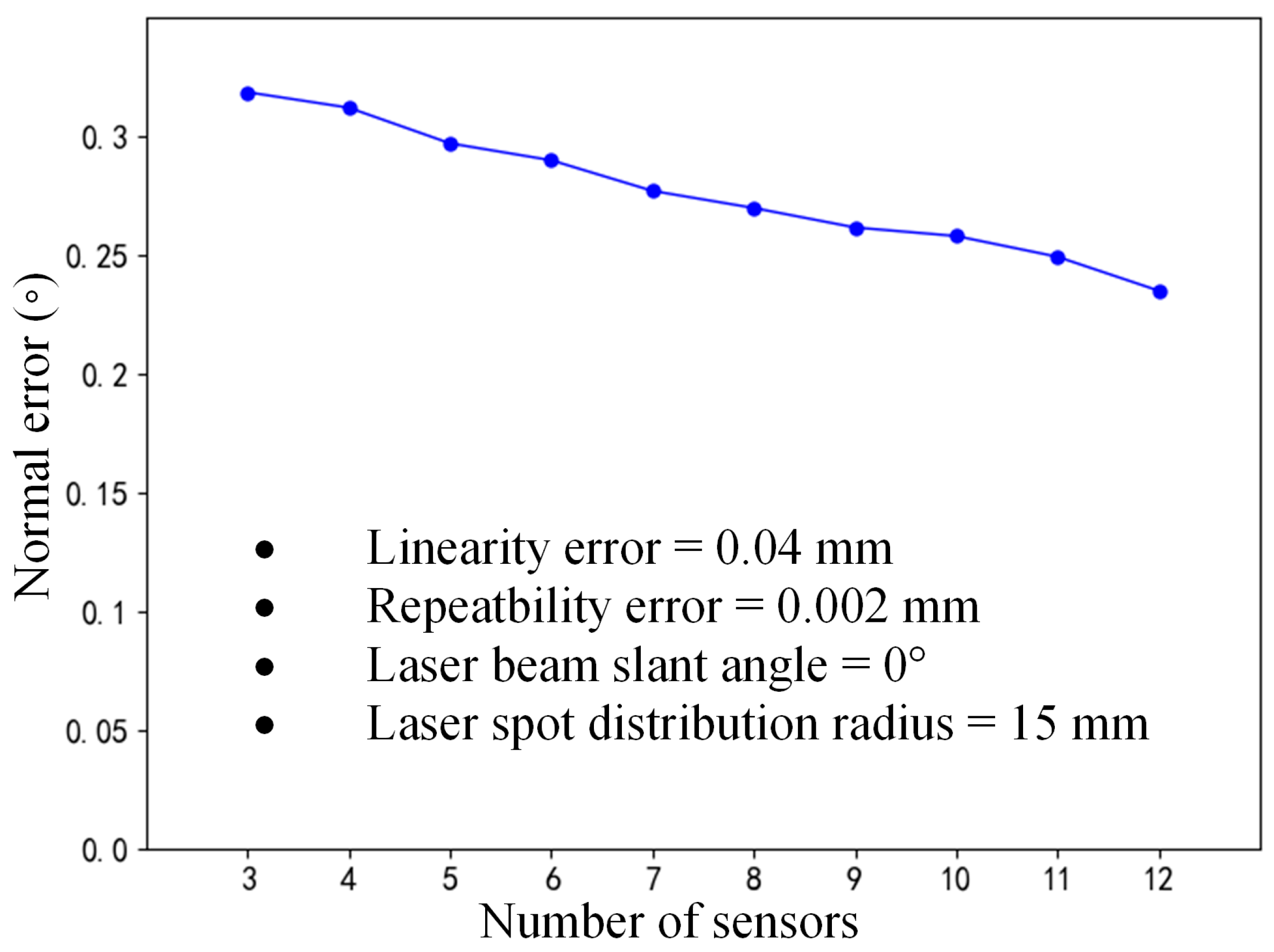
3.4.1. Normal Errors Influenced by Laser Sensor Quantity
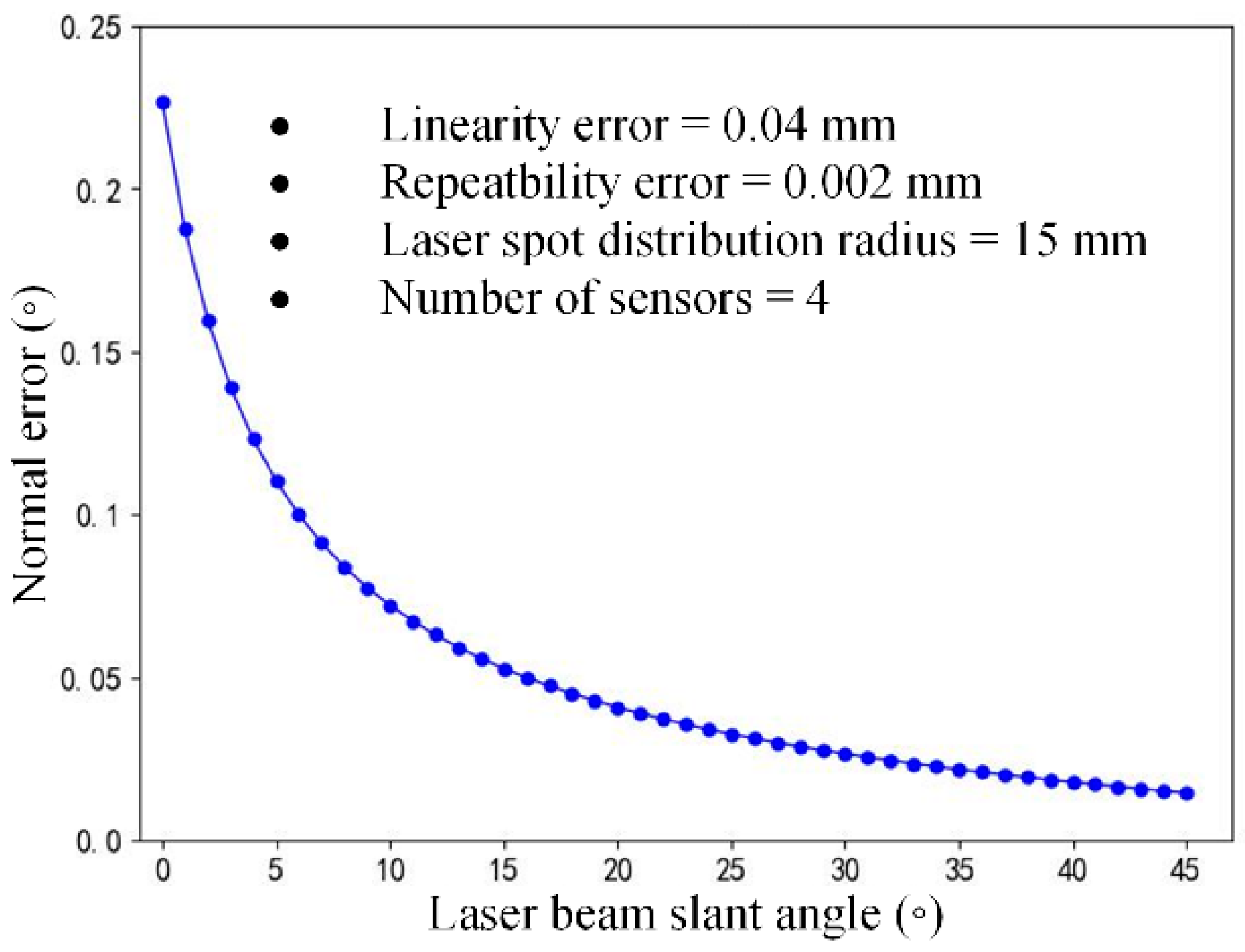
3.4.2. Normal Error Influenced by Laser Beam Slant
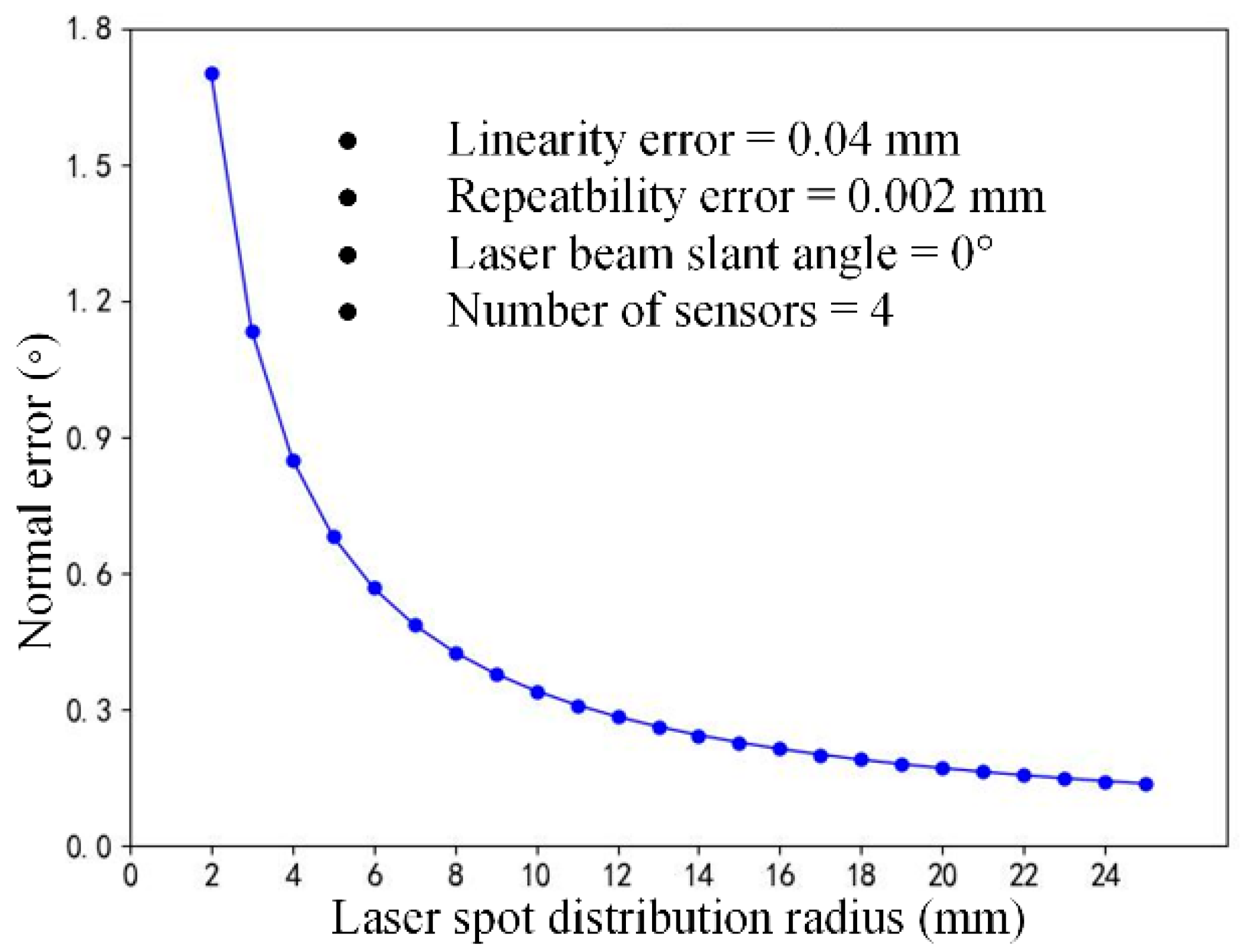
3.4.3. Normal Error Influenced by Laser Spot Distribution
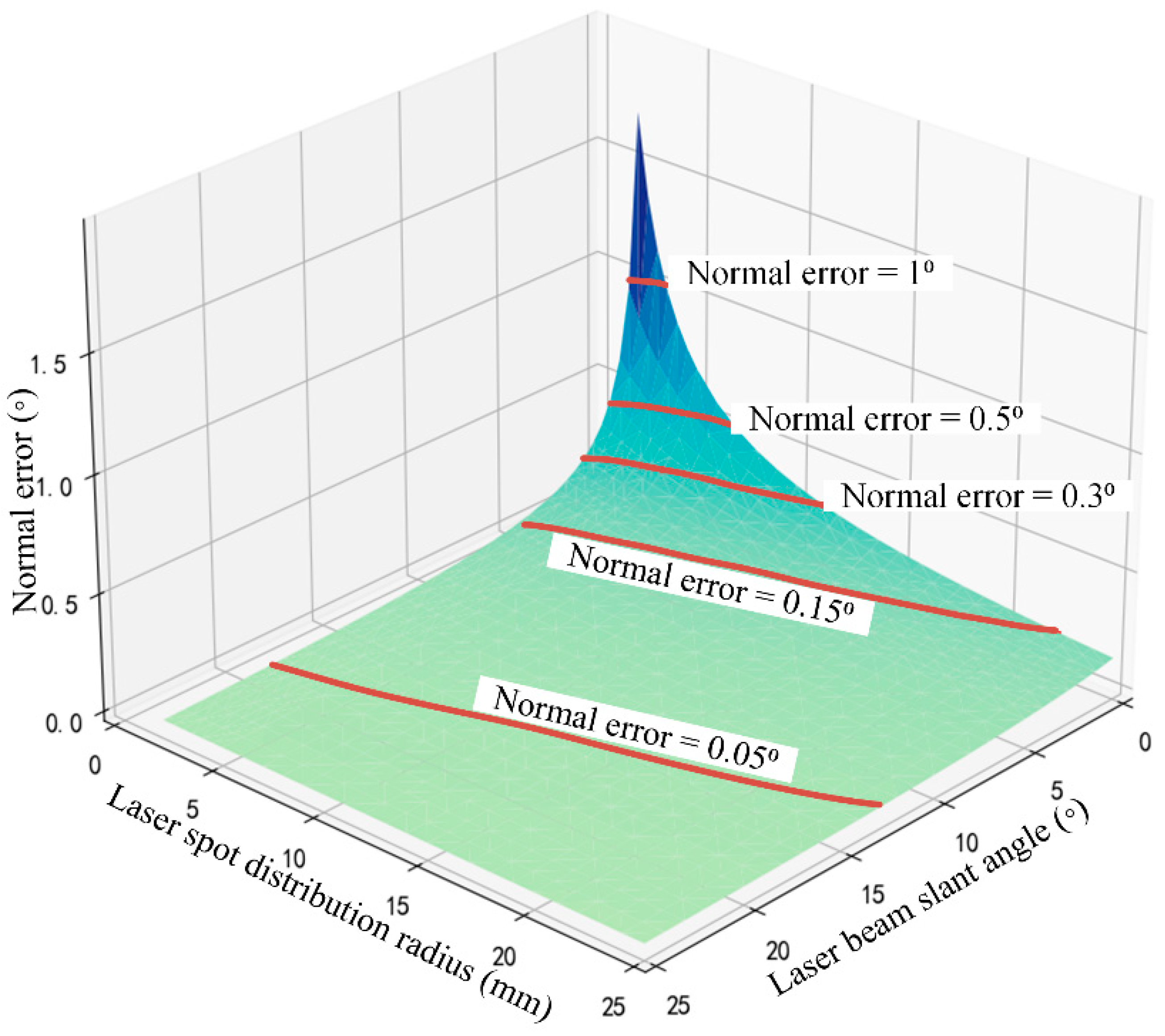
3.4.4. Normal Error Coupling Influenced by Both Laser Beam Slant and Laser Spot Distribution
4. Experimental Verification
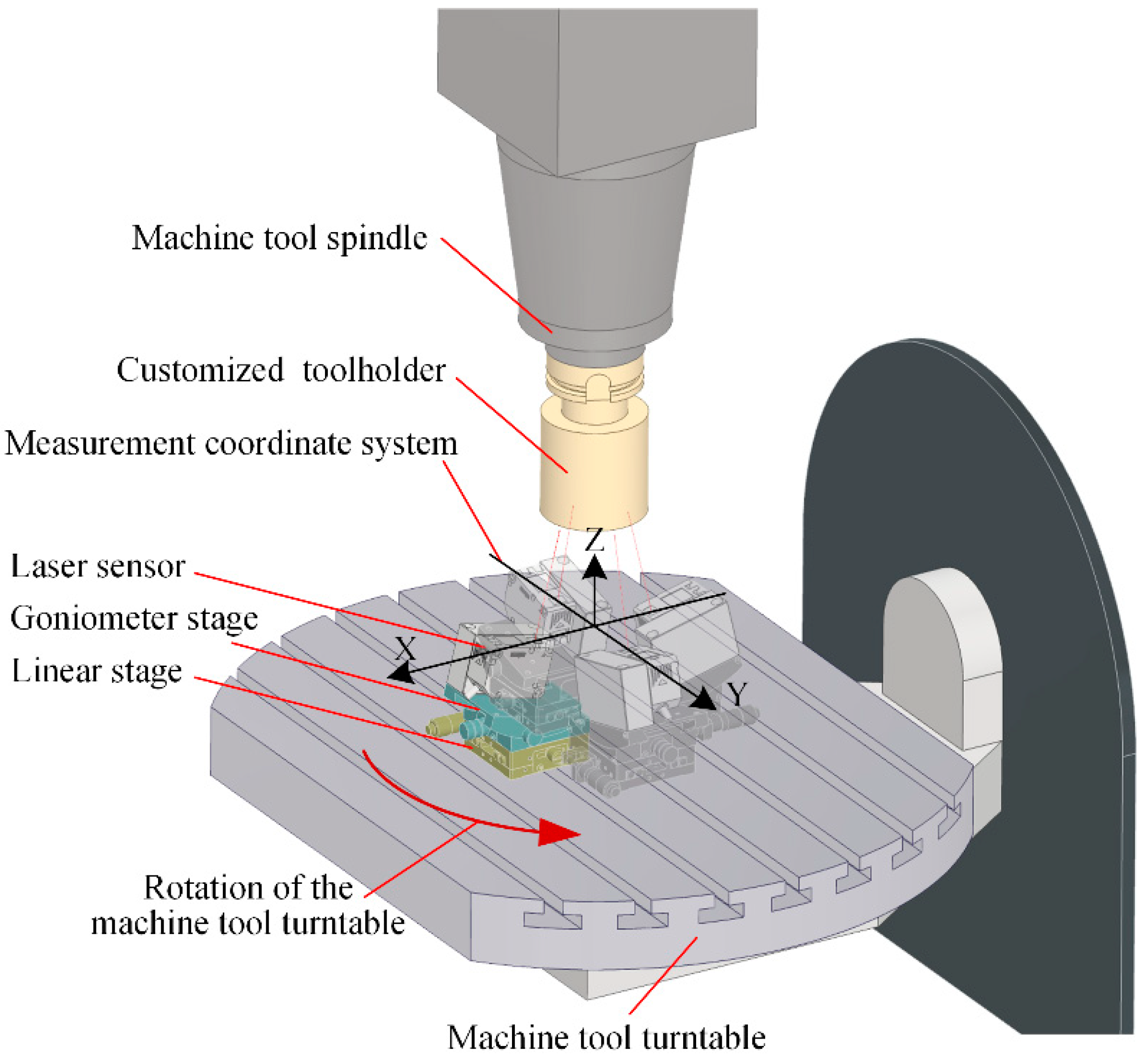
4.1. Experimental Platform
4.2. Experimental Process
5. Result and Discussion
6. Conclusions
- (1)
- Laser sensor precision effect: the simulation results demonstrate that an increase in laser sensor precision enhances the normal measurement accuracy.
- (2)
- Structural parameters’ significance: The three geometric parameters of the normal measurement device, including the number of sensors n, the laser beam slant angle γ, and laser spot distribution radius r, significantly influence the normal measurement accuracy. The increase in parameters n, γ and r all contribute to enhancing the normal measurement accuracy.
- (3)
- Layout optimization of the normal measurement device: For a four-sensor normal measurement device, when the laser beam slant angle is ≥5°, the laser spot distribution radius is ≥7 mm, and the normal measurement error can be maintained within 0.15°, thereby satisfying the requirements for drilling assembly holes. When the laser beam slant angle is ≥15°, the laser spot distribution radius is ≥19 mm, and the normal measurement error is reduced to ≤0.05°, resulting in a negligible effect on normal measurements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Der Sypt, P.; Chérif, M.; Bois, C. Analysis of the fatigue behaviour of laminated composite holes subjected to pin-bearing loads. Int. J. Fatigue 2017, 103, 86–98. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhang, N.; Wang, Q.Y. Tensile behaviour of open-hole and bolted steel plates reinforced by CFRP strips. Compos. Part B-Eng. 2016, 100, 101–113. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Li, L.H.; Liu, Y.J.; Wang, Q.Y. Fatigue Property of Open-Hole Steel Plates Influenced by Bolted Clamp-up and Hole Fabrication Methods. Materials 2016, 9, 698. [Google Scholar] [CrossRef]
- Liu, J.; Shao, X.J.; Liu, Y.J.; Liu, Y.S.; Yue, Z.F. The effect of holes quality on fatigue life of open hole. Mat. Sci. Eng. A-Struct. 2007, 467, 8–14. [Google Scholar] [CrossRef]
- Ralph, W.C.; Johnson, W.S.; Makeev, A.; Newman, J.C. Fatigue performance of production-quality aircraft fastener holes. Int. J. Fatigue 2006, 1, 1319–1327. [Google Scholar] [CrossRef]
- Wang, Z.X.; Qin, X.S.; Bai, J.; Tan, X.Q.; Li, J. Design and Implementation of Multifunctional Automatic Drilling End Effector. In Proceedings of the 2016 Second International Conference on Mechanical and Aeronautical Engineering (ICMAE) (2016), Hong Kong, China, 30 December 2016–1 January 2017; Volume 187, pp. 12032–12037. [Google Scholar]
- Mei, B.A.; Wang, H.J.; Zhu, W.D. Pose and shape error control in automated machining of fastener holes for composite/metal wing-box assembly. J. Manuf. Process 2021, 66, 101–114. [Google Scholar] [CrossRef]
- Miyake, Y.; Kondo, Y. A study on new machining method applied to a collaborative robot for drilling. Robot. Comput.-Integr. Manuf. 2022, 78, 102409–102416. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X. A novel algorithm of normal attitude regulation for the designed end-effector of a flexible drilling robot. J. Southeast Univ. (Engl. Ed.) 2012, 28, 29–34. [Google Scholar]
- Zhang, Q.; Liu, J.T.; Zheng, S.G.; Yu, C.J. A novel accurate positioning method of reference hole for complex surface in aircraft assembly. Int. J. Adv. Manuf. Technol. 2022, 119, 571–586. [Google Scholar] [CrossRef]
- Sa, J.M.; Gu, H.W.; An, Y.L.; Luo, Y.J.; Zhang, Z.S.Y. Study on Curved Surface Fitting of Countersink Based on Point Cloud. IEEE Access 2020, 8, 106464–106470. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Bi, Q.Z.; Yu, L.; Wan, Y.H. Online adaptive measurement and adjustment for flexible part during high precision drilling process. Int. J. Adv. Manuf. Technol. 2012, 89, 3579–3599. [Google Scholar] [CrossRef]
- Yuan, P.J.; Wang, Q.S.; Wang, T.M.; Wang, C.K.; Song, B. Surface Normal Measurement in the End Effector of a Drilling Robot for Aviation. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 4481–4486. [Google Scholar]
- Mei, B.; Liang, Z.S.; Zhu, W.D.; Ke, Y.L. Positioning variation synthesis for an automated drilling system in wing assembly. Robot. Comput.-Integr. Manuf. 2021, 67, 102044. [Google Scholar] [CrossRef]
- Lin, M.Q.; Yuan, P.J.; Tan, H.J.; Liu, Y.W.; Zhu, Q.C.; Li, Y. Improvements of Robot Positioning Accuracy and Drilling Perpendicularity for Autonomous Drilling Robot System. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (IEEE-Robio), Zhuhai, China, 6–9 December 2015; pp. 1483–1488. [Google Scholar]
- Gao, Y.H.; Wu, D.; Dong, Y.F.; Ma, X.G.; Chen, K. The Method of Aiming towards the Normal Direction for Robotic Drilling. Int. J. Precis. Eng. Man. 2017, 18, 787–794. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, W.X.; Zhou, W.; Liao, W.H.; Zeng, Y.F. Auto-normalization algorithm for robotic precision drilling system in aircraft component assembly. Chin. J. Aeronaut. 2013, 26, 495–500. [Google Scholar] [CrossRef]
- Wang, S.; Cheung, C.F.; Kong, L.; Ren, M. Fiducial-aided calibration of a displacement laser probing system for in-situ measurement of optical freeform surfaces on an ultra-precision fly-cutting machine. Opt. Express 2020, 28, 27415–27432. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.D.; Yuan, P.J.; Wang, T.M.; Cai, Y.; Tang, H.Y. A Normal Sensor Calibration Method Based on an Extended Kalman Filter for Robotic Drilling. Sensors 2018, 18, 3485. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, H.C.; Zhao, C.F.; Zhou, Y.G.; Cao, G.H. Detecting the normal-direction in automated aircraft manufacturing based on adaptive alignment. Sci. Prog. 2020, 103, 0036850420981212. [Google Scholar] [CrossRef]
- Gao, Y.H.; Wu, D.; Nan, C.G.; Chen, K. Normal direction measurement in robotic drilling and precision calculation. Int. J. Adv. Manuf. Technol. 2015, 76, 1311–1318. [Google Scholar] [CrossRef]
- Sun, J.H.; Zhang, J.; Liu, Z.; Zhang, G.J. High-dynamic angle measurement based on laser displacement sensors. Appl. Opt. 2013, 52, 5676–5685. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, J.H.; Liu, Z.; Zhang, G.J. A flexible calibration method for laser displacement sensors based on a stereo-target. Meas. Sci. Technol. 2014, 25, 1051031–1051039. [Google Scholar] [CrossRef]
- Nan, Z.J.; Tao, W.; Zhao, H. Automatic optical structure optimization method of the laser triangulation ranging system under the Scheimpflug rule. Opt. Express 2022, 30, 18667–18683. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.M.; Li, Y.M.; Xue, G.P.; Tao, Y.H.; Li, X.H. Laser triangulation measurement system with Scheimpflug calibration based on the Monte Carlo optimization strategy. Opt. Express 2022, 430, 25290–25307. [Google Scholar] [CrossRef] [PubMed]







| Technical Parameters | Expression Symbols |
|---|---|
| Maximum measurement distance of laser sensor | lmax |
| Minimum measurement distance of laser sensor | lmin |
| Median value of laser sensor measuring range | lmid |
| Measurement range of laser sensor | lr |
| Measurement error of laser sensor | e |
| Linearity of laser sensor | el |
| Repeatability of laser sensor | er |
| Number of laser sensors | n |
| The angle between the laser beam and the Z-axis of the measurement coordinate system | γ |
| Distribution radius of laser spot when each of the sensor values equals lmid | r |
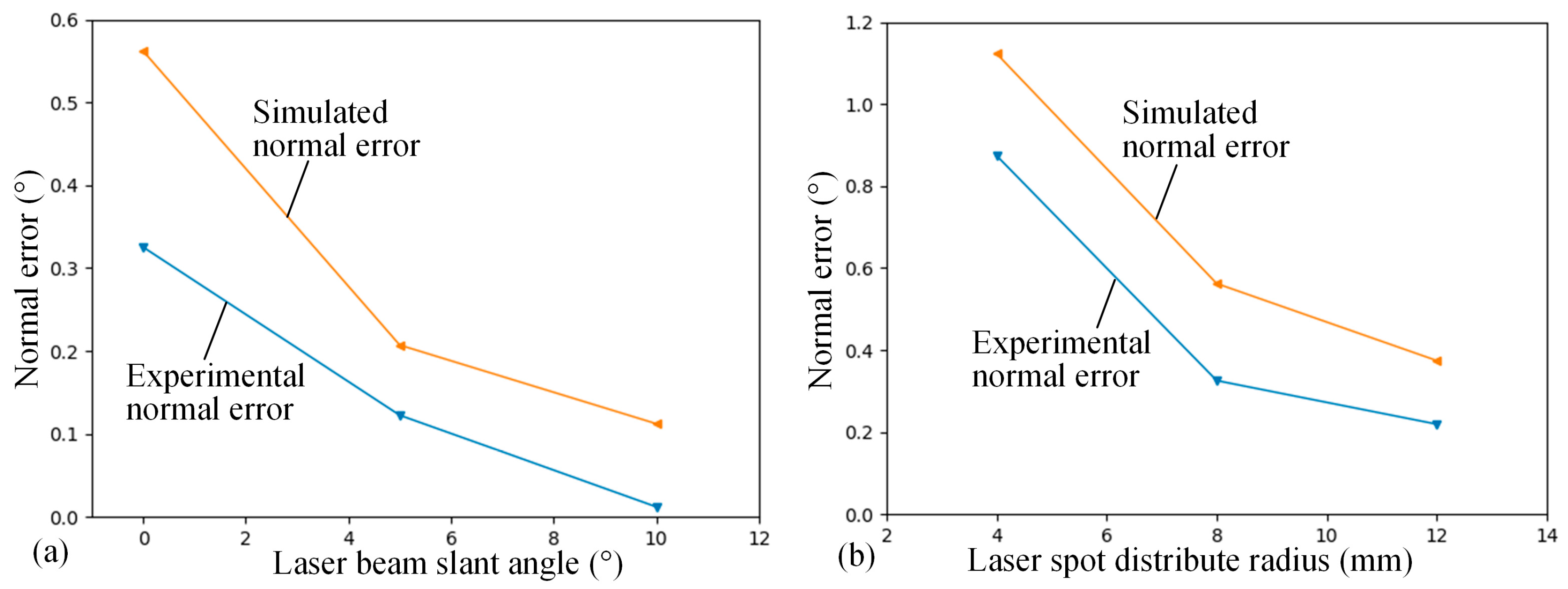
| No. | Slant Angle γ (°) | Experimental Normal Error (°) | Simulated Normal Error (°) |
|---|---|---|---|
| 1 | 0 | 0.325 | 0.562 |
| 2 | 5 | 0.124 | 0.207 |
| 3 | 10 | 0.012 | 0.112 |
| No. | Laser Spot Distribution Radius r (mm) | Experimental Normal Error (°) | Simulated Normal Error (°) |
|---|---|---|---|
| 1 | 4 | 0.874 | 1.123 |
| 2 | 8 | 0.325 | 0.562 |
| 3 | 12 | 0.219 | 0.374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Yang, G.; Yang, J.; Lu, H.; Dong, Z.; Kang, R.; Guo, D.; Qin, Y. Error Analysis of Normal Surface Measurements Based on Multiple Laser Displacement Sensors. Sensors 2024, 24, 2059. https://doi.org/10.3390/s24072059
Meng F, Yang G, Yang J, Lu H, Dong Z, Kang R, Guo D, Qin Y. Error Analysis of Normal Surface Measurements Based on Multiple Laser Displacement Sensors. Sensors. 2024; 24(7):2059. https://doi.org/10.3390/s24072059
Chicago/Turabian StyleMeng, Fantong, Guolin Yang, Jiankun Yang, Haibo Lu, Zhigang Dong, Renke Kang, Dongming Guo, and Yan Qin. 2024. "Error Analysis of Normal Surface Measurements Based on Multiple Laser Displacement Sensors" Sensors 24, no. 7: 2059. https://doi.org/10.3390/s24072059
APA StyleMeng, F., Yang, G., Yang, J., Lu, H., Dong, Z., Kang, R., Guo, D., & Qin, Y. (2024). Error Analysis of Normal Surface Measurements Based on Multiple Laser Displacement Sensors. Sensors, 24(7), 2059. https://doi.org/10.3390/s24072059






