Photon Phase Delay Sensing with Sub-Attosecond Uncertainty
Abstract
:1. Introduction
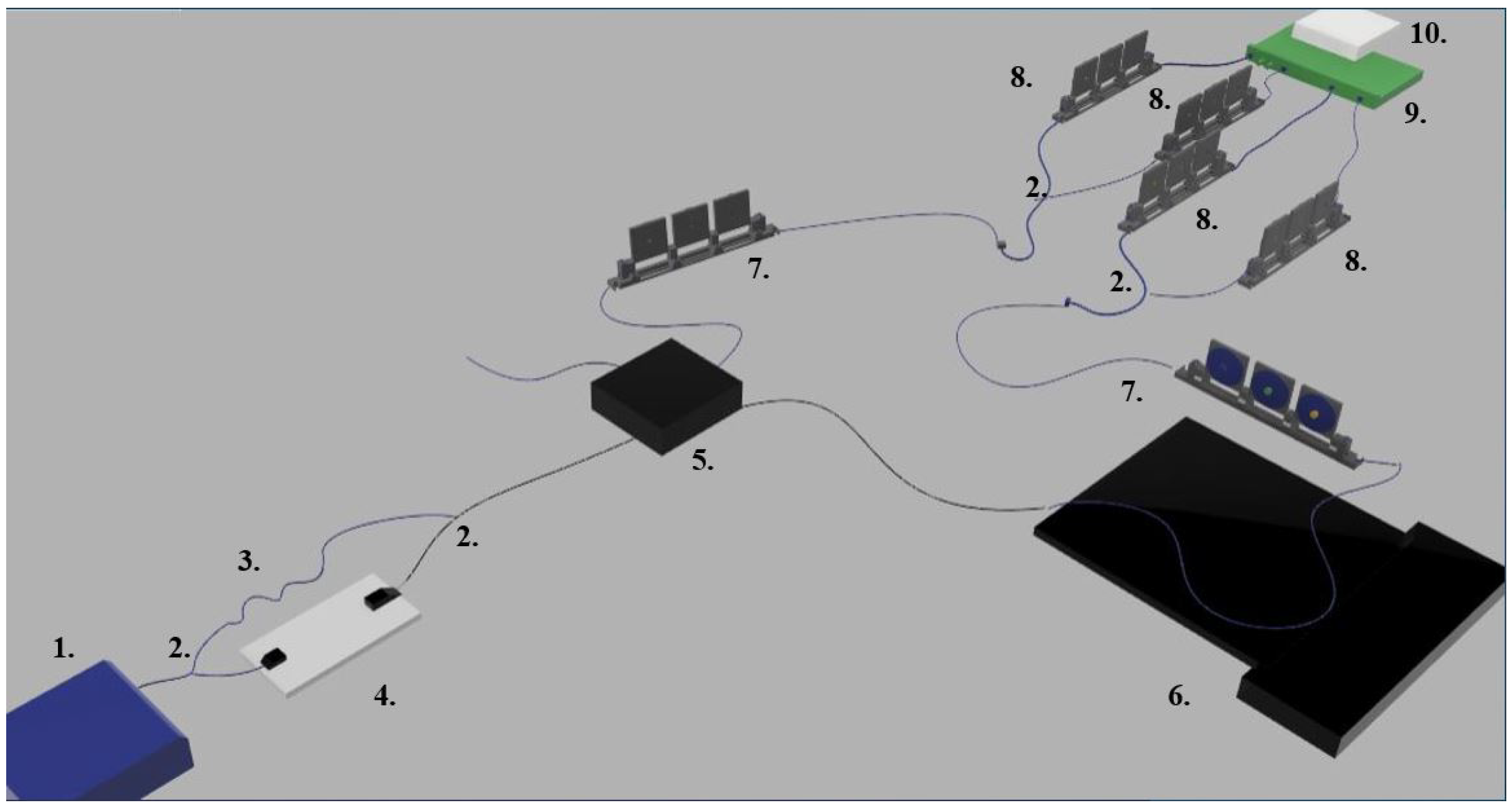
2. Experimental Setup
3. Theoretical Framework
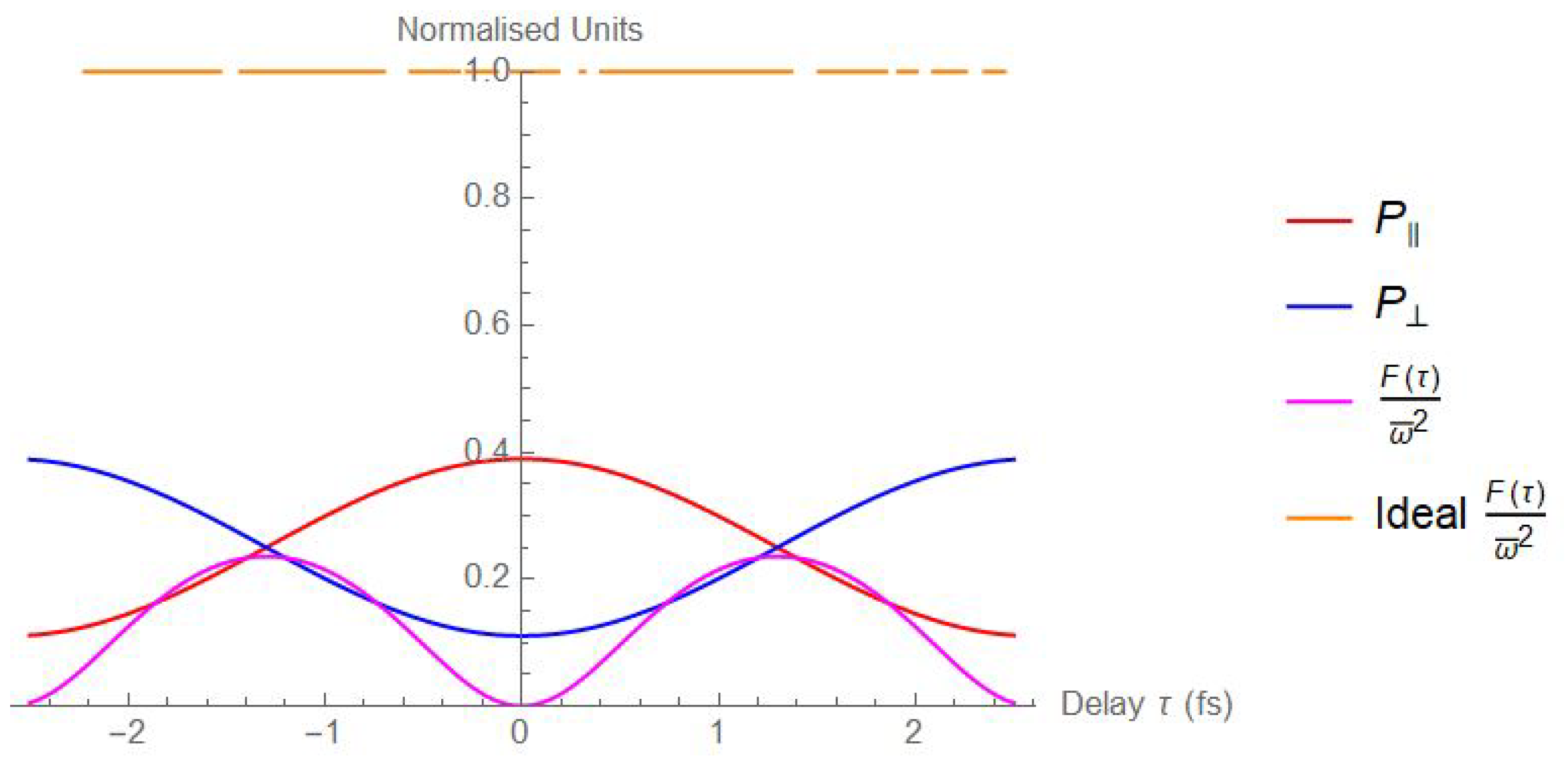
3.1. Outcome Probabilities for Delayed-Choice Temporal Quantum Eraser Experiment
3.2. Fisher Information Analysis
4. Results and Discussion
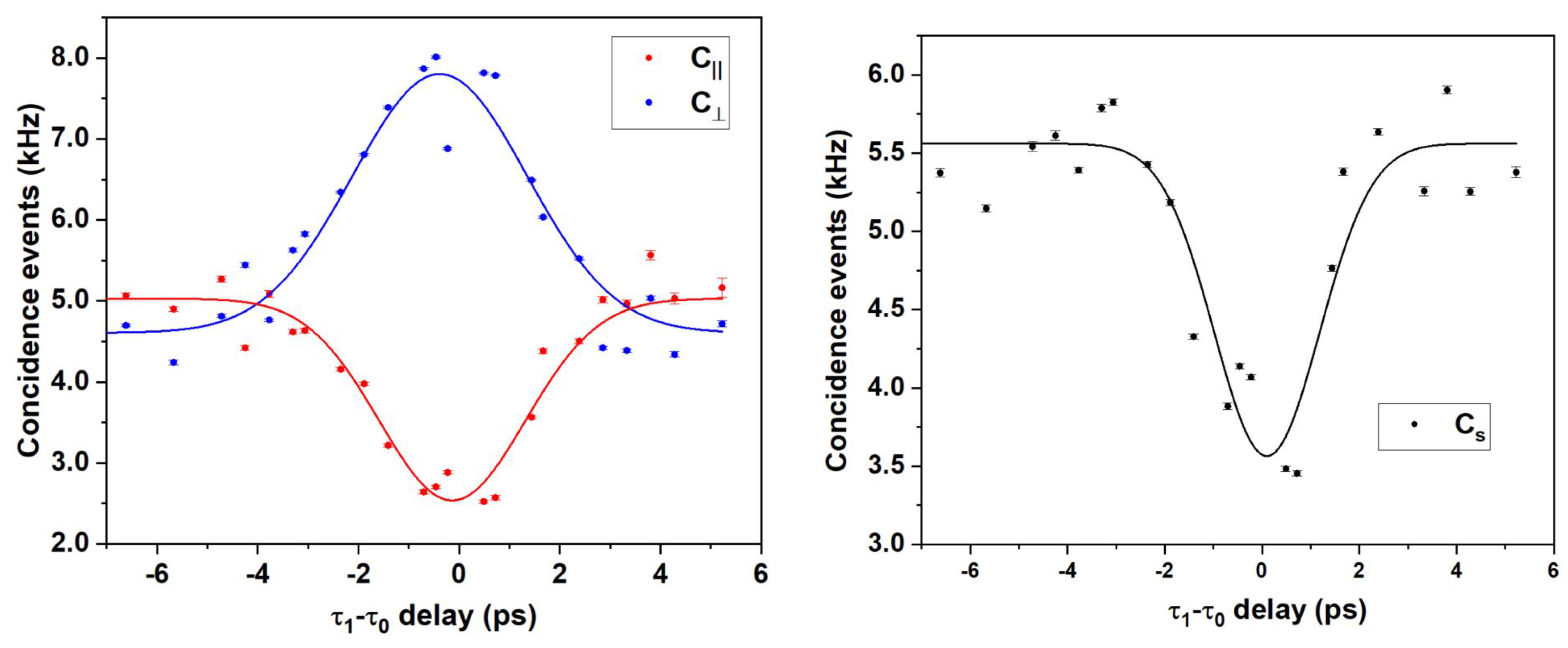
4.1. Reconstruction of the Hong–Ou–Mandel Feature
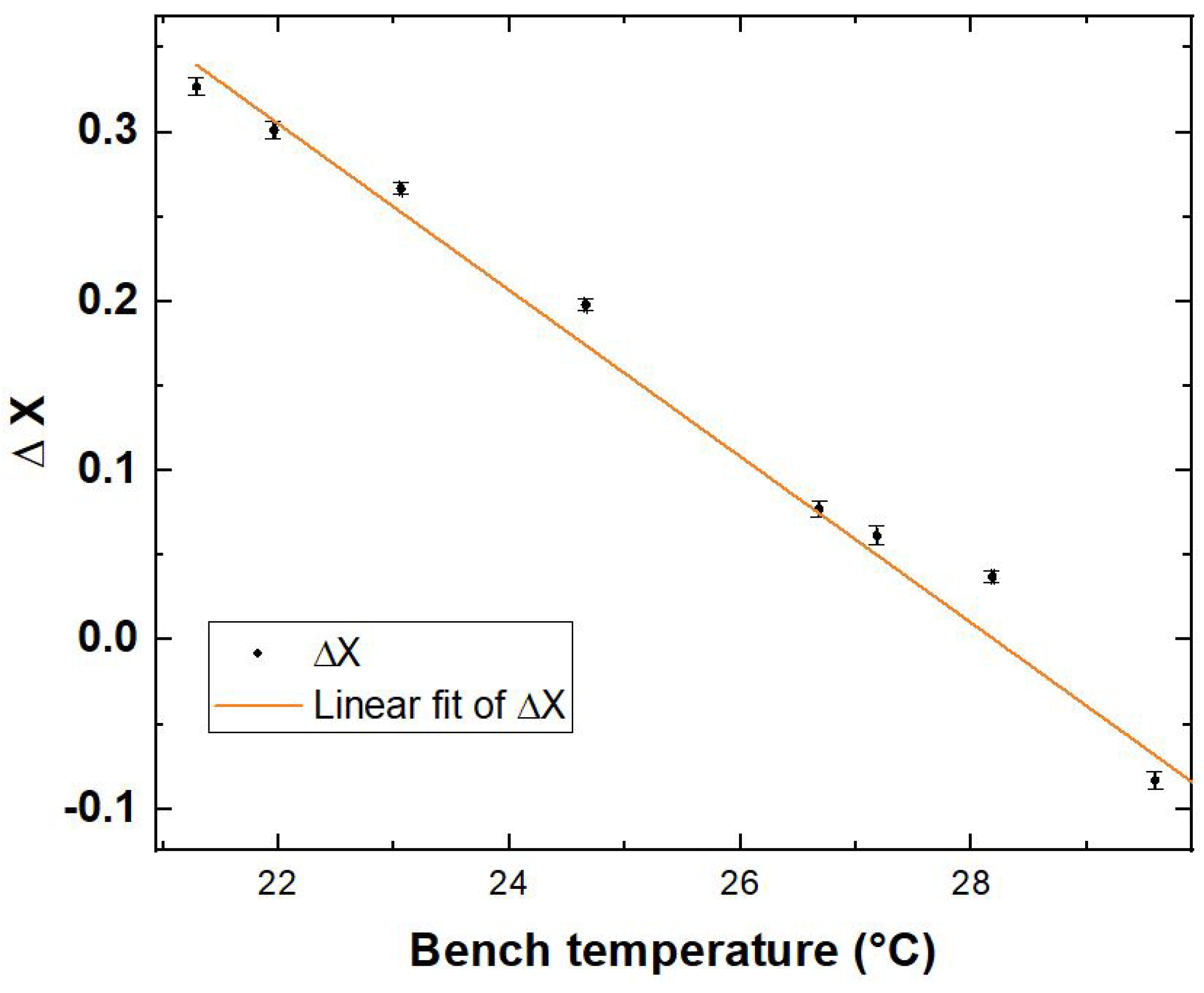
4.2. Temperature-Induced Interferometric Fringes
4.3. Calibration of the Delay Sensor
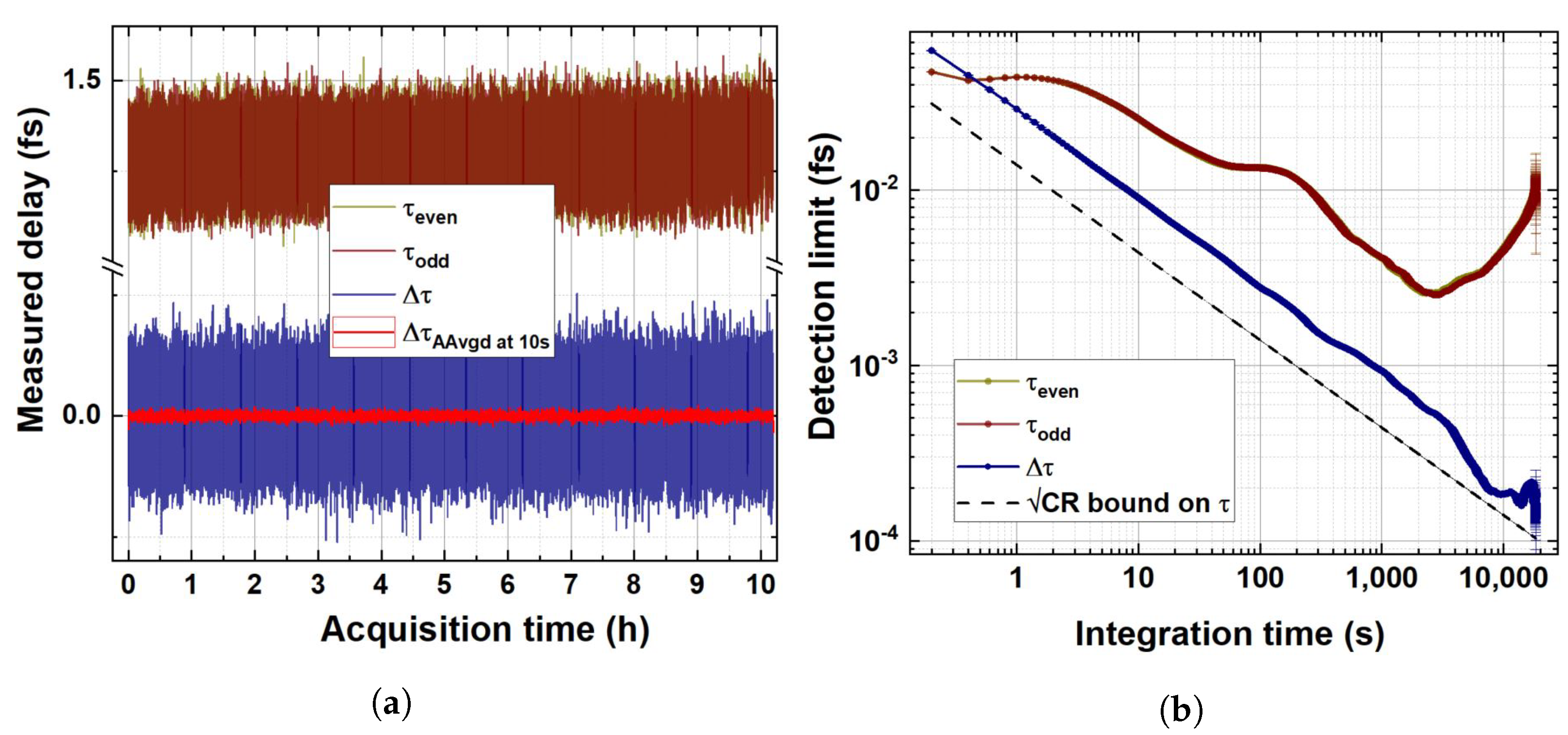
4.4. Long-Term Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Probability Calculations for the Experimental Set-Up of Figure 1
References
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044–2046. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, F.; Sit, A.; Zhang, Y.; Fickler, R.; Miatto, F.M.; Yao, Y.; Sciarrino, F.; Karimi, E. Two-photon interference: The Hong–Ou–Mandel effect. Rep. Prog. Phys. 2020, 84, 012402. [Google Scholar] [CrossRef] [PubMed]
- Ulanov, A.E.; Fedorov, I.A.; Sychev, D.; Grangier, P.; Lvovsky, A.I. Loss-tolerant state engineering for quantum-enhanced metrology via the reverse Hong–Ou–Mandel effect. Nat. Commun. 2016, 7, 11925. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ecker, S.; Wengerowsky, S.; Bulla, L.; Joshi, S.K.; Steinlechner, F.; Ursin, R. Polarization Entanglement by Time-Reversed Hong-Ou-Mandel Interference. Phys. Rev. Lett. 2018, 121, 200502. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ecker, S.; Chen, L.; Steinlechner, F.; Huber, M.; Ursin, R. Temporal distinguishability in Hong-Ou-Mandel interference for harnessing high-dimensional frequency entanglement. npj Quantum Inf. 2021, 7, 167. [Google Scholar] [CrossRef]
- Ndagano, B.; Defienne, H.; Branford, D.; Shah, Y.D.; Lyons, A.; Westerberg, N.; Gauger, E.M.; Faccio, D. Quantum microscopy based on Hong–Ou–Mandel interference. Nat. Photon. 2022, 16, 384–389. [Google Scholar] [CrossRef]
- Dorfman, K.E.; Asban, S.; Gu, B.; Mukamel, S. Hong-Ou-Mandel interferometry and spectroscopy using entangled photons. Commun. Phys. 2021, 4, 49. [Google Scholar] [CrossRef]
- Branning, D.; Migdall, A.L.; Sergienko, A.V. Simultaneous measurement of group and phase delay between two photons. Phys. Rev. A 2000, 62, 063808. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology—The lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Dauler, E.; Jaeger, G.; Muller, A.; Migdall, A.; Sergienko, A. Tests of a two-photon technique for measuring polarization mode dispersion with subfemtosecond precision. J. Res. Natl. Inst. Stand. Technol. 1999, 104, 1. [Google Scholar] [CrossRef]
- Russo, S.D.; Elefante, A.; Dequal, D.; Pallotti, D.K.; Amato, L.S.; Sgobba, F.; de Cumis, M.S. Advances in Mid-Infrared Single-Photon Detection. Photonics 2022, 9, 470. [Google Scholar] [CrossRef]
- Nomerotski, A.; Keach, M.; Stankus, P.; Svihra, P.; Vintskevich, S. Counting of Hong-Ou-Mandel Bunched Optical Photons Using a Fast Pixel Camera. Sensors 2020, 20, 3475. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; de Oliveira, A.N.; Pádua, S.; Monken, C.H. Multimode Hong-Ou-Mandel Interference. Phys. Rev. Lett. 2003, 90, 143601. [Google Scholar] [CrossRef] [PubMed]
- D’Ambrosio, V.; Carvacho, G.; Agresti, I.; Marrucci, L.; Sciarrino, F. Tunable Two-Photon Quantum Interference of Structured Light. Phys. Rev. Lett. 2019, 122, 013601. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Lee, S.M.; Kwon, O.; Moon, H.S. Two-photon interference of polarization-entangled photons in a Franson interferometer. Sci. Rep. 2017, 7, 5772. [Google Scholar] [CrossRef] [PubMed]
- Yepiz-Graciano, P.; Martínez, A.M.A.; Lopez-Mago, D.; Cruz-Ramirez, H.; U’Ren, A.B. Spectrally resolved Hong–Ou–Mandel interferometry for quantum-optical coherence tomography. Photonics Res. 2020, 8, 1023. [Google Scholar] [CrossRef]
- Triggiani, D.; Psaroudis, G.; Tamma, V. Ultimate Quantum Sensitivity in the Estimation of the Delay between two Interfering Photons through Frequency-Resolving Sampling. Phys. Rev. Appl. 2023, 19, 044068. [Google Scholar] [CrossRef]
- Jin, R.B.; Gerrits, T.; Fujiwara, M.; Wakabayashi, R.; Yamashita, T.; Miki, S.; Terai, H.; Shimizu, R.; Takeoka, M.; Sasaki, M. Spectrally resolved Hong-Ou-Mandel interference between independent photon sources. Opt. Express 2015, 23, 28836. [Google Scholar] [CrossRef]
- Kobayashi, T.; Ikuta, R.; Yasui, S.; Miki, S.; Yamashita, T.; Terai, H.; Yamamoto, T.; Koashi, M.; Imoto, N. Frequency-domain Hong–Ou–Mandel interference. Nat. Photonics 2016, 10, 441–444. [Google Scholar] [CrossRef]
- Orre, V.V.; Goldschmidt, E.A.; Deshpande, A.; Gorshkov, A.V.; Tamma, V.; Hafezi, M.; Mittal, S. Interference of Temporally Distinguishable Photons Using Frequency-Resolved Detection. Phys. Rev. Lett. 2019, 123, 123603. [Google Scholar] [CrossRef]
- Xue, Y.; Yoshizawa, A.; Tsuchida, H. Hong-Ou-Mandel dip measurements of polarization-entangled photon pairs at 1550 nm. Opt. Express 2010, 18, 8182. [Google Scholar] [CrossRef] [PubMed]
- Tsujimoto, Y.; Wakui, K.; Fujiwara, M.; Sasaki, M.; Takeoka, M. Ultra-fast Hong-Ou-Mandel interferometry via temporal filtering. Opt. Express 2021, 29, 37150. [Google Scholar] [CrossRef] [PubMed]
- Lyons, A.; Knee, G.C.; Bolduc, E.; Roger, T.; Leach, J.; Gauger, E.M.; Faccio, D. Attosecond-resolution Hong-Ou-Mandel interferometry. Sci. Adv. 2018, 4, eaap9416. [Google Scholar] [CrossRef] [PubMed]
- Pittman, T.B.; Strekalov, D.V.; Migdall, A.; Rubin, M.H.; Sergienko, A.V.; Shih, Y.H. Can Two-Photon Interference be Considered the Interference of Two Photons? Phys. Rev. Lett. 1996, 77, 1917–1920. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Steinberg, A.M.; Chiao, R.Y. Observation of a “quantum eraser”: A revival of coherence in a two-photon interference experiment. Phys. Rev. A 1992, 45, 7729–7739. [Google Scholar] [CrossRef]
- Wheeler, J.A. The “Past” and the “Delayed-Choice” Double-Slit Experiment. In Mathematical Foundations of Quantum Theory; Elsevier: Amsterdam, The Netherlands, 1978; pp. 9–48. [Google Scholar] [CrossRef]
- Scully, M.O.; Drühl, K. Quantum eraser: A proposed photon correlation experiment concerning observation and “delayed choice” in quantum mechanics. Phys. Rev. A 1982, 25, 2208–2213. [Google Scholar] [CrossRef]
- Kim, Y.H.; Yu, R.; Kulik, S.P.; Shih, Y.; Scully, M.O. Delayed “Choice” Quantum Eraser. Phys. Rev. Lett. 2000, 84, 1–5. [Google Scholar] [CrossRef]
- Sgobba, F.; Andrisani, A.; Dello Russo, S.; Siciliani de Cumis, M.; Santamaria Amato, L. Attosecond-Level Delay Sensing via Temporal Quantum Erasing. Sensors 2023, 23, 7758. [Google Scholar] [CrossRef]
- Harnchaiwat, N.; Zhu, F.; Westerberg, N.; Gauger, E.; Leach, J. Tracking the polarisation state of light via Hong-Ou-Mandel interferometry. Opt. Express 2020, 28, 2210. [Google Scholar] [CrossRef]
- Kay, S.M. Statistical Signal Processing: Estimation Theory; Prentice Hall: Hoboken, NJ, USA, 1993; Volume 1, Chapter 3. [Google Scholar]
- Wolfowitz, J. Asymptotic efficiency of the maximum likelihood estimator. Theory Probab. Its Appl. 1965, 10, 247–260. [Google Scholar] [CrossRef]
- Hamilton, M.W. Phase shifts in multilayer dielectric beam splittersp. Am. J. Phys. 2000, 68, 186–191. [Google Scholar] [CrossRef]

| a (C−1) | b | Reduced- |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sgobba, F.; Andrisani, A.; Santamaria Amato, L. Photon Phase Delay Sensing with Sub-Attosecond Uncertainty. Sensors 2024, 24, 2202. https://doi.org/10.3390/s24072202
Sgobba F, Andrisani A, Santamaria Amato L. Photon Phase Delay Sensing with Sub-Attosecond Uncertainty. Sensors. 2024; 24(7):2202. https://doi.org/10.3390/s24072202
Chicago/Turabian StyleSgobba, Fabrizio, Andrea Andrisani, and Luigi Santamaria Amato. 2024. "Photon Phase Delay Sensing with Sub-Attosecond Uncertainty" Sensors 24, no. 7: 2202. https://doi.org/10.3390/s24072202
APA StyleSgobba, F., Andrisani, A., & Santamaria Amato, L. (2024). Photon Phase Delay Sensing with Sub-Attosecond Uncertainty. Sensors, 24(7), 2202. https://doi.org/10.3390/s24072202







