Classification of Corrosion Severity in SPCC Steels Using Eddy Current Testing and Supervised Machine Learning Models
Abstract
:1. Introduction
2. Experiments and Metrology
2.1. SPCC Steel Samples
2.2. ECT Principle
2.3. Experiments
3. Classification Algorithms
3.1. Gaussian Mixture Model
3.2. Logistic Regression Model
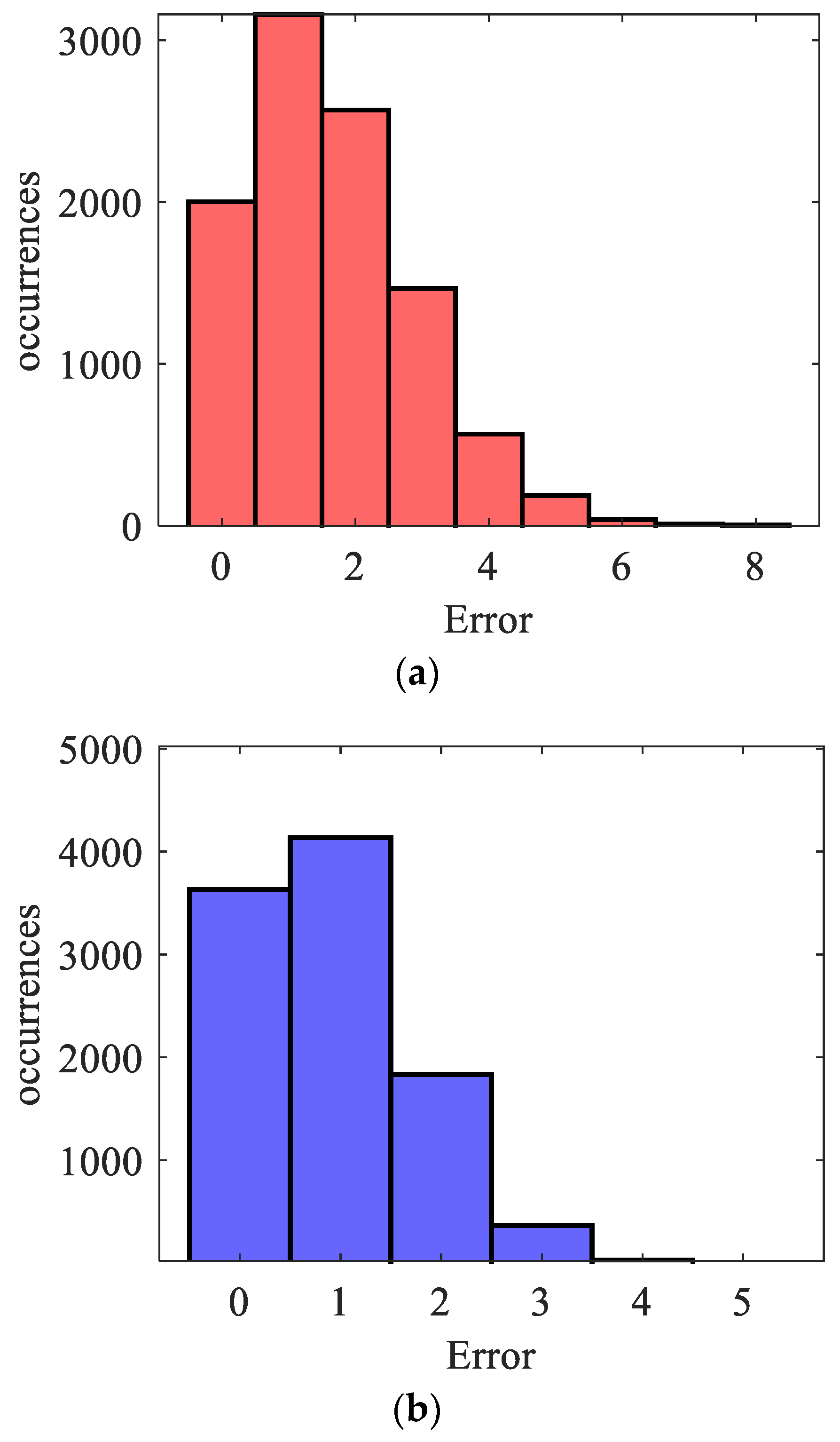
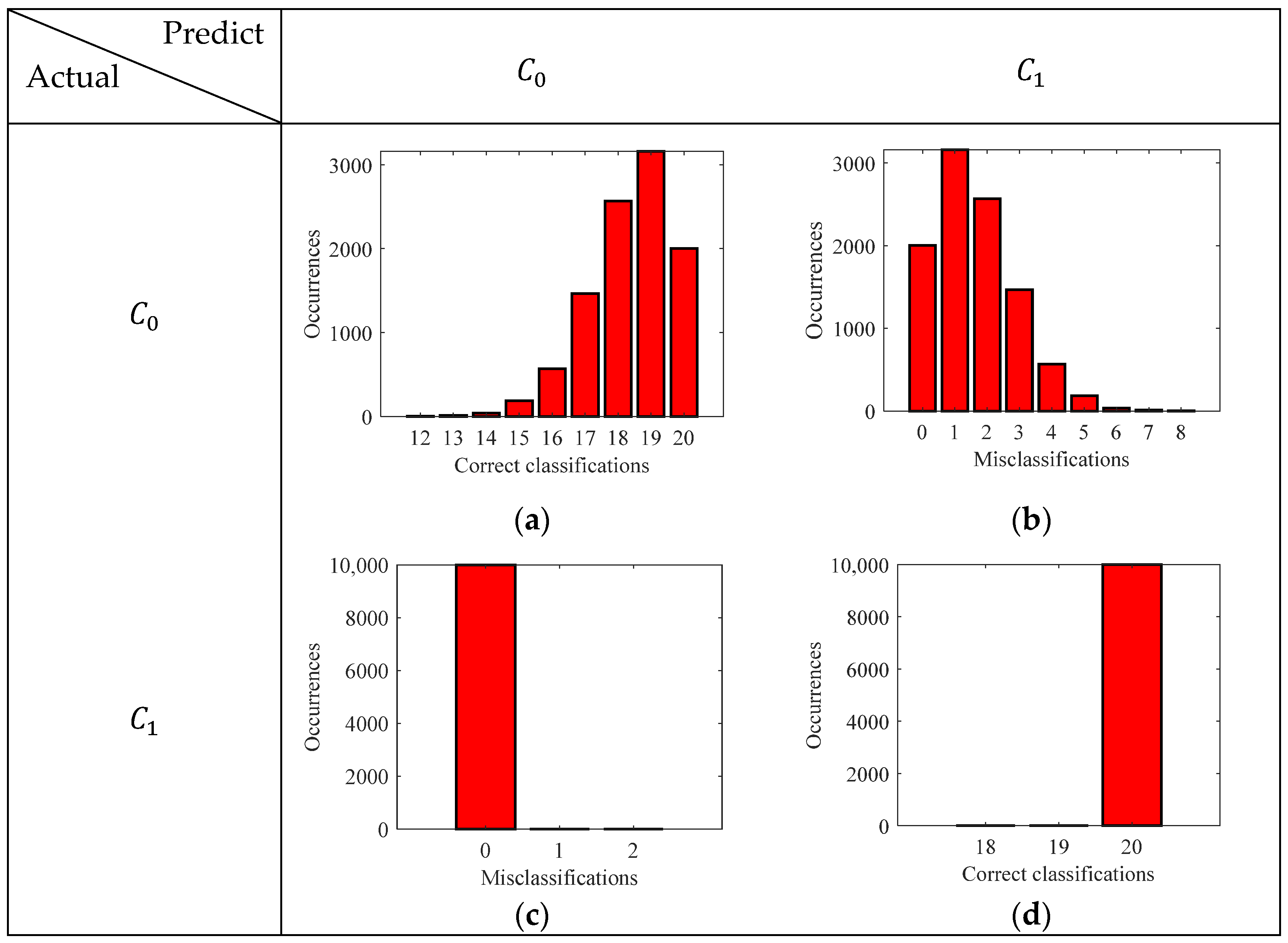
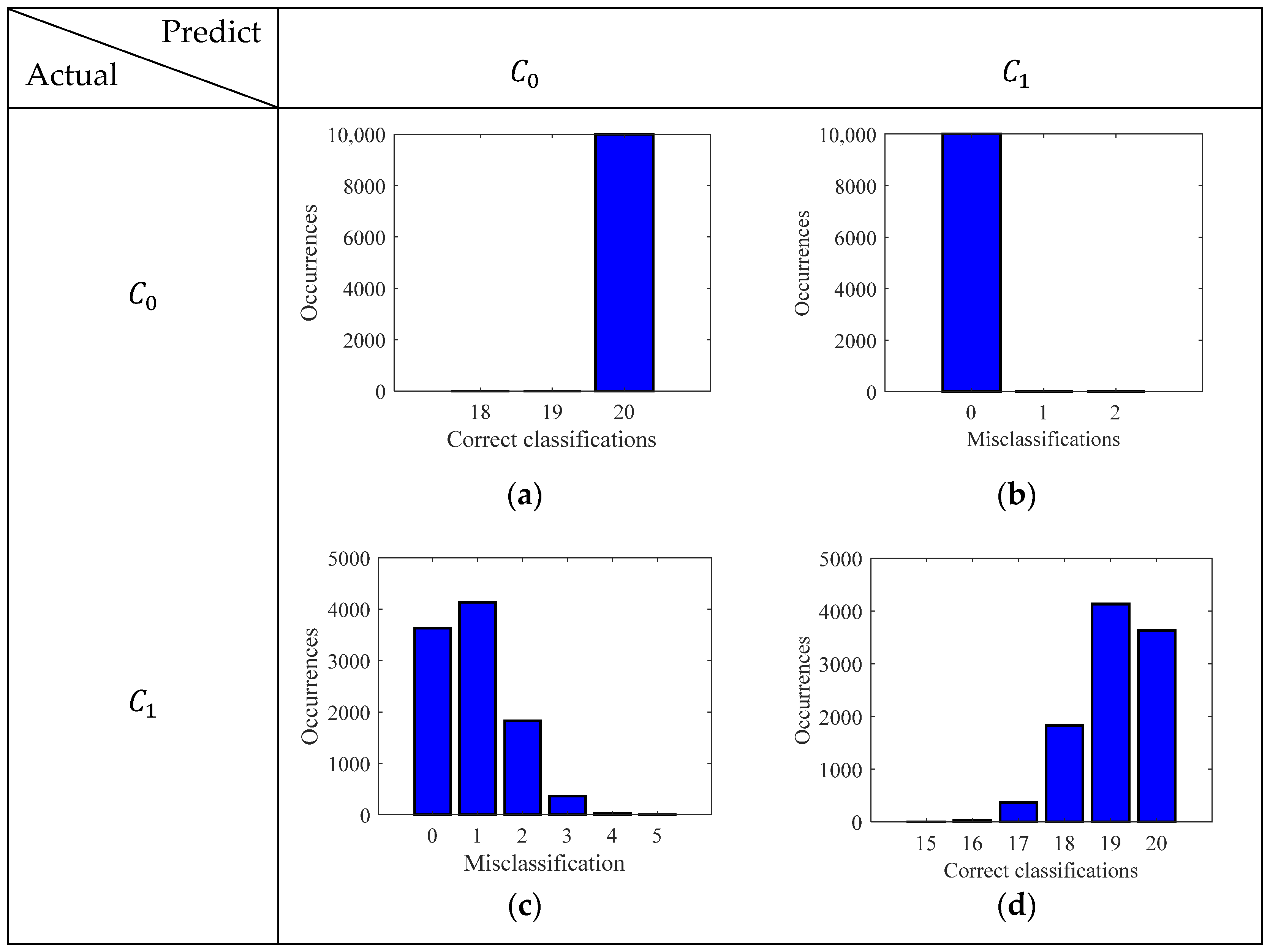
3.3. Classification Results and Discussion
4. Conclusions
- Both the models, GMM and logistic regression model, can classify the corrosive state of the steel samples, using features from the perturbed magnetic flux density components.
- The GMM model has a recall score of 1, indicating that it never misclassifies the samples that are highly corroded (state-2). On the other hand, the logistic regression model occasionally misclassifies the state-2 samples.
- The logistic regression model has a precision score of 1, indicating that it never misclassifies those samples that are less corroded (state-1), while the GMM model occasionally misclassifies them.
- Both the models have a good F1 score indicating the potential application of these models to classify the corrosive state of steels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, C.-H.; Lee, J.-R. Characterization of SPCC Steel Stress Behaviour in Brine Water Environment. Int. J. Electrochem. Sci. 2019, 14, 2321–2332. [Google Scholar] [CrossRef]
- Corrosion Mechanisms in Theory and Practice, 3rd ed.; Marcus, P. (Ed.) Corrosion technology; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-4200-9462-6. [Google Scholar]
- Revie, R.W.; Uhlig, H.H. Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering, 4th ed.; Wiley-Interscience; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; ISBN 978-0-470-27725-6. [Google Scholar]
- Biezma, M.V.; San Cristóbal, J.R. Methodology to Study Cost of Corrosion. Corros. Eng. Sci. Technol. 2005, 40, 344–352. [Google Scholar] [CrossRef]
- Doğan, F.; Duru, E.; Akbulut, H.; Aslan, S. How the Duty Cycle Affects Wear and Corrosion: A Parametric Study in the Ni–B–TiN Composite Coatings. Results Surf. Interfaces 2023, 11, 100112. [Google Scholar] [CrossRef]
- Refait, P.; Grolleau, A.-M.; Jeannin, M.; Rémazeilles, C.; Sabot, R. Corrosion of Carbon Steel in Marine Environments: Role of the Corrosion Product Layer. Corros. Mater. Degrad. 2020, 1, 198–218. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Chen, H.; Huang, Y. Understanding the Interaction between Erosion and Corrosion of Pipeline Steel in Acid Solution of Different pH. J. Mater. Res. Technol. 2023, 25, 6550–6566. [Google Scholar] [CrossRef]
- Fregonese, M.; Idrissi, H.; Mazille, H.; Renaud, L.; Cetre, Y. Initiation and Propagation Steps in Pitting Corrosion of Austenitic Stainless Steels: Monitoring by Acoustic Emission. Corros. Sci. 2001, 43, 627–641. [Google Scholar] [CrossRef]
- Edalati, K.; Rastkhah, N.; Kermani, A.; Seiedi, M.; Movafeghi, A. The Use of Radiography for Thickness Measurement and Corrosion Monitoring in Pipes. Int. J. Press. Vessels Pip. 2006, 83, 736–741. [Google Scholar] [CrossRef]
- He, Y.; Tian, G.; Zhang, H.; Alamin, M.; Simm, A.; Jackson, P. Steel Corrosion Characterization Using Pulsed Eddy Current Systems. IEEE Sens. J. 2012, 12, 2113–2120. [Google Scholar] [CrossRef]
- Ishkov, A.V.; Dmitriev, S.F.; Katasonov, A.O.; Fadeev, D.A.; Malikov, V.N. Inspection of Corrosion Defects of Steel Pipes by Eddy Current Method. J. Phys. Conf. Ser. 2021, 1728, 012006. [Google Scholar] [CrossRef]
- Frankowski, P.K. Corrosion Detection and Measurement Using Eddy Current Method. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Swinoujście, Poland, 9–12 May 2018; IEEE: San Francisco, CA, USA, 2018; pp. 398–400. [Google Scholar]
- Yusa, N.; Perrin, S.; Mizuno, K.; Chen, Z.; Miya, K. Eddy Current Inspection of Closed Fatigue and Stress Corrosion Cracks. Meas. Sci. Technol. 2007, 18, 3403–3408. [Google Scholar] [CrossRef]
- Li, Y.; Yan, B.; Li, D.; Jing, H.; Li, Y.; Chen, Z. Pulse-Modulation Eddy Current Inspection of Subsurface Corrosion in Conductive Structures. NDT E Int. 2016, 79, 142–149. [Google Scholar] [CrossRef]
- Xue, C.; Zhang, Y.; Ding, S.; Song, C.; Wang, Y. Comparison Research on Characterization and Evaluation Approaches for Paint Coated Corrosion Using Eddy Current Pulsed Thermography. Sensors 2023, 23, 6889. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Tian, G.; Zhu, J.; Chen, X.; Wang, Y.; Chen, Y. Characterisation and Evaluation of Paint-Coated Marine Corrosion in Carbon Steel Using Eddy Current Pulsed Thermography. NDT E Int. 2022, 130, 102678. [Google Scholar] [CrossRef]
- Hernandez, J.; Fouliard, Q.; Vo, K.; Raghavan, S. Detection of Corrosion under Insulation on Aerospace Structures via Pulsed Eddy Current Thermography. Aerosp. Sci. Technol. 2022, 121, 107317. [Google Scholar] [CrossRef]
- Kopf, L.; Tighe, R. Thermographic Identification of Hidden Corrosion. In Proceedings of the 2021 36th International Conference on Image and Vision Computing New Zealand (IVCNZ), Tauranga, New Zealand, 9 December 2021; IEEE: San Francisco, CA, USA, 2021; pp. 1–6. [Google Scholar]
- Alamin, M.; Tian, G.Y.; Andrews, A.; Jackson, P. Principal Component Analysis of Pulsed Eddy Current Response from Corrosion in Mild Steel. IEEE Sens. J. 2012, 12, 2548–2553. [Google Scholar] [CrossRef]
- Postolache, O.; Ramos, H.G.; Ribeiro, A.L. Detection and Characterization of Defects Using GMR Probes and Artificial Neural Networks. Comput. Stand. Interfaces 2011, 33, 191–200. [Google Scholar] [CrossRef]
- Ameli, Z.; Nesheli, S.J.; Landis, E.N. Deep Learning-Based Steel Bridge Corrosion Segmentation and Condition Rating Using Mask RCNN and YOLOv8. Infrastructures 2023, 9, 3. [Google Scholar] [CrossRef]
- Mayakuntla, P.K.; Ganguli, A.; Smyl, D. Gaussian Mixture Model-Based Classification of Corrosion Severity in Concrete Structures Using Ultrasonic Imaging. J. Nondestruct. Eval. 2023, 42, 28. [Google Scholar] [CrossRef]
- Jalali, H.; Misra, R.; Dickerson, S.J.; Rizzo, P. Detection and Classification of Corrosion-Related Damage Using Solitary Waves. Res. Nondestruct. Eval. 2022, 33, 78–97. [Google Scholar] [CrossRef]
- Yusa, N.; Tomizawa, T.; Song, H.; Hashizume, H. Probability of Detection Analyses of Eddy Current Data for the Detection of Corrosion. Badania Nieniszcz. Diagn. 2018, 3, 3–7. [Google Scholar] [CrossRef]
- Arenas, M.P.; Rocha, T.J.; Angani, C.S.; Ribeiro, A.L.; Ramos, H.G.; Eckstein, C.B.; Rebello, J.M.A.; Pereira, G.R. Novel Austenitic Steel Ageing Classification Method Using Eddy Current Testing and a Support Vector Machine. Measurement 2018, 127, 98–103. [Google Scholar] [CrossRef]
- Ramos, H.M.G.; Postolache, O.; Alegria, F.C.; Lopes Ribeiro, A. Using the Skin Effect to Estimate Cracks Depths in Mettalic Structures. In Proceedings of the 2009 IEEE Intrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; IEEE: San Francisco, CA, USA, 2009; pp. 1361–1366. [Google Scholar]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Olakanmi, O.; Akinjobi, J. Supervised Machine Learning Algorithms: Classification and Comparison. Int. J. Comput. Trends Technol. 2017, 48, 128–138. [Google Scholar] [CrossRef]
- Wong, P.T.; Lai, W.W.; Poon, C. Classification of Concrete Corrosion States by GPR with Machine Learning. Constr. Build. Mater. 2023, 402, 132855. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
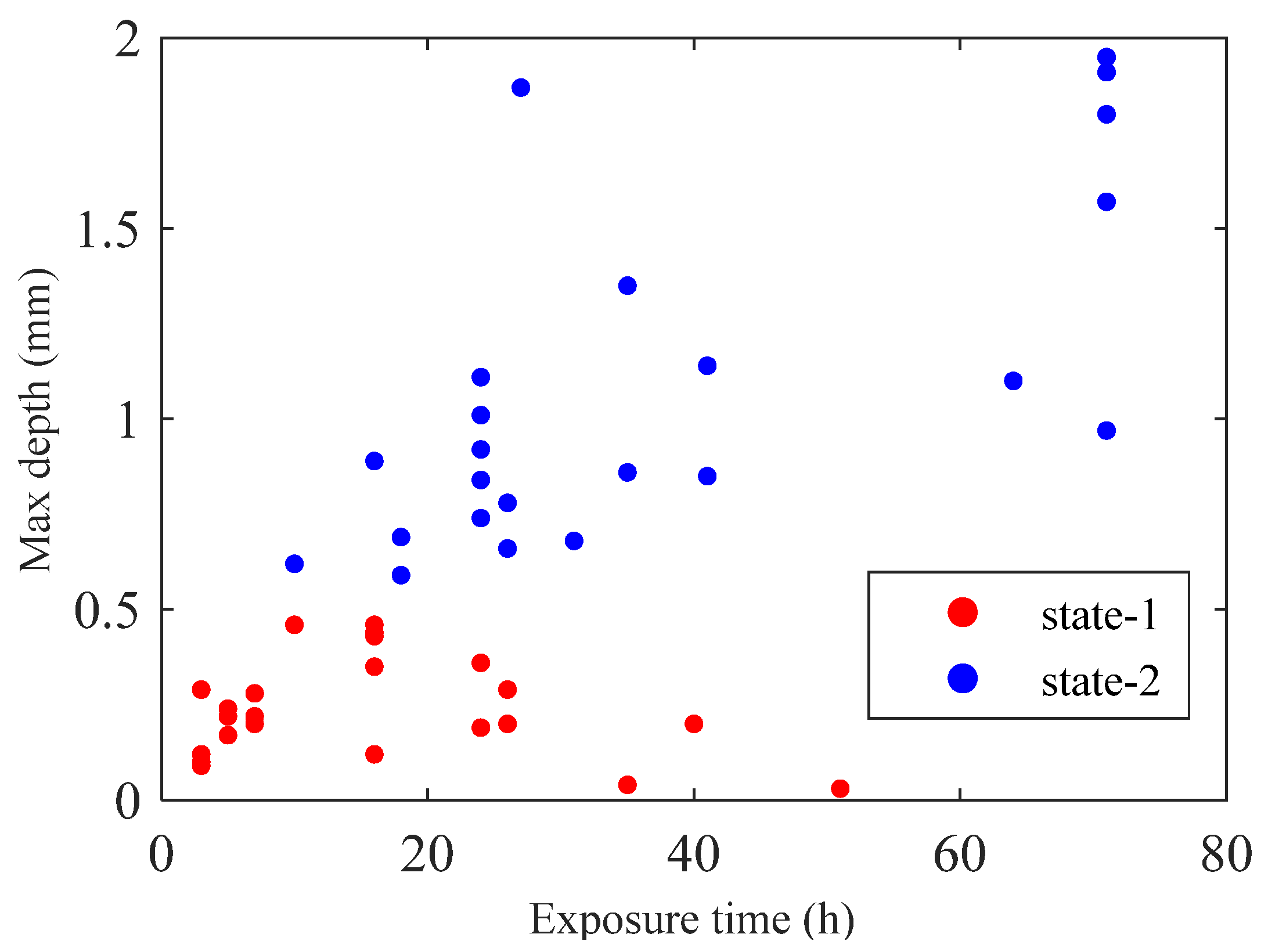





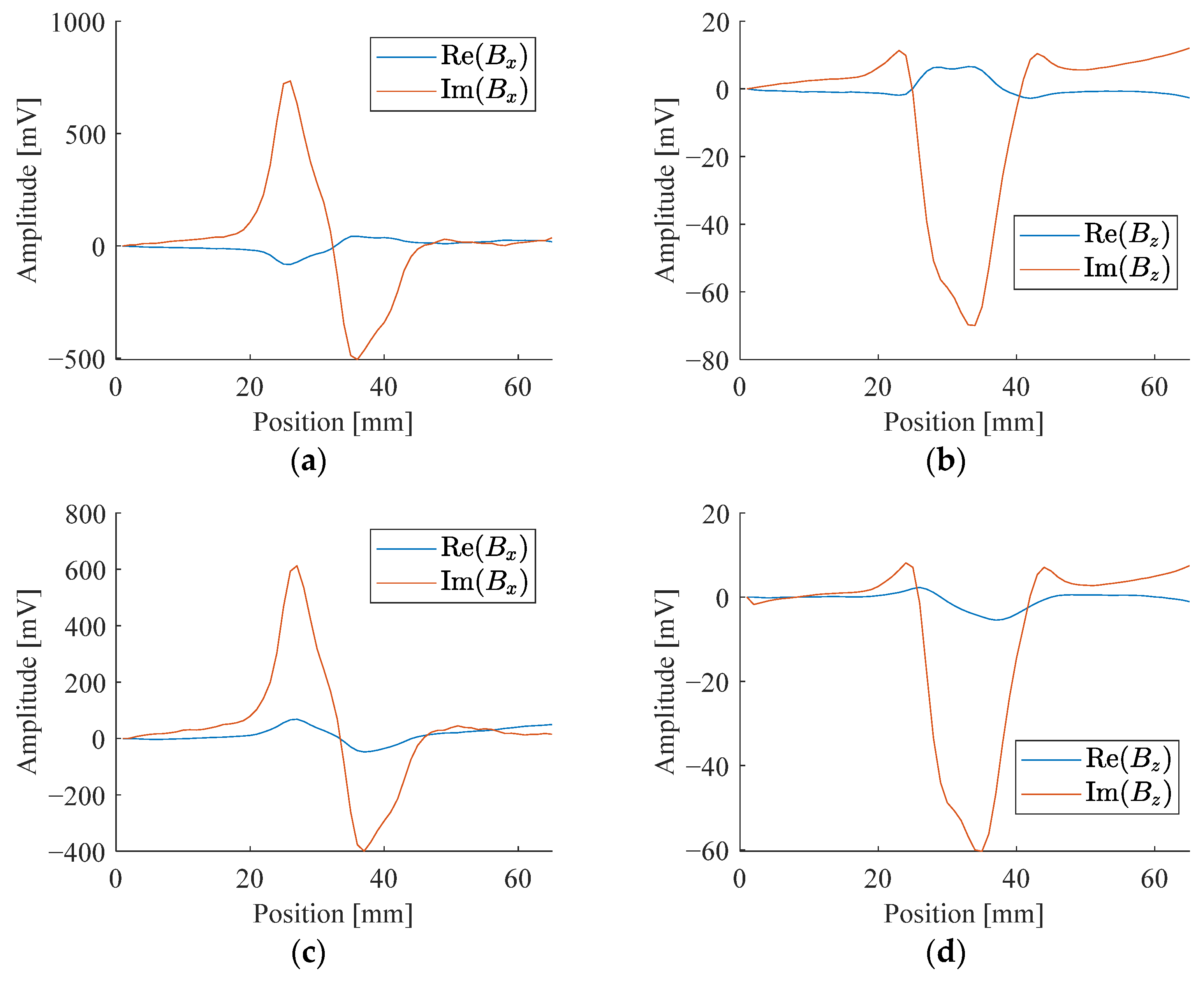
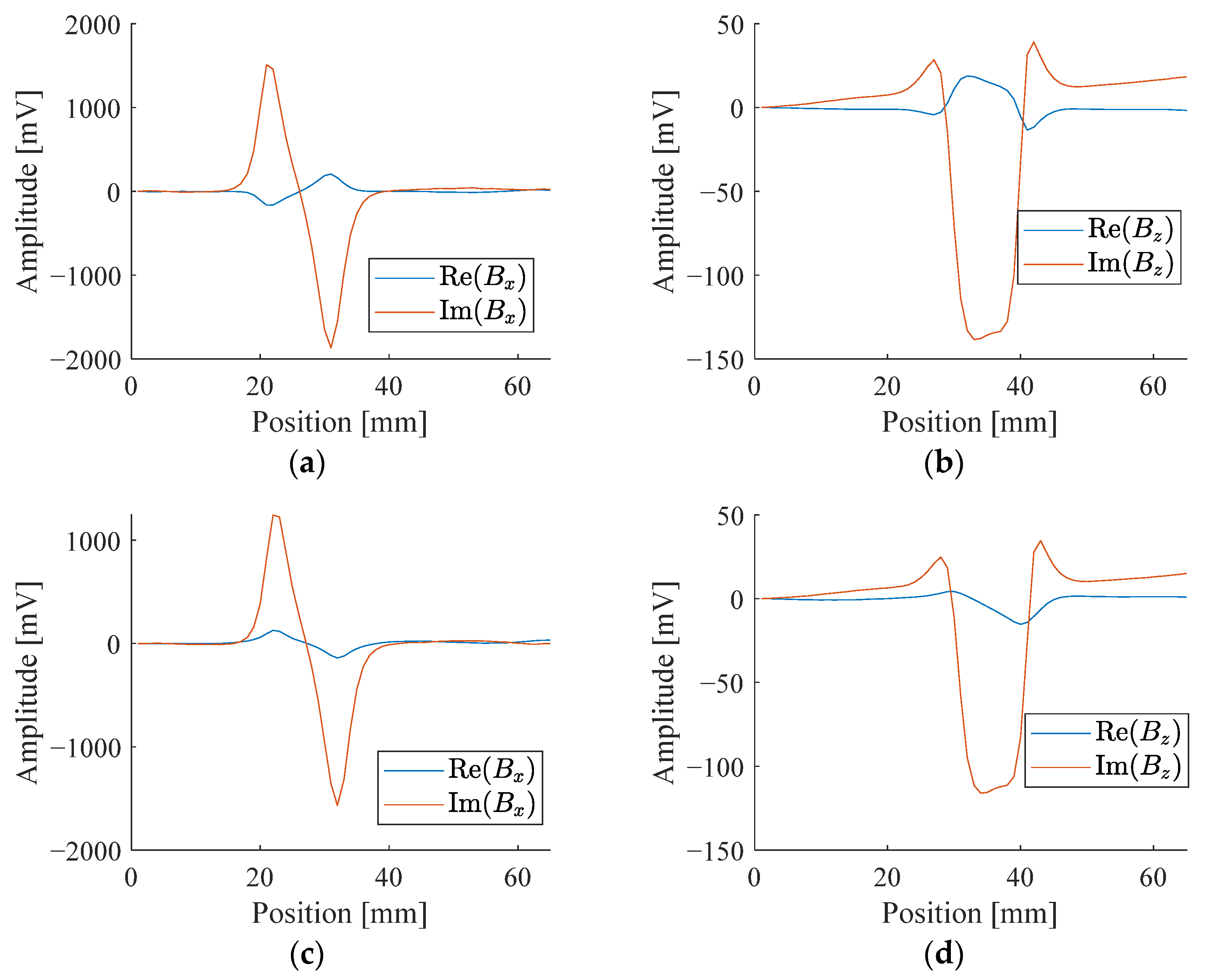



| No. | Features |
|---|---|
| 1 | Max(abs(Re (Bx))) at 2.5 kHz |
| 2 | Max(abs(Im(Bx))) at 2.5 kHz |
| 3 | Max(abs(Re (Bz))) at 2.5 kHz |
| 4 | Max(abs(Im (Bz))) at 2.5 kHz |
| 5 | Max(abs(Re (Bx))) at 5.0 kHz |
| 6 | Max(abs(Im(Bx))) at 5.0 kHz |
| 7 | Max(abs(Re (Bz))) at 5.0 kHz |
| 8 | Max(abs(Im (Bz))) at 5.0 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Baskaran, P.; Ribeiro, A.L.; Alegria, F.C.; Ramos, H.G. Classification of Corrosion Severity in SPCC Steels Using Eddy Current Testing and Supervised Machine Learning Models. Sensors 2024, 24, 2259. https://doi.org/10.3390/s24072259
Xie L, Baskaran P, Ribeiro AL, Alegria FC, Ramos HG. Classification of Corrosion Severity in SPCC Steels Using Eddy Current Testing and Supervised Machine Learning Models. Sensors. 2024; 24(7):2259. https://doi.org/10.3390/s24072259
Chicago/Turabian StyleXie, Lian, Prashanth Baskaran, Artur L. Ribeiro, Francisco C. Alegria, and Helena G. Ramos. 2024. "Classification of Corrosion Severity in SPCC Steels Using Eddy Current Testing and Supervised Machine Learning Models" Sensors 24, no. 7: 2259. https://doi.org/10.3390/s24072259
APA StyleXie, L., Baskaran, P., Ribeiro, A. L., Alegria, F. C., & Ramos, H. G. (2024). Classification of Corrosion Severity in SPCC Steels Using Eddy Current Testing and Supervised Machine Learning Models. Sensors, 24(7), 2259. https://doi.org/10.3390/s24072259






