Temperature Uncertainty Reduction Algorithm Based on Temperature Distribution Prior for Optical Sensors in Oil Tank Ground Settlement Monitoring
Abstract
:1. Introduction
2. Theoretical Background
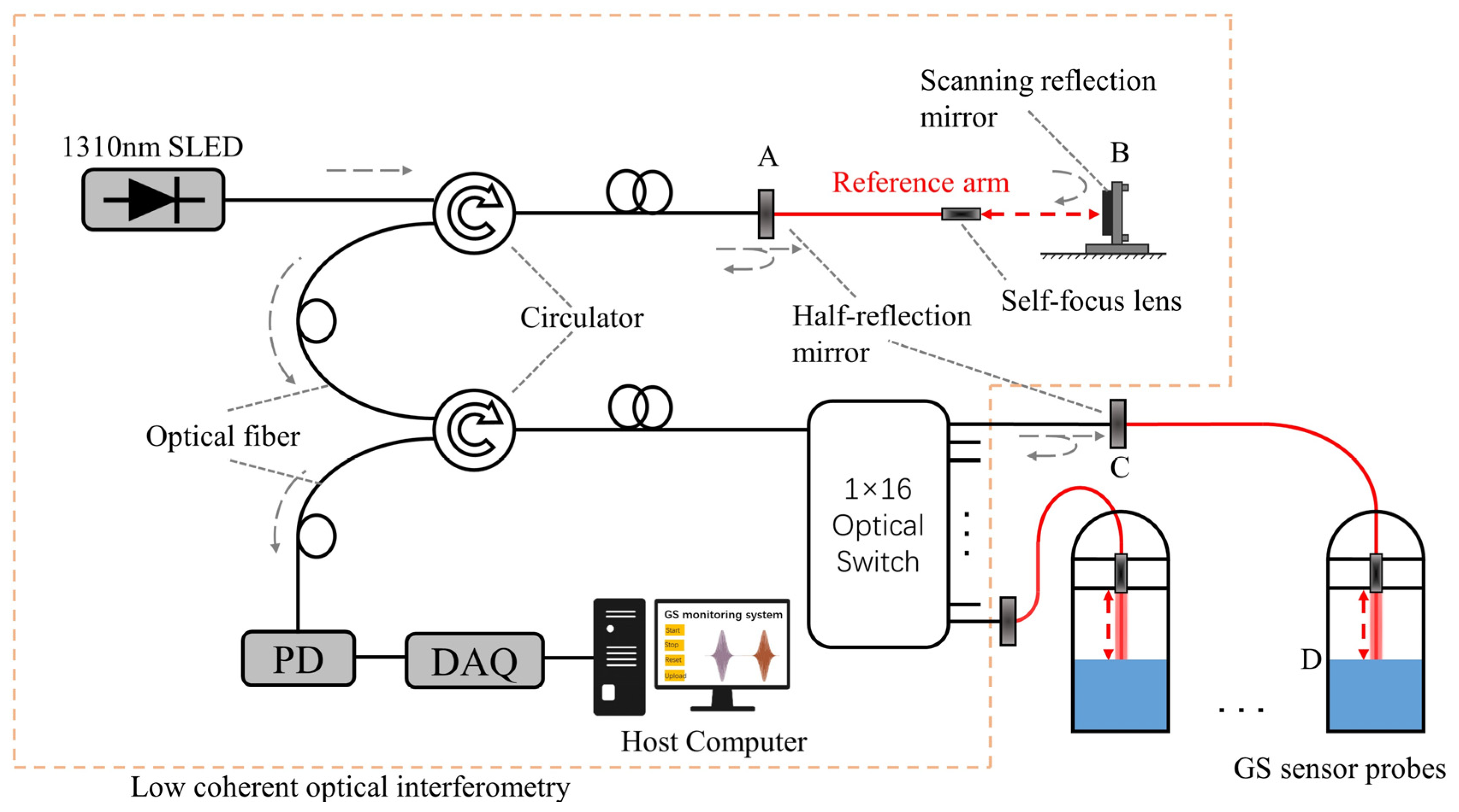
2.1. The Configuration of the Optical GS Sensor
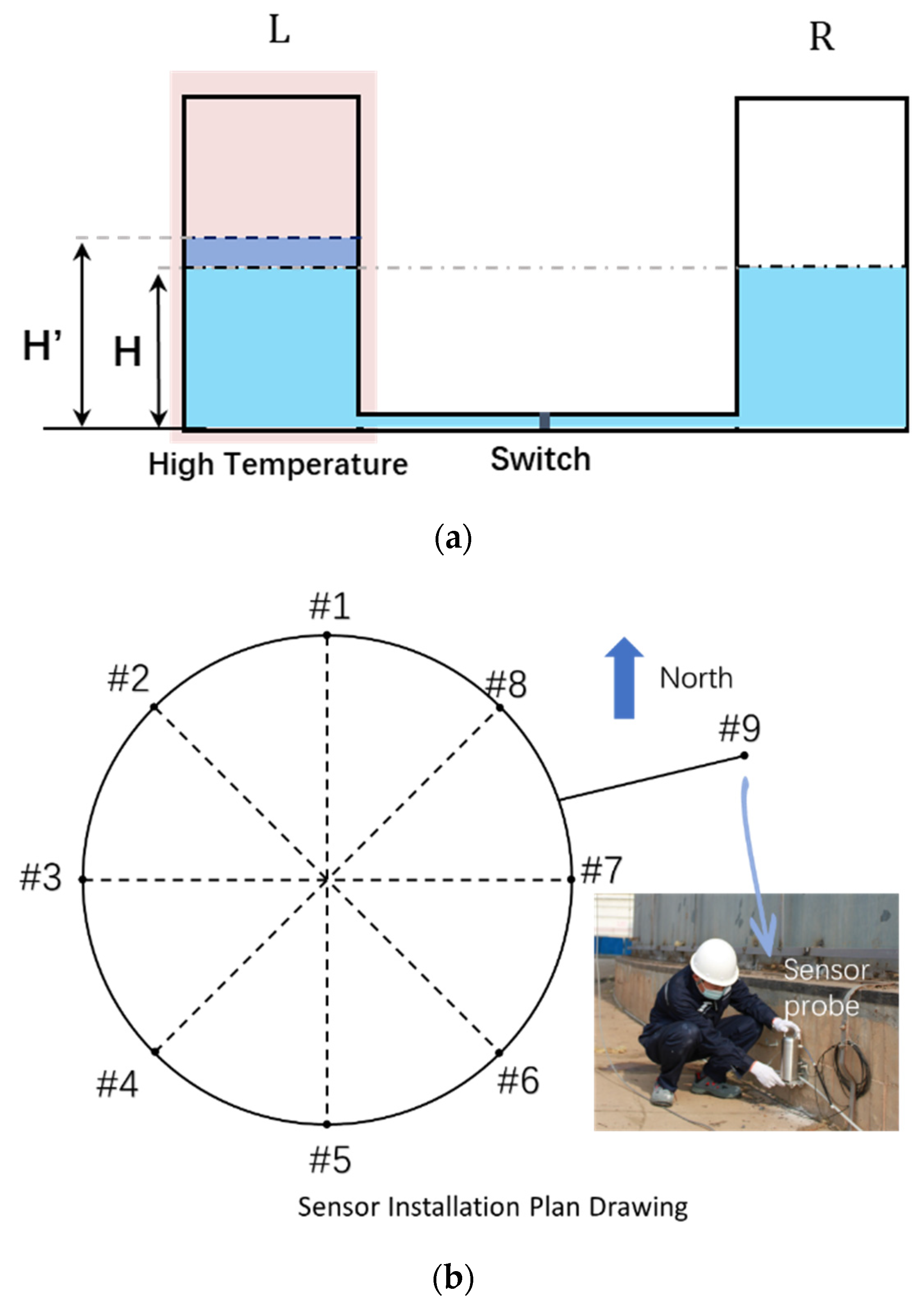
2.2. Source of Temperature Uncertainty
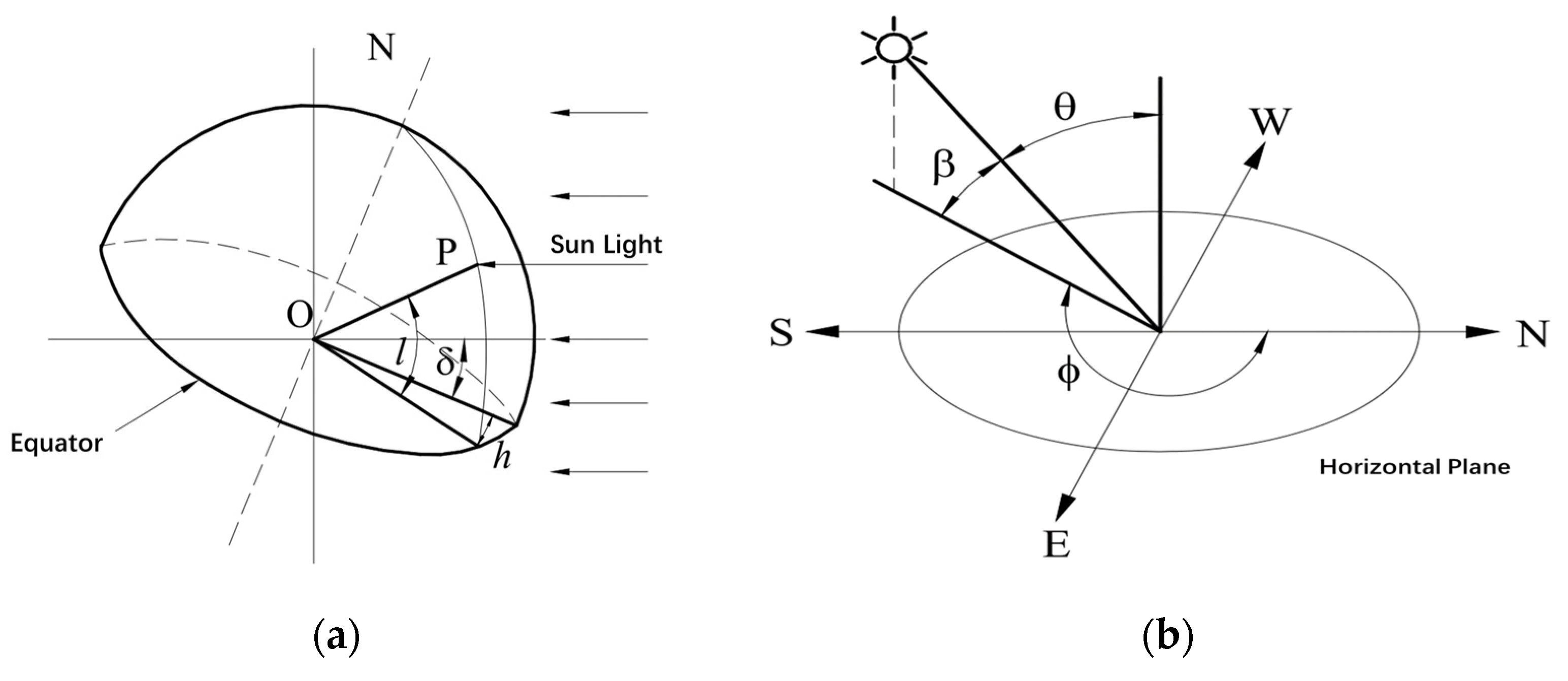
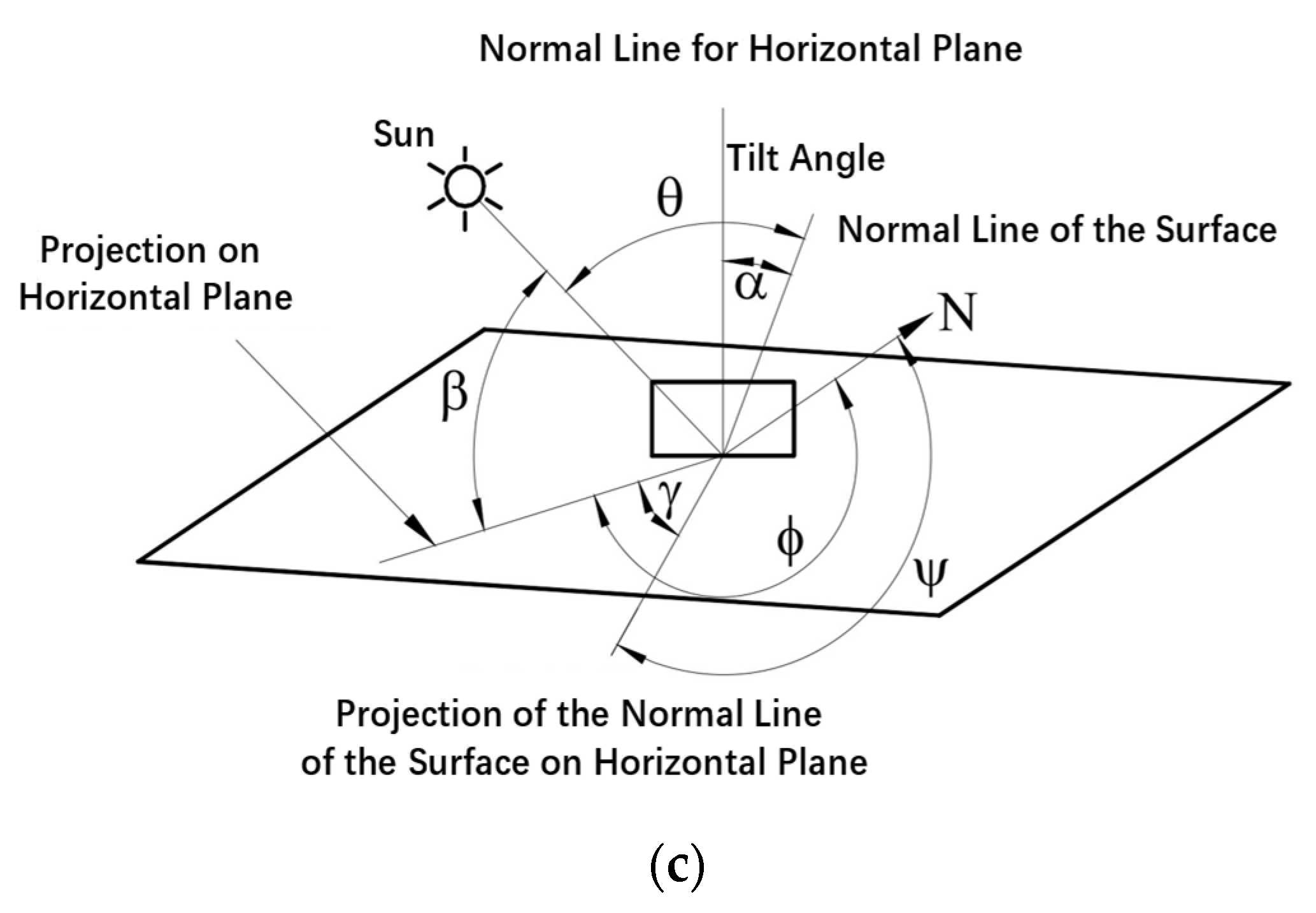
2.3. Solar Radiation Model
2.4. Heat Transfer Model
3. Algorithm Research
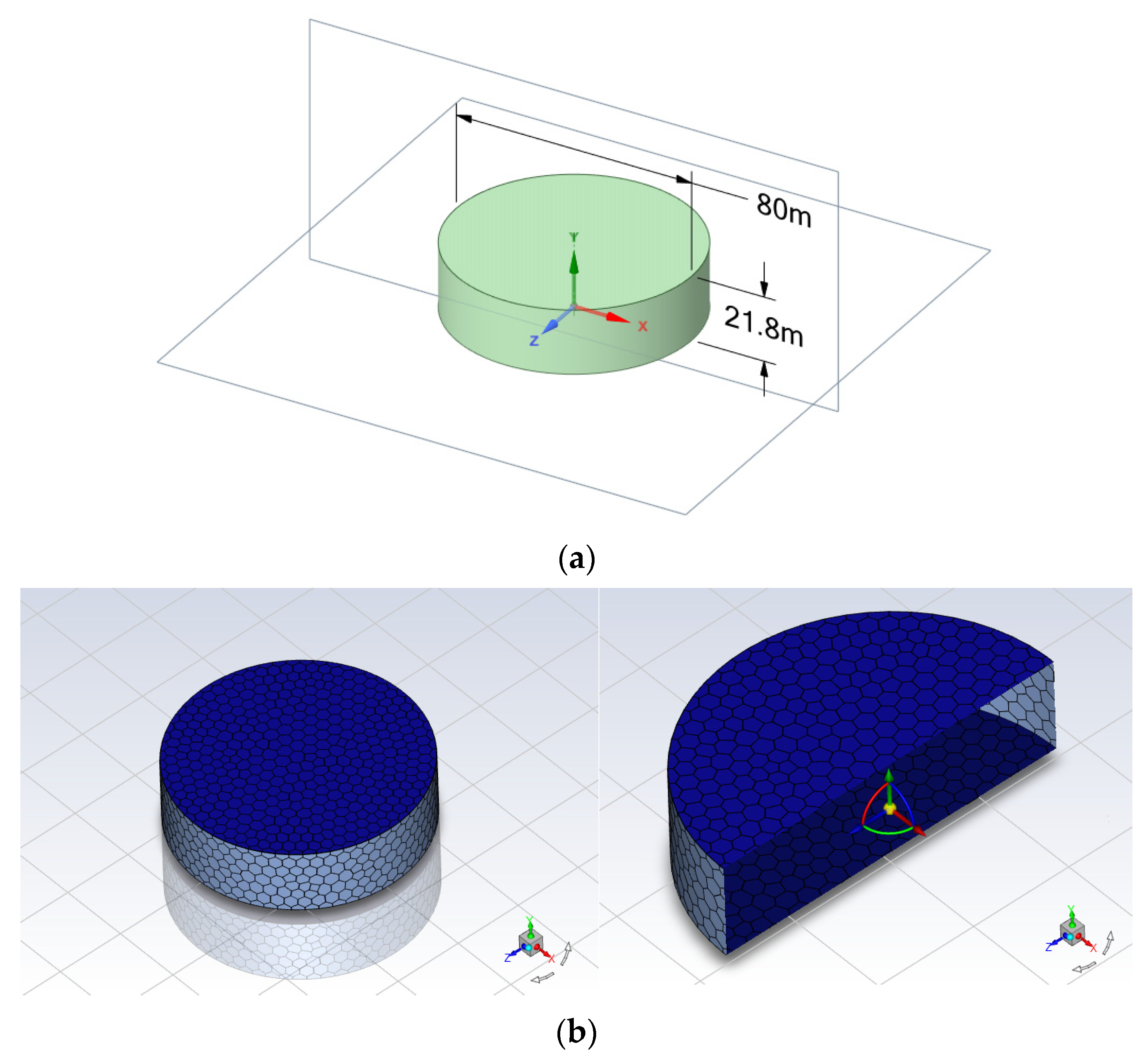
3.1. Finite Element Analysis on Temperature Field of Oil Tank
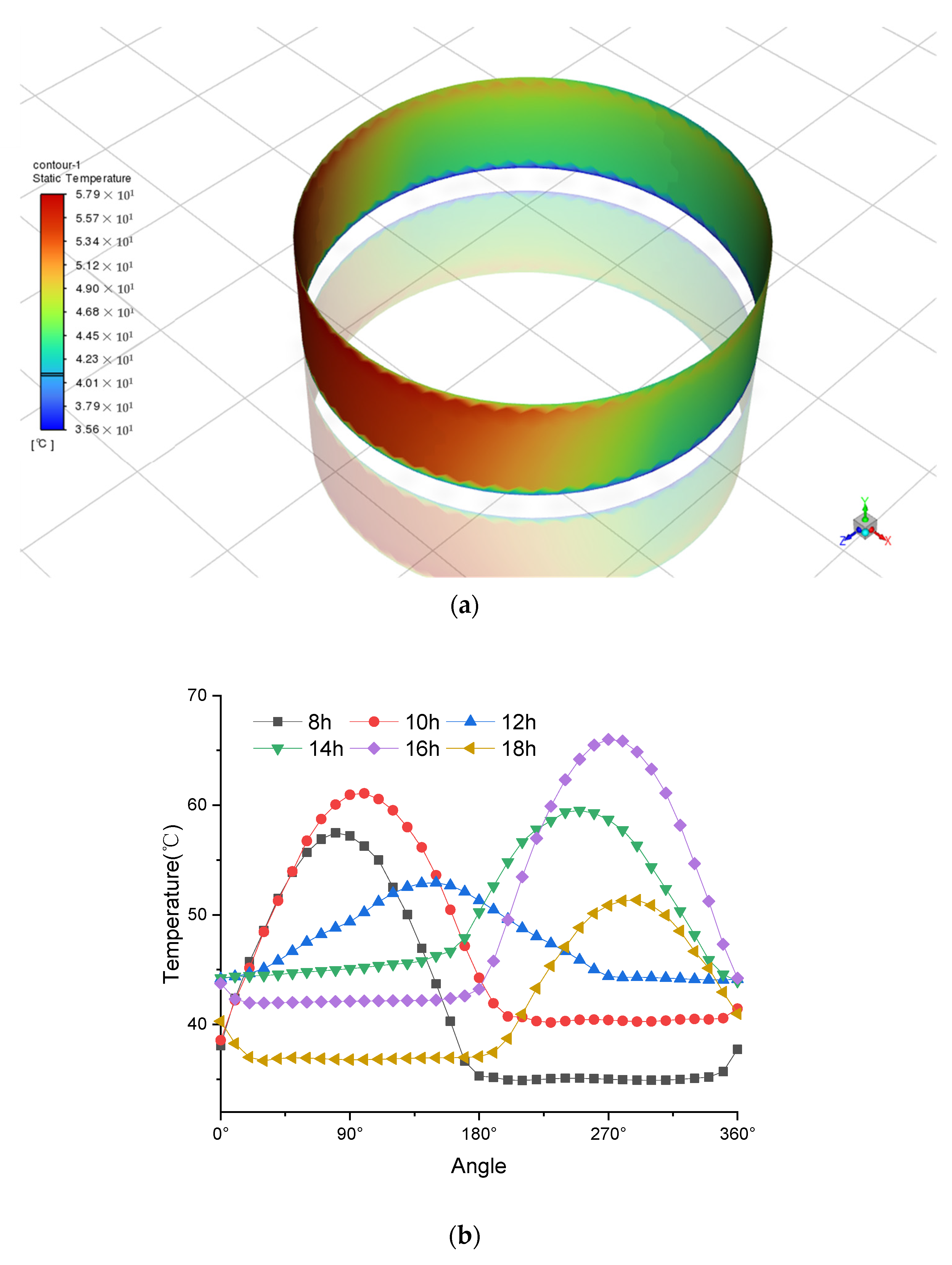
3.2. Result of Simulation
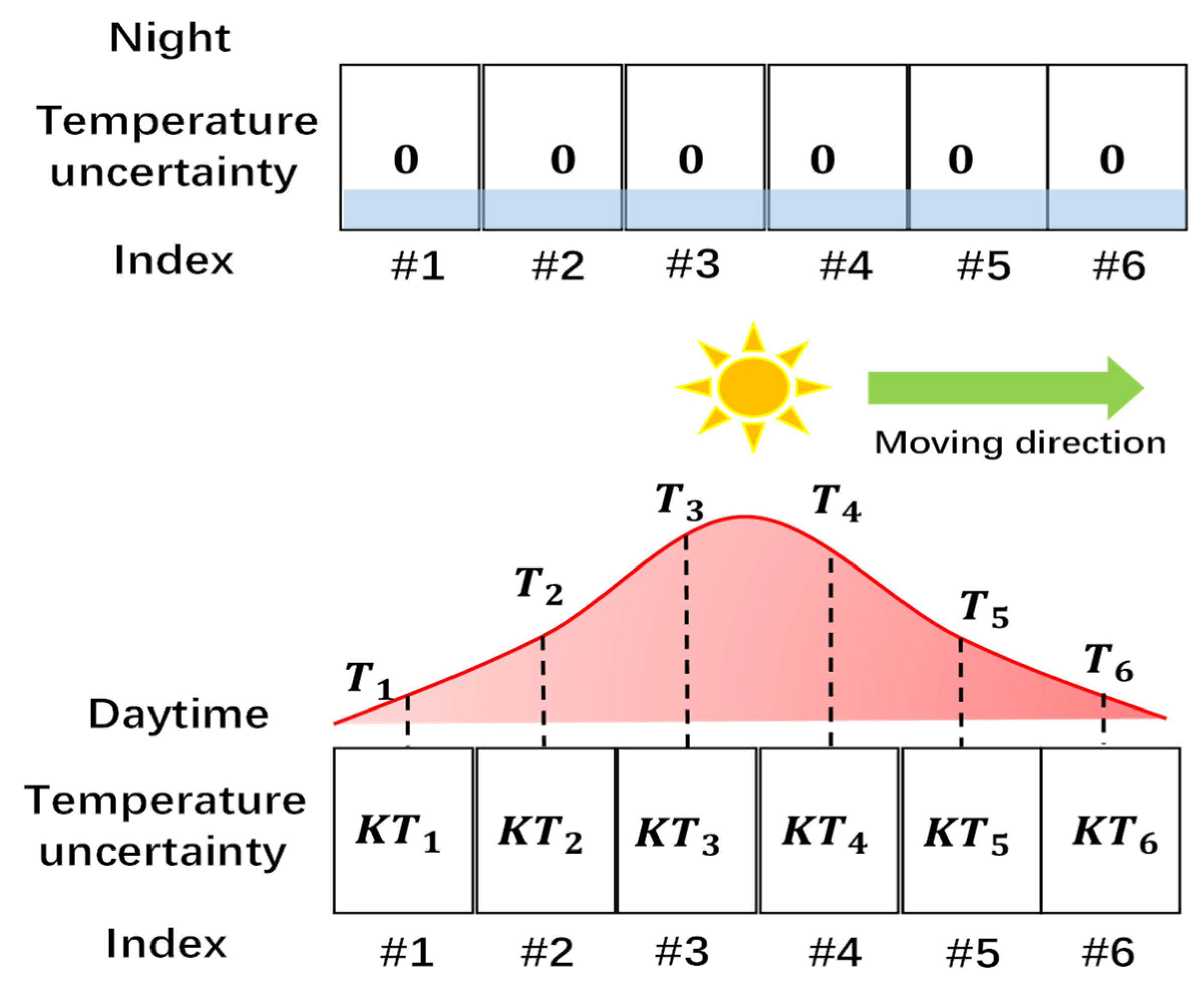
3.3. Temperature Uncertainty Reduction Algorithm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cirimello, P.G.; Otegui, J.L.; Ramajo, D.; Carfi, G. A major leak in a crude oil tank: Predictable and unexpected root causes. Eng. Fail. Anal. 2019, 100, 456–469. [Google Scholar] [CrossRef]
- Sun, B.; Ma, D.; Gao, L.; He, M.; Peng, Z.; Li, X.; Wang, W. Wind Buckling Analysis of a Large-Scale Open-Topped Steel Tank with Harmonic Settlement-Induced Imperfection. Buildings 2022, 12, 1973. [Google Scholar] [CrossRef]
- Bohra, H.; Guzey, S. Fitness-for-service of open-top storage tanks subjected to differential settlement. Eng. Struct. 2020, 225, 141–296. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, J.; Zhang, J.; Zhang, J.; Zheng, Y. Principle and application of in-situ monitoring system for ground displacement induced by shield tunnelling. Tunn. Undergr. Space Technol. 2021, 112, 103905. [Google Scholar] [CrossRef]
- Shaghaleh, H.; Hamoud, Y.A.; Sun, Q. Functionalized nanocellulose nanocomposite hydrogels for soil and water pollution prevention, remediation, and monitoring: A critical review on fabrication, application properties, and potential mechanisms. J. Environ. Chem. Eng. 2024, 12, 111892. [Google Scholar] [CrossRef]
- Ta, Q.T.H.; Tran, N.M.; Tri, N.N.; Sreedhar, A.; Noh, J.S. Highly surface-active Si-doped TiO2/Ti3C2Tx heterostructure for gas sensing and photodegradation of toxic matters. Chem. Eng. J. 2021, 425, 131437. [Google Scholar] [CrossRef]
- Brzeziński, K.; Ciężkowski, P.; Kwaśniewski, A.; Michalczyk, R.; Bak, S.; Jozefiak, K. Soil compaction monitoring via photogrammetric settlement measurement–Feasibility study. Measurement 2022, 205, 112164. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Zhang, Y.; Lin, Y. Research on Foundation Settlement Detection Method of Large Crude Oil Storage Tank. In Proceedings of the 2021 IEEE Far East NDT New Technology & Application Forum (FENDT), Kunming, China, 14–17 December 2021; pp. 134–139. [Google Scholar]
- Kamiński, W. The Concept of Accuracy Analysis of the Vertical Displacements Gained from the Hydrostatic Levelling Systems’ Measurements. Sensors 2021, 21, 4842. [Google Scholar] [CrossRef] [PubMed]
- Al-QaBas, I.A.; Farahan, M.; Fawzy, H. Surrounding Factors’ Influence on the Accuracy of the Digital Level and Total Station. J. Eng. Res-Kuwait. 2020, 8, 45–62. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, J.; Xi, W.; Zhao, P.; Qiao, X.; Deng, X.; Liu, Q. Analysis of tunnel displacement accuracy with total station. Measurement 2016, 83, 29–37. [Google Scholar] [CrossRef]
- Liu, T.; Liu, G.; Liu, G.; Lu, Z.; Wang, K.; Kiesewetter, D.; Jiang, T.; Victor, M.; Sun, C. Loading test on the oil tank ground settlement performance monitored by an optical parallel scheme. Appl. Opt. 2023, 62, 4691–4698. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Liu, G.; Jiang, T.; Li, H.; Sun, C. Curve Similarity Analysis for Reducing the Temperature Uncertainty of Optical Sensor for Oil-Tank Ground Settlement Monitoring. Sensors 2023, 23, 8287. [Google Scholar] [CrossRef] [PubMed]
- Qi, W.; Xing, X.; Kai, Z.; Guoxing, C. A Modified Model for the Temperature Effect-Induced Error in Hydrostatic Leveling Systems. IEEE Sens. J. 2022, 22, 9473–9482. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Hecht, E. Principles of Optics Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Phys. Today 2000, 53, 77–78. [Google Scholar] [CrossRef]
- McQuiston, F.C.; Parker, J.D.; Spitler, J.D.; Taherian, H. Heating, Ventilating, and Air Conditioning: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Wang, X.; Huang, X.; Kwon, O.-S.; Bentz, E.; Tcherner, J.; DeMerchant, M.; Moland, M. Evaluation of the thermal strain of an NPP containment structure during leakage rate tests. Eng. Struct. 2019, 201, 109761. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Guermoui, M.; Melgani, F.; Gairaa, K.; Mekhalfi, M.L. A comprehensive review of hybrid models for solar radiation forecasting. J. Clean. Prod. 2020, 258, 120357. [Google Scholar] [CrossRef]
- Wong, L.T.; Chow, W.K. Solar radiation model. Appl. Energy 2001, 69, 191–224. [Google Scholar] [CrossRef]
- Han, J.C.; Wright, L.M. Analytical Heat Transfer; Taylor & Francis: Abingdon, UK, 2022. [Google Scholar]
- DiLaura, D.L.; Burkett, R.J.; Clark, F.; Fink, W.L.; Gillette, G.; Goodbar, I. Recommended practice for the calculation of daylight availability. J. Illum. Eng. Soc. 1984, 13, 381–392. [Google Scholar] [CrossRef]
- Matsson, J.E. An Introduction to ANSYS Fluent 2022; Sdc Publications: Mission, KS, USA, 2022. [Google Scholar]

| Thermal Property | Value | Unit |
|---|---|---|
| Conductivity, | 16.27 | |
| Density, | 8030 | |
| Specific heat, | 502.48 | |
| Inter-emissivity, | 0.95 | - |
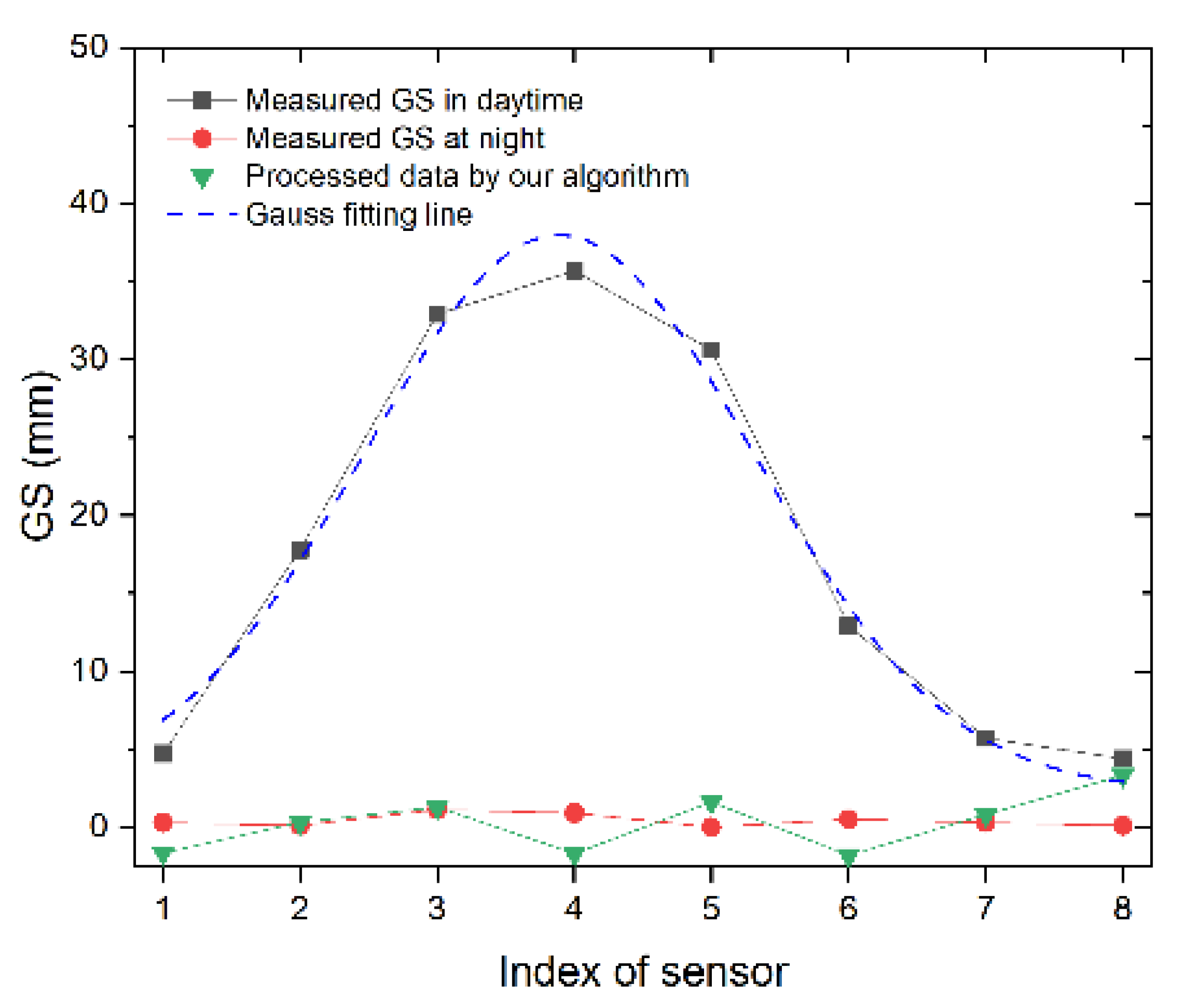
| Index of Sensor | GS in Daytime (mm) | GS at Night (mm) | Processed Data by Algorithm (mm) | Difference between Daytime and Night (mm) | Difference between Processed Data and Night (mm) |
|---|---|---|---|---|---|
| #1 | 4.70 | 0.30 | −1.65 | 4.40 | 1.95 |
| #2 | 17.80 | 0.10 | 0.30 | 17.70 | 0.20 |
| #3 | 32.90 | 1.13 | 1.29 | 31.77 | 0.16 |
| #4 | 35.70 | 0.90 | −1.69 | 34.80 | 2.59 |
| #5 | 30.60 | 0.00 | 1.62 | 30.60 | 1.62 |
| #6 | 12.90 | 0.50 | −1.81 | 12.40 | 2.31 |
| #7 | 5.70 | 0.30 | 0.81 | 5.40 | 0.51 |
| #8 | 4.40 | 0.10 | 3.33 | 4.30 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Jiang, T.; Liu, G.; Sun, C. Temperature Uncertainty Reduction Algorithm Based on Temperature Distribution Prior for Optical Sensors in Oil Tank Ground Settlement Monitoring. Sensors 2024, 24, 2341. https://doi.org/10.3390/s24072341
Liu T, Jiang T, Liu G, Sun C. Temperature Uncertainty Reduction Algorithm Based on Temperature Distribution Prior for Optical Sensors in Oil Tank Ground Settlement Monitoring. Sensors. 2024; 24(7):2341. https://doi.org/10.3390/s24072341
Chicago/Turabian StyleLiu, Tao, Tao Jiang, Gang Liu, and Changsen Sun. 2024. "Temperature Uncertainty Reduction Algorithm Based on Temperature Distribution Prior for Optical Sensors in Oil Tank Ground Settlement Monitoring" Sensors 24, no. 7: 2341. https://doi.org/10.3390/s24072341
APA StyleLiu, T., Jiang, T., Liu, G., & Sun, C. (2024). Temperature Uncertainty Reduction Algorithm Based on Temperature Distribution Prior for Optical Sensors in Oil Tank Ground Settlement Monitoring. Sensors, 24(7), 2341. https://doi.org/10.3390/s24072341





