Chromatic Aberration Correction in Harmonic Diffractive Lenses Based on Compressed Sensing Encoding Imaging
Abstract
1. Introduction
2. Diffractive Lens Imaging Model
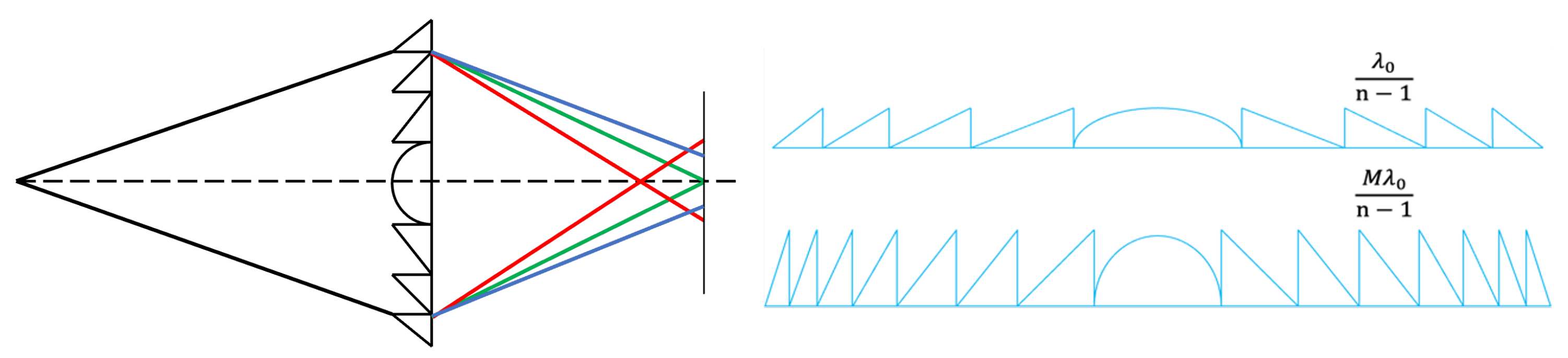
3. Harmonic Diffractive Lens Design
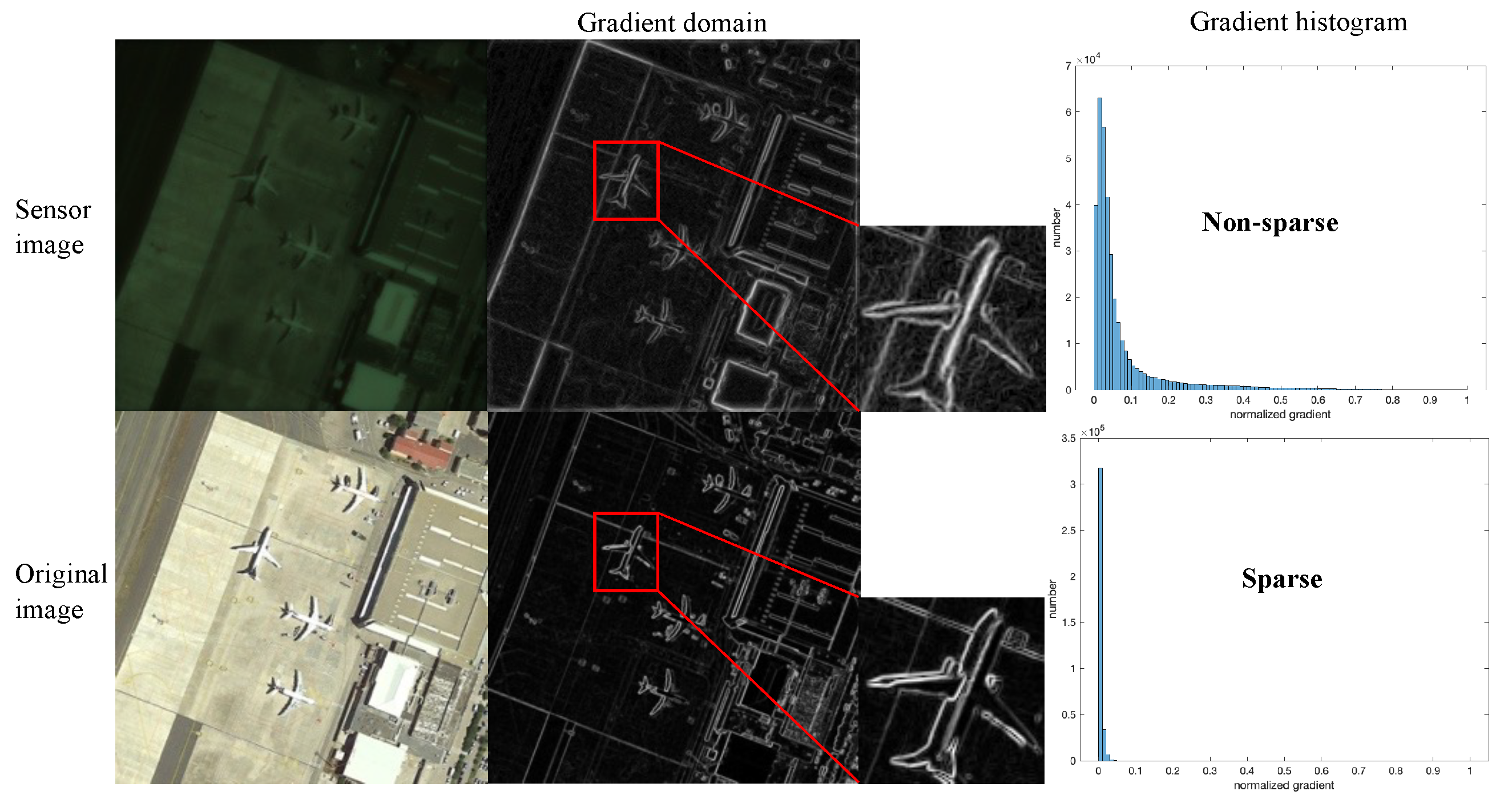
4. Compressive Sensing
5. Algorithm Recovery Model
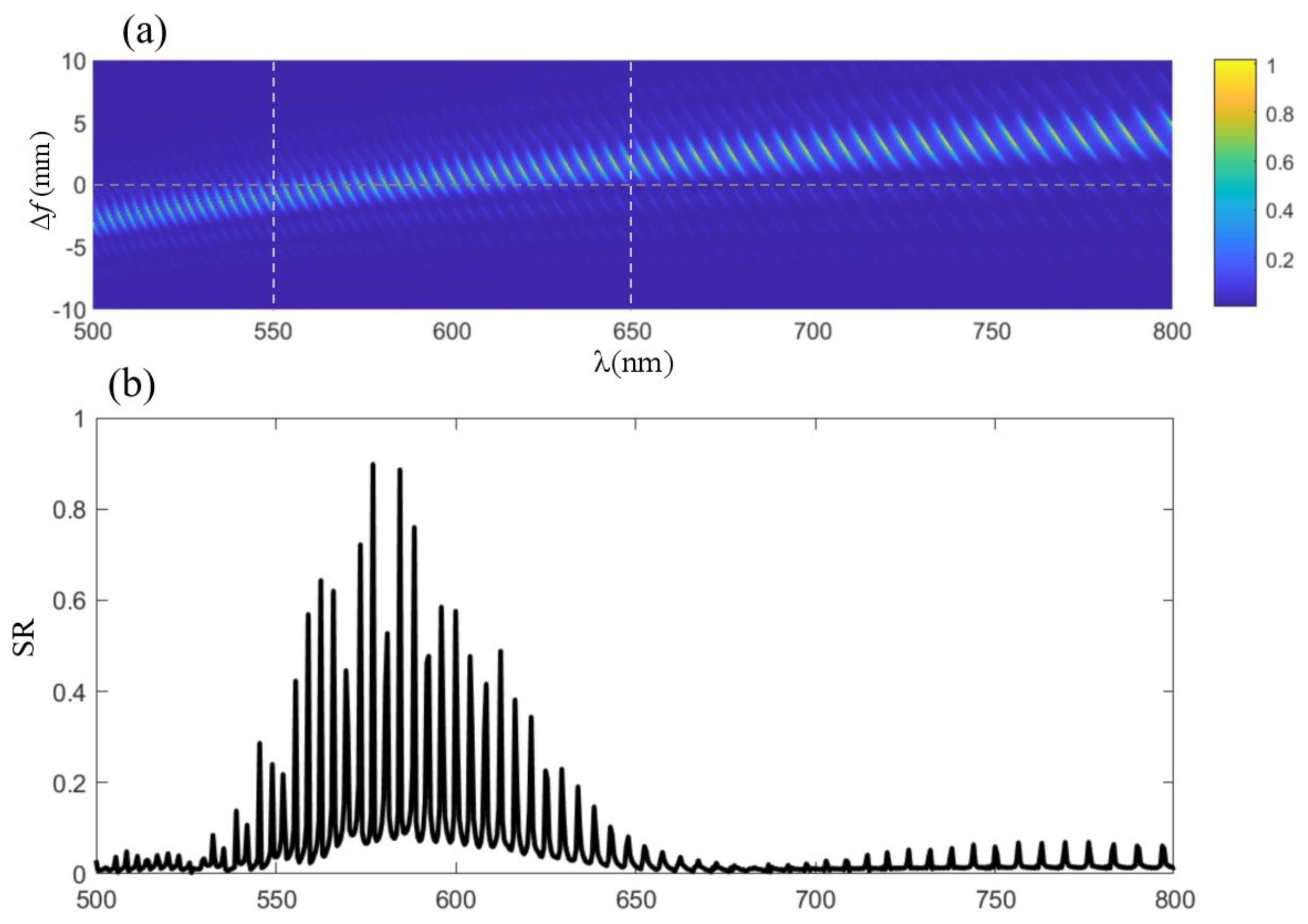
6. Result
7. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meyer-Arendt, J.R. Introduction to Classical and Modern Optics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Soifer, V.A.; Doskolovich, L.; Golovashkin, D.; Kazanskiy, N.; Kharitonov, S.; Khonina, S.; Kotlyar, V.; Pavelyev, V.; Skidanov, R.; Solovyev, V.; et al. Methods for Computer Design of Diffractive Optical Elements; John Willey & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Cheng, X.; Xie, W.; Bai, Y.; Jia, X.; Xing, T. Athermal design for infrared refractive, diffractive, reflective hybrid optical system. In Proceedings of the 7th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes, Harbin, China, 26–29 April 2014; SPIE: Bellingham, WT, USA, 2014; Volume 9280, pp. 292–298. [Google Scholar]
- Suo, J.; Ji, X.; Dai, Q. An overview of computational photography. Sci. China Inf. Sci. 2012, 55, 1229–1248. [Google Scholar] [CrossRef]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhong, J. Three-dimensional single-pixel imaging with far fewer measurements than effective image pixels. Opt. Lett. 2016, 41, 2497–2500. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiao, S.; Yao, M.; Li, X.; Zhong, J. Secured single-pixel broadcast imaging. Opt. Express 2018, 26, 14578–14591. [Google Scholar] [CrossRef]
- Batlle, J.; Mouaddib, E.; Salvi, J. Recent progress in coded structured light as a technique to solve the correspondence problem: A survey. Pattern Recognit. 1998, 31, 963–982. [Google Scholar] [CrossRef]
- Mudanyali, O.; Tseng, D.; Oh, C.; Isikman, S.O.; Sencan, I.; Bishara, W.; Oztoprak, C.; Seo, S.; Khademhosseini, B.; Ozcan, A. Compact, light-weight and cost-effective microscope based on lensless incoherent holography for telemedicine applications. Lab Chip 2010, 10, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, H.; Zhang, W.; Jin, G.; Cao, L.; Barbastathis, G. Single-shot lensless imaging with fresnel zone aperture and incoherent illumination. Light. Sci. Appl. 2020, 9, 53. [Google Scholar] [CrossRef]
- Tian, L.; Li, X.; Ramchandran, K.; Waller, L. Multiplexed coded illumination for Fourier Ptychography with an LED array microscope. Biomed. Opt. Express 2014, 5, 2376–2389. [Google Scholar] [CrossRef]
- Yue, J.; Han, J.; Li, L.; Bai, L. Denoising analysis of spatial pixel multiplex coded spectrometer with Hadamard H-matrix. Opt. Commun. 2018, 407, 355–360. [Google Scholar] [CrossRef]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Brady, D.J.; Gehm, M.E. Compressive imaging spectrometers using coded apertures. In Proceedings of the Visual Information Processing XV, Orlando (Kissimmee), FL, USA, 17–21 April 2006; SPIE: Bellingham, WT, USA, 2006; Volume 6246, pp. 80–88. [Google Scholar]
- Peng, Y.; Fu, Q.; Heide, F.; Heidrich, W. The diffractive achromat full spectrum computational imaging with diffractive optics. In Proceedings of the SIGGRAPH ASIA 2016 Virtual Reality Meets Physical Reality: Modelling and Simulating Virtual Humans and Environments, Macau, China, 5–8 December 2016; pp. 1–2. [Google Scholar]
- Dun, X.; Ikoma, H.; Wetzstein, G.; Wang, Z.; Cheng, X.; Peng, Y. Learned rotationally symmetric diffractive achromat for full-spectrum computational imaging. Optica 2020, 7, 913–922. [Google Scholar] [CrossRef]
- Nikonorov, A.; Skidanov, R.; Fursov, V.; Petrov, M.; Bibikov, S.; Yuzifovich, Y. Fresnel lens imaging with post-capture image processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 33–41. [Google Scholar]
- Sitzmann, V.; Diamond, S.; Peng, Y.; Dun, X.; Boyd, S.; Heidrich, W.; Heide, F.; Wetzstein, G. End-to-end optimization of optics and image processing for achromatic extended depth of field and super-resolution imaging. ACM Trans. Graph. (TOG) 2018, 37, 1–13. [Google Scholar] [CrossRef]
- Jeon, D.S.; Baek, S.H.; Yi, S.; Fu, Q.; Dun, X.; Heidrich, W.; Kim, M.H. Compact snapshot hyperspectral imaging with diffracted rotation. ACM Trans. Graph. 2019, 38, 117. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.; Song, W.; Zhang, L.; Xiong, Z.; Huang, H. Quantization-aware Deep Optics for Diffractive Snapshot Hyperspectral Imaging Supplementary Material. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Wu, Y.; Boominathan, V.; Chen, H.; Sankaranarayanan, A.; Veeraraghavan, A. Phasecam3d—learning phase masks for passive single view depth estimation. In Proceedings of the 2019 IEEE International Conference on Computational Photography (ICCP), Tokyo, Japan, 15–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–12. [Google Scholar]
- Chang, J.; Wetzstein, G. Deep optics for monocular depth estimation and 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10193–10202. [Google Scholar]
- Sun, Q.; Wang, C.; Qiang, F.; Xiong, D.; Wolfgang, H. End-to-end complex lens design with differentiable ray tracing. ACM Trans. Graph 2021, 40, 1–13. [Google Scholar]
- Reddy, G.S.; Nanmaran, R.; Paramasivam, G. Image Restoration Using Lucy Richardson Algorithm for Deblurring Images with Improved PSNR, SSIM, NC in Comparison with Wiener Filter. Alinteri J. Agric. Sci. 2021, 36, 642. [Google Scholar] [CrossRef]
- Sun, T.; Peng, Y.; Heidrich, W. Revisiting cross-channel information transfer for chromatic aberration correction. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3248–3256. [Google Scholar]
- Apai, D.; Milster, T.D.; Kim, D.; Kim, Y.; Schneider, G.; Rackham, B.V.; Arenberg, J.W.; Choi, H.J.; Esparza, M.A.; Wang, Z.; et al. Nautilus Space Observatory: A very large aperture space telescope constellation enabled by scalable optical manufacturing technologies. In Proceedings of the Optical Engineering + Applications, Kunming, China, 11–13 November 2022. [Google Scholar]
- Nikonorov, A.V.; Petrov, M.V.; Bibikov, S.A.; Yakimov, P.Y.; Kutikova, V.V.; Yuzifovich, Y.V.; Morozov, A.A.; Skidanov, R.V.; Kazanskiy, N.L. Toward Ultralightweight Remote Sensing with Harmonic Lenses and Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3338–3348. [Google Scholar] [CrossRef]
- Wang, Z.; Kim, Y.; Milster, T.D. High-harmonic diffractive lens color compensation. Appl. Opt. 2021, 60, D73–D82. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Mohammad, N.; Meem, M.; Shen, B.; Wang, P.; Menon, R. Broadband imaging with one planar diffractive lens. Sci. Rep. 2018, 8, 2799. [Google Scholar] [CrossRef]
- Meem, M.; Banerji, S.; Pies, C.; Oberbiermann, T.; Majumder, A.; Sensale-Rodriguez, B.; Menon, R. Large-area, high-numerical-aperture multi-level diffractive lens via inverse design. Optica 2020, 7, 252–253. [Google Scholar] [CrossRef]
- Evdokimova, V.V.; Podlipnov, V.V.; Ivliev, N.A.; Petrov, M.V.; Ganchevskaya, S.V.; Fursov, V.A.; Yuzifovich, Y.; Stepanenko, S.O.; Kazanskiy, N.L.; Nikonorov, A.V.; et al. Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction. Sensors 2023, 23, 415. [Google Scholar] [CrossRef] [PubMed]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, J.; Zhao, X.; Zhong, S.; Zhang, T.; Fan, B. Chromatic Aberration Correction in Harmonic Diffractive Lenses Based on Compressed Sensing Encoding Imaging. Sensors 2024, 24, 2471. https://doi.org/10.3390/s24082471
Chan J, Zhao X, Zhong S, Zhang T, Fan B. Chromatic Aberration Correction in Harmonic Diffractive Lenses Based on Compressed Sensing Encoding Imaging. Sensors. 2024; 24(8):2471. https://doi.org/10.3390/s24082471
Chicago/Turabian StyleChan, Jianying, Xijun Zhao, Shuo Zhong, Tao Zhang, and Bin Fan. 2024. "Chromatic Aberration Correction in Harmonic Diffractive Lenses Based on Compressed Sensing Encoding Imaging" Sensors 24, no. 8: 2471. https://doi.org/10.3390/s24082471
APA StyleChan, J., Zhao, X., Zhong, S., Zhang, T., & Fan, B. (2024). Chromatic Aberration Correction in Harmonic Diffractive Lenses Based on Compressed Sensing Encoding Imaging. Sensors, 24(8), 2471. https://doi.org/10.3390/s24082471




