A Laboratory Machine Verifying the Operation of a Hydraulic Rope Equalizer with Tensometric Sensors
Abstract
:1. Introduction
2. Materials and Methods
3. Results
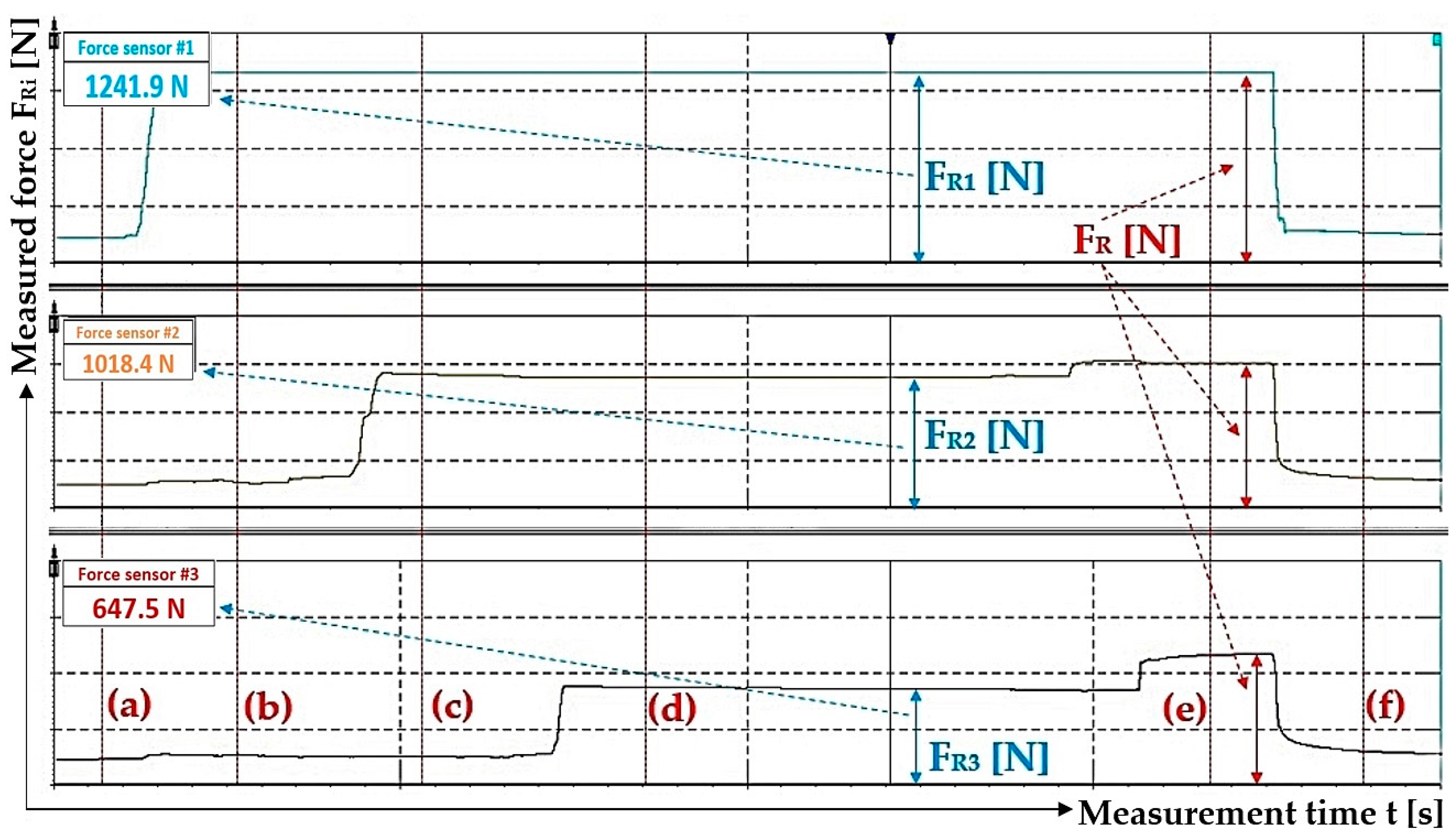
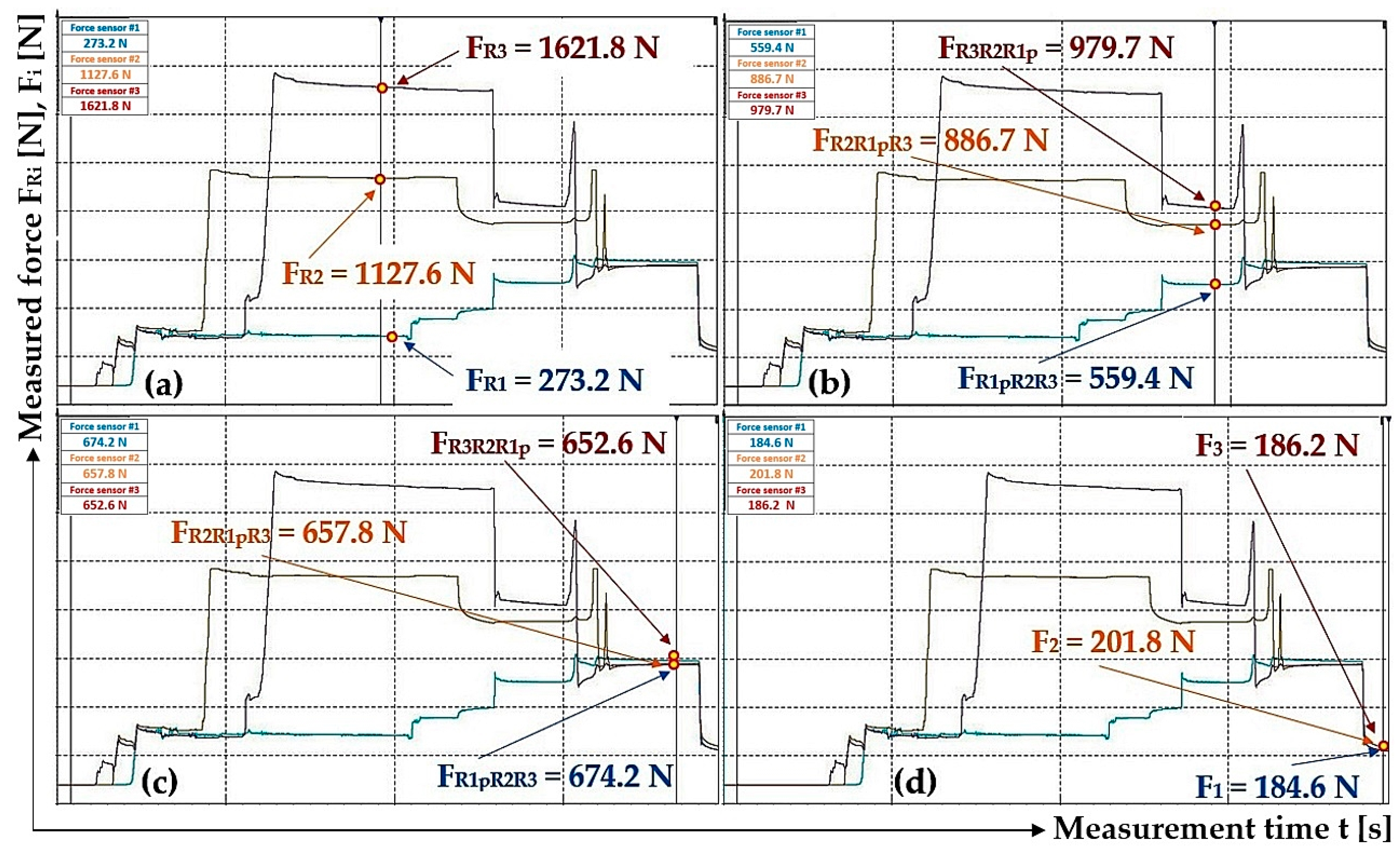
3.1. The Magnitude of the Resulting Hydraulic Oil Pressure Is Affected by the Different Values of the Hydraulic Oil Pressures in the Hydraulic Cylinders and the Pressure in the Supply Pipe

| n | FR1 | FR2 | FR3 | pp1 | pp2 | pp3 = pp |
|---|---|---|---|---|---|---|
| [N] | [106·Pa] | |||||
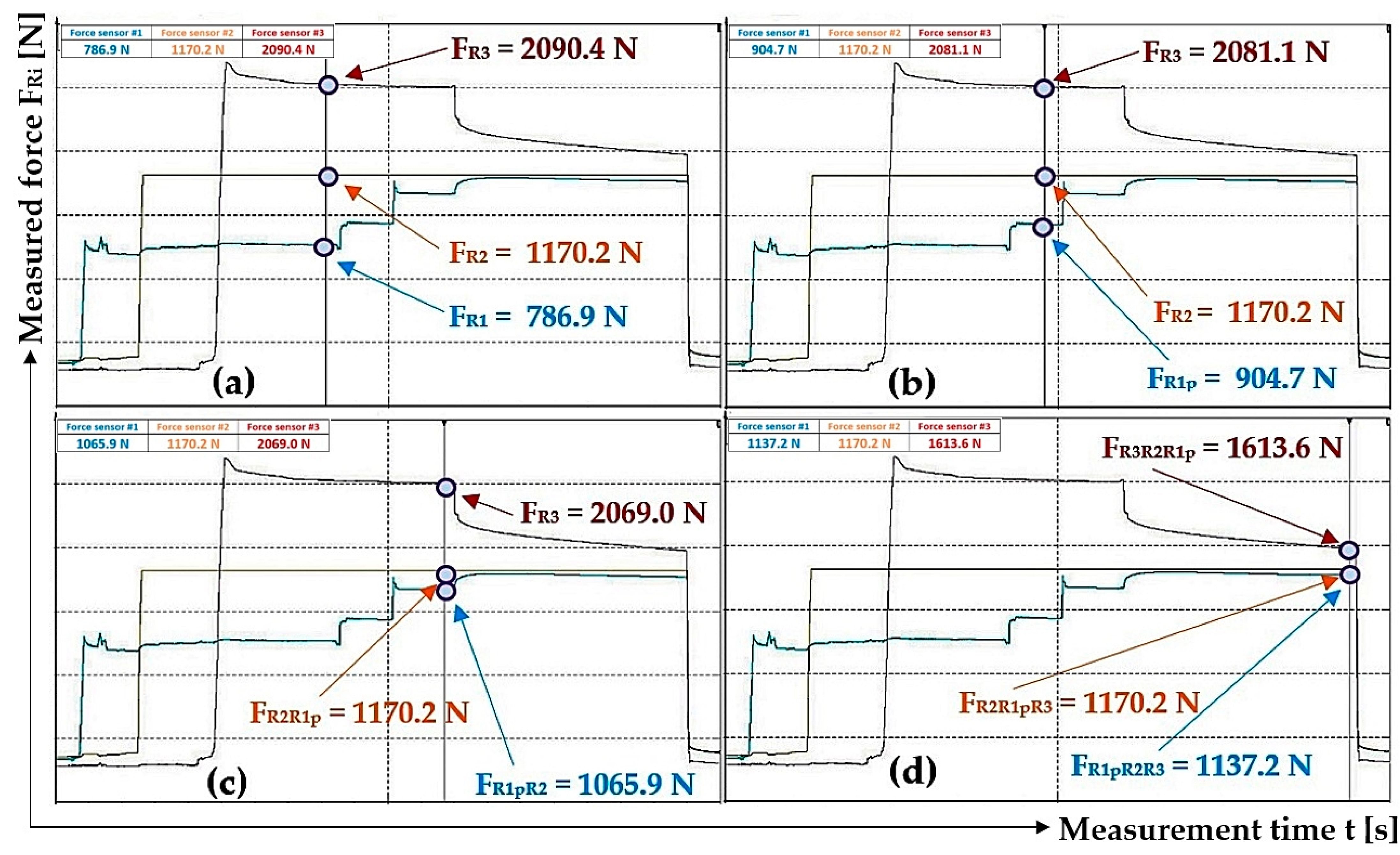
| 1 | 786.9 1 | 1170.2 1 | 2090.4 1 | 1.61 2 | 2.39 2 | 4.27 2 |
| 2 | 1158.7 | 531.9 | 2127.8 | 2.36 3 | 1.09 3 | 4.34 3 |
| 3 | 696.1 | 1170.2 | 2203.5 | 1.42 | 2.39 | 4.50 |
| n | FR1p | FR1pR2 | FR2R1p | FR1pR2R3 | FR2R1pR3 | FR3R2R1p | pp3p2p1p = ppr |
|---|---|---|---|---|---|---|---|
| [N] | [106·Pa] | ||||||
| 1 | 904.7 1 | 1065.9 2 | 1170.2 2 | 1137.2 3 | 1170.2 3 | 1613.6 3 | 3.29 |
| 2 | 1158.7 | 1158.7 | 806.1 | 1158.7 | 1009.4 | 1404.1 | 2.86 |
| 3 | 878.9 | 1170.2 | 2175.5 | 1052.5 | 1170.2 | 1623.7 | 3.31 |
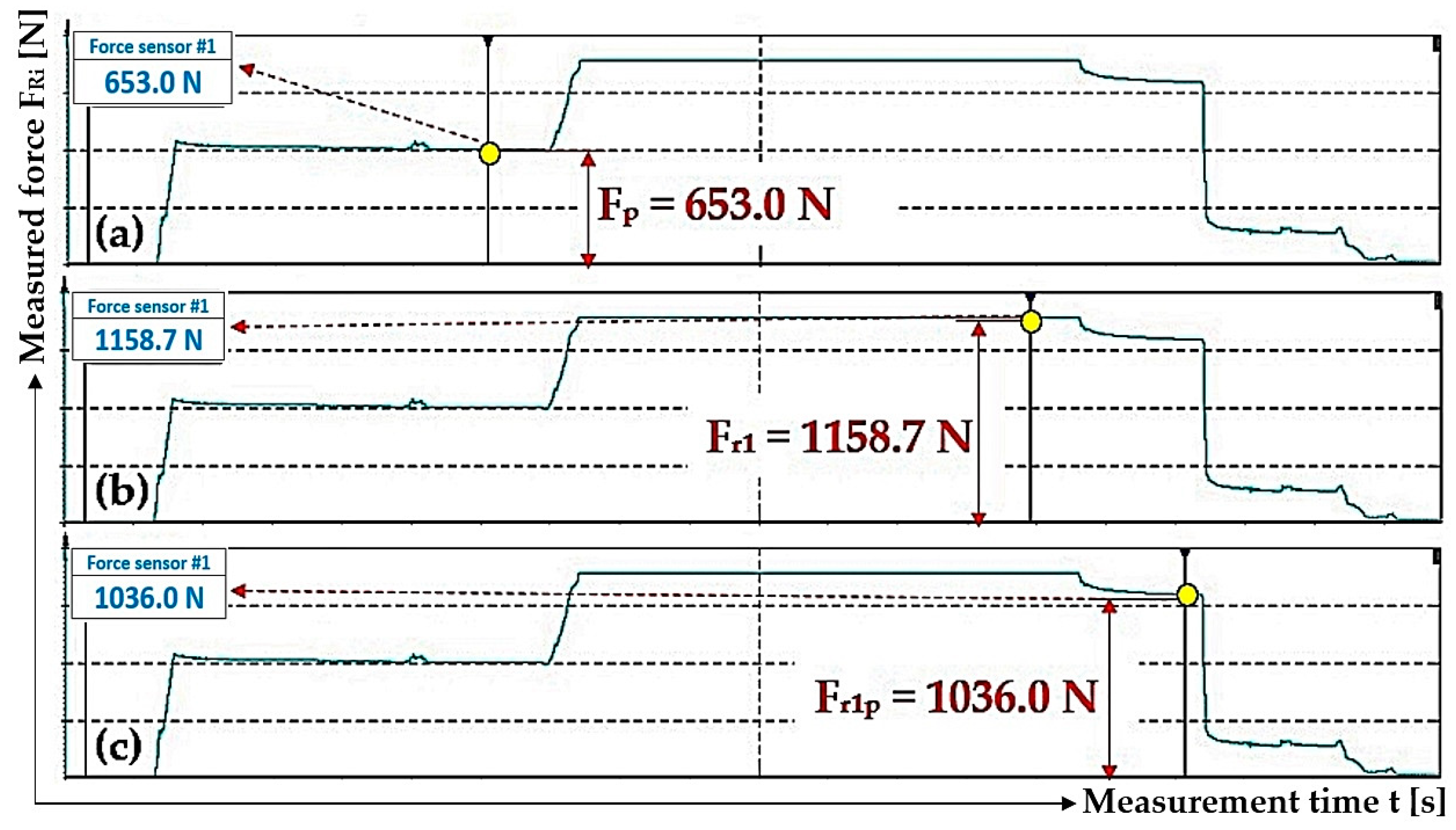
3.2. The Magnitude of the Resulting Pressure of the Hydraulic Oil Affected by the Change in the Different Magnitudes of the Pulling Forces in the Ropes
| n | Fp1 | Fp2 | Fp3 | FR1 | FR2 | FR3 | pp | pp1 | pp2 | pp3 |
|---|---|---|---|---|---|---|---|---|---|---|
| [N] | [MPa] | |||||||||
| 1 | 285.9 1 | 318.6 1 | 297.2 1 | 642.3 2 | 1170.2 2 | 1921.5 2 | 0.58 | 1.31 | 2.39 | 3.92 |
| 2 | 606.3 | 615.6 | 618.0 | 1034.5 | 1170.2 | 1677.8 | 2.24 | 1.26 | 2.39 | 3.42 |
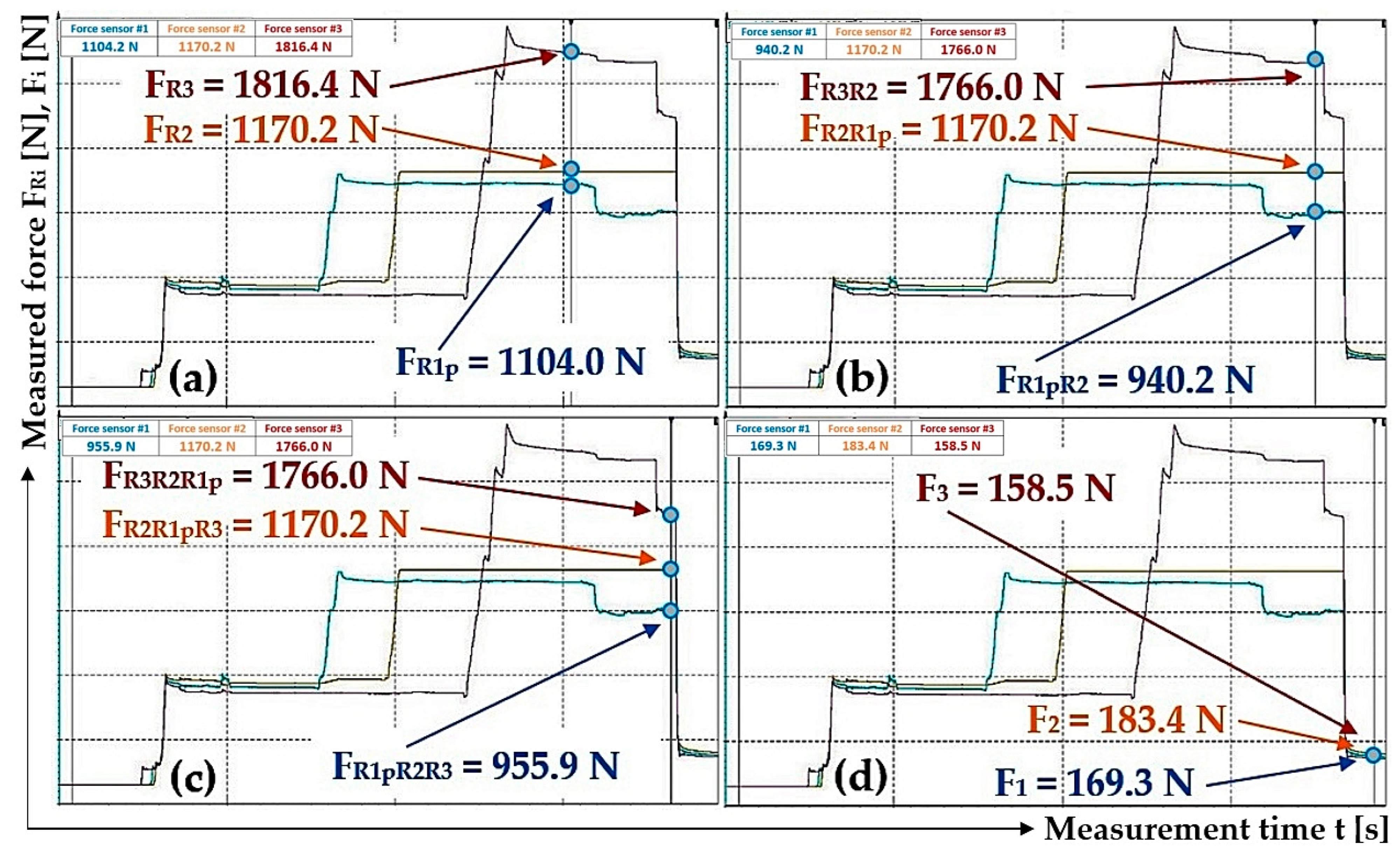
| 3 | 534.5 | 556.5 | 503.4 | 1104.0 | 1170.2 | 1816.4 | 1.09 | 2.25 | 2.39 | 3.71 |

4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DIN EN 81-20; Safety Rules for the Construction and Installation of Lifts—Lifts for the Transport of Persons and Goods—Part 20: Passenger and Goods Passenger Lifts (In Czech: Bezpečnostní Předpisy pro Konstrukci a Montáž Výtahů—Výtahy pro Dopravu Osob a Nákladů—Část 20: Výtahy pro Dopravu Osob a Osob a Nákladů). European Standard: Brussels, Belgium, 2020. Available online: https://www.technickenormy.cz/din-en-81-20-safety-rules-for-the-construction-and-installation-of-lifts-lifts-for-the-transport-of-persons-and-goods-part-20-passenger-and-goods-passenger-lifts-7/ (accessed on 1 June 2020).
- EN 12385-5:2002; Steel Wire Ropes—Safety—Part 5: Stranded Ropes for Lifts (In Czech: Ocelová Drátěná Lana—Bezpečnost—Část 5: Pramenná Lana pro Výtahy). European Standard: Brussels, Belgium, 2021. Available online: https://www.technickenormy.cz/csn-en-12385-5-ocelova-dratena-lana-bezpecnost-cast-5-pramenna-lana-pro-vytahy-3/ (accessed on 1 November 2021).
- Směrnice Evropského Parlamentu a Rady 2000/9/ES. Available online: https://eur-lex.europa.eu/legal-content/CS/TXT/PDF/?uri=CELEX:32000L0009 (accessed on 20 March 2020).
- Zákon č. 22/1997 Sb.: Zákon o Technických Požadavcích na Výrobky a o Změně a Doplnění Některých Zákonů. Available online: https://www.zakonyprolidi.cz/cs/1997-22 (accessed on 27 February 1997).
- Nařízení vlády č. 122/2016 Sb.: Nařízení Vlády o Posuzování Shody Výtahů a Jejich Bezpečnostních Komponent. Available online: https://www.zakonyprolidi.cz/cs/2016-122 (accessed on 18 April 2016).
- Toralkar, S. Traction in Elevators; Elevator World India: Bangalore, India, 2009; pp. 84–88. [Google Scholar]
- Yuda, S.M.; Pane, M.; Elyes, F. Design of Top Traction Elevator in Building 6 Floor. VANOS J. Mech. Eng. Educ. 2021, 6, 107–115. [Google Scholar] [CrossRef]
- Soyaslan, M.; Avsar, Y.; Fenercioglu, A.; Sarihan, F. Design and production of belt drive elevator traction machine: Modelling of double side belt system. Politek. Derg. 2023, 1. [Google Scholar] [CrossRef]
- Annett, F.A. Elevators: Electric and Electrohydraulic Elevators, Escalators, Moving Sidewalks and Ramps. 1960. Available online: https://cir.nii.ac.jp/crid/1130282270583238784 (accessed on 15 May 2022).
- Wrap Traction Overhead Type Elevator. Available online: https://crownelevators.in/images/ropes/elevator-cable-setups.png (accessed on 3 June 2023).
- Hrabovsky, L.; Maslaric, M. Device designed for detection and setting the required tensile force in ropes. Adv. Sci. Technol. Res. J. 2018, 12, 200–206. [Google Scholar] [CrossRef] [PubMed]
- Hrabovsky, L.; Michalik, P. A tension equalizer in lift carrying ropes. Adv. Sci. Technol. Res. J. 2017, 11, 326–332. [Google Scholar] [CrossRef] [PubMed]
- Mingxiang, H.; Dequan, C.; Lizhi, P.; Longbin, Z.; Bo, T. Design of Monitoring Sensors for Rope Force in Assembling Tower with Inside Suspension Pole. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–6. [Google Scholar]
- Barnes, M.; Rhiner, M. Constructional Stretch and Hoist-Rope Tension. Available online: https://elevatorbooks.com/wp-content/uploads/2019/02/EW0712.pdf (accessed on 20 March 2024).
- Kim, D.B.; Kim, G.S. A Study on the Development of an Elevator Rope Tension Automatic Equalizer. J. Korean Soc. Manuf. Process Eng. 2020, 19, 60–66. [Google Scholar] [CrossRef]
- Cvik, K.; Golasowski, J.; Hinner, V. Experience with operation of multi-rope hoisting equipment without any device for automatic equalization of tension in hoisting ropes. Uhli (Czechoslovakia) 1989, 37, 374–377. [Google Scholar]
- Zhang, X.; Jin, H. Design of strain tension sensor of steel wire rope used in the coal mine. In Proceedings of the Seventh International Symposium on Precision Mechanical Measurements, Xiamen, China, 29–31 January 2016. [Google Scholar]
- Liu, P.; Zhang, X.; Huang, Y.K.; Rong, J.X. The analysis of wire rope tension sensor elastic body based on solidworks. Adv. Mater. Res. 2012, 591–593, 1603–1606. [Google Scholar] [CrossRef]
- Singh, M.K.; Mahto, A.; Thakur, R.N.; Sinha, A. Failure analysis of wire rope used for hoisting in mining: A case study. J. Fail. Anal. Prev. 2007, 7, 87–91. [Google Scholar] [CrossRef]
- Jin, H.W.; Zhang, X. Design of dynamic tension detection system of multi-hoisting wire rope. Appl. Mech. Mater. 2012, 201, 565–568. [Google Scholar] [CrossRef]
- Lei, G.; Xu, G.; Zhang, X.; Zhang, Y.; Song, Z.; Xu, W. Study on dynamic monitoring of wire rope tension based on the particle damping sensor. Sensors 2019, 19, 388. [Google Scholar] [CrossRef] [PubMed]
- Hrabovsky, L. Tension force equalizer in a rope system using a proximity sensor. Zesz. Nauk. Transp./Politech. Śląska 2021, 110, 35–44. [Google Scholar] [CrossRef]
- Yao, M.; Jin, Y.; Zhao, M.; Xu, S. Research and Application of Heavy-Equipment Parachute Rope Tension Sensor. J. Sens. 2018, 7631727. [Google Scholar] [CrossRef]
- Zhao, M.; Tian, X.H.; Zhang, R.Y.; Wu, L.L. A wireless passive tension sensor. In Proceedings of the 16th International Conference on Mechatronics-Mechatronika, Brno, Czech Republic, 3–5 December 2014; pp. 473–476. [Google Scholar]
- Xu, G.; Da, J.; Zhang, X.; Han, M.; Xia, T. A novel tension monitoring device of multi-rope friction hoister by using acoustic filtering sensor. J. Vibroeng. 2016, 18, 5537–5552. [Google Scholar] [CrossRef]
- Hrabovsky, L.; Borovsky, D. Laboratory device for checking the functionality of the elevator rope sensors. Manag. Syst. Prod. Eng. 2021, 29, 59–64. [Google Scholar] [CrossRef]
- Lei, G.; Xu, G.; Zhang, X.; Tian, B. Study on dynamic characteristics and compensation of wire rope tension based on oil pressure sensor. Adv. Mech. Eng. 2019, 11, 1687814019836024. [Google Scholar] [CrossRef]
- Mitsantisuk, C.; Ohishi, K.; Katsura, S. Control of interaction force of twin direct-drive motor system using variable wire rope tension with multisensor integration. IEEE Trans. Ind. Electron. 2012, 59, 498–510. [Google Scholar] [CrossRef]
- Daifuku, S.; Li, B.; Yamaguchi, Y.; Nagatoshi, M.; Imado, K. Development of tension meter for wire rope and lashing belt. J. Mech. Syst. Transp. Logist. 2013, 6, 65–72. [Google Scholar] [CrossRef]
- Frydrysek, K.; Michenkova, S.; Pleva, L.; Koutecky, J.; Fries, J.; Peterek, D.K.; Pokorny, J. Mechanics of screw joints solved as beams placed in a tangential elastic foundation. Appl. Sci. 2021, 11, 5616. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, X.; Ni, M.; Liu, Z.; Mo, L. Tension measurement for wire ropes based on magneto-elastic effect. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 50–56. [Google Scholar]
- Konstantinov, M.Y.; Kiseleva, M.V.; Novikov, A.F. Equalizing forces in ropes of a multi-rope hoisting system. Ugol’Ukr (Ukrainian SSR) 1981, 5, 32–33. [Google Scholar]
- Ruční Olejová Pumpa Jednočinná s Nádrží 3L. Available online: https://www.kardanka.cz/rucni-olej-pumpa-jednocinna-s-nadrzi-3l-23987 (accessed on 20 January 2023).
- Standardní Dvoučinný Hydraulický válec 32/20/50. Available online: https://www.kardanka.cz/standardni-dvoucinny-hydraulicky-valec-32/20/50-205-mm-35722 (accessed on 11 August 2023).
- Šestipramenné lano 6x19M-WSC. Available online: https://www.lana-retezy.cz/sestipramenna-lana/sestipramenne-lano-6x19m-wsc/ (accessed on 26 December 2022).
- ČSN EN 12385-4; Steel Wire Ropes—Safety—Part 4: Stranded Ropes for General Lifting Applications (In Czech: Ocelová Drátěná Lana—Bezpečnost—Část 4: Pramenná Lana pro Všeobecné Zdvíhací Účely). TECHNOR print, s.r.o.: Hradec Kralove, Czech Republic, 2004. Available online: https://www.technicke-normy-csn.cz/csn-en-12385-4-024302-162155.html (accessed on 20 May 2004).
- AST—Snímač Typu “S”. Available online: https://www.format1.cz/files/products_files/a/AST.pdf (accessed on 13 January 2023).
- Technical Reference Manual DEWESoft DS-NET V20-1. Available online: https://d36j349d8rqm96.cloudfront.net/3/6/Dewesoft-DS-NET-Manual-EN.pdf (accessed on 26 April 2012).
- DEWESoft Previous Releases. DEWESoft® X2 SP5. Available online: https://dewesoft.com/download/dewesoftx-previous-releases (accessed on 11 July 2002).
- DIN ISO 6022:2008-06; Hydraulic Fluid Power—Mounting Dimensions for Single Rod Cylinders, 25 MPa (250 bar) Series. NORMSERVIS: Hamry nad Sázavou, Czech Republic, 2008. Available online: https://eshop.normservis.cz/norma/diniso-6022-1.6.2008.html (accessed on 1 July 2008).
- Hrabovsky, L. Apparatus producing an even distribution of strain into carriers. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022097. [Google Scholar] [CrossRef]

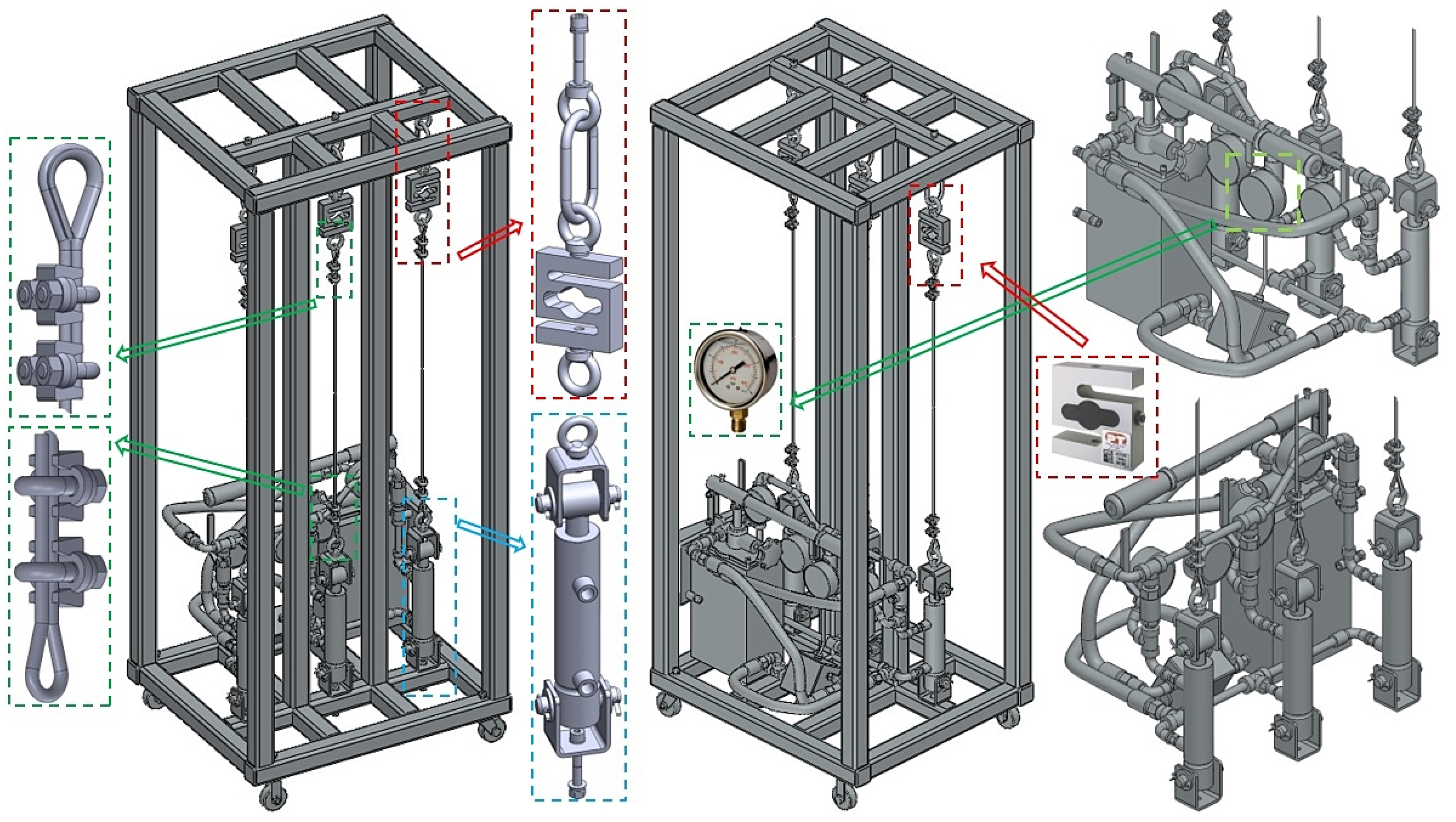
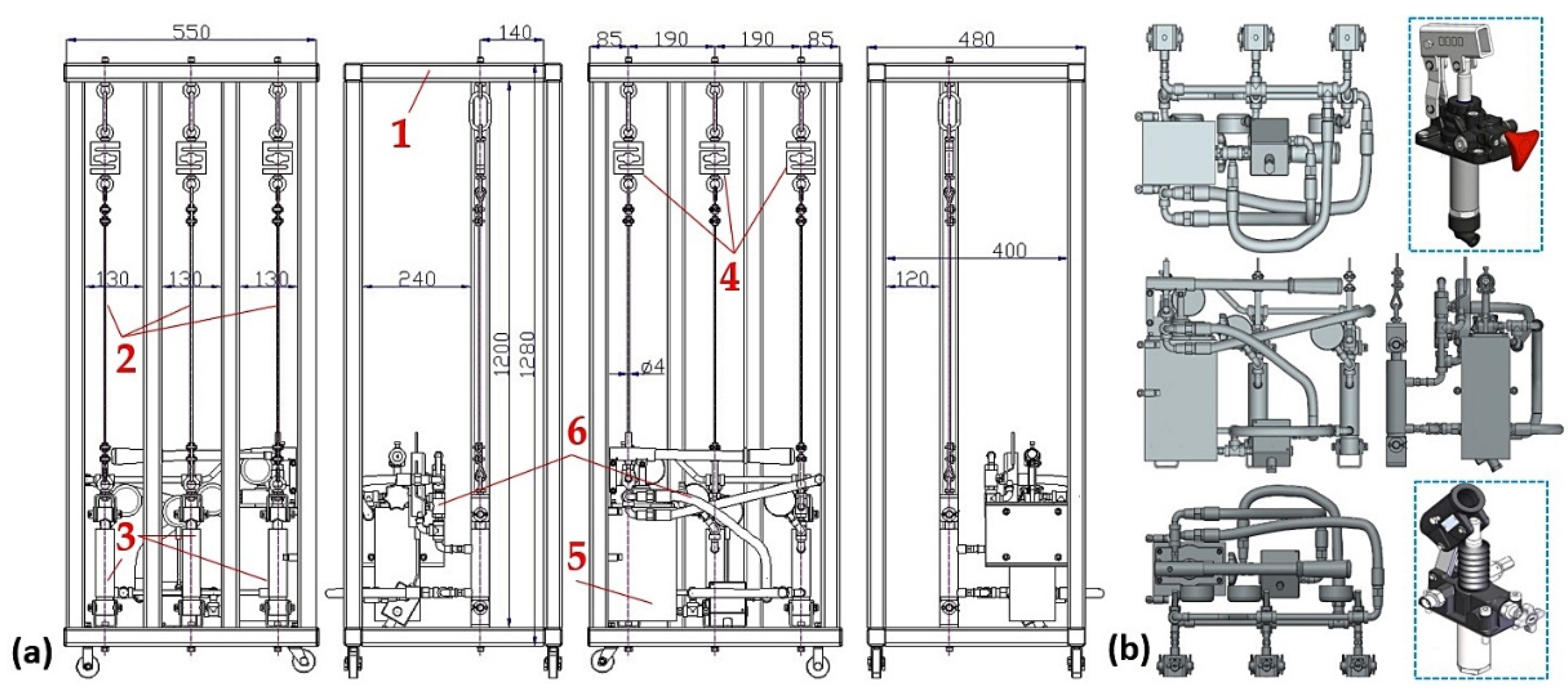



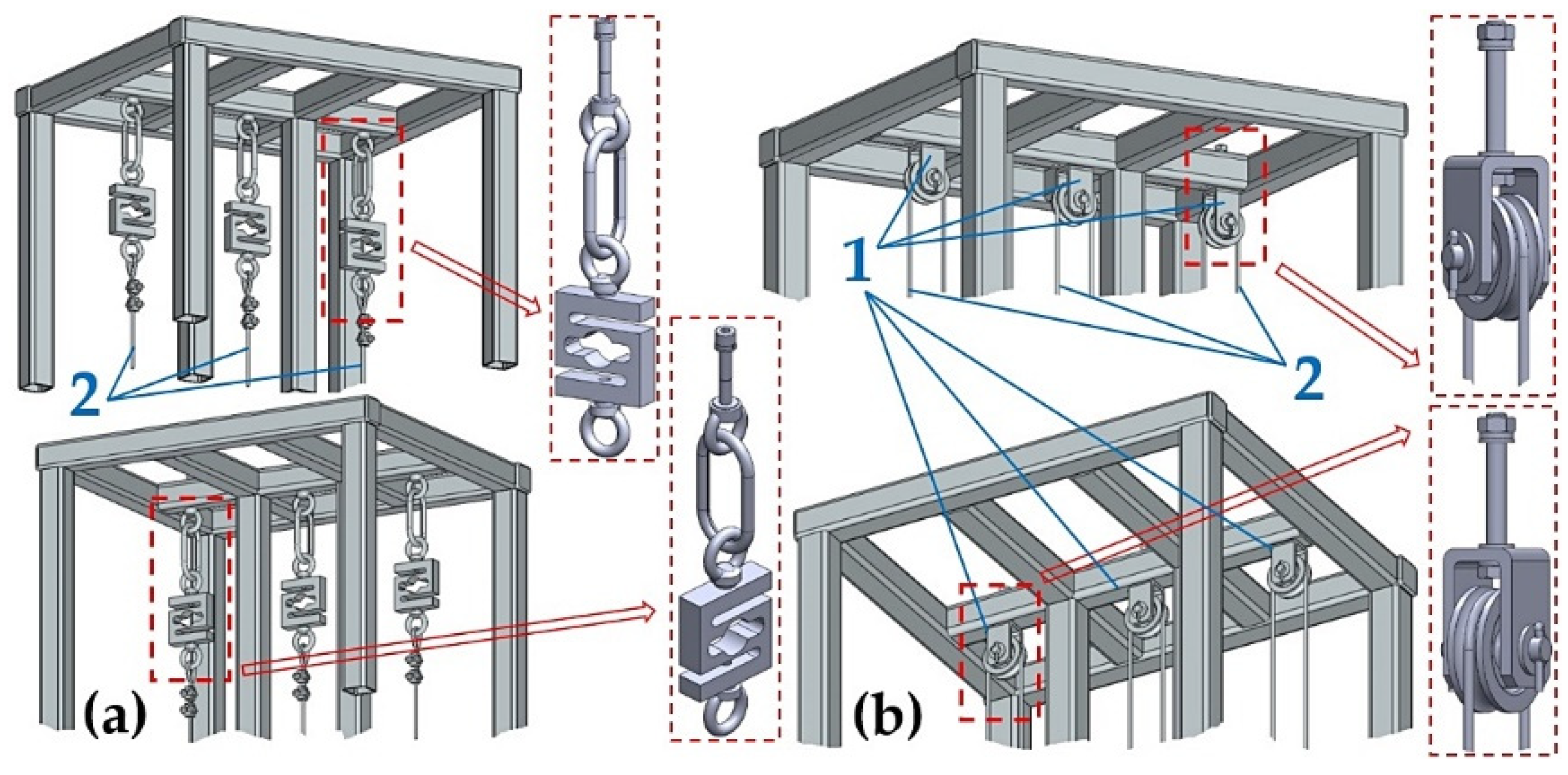
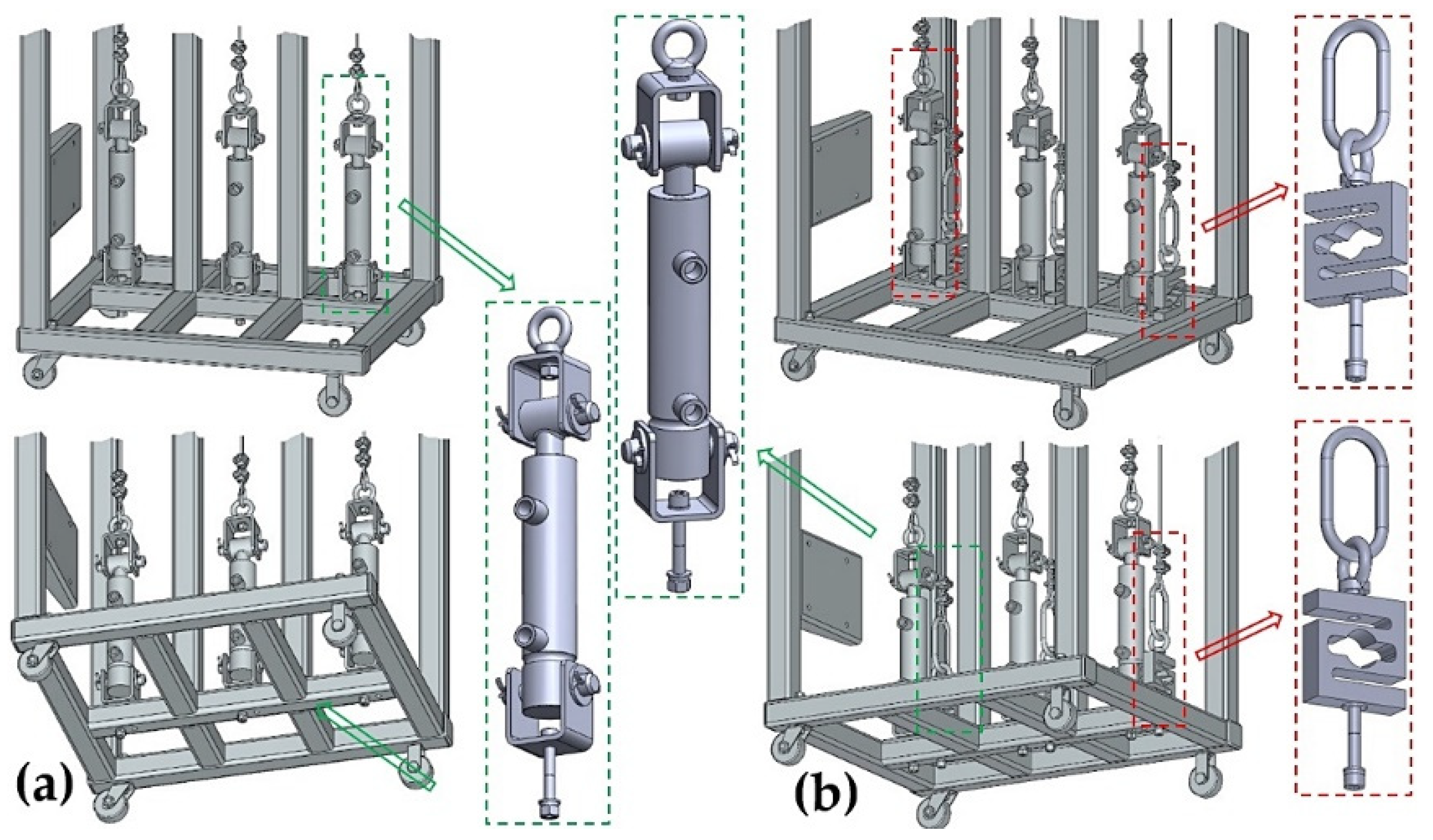



| n | Fp | FR1 | pp | pp1 | FR1p | pp1p |
|---|---|---|---|---|---|---|
| [N] | [MPa] | [N] | [MPa] | |||
| 1 | 653.0 1 | 1158.7 2 | 1.33 | 2.36 | 1036.0 3 | 2.11 |
| 2 | 285.9 | 618.5 | 0.58 | 1.26 | 593.7 | 1.21 |
| 3 | 406.5 | 938.2 | 0.83 | 1.91 | 912.4 | 1.86 |
| n | FR1p1 | FR2R1p1 | FR1p1R2 | FR3R2 | FR3R2R1p | FR1pR2R3 | FR2R1pR3 | F1 | F2 | F3 |
|---|---|---|---|---|---|---|---|---|---|---|
| [N] | ||||||||||
| 1 | 593.0 1 | 947.6 2 | 604.7 2 | 1867.4 2 | 1170.7 3 | 749.5 3 | 961.5 3 | 184.1 4 | 200.1 4 | 178.0 4 |
| 2 | 1034.5 | 955.6 | 1170.2 | 1656.7 | 1005.4 | 1170.2 | 1358.9 | 534.5 | 556.5 | 503.4 |
| 3 | 1104.0 5 | 1170.2 6 | 940.2 6 | 1766.0 6 | 1766.0 7 | 955.9 7 | 1170.2 7 | 169.3 8 | 183.4 8 | 158.5 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hrabovský, L.; Fries, J.; Pravda, Š. A Laboratory Machine Verifying the Operation of a Hydraulic Rope Equalizer with Tensometric Sensors. Sensors 2024, 24, 2588. https://doi.org/10.3390/s24082588
Hrabovský L, Fries J, Pravda Š. A Laboratory Machine Verifying the Operation of a Hydraulic Rope Equalizer with Tensometric Sensors. Sensors. 2024; 24(8):2588. https://doi.org/10.3390/s24082588
Chicago/Turabian StyleHrabovský, Leopold, Jiří Fries, and Štěpán Pravda. 2024. "A Laboratory Machine Verifying the Operation of a Hydraulic Rope Equalizer with Tensometric Sensors" Sensors 24, no. 8: 2588. https://doi.org/10.3390/s24082588
APA StyleHrabovský, L., Fries, J., & Pravda, Š. (2024). A Laboratory Machine Verifying the Operation of a Hydraulic Rope Equalizer with Tensometric Sensors. Sensors, 24(8), 2588. https://doi.org/10.3390/s24082588





