Implementing Gait Kinematic Trajectory Forecasting Models on an Embedded System
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
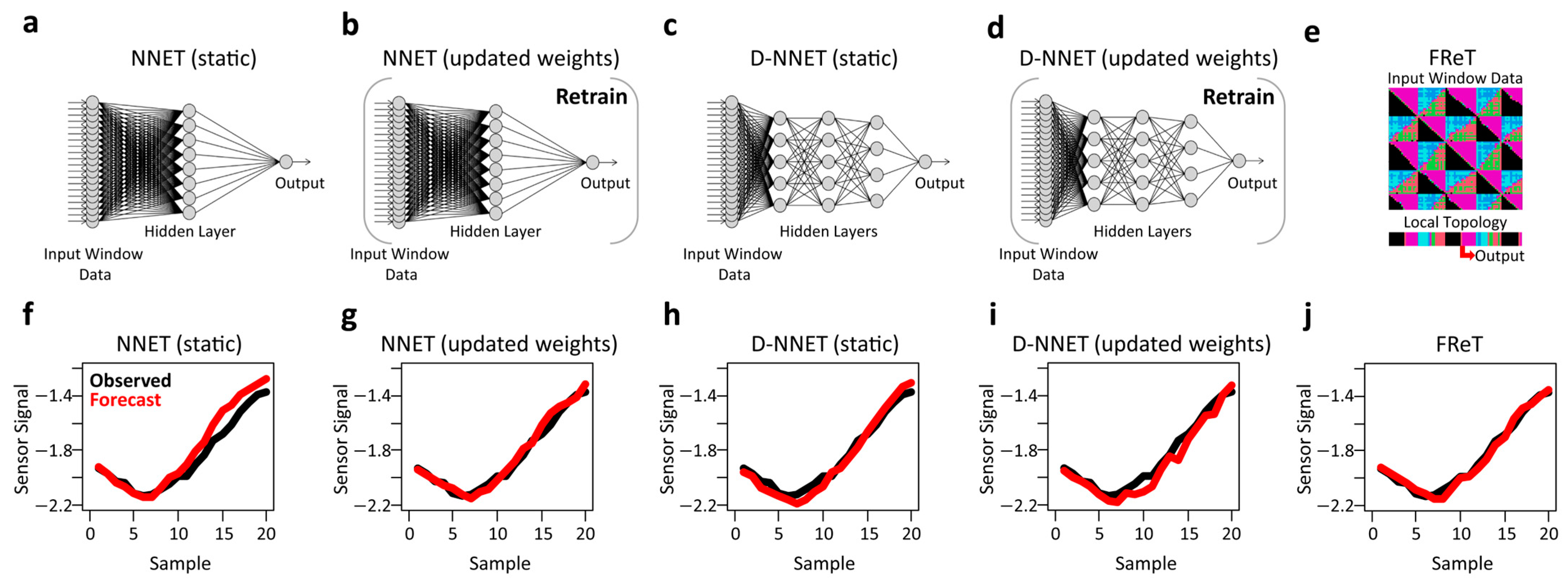
3.1. Artificial Neural Network Models
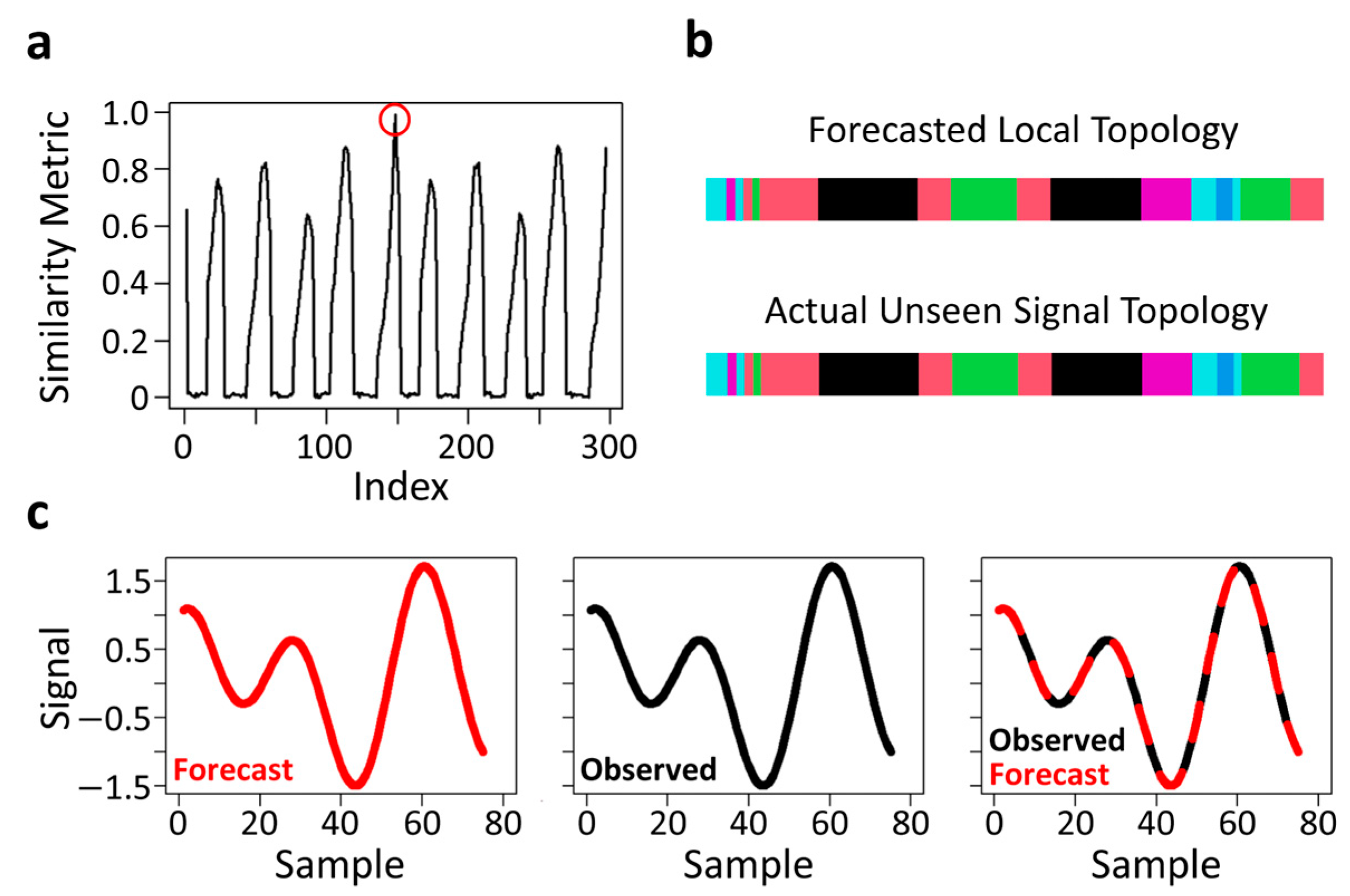
3.2. Forecasting through Recurrent Topology
3.3. Kinematic Trajectory Forecasting
3.4. Gait Sensor
3.5. Gait Data
3.6. Embedded System
3.7. Model Deployment
3.8. Data Analysis
4. Results
4.1. Forecasting Models
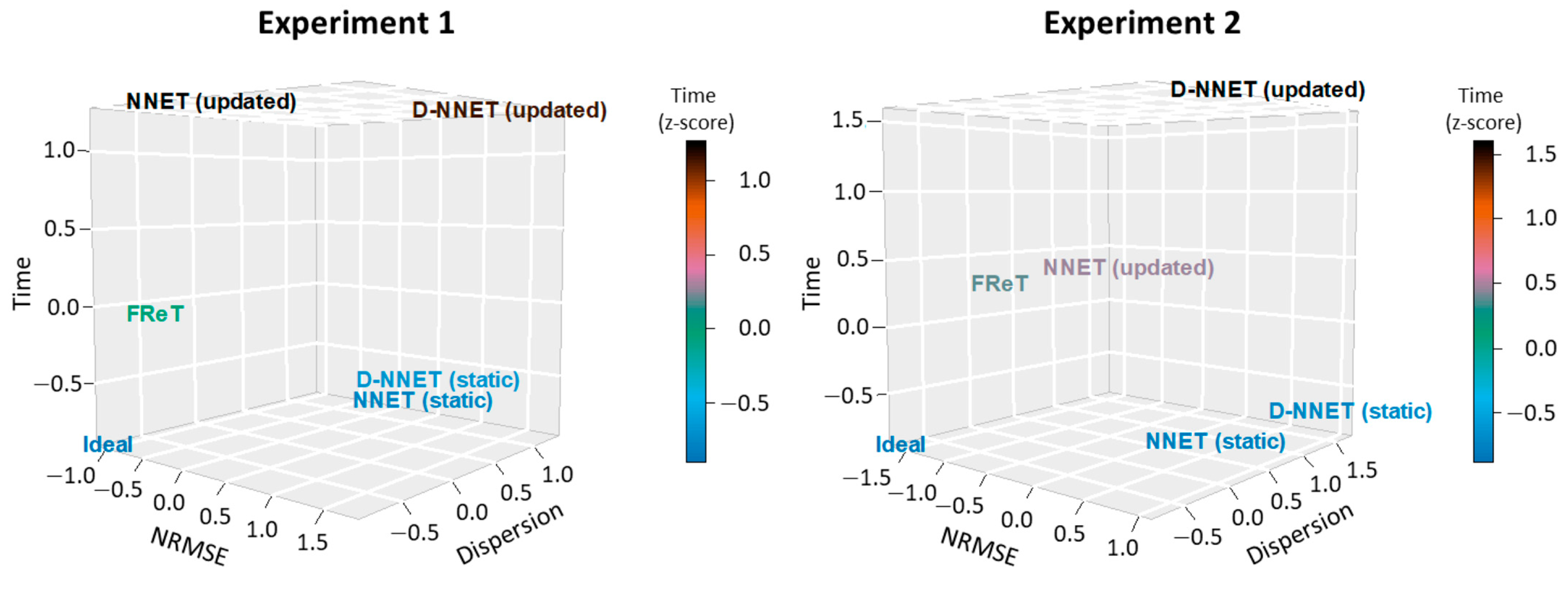
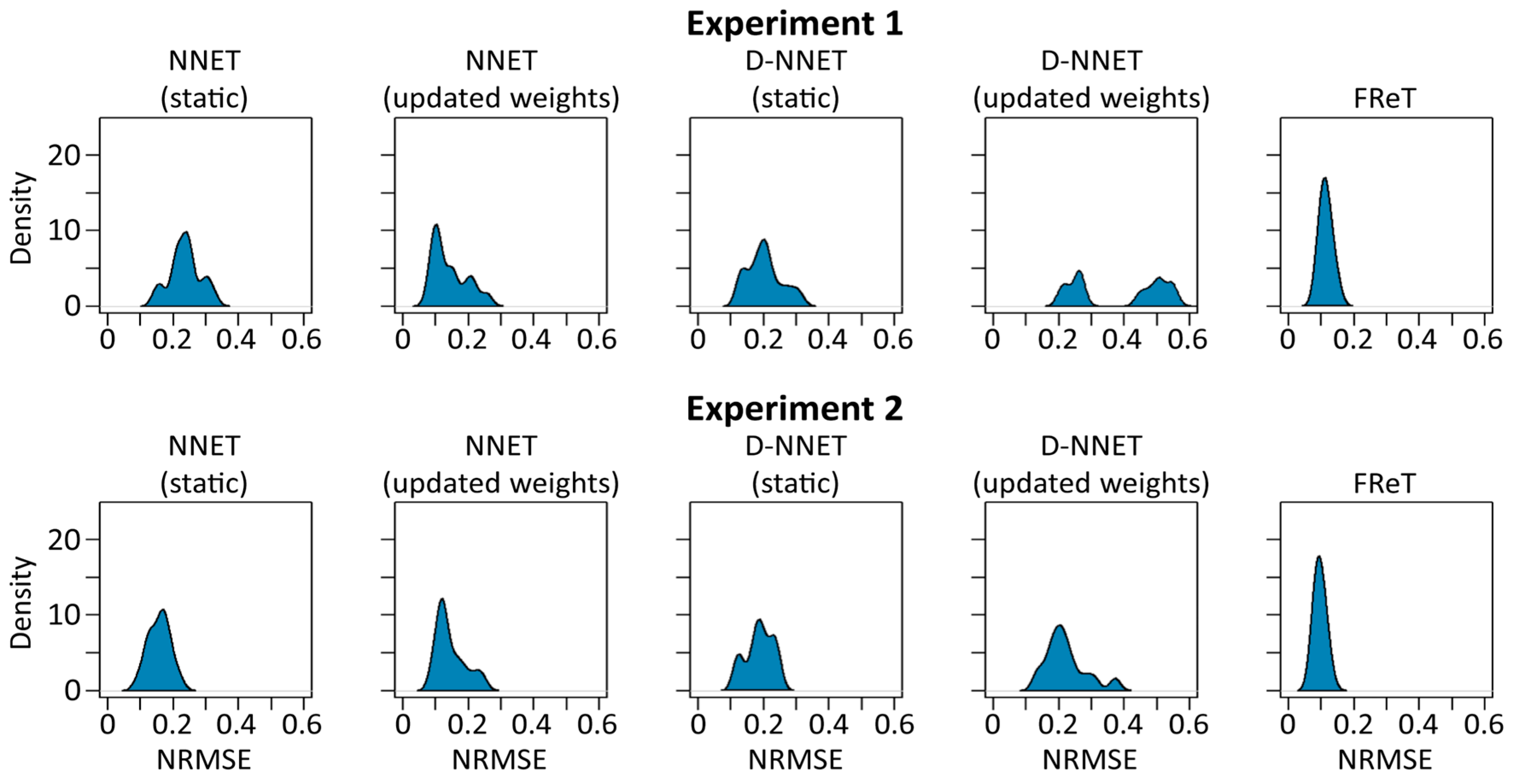
4.2. Model Accuracy, Intra-Individual Variability, and Computational Time
4.3. Model Inter-Individual Variability
5. Discussion
5.1. Complex Prediction Models
5.2. Embedded Systems
5.3. Study Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karakish, M.; Fouz, M.A.; ELsawaf, A. Gait Trajectory Prediction on an Embedded Microcontroller Using Deep Learning. Sensors 2022, 22, 8441. [Google Scholar] [CrossRef] [PubMed]
- Mobarak, R.; Tigrini, A.; Verdini, F.; Al-Timemy, A.H.; Fioretti, S.; Burattini, L.; Mengarelli, A. A Minimal and Multi-Source Recording Setup for Ankle Joint Kinematics Estimation During Walking Using Only Proximal Information from Lower Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 812–821. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-P.; Cao, G.-Z.; Li, L.-L.; Diao, D.-F. Interactive Control of Lower Limb Exoskeleton Robots: A Review. IEEE Sens. J. 2024, 24, 5759–5784. [Google Scholar] [CrossRef]
- Rupal, B.S.; Rafique, S.; Singla, A.; Singla, E.; Isaksson, M.; Virk, G.S. Lower-Limb Exoskeletons: Research Trends and Regulatory Guidelines in Medical and Non-Medical Applications. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417743554. [Google Scholar] [CrossRef]
- Young, A.J.; Ferris, D.P. State of the Art and Future Directions for Lower Limb Robotic Exoskeletons. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Su, B.; Gutierrez-Farewik, E.M. Gait Trajectory and Gait Phase Prediction Based on an LSTM Network. Sensors 2020, 20, 7127. [Google Scholar] [CrossRef] [PubMed]
- Tiboni, M.; Borboni, A.; Vérité, F.; Bregoli, C.; Amici, C. Sensors and Actuation Technologies in Exoskeletons: A Review. Sensors 2022, 22, 884. [Google Scholar] [CrossRef] [PubMed]
- Murray, S.; Goldfarb, M. Towards the Use of a Lower Limb Exoskeleton for Locomotion Assistance in Individuals with Neuromuscular Locomotor Deficits. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; Volume 2012, p. 1912. [Google Scholar] [CrossRef]
- Kim, M.; Hargrove, L.J. A Gait Phase Prediction Model Trained on Benchmark Datasets for Evaluating a Controller for Prosthetic Legs. Front. Neurorobot. 2023, 16, 288. [Google Scholar] [CrossRef] [PubMed]
- Anam, K.; Al-Jumaily, A.A. Active Exoskeleton Control Systems: State of the Art. Procedia Eng. 2012, 41, 988–994. [Google Scholar] [CrossRef]
- Taborri, J.; Scalona, E.; Rossi, S.; Palermo, E.; Patane, F.; Cappa, P. Real-Time Gait Detection Based on Hidden Markov Model: Is It Possible to Avoid Training Procedure? In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA) Proceedings, Turin, Italy, 7–9 May 2015; pp. 141–145. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, S.; Xue, Q. Lower Limb Rehabilitation Exoskeleton Robot: A Review. Adv. Mech. Eng. 2021, 13, 16878140211011862. [Google Scholar] [CrossRef]
- Androwis, G.J.; Sandroff, B.M.; Niewrzol, P.; Fakhoury, F.; Wylie, G.R.; Yue, G.; DeLuca, J. A Pilot Randomized Controlled Trial of Robotic Exoskeleton-Assisted Exercise Rehabilitation in Multiple Sclerosis. Mult. Scler. Relat. Disord. 2021, 51, 102936. [Google Scholar] [CrossRef] [PubMed]
- van Nes, I.J.W.; van Dijsseldonk, R.B.; van Herpen, F.H.M.; Rijken, H.; Geurts, A.C.H.; Keijsers, N.L.W. Improvement of Quality of Life after 2-Month Exoskeleton Training in Patients with Chronic Spinal Cord Injury. J. Spinal Cord Med. 2022. [Google Scholar] [CrossRef]
- Asano, M.; Rushton, P.; Miller, W.C.; Deathe, B.A. Predictors of Quality of Life among Individuals Who Have a Lower Limb Amputation. Prosthet. Orthot. Int. 2008, 32, 231–243. [Google Scholar] [CrossRef]
- Chen, B.; Ma, H.; Qin, L.Y.; Gao, F.; Chan, K.M.; Law, S.W.; Qin, L.; Liao, W.H. Recent Developments and Challenges of Lower Extremity Exoskeletons. J. Orthop. Transl. 2016, 5, 26–37. [Google Scholar] [CrossRef]
- Vu, H.T.T.; Dong, D.; Cao, H.L.; Verstraten, T.; Lefeber, D.; Vanderborght, B.; Geeroms, J. A Review of Gait Phase Detection Algorithms for Lower Limb Prostheses. Sensors 2020, 20, 3972. [Google Scholar] [CrossRef]
- Clemens, S.; Kim, K.J.; Gailey, R.; Kirk-Sanchez, N.; Kristal, A.; Gaunaurd, I. Inertial Sensor-Based Measures of Gait Symmetry and Repeatability in People with Unilateral Lower Limb Amputation. Clin. Biomech. 2020, 72, 102–107. [Google Scholar] [CrossRef]
- Lai, D.T.H.; Begg, R.K.; Palaniswami, M. Computational Intelligence in Gait Research: A Perspective on Current Applications and Future Challenges. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 687–702. [Google Scholar] [CrossRef] [PubMed]
- Sawicki, G.S.; Beck, O.N.; Kang, I.; Young, A.J. The Exoskeleton Expansion: Improving Walking and Running Economy. J. Neuroeng. Rehabil. 2020, 17, 25. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.T.; Chang, C.C.; Sun, P.Y.; Lee, C.L.; Lin, T.C.; Yen, C.K.; Yang, Y.S. Development of Multi-Axis Motor Control Systems for Lower Limb Robotic Exoskeleton. J. Med. Biol. Eng. 2019, 39, 752–763. [Google Scholar] [CrossRef]
- Tanghe, K.; De Groote, F.; Lefeber, D.; De Schutter, J.; Aertbelien, E. Gait Trajectory and Event Prediction from State Estimation for Exoskeletons during Gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 211–220. [Google Scholar] [CrossRef]
- Zaroug, A.; Proud, J.K.; Lai, D.T.H.; Mudie, K.; Billing, D.; Begg, R. Overview of Computational Intelligence (CI) Techniques for Powered Exoskeletons. Stud. Comput. Intell. 2019, 776, 353–383. [Google Scholar] [CrossRef]
- Torricelli, D.; Cortés, C.; Lete, N.; Bertelsen, Á.; Gonzalez-Vargas, J.E.; Del-Ama, A.J.; Dimbwadyo, I.; Moreno, J.C.; Florez, J.; Pons, J.L. A Subject-Specific Kinematic Model to Predict Human Motion in Exoskeleton-Assisted Gait. Front. Neurorobot. 2018, 12, 18. [Google Scholar] [CrossRef]
- Wu, X.; Liu, D.X.; Liu, M.; Chen, C.; Guo, H. Individualized Gait Pattern Generation for Sharing Lower Limb Exoskeleton Robot. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1459–1470. [Google Scholar] [CrossRef]
- Slade, P.; Kochenderfer, M.J.; Delp, S.L.; Collins, S.H. Personalizing Exoskeleton Assistance While Walking in the Real World. Nature 2022, 610, 277–282. [Google Scholar] [CrossRef] [PubMed]
- Dobson, A.; Murray, K.; Manolov, N.; Davanzo, J.E. Economic Value of Orthotic and Prosthetic Services among Medicare Beneficiaries: A Claims-Based Retrospective Cohort Study, 2011–2014. J. Neuroeng. Rehabil. 2018, 15, 55. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Megharjun, V.N.; Talasila, V. Forecasting a Gait Cycle Parameter Region to Enable Optimal FES Triggering. IFAC-PapersOnLine 2020, 53, 232–239. [Google Scholar] [CrossRef]
- Rahman, H.; Kumbla, A.; Megharjun, V.N.; Talasila, V. Real-Time Heel Strike Parameter Estimation for FES Triggering. Lect. Notes Electr. Eng. 2022, 903, 749–760. [Google Scholar] [CrossRef]
- Zaroug, A.; Lai, D.T.H.; Mudie, K.; Begg, R. Lower Limb Kinematics Trajectory Prediction Using Long Short-Term Memory Neural Networks. Front. Bioeng. Biotechnol. 2020, 8, 362. [Google Scholar] [CrossRef]
- Kale, A.; Sundaresan, A.; Rajagopalan, A.N.; Cuntoor, N.P.; Roy-Chowdhury, A.K.; Krüger, V.; Chellappa, R. Identification of Humans Using Gait. IEEE Trans. Image Process. 2004, 13, 1163–1173. [Google Scholar] [CrossRef]
- Borovicka, T.; Jirina , M., Jr.; Kordik, P.; Jirina, M. Selecting Representative Data Sets. In Advances in Data Mining Knowledge Discovery and Applications; BoD: Stafford, VA, USA, 2012; Volume 12, pp. 43–70. [Google Scholar] [CrossRef]
- Finlayson, S.G.; Subbaswamy, A.; Singh, K.; Bowers, J.; Kupke, A.; Zittrain, J.; Kohane, I.S.; Saria, S. The Clinician and Dataset Shift in Artificial Intelligence. N. Engl. J. Med. 2021, 385, 283–286. [Google Scholar] [CrossRef]
- Pinto, B.; Correia, M.V.; Paredes, H.; Silva, I. Detection of Intermittent Claudication from Smartphone Inertial Data in Community Walks Using Machine Learning Classifiers. Sensors 2023, 23, 1581. [Google Scholar] [CrossRef] [PubMed]
- Crone, S.F.; Kourentzes, N. Naive Support Vector Regression and Multilayer Perceptron Benchmarks for the 2010 Neural Network Grand Competition (NNGC) on Time Series Prediction. In Proceedings of the The 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010. [Google Scholar] [CrossRef]
- Zhang, G.P. Neural Networks for Time-Series Forecasting. Handb. Nat. Comput. 2012, 1, 461–477. [Google Scholar] [CrossRef]
- Zaroug, A.; Garofolini, A.; Lai, D.T.H.; Mudie, K.; Begg, R. Prediction of Gait Trajectories Based on the Long Short Term Memory Neural Networks. PLoS ONE 2021, 16, e0255597. [Google Scholar] [CrossRef] [PubMed]
- Chomiak, T.; Hu, B. Time-Series Forecasting through Recurrent Topology. Commun. Eng. 2024, 3, 9. [Google Scholar] [CrossRef]
- Kaastra, I.; Boyd, M. Designing a Neural Network for Forecasting Financial and Economic Time Series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Chomiak, T.; Rasiah, N.P.; Molina, L.A.; Hu, B.; Bains, J.S.; Füzesi, T. A Versatile Computational Algorithm for Time-Series Data Analysis and Machine-Learning Models. npj Park. Dis. 2021, 7, 97. [Google Scholar] [CrossRef] [PubMed]
- Mallikarjuna, M.; Rao, R.P. Evaluation of Forecasting Methods from Selected Stock Market Returns. Financ. Innov. 2019, 5, 40. [Google Scholar] [CrossRef]
- Moreira, F.R.D.S.; Verri, F.A.N.; Yoneyama, T. Maximum Visibility: A Novel Approach for Time Series Forecasting Based on Complex Network Theory. IEEE Access 2022, 10, 8960–8973. [Google Scholar] [CrossRef]
- Di Narzo, A.F.; Aznarte, J.L.; Stigler, M. TsDyn: Nonlinear Time Series Models with Regime Switching, R package version 11.0.4.1; 2022. Available online: https://cran.r-project.org/web/packages/tsDyn/tsDyn.pdf (accessed on 16 April 2024).
- Gers, F.; Eck, D.; Schmidhuber, J. Applying LSTM to Time Series Predictable through Time-Window Approaches. In Artificial Neural Networks—ICANN 2001; Dorffner, G., Bischof, H., Hornik, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2130, pp. 669–676. [Google Scholar]
- Kourentzes, N. Time Series Forecasting with Neural Networks 2022, R Package “nnfor” version 0.9.9. Available online: https://cran.r-project.org/web/packages/nnfor/nnfor.pdf (accessed on 16 April 2024).
- Han, Z.; Zhao, J.; Leung, K.F.; Ma, F.; Wang, W. A Review of Deep Learning Models for Time Series Prediction. IEEE Sens. J. 2021, 21, 7833–7848. [Google Scholar] [CrossRef]
- Chomiak, T.; Sidhu, A.; Watts, A.; Su, L.; Graham, B.; Wu, J.; Classen, S.; Falter, B.; Hu, B. Development and Validation of Ambulosono: A Wearable Sensor for Bio-Feedback Rehabilitation Training. Sensors 2019, 19, 686. [Google Scholar] [CrossRef]
- Chomiak, T.; Pereira, F.V.; Meyer, N.; de Bruin, N.; Derwent, L.; Luan, K.; Cihal, A.; Brown, L.A.; Hu, B. A New Quantitative Method for Evaluating Freezing of Gait and Dual-Attention Task Deficits in Parkinson’s Disease. J. Neural Transm. 2015, 122, 1523–1531. [Google Scholar] [CrossRef] [PubMed]
- Chomiak, T.; Xian, W.; Pei, Z.; Hu, B. A Novel Single-Sensor-Based Method for the Detection of Gait-Cycle Breakdown and Freezing of Gait in Parkinson’s Disease. J. Neural Transm. 2019, 126, 1029–1036. [Google Scholar] [CrossRef] [PubMed]
- Tahmazian, I.; Watts, A.; Chen, O.; Ferrara, H.J.; McCrimmon, A.; Hu, B.; Chomiak, T. A Wearable Device-Enabled Therapeutic Approach to Improve Joint Attention in Autism Spectrum Disorder: A Prospective Pilot Study. J. Neural Transm. 2023, 130, 1601–1607. [Google Scholar] [CrossRef] [PubMed]
- Stolze, H.; Kuhtz-Buschbeck, J.P.; Drucke, H.; Johnk, K.; Illert, M.; Deuschl, G. Comparative Analysis of the Gait Disorder of Normal Pressure Hydrocephalus and Parkinson’s Disease. J. Neurol. Neurosurg. Psychiatry 2001, 70, 289–297. [Google Scholar] [CrossRef]





| Experiment 1 | Experiment 2 | |||
|---|---|---|---|---|
| Model | NRMSE | Dispersion | NRMSE | Dispersion |
| NNET (static) | 0.237 | 0.047 | 0.157 | 0.027 |
| NNET (updated) | 0.143 | 0.004 | 0.146 | 0.008 |
| D-NNET (static) | 0.203 | 0.055 | 0.188 | 0.054 |
| D-NNET (updated) | 0.535 | 0.023 | 0.221 | 0.014 |
| FReT | 0.115 | 0.000 | 0.097 | 0.000 |
| Experiment 1 | Experiment 2 | |
|---|---|---|
| Model | ms | ms |
| NNET (static) | 9.534 | 11.11 |
| NNET (updated) | 195.0 | 218.8 |
| D-NNET (static) | 17.83 | 19.99 |
| D-NNET (updated) | 186.6 | 395.3 |
| FReT | 80.02 | 200.4 |
| Experiment 1 | Experiment 2 | |
|---|---|---|
| Model | Euclidean Distance | Euclidean Distance |
| NNET (static) | 2.32 | 2.40 |
| NNET (updated) | 2.33 | 2.36 |
| D-NNET (static) | 2.52 | 3.55 |
| D-NNET (updated) | 3.74 | 3.83 |
| FReT | 1.10 | 1.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shayne, M.; Molina, L.A.; Hu, B.; Chomiak, T. Implementing Gait Kinematic Trajectory Forecasting Models on an Embedded System. Sensors 2024, 24, 2649. https://doi.org/10.3390/s24082649
Shayne M, Molina LA, Hu B, Chomiak T. Implementing Gait Kinematic Trajectory Forecasting Models on an Embedded System. Sensors. 2024; 24(8):2649. https://doi.org/10.3390/s24082649
Chicago/Turabian StyleShayne, Madina, Leonardo A. Molina, Bin Hu, and Taylor Chomiak. 2024. "Implementing Gait Kinematic Trajectory Forecasting Models on an Embedded System" Sensors 24, no. 8: 2649. https://doi.org/10.3390/s24082649
APA StyleShayne, M., Molina, L. A., Hu, B., & Chomiak, T. (2024). Implementing Gait Kinematic Trajectory Forecasting Models on an Embedded System. Sensors, 24(8), 2649. https://doi.org/10.3390/s24082649






