Compressed Sensing for Biomedical Photoacoustic Imaging: A Review
Abstract
1. Introduction
2. Biomedical Photoacoustic Technique
2.1. Photoacoustic Effect
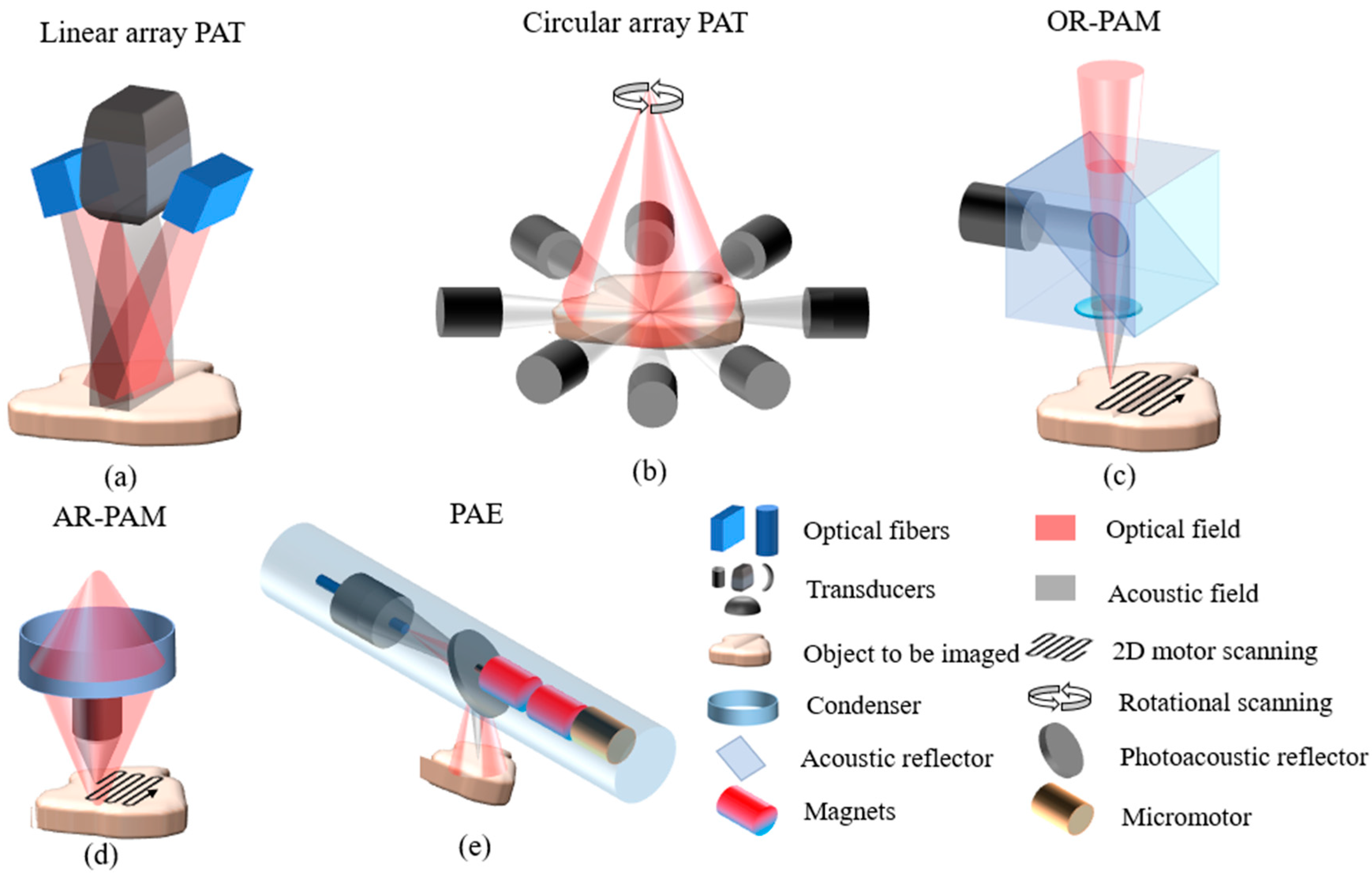
2.2. Biomedical Photoacoustic Imaging
2.3. Biomedical Application of Photoacoustic Technique
3. Compressed Sensing
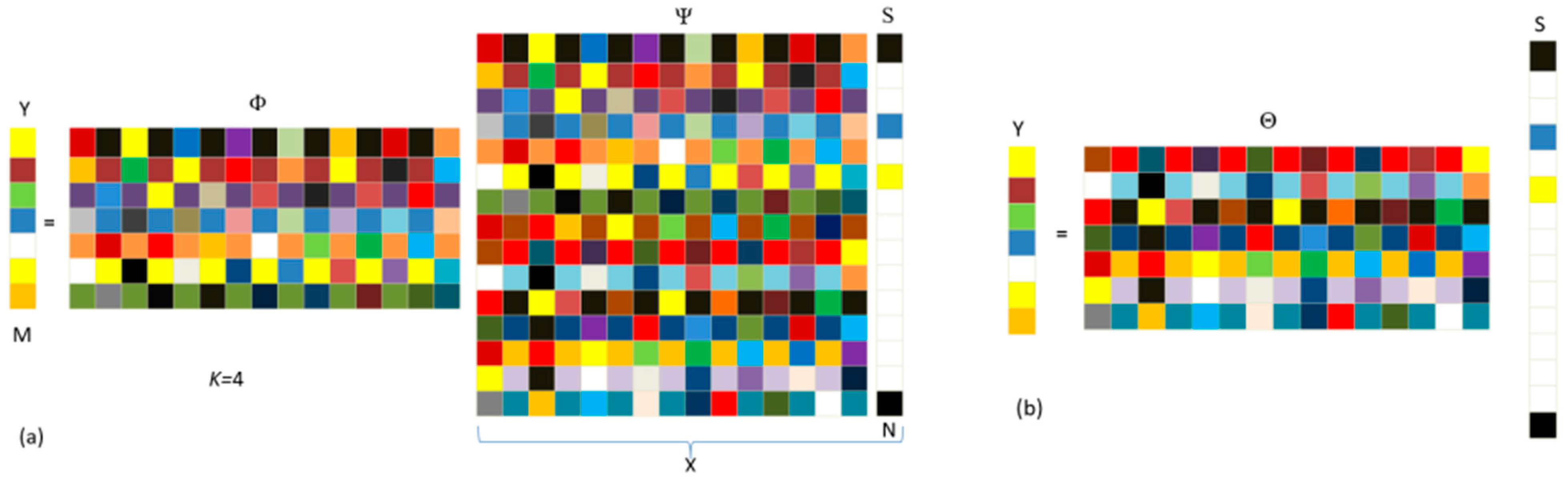
3.1. Sparse Representation
3.2. Compression Measurement
3.3. Signal Reconstruction
4. Photoacoustic Imaging Based on Compressed Sensing
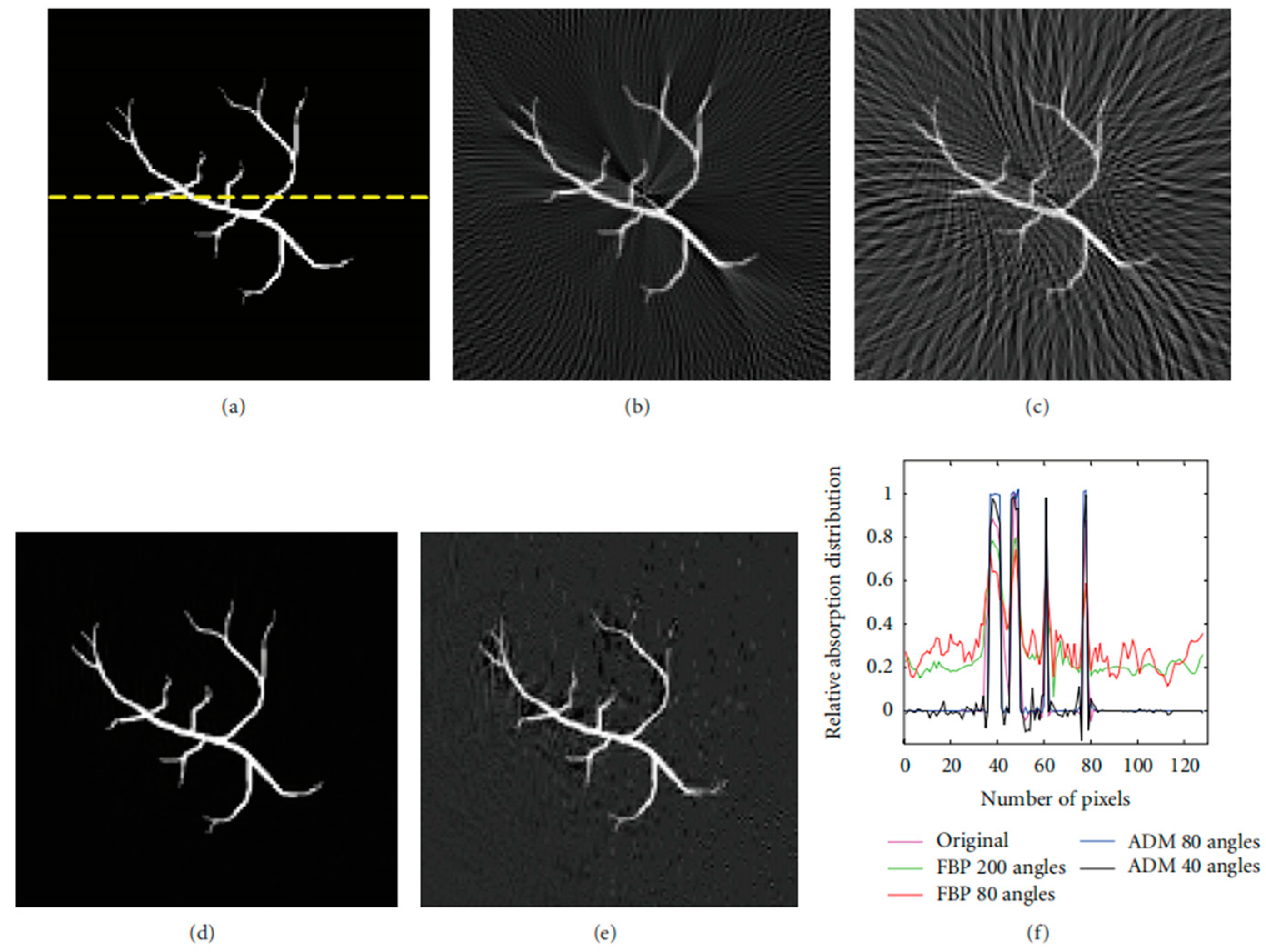
4.1. Physical Transmission Model-Based Compressed Sensing Method
4.2. Two-Stage Reconstruction-Based Compressed Sensing Method
4.3. Single-Pixel Camera-Based Compressed Sensing Method
4.4. Other Valuable Methods (Virtual Detector, Multiscale Decomposition of Wave Equation, Motion Estimation Framework, Undersampled Fourier Measurements, Laplacian Sparsity, and Deep Learning)
5. Comparisons between Different Methods
6. Discussion (Challenges and Future Perspectives)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andresen, B.F.; McMackin, L.; Herman, M.A.; Chatterjee, B.; Weldon, M.; Fulop, G.F.; Norton, P.R. A high-resolution SWIR camera via compressed sensing. In Proceedings of the Infrared Technology and Applications XXXVIII, Baltimore, MD, USA, 23–27 April 2012; pp. 835303–835310. [Google Scholar]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Haykin, S.; Moher, M. Introduction to Analog and Digital Communications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hae-Seung, L.; Sodini, C.G. Analog-to-Digital Converters: Digitizing the Analog World. Proc. IEEE 2008, 96, 323–334. [Google Scholar] [CrossRef]
- Stojanovic, N.; Mao, B.; Zhao, Y. Digital Phase Detector for Nyquist and Faster than Nyquist Systems. IEEE Commun. Lett. 2014, 18, 511–514. [Google Scholar] [CrossRef]
- Lu, J.; Verma, N.; Jha, N.K. Compressed Signal Processing on Nyquist-Sampled Signals. IEEE Trans. Comput. 2016, 65, 3293–3303. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I. Nyquist Sampling Requirements for Polar Grids in Bistatic Time-Domain Algorithms. IEEE Trans. Signal Process. 2015, 63, 457–465. [Google Scholar] [CrossRef]
- Ma, H.; Yuan, X.; Wang, J.; Li, B. Revisiting Model Order Selection: A Sub-Nyquist Sampling Blind Spectrum Sensing Scheme. IEEE Trans. Wirel. Commun. 2023, 22, 3371–3383. [Google Scholar] [CrossRef]
- Nagib, K.; Mezgebo, B.; Fernando, N.; Kordi, B.; Sherif, S.S. Generalized Image Reconstruction in Optical Coherence Tomography Using Redundant and Non-Uniformly-Spaced Samples. Sensors 2021, 21, 7057. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar]
- Lin, J.; Ma, X.; Yang, L.; Lin, G. A Large-Scale Sonar Signal Acquisition and Storage System Based on FPGA. In Proceedings of the 2014 Fourth International Conference on Instrumentation and Measurement, Computer, Communication and Control, Harbin, China, 18–20 September 2014; pp. 21–24. [Google Scholar]
- Makarichev, V.; Lukin, V. Combined Lossless/Lossy Compression of Three-channel Images. In Proceedings of the 2023 13th International Conference on Dependable Systems, Services and Technologies (DESSERT), Greece, Athens, 13–15 October 2023; pp. 1–5. [Google Scholar]
- Tan, Y.F.; Tan, W.N. Image compression technique utilizing reference points coding with threshold values. In Proceedings of the International Conference on Audio, Shanghai, China, 16–18 July 2012. [Google Scholar]
- Koc, B.; Arnavut, Z.; Kocak, H. Concurrent Encryption and Lossless Compression using Inversion Ranks. In Proceedings of the 2022 Data Compression Conference (DCC), Snowbird, UT, USA, 22–25 March 2022; p. 459. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wang, H. Compressed Sensing: Theory and Applications. J. Phys. Conf. Ser. 2023, 2419, 012042. [Google Scholar] [CrossRef]
- Rauhut, H.; Schnass, K.; Vandergheynst, P. Compressed Sensing and Redundant Dictionaries. IEEE Trans. Inf. Theory 2008, 54, 2210–2219. [Google Scholar] [CrossRef]
- Tsaig, Y.; Donoho, D.L. Extensions of compressed sensing. Signal Process. 2006, 86, 549–571. [Google Scholar] [CrossRef]
- Duarte, M.F.; Eldar, Y.C. Structured Compressed Sensing: From Theory to Applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Zymnis, A.; Boyd, S.; Candes, E. Compressed Sensing with Quantized Measurements. IEEE Signal Process. Lett. 2010, 17, 149–152. [Google Scholar] [CrossRef]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. From Denoising to Compressed Sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Potter, L.C.; Ertin, E.; Parker, J.T.; Cetin, M. Sparsity and Compressed Sensing in Radar Imaging. Proc. IEEE 2010, 98, 1006–1020. [Google Scholar] [CrossRef]
- Haupt, J.; Bajwa, W.U.; Rabbat, M.; Nowak, R. Compressed Sensing for Networked Data. IEEE Signal Process. Mag. 2008, 25, 92–101. [Google Scholar] [CrossRef]
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Xia, J.; Wang, L.V. Small-Animal Whole-Body Photoacoustic Tomography: A Review. IEEE Trans. Biomed. Eng. 2014, 61, 1380–1389. [Google Scholar] [CrossRef]
- Feng, N.; Sun, M.; Ma, L. Compressed Sensing Photoacoustic Imaging based on Correlation Criterion. Int. J. Adv. Comput. Technol. 2011, 3, 201–207. [Google Scholar] [CrossRef]
- Manwar, R.; Zafar, M.; Xu, Q. Signal and Image Processing in Biomedical Photoacoustic Imaging: A Review. Optics 2020, 2, 1–24. [Google Scholar] [CrossRef]
- Ahmed, I.; Khalil, A.; Ahmed, I.; Frnda, J. Sparse Signal Representation, Sampling, and Recovery in Compressive Sensing Frameworks. IEEE Access 2022, 10, 85002–85018. [Google Scholar] [CrossRef]
- Tzagkarakis, G.; Nolan, J.P.; Tsakalides, P. Compressive Sensing Using Symmetric Alpha-Stable Distributions for Robust Sparse Signal Reconstruction. IEEE Trans. Signal Process. 2019, 67, 808–820. [Google Scholar] [CrossRef]
- Hu, L.; Zhou, J.; Shi, Z.; Fu, Q. A Fast and Accurate Reconstruction Algorithm for Compressed Sensing of Complex Sinusoids. IEEE Trans. Signal Process. 2013, 61, 5744–5754. [Google Scholar] [CrossRef]
- Ravelomanantsoa, A.; Rabah, H.; Rouane, A. Compressed Sensing: A Simple Deterministic Measurement Matrix and a Fast Recovery Algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 3405–3413. [Google Scholar] [CrossRef]
- Taruttis, A.; Ntziachristos, V. Advances in real-time multispectral optoacoustic imaging and its applications. Nat. Photonics 2015, 9, 219–227. [Google Scholar] [CrossRef]
- Liu, X.; Peng, D.; Ma, X.; Guo, W.; Liu, Z.; Han, D.; Yang, X.; Tian, J. Limited-view photoacoustic imaging based on an iterative adaptive weighted filtered backprojection approach. Appl. Opt. 2013, 52, 3477–3483. [Google Scholar] [CrossRef]
- Wu, D.; Tao, C.; Liu, X.-J.; Wang, X.-D. Influence of limited-view scanning on depth imaging of photoacoustic tomography. Chin. Phys. B 2012, 21, 014301. [Google Scholar] [CrossRef]
- Anderson, R.R.; Parrish, J.A. The Optics of Human Skin. J. Investig. Dermatol. 1981, 77, 13–19. [Google Scholar] [CrossRef]
- Rosencwaig, A. Photoacoustic spectroscopy of solids. Phys. Today 1975, 28, 23–30. [Google Scholar] [CrossRef]
- Su, J.L.; Wang, B.; Wilson, K.E.; Bayer, C.L.; Chen, Y.S.; Kim, S.; Homan, K.A.; Emelianov, S.Y. Advances in Clinical and Biomedical Applications of Photoacoustic Imaging. Expert Opin. Med. Diagn. 2010, 4, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Harshbarger, W.R.; Robin, M.B. Opto-acoustic effect. Revival of an old technique for molecular spectroscopy. Acc. Chem. Res. 1973, 6, 329–334. [Google Scholar] [CrossRef]
- Favazza, C.P.; Cornelius, L.A.; Wang, L.V. In vivo functional photoacoustic microscopy of cutaneous microvasculature in human skin. J. Biomed. Opt. 2011, 16, 026004. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhu, L.; Ma, C.; Lin, L.; Yao, J.; Wang, L.; Maslov, K.; Zhang, R.; Chen, W.; Shi, J.; et al. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 2017, 1, 0071. [Google Scholar] [CrossRef] [PubMed]
- Kye, H.; Song, Y.; Ninjbadgar, T.; Kim, C.; Kim, J. Whole-Body Photoacoustic Imaging Techniques for Preclinical Small Animal Studies. Sensors 2022, 22, 5130. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21, 803–806. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Hu, S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Liu, H.; Wang, L.V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photonics 2011, 5, 154–157. [Google Scholar] [CrossRef]
- Wang, L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 2009, 3, 503–509. [Google Scholar] [CrossRef]
- Culver, J.P.; Ntziachristos, V.; Holboke, M.J.; Yodh, A.G. Optimization of optode arrangements for diffuse optical tomography: A singular-value analysis. Opt. Lett. 2001, 26, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wang, L.V. Photoacoustic tomography and sensing in biomedicine. Phys. Med. Biol. 2009, 54, R59. [Google Scholar] [CrossRef] [PubMed]
- Lou, C.; Yang, S.; Ji, Z.; Chen, Q.; Xing, D. Ultrashort microwave-induced thermoacoustic imaging: A breakthrough in excitation efficiency and spatial resolution. Phys. Rev. Lett. 2012, 109, 218101. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Zheng, Z.; Liu, S.; Zhang, R.; Liao, X.; Liu, S.; Zheng, Y. Pre-migration: A General Extension for Photoacoustic Imaging Reconstruction. IEEE Trans. Comput. Imaging 2020, 6, 1097–1105. [Google Scholar] [CrossRef]
- Liu, S.; Feng, X.; Jin, H.; Zhang, R.; Luo, Y.; Zheng, Z.; Gao, F.; Zheng, Y. Handheld Photoacoustic Imager for Theranostics in 3D. IEEE Trans. Med. Imaging 2019, 38, 2037–2046. [Google Scholar] [CrossRef] [PubMed]
- Baumann, B.; Wolff, M.; Kost, B.; Groninga, H. Finite element calculation of photoacoustic signals. Appl. Opt. 2007, 46, 1120–1125. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Tang, K.; Feng, X.; Jin, H.; Gao, F.; Zheng, Y. Toward Wearable Healthcare: A Miniaturized 3D Imager with Coherent Frequency-Domain Photoacoustics. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1417–1424. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V. Tutorial on Photoacoustic Microscopy and Computed Tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Zhou, Y.; Yao, J.; Wang, L.V. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016, 21, 061007. [Google Scholar] [CrossRef]
- Wang, L.V.; Yao, J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods 2016, 13, 627–638. [Google Scholar] [CrossRef]
- Attia, A.B.E.; Balasundaram, G.; Moothanchery, M.; Dinish, U.S.; Bi, R.; Ntziachristos, V.; Olivo, M. A review of clinical photoacoustic imaging: Current and future trends. Photoacoustics 2019, 16, 100144. [Google Scholar] [CrossRef]
- Xia, J.; Yao, J.; Wang, L.V. Photoacoustic tomography: Principles and advances. Electromagn. Waves 2014, 147, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Roberts, W.W.; Carson, P.L.; Wood, D.P.; Fowlkes, J.B. Photoacoustic tomography: A potential new tool for prostate cancer. Biomed. Opt. Express 2010, 1, 1117–1126. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E 2005, 71, 016706. [Google Scholar] [CrossRef]
- Haltmeier, M.; Scherzer, O.; Burgholzer, P.; Nuster, R.; Paltauf, G. Thermoacoustic Tomography and the Circular Radon Transform: Exact Inversion Formula. Math. Models Methods Appl. Sci. 2011, 17, 635–655. [Google Scholar] [CrossRef]
- Köstli, K.P.; Beard, P.C. Two-dimensional photoacoustic imaging by use of Fourier-transform image reconstruction and a detector with an anisotropic response. Appl. Opt. 2003, 42, 1899–1908. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.F.; Maslov, K.; Stoica, G.; Wang, L.V. Functional photoacoustic microscopy for high-resolution and noninvasive in vivo imaging. Nat. Biotechnol. 2006, 24, 848–851. [Google Scholar] [CrossRef]
- Hu, S.; Maslov, K.; Wang, L.V. Second-generation optical-resolution photoacoustic microscopy with improved sensitivity and speed. Opt. Lett. 2011, 36, 1134–1136. [Google Scholar] [CrossRef]
- Xie, Z.; Roberts, W.; Carson, P.; Liu, X.; Tao, C.; Wang, X. Evaluation of bladder microvasculature with high-resolution photoacoustic imaging. Opt. Lett. 2011, 36, 4815–4817. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, X.; Gong, H.; Luo, Q. Adaptive synthetic-aperture focusing technique for microvasculature imaging using photoacoustic microscopy. Opt. Express 2012, 20, 7555–7563. [Google Scholar] [CrossRef]
- Yang, J.-M.; Favazza, C.; Chen, R.; Yao, J.; Cai, X.; Maslov, K.; Zhou, Q.; Shung, K.K.; Wang, L.V. Simultaneous functional photoacoustic and ultrasonic endoscopy of internal organs in vivo. Nat. Med. 2012, 18, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Dong, B.; Chen, S.; Zhang, Z.; Sun, C.; Zhang, H.F. Photoacoustic probe using a microring resonator ultrasonic sensor for endoscopic applications. Opt. Lett. 2014, 39, 4372–4375. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Gao, L. Photoacoustic Microscopy and Computed Tomography: From Bench to Bedside. Annu. Rev. Biomed. Eng. 2014, 16, 155–185. [Google Scholar] [CrossRef] [PubMed]
- Luke, G.P.; Yeager, D.; Emelianov, S.Y. Biomedical Applications of Photoacoustic Imaging with Exogenous Contrast Agents. Ann. Biomed. Eng. 2011, 40, 422–437. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, I.; Huland, D.M.; Vermesh, O.; Frostig, H.E.; Tummers, W.S.; Gambhir, S.S. Photoacoustic clinical imaging. Photoacoustics 2019, 14, 77–98. [Google Scholar] [CrossRef]
- Jin, T.; Qi, W.; Liang, X.; Guo, H.; Liu, Q.; Xi, L. Photoacoustic Imaging of Brain Functions: Wide Filed-of-View Functional Imaging with High Spatiotemporal Resolution. Laser Photonics Rev. 2021, 16, 2100304. [Google Scholar] [CrossRef]
- Das, D.; Sharma, A.; Rajendran, P.; Pramanik, M. Another decade of photoacoustic imaging. Phys. Med. Biol. 2021, 66, 05TR01. [Google Scholar] [CrossRef]
- Ward, R. Compressed Sensing With Cross Validation. IEEE Trans. Inf. Theory 2009, 55, 5773–5782. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Candes, E.; Elad, M.; Yi, M. Applications of Sparse Representation and Compressive Sensing [Scanning the Issue]. Proc. IEEE 2010, 98, 906–909. [Google Scholar] [CrossRef]
- Yang, X.; Tao, X.; Dutkiewicz, E.; Huang, X.; Guo, Y.J.; Cui, Q. Energy-Efficient Distributed Data Storage for Wireless Sensor Networks Based on Compressed Sensing and Network Coding. IEEE Trans. Wirel. Commun. 2013, 12, 5087–5099. [Google Scholar] [CrossRef]
- Chen, F.; Chandrakasan, A.P.; Stojanovic, V.M. Design and Analysis of a Hardware-Efficient Compressed Sensing Architecture for Data Compression in Wireless Sensors. IEEE J. Solid-State Circuits 2012, 47, 744–756. [Google Scholar] [CrossRef]
- Gilbert, A.C.; Indyk, P.; Iwen, M.; Schmidt, L. Recent Developments in the Sparse Fourier Transform: A compressed Fourier transform for big data. IEEE Signal Process. Mag. 2014, 31, 91–100. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Sapiro, G. Learning to Sense Sparse Signals: Simultaneous Sensing Matrix and Sparsifying Dictionary Optimization. IEEE Trans. Image Process. 2009, 18, 1395–1408. [Google Scholar] [CrossRef]
- Kulkarni, N.; Nagesh, P.; Gowda, R.; Li, B. Understanding Compressive Sensing and Sparse Representation-Based Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 778–789. [Google Scholar] [CrossRef]
- Peyre, G. Best Basis Compressed Sensing. IEEE Trans. Signal Process. 2010, 58, 2613–2622. [Google Scholar] [CrossRef]
- Almasri, N.; Sadhu, A.; Ray Chaudhuri, S. Toward Compressed Sensing of Structural Monitoring Data Using Discrete Cosine Transform. J. Comput. Civ. Eng. 2020, 34, 04019041. [Google Scholar] [CrossRef]
- Wu, S.; Dimakis, A.; Sanghavi, S.; Yu, F.; Holtmann-Rice, D.; Storcheus, D.; Rostamizadeh, A.; Kumar, S. Learning a compressed sensing measurement matrix via gradient unrolling. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6828–6839. [Google Scholar]
- Tillmann, A.M.; Pfetsch, M.E. The Computational Complexity of the Restricted Isometry Property, the Nullspace Property, and Related Concepts in Compressed Sensing. IEEE Trans. Inf. Theory 2014, 60, 1248–1259. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N.; El Ghazi, H.; Tamtaoui, A. A performance comparison of measurement matrices in compressive sensing. Int. J. Commun. Syst. 2018, 31, e3576. [Google Scholar] [CrossRef]
- Gu, B.; Chen, Y.; Liu, X.; Zhou, F.; Jiang, R. Distributed Convex Optimization Compressed Sensing Method for Sparse Planar Array Synthesis in 3-D Imaging Sonar Systems. IEEE J. Ocean. Eng. 2020, 45, 1022–1033. [Google Scholar] [CrossRef]
- Liu, E.; Temlyakov, V.N. The Orthogonal Super Greedy Algorithm and Applications in Compressed Sensing. IEEE Trans. Inf. Theory 2012, 58, 2040–2047. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Bilen, C.; Puy, G.; Gribonval, R.; Daudet, L. Convex Optimization Approaches for Blind Sensor Calibration Using Sparsity. IEEE Trans. Signal Process. 2014, 62, 4847–4856. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, J.; Xu, S.; Wang, Y.; Qiao, Z. Compressive sensing for noisy solder joint imagery based on convex optimization. Solder. Surf. Mt. Technol. 2016, 28, 114–122. [Google Scholar] [CrossRef]
- Vincent, P.; Bengio, Y. Kernel Matching Pursuit. Mach. Learn. 2002, 48, 165–187. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- You, C.; Robinson, D.; Vidal, R. Scalable sparse subspace clustering by orthogonal matching pursuit. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3918–3927. [Google Scholar]
- Zhu, H.; Chen, W.; Wu, Y. Efficient Implementations for Orthogonal Matching Pursuit. Electronics 2020, 9, 1507. [Google Scholar] [CrossRef]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian Compressive Sensing Via Belief Propagation. IEEE Trans. Signal Process. 2010, 58, 269–280. [Google Scholar] [CrossRef]
- Kratkiewicz, K.; Pattyn, A.; Alijabbari, N.; Mehrmohammadi, M. Ultrasound and Photoacoustic Imaging of Breast Cancer: Clinical Systems, Challenges, and Future Outlook. J. Clin. Med. 2022, 11, 1165. [Google Scholar] [CrossRef]
- Oraevsky, A.A.; Cox, B.T.; Wang, L.V.; Laufer, J.G.; Beard, P.C. The challenges for quantitative photoacoustic imaging. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2009, San Jose, CA, USA, 25–28 January 2009. [Google Scholar]
- Wang, L.V. Prospects of photoacoustic tomography. Med. Phys. 2008, 35, 5758–5767. [Google Scholar] [CrossRef]
- Paltauf, G.; Nuster, R.; Burgholzer, P. Weight factors for limited angle photoacoustic tomography. Phys. Med. Biol. 2009, 54, 3303. [Google Scholar] [CrossRef]
- Tao, C.; Liu, X.J. Reconstruction of high quality photoacoustic tomography with a limited-view scanning. Opt. Express 2010, 18, 2760–2766. [Google Scholar] [CrossRef]
- Guan, S.; Khan, A.A.; Sikdar, S.; Chitnis, P.V. Limited-View and Sparse Photoacoustic Tomography for Neuroimaging with Deep Learning. Sci. Rep. 2020, 10, 8510. [Google Scholar] [CrossRef]
- John, M.J.; Barhumi, I. Compressive Sensing Based Algorithms for Limited-View PAT Image Reconstruction. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Taipei, Taiwan, 31 October–3 November 2023; pp. 1317–1322. [Google Scholar]
- Meng, J.; Liu, C.; Kim, J.; Kim, C.; Song, L. Compressed Sensing with a Gaussian Scale Mixture Model for Limited View Photoacoustic Computed Tomography In Vivo. Technol. Cancer Res. Treat. 2018, 17, 1533033818808222. [Google Scholar] [CrossRef]
- Yang, D.W.; Xing, D.; Gu, H.M.; Tan, Y.; Zeng, L.M. Fast multielement phase-controlled photoacoustic imaging based on limited-field-filtered back-projection algorithm. Appl. Phys. Lett. 2005, 87, 194101. [Google Scholar] [CrossRef]
- Gao, M.; Si, G.; Bai, Y.; Wang, L.V.; Liu, C.; Meng, J. Graphics processing unit accelerating compressed sensing photoacoustic computed tomography with total variation. Appl. Opt. 2020, 59, 712–719. [Google Scholar] [CrossRef]
- Haltmeier, M.; Berer, T.; Moon, S.; Burgholzer, P. Compressed sensing and sparsity in photoacoustic tomography. J. Opt. 2016, 18, 114004. [Google Scholar] [CrossRef]
- Liu, X.; Peng, D.; Guo, W.; Ma, X.; Yang, X.; Tian, J. Compressed Sensing Photoacoustic Imaging Based on Fast Alternating Direction Algorithm. Int. J. Biomed. Imaging 2012, 2012, 206214. [Google Scholar] [CrossRef]
- Kratkiewicz, K.; Manwar, R.; Zhou, Y.; Mozaffarzadeh, M.; Avanaki, K. Technical considerations in the Verasonics research ultrasound platform for developing a photoacoustic imaging system. Biomed. Opt. Express 2021, 12, 1050–1084. [Google Scholar] [CrossRef]
- Guo, Y.; Li, B.; Yin, X. Dual-compressed photoacoustic single-pixel imaging. Natl. Sci. Rev. 2023, 10, nwac058. [Google Scholar] [CrossRef]
- Green, D.; Gelb, A.; Luke, G.P. Sparsity-Based Recovery of Three-Dimensional Photoacoustic Images from Compressed Single-Shot Optical Detection. J. Imaging 2021, 7, 201. [Google Scholar] [CrossRef]
- Paul, S.; Mandal, S.; Singh, M.S. Noise Adaptive Beamforming for Linear Array Photoacoustic Imaging. IEEE Trans. Instrum. Meas. 2021, 70, 4006511. [Google Scholar] [CrossRef]
- Huo, H.; Deng, H.; Gao, J.; Duan, H.; Ma, C. Mitigating Under-Sampling Artifacts in 3D Photoacoustic Imaging Using Res-UNet Based on Digital Breast Phantom. Sensors 2023, 23, 6970. [Google Scholar] [CrossRef]
- Provost, J.; Lesage, F. The Application of Compressed Sensing for Photo-Acoustic Tomography. IEEE Trans. Med. Imaging 2009, 28, 585–594. [Google Scholar] [CrossRef]
- Oraevsky, A.A.; Guo, Z.; Wang, L.V.; Li, C.; Song, L.; Wang, L.V. Compressed sensing in photoacoustic tomography with in vivo experiments. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2010, San Francisco, CA, USA, 24–26 January 2010. [Google Scholar]
- Treeby, B.E.; Zhang, E.Z.; Cox, B.T. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Probl. 2010, 26, 115003. [Google Scholar] [CrossRef]
- Ding, L.; Razansky, D.; Dean-Ben, X.L. Model-Based Reconstruction of Large Three-Dimensional Optoacoustic Datasets. IEEE Trans. Med. Imaging 2020, 39, 2931–2940. [Google Scholar] [CrossRef]
- Rosenthal, A.; Ntziachristos, V.; Razansky, D. Model-based optoacoustic inversion with arbitrary-shape detectors. Med. Phys. 2011, 38, 4285–4295. [Google Scholar] [CrossRef]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Fast Semi-Analytical Model-Based Acoustic Inversion for Quantitative Optoacoustic Tomography. IEEE Trans. Med. Imaging 2010, 29, 1275–1285. [Google Scholar] [CrossRef]
- Liu, S.; Lu, Y.; Zhu, X.; Jin, H. Measurement matrix uncertainty model-based microwave induced thermoacoustic sparse reconstruction in acoustically heterogeneous media. Appl. Phys. Lett. 2021, 119, 263701. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Wang, J. Efficient block-sparse model-based algorithm for photoacoustic image reconstruction. Biomed. Signal Process. Control. 2016, 26, 11–22. [Google Scholar] [CrossRef]
- Dean-Ben, X.L.; Buehler, A.; Ntziachristos, V.; Razansky, D. Accurate Model-Based Reconstruction Algorithm for Three-Dimensional Optoacoustic Tomography. IEEE Trans. Med. Imaging 2012, 31, 1922–1928. [Google Scholar] [CrossRef]
- Deán-Ben, X.L.; Razansky, D. A practical guide for model-based reconstruction in optoacoustic imaging. Front. Phys. 2022, 10, 1028258. [Google Scholar] [CrossRef]
- Park, H.; Yao, J.; Jing, Y. A frequency-domain model-based reconstruction method for transcranial photoacoustic imaging: A 2D numerical investigation. Photoacoustics 2023, 33, 100561. [Google Scholar] [CrossRef]
- Guo, Z.; Li, C.; Song, L.; Wang, L.V. Compressed sensing in photoacoustic tomography in vivo. J. Biomed. Opt. 2010, 15, 021311. [Google Scholar] [CrossRef]
- Jing, M.; Liang, D.; Song, L. Compressed sensing photoacoustic tomography in vivo in time and frequency domains. In Proceedings of the 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics, Hong Kong, China, 5–7 January 2012; pp. 717–720. [Google Scholar]
- Liu, X.; Dai, S.; Wang, M.; Zhang, Y.; Akers, W. Compressed Sensing Photoacoustic Imaging Reconstruction Using Elastic Net Approach. Mol. Imaging 2022, 2022, 7877049. [Google Scholar] [CrossRef]
- Chiu, C.H.; Li, M.L. Compressive-sensing like grating-lobe suppressed image reconstruction for photoacoustic linear array imaging. In Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014; pp. 1277–1279. [Google Scholar]
- Francis, K.J.; Rajalakshmi, P.; Channappayya, S.S. Distributed compressed sensing for photo-acoustic imaging. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 1513–1517. [Google Scholar]
- Moein, M.; Ali, M.; Mohammadreza, N.; Mahdi, O. Model-based photoacoustic image reconstruction using compressed sensing and smoothed L0 norm. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2018, San Francisco, CA, USA, 28 January–1 February 2018; p. 104943. [Google Scholar]
- Wang, Z.-X.; Wang, H.-Q.; Ren, S.-L. Research on ADMM Reconstruction Algorithm of Photoacoustic Tomography with Limited Sampling Data. IEEE Access 2021, 9, 113631–113641. [Google Scholar] [CrossRef]
- Qin, Z.; Ma, Y.; Ma, L.; Liu, G.; Sun, M. Convolutional sparse coding for compressed sensing photoacoustic CT reconstruction with partially known support. Biomed. Opt. Express 2024, 15, 524–539. [Google Scholar] [CrossRef]
- Bu, S.; Liu, Z.; Shiina, T.; Fukutani, K. Matrix Compression and Compressed Sensing Reconstruction for Photoacoustic Tomography. Electron. Electr. Eng. 2012, 18, 101–104. [Google Scholar] [CrossRef]
- Lin, X.; Feng, N.; Qu, Y.; Chen, D.; Shen, Y.; Sun, M. Compressed sensing in synthetic aperture photoacoustic tomography based on a linear-array ultrasound transducer. Chin. Opt. Lett. 2017, 15, 101102. [Google Scholar] [CrossRef]
- Cao, M.; Yuan, J.; Du, S.; Xu, G.; Wang, X.; Carson, P.L.; Liu, X. Full-view photoacoustic tomography using asymmetric distributed sensors optimized with compressed sensing method. Biomed. Signal Process. Control. 2015, 21, 19–25. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y.; Wang, Z.; Wang, X. Three-Dimensional Microwave-Induced Thermoacoustic Imaging Based on Compressive Sensing Using an Analytically Constructed Dictionary. IEEE Trans. Microw. Theory Tech. 2020, 68, 377–386. [Google Scholar] [CrossRef]
- Qin, T.; Wang, X.; Qin, Y.; Wan, G.; Witte, R.S.; Xin, H. Quality Improvement of Thermoacoustic Imaging Based on Compressive Sensing. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1200–1203. [Google Scholar] [CrossRef]
- Wang, B.; Ma, X.; Liu, S.; Zhu, X. Efficient dictionary construction method for microwave induced thermoacoustic compressive sensing imaging. Appl. Phys. Lett. 2018, 113, 053701. [Google Scholar] [CrossRef]
- Xiaozhang, Z.; Zhiqin, Z.; Jinguo, W.; Jian, S.; Qing Huo, L. Microwave-Induced Thermal Acoustic Tomography for Breast Tumor Based on Compressive Sensing. IEEE Trans. Biomed. Eng. 2013, 60, 1298–1307. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, Z.; Zhu, X.; Lu, Y.; Wang, B.; Nie, Z.; Liu, Q.-H. Block based compressive sensing method of microwave induced thermoacoustic tomography for breast tumor detection. J. Appl. Phys. 2017, 122, 024702. [Google Scholar] [CrossRef]
- Hu, D.; Wang, J.; Fang, E.; Zhou, W.; Zhou, Y. The application of compressed sensing method in photoacoustic image reconstruction. In Proceedings of the 2014 4th IEEE International Conference on Information Science and Technology, Shenzhen, China, 26–28 April 2014; pp. 256–259. [Google Scholar]
- Arridge, S.; Beard, P.; Betcke, M.; Cox, B.; Huynh, N.; Lucka, F.; Ogunlade, O.; Zhang, E. Accelerated high-resolution photoacoustic tomography via compressed sensing. Phys. Med. Biol. 2016, 61, 8908–8940. [Google Scholar] [CrossRef]
- Sandbichler, M.; Krahmer, F.; Berer, T.; Burgholzer, P.; Haltmeier, M. A Novel Compressed Sensing Scheme for Photoacoustic Tomography. SIAM J. Appl. Math. 2015, 75, 2475–2494. [Google Scholar] [CrossRef]
- Oraevsky, A.A.; Wang, L.V.; Burgholzer, P.; Sandbichler, M.; Krahmer, F.; Berer, T.; Haltmeier, M. Sparsifying transformations of photoacoustic signals enabling compressed sensing algorithms. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2016, San Francisco, CA, USA, 13–18 February 2016. [Google Scholar]
- Burgholzer, P.; Bauer-Marschallinger, J.; Grün, H.; Haltmeier, M.; Paltauf, G. Temporal back-projection algorithms for photoacoustic tomography with integrating line detectors. Inverse Probl. 2007, 23, S65–S80. [Google Scholar] [CrossRef]
- Lili, Z.; Jiajun, W.; Danfeng, H. The application of dictionary based compressed sensing for photoacoustic image. In Proceedings of the 2014 International Conference on Machine Learning and Cybernetics, Lanzhou, China, 13–16 July 2014; pp. 98–102. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Zheng, S.; Xiangyang, Y. Image reconstruction based on compressed sensing for sparse-data endoscopic photoacoustic tomography. Comput. Biol. Med. 2020, 116, 103587. [Google Scholar] [CrossRef]
- Betcke, M.M.; Cox, B.T.; Huynh, N.; Zhang, E.Z.; Beard, P.C.; Arridge, S.R. Acoustic Wave Field Reconstruction from Compressed Measurements With Application in Photoacoustic Tomography. IEEE Trans. Comput. Imaging 2017, 3, 710–721. [Google Scholar] [CrossRef]
- Candès, E.J.; Donoho, D.L. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Commun. Pure Appl. Math. 2004, 57, 219–266. [Google Scholar] [CrossRef]
- Sampsell, J.B. Digital micromirror device and its application to projection displays. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1994, 12, 3242–3246. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2018, 13, 13–20. [Google Scholar] [CrossRef]
- Kuusela, T.A. Single-pixel camera. Am. J. Phys. 2019, 87, 846–850. [Google Scholar] [CrossRef]
- Sun, M.; Feng, N.; Shen, Y.; Shen, X.; Ma, L.; Li, J.; Wu, Z. Photoacoustic imaging method based on arc-direction compressed sensing and multi-angle observation. Opt. Express 2011, 19, 14801–14806. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, H.F.; Ying, L. Compressed-sensing Photoacoustic Imaging based on random optical illumination. Int. J. Funct. Inform. Pers. Med. 2009, 2, 394–406. [Google Scholar] [CrossRef]
- Huynh, N.; Lucka, F.; Zhang, E.; Betcke, M.; Arridge, S.R.; Beard, P.C.; Cox, B.T. Single-pixel camera photoacoustic tomography. J. Biomed. Opt. 2019, 24, 121907. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, M.; Wang, Q.; Feng, N.; Shen, Y. Compressive sampling photoacoustic tomography based on edge expander codes and TV regularization. Chin. Opt. Lett. 2014, 12, 101102. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Hecht, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Phys. Today 2000, 53, 77–78. [Google Scholar] [CrossRef]
- Tromberg, B.J.; Yodh, A.G.; Sevick-Muraca, E.M.; Alfano, R.R.; Farina, A.; Betcke, M.; Di Sieno, L.; Bassi, A.; Ducros, N.; Pifferi, A.; et al. Diffuse optical tomography based on time-resolved compressive sensing. In Proceedings of the Optical Tomography and Spectroscopy of Tissue XII, San Francisco, CA, USA, 30 January–1 February 2017. [Google Scholar]
- Jin, H.; Wu, E.; Luo, Y.; Li, L.; Zhang, R.; Zheng, Y. A Compressed Sensing Based Miniaturized Photoacoustic Imaging System. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–9. [Google Scholar]
- Antholzer, S.; Schwab, J.; Haltmeier, M. Deep Learning Versus ℓ1-Minimization for Compressed Sensing Photoacoustic Tomography. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 206–212. [Google Scholar]
- Meng, J.; Liu, C.; Zheng, J.; Lin, R.; Song, L. Compressed sensing based virtual-detector photoacoustic microscopy in vivo. J. Biomed. Opt. 2014, 19, 36003. [Google Scholar] [CrossRef] [PubMed]
- Zangerl, G.; Haltmeier, M. Multiscale Factorization of the Wave Equation with Application to Compressed Sensing Photoacoustic Tomography. SIAM J. Imaging Sci. 2021, 14, 558–579. [Google Scholar] [CrossRef]
- Lucka, F.; Huynh, N.; Betcke, M.; Zhang, E.; Beard, P.; Cox, B.; Arridge, S. Enhancing Compressed Sensing 4D Photoacoustic Tomography by Simultaneous Motion Estimation. SIAM J. Imaging Sci. 2018, 11, 2224–2253. [Google Scholar] [CrossRef]
- Alberti, G.S.; Campodonico, P.; Santacesaria, M. Compressed Sensing Photoacoustic Tomography Reduces to Compressed Sensing for Undersampled Fourier Measurements. SIAM J. Imaging Sci. 2021, 14, 1039–1077. [Google Scholar] [CrossRef]
- Haltmeier, M.; Sandbichler, M.; Berer, T.; Bauer-Marschallinger, J.; Burgholzer, P.; Nguyen, L. A sparsification and reconstruction strategy for compressed sensing photoacoustic tomography. J. Acoust. Soc. Am. 2018, 143, 3838–3848. [Google Scholar] [CrossRef] [PubMed]
- Antholzer, S.; Schwab, J.; Bauer-Marschallinger, J.; Burgholzer, P.; Haltmeier, M. NETT regularization for compressed sensing photoacoustic tomography. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2019, San Francisco, CA, USA, 3–6 February 2019. [Google Scholar]
- Lan, H.; Zhang, J.; Yang, C.; Gao, F. Compressed sensing for photoacoustic computed tomography based on an untrained neural network with a shape prior. Biomed. Opt. Express 2021, 12, 7835–7848. [Google Scholar] [CrossRef]
- Pan, B.; Arridge, S.R.; Lucka, F.; Cox, B.T.; Huynh, N.; Beard, P.C.; Zhang, E.Z.; Betcke, M.M. Photoacoustic Reconstruction Using Sparsity in Curvelet Frame: Image Versus Data Domain. IEEE Trans. Comput. Imaging 2021, 7, 879–893. [Google Scholar] [CrossRef]










| Positions | Iterations | Experimental CPU Time (s) | SNR (dB) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Magic | SPG | ADM | Magic | SPG | ADM | Magic | SPG | ADM | |
| 16 | 67 | 340 | 88 | 471.2 | 16.3 | 5.5 | −3.8 | −3.6 | −3.5 |
| 24 | 75 | 422 | 73 | 692.1 | 28.7 | 3.4 | 0.7 | 0.9 | 3.9 |
| 32 | 77 | 345 | 68 | 831.5 | 29.5 | 7.9 | 3.3 | 3.4 | 3.6 |
| 40 | 78 | 350 | 58 | 877.5 | 37.5 | 6.6 | 11.1 | 12.l | 13.4 |
| 48 | 80 | 337 | 53 | 1280.7 | 43.2 | 9.3 | 11.1 | 11.7 | 13.8 |
| 56 | 79 | 317 | 46 | 1294.2 | 45.3 | 4.1 | 20.3 | 24.6 | 28.6 |
| 64 | 79 | 429 | 43 | 1179.6 | 64.5 | 5.0 | 20.4 | 22.1 | 25.9 |
| 72 | 81 | 367 | 46 | 1711.9 | 66.4 | 6.0 | 21.2 | 22.9 | 28.7 |
| 80 | 84 | 366 | 42 | 1580.9 | 68.7 | 11.4 | 22.7 | 29.1 | 29.7 |
| Average | 1102.2 | 44.5 | 6.6 | ||||||
| SDNR | Q | MSE | ||
|---|---|---|---|---|
| Breast cancer | Traditional PAT | 0.8792 | 0.3070 | 0.1140 |
| Improved PAT + CS | 0.9125 | 0.3443 | 0.1044 | |
| Improvement (%) | 3.79 | 12.15 | 8.42 | |
| Stomach | Traditional PAT | 1.7540 | 0.4020 | 0.0815 |
| Improved PAT + CS | 1.8225 | 0.4395 | 0.0739 | |
| Improvement (%) | 3.91 | 9.33 | 9.33 | |
| Intestine | Traditional PAT | 0.6494 | 0.3280 | 0.1093 |
| Improved PAT + CS | 0.6680 | 0.3785 | 0.1000 | |
| Improvement (%) | 2.86 | 15.40 | 8.51 | |
| Hip bone | Traditional PAT | 0.3550 | 0.3511 | 0.0648 |
| Improved PAT + CS | 0.3517 | 0.4166 | 0.0564 | |
| Imp roveme nt (%) | −0.93 | 18.66 | 12.96 | |
| Points | Direct Reconstruction | CS with DCT | CS with K-SVD |
|---|---|---|---|
| 150 | 0.003 | 0.002 | 0.002 |
| 100 | 0.008 | 0.004 | 0.003 |
| 50 | 0.017 | 0.012 | 0.001 |
| Points | Direct Reconstruction | CS with DCT | CS with K-SVD |
|---|---|---|---|
| 150 | 73.085 | 75.313 | 76.039 |
| 100 | 69.006 | 72.432 | 73.280 |
| 50 | 65.804 | 67.208 | 68.224 |
| Time Reversal | Two Stage Method | Physical Transmission Model Based CS Method | |
|---|---|---|---|
| MSE | 0.026 | 0.011 | 0.003 |
| SSIM | 0.553 | 0.621 | 0.791 |
| PSNR | 16.023 | 18.703 | 25.005 |
| SNR | 18.817 | 22.867 | 25.272 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, Y.; Zhao, Y.; Liu, S. Compressed Sensing for Biomedical Photoacoustic Imaging: A Review. Sensors 2024, 24, 2670. https://doi.org/10.3390/s24092670
Wang Y, Chen Y, Zhao Y, Liu S. Compressed Sensing for Biomedical Photoacoustic Imaging: A Review. Sensors. 2024; 24(9):2670. https://doi.org/10.3390/s24092670
Chicago/Turabian StyleWang, Yuanmao, Yang Chen, Yongjian Zhao, and Siyu Liu. 2024. "Compressed Sensing for Biomedical Photoacoustic Imaging: A Review" Sensors 24, no. 9: 2670. https://doi.org/10.3390/s24092670
APA StyleWang, Y., Chen, Y., Zhao, Y., & Liu, S. (2024). Compressed Sensing for Biomedical Photoacoustic Imaging: A Review. Sensors, 24(9), 2670. https://doi.org/10.3390/s24092670







