Analysis and Compensation of Lorentz Force Magnetic Bearing Magnetic Flux Density Uniformity Error
Abstract
:1. Introduction
2. LFMB Structure and Error Analysis
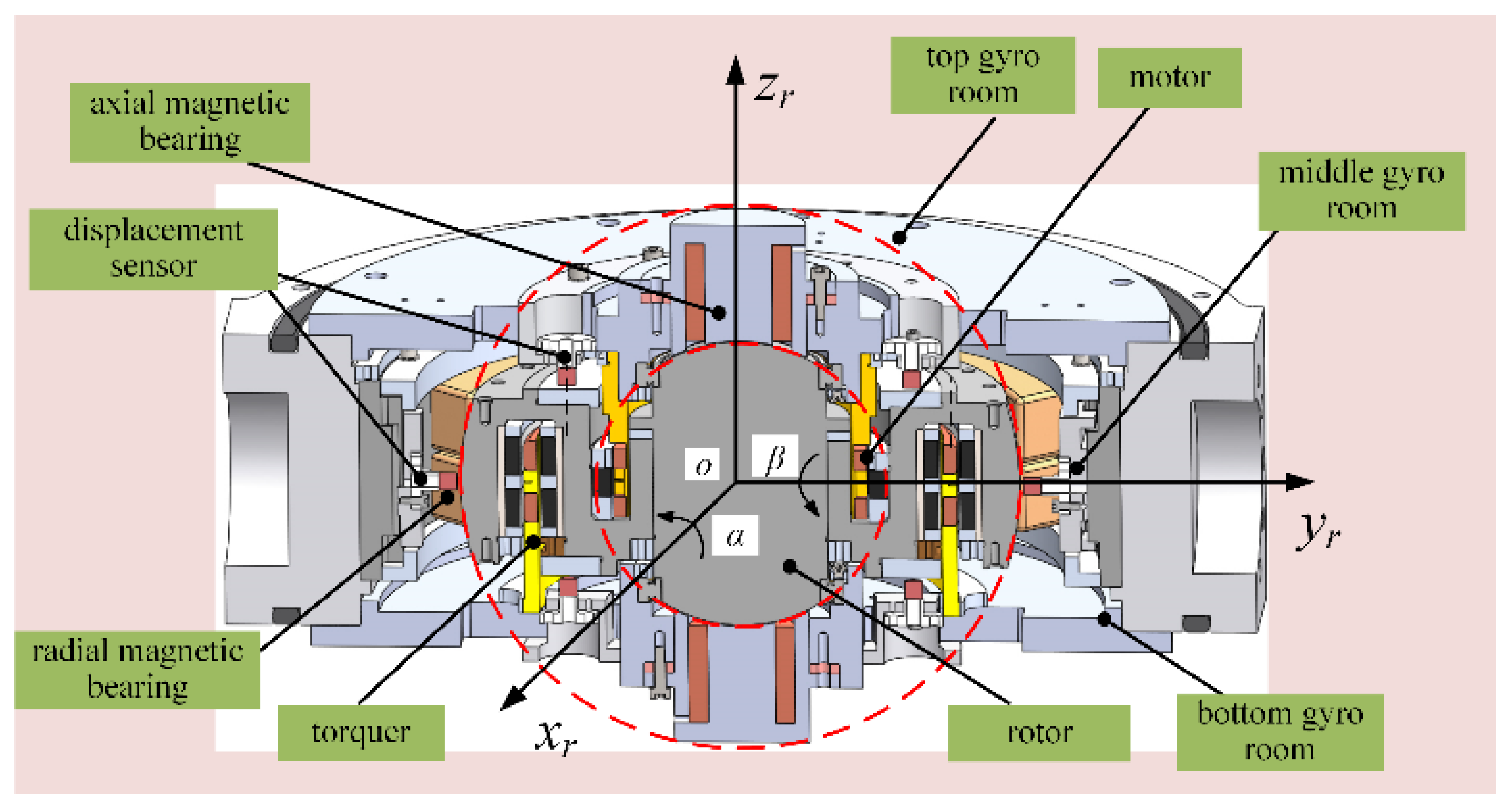
2.1. MSCSG Structure
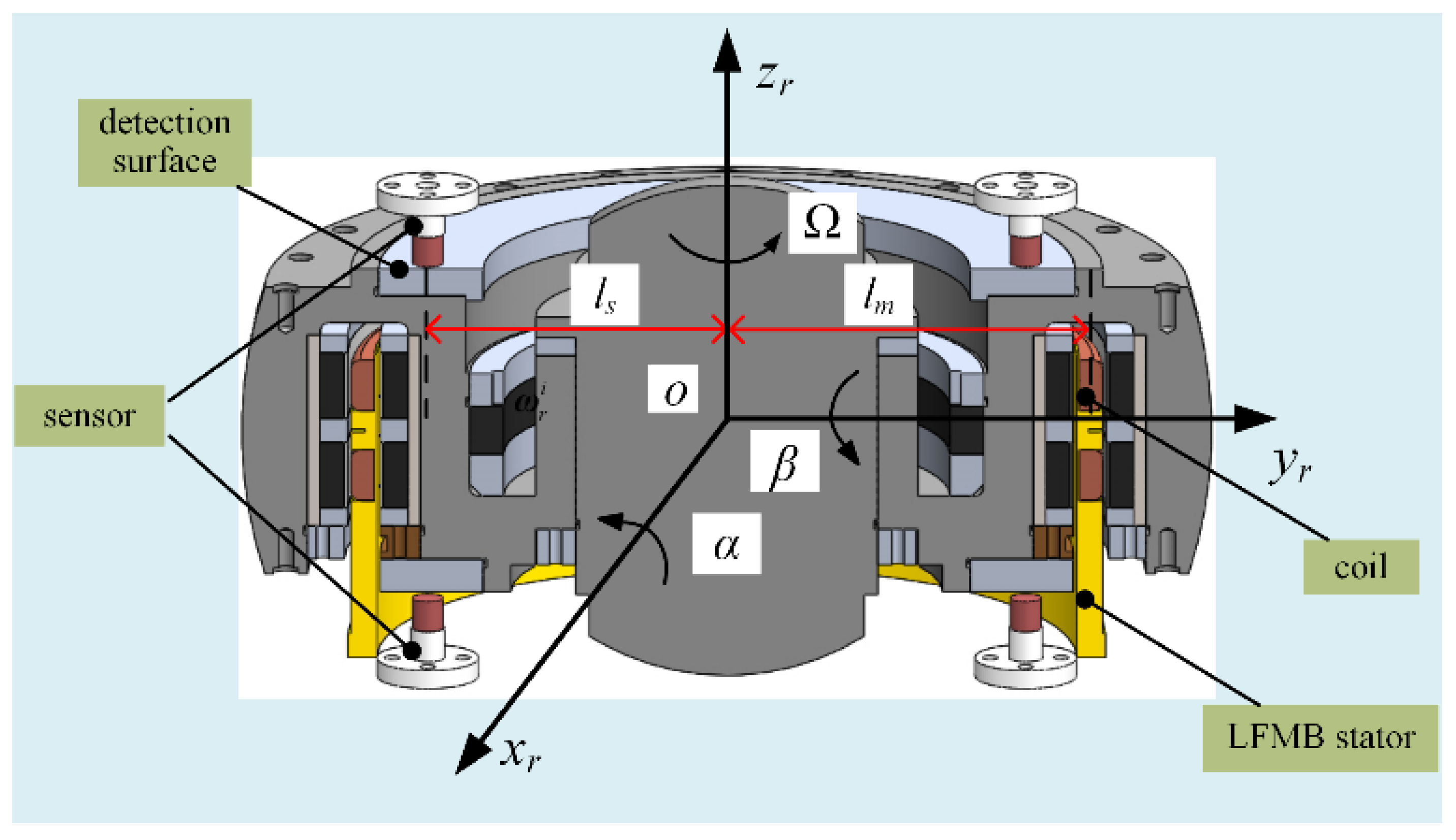
2.2. LFMB Structure and Sensitivity Principle
2.3. LFMB Magnetic Flux Density Error Analysis
3. LFMB Magnetic Flux Density Simulation Analysis and Error Compensation
3.1. Simulation Analysis of LFMB Magnetic Field
3.2. LFMB Magnetic Flux Density Error Compensation
4. Simulation and Experimental Results
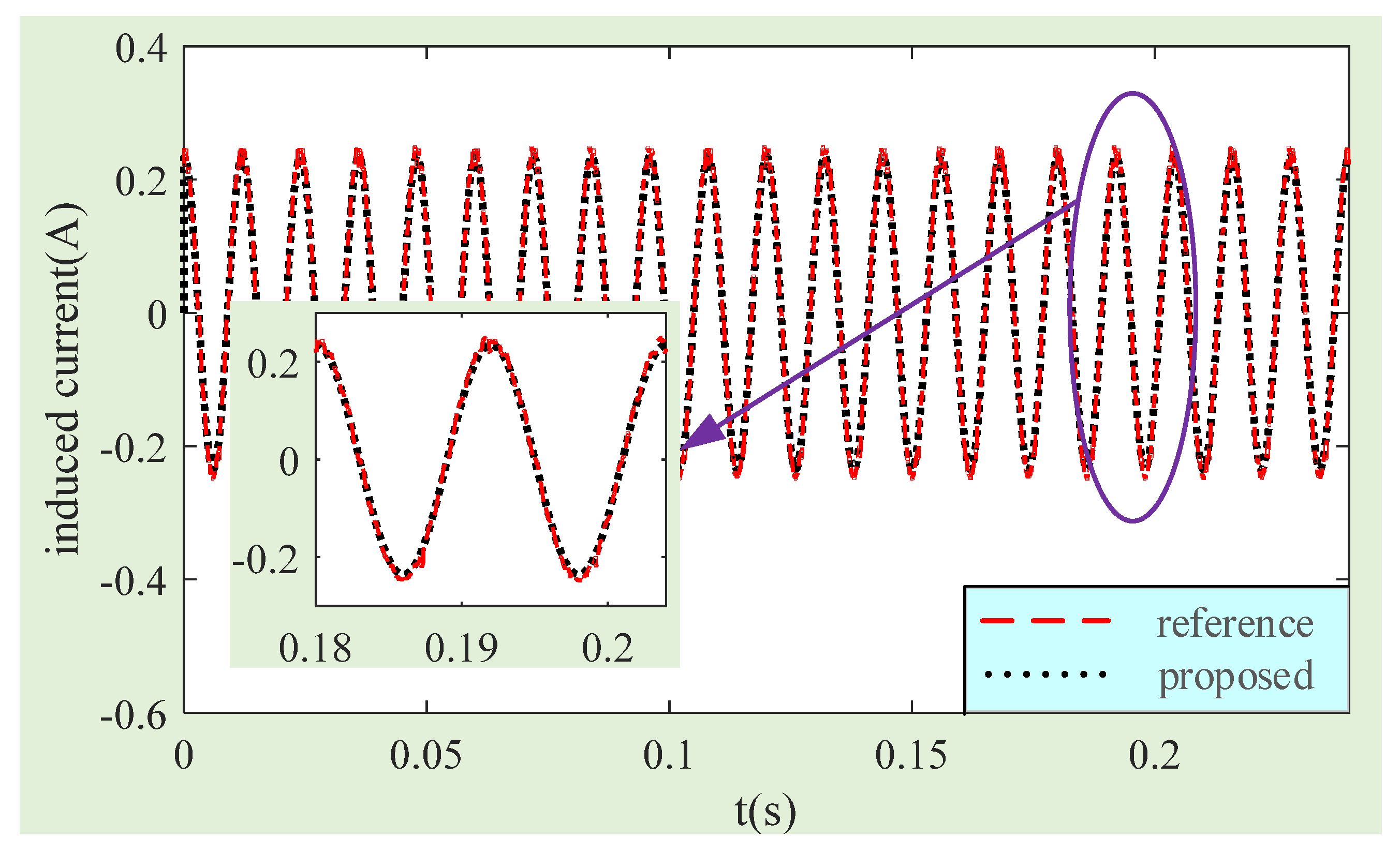
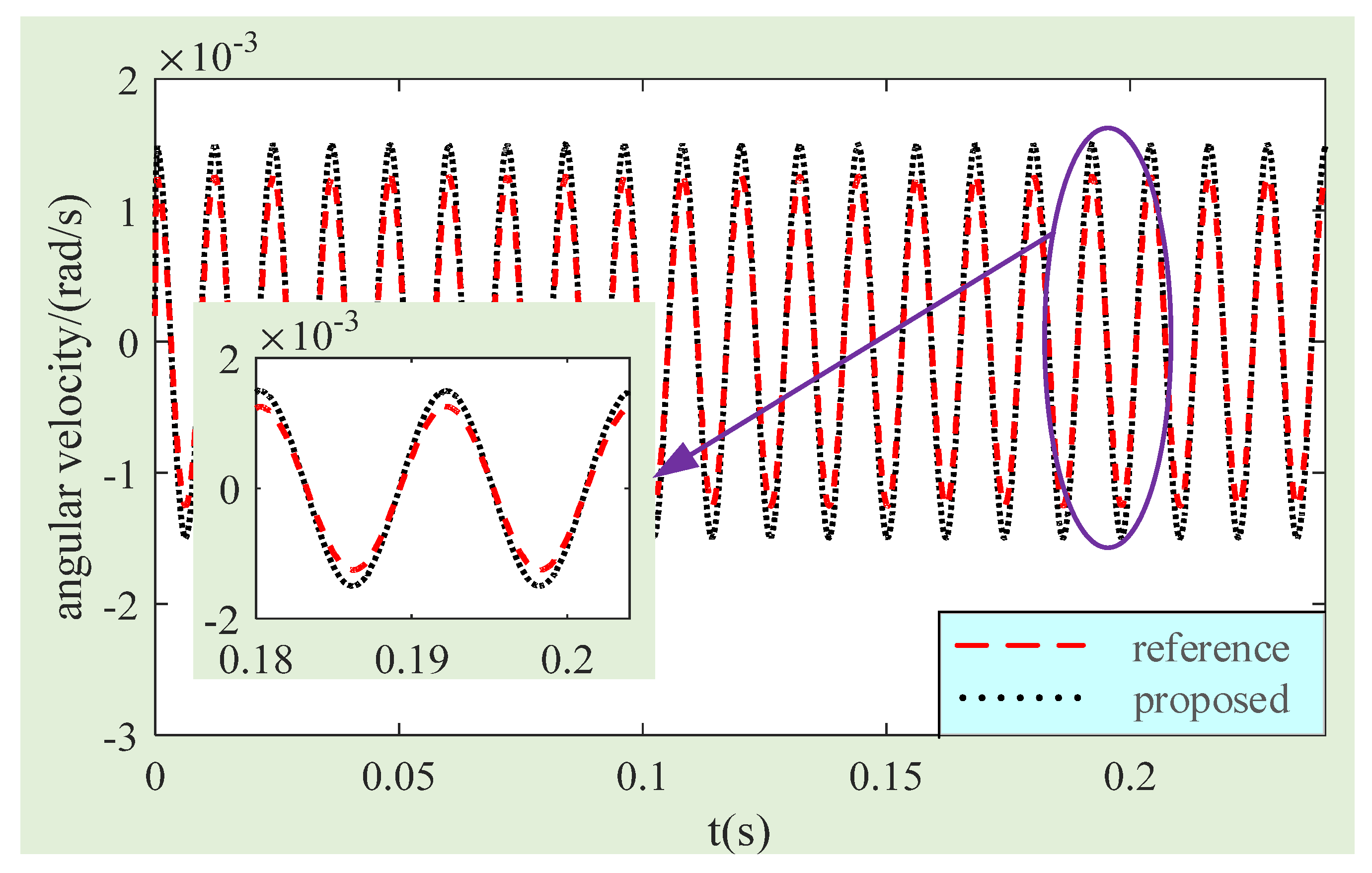
4.1. Simulation Verification of Compensation Method
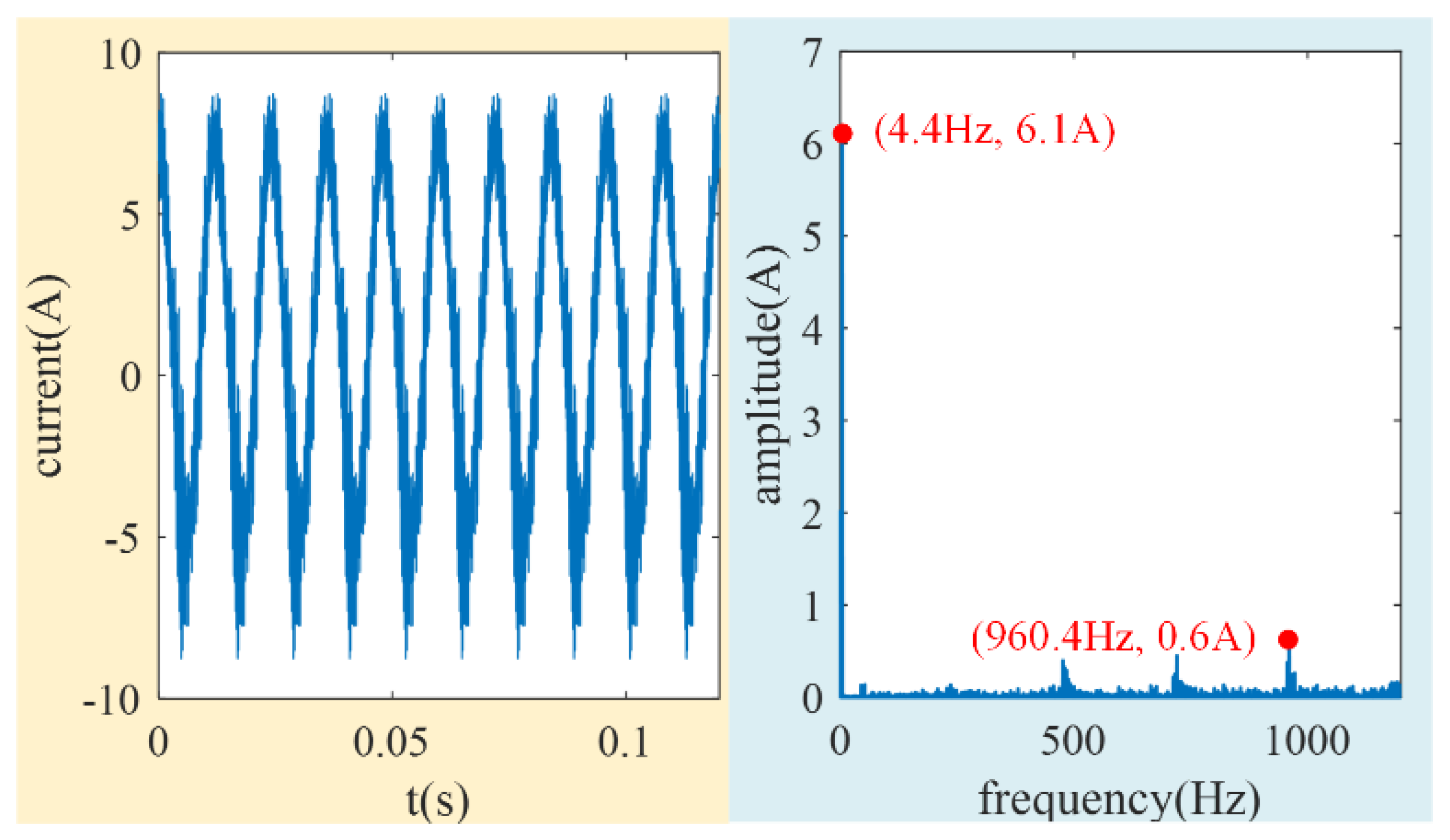
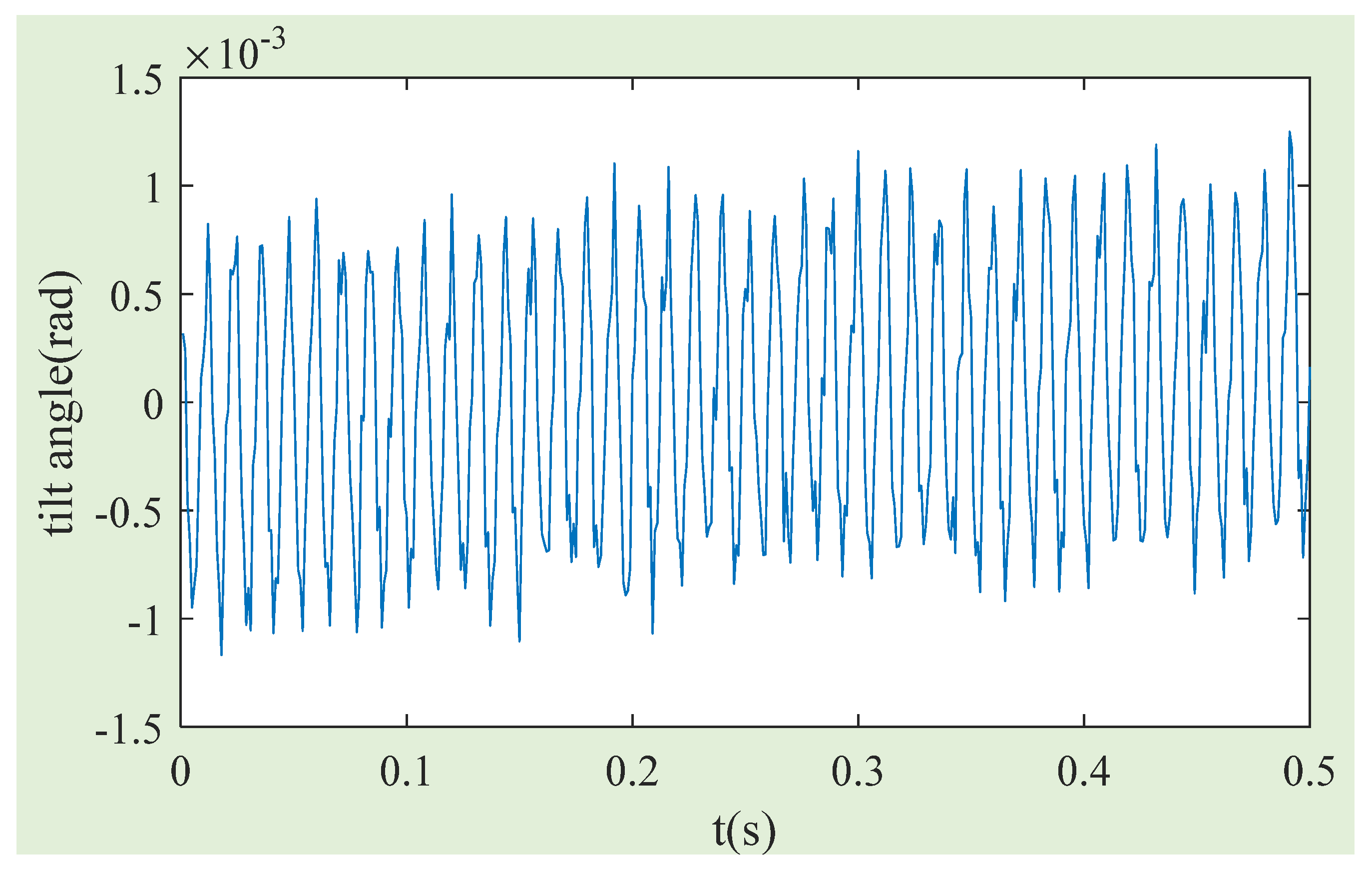
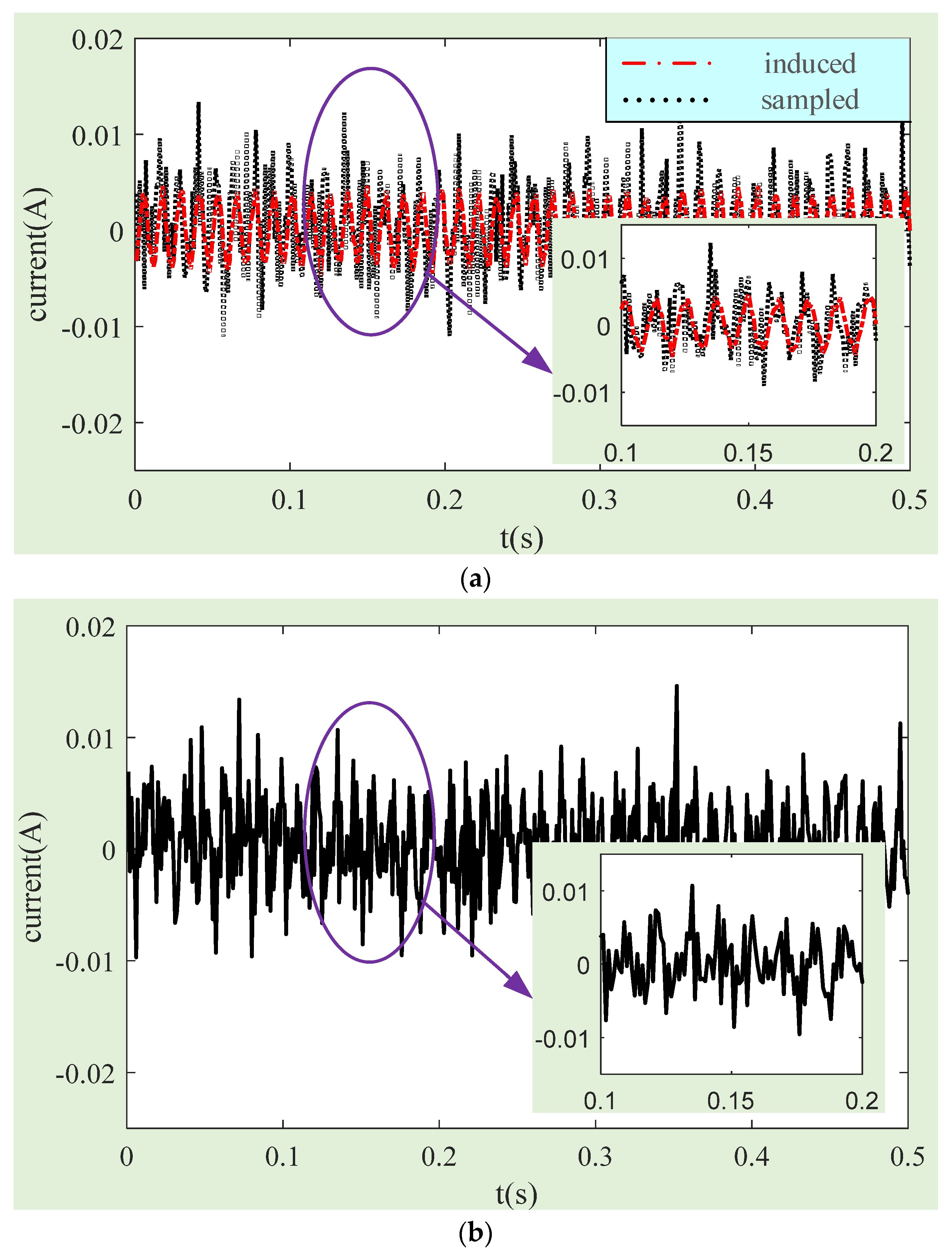
4.2. Experimental Verification of Compensation Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Liu, G.; Zheng, S.; Cui, P.; Chen, Q. Micro-Jitter Control of Magnetically Suspended Control Moment Gyro Using Adaptive LMS Algorithm. IEEE-ASME Trans. Mech. 2022, 27, 327–335. [Google Scholar] [CrossRef]
- Cui, P.; Du, L.; Zhou, X.; Li, J.; Li, Y.; Wu, Y. Synchronous vibration moment suppression for AMBs rotor system in control moment gyros considering rotor dynamic unbalance. IEEE-ASME Trans. Mechatron. 2022, 27, 3210–3218. [Google Scholar] [CrossRef]
- Yang, H.; Gao, S.; Liu, S.; Zhang, L.; Luo, S. Research on Identification and Suppression of Vibration Error for MEMS Inertial Sensor in Near-Bit Inclinometer. IEEE Sens. J. 2022, 22, 19645–19655. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, C. Rotor balancing for magnetically levitated TMPs integrated with vibration self-sensing of magnetic bearings. IEEE/ASME Trans. Mechatron. 2021, 26, 3031–3039. [Google Scholar] [CrossRef]
- Xu, S.; Sun, J.; Ren, H. An active magnetic bearing with controllable permanent-magnet bias field. IEEE-ASME Trans. Mech. 2022, 27, 3474–3481. [Google Scholar] [CrossRef]
- Chai, S.; Wang, S.; Liu, C.; Liu, T.; Liu, X.; Xing, K. Using Semantic Segmentation Network to Measure Vibration Displacement of Rotating Body. IEEE Sens. J. 2023, 23, 7977–7991. [Google Scholar] [CrossRef]
- Fang, J.; Zheng, S.; Han, B. Attitude Sensing and Dynamic Decoupling Based on Active Magnetic Bearing of MSDGCMG. IEEE Trans. Instrum. Meas. 2020, 67, 4066–4076. [Google Scholar] [CrossRef]
- Yunus, M.A.M.; Khairi, M.T.M.; Ibrahim, S. Narrow Band Vibration Measurement System with Electrodynamic Transducer Seismograph and Modeling Verification. IEEE Sens. J. 2020, 20, 4768–4777. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Liu, K.; Wei, J.; Hu, H. Modeling and control strategies of a novel axial hybrid magnetic bearing for flywheel energy storage system. IEEE/ASME Trans. Mechatron. 2022, 27, 3819–3829. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, B.; Ge, Q.; Liu, Y. Design and Analysis of a High Thrust Linear Voice Coil Motor Using for the Stiffness Test of Linear Motor Servo System. IEEE Trans. Magn. 2022, 58, 8200505. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Liu, C.-S.; Chen, I.-W.; Tsai, M.-S.; Tseng, H.-C. Open-Loop Control of Voice Coil Motor with Magnetic Restoring Force Using High-Low Frequency Composite Signals. IEEE Access 2019, 7, 146258–146263. [Google Scholar] [CrossRef]
- Chen, F.; Wang, W.; Wang, S. Rotating Lorentz Force Magnetic Bearings’ Dynamics Modeling and Adaptive Controller Design. Sensors 2023, 23, 8543. [Google Scholar] [CrossRef] [PubMed]
- Geng, M.; Ren, Y.; Fan, Y.; Wang, L.; Wu, C. Random error test and error source analysis of MSCSG. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1697–1704. [Google Scholar]
- Li, Z.; Wang, W.; Wang, L.; Ren, Y.; Fan, Y.; Li, L. Dynamics and Decoupling Control Method of Double Radial Lorentz Force Magnetic Bearings. J. Beihang Univ. 2024, 1–15. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, Z.; Han, C. Active vibration control of magnetically suspended wheel using active shaft deflection. IEEE Trans. Ind. Electron. 2017, 64, 6528–6537. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, Z.; Han, C. Fuzzy adaptive back-stepping sliding mode controller for high-precision deflection control of the magnetically suspended momentum wheel. IEEE Trans. Ind. Electron. 2018, 65, 3530–3538. [Google Scholar] [CrossRef]
- Xu, G.; Cai, Y.; Ren, Y.; Fan, Y.; Sun, J.; Zhao, H. Design and analysis on uniformity of magnetic flux density in Lorentz force-type magnetic bearing. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 559–566. [Google Scholar]
- Liu, Q.; Zhao, Y.; Dai, F.; Ren, Y.; Wang, W. Novel internal Lorentz magnetic bearing for magnetic bearing gyrowheel. Opt. Precis. Eng. 2018, 26, 399–409. [Google Scholar]
- Fu, B.; Wang, W.; Wang, Y.; Fan, Y.; Nie, C.; Jia, H. Design and analysis of high precision for spherical Lorentz force magnetic bearing. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 2222–2229. [Google Scholar]
- Zhao, Y.; Liu, Q.; Ma, L.; Wang, K. Novel Lorentz force-type magnetic bearing with flux congregating rings for magnetically suspended gyrowheel. IEEE Trans. Magn. 2019, 55, 8002208. [Google Scholar] [CrossRef]
- Xin, C.; Cai, Y.; Ren, Y.; Fan, Y.; Su, Y. Real-time compensation of errors caused by the flux density non-uniformity for a magnetically suspended sensitive gyroscope. J. Magn. 2017, 22, 315–325. [Google Scholar]
- Yu, C.; Cai, Y.W.; Ren, Y.; Fan, Y.; Wang, W.; Nie, C. Angular Rate Sensitive Method of Magnetically Suspended Control & Sensing Gyroscope Based on Deflection Current and Angle. IEEE Sens. J. 2021, 21, 12068–12076. [Google Scholar]










| Symbol | Quantity | Value |
|---|---|---|
| Jr | Transverse moments of inertia | 0.0097 kg·m2 |
| Jz | Polar moments of inertia | 0.0167 kg·m2 |
| L | Circumferential length of the coil | 80 mm |
| N | Coil turns | 200 |
| Ω | Rotor speed | 5000 r/min |
| lm | Radius of LFMB stator | 59 mm |
| ls | Radius of LFMB coil | 48.5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Cai, Y.; Wang, W.; Han, W.; Yin, Z.; Han, W. Analysis and Compensation of Lorentz Force Magnetic Bearing Magnetic Flux Density Uniformity Error. Sensors 2024, 24, 2683. https://doi.org/10.3390/s24092683
Yu C, Cai Y, Wang W, Han W, Yin Z, Han W. Analysis and Compensation of Lorentz Force Magnetic Bearing Magnetic Flux Density Uniformity Error. Sensors. 2024; 24(9):2683. https://doi.org/10.3390/s24092683
Chicago/Turabian StyleYu, Chunmiao, Yuanwen Cai, Weijie Wang, Wenjing Han, Zengyuan Yin, and Wenting Han. 2024. "Analysis and Compensation of Lorentz Force Magnetic Bearing Magnetic Flux Density Uniformity Error" Sensors 24, no. 9: 2683. https://doi.org/10.3390/s24092683
APA StyleYu, C., Cai, Y., Wang, W., Han, W., Yin, Z., & Han, W. (2024). Analysis and Compensation of Lorentz Force Magnetic Bearing Magnetic Flux Density Uniformity Error. Sensors, 24(9), 2683. https://doi.org/10.3390/s24092683





