Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Viaduct
2.2. Measurements of Strains under Passages of Calibration Vehicles
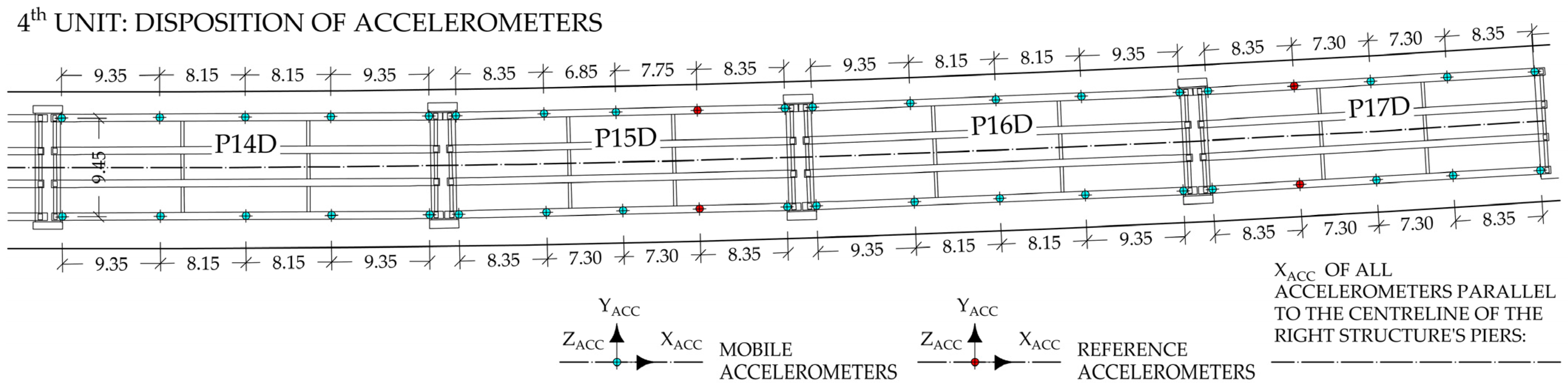
2.3. Ambient and Traffic-Induced Vibration Tests
2.4. Finite Element (FE) Model
2.4.1. Geometry and Materials
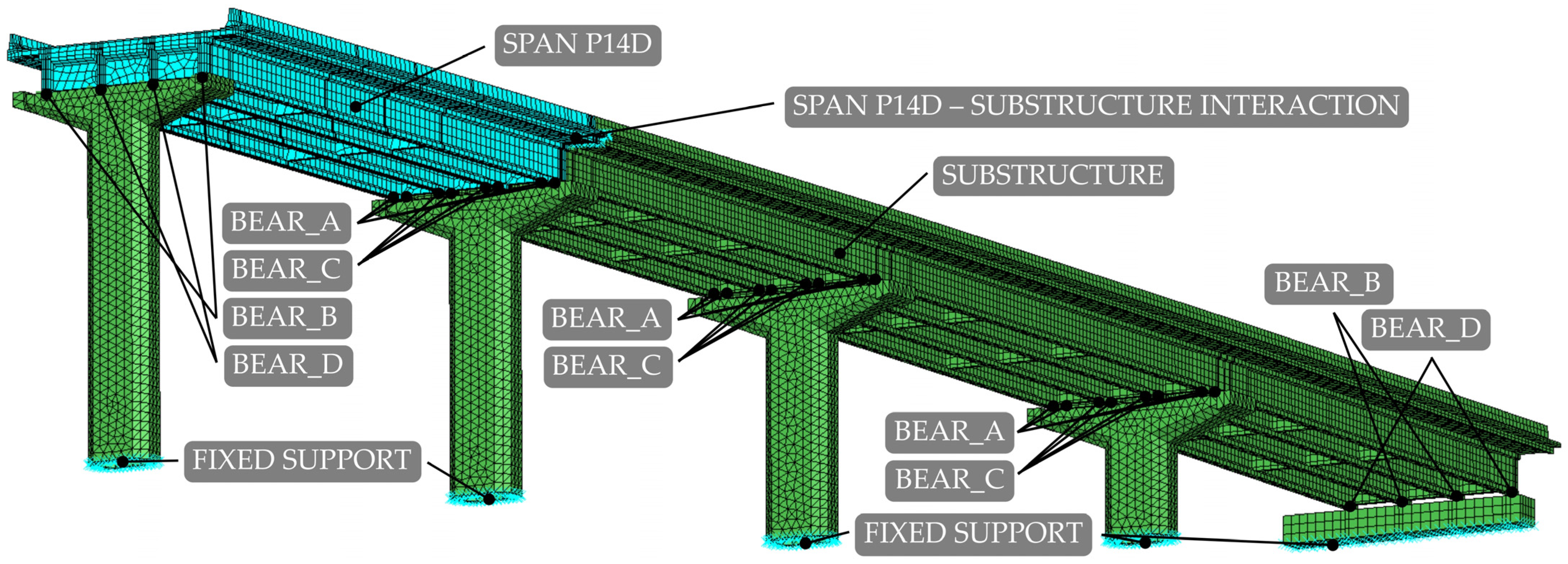
2.4.2. Interactions
2.4.3. Boundary Conditions and Interaction with Adjacent Unit
2.4.4. FE Mesh
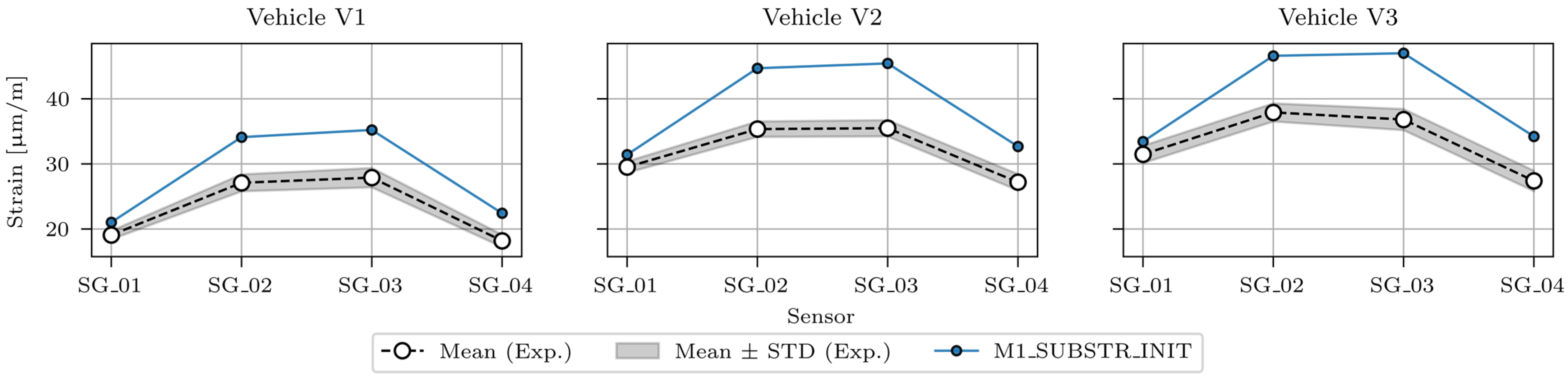
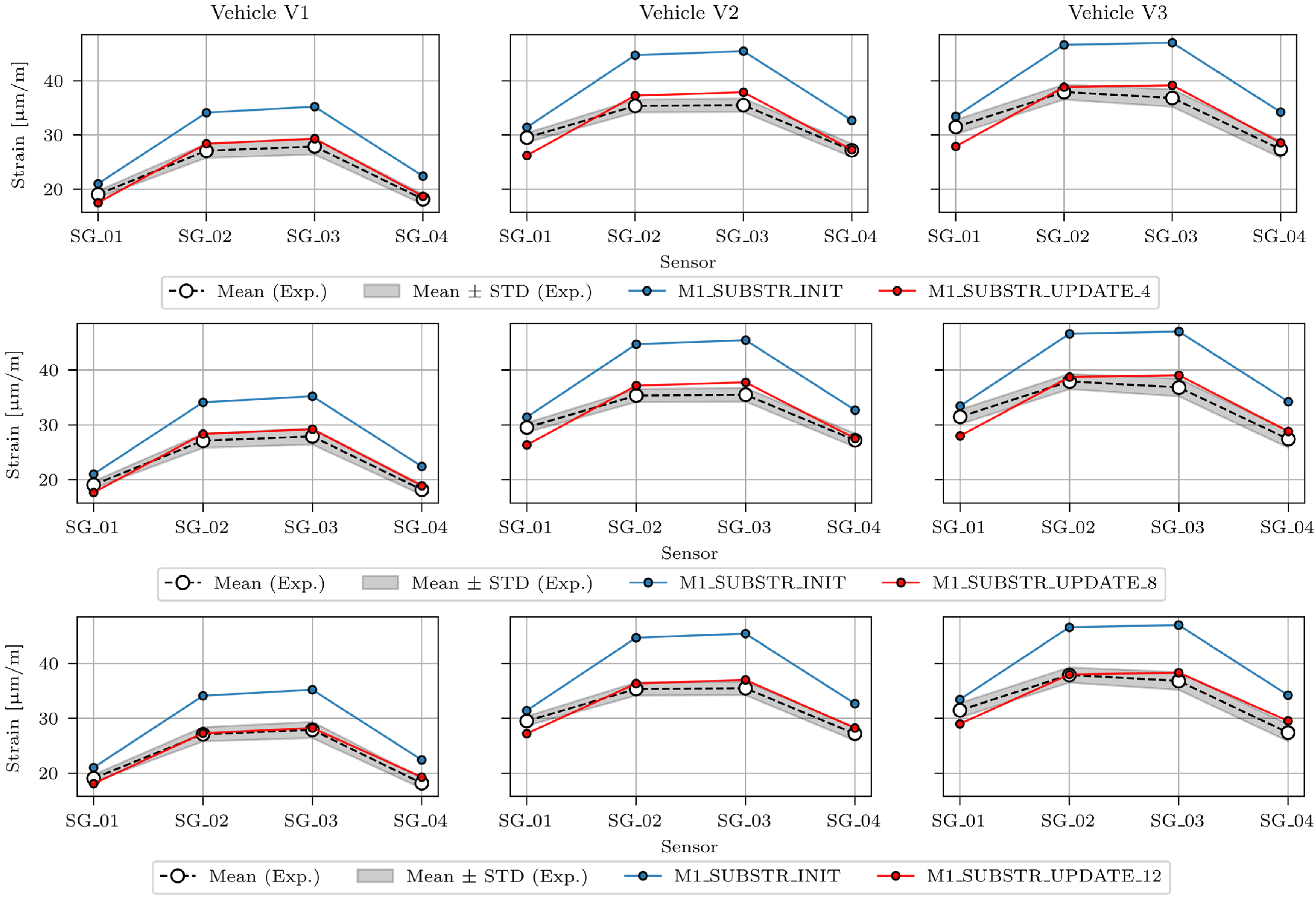
2.5. Comparison of the Initial FE Model M1_SUBSTR_INIT and Experiment
2.6. Finite Element Model Updating (FEMU): Residual Minimisation
2.6.1. Objective Functions for Acceleration-Based FEMU
2.6.2. Objective Function for Strain-Based FEMU
- denotes the main girder index;
- denotes the number of main girders considered (four in this study);
- denotes the number of strain gauges considered in a given girder g (two or three in this study);
- denotes the number of calibration vehicles considered (three in this study);
- denotes the number of vehicle v passages;
- denotes the passage index of the selected calibration vehicle;
- denotes the strain-gauge sensor index on the selected main girder;
- denotes the standard deviation of measured strains for main girder g and vehicle v;
- denotes the calibration vehicle index;
- denotes the maximum measured longitudinal strain (section) in the th strain-gauge sensor on the th main girder, caused by the th calibration vehicle during th passage;
- denotes the FE model longitudinal strain, oriented parallel to the X (longitudinal) direction of the viaduct, in the selected node that corresponds to the th strain-gauge sensor on the th main girder, caused by the th calibration vehicle positioned on the location that results in the maximum strain at sensors SG_0g.
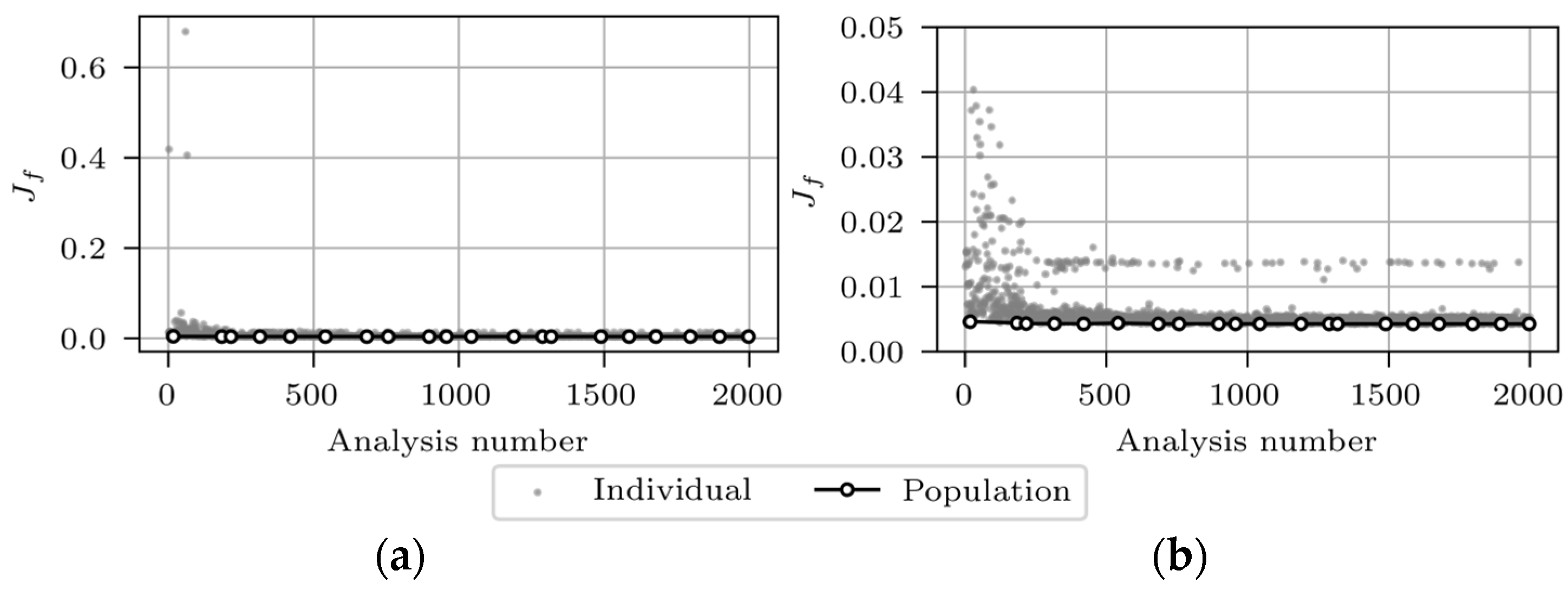
2.6.3. Optimisation Algorithm
2.7. FEMU: Error-Domain Model Falsification (EDMF)
3. Results
3.1. Sensitivity Study
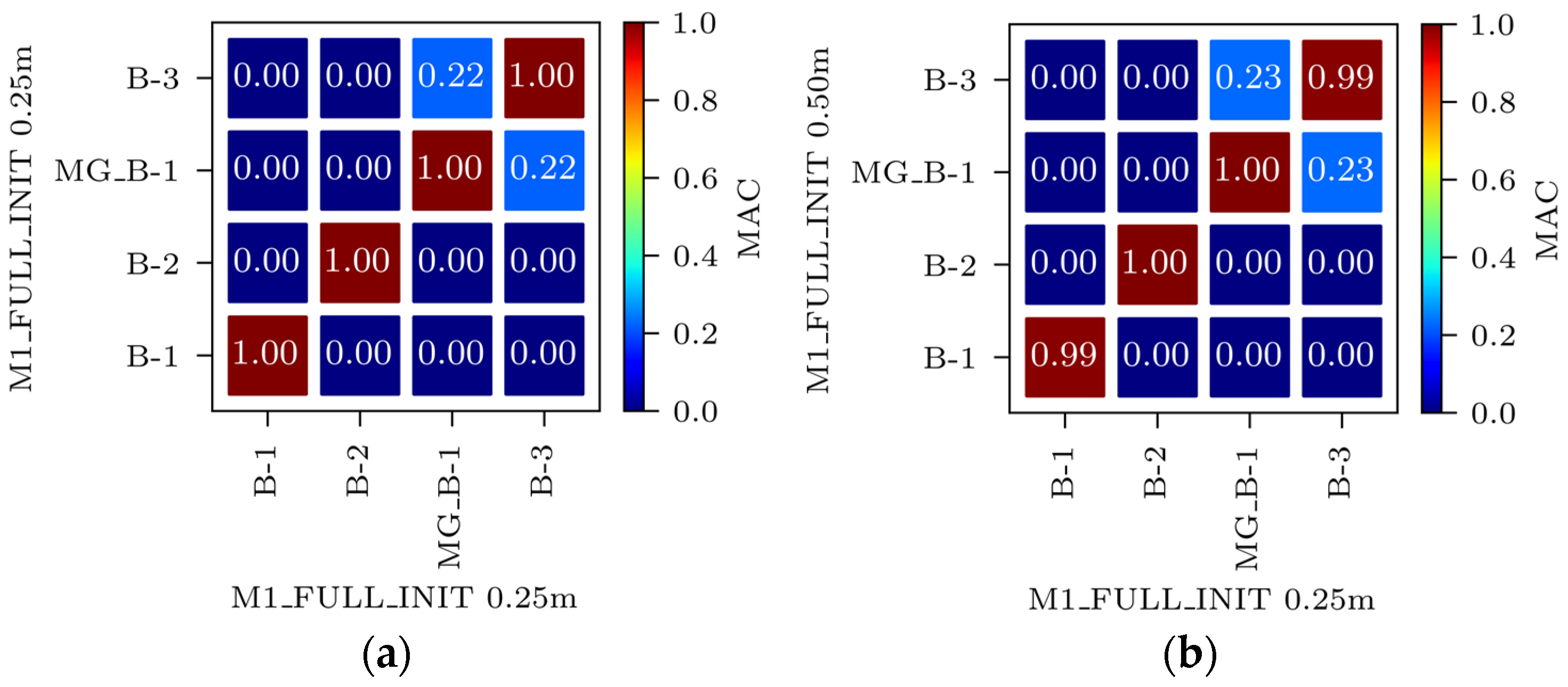
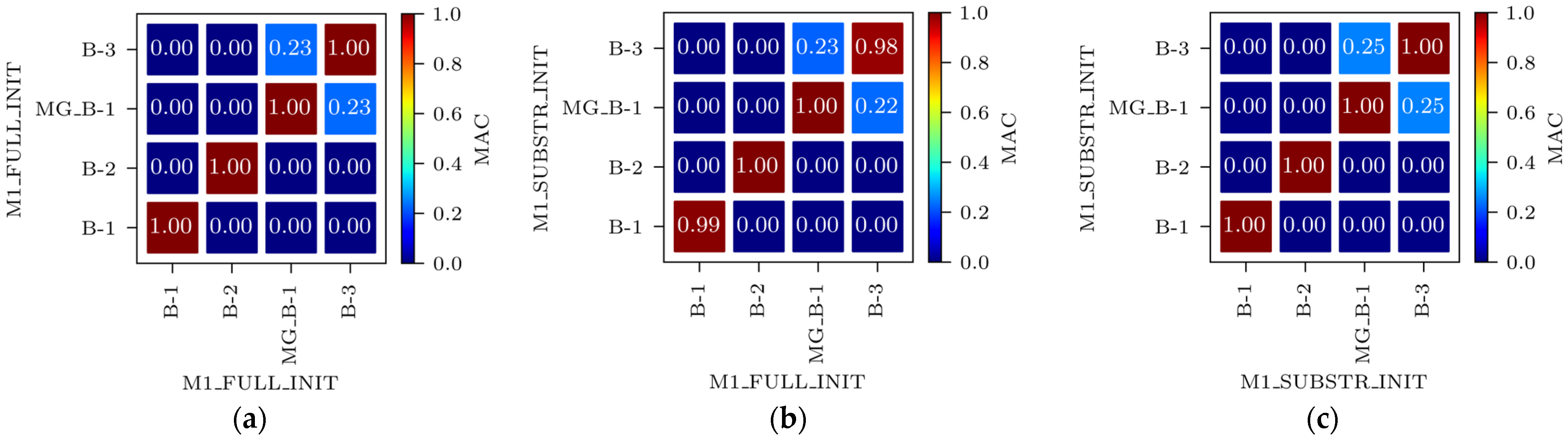
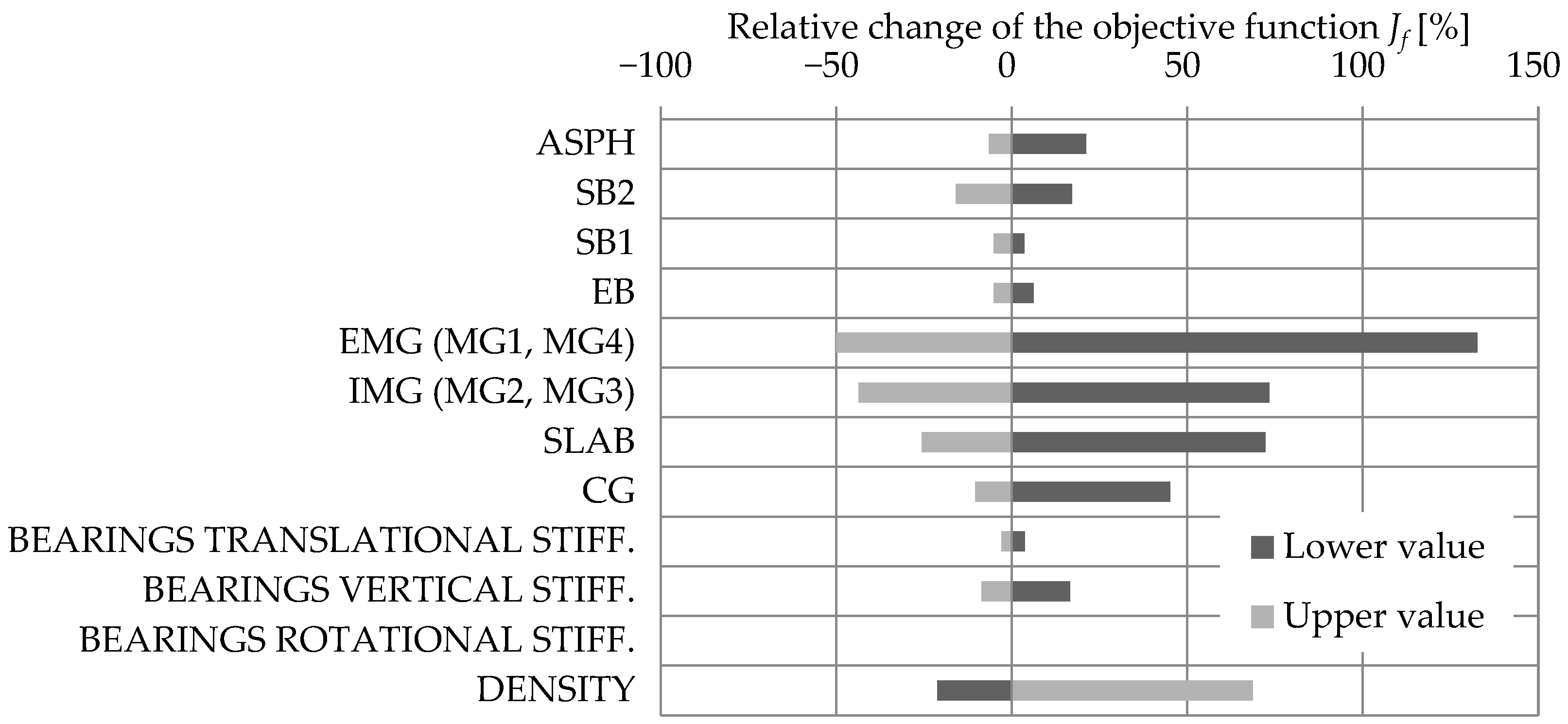
3.1.1. Variables
3.1.2. Acceleration-Based FEMU
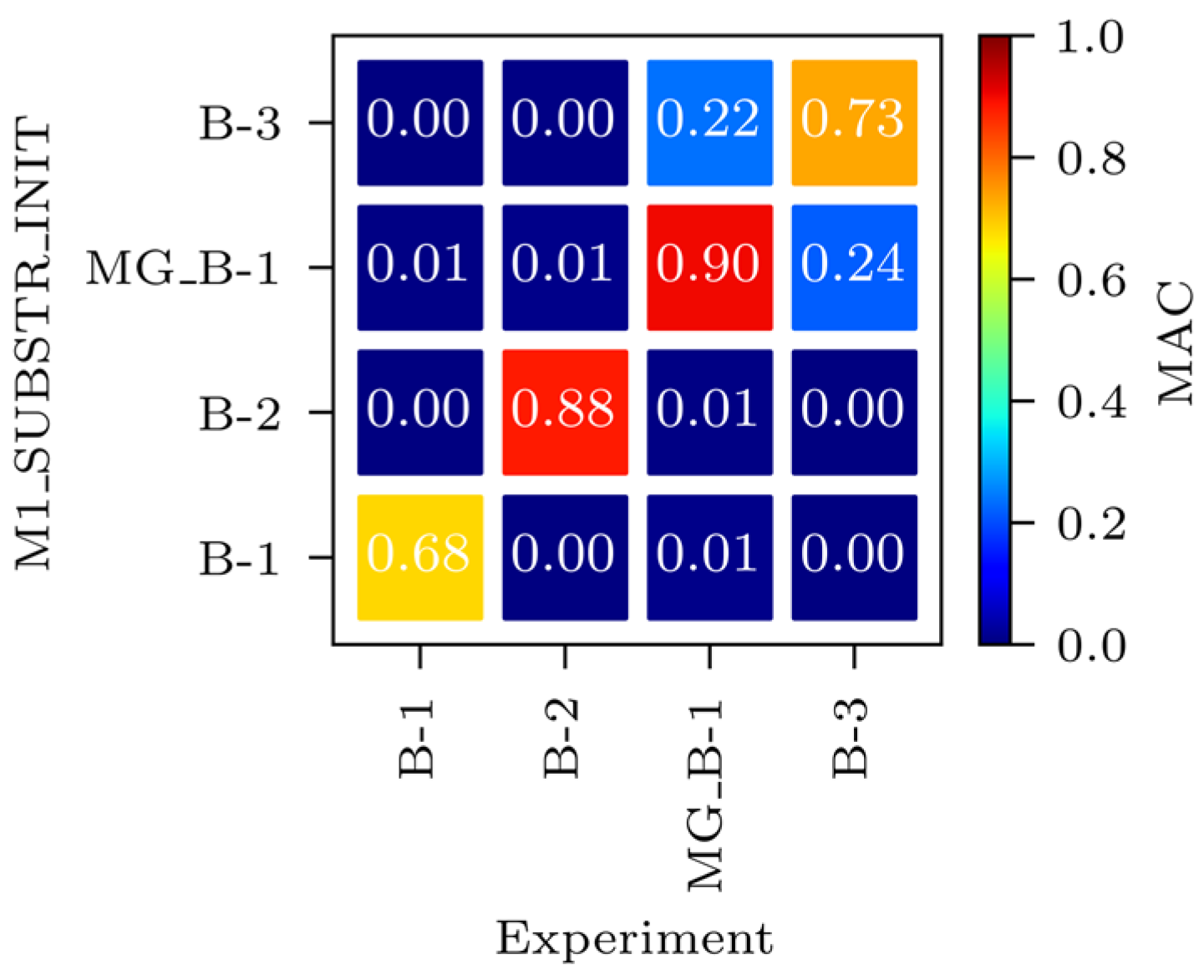
3.1.3. Strain-Based FEMU
3.1.4. Variables Selected for FEMU
3.2. Updated FE Model
3.2.1. List of Analyses
3.2.2. FEMU Results: Residual Minimisation
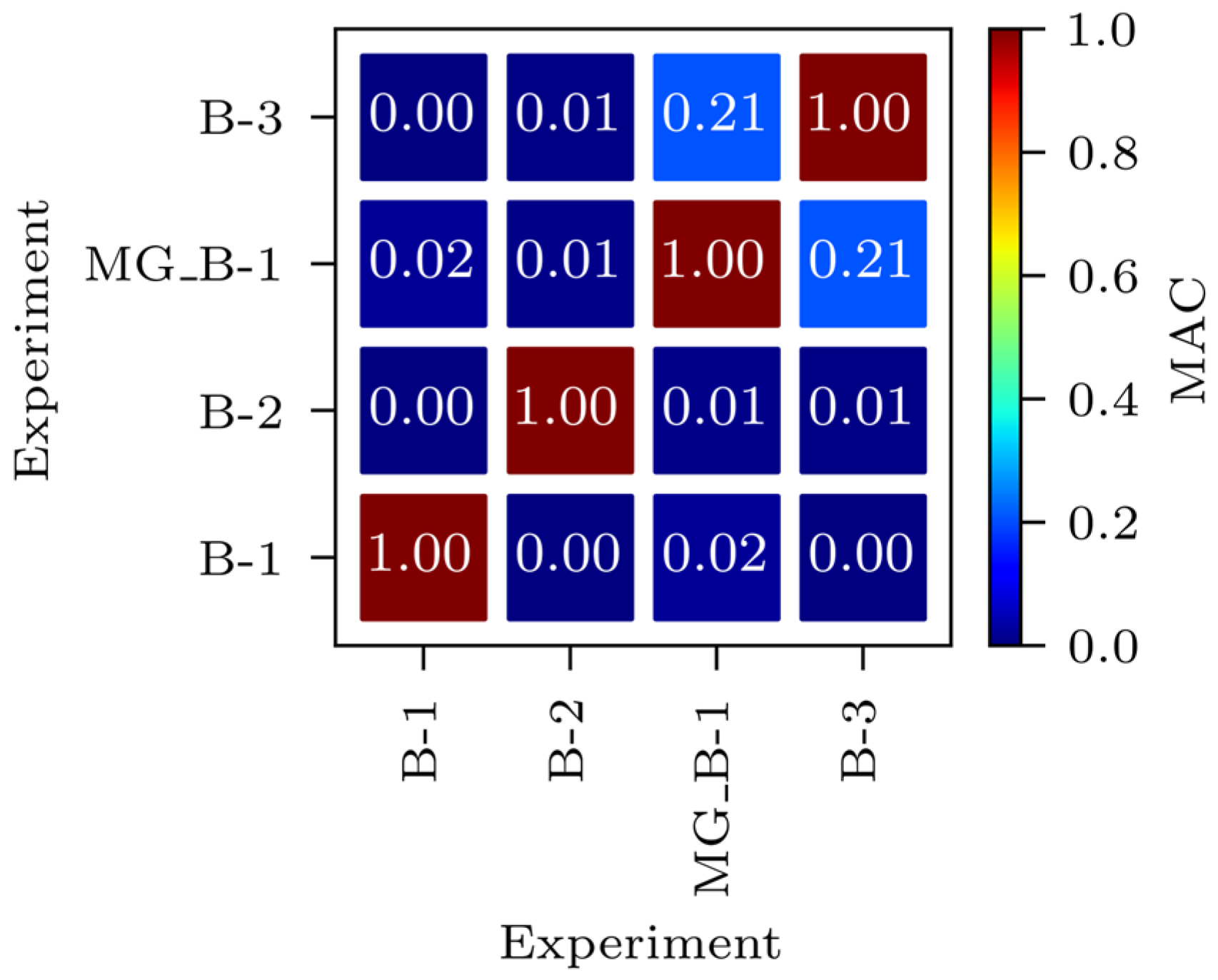
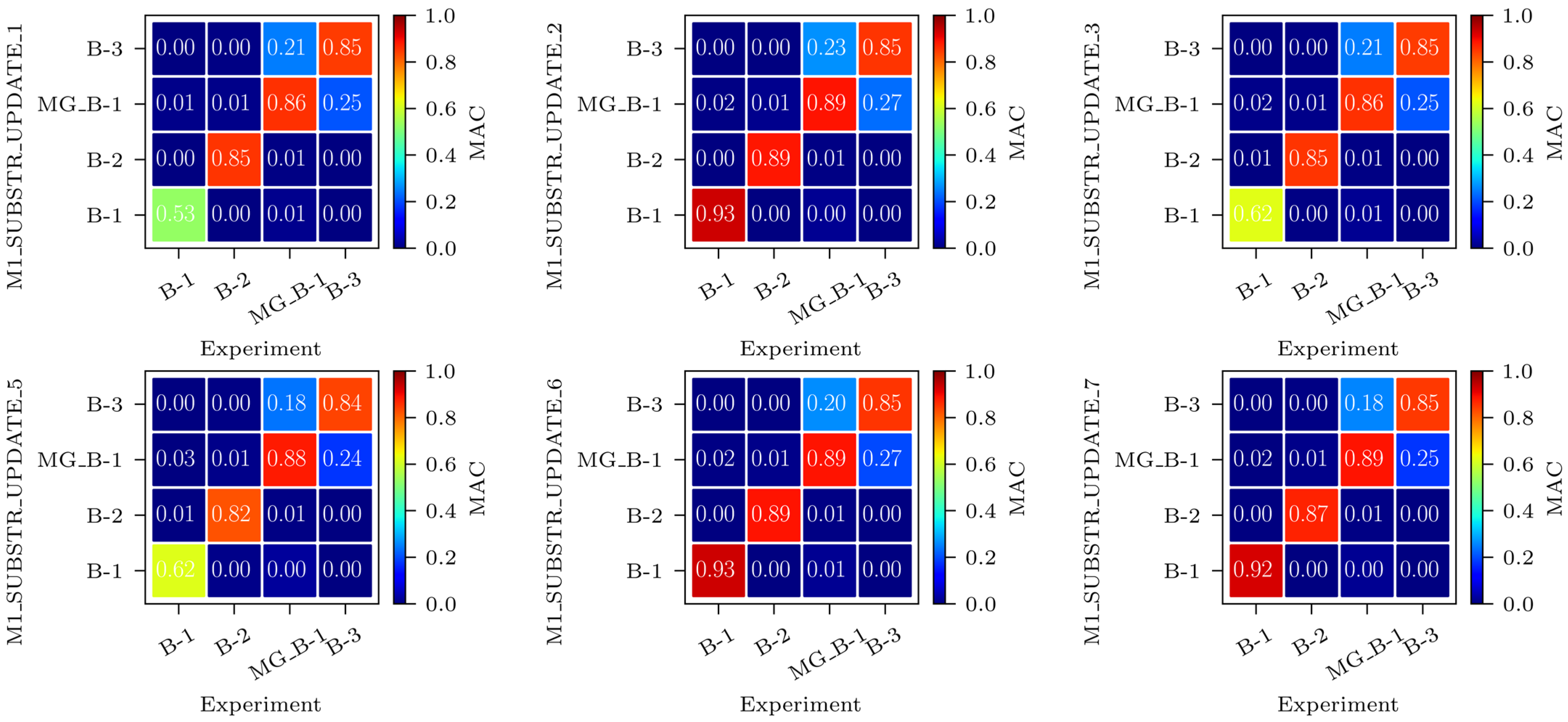
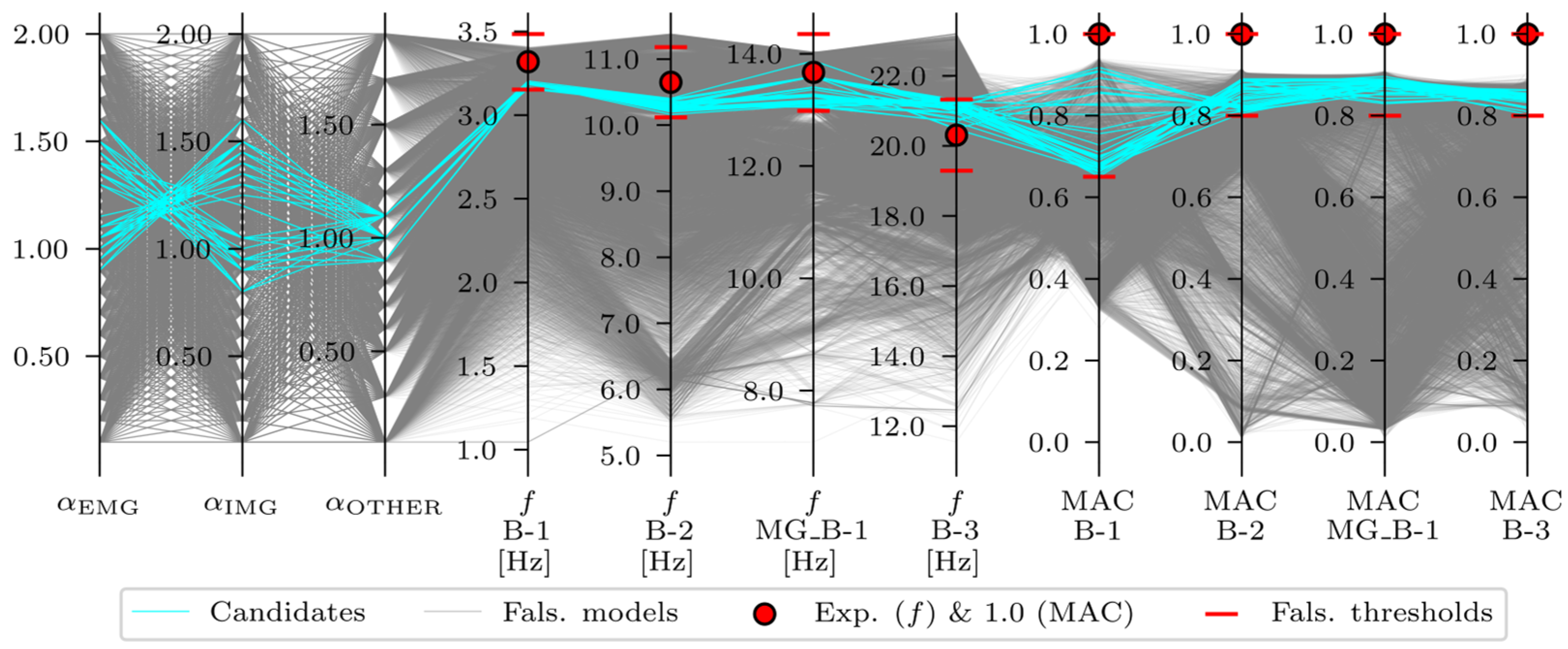
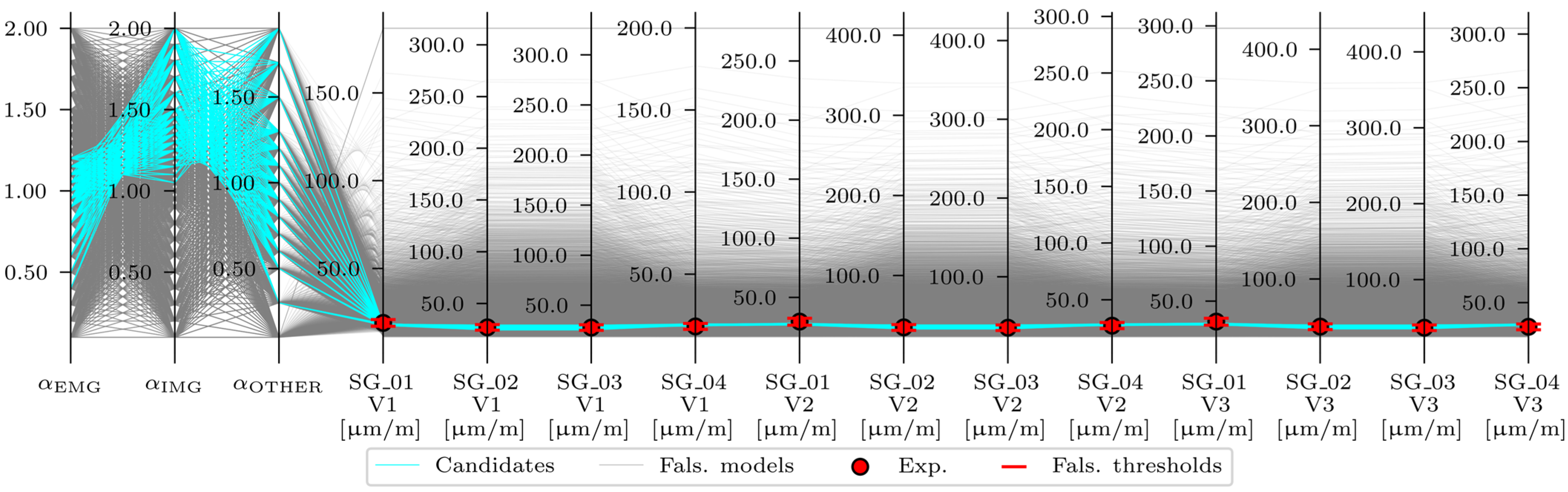
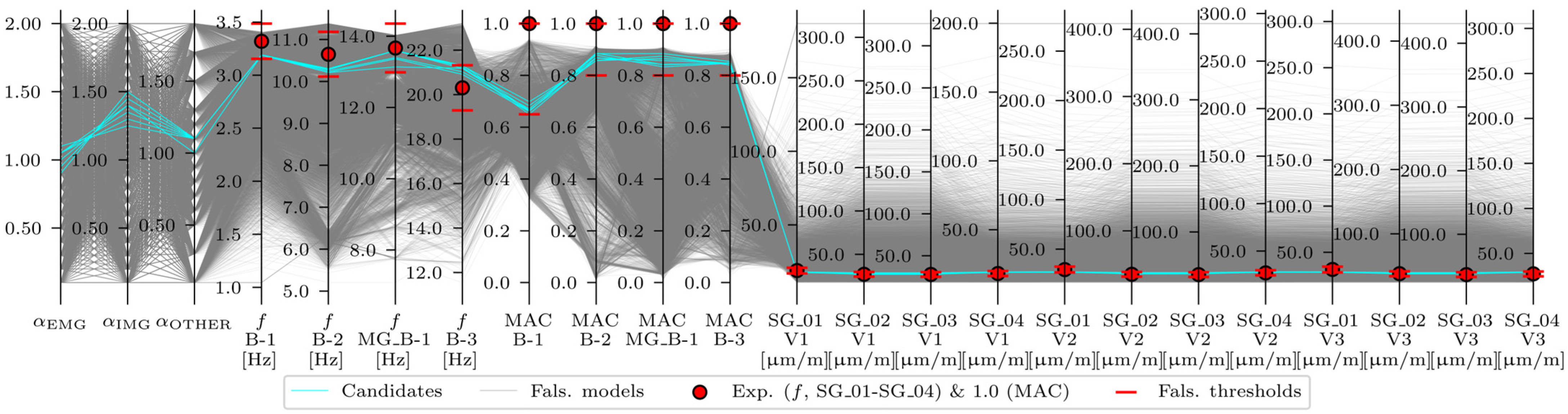
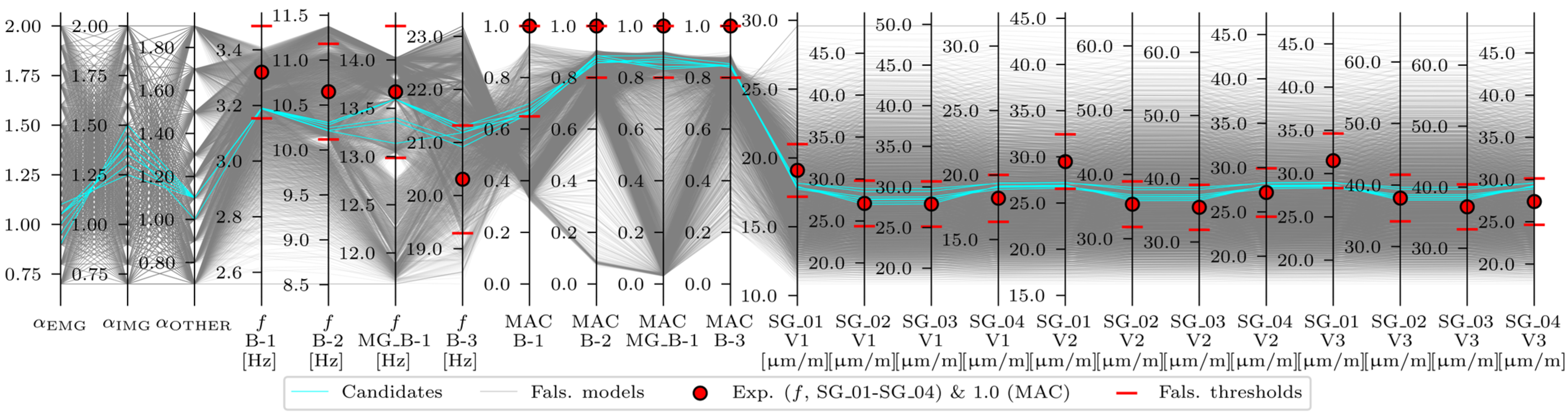
3.2.3. FEMU Results: EDMF
- All frequencies and all MACs (acceleration-based EDMF, analysis number 13);
- All strains (strain-based EDMF, analysis number 14);
- All frequencies, all MACs, and all strains (acceleration-and-strain-based EDMF, analysis number 15).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pour-Ghaz, M.; Isgor, O.B.; Ghods, P. The Effect of Temperature on the Corrosion of Steel in Concrete. Part 1: Simulated Polarization Resistance Tests and Model Development. Corros. Sci. 2009, 51, 415–425. [Google Scholar] [CrossRef]
- Nasr, A.; Kjellström, E.; Björnsson, I.; Honfi, D.; Ivanov, O.L.; Johansson, J. Bridges in a Changing Climate: A Study of the Potential Impacts of Climate Change on Bridges and Their Possible Adaptations. Struct. Infrastruct. Eng. 2020, 16, 738–749. [Google Scholar] [CrossRef]
- Cho, R. What Uncertainties Remain in Climate Science? Available online: https://news.climate.columbia.edu/2023/01/12/what-uncertainties-remain-in-climate-science/ (accessed on 18 December 2023).
- Tabari, H. Climate Change Impact on Flood and Extreme Precipitation Increases with Water Availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Clare Nullis Economic Costs of Weather-Related Disasters Soars but Early Warnings Save Lives. Available online: https://public-old.wmo.int/en/media/press-release/economic-costs-of-weather-related-disasters-soars-early-warnings-save-lives (accessed on 18 December 2023).
- International Transport Forum. ITF Transport Outlook; OECD: Paris, France, 2023. [Google Scholar]
- Kos, M. Experimental Statistics: Road Traffic Counting 2022. Available online: https://www.stat.si/StatWeb/News/Index/11293 (accessed on 20 December 2023). (In Slovene).
- Slovenian Infrastructure Agency Traffic Loads from 1997 Onwards. Available online: https://podatki.gov.si/dataset/pldp-karte-prometnih-obremenitev (accessed on 20 December 2023). (In Slovene)
- Žnidarič, A.; Pakrashi, V.; OBrien, E.J.; O’Connor, A. A Review of Road Structure Data in Six European Countries. Proc. Inst. Civ. Eng. Urban Des. Plan. 2011, 164, 225–232. [Google Scholar] [CrossRef]
- Nowak, A.S.; Latsko, O. Are Our Bridges Safe? Bridge 2018, 48, 26–30. [Google Scholar]
- Gartner, N.; Kosec, T.; Legat, A. Monitoring the Corrosion of Steel in Concrete Exposed to a Marine Environment. Materials 2020, 13, 407. [Google Scholar] [CrossRef]
- Page, C.L. Mechanism of Corrosion Protection in Reinforced Concrete Marine Structures. Nature 1975, 258, 514–515. [Google Scholar] [CrossRef]
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Redaelli, E.; Polder, R.B. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 3527651713. [Google Scholar]
- Scope, C.; Vogel, M.; Guenther, E. Greener, Cheaper, or More Sustainable: Reviewing Sustainability Assessments of Maintenance Strategies of Concrete Structures. Sustain. Prod. Consum. 2021, 26, 838–858. [Google Scholar] [CrossRef]
- Brücken an Bundesfernstraßen: Bilanz und Ausblick (Only in German); BMDV: Bonn, Germany, 2022.
- Gkoumas, K.; Marques Dos Santos, F.; Van Balen, M.; Tsakalidis, A.; Ortega Hortelano, A.; Grosso, M.; Haq, A.; Pekar, F. Research and Innovation in Bridge Maintenance, Inspection and Monitoring; Publications Office of the European Union: Luxembourg, 2019.
- Bigaj-van Vliet, A.; Allaix, D.L.; Köhler, J.; Scibilia, E. Standardisation in Monitoring, Safety Assessment and Maintenance of the Transport Infrastructure: Current Status and Future Perspectives. In Proceedings of the 1st Conference of the European Association on Quality Control of Bridges and Structures, Padua, Italy, 29 August–1 September 2021; Pellegrino, C., Faleschini, F., Zanini, M.A., Matos, J.C., Casas, J.R., Strauss, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 1152–1162. [Google Scholar]
- James, G.; Pianigiani, G.; White, J.; Karthik, P. Genoa Bridge Collapse: The Road to Tragedy. Available online: https://www.nytimes.com/interactive/2018/09/06/world/europe/genoa-italy-bridge.html (accessed on 18 December 2023).
- Woof, M.J. Italy Bridge Monitoring Tender. Available online: https://www.worldhighways.com/wh9/news/italy-bridge-monitoring-tender#:~:text=An important tender is underway,condition of bridges and viaducts (accessed on 18 December 2023).
- Ereiz, S.; Duvnjak, I.; Fernando Jiménez-Alonso, J. Review of Finite Element Model Updating Methods for Structural Applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Xia, Z.; Li, A.; Li, J.; Shi, H.; Duan, M.; Zhou, G. Model Updating of an Existing Bridge with High-Dimensional Variables Using Modified Particle Swarm Optimization and Ambient Excitation Data. Measurement 2020, 159, 107754. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; De Roeck, G.; Bui-Tien, T.; Nguyen-Ngoc, L.; Abdel Wahab, M. Model Updating for Nam O Bridge Using Particle Swarm Optimization Algorithm and Genetic Algorithm. Sensors 2018, 18, 4131. [Google Scholar] [CrossRef]
- Cheng, X.X.; Song, Z.Y. Modal Experiment and Model Updating for Yingzhou Bridge. Structures 2021, 32, 746–759. [Google Scholar] [CrossRef]
- Casas, J.R.; Moughty, J.J. Bridge Damage Detection Based on Vibration Data: Past and New Developments. Front. Built Environ. 2017, 3, 4. [Google Scholar] [CrossRef]
- Scozzese, F.; Dall’Asta, A. Nonlinear Response Characterization of Post-Tensioned R.C. Bridges through Hilbert–Huang Transform Analysis. Struct. Control Health Monit. 2024, 2024, 5960162. [Google Scholar] [CrossRef]
- Hester, D.; Koo, K.; Xu, Y.; Brownjohn, J.; Bocian, M. Boundary Condition Focused Finite Element Model Updating for Bridges. Eng. Struct. 2019, 198, 109514. [Google Scholar] [CrossRef]
- Ticona Melo, L.R.; Malveiro, J.; Ribeiro, D.; Calçada, R.; Bittencourt, T. Dynamic Analysis of the Train-Bridge System Considering the Non-Linear Behaviour of the Track-Deck Interface. Eng. Struct. 2020, 220, 110980. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Sun, R. Response Analysis of Orthotropic Steel Deck Pavement Based on Interlayer Contact Bonding Condition. Sci. Rep. 2021, 11, 23692. [Google Scholar] [CrossRef]
- Wang, H.; Li, A.; Li, J. Progressive Finite Element Model Calibration of a Long-Span Suspension Bridge Based on Ambient Vibration and Static Measurements. Eng. Struct. 2010, 32, 2546–2556. [Google Scholar] [CrossRef]
- Meixedo, A.; Ribeiro, D.; Santos, J.; Calçada, R.; Todd, M. Progressive Numerical Model Validation of a Bowstring-Arch Railway Bridge Based on a Structural Health Monitoring System. J. Civ. Struct. Health Monit. 2021, 11, 421–449. [Google Scholar] [CrossRef]
- Chen, S.-Z.; Wu, G.; Feng, D.-C. Damage Detection of Highway Bridges Based on Long-Gauge Strain Response under Stochastic Traffic Flow. Mech. Syst. Signal Process. 2019, 127, 551–572. [Google Scholar] [CrossRef]
- Hekič, D.; Anžlin, A.; Kreslin, M.; Žnidarič, A.; Češarek, P. Model Updating Concept Using Bridge Weigh-in-Motion Data. Sensors 2023, 23, 2067. [Google Scholar] [CrossRef]
- VA0174 Ravbarkomanda Viaduct Rehabilitation Plan (in Slovene): Notebook 3/1.1-General Part, Technical Part; Promico d.o.o.: Ljubljana, Slovenia, 2019.
- Kalin, J.; Žnidarič, A.; Anžlin, A.; Kreslin, M. Measurements of Bridge Dynamic Amplification Factor Using Bridge Weigh-in-Motion Data. Struct. Infrastruct. Eng. 2022, 18, 1164–1176. [Google Scholar] [CrossRef]
- DEWESoft. DEWESoft IOLITEi 3xMEMC-ACC. Available online: https://downloads.dewesoft.com/brochures/dewesoft-iolitei-3xmems-acc-datasheet-en.pdf (accessed on 26 December 2023).
- DEWESoft DewesoftX 2023, Version 2023.5. Available online: https://dewesoft.com/products/dewesoftx (accessed on 26 December 2023).
- Structural Vibration Solutions A/S ARTeMIS Modal Pro 2023. Available online: https://www.svibs.com/artemis-modal-pro/ (accessed on 26 December 2023).
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis; Wiley Online Library: Hoboken, NJ, USA, 2015; ISBN 9781119963158. [Google Scholar]
- Allemang, R. The Modal Assurance Criterion—Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Ewins, D.J. Model Validation: Correlation for Updating. Sadhana 2000, 25, 221–234. [Google Scholar] [CrossRef]
- Dassault Systemes SIMULIA User Assistance 2019: Abaqus/CAE User’s Guide 2019; Dassault Systemes: Waltham, MA, USA, 2019.
- Technical Report about the General Project of the Ravbarkomanda Viaduct (in Slovene); Tehnogradnja Maribor: Maribor, Slovenia, 1970.
- Goulet, J.-A.; Smith, I.F.C. Structural Identification with Systematic Errors and Unknown Uncertainty Dependencies. Comput. Struct. 2013, 128, 251–258. [Google Scholar] [CrossRef]
- Schlune, H.; Plos, M.; Gylltoft, K. Improved Bridge Evaluation through Finite Element Model Updating Using Static and Dynamic Measurements. Eng. Struct. 2009, 31, 1477–1485. [Google Scholar] [CrossRef]
- Kurent, B.; Brank, B.; Ao, W.K. Model Updating of Seven-Storey Cross-Laminated Timber Building Designed on Frequency-Response-Functions-Based Modal Testing. Struct. Infrastruct. Eng. 2023, 19, 178–196. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. {SciPy} 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Cao, W.-J.; Koh, C.G.; Smith, I.F.C. Enhancing Static-Load-Test Identification of Bridges Using Dynamic Data. Eng. Struct. 2019, 186, 410–420. [Google Scholar] [CrossRef]
- Bertola, N.J.; Henriques, G.; Brühwiler, E. Assessment of the Information Gain of Several Monitoring Techniques for Bridge Structural Examination. J. Civ. Struct. Health Monit. 2023, 13, 983–1001. [Google Scholar] [CrossRef]
- Pai, S.G.S.; Smith, I.F.C. Methodology Maps for Model-Based Sensor-Data Interpretation to Support Civil-Infrastructure Management. Front. Built Environ. 2022, 8, 801583. [Google Scholar] [CrossRef]
- Jiao, Y.; Liu, H.; Wang, X.; Zhang, Y.; Luo, G.; Gong, Y. Temperature Effect on Mechanical Properties and Damage Identification of Concrete Structure. Adv. Mater. Sci. Eng. 2014, 2014, 191360. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Naranjo-Perez, J.; Pavic, A.; Sáez, A. Maximum Likelihood Finite-Element Model Updating of Civil Engineering Structures Using Nature-Inspired Computational Algorithms. Struct. Eng. Int. 2021, 31, 326–338. [Google Scholar] [CrossRef]








| 1st Axle | 2nd Axle | 3rd Axle | 4th Axle | 5th Axle | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vehicle | Load [kN] | Spacing [m] | Load [kN] | Spacing [m] | Load [kN] | Spacing [m] | Load [kN] | Spacing [m] | Load [kN] | GVW [kN] |
| V1 | 67.69 | 3.30 | 85.35 | 1.35 | 88.29 | / | / | / | / | 241.33 |
| V2 | 68.67 | 3.60 | 93.20 | 5.60 | 76.52 | 1.30 | 75.54 | 1.30 | 76.52 | 390.44 |
| V3 | 68.67 | 3.30 | 87.31 | 1.35 | 87.31 | 5.17 | 76.52 | 1.33 | 76.52 | 396.32 |
| n, Mean [μm/m], STD [μm/m], CV [%] | V1 | V2 | V3 | |
|---|---|---|---|---|
| SG_01 | n | 32 | 34 | 36 |
| Mean | 19.1 | 29.5 | 31.5 | |
| STD | 0.7 | 0.9 | 1.3 | |
| CV | 3.5 | 2.9 | 4.2 | |
| SG_02 | n | 48 | 51 | 54 |
| Mean | 27.1 | 35.4 | 37.9 | |
| STD | 1.3 | 1.2 | 1.4 | |
| CV | 4.8 | 3.4 | 3.7 | |
| SG_03 | n | 48 | 51 | 54 |
| Mean | 27.9 | 35.5 | 36.8 | |
| STD | 1.5 | 1.3 | 1.6 | |
| CV | 5.3 | 3.5 | 4.4 | |
| SG_04 | n | 48 | 51 | 54 |
| Mean | 18.2 | 27.2 | 27.4 | |
| STD | 0.9 | 1.2 | 1.6 | |
| CV | 5.2 | 4.6 | 5.7 | |
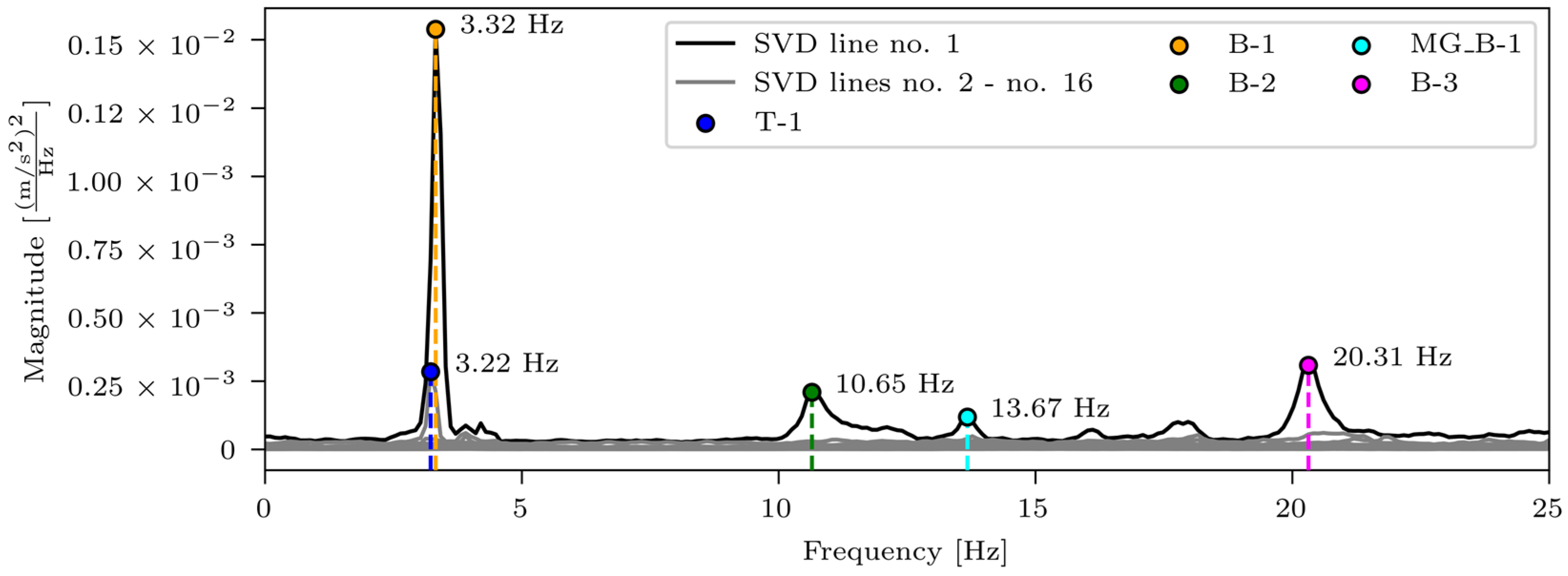
| T-1 | B-1 | B-2 | MG_B-1 | B-3 |
|---|---|---|---|---|
| 3.22 Hz | 3.32 Hz | 10.65 Hz | 13.67 Hz | 20.31 Hz |
 |  |  |  |  |
 |  |  |  |  |
| Element | Abbreviation | Young’s Modulus [GPa] | Poisson Ratio | Density [t/m3] 1 |
|---|---|---|---|---|
| Piers | / | 34 | 0.20 | 2.500 |
| Slab | SLAB | 33 | 0.20 | 2.500 |
| External main girders | EMG (MG1, MG4) | 35 | 0.20 | 2.575 |
| Internal main girders | IMG (MG2, MG3) | 34 | 0.20 | 2.575 |
| Cross-girders | CG | 35 | 0.20 | 2.500 |
| Safety barriers 1 | SB1 | 33 | 0.20 | 2.500 |
| Safety barriers 2 | SB2 | 33 | 0.20 | 2.500 |
| Edge beams | EB | 33 | 0.20 | 2.500 |
| Asphalt | ASPH | 8 | 0.35 | 2.582 |
| Mode | Natural Frequencies [Hz] for 0.25 m Global Element Size | Natural Frequencies [Hz] for 0.50 m Global Element Size |
|---|---|---|
| B-1 | 3.00 | 3.00 |
| B-2 | 9.81 | 9.80 |
| MG_B-1 | 12.83 | 12.78 |
| B-3 | 20.39 | 20.37 |
| Mode | B-1 | B-2 | MG_B-1 | B-3 | |
|---|---|---|---|---|---|
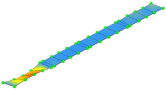
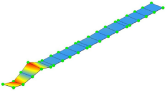
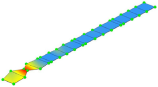
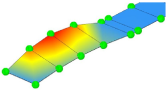
| FE model M1_SUBSTR_INIT | Frequency | 3.00 Hz | 9.83 Hz | 13.07 Hz | 20.48 Hz |
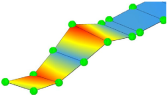
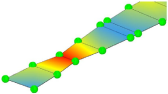
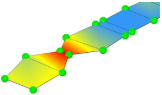
| Mode Shape (Full) |  | 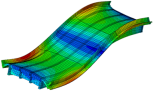 |  | 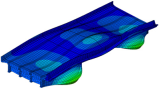 | |
| Mode Shape (Z Cut) |  | 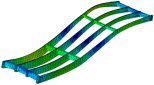 |  | 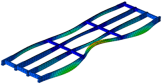 | |
| Experiment | Frequency | 3.32 Hz | 10.65 Hz | 13.67 Hz | 20.31 Hz |
| Mode Shape | 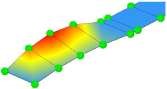 |  | 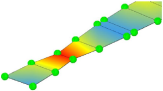 | 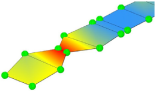 |
| Strains [μm/m] | V1 | V2 | V3 | ||||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
| SG_01 | M1_SUSBSTR_INIT | 21.0 | / | 31.4 | / | 33.4 | / |
| Experiment | 19.1 | 0.7 | 29.5 | 0.9 | 31.5 | 1.3 | |
| SG_02 | M1_SUSBSTR_INIT | 34.1 | / | 44.7 | / | 46.6 | / |
| Experiment | 27.1 | 1.3 | 35.4 | 1.2 | 37.9 | 1.4 | |
| SG_03 | M1_SUSBSTR_INIT | 35.2 | / | 45.5 | / | 47.0 | / |
| Experiment | 27.9 | 1.5 | 35.5 | 1.3 | 36.8 | 1.6 | |
| SG_04 | M1_SUSBSTR_INIT | 22.4 | / | 32.7 | / | 34.2 | / |
| Experiment | 18.2 | 0.9 | 27.2 | 1.2 | 27.4 | 1.6 | |
| Element/Variable/Property | Lower Value 1 | Upper Value 1 | Description |
|---|---|---|---|
| ASPH, SB1, SB2, EB, EMG (MG1, MG4), IMG (MG2, MG3), SLAB, CG | 0.75 × design | 1.25 × design | Young’s modulus change |
| BEARINGS TRANSL. STIFF. | 0.75 × design | 1.25 × design | Horizontal (X and Y) stiffness change |
| BEARINGS VERT. STIFF. | 0.75 × design | 1.25 × design | Vertical (Z) stiffness change |
| BEARINGS ROT. STIFF. | 0.75 × design | 1.25 × design | Rot. (around Y) stiffness change |
| DENSITY | 0.95 × design | 1.05 × design | Change in the density of elements ASPH, SB1, SB2, EB, EMG (MG1, MG4), IMG (MG2, MG3), SLAB, and CG |
| Variable | Description | Range | |
|---|---|---|---|
| Res. Min. | EDMF | ||
| Young’s modulus adjustment factor for ASPH, SB2, SB1, EB, EMG, IMG, SLAB, and CG | [0.9, 1.5] | / | |
| Young’s modulus adjustment factor for EMG and IMG | [0.9, 1.5] | / | |
| Young’s modulus adjustment factor for ASPH, SB2, SB1, EB, SLAB, and CG | [0.9, 1.5] | [0.10, 1.90] | |
| Young’s modulus adjustment factor for EMG | [0.9, 1.5] | [0.10, 2.00] | |
| Young’s modulus adjustment factor for IMG | [0.9, 1.5] | [0.10, 2.00] | |
| Analysis Number | Analysis Type | Mode Shapes/Vehicles Considered | Variables | Acceleration-Based | ) | ||
|---|---|---|---|---|---|---|---|
| ) | ) | ) | |||||
| 1 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 2 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 3 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 4 | Res. min. | V1, V2, V3 | X | ||||
| 5 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 6 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 7 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 8 | Res. min. | V1, V2, V3 | X | ||||
| 9 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 10 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 11 | Res. min. | B-1, B-2, MG_B-1, B-3 | X | ||||
| 12 | Res. min. | V1, V2, V3 | X | ||||
| 13 | EDMF | B-1, B-2, MG_B-1, B-3 | X | ||||
| 14 | EDMF | V1, V2, V3 | X | ||||
| 15 | EDMF | B-1, B-2, MG_B-1, B-3 & V1, V2, V3 | X | X | |||
| Analysis Number | Variables | Acceleration-Based | Strain-Based | ||
|---|---|---|---|---|---|
| Frequency-Based | MAC-Based | Frequency-and-MAC-Based | |||
| 1, 2, 3, 4 | 1.18 | 0.99 | 1.18 | 1.21 | |
| 5, 6, 7, 8 | 1.20, 1.09 | 0.96, 0.90 | 0.97, 1.33 | 1.17, 1.50 | |
| 9, 10, 11, 12 | 0.91, 1.50 1.17 | 0.90, 0.96, 1.02 | 1.36, 0.93, 1.09 | 0.90, 1.50, 1.01 | |
| Analysis Number (i) | Experiment [Hz] | M1_SUBSTR_INIT [Hz] | M1_SUBSTR_UPDATE_i [Hz] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B-1 | B-2 | MG_B-1 | B-3 | B-1 | B-2 | MG_B-1 | B-3 | B-1 | B-2 | MG_B-1 | B-3 | |
| 1 | 3.32 | 10.65 | 13.67 | 20.31 | 3.00 | 9.83 | 13.07 | 20.48 | 3.20 | 10.35 | 14.06 | 21.33 |
| 2 | 2.95 | 9.69 | 13.05 | 20.22 | ||||||||
| 3 | 3.19 | 10.35 | 14.06 | 21.33 | ||||||||
| 5 | 3.25 | 10.36 | 13.59 | 21.43 | ||||||||
| 6 | 2.93 | 9.59 | 12.39 | 20.13 | ||||||||
| 7 | 3.08 | 10.18 | 14.14 | 20.80 | ||||||||
| 9 | 3.24 | 10.31 | 13.59 | 20.86 | ||||||||
| 10 | 2.94 | 9.67 | 13.06 | 20.14 | ||||||||
| 11 | 3.17 | 10.33 | 13.59 | 21.04 | ||||||||
| Variable | Initial Range |
|---|---|
| [0.10, 0.20, …, 0.90, 0.95, …, 1.50, 1.60, …, 2.00] | |
| [0.10, 0.20, …, 0.90, 0.95, …, 1.50, 1.60, …, 2.00] | |
| [0.10, 0.30, …, 0.50, 0.60, …, 1.30, 1.50, …, 1.90] |
| Analysis Number | Source | Falsification Thresholds 1 | ||
|---|---|---|---|---|
| Min | Max | |||
| 13 | Acc.-Based | Frequencies | −5%, −5%, −5%, −5% | +5%, +5%, +5%, +5% |
| MAC values | 0.35, 0.20, 0.20, 0.20 | 0, 0, 0, 0 | ||
| 14 | Strain-Based | Strains | −10%, −10%, −10%, −10% | +10%, +10%, +10%, +10% |
| 15 | Acc.-and-Strain-Based | Frequencies | −5%, −5%, −5%, −5% | +5%, +5%, +5%, +5% |
| MAC values | 0.35, 0.20, 0.20, 0.20 | 0, 0, 0, 0 | ||
| Strains | −10%, −10%, −10%, −10% | +10%, +10%, +10%, +10% | ||
| Variable | Initial Range | Range after EDMF | ||
|---|---|---|---|---|
| Analysis No. 13 | Analysis No. 14 | Analysis No. 15 | ||
| Acceleration-Based | Strain-Based | Acceleration-and-Strain-Based | ||
| n = 9464 | n = 35 | n = 199 | n = 7 | |
| [0.10, 2.00] | [0.90, 1.60] | [0.40, 1.20] | [0.90, 1.10] | |
| [0.10, 2.00] | [0.80, 1.60] | [1.05, 2.00] | [1.25, 1.50] | |
| [0.10, 1.90] | [0.90, 1.10] | [0.30, 1.90] | [1.00, 1.10] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hekič, D.; Ribeiro, D.; Anžlin, A.; Žnidarič, A.; Češarek, P. Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data. Sensors 2024, 24, 2788. https://doi.org/10.3390/s24092788
Hekič D, Ribeiro D, Anžlin A, Žnidarič A, Češarek P. Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data. Sensors. 2024; 24(9):2788. https://doi.org/10.3390/s24092788
Chicago/Turabian StyleHekič, Doron, Diogo Ribeiro, Andrej Anžlin, Aleš Žnidarič, and Peter Češarek. 2024. "Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data" Sensors 24, no. 9: 2788. https://doi.org/10.3390/s24092788
APA StyleHekič, D., Ribeiro, D., Anžlin, A., Žnidarič, A., & Češarek, P. (2024). Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data. Sensors, 24(9), 2788. https://doi.org/10.3390/s24092788









